Keywords

1 Introduction

Transportation by ships plays a significant role in international trade and passenger traffic between countries within marine regions as Mediterranean Sea, Black Sea etc. as well as between continents. For some countries with long shorelines, navigable rivers or with multiple islands, transportation by ships also plays an important role in regional or local trade [1, 16, 26]. Nowadays, among such traditional marine cargo as coal, oil, cement etc., natural gas is an important cargo in marine shipping taking into account that liquefaction ports transform gas into liquefied natural gas [12]. The most important and complex problems for all kinds of marine transportation are the routing and scheduling of vessels in marine environment, which is fuzzy and uncertain because of strong disturbances and different influences of weather, distance and others. Some special characteristics of ship routing and scheduling problems are [1, 12, 36, 42, 44]:

  • a fleet is mostly heterogeneous, ships may have various deadweights and loading capacities, cruise speed and special constructions for different kind of cargoes (tankers, bulkers, dry-ships etc.);

  • sometimes the distance between two ports is an uncertain value (parameter) and in some cases it is necessary to change destination while at sea to cope with increasing travel times between departure and arrival ports;

  • the weather may have strong impact on ships during long trips, speed and travelling time usually depend on wind, current and wave influences;

  • loading and unloading processes at the ports usually depend on specific working time windows and cost penalties are to be calculated as a function of the relation between opening and closing of cargo processing at a port on one side and the arrival time of a ship on the other side.

Maritime transportation planning problems can be classified [1] with respect to the corresponding planning horizon into strategic, tactical and operational problems and according to the up-dated classification for modes of ship’s operations they can be divided into the three different categories: liner, tramp and industrial operations, but there are no clear bounds between the abovementioned categories.

Taking into account uncertain sea environment it is necessary to use efficient methods for mathematical formalization of marine transportation problems. In particular, for mathematical formalization of various processes and systems in uncertainty it is beneficial to use the theory of fuzzy sets, developed by Zadeh [48]. Specialists have a great interest in such intelligent approaches in terms of practical applications of its mathematical methods in different fields: business process management [2, 4,5,6, 8, 23], engineering [14], economics [7, 9,], finances [10, 30], decision-making [3, 11, 20, 31,32,33, 46, 47], medical and technical diagnostics, transport logistics [18, 22, 24], etc. There are multiple fundamental theoretical contributions to the development of fuzzy sets and fuzzy logic theory and their applications for solving optimization problems made by scientists all over the world [9, 19, 25, 29, 34, 38,39,40, 49, 50]. For example, the solution of a classical transportation problem with uncertain information about transportation cost of cargo unit was proposed by Arnold Kaufmann (France) and Jaime Gil-Aluja (Spain) in [15]. This solution is based on the simplex method of linear optimization and implementation of triangular fuzzy numbers for decreasing uncertainty. This proposed fuzzy approach [15] can be successfully applied to solve marine transportation problems under uncertainty.

In this article we focus on a real-world problem which deals with planning and optimization of a bunkering tanker routing problem in conditions when a priori orders in nodes are uncertain.

2 Problem Statement

The routing problem for bunkering tankers is one of the most important and complicated VRP in marine transportation [7, 15, 16]. Bunkering tankers should provide bunkering operations (transportation and unloading) for various ships to be served. These serviced ships can be located in different geographically distributed marine ports and open sea points. Marine practice shows that very often the information about fuel demands of serviced ships is uncertain. Usually the ship-owner sends an approximate order to the bunkering company. For example, the ship-owner sends an order for fuel supply using such uncertain terms as “approximately A”, “about B”, “between C and D”, “at least R”, “not less than S”, “not more than K” and so on. It is possible to represent such kind of orders as fuzzy demands, for example, as fuzzy numbers with triangular membership function [2, 20, 21, 43]. The classical VRP [28, 37], taking into account the restricted fuel capacity Cap of each tanker, can be transformed to [13, 17, 37, 41, 42] a capacitated vehicle routing problem (CVRP) under uncertainty. Solving such CVRPFD (CVRP in the conditions of fuzzy demands) deals with (a) minimization of both total length of planned tanker routes and (b) used fleet size of tankers, (c) satisfaction of orders in all destinations and (d) maximization of total value of unloaded fuel. So we will consider a CVRPFD as bi- or multi-criteria optimization problem under uncertainty. Two alternative fuzzy approaches will be considered for solving marine CVRPFD.

3 First Alternative Fuzzy Approach Based on Iterative Heuristic Algorithm

3.1 Mathematical Model for Solving CVRPFD

A first suggested fuzzy multi-criteria approach for solving CVRPFD, where fuzzy demands at nodes are presented by fuzzy numbers \( {\tilde{\text{d}}}_{\text{j}} \) with triangular membership functions \( {\tilde{\text{d}}}_{\text{j}} = \left( {{\underline{\text{d} }}_{\text{j}} ,{\hat{\text{d}}}_{\text{j}} ,{\bar{\text{d}}}_{\text{j}} } \right),{\text{j}} = 1\ldots {\text{N}} \), is based on a mixed integer linear mathematical programming model. The first compromise solution can be interactively modified to meet the decision makers’ requirements with respect to different criteria [39, 40, 42]. Indices i,j = 0,1,…,N are for the depot and different ports, and k = 1,…,K are for routes. The objective function of the considered CVRP is to minimize the total travel distance:

$$ { \hbox{min} }\quad \sum\limits_{{{\text{i}} = 0}}^{\text{N}} {\sum\limits_{{{\text{j}} = 0}}^{\text{N}} {\sum\limits_{{{\text{k}} = 1}}^{\text{K}} {{\text{c}}_{\text{ij}} \,{\text{x}}_{\text{ijk}} } } } $$
(1)

and the capacity Cap of each tanker should be sufficient to meet the fuzzy demands \( {\tilde{\text{D}}}_{\text{k}} = \sum\nolimits_{{{\text{j}} = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{jk}} ,\quad {\text{k}} = 1, \ldots ,{\text{N}} \) of all ports on the k-th planned route:

$$ \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{jk}} \le {\text{Cap}},\quad {\text{k}} = 1 ,\ldots , {\text{N}} $$
(2)

where \( {\text{c}}_{\text{ij}} \) is the distance from i-th port to j-th port, \( {\text{i}},{\text{j}} = 0, \ldots ,{\text{N}} \),

$$ x_{ijk} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,{\text{j}}\,\,{\text{follows}}\,{\text{i}}\,{\text{on}}\,{\text{route}}\,{\text{k}}} \hfill \\ 0 \hfill & {\text{else}} \hfill \\ \end{array} } \right., $$
$$ {\text{y}}_{\text{jk}} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,{\text{port}}\,{\text{j}}\,{\text{belongs}}\,{\text{to}}\,{\text{route}}\,{\text{k}}} \hfill \\ 0 \hfill & {\text{else}} \hfill \\ \end{array} } \right., $$

\( u_{\text{jk}} \ge 0 \) is the sequence no. of port j on route k

Each port j belongs to exactly one of the routes except port 0 with the depot

$$ \sum\limits_{{{\text{k}} = 1}}^{\text{K}} {{\text{y}}_{\text{jk}} = 1,{\text{j}} = 1, \ldots ,{\text{N}}} . $$
(3)

Each port j on the route must be entered exactly once on the trip

$$ \sum\limits_{{{\text{i}} = 0}}^{\text{N}} {{\text{x}}_{\text{ijk}} = {\text{y}}_{\text{jk}} } ,{\text{j}} = 0, \ldots ,{\text{N}},{\text{k}} = 1, \ldots ,{\text{K}}. $$
(4)

Each port i on the route must be exited exactly once on the trip

$$ \sum\limits_{{{\text{j}} = 0}}^{\text{N}} {{\text{x}}_{\text{ijk}} = {\text{y}}_{\text{ik}} } ,{\text{i}} = 0, \ldots ,{\text{N}},{\text{k}} = 1, \ldots ,{\text{K}}. $$
(5)

No port can follow itself on the route

$$ {\text{x}}_{\text{iik}} = 0,\quad {\text{i}} = 0 ,\ldots ,{\text{N}},{\text{k}} = 1, \ldots ,{\text{K}} . $$
(6)

Sub-routes are forbidden

$$ {\text{u}}_{\text{jk}} \ge {\text{u}}_{\text{ik}} + 1- \left( { 1- {\text{x}}_{\text{ijk}} } \right){\text{N}},\,\,{\text{i}} = 0 ,\ldots ,{\text{N}},{\text{j}} = 1, \ldots ,{\text{N}},{\text{j}} \ne {\text{i}}. $$
(7)

Each trip starts in the depot

$$ {\text{u}}_{{0{\text{k}}}} = 1,\quad {\text{k}} = 1, \ldots ,{\text{N}} . $$
(8)

To model fuzzy demands it is suggested to consider the possibility that the actual demand of all ships on one route is less or equal to the capacity Cap of the tanker. If the demand is not known exactly, it is possible to find a solution for which the possibility to serve the demand is required at least [10] to a certain degree \( \upalpha \in \left[ {0,1} \right]. \)

The decision maker has to determine \( \upalpha \) in advance. Considering a fuzzy number as a method of representing uncertainty in a given quantity by defining a possibility distribution for the quantity is analyzed in [13, 41, 42]

$$ {\text{Pos}}\left( {\sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} \le {\text{Cap}}} \right) \ge\upalpha,\quad {\text{k}} = 1, \ldots ,{\text{N}};\quad\upalpha \in \left[ {0,1} \right]. $$
(9)

An even stronger condition is to determine a certain degree of necessity β that the demand on the route can be served

$$ {\text{Nec}}\left( {\sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} \le {\text{Cap}}} \right) \ge\upbeta ,\quad {\text{k}} = 1, \ldots ,{\text{N}};\quad\upbeta \in \left[ {0,1} \right]. $$
(10)

The requirements (9) and (10) for capacity can be transformed as follows

$$ {\text{Pos}}\left( {{\text{Cap}} - \sum\limits_{\text{j = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} \ge 0} \right) \ge\upalpha,\quad {\text{k}} = 1, \ldots ,{\text{N;}}\quad\upalpha \in \left[ { 0 , 1} \right], $$
(11)
$$ {\text{Nec}}\left( {{\text{Cap}} - \sum\limits_{\text{j = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} \ge 0} \right) \ge\upbeta,\quad {\text{k}} = 1, \ldots ,{\text{N}};\quad\upbeta \in \left[ {0,1} \right]. $$
(12)

and for triangular fuzzy numbers \( {\tilde{\text{d}}}_{\text{j}} = \left( {{\underline{\text{d}}}_{\text{j}} ,{\hat{\text{d}}}_{\text{j}} ,{\bar{\text{d}}}_{\text{j}} } \right) \) the fuzzy number

\( \left( {{\text{Cap}} - \sum\nolimits_{\text{j = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} } \right) \) can be presented also as triangular fuzzy number as follows

$$ {\text{Cap}} - \sum\limits_{\text{j = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} = \left( {{\text{Cap}} - \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\bar{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} , {\text{Cap}} - \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} ,{\text{Cap}} - \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\underline{\text{d}}}_{\text{j}} } {\text{y}}_{\text{ik}} } \right). $$
(13)

The mathematical models for possibility \( {\text{Pos}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) \) and necessity \( {\text{Nec}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) \) that the capacity Cap of the tanker is sufficient to serve all demands \( {\tilde{\text{D}}}_{\text{k}} \) on k-th route are

$$ {\text{Pos}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) = \left\{ {\begin{array}{*{20}l} { 1 ,} \hfill & {{\text{Cap}} \ge \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } } \hfill \\ {\frac{{{\text{Cap}} - \sum\nolimits_{{{\text{j}} = 1}}^{\text{N}} {\underline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} } }}{{\sum\nolimits_{{{\text{j}} = 1}}^{\text{N}} {({\hat{\text{d}}}_{\text{j}} - \underline{\text{d}}_{\text{j}} ) {\text{ y}}_{\text{jk}} } }} ,} \hfill & { \, \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {\underline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} < {\text{Cap}} \le \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } \, } } \hfill \\ { 0 ,} \hfill & {{\text{Cap}} < \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {\underline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} } } \hfill \\ \end{array} } \right., $$
(14)
$$ {\text{Nec}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) = \left\{ {\begin{array}{*{20}l} { 1 ,} \hfill & {{\text{Cap}} \ge \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {\overline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} } } \hfill \\ {\frac{{{\text{Cap}} - \sum\nolimits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } }}{{\sum\nolimits_{j = 1}^{N} {(\overline{\text{d}}_{\text{j}} - {\hat{\text{d}}}_{\text{j}} ) {\text{ y}}_{\text{jk}} } }} ,} \hfill & {\sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} < {\text{Cap}} \le \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {\overline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} } } } \hfill \\ { 0 ,} \hfill & {{\text{ Cap < }}\sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } } \hfill \\ \end{array} } \right.. $$
(15)

According to [42] the following relation applies

$$ {\text{Pos}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) < 1\Rightarrow {\text{Nec}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) = 0 $$
(16)

and it is more demanding to request the necessity to be greater than 0 than to request the possibility to be less or equal to 1.

For \( \upalpha > 0 \) we can model the following constraints as crisp equivalents for the fuzzy constraint (2):

$$ {\text{Pos}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) \ge\upalpha \Leftrightarrow \sum\limits_{\text{j = 1}}^{\text{N}} {\left( {\upalpha\,{\hat{\text{d}}}_{\text{j}} + \left( {1 -\upalpha} \right)\underline{\text{d}}_{\text{j}} } \right){\text{y}}_{\text{jk}} \le {\text{Cap}},{\text{k}} = 1, \ldots ,{\text{K}},\upalpha \in \left( {0,1} \right]} $$
(17)

and for \( \beta > 0 \), respectively:

$$ {\text{Nec}}\left( {{\text{Serve}}\,{\tilde{\text{D}}}_{\text{k}} } \right) <\upbeta \Leftrightarrow \sum\limits_{\text{j = 1}}^{\text{N}} {\left( {\upbeta\overline{\text{d}}_{\text{j}} + \left( { 1-\upbeta} \right){\hat{\text{d}}}_{\text{j}} } \right){\text{y}}_{\text{jk}} \le {\text{Cap}},{\text{k}} = 1, \ldots ,{\text{K}},\upbeta \in \left( {0,1} \right]} $$
(18)

To solve this fuzzy mathematical programming model, it is suggested to determine the optimal solutions with respect to a given degree of possibility \( \upalpha \) or even stronger a given degree of necessity \( \upbeta \) that the capacity Cap is sufficient to meet the total demand \( {\tilde{\text{D}}}_{\text{k}} \) of the served ships on each of the K routes.

3.2 Multi-criteria Optimization for CVRPFD Based on Fuzzy Approach

A bunkering company usually wants to serve all the demands and sell as much fuel as possible. Sales are restricted by the demands and by the capacity of the tanker for a route. A solution is preferable if the amount of the demand served is high. To maximize sales in this considered fuzzy context means to determine and maximize a fuzzy set which depends on the fuzzy demand, the route and the capacity of the tanker.

The fuzzy set sales \( {\tilde{\text{S}}}_{\text{k}} \) on route k can be calculated as the minimum of demand \( {\tilde{\text{D}}}_{\text{k}} \) and the capacity of the tanker. The membership results as

$$ \upmu_{{{\tilde{\text{S}}}_{\text{k}} }} ( {\text{x)}} = \left\{ {\begin{array}{*{20}c} {\upmu_{{{\tilde{\text{D}}}_{\text{k}} }} ( {\text{x),}}} & {{\text{x}} < {\text{Cap}}} \\ {{\text{Pos }}\left( {{\tilde{\text{S}}}_{\text{k}} \ge {\text{Cap}}} \right),} & {{\text{x}} = {\text{Cap}} .} \\ { 0 ,} & {{\text{x}} > {\text{Cap}}} \\ \end{array} } \right. $$
(19)

It is suggested to use the following defuzzyfication method [40,41,42, 44] to determine the crisp approximation \( {\text{D}}\,{\tilde{\text{S}}}_{\text{k}} \) for the sales on the k-th route

$$ {\text{D}}\,{\tilde{\text{S}}}_{\text{k}} = \frac{ 1}{ 3}\left( {{ \hbox{min} }\left\{ {\sum\limits_{\text{j = 1}}^{\text{N}} {\underline{\text{d}}_{\text{j}} {\text{y}}_{\text{jk}} ,} {\text{Cap}}} \right\} + { \hbox{min} }\left\{ {\sum\limits_{\text{j = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} ,{\text{Cap}}} } \right\} + { \hbox{min} }\left\{ {\sum\limits_{\text{j = 1}}^{\text{N}} {{\bar{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } ,{\text{Cap}}} \right\}} \right) $$
(20)

Let \( \sum\nolimits_{\text{k = 1}}^{\text{K}} {{\tilde{\text{S}}}_{\text{k}} } \) be a fuzzy set of the total sales (depended on all K routes) with corresponding membership function

$$ \upmu_{{\sum {{\tilde{\text{S}}}_{\text{k}} } }} ( {\text{z)}} = \mathop { \sup }\limits_{{\sum\nolimits_{\text{k = 1}}^{\text{K}} {{\text{x}}_{\text{k}} = {\text{z}}} }} \, \mathop { \hbox{min} }\limits_{{{\text{k}} = 1}}^{\text{K}} \left\{ { \,\upmu_{{{\tilde{\text{S}}}_{\text{k}} }} \left( {{\text{x}}_{\text{k}} } \right)} \right\}. $$
(21)

and \( \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } \) is a crisp approximation of total sales \( \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {{\tilde{\text{S}}}_{\text{k}} } \).

The fuzzy multi-criteria approach for mathematical formalization of such kind of corresponding optimization problems for tankers CVRP and trucks CVRP are presented in [41, 42]. The multi-criteria model in a fuzzy context has to be considered in more detail. It is based on the minimization of total length of planned tanker’s routes

$$ { \hbox{min} }\,{\text{Z}}^{1} ({\text{x}},{\text{y}},{\text{u}}) \, = \, \sum\limits_{\text{i = 0}}^{\text{N}} {\sum\limits_{\text{j = 0}}^{\text{N}} {\sum\limits_{\text{k = 1}}^{\text{K}} {{\text{c}}_{\text{ij}} {\text{x}}_{\text{ijk}} } } } $$
(22)

and the maximization of total value of unloaded cargo (fuel) on all routes

$$ { \hbox{max} }\,{\text{Z}}^{2} ({\text{x}},{\text{y}},{\text{u}}) = \sum\limits_{\text{k = 1}}^{\text{K}} {,{\tilde{\text{min}}}} \left\{ {\sum\limits_{\text{j = 1}}^{\text{N}} {{\tilde{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } ,{\text{Cap}}} \right\}, $$
(23)

according to constraints (3)–(8), fuzzy relations (11), (12) and their crisp equivalents (17), (18), where x, y and u stand for the vectors of variables in the considered model and operator \( \left( {\text{m}} {\tilde{\text{i}}}{\text{n}} \right) \) means the extended minimum of the two fuzzy sets \( {\tilde{\text{D}}}_{k} \) and \( {\text{Cap}} \Leftrightarrow {\text{C}}\,{\tilde{\text{a}}\text{p }} = \left( {{\text{Cap}},{\text{Cap}},{\text{Cap}}} \right) \). For this model we assume that the number of vehicles is not restricted, the fleet of vehicles is homogeneous and each single demand is less than the capacity of the vehicle Cap.

For finding the optimal solution of CVRPFD (22), (23), (11), (12), (3)–(8) the modified iterative method developed in [12, 13] is used.

Step 1. The optimization criterion is (22) and simultaneously criterion (23) can be transformed to constraint

$$ \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\underline{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } \le {\text{Cap}},\quad {\text{k}} = 1, \ldots ,{\text{K}}, $$
(24)

that means that at least the lower bound of the fuzzy demand \( \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {\sum\nolimits_{{{\text{j}} = 1}}^{\text{N}} {{\underline{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } } \) is served. The individual optimum of \( {\text{Z}}^{1} \) (the minimal total distance) \( {\text{Z}}^{1} \left( {{\text{x}}^{1} ,{\text{y}}^{1} ,{\text{u}}^{1} } \right) = {\text{Z}}^{1*} \) can be determined by the solution algorithm and corresponding optimal parameters are \( {\text{x}}_{\text{ijk}}^{1} \), \( {\text{y}}_{\text{jk}}^{1} \) and \( {\text{u}}_{\text{jk}}^{1} \), where i, j = 0,…,N; k = 1,…,K.

Step 2. The value \( {\text{Z}}^{2} ({\text{x}}^{1} ,{\text{y}}^{1} ,{\text{u}}^{1} ) = {\text{Z}}_{*}^{2} \) should be calculated using (23) taking into account that

$$ {\text{Z}}^{2} \left( {{\text{x}}^{1} ,{\text{y}}^{1} ,{\text{u}}^{1} } \right) \ge \sum\limits_{{{\text{k}} = 1}}^{\text{K}} {\sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\underline{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} } } . $$
(25)

Step 3. Transform the second criterion (23) using the crisp approximation \( {\text{D}}\,{\tilde{\text{S}}}_{\text{k}} \) (20) to the following form

$$ { \hbox{max} }\,{\text{Z}}^{2} \left( {{\text{x}},{\text{y}},{\text{u}}} \right) \, = \sum\limits_{{{\text{k}} = 1}}^{\text{K}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } \ge {\text{Z}}^{2} ({\text{x}}^{1} ,{\text{y}}^{1} ,{\text{u}}^{1} ). $$
(26)

To determine the individual optimum of \( Z^{2} \) and fuzzy efficient solution it is necessary to consider all alternative solutions \( \left( {{\text{x}}^{2} ,{\text{y}}^{2} ,{\text{u}}^{2} } \right) \) and choose best solutions with the fulfilment of condition

$$ { \hbox{min} }\,{\text{Z}}^{1} \left( {{\text{x}}^{2} ,{\text{y}}^{2} ,{\text{u}}^{2} } \right) \le {\text{Z}}^{ 1} \left( {{\text{x}}^{1} ,{\text{y}}^{1} ,{\text{u}}^{1} } \right). $$
(27)

In this case optimal solutions according to criterion (23) will satisfy constraint (18) for the strongest condition: \( \upbeta = 1 \) and, practically, a fuzzy efficient individual optimum \( Z^{2} \) can be found solving model (1) with constraints (3)–(8) and with constraint (2) modified as follows

$$ \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\bar{\text{d}}}_{\text{j}} {\text{y}}_{\text{jk}} \le {\text{Cap}},} \quad {\text{k}} = 1, \ldots ,{\text{K}}. $$
(28)

As a result, the optimal solution is \( \left( {{\text{x}}^{2} ,{\text{y}}^{2} ,{\text{z}}^{2} } \right) \) for which \( {\text{Z}}^{ 2} \left( {{\text{x}}^{2} ,{\text{y}}^{2} ,{\text{z}}^{2} } \right) = {\text{Z}}^{2*} \) and \( {\text{Z}}^{ 1} \left( {{\text{x}}^{2} ,{\text{y}}^{2} ,{\text{u}}^{2} } \right) = {\text{Z}}_{*}^{1} \).

Step 4. Consider goal functions (22) and (23) as fuzzy sets and define their membership functions \( \upmu_{{Z^{1} }} ({\text{x}}), \,\upmu_{{Z^{ 2} }} ( {\text{x}}) \) using individual optimal values \( {\text{Z}}^{ 1 *} , {\text{ Z}}^{ 2 *} \) and pessimistic solutions \( {\text{Z}}_{ *}^{ 1} , {\text{ Z}}_{ *}^{ 2} \):

$$ \upmu_{{{\text{Z}}^{1} }} ({\text{x}}) = \, \left\{ {\begin{array}{*{20}c} {1,} & {{\text{Z}}^{1} ({\text{x}},{\text{y}},{\text{u}}) \le {\text{Z}}^{1*} } \\ {\frac{{{\text{Z}}_{*}^{1} - {\text{Z}}^{1} ({\text{x}},{\text{y}},{\text{u}})}}{{{\text{Z}}_{*}^{1} - {\text{Z}}^{1*} }},} & {{\text{Z}}^{1*} < {\text{Z}}^{1} ({\text{x}},{\text{y}},{\text{u}}) < {\text{Z}}_{*}^{1} } \\ {0,} & {{\text{Z}}^{1} ({\text{x}},{\text{y}},{\text{u}}) \ge {\text{Z}}_{*}^{1} } \\ \end{array} } \right., $$
(29)
$$ \upmu_{{{\text{Z}}^{2} }} ({\text{x}}) = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{Z}}^{ 2} ({\text{x}},{\text{y}},{\text{u}}) \ge {\text{Z}}^{ 2 *} } \\ {\frac{{{\text{Z}}^{ 2} ({\text{x}},{\text{y}},{\text{u}}) - {\text{Z}}_{ *}^{2} }}{{{\text{Z}}^{ 2 *} - {\text{Z}}_{ *}^{ 2} }},} & {{\text{Z}}_{ *}^{ 2} < {\text{Z}}^{ 2} ({\text{x}},{\text{y}},{\text{u}}) < {\text{Z}}^{ 2 *} } \\ { 0,} & {{\text{Z}}^{ 2} ({\text{x}},{\text{y}},{\text{u}}) \le {\text{Z}}_{ *}^{ 2} } \\ \end{array} } \right.. $$
(30)

Step 5. Set the first compromise model in the following way

$$ { \hbox{max} }\,\uplambda $$
(31)

subject to

$$ \left( {{\text{Z}}_{ *}^{ 1} - Z^{1*} } \right)\uplambda + \sum\limits_{{{\text{i}} = 0}}^{\text{N}} {\sum\limits_{{{\text{j}} = 0}}^{\text{N}} {\sum\limits_{{{\text{k}} = 1}}^{\text{K}} {{\text{c}}_{\text{ij}} {\text{x}}_{\text{ijk}} } } } \le {\text{Z}}_{*}^{1} , $$
(32)
$$ \left( {{\text{Z}}_{ *}^{ 2} - {\text{Z}}^{2*} } \right)\uplambda + \sum\limits_{\text{k = 1}}^{\text{K}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } \ge {\text{Z}}_{*}^{2} , $$
(33)
$$ \lambda \in \left[ {0,1} \right] $$
(34)

and constraints (3)–(8).

Step 6. An equivalent linear model is given by constraints (31), (32), (34), (3)–(8) and substituting the following linear constraints for the nonlinear constraint (33)

$$ \left( {Z_{*}^{2} - Z^{2*} } \right)\uplambda + \sum\limits_{{{\text{k}} = 1}}^{\text{K}} {\frac{{\left( {{\underline{\text{g}}}_{\text{k}} + {\hat{\text{g}}}_{\text{k}} + {\bar{\text{g}}}_{\text{k}} } \right)}}{3}} \ge {\text{Z}}_{*}^{2} , $$
(35)
$$ {\underline{\text{g}}}_{\text{k}} \le \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\underline{\text{d}}}_{\text{j}} } {\text{y}}_{\text{jk}} ,\quad {\text{k}} = 1 ,\ldots ,{\text{K,}} $$
(36)
$$ {\hat{\text{g}}}_{\text{k}} \le \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\hat{\text{d}}}_{\text{j}} } {\text{y}}_{\text{jk}} ,\quad {\text{k}} = 1, \ldots ,{\text{K,}} $$
(37)
$$ {\bar{\text{g}}}_{\text{k}} \le \sum\limits_{{{\text{j}} = 1}}^{\text{N}} {{\bar{\text{d}}}_{\text{j}} } {\text{y}}_{\text{jk}} ,\quad {\text{k}} = 1, \ldots ,{\text{K,}} $$
(38)
$$ 0 \le {\underline{\text{g}}}_{\text{k}} ,{\hat{\text{g}}}_{\text{k}} ,{\bar{\text{g}}}_{\text{k}} \le {\text{Cap}},\quad {\text{k}} = 1 ,\ldots , {\text{K}} . $$
(39)

Step 7. To solve the linear optimization model of CVRPFD in Step 6 with (31), (32), (34), (3)–(8) and (35)–(39) it is necessary to determine:

  1. (a)

    all nodes (ports, served ships or destination points) on every route k, k = 1,…,K and the set of completed routes;

  2. (b)

    the length \( {\text{L}}_{\text{k}} \) of each route k (total distance), k = 1,…,K;

  3. (c)

    the calculated values of sales \( {\text{D}}\,{\tilde{\text{S}}}_{\text{k}} \) for the realization of each route k, k = 1,…,K;

  4. (d)

    the total length (distance) \( {\text{L}}_{\text{total}} = \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {{\text{L}}_{\text{k}} } = Z_{1} \) for the realization of all planned routes;

  5. (e)

    total sales \( \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } = Z_{2} \) for the realization of all planned routes.

Step 8. Solve the local TSP (Travelling Salesperson Problem) separately for the nodes of each preliminary planned route k, k = 1,…,K. So the length for each route is minimized with fixed values of sales by using any well-known TSP exact algorithms, TSP heuristics [27, 44] or evolutionary optimization algorithms [35] (genetic algorithm, bio-geography optimization algorithm, etc.) depending on the number of nodes at a route. As a result, the optimal or nearly optimal length \( {\text{L}}_{\text{k}}^{\text{opt}} \) of each route k of the corresponding TSP is ascertained.

Step 9. The total optimal length for the realization of all optimized routes is \( {\text{L}}_{\text{total}}^{\text{opt}} = \sum\nolimits_{{{\text{k}} = 1}}^{\text{K}} {{\text{L}}_{\text{k}}^{\text{opt}} } = Z_{1}^{opt} \) .

Step 10. If \( {\text{L}}_{\text{total}}^{\text{opt}} < {\text{L}}_{\text{total}} \) then the sequence and consequences of port’s visits for tankers have to be changed according to the optimization process in Step 8, providing additional minimization of total length of all planned routes, else for \( {\text{L}}_{\text{total}}^{\text{opt}} = {\text{L}}_{\text{total}} \), no change is required.

3.3 Discussion of Modelling Results with Additional Route Optimization

Using the above-considered optimization models and the presented iterative algorithm, all routes and sales for the same input data as in the example published in [41] are determined. The CVRPFD (Fig. 1) consists of 75 ports, which are situated at locations characterized by their corresponding coordinates in the plane \( \left( {{\text{x}}_{\text{j}} ,{\text{y}}_{\text{j}} } \right),{\text{j}} = 1, \ldots , 7 5 \) and with Deport 0 with coordinates (40, 40). The tanker fleet is homogeneous with capacity Cap = 160 of each tanker and fuzzy demands are identical to those in [41].

Fig. 1
figure 1

Location of ports and depot

Full size image

The modelling results after the first seven steps of the suggested iterative algorithm are presented in Table 1. The number of planned routes is 10.

Table 1 Modelling results for routes 1–10
Full size table

The total distance

$$ {\text{L}}_{\text{total}} { = }\sum\limits_{\text{k = 1}}^{\text{K}} {{\text{L}}_{\text{k}} } = Z_{1} $$

and total sales

$$ \sum\limits_{{{\text{k}} = 1}}^{\text{K}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } = Z_{2} $$

are calculated based on the modelling data from each planned route, including length \( {\text{L}}_{\text{k}} \), fuzzy demands \( {\tilde{\text{D}}}_{\text{k}} = \left( {{\underline{\text{D}}}_{\text{k}} ,{\hat{\text{d}}}_{\text{k}} ,{\bar{\text{D}}}_{\text{k}} } \right) \) and sales \( {\text{D}}\,{\tilde{\text{S}}}_{\text{k}} ,{\text{k}} = 1, \ldots ,{\text{N}} \) for each route (Table 2).

Table 2 Characteristics of the routes 1–10
Full size table

All modelling results are obtained for \( \alpha = 1 \) and different values of \( \beta \). The resulting values after the first seven steps of the suggested iterative algorithm for CVRPFD are

$$ {\text{L}}_{\text{total}} = 8 7 6. 3 6\approx 876, $$
$$ \sum\limits_{{{\text{k}} = 1}}^{\text{N}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } = 1 3 3 9. 6 7\approx 1 3 4 0. $$

Then for continuing the decision making process with the goal to find the best solution it is necessary to realize the TSP-improvement by Steps 8–10.

Using a 2-opt heuristic [27, 44] the same node sequences for routes 1,2,3,4,5,6,9 result. But routes 7, 8 and 10 are improved in this case (Table 3).

Table 3 Final versions of improved routes after TSP-optimization on the steps 8–10 of the proposed iterative algorithm
Full size table

The lengths of the improved routes are

$$ {\text{L}}_{ 7}^{\text{opt}} = 80.63,{\text{L}}_{ 8}^{\text{opt}} = 126.02,{\text{L}}_{ 1 0}^{\text{opt}} = 135.48 $$

and total optimized distance for all routes is

$$ {\text{L}}_{\text{total}}^{\text{opt}} = 870.77 $$

taking into account that

$$ \begin{aligned} & {\text{D}}\,{\tilde{\text{S}}}_{7} = 142,{\text{D}}\,{\tilde{\text{S}}}_{8} = 139,{\text{D}}\,{\tilde{\text{S}}}_{10} = 137, \\ & \sum\limits_{{{\text{k}} = 1}}^{\text{N}} {{\text{D}}\,{\tilde{\text{S}}}_{\text{k}} } = 1339.67 = {\text{const}}. \\ \end{aligned} $$

Analyzing all modelling results it can be seen that after 2-opt TSP- improvement (Steps 8,9) (Fig. 2)

Fig. 2
figure 2

Final CVRPFD solution after additional TSP-optimization

Full size image
$$ {\text{L}}_{7}^{\text{opt}} < {\text{L}}_{7} ,{\text{ L}}_{8}^{\text{opt}} < {\text{ L}}_{8} ,{\text{L}}_{10}^{\text{opt}} < {\text{L}}_{10} $$

and the above-mentioned condition of Step 10

$$ {\text{L}}_{\text{total}}^{\text{opt}} < {\text{L}}_{\text{total}} $$

is satisfied. Finally, it is necessary to choose the optimized routes (Table 3) for the practical realization of CVRPFD taking into account that

$$ \Delta {\text{L}}_{\text{total}}^{\text{opt}} = {\text{ L}}_{\text{total}} - {\text{L}}_{\text{total}}^{\text{opt}} \,\approx \, 5. 5 9> { 0}. $$

This value illustrates the improved result compared to the modelling results in [14].

4 Second Alternative Fuzzy Approach Based on Evaluation of Satisfaction Value

4.1 Description of Conflict Situation in Route Planning

For implementation of the second alternative fuzzy approach it is suggested to form the intelligent model and planning algorithm for CVRPFD in the following way.

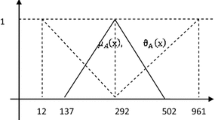
First of all, it is necessary to form mathematical models of fuzzy demands \( {\mathop{\text{q}}\limits_{\sim}}{_{\text{j}}} = \left( {{\underline{\text{q}}}_{\text{j}} ,{\hat{\text{q}}}_{\text{j}} ,{\bar{\text{q}}}_{\text{j}} } \right),{\text{j}} = 1\ldots {\text{N}} \) at nodes by the expert evaluation method. Three examples of demands \( {\mathop{\text{q}}\limits_{\sim}}{_{\text{j}}} = \left( {{\underline{\text{q}}}_{\text{j}} ,{\hat{\text{q}}}_{\text{j}} ,{\bar{\text{q}}}_{\text{j}} } \right),{\text{j}} = 1\ldots {\text{N}} \) are represented by fuzzy sets \( {\mathop{\text{A}}\limits_{\sim}}, {\mathop{\text{B}}\limits_{\sim}} \) and \( {\mathop{\text{C}}\limits_{\sim}} \) and shown in Fig. 3, where fuzzy set \( {\mathop{\text{A}}\limits_{\sim}} \) is a model of fuzzy demand of type “not less than 150 ”, fuzzy set \( {\mathop{\text{B}}\limits_{\sim}} \) is a model of fuzzy demand of type “not more than 500”, fuzzy set \( {\mathop{\text{C}}\limits_{\sim}} \) is a model of fuzzy demand of type “about 350” or “between 250 and 450”, \( \upmu_{\mathop{\text{X}}\limits_{\sim}} \left( {\text{q}} \right) \) is a membership function, \( {\mathop{\text{X}}\limits_{\sim}} = \left\{ {\mathop{\text{A}}\limits_{\sim}},{\mathop{\text{B}}\limits_{\sim}},{\mathop{\text{C}}\limits_{\sim}} \right\} \).

Fig. 3
figure 3

Fuzzy models of uncertain demands

Full size image

In the next step it is necessary to solve the Traveling Salesperson Problem for the total number of nodes \( {\text{N}} \) using one of the heuristic algorithms [27, 45], such as sweep-algorithm, tabu search algorithm, genetic algorithm, bio-geography optimization algorithm, simulated anneling, ant colony optimization algorithm or others. For example, Clarke and Write savings algorithm is based on calculating value \( {\text{s}}_{\text{ij}} \) for each pair of nodes (i,j):

$$ {\text{s}}_{\text{ij}} = {\text{L}}_{{0{\text{i}}}} + {\text{L}}_{{0{\text{j}}}} - {\text{L}}_{\text{ij}} ,\left( {{\text{i}} = 1 \ldots {\text{N}};{\text{j}} = 1 \ldots {\text{N}};{\text{i}} \ne {\text{j}}} \right), $$
(40)

The result of TSP solving depends on the number of nodes and on the selected heuristic. For example, for 35 nodes \( \left\{ {12,13,14, \ldots ,45,46} \right\} \) with coordinates, presented in Fig. 1 [41], and central depot with coordinates (\( {\text{x}}_{0} = 40 \), \( {\text{y}}_{0} = 40 \)) TSP solutions are:

  1. (a)

    for Clarke and Write saving algorithm:

    $$ \begin{aligned} & [ 0 \text{-42-41-43-23-24-18-25-31-38-14-19-35-13-15-20-37-36-21-28-22-} \\ & 3 3 \text{-16-44-32-39-40-12-17-26-46-34-27-29-45-30-0}] \\ \end{aligned} $$

    and the total length of this Hamiltonian circuit is 386,98;

  2. (b)

    for sweep algorithm:

    $$ \begin{aligned} & [ 0 \text{-38-14-35-19-46-34-13-27-15-20-45-29-37-36-30-21-28-22-42-43-} \\ & 4 1 \text{-33-23-16-24-44-18-17-32-40-25-39-12-31-26-0}] \\ \end{aligned} $$

    and the total length of this Hamiltonian circuit is 486,80;

  3. (c)

    for ant colony algorithm:

    $$ \begin{aligned} & [ 0 \text{-26-17-12-40-32-44-16-33-30-29-45-27-13-15-20-37-36-21-28-22-} \\ & 4 2 \text{-41-43-23-24-18-25-39-31-38-14-19-35-46-34-0}] \\ \end{aligned} $$

    and the total length of this Hamiltonian circuit is 343,74.

The procedure of route planning is based on the used TSP-solution (Hamiltonian circuit) which was created at the previous step. It is necessary to find nodes which should be included in the corresponding route taking into account possibilities for service of each node with fuzzy demands and constraint tanker capacity.

Figure 4 shows the route planning procedure for 1-st node’s demand \( {\mathop{\text{q}}\limits_{\sim}}{_{1}} \), Fig. 5 that for 2-nd node’s demand \( {\mathop{\text{q}}\limits_{\sim}}{_{2}} \) and Fig. 6 applies for 3-rd node’s demand \( {\mathop{\text{q}}\limits_{\sim}}{_{3}} \), where

Fig. 4
figure 4

Procedure of route planning (for 1-st node in TSP-solution)

Full size image
Fig. 5
figure 5

Procedure of route planning (for 2-nd node in TSP-solution)

Full size image
Fig. 6
figure 6

Procedure of route planning (for 3-rd node in TSP-solution)

Full size image

\( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{0}} = \left( {\Delta {\underline{\text{Q}}}_{0} ,\Delta {\hat{\text{Q}}}_{0} ,\Delta {\bar{\text{Q}}}_{0} } \right) \) is the initial value (Fig. 4) of cargo capacity of a tanker, which is presented as crisp number \( {\text{D}} \) in the style of triangular fuzzy number \( {\mathop{\text{D}}\limits_{\sim}} = \Delta {\mathop{\text{D}}\limits_{\sim}}{_{0}} = \left( {{\text{D}},{\text{D}},{\text{D}}} \right) \);

\( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{1}} = \left( {\Delta {\underline{\text{Q}}}_{1} ,\Delta {\hat{\text{Q}}}_{1} ,\Delta {\bar{\text{Q}}}_{1} } \right) \) is remaining cargo capacity on tanker (Fig. 5) after including 1-st node to the route, \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{1}} = \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{0}} - {\mathop{\text{Q}}\limits_{\sim}}{_{1}} \);

\( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{2}} = \left( {\Delta {\underline{\text{Q}}}_{2} ,\Delta {\hat{\text{Q}}}_{2} ,\Delta {\bar{\text{Q}}}_{2} } \right) \) is remaining cargo capacity (Fig. 6) on tanker after including 2-nd node to the route, \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{2}} = \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{1}} - {\mathop{\text{Q}}\limits_{\sim}}{_{2}} \);

\( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{3}} = \left( {\Delta {\underline{\text{Q}}}_{ 3} ,\Delta {\hat{\text{Q}}}_{ 3} ,\Delta {\bar{\text{Q}}}_{3} } \right) \) is remaining cargo on tanker after including 3-rd node to the route, \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{3}} { = }\Delta {\mathop{\text{Q}}\limits_{\sim}}{_{2}} - {\mathop{\text{q}}\limits_{\sim}}{_{3}} \).

All first three nodes (Figs. 4, 5, and 6), a sequence of which was taken from TSP solution, are included in the planning route because fuzzy values of remaining cargo on the tanker are higher than the fuzzy values of corresponding demands (Steps 1, 2, 3).

The conflict situation always appears during the route planning process for CVRP on the corresponding step and it is necessary to make a decision about including or excluding the corresponding “conflict” node in the route.

Let’s denote, that the conflict situation for the (j +1)-th port-applicant appears on condition that the highest value \( {\bar{\text{q}}}_{{{\text{j}} + 1}} \) of the fuzzy demand \( {\mathop{\text{q}}\limits_{\sim}}{_{{\text{j}} + 1}} = \left( {{\underline{\text{q}}}_{{{\text{j}} + 1}} ,{\hat{\text{q}}}_{{{\text{j}} + 1}} , {\bar{\text{q}}}_{{{\text{j}} + 1}} } \right) \) is higher than the lowest value \( \left( {{\text{D}} - \sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{\bar{\text{q}}}_{\text{s}} } } \right) \) of the fuzzy remaining tanker’s cargo quantity \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{\text{j}}} = \left( {{\text{D}} - \sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{\bar{\text{q}}}_{\text{s}} } , {\text{D - }}\sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{\hat{\text{q}}}_{\text{s}} } , {\text{D}} - \sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{\underline{\text{q}}}_{\text{s}} } } \right) \), or in other words, in the situation when

$$ {\underline{\text{q}}}_{\text{j + 1}} { < }\left( {{\text{D - }}\sum\limits_{\text{s = 1}}^{\text{j}} {{\bar{\text{q}}}_{\text{s}} } } \right). $$

Figure 7 shows the conflict situation during route planning procedure for 4-th node (Step 4). During the planning procedure for the current route (Figs. 4, 5 and 6), fuzzy values of remaining tanker’s cargo \( \Delta {{\underline{\text{Q}} }}_{\text{j}} { = }\left( {{\text{D}} - \sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{\bar{\text{q}}}_{\text{s}} } ,{\text{D}} - \sum\nolimits_{\text{s = 1}}^{\text{j}} {{\mathop{\text{q}}\limits^{\frown} }}_{\text{s}} } ,{\text{D}} - \sum\nolimits_{{{\text{s}} = 1}}^{\text{j}} {{{\underline{\text{q}}}_{\text{s}} } } \right) \) step by step (Steps 1, 2, 3) shift to the left. Triangular fuzzy number \( {\mathop{\Delta}\limits_{\sim}}{\text{Q}}_{\text{j}} \) is crossed with a triangular fuzzy number \( {\mathop{\text{q}}\limits_{\sim}}{_{\text{j + 1}}} \) (Fig. 7, j = 3) on the 4-th Step or placed to the left of it (as for fuzzy demand \( {\underline{\text{q}}}{_{\text{j + 1}}}^{\prime } = {underline{\text{q}}}{{_{ 4} }}^{\prime } \) of (j + 1)-th node, shown in Fig. 7 by dashed lines).

Fig. 7
figure 7

The conflict situation in route planning procedure for 4-th node in TSP-solution

Full size image

In the last case of intersection of fuzzy sets \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{\text{j}}} \) and \( {\mathop{\text{q}}\limits_{\sim}}{_{\text{j+1}}} \), the possibility degree of demand implementation decreases with increasing degree of shifting triangular fuzzy number \( \Delta {\mathop{\text{Q}}\limits_{\sim}}{_{\text{j}}} \) to the left.

4.2 Fuzzy Decision-Making Based on Satisfaction Value

It is propose to make a decision about including considered port \( {\text{P}}_{\text{j + 1}} \) in the current route (using developed fuzzy knowledge-based system—FKBS) based on the condition [16, 17]

$$ \lambda_{j + 1} \ge \lambda^{ *} , $$
(41)

where \( \lambda^{ *} \) is a desired satisfaction (preference) value; \( \lambda_{j + 1} \) is a current value of satisfaction level. Such satisfaction level \( \lambda_{j + 1} \) can be calculated at each serviced port \( \left( {{\text{P}}_{\text{j}} } \right) \) as possible level of the satisfaction of required order for the next serviced port \( \left( {{\text{P}}_{\text{j + 1}} } \right) \) with its fuzzy demand \( {\mathop{\text{q}}\limits_{\sim}}{_{\text{j + 1}}} \).

The developed decision-making algorithm based on fuzzy logic [16, 17] can be presented in the following way:

$$ \lambda_{j + 1} = FKBS \left[ { FRB\left( { {\mathop{\text{x}}\limits_{\sim}} {_{1}} ,{\mathop{\text{x}}\limits_{\sim}} {_{2}} ,x_{3} } \right) } \right]. $$
(42)

In (42) we used the following notations:

  • FKBS is a fuzzy knowledge–based system;

  • FRB is a fuzzy rule base with the following structure of fuzzy rules. For example,

“IF (input signal \( {\mathop{x}\limits_{\sim}}{_{1}} \) is Low) AND (input signal \( {\mathop{x}\limits_{\sim}}{_{2}} \) is Middle) AND (input signal \( x_{3} \) is High) THEN (output signal \( \lambda_{j} \) is High)”;

  • \( \lambda_{j + 1} \) is a value of satisfaction level for each alternative decision-making;

  • \( {\mathop{x}\limits_{\sim}} {_{1}} = \tilde{q}_{j + 1} /\Delta \tilde{Q}_{i} \) is the ration of fuzzy demands of the next \( \left( {j + 1} \right) \)-th port \( \tilde{q}_{j + 1} \) to the fuzzy value of the remaining tanker cargo \( \Delta \tilde{Q}_{i} \);

  • \( {\mathop{x}\limits_{\sim}} {_{2}} = \Delta \tilde{Q}_{i} /Q_{i} \)—ration of fuzzy numbers \( \Delta \tilde{Q}_{i} \) to tanker capacity \( Q_{i} \);

  • \( x_{3} = L_{1} /L_{ 2} \) is the ration of length \( L_{1} \) to \( L_{ 2} \) of two alternative routes \( R_{1} \) and \( R_{2} \) (\( R_{1} \) is the route with 1st level of search of the next route candidate port and \( R_{2} \) is the route of the 2nd level of search);

  • \( \Delta \tilde{Q}_{i} = \left( {Q_{i} - \sum\nolimits_{j = 1}^{k} {\bar{q}_{j} } ,\;Q_{i} - \sum\nolimits_{j = 1}^{k} {\hat{q}_{j} } ,\;Q_{i} - \sum\nolimits_{j = 1}^{k} {\underline{q}_{j} } } \right) \) is a fuzzy value of the remaining tanker cargo, where k is the number of served ships on the i-th route before the current decision; \( \left\{ {Low,Middle,High} \right\} \) is a set of the corresponding linguistic terms for input \( {\mathop{x}\limits_{\sim}} {_{1}}, {\mathop{x}\limits_{\sim}} {_{2}}, {\mathop{x}\limits_{\sim}} {_{3}}\) and output \( \lambda_{j + 1} \) signals.

The characterized surface

$$ Surf\left( {x_{1} ,x_{3} } \right),x_{2} = const, $$

of the fuzzy rule base FRB (42) for fixed input signal \( x_{2} = Middle \) is presented in Fig. 8.

Fig. 8
figure 8

Characteristic surface of FKBS (42) with fixed value of input signal \( x_{2} \)

Full size image

If the condition (41) is correct for the 4-st node (Fig. 7), then this node will be included in the current planning route. Next node in the TSP-solution will be a first node in the next planning route and so on.

After planning all routes according to the proposed second fuzzy approach it is necessary to realize an additional optimization procedure by solving TSP for each separate route \( {\text{R}}_{\text{s}} ,\left( {{\text{s}} = 1\ldots {\text{r}}} \right) \) that provides the minimization of the length of each separate route, as well as the total length of all routes \( {\text{L}}_{{\Sigma {\text{s}}}} ,\left( {{\text{s}} = 1\ldots {\text{r}}} \right) \).

The final solution of the CVRPFD can be implemented for the practical realization of the respective bunkering program for r tankers.

Modelling results [16, 17] confirm the efficiency of the proposed fuzzy approach based on FKBS application as second alternative for solving CVRPFD.

5 Conclusions

The suggested theoretical approach, based on the fuzzy multi-criteria models and iterative multistage algorithm, allows to receive in a fuzzy context optimal solutions for the CVRPFD. Modelling results confirm the efficiency of the suggested multi-objective optimization approach as first alternative. Using FKBS is the base for the second alternative for efficiently solving CVRPFD. Nevertheless, successful implementation of the second fuzzy approach significantly depends on the choice of the desired satisfaction value \( \lambda^{*} \). In future research work it is appropriate to extend the proposed models and algorithm for CVRPFD by solving time-windows problem.