Normal Numbers and Computer Science

Abstract

Émile Borel defined normality more than 100 years ago to formalize the most basic form of randomness for real numbers. A number is normal to a given integer base if its expansion in that base is such that all blocks of digits of the same length occur in it with the same limiting frequency. This chapter is an introduction to the theory of normal numbers. We present five different equivalent formulations of normality, and we prove their equivalence in full detail. Four of the definitions are combinatorial, and one is, in terms of finite automata, analogous to the characterization of Martin-Löf randomness in terms of Turing machines. All known examples of normal numbers have been obtained by constructions. We show three constructions of numbers that are normal to a given base and two constructions of numbers that are normal to all integer bases. We also prove Agafonov’s theorem that establishes that a number is normal to a given base exactly when its expansion in that base is such that every subsequence selected by a finite automaton is also normal.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

Flip a coin a large number of times, and roughly half of the flips will come up heads and half will come up tails. Normality makes analogous assertions about the digits in the expansion of a real number. Precisely, let b be an integer greater than or equal to 2. A real number is normal to base b if each of the digits 0, …, b − 1 occurs in its expansion with the same asymptotic frequency 1/b, each of the blocks of two digits occurs with frequency 1/b², each of the blocks of three digits occurs with frequency 1/b³, and so on, for every block length. A number is absolutely normal if it is normal to every base. Émile Borel [99] defined normality more than 100 years ago to formalize the most basic form of randomness for real numbers. Many of his questions are still open, such as whether any of π, e, or $\sqrt {2}$ is normal in some base, as well as his conjecture that the irrational algebraic numbers are absolutely normal [100].

In this chapter, we give an introduction to the theory of normal numbers. We start by considering five different equivalent formulations of normality, and we prove their equivalence in full detail. These proofs have not appeared all together in the literature before. Four of the definitions are combinatorial, and one is, in terms of finite automata, analogous to the characterization of Martin-Löf randomness [198] in terms of Turing machines. This characterization of normality holds for various enrichments of finite automata [57, 131], but the relation with deterministic push-down automata remains unsolved. We also briefly mention another well-known equivalent definition of normality, in terms of uniform distribution modulo 1, that will be further considered in Chapter 8.

All known examples of normal numbers have been obtained by constructions. We first focus in three selected constructions of numbers that are normal to a given base. We then present two constructions of absolutely normal numbers, one is a slightly simplified version of the pioneer work done by Alan Turing and the other is a simplified version of the polynomial time algorithm in [53].

Finally we consider the problem of preserving normality by selection by finite automata of a subsequence of a give sequence. We give the proof of Agafonov’s theorem [6] showing that a number is normal to a given base exactly when its expansion in that base is such that every subsequence selected by a finite automata is also normal.

Notation

Let A be finite set of symbols that we refer as the alphabet. We write A^ω for the set of all infinite words in alphabet A, A^∗ for the set of all finite words, A^≤k for the set of all words of length up to k, and A^k for the set of words of length exactly k. The length of a finite word w is denoted by |w|. The positions of finite and infinite words are numbered starting at 1. To denote the symbol at position i of a word w, we write w[i], and to denote the substring of w from position i to j, we write w[i…j]. The empty word is denoted by λ.

For two words w and u, the number |w| _u of occurrences of u in w and the number of aligned occurrences of u in w are, respectively, given by

For example, |aaaaa| _aa  = 4 and . Notice that the definition of aligned occurrences has the condition i ≡ 1mod|u| instead of i ≡ 0mod|u|, because the positions are numbered starting at 1. When a word u is just a symbol, |w| _u and coincide. Counting aligned occurrences of a word of length r over alphabet A is the same as counting occurrences of the corresponding symbol over alphabet A^r. Precisely, consider alphabet A, a length r, and an alphabet B with |A|^r symbols. The set of words of length r over alphabet A and the set B are isomorphic, as witnessed by the isomorphism π : A^r → B induced by the lexicographic order in the respective sets. Thus, for any w ∈ A^∗ such that |w| is a multiple of r, π(w) has length |w|/r and π(u) has length 1, as it is just a symbol in B. Then, for any u ∈ A^r, .

7.2 Borel’s Definition of Normality

A base is an integer greater than or equal to 2. For a real number x in the unit interval, the expansion of x in base b is a sequence a ₁ a ₂ a ₃… of integers from {0, 1, …, b − 1} such that

$$\displaystyle \begin{aligned} x= \sum_{k\geq 1} {a_k}{b^{-k}} = 0.a_1 a_2 a_3\ldots\end{aligned} $$

To have a unique representation of all rational numbers, we require that expansions do not end with a tail of b − 1. We will abuse notation, and whenever the base b is understood, we will denote the first n digits in the expansion of x with x[1…n].

Definition 7.2.1 (Strong Aligned Normality, Borel [99])

A real number x is simply normal to base b if, in the expansion of x in base b, each digit d occurs with limiting frequency equal to 1/b,

$$\displaystyle \begin{aligned} \lim_{n\to\infty } \frac{|x[1\ldots n]|{}_{d}}{n}=\frac{1}{b} \end{aligned}$$

A real number x is normal to base b if each of the reals x, bx, b² x, … are simply normal to bases b¹, b², b³, …. A real x is absolutely normal if x is normal to every integer base greater than or equal to 2.

Theorem 7.2.2 (Borel [99])

Almost all real numbers (with respect to Lebesgue measure) are absolutely normal.

Are the usual mathematical constants, such as π, e, or $\sqrt {2}$, absolutely normal? Or at least simply normal to some base? The question remains open.

Conjecture 7.2.3 (Borel [100])

Irrational algebraic numbers are absolutely normal.

The most famous example of a normal number is due to Champernowne [141]. He proved that the number

$$\displaystyle \begin{aligned} 0.12345678910112131415161718192021222324252627\ldots \end{aligned}$$

is normal to base 10. The construction can be done in any base, obtaining a number normal to that base. It is unknown whether Champernowne numbers are normal to the bases that are multiplicatively independent to the base used in the construction. Champernowne’s construction has been generalized in many interesting ways. There are also some other methods to obtain examples of numbers that are normal to a given base. In Section 7.7, we comment on the different methods, and we present three selected constructions.

All known examples of absolutely normal numbers are given by constructions. The oldest were not even computable. The first computable construction is due to A. Turing [52, 570]. In Section 7.8, we give references of known constructions, and we present two of them.

7.3 Equivalences Between Combinatorial Definitions of Normality

Borel’s original definition of normality turned out to be redundant. Pillai in 1940, see [118, Theorem 4.2], proved the equivalence between Definition 7.2.1 and the following.

Definition 7.3.1 (Aligned Normality)

A real number x is normal to base b if x is simply normal to bases b¹, b², b³, ….

Niven and Zuckerman in 1951, see [118, Theorem 4.5], proved yet another equivalent formulation of normality by counting occurrences of blocks but not aligned. This formulation was stated earlier by Borel himself, without proof.

Definition 7.3.2 (Non-aligned Normality)

A real number x is normal to base b if for every block u,

$$\displaystyle \begin{aligned} \lim_{n\to\infty } \frac{|x[1\ldots n]|{}_{u}}{n}=\frac{1}{b^{|u|}}. \end{aligned}$$

We will prove that Definitions 7.2.1, 7.3.1 and 7.3.2 are equivalent. The following lemma gives a central limit theorem that bounds the number of words in alphabet A of length k having too few or too many occurrences of some block w.

Definition 7.3.3

Let A be an alphabet of b symbols. We define the set of words of length k such that a given word w has a number of occurrences that differs from the expected value in plus or minus εk,

$$\displaystyle \begin{aligned} Bad(A, k,w, \varepsilon)= \left\{ v \in A^{k} : \left| \frac{|v|{}_{w}}{ k} - b^{-|w|} \right| \geq \varepsilon \right\}. \end{aligned}$$

Lemma 7.3.4 (Adapted from Hardy and Wright [283, proof of Theorem 148])

Let b be an integer greater than or equal to 2, and let k be a positive integer. If 6/k ≤ ε ≤ 1/b, then for every d ∈ A,

$$\displaystyle \begin{aligned} \left|Bad(A, k,d,\varepsilon)\right| < 4 b^k e^{- b \varepsilon^2 k/6}. \end{aligned}$$

Proof

Observe that for any d ∈ A,

$$\displaystyle \begin{aligned} Bad(A, k,d,\varepsilon)= \sum_{ n \leq k/b-\varepsilon k} \binom{k}{n} (b-1)^{k-n} + \sum_{ n \geq k/b+\varepsilon k} \binom{k}{n} (b-1)^{k-n} \end{aligned}$$

Fix b and k and write N(n) for

$$\displaystyle \begin{aligned} \binom{k}{n} (b-1)^{k-n}.\end{aligned} $$

For all n < k/b, we have that N(n) < N(n + 1) and the quotients

$$\displaystyle \begin{aligned} \frac{N(n)}{N(n+1)}=\frac{(n+1)(b-1)}{k-n} \end{aligned}$$

decrease as n increases. Similarly, for all n > k/b, we have that N(n) < N(n − 1) and the quotients

$$\displaystyle \begin{aligned} \frac{N(n)}{N(n-1)}=\frac{k-n+1}{n(b-1)} \end{aligned}$$

increase as n decreases. The strategy will be to “shift” each of the sums m positions.

We bound the first sum as follows. For any n we can write

$$\displaystyle \begin{aligned} N(n) = \frac{N(n)}{N(n+1)} \cdot \frac{N(n+1)}{N(n+2)} \cdot \ldots \cdot \frac{N(n + m -1 )} {N(n + m)} \cdot N(n + m) \end{aligned}$$

Let

$$\displaystyle \begin{aligned} m=\left\lfloor \varepsilon k/2\right\rfloor \text{ and } p=\lfloor k/b -\varepsilon k\rfloor\end{aligned} $$

For each n such that n ≤ p + m − 1, we have that n + m < k/b, so

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \frac{N(n)}{N(n+1)} &\displaystyle \leq&\displaystyle \frac{ N(p+ m -1 )} {N( p+m )}\\ &\displaystyle =&\displaystyle \frac{(p+m)(b-1)}{k-p-m+1}\\ &\displaystyle <&\displaystyle \frac{(k/b -\varepsilon k/2)(b-1)}{k-k/b+\varepsilon k/2}\\ &\displaystyle =&\displaystyle 1-\frac{\varepsilon b/2}{1-1/b+\varepsilon/2}\\ &\displaystyle <&\displaystyle 1-\varepsilon b/2 \qquad (\text{using the hypothesis }\varepsilon\leq 1/b).\\ &\displaystyle < &\displaystyle e^{-b\varepsilon/2}. \end{array} \end{aligned} $$

Then,

$$\displaystyle \begin{aligned} \begin{array}{rcl} N(n) &\displaystyle < &\displaystyle \left(e^{-b\varepsilon/2}\right)^m \ N(n + m) \\ &\displaystyle \leq&\displaystyle e^{-b\varepsilon (\varepsilon k/2 -1)/2} \ N(n + m) \\ &\displaystyle \leq &\displaystyle 2 e^{-b\varepsilon^2 k/4} \ N(n + m), \qquad (\text{the hypothesis }\varepsilon\leq 1/b\text{ implies }e^{b\varepsilon/2} < 2) \end{array} \end{aligned} $$

We obtain,

$$\displaystyle \begin{aligned} \sum_{n \leq u } N(n) < 2 e^{-b\varepsilon^2 k/2} \sum_{n\leq u}\ N(n+m) \leq 2\ b^{k} e^{-b\varepsilon^2 k/4} . \end{aligned}$$

We now bound the second sum, shifting it m positions. For any n we can write

$$\displaystyle \begin{aligned} N(n) = \frac{N(n)}{N(n-1)} \cdot \frac{N(n-1)}{N(n-2)} \cdot \ldots\cdot \frac{N(n - m+1)}{N(n -m ) }\cdot N(n-m) \end{aligned}$$

Let

$$\displaystyle \begin{aligned} m=\lfloor \varepsilon k /2\rfloor \text{ and } q=\lceil k/b +\varepsilon k\rceil. \end{aligned}$$

For each n such that n ≥ q − m + 1, we have n − m > k/b, so

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \frac{N(n)}{N(n-1)} &\displaystyle \leq&\displaystyle \frac{ N(q-m+1)} {N( q-m)}\\ {} &\displaystyle = &\displaystyle \frac{k-q+m}{(q-m+1)(b-1)}\\ {} &\displaystyle =&\displaystyle \frac{k-\lceil k/b +\varepsilon k\rceil + \lfloor \varepsilon k/2\rfloor}{(\lceil k/b +\varepsilon k\rceil -\lfloor \varepsilon k /2\rfloor+1)(b-1)}\\ {} &\displaystyle \leq&\displaystyle \frac{k-k/b-\varepsilon k/2 }{(k/b+\varepsilon k/2 +1)(b-1)}\\ {} &\displaystyle <&\displaystyle \frac{1-1/b-\varepsilon /2}{(1/b+\varepsilon /2 )(b-1)} \end{array} \end{aligned} $$

Now

$$\displaystyle \begin{aligned}\begin{array}{crl} &\frac{1-1/b-\varepsilon /2}{(1/b+\varepsilon /2 )(b-1)} &\leq \ 1-b\varepsilon/3 \\ {} \Leftrightarrow& 1-1/b-\varepsilon /2 &\leq\ (1-b\varepsilon/3)(1/b+\varepsilon /2 )(b-1) \\ {} \Leftrightarrow& (b-1)/b-\varepsilon /2 &\leq\ ( 1/b + \varepsilon/2 )(b-1) - (b\varepsilon/3)(1/b+\varepsilon /2 )(b-1) \\ {} \Leftrightarrow& (b\varepsilon/3)(1/b+\varepsilon /2 )(b-1) &\leq\ b\varepsilon/2 \\ {} \Leftrightarrow & (1/b+\varepsilon /2 )(b-1) &\leq\ 3/2. \end{array}\end{aligned}$$

Since ε ≤ 1/b, we obtain the required inequality,

$$\displaystyle \begin{aligned} (1/b+\varepsilon/2) (b-1) \leq (1/b + 1/(2b)) (b-1) = 3/(2b) (b-1) \leq 3/2 \end{aligned}$$

We conclude,

$$\displaystyle \begin{aligned} \frac{N(n)}{N(n-1)} \leq 1-b\varepsilon/3 \leq e^{-b\varepsilon/3 }. \end{aligned} $$

Then,

$$\displaystyle \begin{aligned} N(n) &< \left(e^{-b\varepsilon/3}\right)^{m} N(n - m) \\ &\leq e^{-b\varepsilon \lfloor \varepsilon k/2\rfloor /3} N(n - m) \\ &\leq e^{-b\varepsilon ( \varepsilon k/2-1) /3} N(n - m) \\ &\leq 2 \ e^{-b\varepsilon^2 k/6} N(n - m),\qquad (\text{the hypothesis }\varepsilon\leq 1/b\text{ implies }e^{b\varepsilon/3}< 2). \end{aligned} $$

Thus,

$$\displaystyle \begin{aligned} \sum_{n \geq q } N(n) < 2\ b^{k} e^{-b\varepsilon^2 k/6}. \end{aligned}$$

This completes the proof.

The next lemma bounds the number of words of k symbols in alphabet A that contain too many or too few occurrences of some block of length ℓ, with respect to a toleration specified by ε.

Lemma 7.3.5

Let A be an alphabet of b symbols. Let k, ℓ be positive integers and ε a real such that 6/⌊k/ℓ⌋≤ ε ≤ 1/b^ℓ . Then,

$$\displaystyle \begin{aligned} \left|\bigcup_{w\in A^\ell}Bad(A, k,w,\varepsilon)\right|< 2 \ell\ b^{k+2\ell} \ e^{- b^\ell \varepsilon^2 k/(6\ell)}. \end{aligned}$$

Proof

Split the set {1, 2, …, k} into the congruence classes modulo ℓ. Each of these classes contains either ⌊k/ℓ⌋ or ⌈k/ℓ⌉ elements. Let M ₀ denote the class of all indices which leave remainder zero when being reduced modulo ℓ. Let n ₀ = |M ₀|.

For each x in A^k, consider the word in $(A^\ell )^{n_0}$

$$\displaystyle \begin{aligned} x[i_1 \ldots (i_1+\ell-1)] x[i_2 \ldots (i_2+\ell-1)] \ldots x[i_{n_0} \ldots (i_{n_0}+\ell-1)] \end{aligned}$$

for $i_1, \ldots i_{n_0}\in M_0$. By Lemma 7.3.4, we have

$$\displaystyle \begin{aligned} \left|Bad(A^\ell, n_0,w,\varepsilon)\right|< 4\ (b^\ell)^{n_0} e^{- b^\ell \varepsilon^2 n_0/6}. \end{aligned}$$

Clearly, similar estimates hold for the indices in the other residue classes. Let n ₁, …, n _ℓ−1 denote the cardinalities of these other residue classes. By assumption n ₀ + ⋯ + n _ℓ−1 = k. Then,

$$\displaystyle \begin{aligned} \left|Bad(A, k,w,\varepsilon)\right|&\leq \sum_{j=0}^{\ell-1} \left|Bad(A^\ell, n_j,w,\varepsilon)\right| \\ &\leq \sum_{j=0}^{\ell-1} 4 (b^\ell)^{n_j} e^{- b^\ell \varepsilon^2 n_j/6} \\ &\leq \sum_{j=0}^{\ell-1} 4 (b^\ell)^{k/\ell+1} e^{- b^\ell \varepsilon^2 k/(6\ell) } \\ &= 4\ \ell \ b^{k+\ell}\ e^{- b^\ell \varepsilon^2 k/(6 \ell)}. \end{aligned} $$

The last inequality holds because

$$\displaystyle \begin{aligned} (b^\ell)^{\lceil k/\ell\rceil } e^{- b^\ell \varepsilon^2 \lceil k/\ell\rceil /6} < (b^\ell)^{k/\ell +1} e^{- b^\ell \varepsilon^2 k/(6\ell)} \end{aligned}$$

and ε ≤ 1/b^ℓ ensures

$$\displaystyle \begin{aligned} (b^\ell)^{\lfloor k/\ell\rfloor } e^{- b^\ell \varepsilon^2 \lfloor k/\ell\rfloor /6} &\leq b^k e^{- b^\ell \varepsilon^2 k/(6\ell)} e^{1 /(6 b^\ell)} \leq b^k e^{- b^\ell \varepsilon^2 k/(6\ell)} b^\ell. \end{aligned} $$

Now, summing up over all w ∈ A^ℓ, we obtain

$$\displaystyle \begin{aligned} \left|\bigcup_{w\in A^\ell}Bad(A, k,w,\varepsilon)\right|< 2 \ell \ b^{k+2\ell} e^{- b^\ell \varepsilon^2 k/(6\ell)} \ . \end{aligned}$$

Instead of the factor 4, we can put the factor 2 because if a word w ∈ A^ℓ occurs fewer times than expected in a given word x ∈ A^k, then there is another word v ∈ A^ℓ that occurs in x more times than expected.

Lemma 7.3.6

Let (x _1,n)_n≥0, (x _2,n)_n≥0, …, (x _k,n)_n≥0 be sequences of real numbers such that $\sum _{i = 1}^k x_{i,n} = 1$ , and let c ₁, c ₂, …, c _k be real numbers such that $\sum _{i = 1}^k c_i = 1$ . Then,

• 1. If for each i, liminf_n→∞ x _i,n ≥ c _i then for each i, lim_n→∞ x _i,n = c _i .

• 2. If for each i, limsup_n→∞ x _i,n ≤ c _i then for each i, lim_n→∞ x _i,n = c _i .

Proof

For any i in {1, …, k},

$$\displaystyle \begin{aligned} \limsup_{n \to \infty} x_{i,n} & = \limsup_{n \to \infty} ( 1 - \sum_{j \neq i} x_{j,n} ) \\&= 1 + \limsup_{n \to \infty} (-\sum_{j \neq i} x_{j,n} ) \\&= 1 - \liminf_{n \to \infty} (\sum_{j \neq i} x_{j,n} ) \\& \leq 1 - \sum_{j \neq i} \liminf_{n \to \infty} x_{j,n} \\& \leq 1 - \sum_{j \neq i} c_j \\&= c_i. \end{aligned} $$

Since

$$\displaystyle \begin{aligned} \liminf \leq \limsup \text{ and } \limsup_{n \to \infty} x_{i,n} \leq c_i \leq \liminf_{n \to \infty} x_{i,n}, \end{aligned}$$

necessarily,

$$\displaystyle \begin{aligned} \liminf_{n \to \infty} x_{i,n} = \limsup_{n \to \infty} = c_i \text{ and } \lim_{n \to \infty} x_{i,n} = c_i. \end{aligned}$$

Theorem 7.3.7

Definitions 7.2.1 , 7.3.1 and 7.3.2 are equivalent.

Proof

Let x be a real number. We use the fact that for every block w ∈ A^∗,

$$\displaystyle \begin{aligned} \lim_{n \to \infty} \frac{|x[1 \ldots n]|{}_{w}}{n} = b^{-|w|} \end{aligned}$$

if and only if there is a positive integer r such that

$$\displaystyle \begin{aligned} \lim_{n \to \infty} \frac{|x[1 \ldots nr]|{}_{w}}{nr} = b^{-|w|}. \end{aligned}$$

A similar fact is true for the limit of .

• 1. We show that strong aligned normality implies non-aligned normality.

  Observe that for any w ∈ A^ℓ,

  

  Then,

  

• 2. We prove that non-aligned normality implies aligned normality. Define

  

  Given w ∈ A^∗, let d be corresponding digit in A^|w|, and observe that for each v ∈ V (w, k, ε), there is $\tilde {v}\in Bad(A^{|w|}, k-1, d,\varepsilon )$ and there are words s, t ∈ A^∗ such that |s| + |t| = |w|− 1 and $v= s\tilde {v}t$. Thus,

  $$\displaystyle \begin{aligned} |V(w,k,\varepsilon)|\leq |w| b^{|w|-1} |Bad(A^{|w|}, k-1, d,\varepsilon)|. \end{aligned}$$

  So by Lemma 7.3.5, for every positive real δ, there is k ₀ such that for every k > 0,

  $$\displaystyle \begin{aligned} |V(w,k,\varepsilon)| \ b^{-(k|w|-1)} < \delta. \end{aligned}$$

  Fix ℓ and assume w ∈ A^ℓ. Then, for any $k\geq \max (2,k_0)$,

  

  To obtain the inequality in the second line, observe that each aligned occurrence of w in a position jℓ + 1, where k − 1 ≤ j < n, is counted (k − 1)ℓ times by for (j + 1 − k)ℓ + 1 ≤ t ≤ jℓ + 1.

  Since the last inequality is true for any δ, ε > 0, we conclude that

  

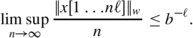
  Applying Lemma 7.3.6, we conclude,

  

• 3. We prove that aligned normality implies strong aligned normality. It is sufficient to prove that if x has aligned normality, then bx also has aligned normality. Define

  $$\displaystyle \begin{aligned} U(k,w,i) = \{ u \in A^k : u[i \ldots i + |w| - 1] = w \}. \end{aligned}$$

  Fix a positive integer ℓ. For any w ∈ A^ℓ and for any positive integer r,

  

  For every r, the following equality holds:

  

  Then, using the inequality obtained above, we have

  

  Since this last inequality holds for every r, we obtain,

  

  Finally, this last inequality is true for every w ∈ A^ℓ; hence, by Lemma 7.3.6,

  

7.4 Normality as a Seemingly Weaker Condition

The following result is due to Piatetski-Shapiro in 1957 [481] and was rediscovered later by Borwein and Bailey [101] who called it the hot spot lemma. In Theorem 7.4.1, we present two versions of this result, one with non-aligned occurrences and one with aligned occurrences. The theorem has been extended relaxing the constant C to a sublinear function; see [118] for the references.

Theorem 7.4.1

Let x be a real and let b be an integer greater than or equal to 2. Let A = {0, …, b − 1}. The following conditions are equivalent,

• 1. The real x is normal to base b.

• 2. There is a constant C such that for infinitely many lengths ℓ and for every w in A ^ℓ

  

• 3. There is a constant C such that for infinitely many lengths ℓ and for every w in A ^ℓ

  $$\displaystyle \begin{aligned} \limsup_{n \to \infty} \frac{|x[1 \ldots n]|{}_{w}}{n} < C \cdot b^{-|w|}. \end{aligned}$$

Proof

The implications 1 ⇒ 2 and 1 ⇒ 3 follow from Theorem 7.3.7.

We now prove 2 ⇒ 1. Define,

Lemma 7.3.5 implies that the size of $\widetilde {Bad}(A^{|w|}, k,w,\varepsilon )$ shrinks exponentially as k increases. Suppose there is C such that for infinitely many lengths ℓ and for every w ∈ A^ℓ,

Fix ℓ and w ∈ A^ℓ. Fix ε > 0 and take k large enough.

Since this is true for all ε > 0,

Finally, this last inequality is true for every w ∈ A^ℓ; hence, by Lemma 7.3.6

The proof of implication 3 ⇒ 1 is similar to 2 ⇒ 1. Consider the set Bad(A, w, k, ε) from Definition 7.3.3, the bound in Lemma 7.3.5, and the following fact. Fix w of length ℓ. Then for any n and k,

Then,

And

Hence,

7.5 Normality as Incompressibility by Finite Automata

The definition of normality can be expressed as a notion of incompressibility by finite automata with output also known as transducers. We consider nondeterministic transducers. We focus on transducers that operate in real time, that is, they process exactly one input alphabet symbol per transition. We start with the definition of a transducer (see Section 1.5.4 for the definition of automata without output).

Definition 7.5.1

A nondeterministic transducer is a tuple $\mathcal {T} = \langle Q,A,B,\delta ,I,F \rangle$, where

• Q is a finite set of states,

• A and B are the input and output alphabets, respectively,

• δ ⊂ Q × A × B^∗× Q is a finite transition relation,

• I ⊆ Q and F ⊆ Q are the sets of initial and final states, respectively.

A transition of such a transducer is a tuple 〈p, a, v, q〉 which is written . A finite (respectively infinite) run is a finite (respectively infinite) sequence of consecutive transitions,

A finite path is written . An infinite path is final if the state q _n is final for infinitely many integers n. In that case, the infinite run is written . An infinite run is accepting if it is final and furthermore its first state q ₀ is initial. This is the classical Büchi acceptance condition. For two infinite words x ∈ A^ω and y ∈ B^ω, we write $\mathcal {T}(x,y)$ whenever there is an accepting run in $\mathcal {T}$.

Definition 7.5.2

A transducer T is bounded-to-one if the function $y \mapsto |\{x : \mathcal {T}(x,y)\}|$ is bounded.

Definition 7.5.3

An infinite word x = a ₁ a ₂ a ₃⋯ is compressible by a nondeterministic transducer if it has an accepting run satisfying

$$\displaystyle \begin{aligned} \liminf_{n \to \infty} \frac{|v_1 v_2 \cdots v_n|}{n}\frac{ \log |B|}{\log |A|} < 1. \end{aligned}$$

It follows from the results in [175, 531] that the words which are not compressible by one-to-one deterministic transducers are exactly the normal words. A direct proof of this result appears in [56]. Extensions of this characterization for nondeterminisms and extra memory appear in [57, 131].

Theorem 7.5.4

An infinite word is normal if and only if it not compressible by a bounded-to-one nondeterministic transducer.

We first show that a non-normal word is compressible. We show a slightly stronger result since the transducer can be chosen deterministic and one-to-one.

Lemma 7.5.5

A non-normal infinite word is compressible by a deterministic one-to-one transducer.

Proof

Assume x ∈ A^ω is not normal. Let us show that x is compressible regardless of the choice of an output alphabet B. Since x is not normal, there is some word u ₀ of length k such that

meaning that the limit on the left side either does not exist or it does exist but it is different from 1/|A|^k. There exists then an increasing sequence (n _i )_i≥0 of integers such that the limit does exists for each word u of length k and furthermore $f_{u_0} \neq 1/|A|{ }^{k}$. Note that $\sum _{u\in A^k}{f_u} = 1$. Let m be an integer to be fixed later. For each word w ∈ A^km, let f _w be defined by $f_w = \prod _{i=1}^m f_{u_i}$ where w is factorized w = u ₁⋯u _m with |u _i | = k for each 1 ≤ i ≤ m. Since $\sum _{w\in A^{km}}{f_w} = 1$, a word v _w  ∈ B^∗ can be associated with each word w ∈ A^km such that $v_w \neq v_{w'}$ for w ≠ w′ , the set {v _w  : w ∈ A^mk} is prefix-free, and for each w ∈ A^km,

$$\displaystyle \begin{aligned} |v_w| \le \lceil -{\log f_w}/{\log |B|} \rceil. \end{aligned}$$

We claim that the words $(v_w)_{w \in A^{km}}$ can be used to construct a deterministic transducer $\mathcal {T}_m$ which compresses x for m large enough. The state set Q _m of $\mathcal {T}_m$ is the set A^<km of words of length less than km. Its initial state is the empty word λ, and all states are final. Its set E _m of transitions is given by

Let us denote by $\mathcal {T}_m(z)$ the output of the transducer $\mathcal {T}_m$ on some finite input word z. Suppose that the word z is factorized z = w ₁⋯w _n w′ where |w _i | = km for each 1 ≤ i ≤ n and |w′| < km. Note that n = ⌊|z|/km⌋. Note also that the transducer $\mathcal {T}_m$ always comes back to its initial state λ after reading km symbols.

Applying this computation to the prefix z = x[1..n] of x gives

$$\displaystyle \begin{aligned} \liminf_{n \to \infty} \frac{|\mathcal{T}_m(x[1..n])\log |B|}{n\log |A|} & \le \lim_{i \to \infty} \frac{|\mathcal{T}_m(x[1..n_i])\log |B|}{n_i\log |A|} \\ & \le \frac{\log |B|}{km\log |A|} + \frac{1}{k\log |A|}\sum_{u \in A^{k}} f_u(-\log f_u). \end{aligned} $$

Since at least one number f _u is not equal to 1/|A|^k, the sum $\sum _{u \in A^{k}} f_u(-\log f_u)$ is strictly less than $k\log |A|$. For m chosen large enough, we obtain that $\mathcal {T}_m$ compresses x.

The following lemma is the key lemma to prove the converse.

Lemma 7.5.6

Let ℓ be a positive integer, and let u ₁, u ₂, u ₃, … be words of length ℓ over the alphabet A such that u ₁ u ₂ u ₃⋯ is simply normal to word length ℓ. Let

be a run where each C _i is a configuration of some kind of transducer. Assume there is a real ε > 0 and a set U ⊆ A^ℓ of at least (1 − ε)|A|^ℓ words such that u _i  ∈ U implies |v _i |≥ ℓ(1 − ε). Then,

$$\displaystyle \begin{aligned} \liminf_{n \to \infty} \frac{|v_1 v_2 \cdots v_n|}{n \ell} \ge (1-\varepsilon)^3. \end{aligned}$$

Proof

Assume words u _i as in the hypothesis. By definition of normality to word length ℓ, let n ₀ be such that for every u ∈ A^ℓ and for every n ≥ n ₀,

$$\displaystyle \begin{aligned} |\{i : 1\leq i \leq n, u_i = u\}| \ge n |A|{}^{-\ell} (1-\varepsilon). \end{aligned}$$

Then, for every n ≥ n ₀,

$$\displaystyle \begin{aligned} |v_1 v_2 \cdots v_n| &= \sum_{i=1}^n |v_i| \\ &\ge \sum_{1\leq i \leq n, u_i \in U} |v_i| \\ &\ge \sum_{1\leq i \leq n, u_i \in U} \ell (1-\varepsilon) \\ &\ge n |A|{}^{-\ell} (1-\varepsilon) \sum_{u \in U} \ell (1-\varepsilon)\\ &\ge n |A|{}^{-\ell} (1-\varepsilon) (1-\varepsilon) |A|{}^\ell \ell (1-\varepsilon) \\ &\ge (1-\varepsilon)^3 n \ell. \end{aligned} $$

We now come back to the proof that normal words are not compressible by bounded-to-one transducers.

Proof

Fix a normal infinite word x = a ₁ a ₂ a ₃⋯, a real ε > 0, a bounded-to-one nondeterministic transducer T = 〈Q, A, B, δ, q ₀, F〉, and an accepting run . It suffices to show that there is ℓ and U such that Lemma 7.5.6 applies to this arbitrary choice of ε, T, and accepting run. For each word u ∈ A^∗, let

be the minimum number of symbols that the processing of u can contribute to the output in the run we fixed. Let

$$\displaystyle \begin{aligned} U_\ell = \{u \in A^\ell: h_u \ge (1-\varepsilon) \ell\}\end{aligned} $$

be the set of words of length ℓ with relatively large contribution to the output. Let t be such that T is t-to-one. For each length ℓ, pair of states p, q that appear in the run, and for each word v, consider the set

Since p and q appear in the run, let be a prefix of the run and be a suffix of the run. This implies goes infinitely often through an accepting state. Thus, for different u ₁, u ₂ ∈ U′, there are accepting runs and , from which it follows that $\mathcal {T}(u_0 u_1 x_0, v_0 v y_0)$ and $\mathcal {T}(u_0 u_2 x_0, v_0 v y_0)$. Therefore, by definition of t, |U′|≤ t.

Thus,

$$\displaystyle \begin{aligned} |U_\ell| \ge |A|{}^\ell - |Q|{}^2 t |B|{}^{(1-\varepsilon)\ell+1}. \end{aligned}$$

Fix ℓ such that |U _ℓ | > |A|^ℓ(1 − ε) and apply Lemma 7.5.6 with U = U _ℓ to the considered run. This completes the proof.

7.6 Normality as Uniform Distribution Modulo 1

Let (x _j )_j≥1 be a sequence of real numbers in the unit interval. The discrepancy of the N first elements is

$$\displaystyle \begin{aligned} D_N((x_j)_{j\geq 1})= \sup_{0\leq u< v\leq 1} \left| \frac{|\{ j : 1\leq j \leq N \text{ and } u\leq x_j \leq v\}|}{N} - (v-u)\ \right|. \end{aligned}$$

The sequence (x _j )_j≥1 is uniformly distributed in the unit interval if

$$\displaystyle \begin{aligned} \lim_{N\to\infty}D_N((x_j)_{j\geq 1})=0. \end{aligned}$$

Schmidt [530] proved that for every sequence (x _j )_j≥1 of reals in the unit interval, there are infinitely many Ns such that

$$\displaystyle \begin{aligned} D_N( (x_j)_{j\geq 1}) \geq \frac{\log N}{100 \ N}. \end{aligned}$$

There are sequences that achieve this lower bound, see [199].

Normality can be expressed in terms of uniform distribution modulo 1.

Theorem 7.6.1 (Wall 1949 [578])

A real number x is normal to base b if and only if the sequence (b^j x)_j≥0 is uniformly distributed modulo 1.

The discrepancy modulo 1 of the sequence (b^j x)_j≥0 gives the speed of convergence to normality to base b. Gál and Gál [236] and Philipp [480] proved that for almost all real numbers x, the discrepancy modulo 1 of the sequence (b^j x)_j≥0 is essentially the same and it obeys the law of iterated logarithm up to a constant factor that depends on b. Fukuyama [233] obtained the precise constant factor.

For a real number x, we write {x} = x −⌊x⌋ to denote the fractional part of x.

Theorem 7.6.2 (Fukuyama 2008 [233])

For every real θ > 1, there is a constant C _θ such that for almost all real numbers x (with respect to Lebesgue measure),

$$\displaystyle \begin{aligned} \limsup_{N\to \infty} \frac{D_N( \{\theta^j x\}_{j\geq 0} ) \sqrt{N}}{\sqrt{\log \log N}} = C_\theta. \end{aligned}$$

For instance, in case θ is an integer greater than or equal to 2,

$$\displaystyle \begin{aligned} C_\theta=\left\{ \begin{array}{ll}\medskip \sqrt{84}/9, & \mathit{\text{ if }} \theta=2 \\ \medskip \sqrt{2 (\theta+1)/(\theta-1)}/2, & \mathit{\text{ if }}\theta\mathit{\text{ is odd}} \\ \medskip \sqrt{2(\theta+1)\theta(\theta-2)/(\theta-1)^3}/2, & \mathit{\text{ if }} \theta\geq 4 \mathit{\text{ is even}}. \end{array} \right. \end{aligned}$$

It remains an open problem to establish the minimal discrepancy that can be achieved by a sequence ({b^j x})_j≥0 for some x.

The formulation of normality in terms of uniform distribution modulo 1 has been used in constructions of numbers that are normal to one base and not normal to another, where analytic tools come into play by way of Weyl’s criterion of equidistribution [118, 364]. We give some references in Section 7.8.

7.7 Constructions of Numbers That Are Normal to a Given Base

Copeland and Erdős [166] generalized Champernowne’s construction [141]. They show that for any increasing sequence of integers which does not grow too fast, the concatenation of its terms yields the expansion of a normal number. In particular, one can take the sequence of prime numbers. There are many other generalizations, such as [180, 435].

Other examples of normal numbers are defined by arithmetic constructions, the first ones are due to Stoneham [553] and Korobov [359]. For b, c be relatively prime integers greater than 1, the real numbers

$$\displaystyle \begin{aligned} \alpha_{b,c}=\sum_{n=1}^\infty \frac{1}{c^n b^{c^n}} \end{aligned}$$

are normal to base b. Bailey and Borwein [31] showed that α _2,3 is normal to base 2 but not to base 6. Noticeably, for any given integer base b, Levin [376] gives an arithmetic construction of a real number x, subtler than the series for α _b,c, such that D _N ({bⁿ x}_n≥0)is in $O((\log N)^2/N)$. This is the lowest discrepancy obtained so far, and it is close to the lower bound of $O(\log (N)/N)$ proved by Schmidt for arbitrary sequences (see Section 7.6 above). It is an open question whether there exists a real x for which D _N ({bⁿ x}_n≥0) reaches Schmidt’s general lower bound.

Yet there is a very different kind of construction of expansions of normal numbers, based on combinatorics on words, specifically on de Bruijn words. This is due to Ugalde in [571].

In all the cases, the constructions have the form of an algorithm or can be turned into an algorithm. Recall that a real number x is computable if there is an algorithm that produces the expansion of x in some base, one digit after the other. The algorithm computes in linear time or has linear time complexity if it produces the first n digits in the expansion of x after performing a number of operations that is linear in n. Similarly, we consider polynomial, exponential, or hyper-exponential complexity. Algorithms with exponential complexity cannot run in human time, but algorithms with sub-exponential complexity can. In this monograph we analyze the computational complexity by counting the number of mathematical operations required to output the first k digits of the expansion of the computed number in a designated base. Thus, we do not count how many elementary operations are implied by each of the mathematical operations, which means that we neglect the computational cost of performing arithmetical operations with arbitrary precision.

In this section we present three constructions of real numbers that are insured to be normal to a given base. Since we care about the normality to just one base, we will just construct infinite words in a given alphabet. We first present the simplest possible construction à la Champernowne. Then we present Ugalde’s construction, and we give a much simpler proof than the one in [571]. Finally we present a subtle construction of a normal word which has a self-similarity condition: the whole infinite word is identical to its subsequence at the even positions. This result is due to Becher, Carton, and Heiber (see [50, Theorem 4.2]).

7.7.1 À la Champernowne

Theorem 7.7.1

Let A be an alphabet. Let w _j be the concatenation of all words over A of length j, in lexicographic order. The infinite word w = w ₁ w ₂ w ₃… is normal to alphabet A.

Proof

Let w = w ₁ w ₂ w ₃… = a ₁ a ₂… where each a _i is a symbol in A. Fix N and let n be such that

$$\displaystyle \begin{aligned} \sum_{j=1}^{n} j|A|{}^{j} \leq N < \sum_{j=1}^{n+1} j|A|{}^{j} \end{aligned}$$

Let u be a block of symbols in alphabet A. The occurrences of u in the prefix of w[1..N] are divided into two classes: those that are fully contained in a single block of length i in some w _i and those that overlap several blocks.

$$\displaystyle \begin{aligned} \frac{|a_1 a_2 \ldots a_N|{}_u}{N} & \leq \frac{|a_1 a_2 \ldots a_{x_{n+1}}|{}_u}{n|A|{}^n} \\ & \leq \frac{1}{n|A|{}^n}\left( \sum_{j=|u|}^{n+1}{(j-|u|+1)|A|{}^{j-|u|}} + \sum_{j=1}^{n+1}{(|u|-1)|A|{}^j} \right) \\ & \leq \frac{(n+1)|A|{}^{-|u|}}{n|A|{}^n}\sum_{j=1}^{n+1}{|A|{}^j} + \frac{|u|}{n|A|{}^n} \sum_{j=1}^{n+1}{|A|{}^j} \\ & \leq \frac{(n+1) }{n(|A|-1)} |A|{}^{-|u|} + \frac{|u| |A|{}^2}{n(|A|-1)}. \end{aligned} $$

The first term accounts for occurrences fully contained in a block and the second of for those that overlap several blocks. It follows that

$$\displaystyle \begin{aligned} \limsup_{N\to\infty} \frac{|a_1 a_2 \ldots a_N|{}_u}{N} \le \frac{2}{|A|-1}|A|{}^{-|u|}. \end{aligned}$$

By Lemma 7.4.1, w is normal to alphabet A.

The infinite word w can be computed very efficiently: the first N symbols can be produced in at most O(N) elementary operations. It is also possible to produce just the N-th symbol of w in $O(\log N)$ many elementary operations.

7.7.2 Infinite de Bruijn Words

See [76] for a fine presentation and history of de Bruijn words.

Definition 7.7.2 ([182, 517])

A (noncyclic) de Bruijn word of order n over alphabet A is a word of length |A|ⁿ + n − 1 such that every word of length n occurs in it exactly once.

Every de Bruijn word of order n over A with |A|≥ 3 can be extended to a de Bruijn word of order n + 1. Every de Bruijn word of order n over A with |A| = 2 can not be extended to order n + 1, but it can be extended to order n + 2. See [55] for a complete proof of this fact. This allows us to define infinite de Bruijn words, as follows.

Definition 7.7.3

An infinite de Bruijn word w = a ₁ a ₂… in an alphabet of at least three symbols is an infinite word such that, for every n, $a_1 \ldots a_{|A|{ }^n +n-1}$ is a de Bruijn word of order n. In case the alphabet has two symbols, an infinite de Bruijn word w = a ₁ a ₂… is such that, for every odd n, $a_1 \ldots a_{|A|{ }^n +n-1}$ is a de Bruijn word of order n.

Ugalde [571] was the first to prove that infinite de Bruijn words are normal.

Theorem 7.7.4

Infinite de Bruijn words are normal.

Proof

In case the alphabet A has two symbols, consider instead the words in the alphabet A′ of four symbols obtained by the morphism mapping blocks two symbols in A to one symbol in A′, and prove normality for alphabet A′.

Suppose that the alphabet A has at least 3 symbols. Let x = a ₁ a ₂… be an infinite de Bruijn word over A. Fix a word u of length ℓ and n > |A|^ℓ + ℓ − 1. Then u occurs in a de Bruijn word of order n ≥ ℓ between |A|^n−ℓ and |A|^n−ℓ + n − ℓ times. To see this, observe if u occurs at a position i, for some i such that 1 ≤ i ≤|A|ⁿ, then position i is the beginning of an occurrence of a word of length n. There are exactly |A|^n−ℓ words of length n whose first ℓ symbols are u. In addition, there are exactly n − ℓ other positions in a de Bruijn word of order n at which a subword of length ℓ may start. Since x is infinite de Bruijn, by definition, for each n, $a_1 \ldots a_{|A|{ }^n+n-1}$ is a de Bruijn word or order n. Fix a position N, and let n be such that

$$\displaystyle \begin{aligned} |A|{}^n +n-1 \leq N< |A|{}^{n+1}+n.\end{aligned} $$

Then,

$$\displaystyle \begin{aligned} \frac{ |a_1\ldots a_N|{}_u }{N } \le \frac{ |a_1\ldots a_{|A|{}^{n+1}+n} |{}_u}{ |A|{}^n+n-1 } \le \frac{ |A|{}^{n+1-\ell}+n-\ell }{ |A|{}^n+n-1 } \leq 2\ |A|{}^{-\ell+1}. \end{aligned} $$

Thus,

$$\displaystyle \begin{aligned} \limsup_{N\to\infty}\frac{ |a_1\ldots a_N|{}_u }{N }< 2\ |A|{}^{-\ell+1}. \end{aligned} $$

By Lemma 7.4.1, using C = 2 |A|, x is normal.

There is an obvious algorithm to compute an infinite de Bruijn word which, for each n ≥ 1, extends a Hamiltonian cycle in a de Bruijn graph of order n to an Eulerian cycle in the same graph. This is done in time exponential in n. No efficient algorithm is known to compute the N-th symbol of an infinite de Bruijn word without computing the first N symbols.

7.7.3 A Normal and Self-Similar Word

For a given finite or infinite word x = a ₁ a ₂ a ₃… where each a _i is a symbol in alphabet A, define even(x) = a ₂ a ₄ a ₆⋯ and odd(x) = a ₁ a ₃ a ₅⋯. Thus, x =even(x) means that a _n  = a _2n for all n.

Theorem 7.7.5 ([50, Theorem 4.2])

There is a normal word x such that x =even(x).

We construct a normal word x = a ₁ a ₂ a ₃⋯ over the alphabet {0, 1} such that a _2n = a _n for every n. The construction can be extended to an alphabet of size k to obtain a word a ₁ a ₂ a ₃⋯ such that a _kn  = a _n for each integer n ≥ 1.

A finite word w is called ℓ-perfect for an integer ℓ ≥ 1, if |w| is a multiple of ℓ and all words of length ℓ have the same number |w|/(ℓ2^ℓ) of aligned occurrences in w.

Lemma 7.7.6

Let w be an ℓ-perfect word such that |w| is a multiple of ℓ2^2ℓ . Then, there exists a 2ℓ-perfect word z of length 2|w| such that even(z) = w.

Proof

Since |w| is a multiple of ℓ2^2ℓ and w is ℓ-perfect, for each word u of length ℓ, is a multiple of 2^ℓ. Consider a factorization of w = w ₁ w ₂⋯w _r such that for each i, |w _i | = ℓ. Thus, r = |w|/ℓ. Since w is ℓ-perfect, for any word u of length ℓ, the set {i : w _i  = u} has cardinality r/2^ℓ. Define z of length 2|w| as z = z ₁ z ₂⋯z _r such that for each i, |z _i | = 2ℓ, even(z _i ) = w _i and for all words u and u′ of length ℓ, the set {i : z _i  = u′∨ u} has cardinality r/2^2ℓ. This latter condition is achievable because, for each word u of length ℓ, the set {i :even(z _i ) = u} has cardinality r/2^ℓ which is a multiple of 2^ℓ, the number of possible words u′.

Corollary 7.7.7

Let w be an ℓ-perfect word for some even integer ℓ. Then there exists an ℓ-perfect word z of length 2|w| such that even(z) = w.

Proof

Since w is ℓ-perfect, it is also ℓ/2-perfect. Furthermore, if u and v are words of length ℓ/2 and ℓ, respectively, then . Thus, the hypothesis of Lemma 7.7.6 is fulfilled with ℓ/2.

Corollary 7.7.8

There exist a sequence (w _n )_n≥1 of words and a sequence of positive integers (ℓ _n )_n≥1 such that |w _n | = 2ⁿ , even(w _n+1) = w _n , w _n is ℓ _n -perfect and (ℓ _n )_n≥1 is nondecreasing and unbounded. Furthermore, it can be assumed that w ₁ = 01.

Proof

We start with w ₁ = 01, ℓ ₁ = 1, w ₂ = 1001, and ℓ ₂ = 1. For each n ≥ 2, if $\ell _n2^{2\ell _n}$ divides |w _n |, then ℓ _n+1 = 2ℓ _n and w _n+1 is obtained by Lemma 7.7.6. Otherwise, ℓ _n+1 = ℓ _n and w _n+1 is obtained by Corollary 7.7.7. Note that the former case happens infinitely often, so (ℓ _n )_n≥1 is unbounded. Also note that each ℓ _n is a power of 2.

Proof (of Theorem 7.7.5)

Let (w _n )_n≥1 be a sequence given by Corollary 7.7.8. Let x = 11w ₁ w ₂ w ₃⋯ We first prove that x satisfies x =even(x). Note that x[2^k + 1..2^k+1] = w _k for each k ≥ 1 and x[1..2^k+1] = 11w ₁⋯w _k . The fact that w _n  =even(w _n+1) implies x[2n] = x[n], for every n ≥ 3. The cases for n = 1 and n = 2 hold because x[1..4] = 1101.

We prove that x is normal. Consider an arbitrary index n ₀. By construction, $w_{n_0}$ is $\ell _{n_0}$-perfect, and for each n ≥ n ₀, w _n is also $\ell _{n_0}$-perfect. For every word u of length $\ell _{n_0}$ and for every n ≥ n ₀,

Then, for every N such that 2ⁿ ≤ N < 2ⁿ⁺¹ and n ≥ n ₀,

For large values of N and n such that 2ⁿ ≤ N < 2ⁿ⁺¹, the expression becomes arbitrarily small. We obtain for every word u of length $\ell _{n_0}$,

Since the choice of ${\ell _{n_0}}$ was arbitrary, the above inequality holds for each ℓ _n . Since (ℓ _n )_n≥1 is unbounded, the hypothesis of Lemma 7.4.1 is fulfilled, with C = 3, so we conclude that x is normal.

It is possible to compute a normal word x such that x = even(x) in linear time.

7.8 Constructions of Absolutely Normal Numbers

The first constructions of absolutely normal numbers were given, independently, by Lebesgue [371] and Sierpiński [547], when the theory of computing was undeveloped. The numbers defined by these two constructions cannot be computed because they are just determined as the infimum of a set defined by infinite unions and intersections. The first example of a computable absolutely normal number was given by Turing [52, 570], and, unfortunately, it has doubly exponential time complexity. The computable reformulation of Sierpiński’s construction [51] has also doubly exponential time complexity.

There are exponential algorithms that use analytic tools, such as Levin’s construction [19, 375] of an absolutely normal number with fast convergence to normality and Schmidt’s construction [529] of a number that is normal to all the bases in a prescribed set but not normal to the bases in the complement, see Theorem 7.9.3.

Some years ago, several efficient algorithms were published. Figueira and Nies gave in [222] an algorithm based on martingales with polynomial time complexity. Becher, Heiber, and Slaman [53] reworked Turing’s strategy and obtained an algorithm with just above quadratic time complexity. Madritsch, Scheerer, and Tichy [397] adapted it and obtained an efficient algorithm to compute a number that is normal to all Pisot bases. Recently Lutz and Mayordomo [395] obtained an algorithm based on martingales with poly-logarithmic linear time complexity.

Another aspect in constructions of absolutely normal numbers is the speed of convergence to normality. Aistleitner et al. [8] constructed an absolutely normal real number x, so that for every integer b greater than or equal to 2 the discrepancy modulo 1 of the sequence (bⁿ x)_n≥0 is strictly below that realized by almost all real numbers (see Section 7.6) The construction yields an exponential algorithm that achieves a discrepancy estimate lower than that in Levin’s work [375]. According to Scheerer’s analysis [525], currently there are no other known constructions achieving a smaller discrepancy. The problem of the existence of an absolutely normal number computable with polynomial complexity having fast rate of convergence to normality remains open.

We will present two algorithms, and we will analyze their computational complexity. We first need some notation.

If v is a block of digits in base b, I _v denotes b-ary interval

$$\displaystyle \begin{aligned} (.v, .v + b^{-|v|})\end{aligned} $$

Definition 7.8.1

Let x be a real in the unit interval, and let x _b be its expansion in base b. We define

$$\displaystyle \begin{aligned} \varDelta_{N}(x_b)= \max_{d\in \{1,\dotsc,b\}} \left| \frac{|x_b[1\ldots N]|{}_d}{N} - \frac{1}{b} \right|.\end{aligned} $$

If w is a finite block of digits in base b, we just write Δ(w) instead of Δ _|w|(w).

7.8.1 Turing’s Construction of Absolutely Normal Numbers

Theorem 7.8.2 (Turing 1937? [52, 570])

There is an algorithm that computes the expansion in base 2 of an absolutely normal number y in the unit interval.

The construction is done by steps. We will use n as the step number, and we will define the following functions of n: N _n is the number of digits looked at step n, b _n is the largest base considered at step n, and ε _n is the maximum difference between the expected frequency of digits and the tolerated frequency of digits at step n. It is required that b _n be nondecreasing and unbounded and ε _n be nonincreasing and goes to zero. Many instantiations of these functions can work.

Definition 7.8.3

Define the following functions of n,

$$\displaystyle \begin{aligned} N_n &= 2^{n_0+2n}, \text{where} n_0 = 11, \\ b_n &= \lfloor \log N_n\rfloor \\ \varepsilon_n&= 1/ b_n. \end{aligned} $$

Define the following sets of real numbers,

$$\displaystyle \begin{aligned} E_{0}&=(0,1), \text{ and for each }n \\ E_{n}&= \bigcap_{b\in\{2,.., b_n\}}\{x\in (0,1): \varDelta_{N_n}(x_b)<\varepsilon_n\}.\end{aligned} $$

The value n ₀ has been selected so that the forthcoming calculations are simple. Observe that for every n, b _n  ≥ 2. Thus, for each n the set E _n consists of all the real numbers whose expansion in the bases 2,3, …, b _n exhibit good frequencies of digits in the first N _n digits. We write μ for Lebesgue measure.

Proposition 7.8.4

For each n, E _n is a finite union of open intervals with rational endpoints, E _n+1 ⊂ E _n , and $\mu E_n > 1- N_n^2$.

Proof

The values of N _n and ε _n satisfy the hypotheses of Lemma 7.3.5 with digits in base b (i.e., let k be N _n , let ℓ be 1, and let ε be ε _n ),

$$\displaystyle \begin{aligned} \mu \{x\in (0,1): \varDelta_{N_n}(x_b)\geq \varepsilon_n\} < 2 b^2 e^{-\varepsilon_n^2 b N_n/6.} \end{aligned}$$

Then, for $b_n\leq \log N_n$, $\varepsilon \geq 1/\log N_n$ and N _n  > e¹⁰ can be checked that

$$\displaystyle \begin{aligned} &\sum_{b=2}^{b_n} 2 b^2 e^{-\varepsilon^2 b N_n/6}< 1/N^2_n.\end{aligned} $$

Hence,

$$\displaystyle \begin{aligned}\mu E_n \geq 1 - \sum_{b=2}^{b_n} 2 b^2 e^{-\varepsilon^2 b N_n/6} \geq 1- 1/ N^2_n. \end{aligned}$$

Proposition 7.8.5

The set ⋂_n≥0 E _n has positive measure and consists just of absolutely normal numbers.

Proof

From Proposition 7.8.4 follows that ⋂_n≥0 E _n has positive measure. Suppose x ∈⋂_n≥0 E _n . Then, for every n, x ∈ E _n , so for each b = 2, 3, …, b _n ,

$$\displaystyle \begin{aligned} \varDelta_{N_n}(x_b) \leq \varepsilon_n. \end{aligned}$$

Let b be an arbitrary base, and let M be an arbitrary position. Let n be such that

$$\displaystyle \begin{aligned} N_n\leq M < N_{n+1}. \end{aligned}$$

For each b smaller than b _n we have that for each digit d in {0, …, b − 1},

$$\displaystyle \begin{aligned} \frac{|x_b[1\ldots M]|{}_d}{M} &<& \frac{|x_b[1\ldots N_{n+1}]|{}_d}{N_n} &<& \frac{N_{n+1}}{N_n} \left(\frac{1}{b} +\varepsilon_{n+1}\right) &= &4 \left(\frac{1}{b} +\varepsilon_{n+1}\right) \\ \frac{|x_b[1\ldots M]|{}_d}{M} &>& \frac{|x_b[1\ldots N_n]|{}_d}{N_{n+1}} &>& \frac{N_n}{N_{n+1}} \left(\frac{1}{b} -\varepsilon_{n}\right) &=& \frac{1}{4} \left(\frac{1}{b} -\varepsilon_{n}\right). \end{aligned} $$

Since ε _n is decreasing in n and goes to 0, we conclude that for each base b = 2, 3…,

$$\displaystyle \begin{aligned} \limsup_{N\to \infty} \frac{|x_b[1\ldots N]|{}_d}{N} < 4 \frac{1}{b}. \end{aligned}$$

Using the morphism that maps digits in base b^ℓ to words in base b, this is equivalent to say that for each base b, for every length ℓ, and for every word u of length ℓ,

By Theorem 7.4.1, x is normal to every base b, hence absolutely normal.

Turing’s construction selects nested binary intervals I ₁, I ₂, … such that, for each n, μI _n  = 1/2ⁿ. Each interval I _n+1 is either the left half or the right half of I _n . The base-2 expansion of the computed number y is denoted with the sequences y ₁, y ₂, … which is the trace of the left/right selection at each step. Recall Definition 7.8.3 where the sets E _n are defined, for every n ≥ 0.

• Initial step, n = 0. I ₀ = (0, 1), E ₀ = (0, 1).

• Recursive step, n > 1. Assume that in the previous step we have computed I _n−1.

  Let $I^0_n$ be left half of I _n−1 and $I^1_n$ be right half of I _n−1.

  If $\mu \left (I^0_n \cap \bigcap _{j=0}^n E_j\right ) > 1/N_n$ then let $I_n=I^0_n$ and y _n  = 0.

  Else let $I_n=I^1_n$ and y _n  = 1.

Proof (of Theorem 7.8.2)

From Algorithm 7.8.1 follows that the intervals I ₁, I ₂, … are nested, and for each n, μI _n  = 1/2ⁿ. To prove the correctness of the algorithm, we need to prove that the following condition is invariant along every step n of the algorithm:

$$\displaystyle \begin{aligned} \mu\left(I_n\cap \bigcap_{j=1}^n E_j\right)>0. \end{aligned}$$

We prove it by induction on n. Recall $N_n=2^{n_0+2n}$.

Base case n = 0.

$$\displaystyle \begin{aligned} \mu(I_0 \cap E_0) = \mu((0,1))> \frac{1}{N^2_0} =\frac{ 1}{ 2^{2 n_0}}. \end{aligned}$$

Inductive case, n > 0. Assume as inductive hypothesis that

$$\displaystyle \begin{aligned} \mu\left(I_n\cap \bigcap_{j=0}^n E_j)\right)> \frac{1}{ N_n}. \end{aligned}$$

We now show it holds for n + 1. Recall $\mu E_n>1- 1/N_n^2$. Then,

$$\displaystyle \begin{aligned} \mu\left(I_n \cap \bigcap_{j=0}^{n+1} E_j\right) &= & \mu\left(I_n \cap \bigcap_{j=0}^n E_j \cap E_{n+1} \right) &>& \frac{1}{N_n} - \frac{1}{N_{n+1}^2} &>& \frac{2}{ N_{n+1}}. \end{aligned} $$

Since the algorithm chooses I _n+1 among $I^0_n$ and $I^1_n$ ensuring $\mu ( I_{n+1} \cap \bigcap _{j=0}^{n+1} E_j ) > 1/N_{n+1}$, we conclude $\mu ( I_{n+1} \cap \bigcap _{j=0}^{n+1} E_j ) > 1/N_{n+1}$ as required.

Finally, since (I _n )_n≥0 is a nested sequence of intervals and $\mu (I_n \cap \bigcap _{j=0}^{n} E_j ) > 0$, for every n, we obtain that

$$\displaystyle \begin{aligned} \bigcap_{n\geq 0} I_n = \bigcap_{n\geq 0} \left(I_n\cap \bigcap_{j=0}^n E_j\right). \end{aligned}$$

contains a unique real number y. By Lemma 7.8.5, all the elements in ⋂_j≥0 E _j are absolutely normal. This concludes the proof of Theorem 7.8.2.

We now bound the number of mathematical operations computed by the algorithm to output the first n digits of the expansion of the computed number in a designated base. We do not count how many elementary operations are implied by each of the mathematical operations, which means that we neglect the computational cost of performing arithmetical operations with arbitrary precision.

Proposition 7.8.6

Turing’s algorithm has double exponential time complexity.

Proof

At step n the algorithm computes the set I _n−1 ∩ E _n by computing first the set

$$\displaystyle \begin{aligned} I_{n-1}\cap E_n= \bigcap_{b\in\{2,..,b_n\}}\{x\in I_{n-1}\cap E_{n-1}: \varDelta_{N_n}(x_b)<\varepsilon_n\} \end{aligned}$$

and choosing one of its halves. Then, the number of words to be examined to compute I _n  ∩ E _n is

$$\displaystyle \begin{aligned} (b_n)^{N_{n} - N_{n-1} -(n -1)}. \end{aligned}$$

Since $N_n=2^{n_0+2n}$ and $b_n=\lfloor \log N_n\rfloor$, this number of words is in the order of

$$\displaystyle \begin{aligned} O\big((2n)^{2^{2n}}\big). \end{aligned}$$

The examination of all these words requires $O\big ((2n)^{2^{2n}}\big )$ mathematical operations. We conclude by noticing that using the set I _n  ∩ E _n at step n the algorithm determines the n − th binary digit of the computed number.

7.8.2 A Fast Construction of Absolutely Normal Numbers

We give a simplified version of the algorithm given by Becher, Heiber, and Slaman in [53].

Theorem 7.8.7

There is an algorithm that computes an absolutely normal number x in nearly quadratic time completely: the first n digits in the expansion of x in base 2 are obtained by performing $O\big (n^2 \sqrt [4]{\log n})$ mathematical operations.

The following two lemmas are not hard to prove.

Lemma 7.8.8 ([53, Lemma 3.1])

Let u and v be blocks and let ε be a positive real number.

• 1. If Δ(u) < ε and Δ(v) < ε then Δ(uv) < ε.

• 2. If Δ(u) < ε, v = a ₁…a _|v| and |v|/|u| < ε then Δ(vu) < 2ε, and for every ℓ such that 1 ≤ ℓ ≤|v|, Δ(ua ₁ a ₂…a _ℓ ) < 2ε.

Lemma 7.8.9 (Lemma 3.4 [53])

For any interval I and any base b, there is a b-ary subinterval J such that μJ ≥ μI/(2b).

The next two definitions are the core of the construction.

Definition 7.8.10

A t-sequence $\overrightarrow {\sigma }$ is a sequence of intervals (σ ₂, …, σ _t ) such that for each base b = 2, …, t, σ _b is b-ary,   for each base b = 3, …, t, σ _b  ⊂ σ _b−1 and μσ _b  ≥ μσ _b−1/(2b).

Observe that the definition implies μσ _t  ≥ (μσ ₂)/(2^t t!).

Definition 7.8.11

A t-sequence $\overrightarrow {\tau }=(\tau _2,\dots ,\tau _{t})$ refines a t′-sequence $\overrightarrow {\sigma }=(\sigma _2,\dots ,\sigma _{t'})$ if t′≤ t and τ _b  ⊂ σ _b for each b = 2, …, t′. A refinement has discrepancy less than ε if for each b = 2, ..t′, there are words u, v such that σ _b  = I _u , τ _b  = I _uv , and Δ(v) < ε.

We say that an interval is b-ary of order n if it is of the form

$$\displaystyle \begin{aligned} \left(\frac{a}{b^n},\frac{a+1}{b^n}\right) \end{aligned}$$

for some integer a such that 0 ≤ a < bⁿ. If σ _b and τ _b are b-ary intervals, and τ _b  ⊆ σ _b , we say that the relative order of τ _b with respect to σ _b is the order of τ _b minus the order of σ _b .

Lemma 7.8.12

Let t be an integer greater than or equal to 2, let t′ be equal to t or to t + 1, and let ε be a positive real less than 1/t. Then, any t-sequence $\overrightarrow \sigma =(\sigma _2,\dotsc ,\sigma _t)$ admits a refinement $\overrightarrow \tau = (\tau _2,\dotsc ,\tau _{t'})$ with discrepancy less than ε. The relative order of τ ₂ can be any integer greater than or equal to $\max ( 6/\varepsilon , 24 (\log _2 t) (\log (t!))/ \varepsilon ^2)$.

Proof

First assume t′ = t. We must pick a t-sequence (τ ₂, …, τ _t ) that refines (σ ₂, …, σ _t ) in a zone of low discrepancy. This is possible because the measure of the zones of large discrepancy decreases at an exponential rate in the order of the interval. To prove the lemma, we need to determine the relative order N of τ ₂ such that the measure of the union of the bad zones inside σ ₂ for the bases b = 2, …t is strictly less than the measure of the set all the possible t-ary subintervals τ _t of σ ₂.

Let L be the largest binary subinterval in σ _t . Consider the partition of L in 2^N binary intervals τ ₂ of equal length. For each τ ₂, apply iteratively Lemma 7.8.9 to define $\tau _3, \ldots , \tau _{t_n}$. In this form, we have defined 2^N many t _n -sequences (τ ₂, …τ _t ). Let S be the union of the set of all possible intervals τ _t over these 2^N many t _n -sequences. Hence, by the definition of t-sequence,

$$\displaystyle \begin{aligned} \mu S \geq {\mu L}/(2^t t!). \end{aligned}$$

By Lemma 7.8.9,

$$\displaystyle \begin{aligned}\mu L\geq {\mu\sigma_{t}}/{4}. \end{aligned}$$

And by the definition of t-sequence again,

$$\displaystyle \begin{aligned}\mu \sigma_t \geq {\mu \sigma_2 }/(2^t t!). \end{aligned}$$

Combining inequalities we obtain,

$$\displaystyle \begin{aligned} \mu S\geq \mu\sigma_2/ (2^t t!\ 4 \ 2^t t!) \end{aligned}$$

Now consider the bad zones inside σ ₂. For each b = 2, …t, for a length N and a real value ε, consider the following set of intervals of relative order ⌈N/log₂ b⌉ with respect to σ ₂,

$$\displaystyle \begin{aligned} B_{b, \lceil N/\log_2 b\rceil, \varepsilon } = \bigcup_ {\substack{u\in \{0, \dotsc, b-1\}^{\lceil N/\log_2 b\rceil }\\ \varDelta(u)\geq\varepsilon}} I_u. \end{aligned}$$

Thus, the actual measure of the bad zones is

$$\displaystyle \begin{aligned} \mu\sigma_2 \ \mu \Big(\bigcup_{b=2,..,t} \mu B_{b, \lceil N/\log_2 b\rceil, \varepsilon }\Big) \end{aligned}$$

Then, N must be such that

$$\displaystyle \begin{aligned} \mu \sigma_2 \ \mu \Big(\bigcup_{b=2,..,t} B_{b, \lceil N/\log_2 b\rceil, \varepsilon }\Big) < \mu S. \end{aligned}$$

Using Lemma 7.3.5 on the left and the inequality above for μS on the right it suffices that N be greater than 6/ε and also N be such that

$$\displaystyle \begin{aligned} 2 t^2 \cdot e^{-\varepsilon^2 (N/3\log_2 t) } < \frac{1}{2^{ t} t! } \frac{1}{4} \frac{1}{2^{t} t!}. \end{aligned}$$

We can take N greater than or equal to $\max ( 6/\varepsilon , 24 (\log _2 t) (\log (t!))/ \varepsilon ^2)$.

The case t′ = t + 1 follows easily by taking first a t-sequence $\overrightarrow \tau$ refining $\overrightarrow \sigma$ with discrepancy less than ε. Definition 7.8.11 does not require any discrepancy considerations for τ _t+1. Take τ _t+1 the largest (t + 1)-ary subinterval of τ _t . By Lemma 7.8.9, μτ _t+1 ≥ (μτ _t )/(2(t + 1)). This completes the proof of the lemma.

The algorithm considers three functions of the step number n: t _n is the maximum base to be considered at step n, ε _n is the maximum discrepancy tolerated at step n, and N _n is the number of digits in base 2 added at step n. It is required that t _n be increasing and ε _n be decreasing. Many instantiations of this functions can work.

The algorithm constructs $\overrightarrow {\sigma }_0,\overrightarrow {\sigma }_1,\overrightarrow {\sigma }_2,\ldots$ such that $\overrightarrow {\sigma }_0=(0,1)$, and for each n ≥ 1, $\overrightarrow {\sigma }_n$ is t _n -sequence that refines $\overrightarrow {\sigma }_{n-1}$ with discrepancy ε _n and such that the order of σ _n,2 is N _n plus the order of σ _n−1,2.

Definition 7.8.13

Define the following functions of n,

$$\displaystyle \begin{aligned} t_n &= \max(2, \lfloor \sqrt[4]{\log n} \rfloor ), \\ \varepsilon_n & = 1/ t_n, \\ N_n &= \lfloor \log n\rfloor + n_{start}, \end{aligned} $$

where n _start is the minimum integer such that it validates the condition in Lemma 7.8.12. Thus, we require that for every positive n,

$$\displaystyle \begin{aligned} \lfloor\log n\rfloor + n_{start} &\geq 6/\varepsilon_n\qquad \mbox{ and}\qquad \\ \lfloor \log n\rfloor + n_{start} &\geq 24 (\log_2 t_n) (\log( t_n!))/ \varepsilon_n^2. \end{aligned} $$

• Initial step, n = 1. $\overrightarrow {\sigma }_1=(\sigma _2)$, with σ ₂ = (0, 1).

• Recursive step, n > 1. Assume $\overrightarrow {\sigma }_{n-1} = (\sigma _2, \dots , \sigma _{t_{n-1}})$. Take $\overrightarrow {\sigma }_n =(\tau _2, \dots , \tau _{t_n})$ the leftmost t _n -sequence such that it is refinement of $\overrightarrow {\sigma }_{n-1}$ with discrepancy less than ε _n such that the relative order of τ ₂ is N _n .

Proof (of Theorem 7.8.7)

Consider Algorithm 7.8.2. The existence of the sequence $\overrightarrow {\sigma }_1, \overrightarrow {\sigma }_2, \ldots$ is guaranteed by Lemma 7.8.12. We have to prove that the real number x defined by the intersection of all the intervals in the sequence is absolutely normal. We pick a base b and show that x is simply normal to base b. Let $\tilde \varepsilon > 0$. Choose n ₀ so that $t_{n_0} \geq b$ and $\varepsilon _{n_0}\leq \tilde \varepsilon / 4$. At each step n after n ₀ the expansion of x in base b was constructed by appending blocks u _n such that $\varDelta (u_n)< \varepsilon _{n_0}$. Thus, by Lemma 7.8.8 (item 1) for any n > n ₀,

$$\displaystyle \begin{aligned} \varDelta(u_{n_0} \ldots u_n) < \varepsilon_{n_0}.\end{aligned} $$

Applying Lemma 7.8.8 (item 2a), we obtain n ₁ such that for any n > n ₁

$$\displaystyle \begin{aligned} \varDelta(u_1 \ldots u_n) < 2\varepsilon_{n_0}. \end{aligned}$$

Let $N^{(b)}_n$ be the relative order of τ _b with respect to σ _b . By Lemma 7.8.9,

$$\displaystyle \begin{aligned} \frac{N_n}{ \log_2 b} \leq N^{(b)}_n\leq \frac{N_n +1}{\log_2 b} +1. \end{aligned}$$

Since $N_n=\lfloor \log n\rfloor + n_{start}$, N _n grows logarithmically and so does $N^{(b)}_n$ for each base b. Then, for n sufficiently large,

$$\displaystyle \begin{aligned} N^{(b)}_n \leq \frac{N_n +1}{\log_2 b} +1 \leq 2\varepsilon_{n_0} \sum_{j=1}^{n-1} \frac{N_j}{\log_2 b} \leq 2\varepsilon_{n_0} \sum_{j=1}^{n-1} N^{(b)}_j. \end{aligned}$$

By Lemma 7.8.8 (item 2b), we conclude that for n sufficiently large, if $u_n= a_1\dots a_{|u_n|}$, then for every ℓ such that 1 ≤ ℓ ≤|u _n |,

$$\displaystyle \begin{aligned} \varDelta_{\ell}(u_1 \dots u_{n-1} a_1\dots a_\ell ) <\ 4 \varepsilon_{n_0} < \tilde \varepsilon. \end{aligned}$$

So, x is simply normal to base b for every b ≥ 2.

We now analyze the computational complexity of the algorithm. Lemma 7.8.12 ensures the existence of the wanted t-sequence at each step n. To effectively find it, we proceed as follows. Divide the interval σ ₂ into

$$\displaystyle \begin{aligned} 2^{N_n} \end{aligned}$$

equal binary intervals. In the worst case, for each of them, we need to check if it allocates a t _n -sequence $(\tau _2, \dots , \tau _{t_n})$ that refines $(\sigma _2 \dots , \sigma _{t_{n-1}})$ with discrepancy less than ε _n . Since we are just counting the number of mathematical operations ignoring the precision, at step n the algorithm performs

$$\displaystyle \begin{aligned} O\big( 2^{N_n} t_n\big) \end{aligned}$$

many mathematical operations. Since N _n is logarithmic in n and t _n is a rational power of $\log (n)$, we conclude that at step n the algorithm performs

$$\displaystyle \begin{aligned} O(n \sqrt[4]{\log n}) \end{aligned}$$

mathematical operations. Finally, in the first k steps, the algorithm will output at least k many digits of the binary expansion of the computed number having performed

$$\displaystyle \begin{aligned} O(k^2 \sqrt[4]{\log k}) \end{aligned}$$

many mathematical operations. This completes the proof of Theorem 7.8.7.

7.9 Normality, Non-normality, and Other Mathematical Properties

Recall that two positive integers are multiplicatively dependent if one is a rational power of the other. Then, 2 and 8 are dependent, but 2 and 6 are independent.

Theorem 7.9.1 (Maxfield 1953 [118])

Let b and b′ multiplicatively dependent. For any real number x, x is normal to base b if and only if x is normal to base b′.

Theorem 7.9.2 (Cassels 1959 [135])

Almost all real numbers in the middle third Cantor set (with respect to the uniform measure) are normal to every base which is not a power of 3.

Theorem 7.9.3 (Schmidt 1961 [529])

For any given set S of bases closed under multiplicative dependence, there are real numbers normal to every base in S and not normal to any base in its complement. Furthermore, there is a real x computable from S.

Theorem 7.9.3 was improved in [58] to obtain lack of simple normality for the bases outside S instead of just lack of normality. Then Becher, Bugeaud, and Slaman [49] obtained the necessary and sufficient conditions on a set S for the existence of real numbers simply normal to every base in S and not simply normal to any base in its complement.

Theorem 7.9.4 (Becher, Bugeaud, and Slaman [49])

Let S be a set of bases. There is a real x that is simply normal to exactly the elements in S if and only if

• 1. for each b, if b ^k in S then b in S,

• 2. if infinitely many powers of b belong to S, then all powers of b belong to S.

Moreover, the real x is computable from the set S. Furthermore, the set of real numbers that satisfy this condition has full Hausdorff dimension.

We end the section with references on the relation of normality and Diophantine approximations. The irrationality exponent m of a real number x reflects how well x can be approximated by rational numbers. Precisely, it is the supremum of the set of real numbers z for which the inequality

$$\displaystyle \begin{aligned} 0< \left| x- \frac{p}{q}\right| < \frac{1}{q^z} \end{aligned}$$

is satisfied by an infinite number of integer pairs (p, q) with q > 0. Rational numbers have irrationality exponent equal to 1. Liouville numbers are those with infinite irrationality exponent. It follows from the fundamental work by [347] that almost all irrational numbers (with respect to Lebesgue measure) have irrationality exponent equal to 2. On the other hand, it follows from the theory of continued fractions that for every m greater than 2 or equal to infinity, there is a real number x with irrationality exponent equal to m.

Absolute normality places no restriction on irrationality exponents of irrational numbers. For every real number z greater than or equal to 2, there is an absolutely normal number with irrationality exponent equal to z. This existential result follows from Kaufman [338]. Bugeaud [117] showed there is an absolutely normal Liouville. In both cases, existence of such real numbers follows from the existence of a measure whose Fourier transform vanishes sufficiently quickly at infinity and which is supported by a subset of the real numbers with the appropriate irrationality exponent. Bugeaud’s argument employs an adaptation of Kaufman’s methods to the set of Liouville numbers due to Bluhm [92]. Becher, Heiber, and Slaman [54] exhibit a computable construction of an absolutely number Liouville number.

7.10 Selection

We consider the selection of symbols from an infinite word and define a word with the selected symbols. The general problem is which forms of selection preserve normality, that is, which families of functions f performing selection guarantee that f(x) is normal when x is normal. Notice that if a selection procedure is allowed to read the symbol being decided, it would be possible to “select only zeroes” or yield similar schemes that do not preserve normality.

We consider three forms of selection. Prefix selection looks at just the prefix of length i − 1 to decide whether the symbol at position i is selected. Suffix selection looks at just the suffix starting at position i + 1 to decide whether symbol at position i is selected. Two-sided selection looks at the prefix of length i − 1 and the suffix starting at position i + 1 to decide the selection of the symbol at position i. Prefix selection is the selection defined by Agafonov [6].

Let x = a ₀ a ₁ a ₂⋯ be an infinite word over alphabet A. Let L ⊆ A^∗ be a set of finite words over A and X ⊆ A^ω a set of infinite words over A.

The word obtained by prefix selection of x by L is $x \upharpoonright L = a_{i_0}a_{i_1}a_{i_2}a_{i_3} \cdots$ where i ₀, i ₁, i ₂, ⋯ is the enumeration in increasing order of all the integers i such that a ₀ a ₂⋯a _i−1 ∈ L.

The word obtained by suffix selection of x by X is $x \upharpoonleft X = a_{i_0}a_{i_1}a_{i_2}a_{i_3} \cdots$ where i ₀, i ₁, i ₂, ⋯ is the enumeration in increasing order of all the integers i such that a _i+1 a _i+2 a _i+3⋯ ∈ X.

Theorem 7.10.1 (Agafonov [6])

If x ∈ A^ω is normal and L ⊂ A^∗ is rational then $x \upharpoonright L$ is also normal.

Before giving the proof of Theorem 7.10.1, we discuss some other results. Agafanov’s theorem can be extended to suffix selection by replacing the rational set of finite words L by a rational set of infinite words X. The proof of this theorem is quite technical, so we do not give it here.

Theorem 7.10.2 ([57])

If x ∈ A^ω is normal and X ⊂ A^ω is rational, then $x \upharpoonleft X$ is also normal.

The prefix and suffix selections cannot be combined to preserve normality: in general, two-sided selection does not preserve normality. For instance, selecting all symbols surrounded by two symbols 1 in a normal word over {0, 1} always destroys normality: the factor 11 occurs more frequently than the factor 00 in the resulting word.

We now give three lemmas to be used in the proof of Theorem 7.10.1.

Lemma 7.10.3

For any set of finite words L, the function $x \mapsto \langle x \upharpoonright L,x \upharpoonright A^* \setminus L \rangle$ is one-to-one.

Proof

Let $y_1 = x \upharpoonright L$ and $y_2 = x \upharpoonright A^* \setminus L$. By definition, y ₁ contains some symbols of x, in the same relative order, and y ₂ contains the complement, also in the same relative order. It is possible to reconstruct x by interleaving appropriately the symbols in y ₁ and y ₂. For each i ≥ 1, the i-th symbol of x comes from y ₁ if and only if the prefix of length i of x is in L. Thus, there is a unique x such that $y_1 = x \upharpoonright L$ and $y_2 = x \upharpoonright A^* \setminus L$.

A (deterministic) two-output transducer is like transducer, but it has two output tapes. Each of its transitions has the form where a is the symbol read on the input tape and v and w are the words written to the first and the second output tape, respectively.

An infinite word x = a ₀ a ₁ a ₂⋯ is compressible by a two-output transducer if there is an accepting run that satisfies

$$\displaystyle \begin{aligned} \liminf_{n \to \infty} \frac{(|v_0 v_2 \cdots v_n| + |w_0 w_2 \cdots w_n|)}{n+1}\frac{\log |B|}{\log |A|} < 1. \end{aligned}$$

The following lemma states that an extra output tape does not help for compressing.

Lemma 7.10.4

An infinite word is compressible by a bounded-to-one two-output transducer if and only if it is compressible by a bounded-to-one transducer.

Proof

The “if” part is immediate by not using one of the output tapes.

Suppose that x is compressible by the bounded-to-one two-output transducer $\mathcal {T}_2$. We construct a transducer $\mathcal {T}_1$ with a single output tape which also compresses x. The main idea is to merge the two outputs into the single tape without losing the bounded-to-one assumption. Let m be an integer to be fixed later. The transducer $\mathcal {T}_1$ simulates $\mathcal {T}_2$ on the input and uses two buffers of size m to store the outputs made by $\mathcal {T}_2$. Whenever one of the two buffers is full and contains m symbols, its content is copied to the output tape of $\mathcal {T}_1$ with an additional symbol in front of it. This symbol is either 0 or 1 to indicate whether the m following symbols comes from the first or the second buffer. This trick preserves the bounded-to-one assumption. This additional symbol for each block of size m increases the length of the output by a factor (m + 1)/m. For m large enough, the transducer $\mathcal {T}_1$ also compresses x.

Lemma 7.10.5

Let x = a ₀ a ₁ a ₂⋯ be a normal word, and let be a run in a deterministic automaton. If the state q is visited infinitely often then liminf_n→∞|{i ≤ n : q _i  = q}|/n > 0.

Proof

Let $\mathcal {A}$ be a deterministic automaton. For a state p and a finite word w, the unique state q such that is denoted p ⋅ w.

Let q = q ₁, …, q _n be the states occurring infinitely often in the run. For 1 ≤ i, j len, let u _i,j be a word such that q _i  ⋅ u _i,j = q _j . Let us define the sequence of words (w _k )_1≤k≤n by w ₁ = λ and w _k+1 = w _k u _i,1 where q _k+1 ⋅ w _k  = q _i . By definition, q _k  ⋅ w _k  = q, and thus the finite run visits the state q for each i since w _i is a prefix of w _n . Since the number of occurrences of w _n in x converges to $1/|A|{ }^{|w_n|}$, the result holds.

Proof (of Theorem 7.10.1)

Let x be a normal word. Let L ⊂ A^∗ be a rational language. We suppose by constriction that $x \upharpoonright L$ is not normal, and we show that x can be compressed, contradicting its normality.

Let $\mathcal {A}$ be a deterministic automaton accepting L. This automaton can be turned into a two-output transducer that outputs $x \upharpoonright L$ and $x \upharpoonright A^* \setminus L$ on its first and second output tapes, respectively. Each transition that leaves a final state copies its input symbol to the first output tape, and each transition that leaves a nonfinal state copies its input symbol to the second output tape. By hypothesis, $x \upharpoonright L$ is not normal and therefore can be compressed by some deterministic transducer. Combining, these two transducers yield a two-output transducer that compresses x. This later result holds because, by Lemma 7.10.5, the states that select symbols from x are visited at least linearly often. Then, by Lemma 7.10.4, x can be compressed and is not normal.