Universally Optimal Gathering Under Limited Visibility

Abstract

We consider the distributed setting of N autonomous mobile robots that operate in Look-Compute-Move (LCM) cycles following the well-celebrated classic oblivious robots model. We study the fundamental problem of gathering N autonomous robots on a plane, which requires all robots to meet at a single point (or to position within a small area) that is not known beforehand. We consider limited visibility under which robots are only able to see other robots up to a constant Euclidean distance and focus on the time complexity of gathering by robots under limited visibility. There exists an $\mathcal{O}(D_G)$ time algorithm for this problem in the fully synchronous setting, assuming that the robots agree on one coordinate axis (say North), where $D_G$ is the diameter of the visibility graph of the initial configuration. In this paper, we provide the first $\mathcal{O}(D_E)$ time algorithm for this problem in the asynchronous setting under the same assumption of robots agreement on one coordinate axis, where $D_E$ is the Euclidean distance between farthest-pair of robots in the initial configuration. The runtime of our algorithm is a significant improvement since, for any initial configuration of $N\ge 1$ robots, $D_E\le D_G$, and, there exist initial configurations for which $D_G$ can be as much as quadratic on $D_E$, i.e., $D_G=\varTheta (D_E^2)$. Moreover, our algorithm is universally (time) optimal since the trivial time lower bound for this problem is $\varOmega (D_E)$.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the classic model of distributed computing by mobile robots, each robot is modeled as a point in the plane [15]. The robots are autonomous (no external control), anonymous (no unique identifiers), indistinguishable (no external identifiers), disoriented (no agreement on local coordinate systems and units of distance measures), oblivious (no memory of past computation), and silent (no direct communication and actions are coordinated via only vision and mobility). They execute the same algorithm. Each robot proceeds in Look-Compute-Move (LCM) cycles: When a robot becomes active, it first gets a snapshot of its surroundings (Look), then computes a destination based on the snapshot (Compute), and finally moves towards the destination (Move) [15].

We consider the gathering problem in the classic oblivious robots model, where starting from any arbitrary (yet connected) initial configuration, all robots are required to meet at a single point (or to position within a small area) that is not known beforehand. Gathering is one of the most fundamental tasks and a central benchmark problem in distributed mobile robotics [17]. Early studies on gathering in the classic model solved it under unlimited visibility, where each robot is assumed to see (the locations of) all other robots [3], i.e., all the robots are connected to each other. Flocchini et al. [16] gave the first algorithm for gathering in the classic model under limited visibility, where each robot can see (the locations of) other robots within a fixed unit distance (viewing range) and each robot is connected to all other robots within that fixed unit distance (connectivity range), i.e., the viewing and connectivity ranges are the same. Subsequently, several algorithms were studied for this problem under different constraints [1, 4, 15, 21, 23]. These studies proved the correctness of the algorithms but gave no runtime analysis (except a proof of finite time termination).

The runtime analysis for gathering has been studied relatively recently [8, 10, 11, 14, 18]. Degener et al. [11] gave the first algorithm for this problem with runtime $\mathcal{O}(N^2)$ in expectation in the fully synchronous setting, where N is the total number of robots. Degener et al. [10] gave an $\mathcal{O}(N^2)$-time algorithm for this problem in the fully synchronous setting. Kempkes et al. [18] gave an $\mathcal{O}(OPT \log OPT)$-time algorithm for this problem under a slightly different continuous time setting, where OPT is the runtime of an optimal algorithm. All above algorithms assume that both the viewing and connectivity ranges are of (fixed) radius 1. Recently, Cord-Landwehr et al. [8] gave an $\mathcal{O}(N)$-time algorithm for this problem for robots positioned on a grid in the fully synchronous setting. In this algorithm, it is assumed that robots have the viewing range of (distance) 20, i.e., each robot can see other robots within a fixed distance of 20, but the connectivity range is 1, i.e., two robots are connected if and only if they are vertical or horizontal neighbors on the grid. Moreover, each robot is assumed to have memory to remember a constant number of previous cycles. Recently, Fischer et al. [14] gave an $\mathcal{O}(N^2)$-time algorithm for gathering on a grid in the fully synchronous setting, if the memory is not available, using the improved viewing range of 7.

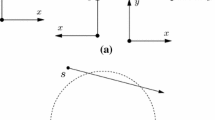
The intriguing open question is whether an universally optimal time algorithm can be designed for gathering under limited visibility, and if possible, under what conditions. We define universal time optimality as follows: Let G be the visibility graph of an arbitrary initial configuration I of $N\ge 1$ robots in a plane. The robots in the system act as nodes of G. There is an edge between any two nodes in G if the distance between these two nodes satisfies the connectivity range. Note that, according to the definitions above, the viewing and connectivity ranges may or may not be the same, and if each robot is connected to all robots within its viewing range, then the viewing range also serves as the connectivity range, otherwise the connectivity range is different than the viewing range. G must be connected otherwise gathering may be unsolvable [15]. G is connected, if the robots (or nodes of G) cannot be separated into two subsets such that no robot of the one subset is connected to any robot of the other subset and vice versa. Let $D_G$ be the diameter of G which is the greatest distance between any pair of nodes in G following the edges of G. Let $D_E$ be the diameter of the initial configuration I, which is the greatest Euclidean distance between any pair of robots in I. Notice that, for any I, $D_E\le D_G$, and for some configurations the gap between $D_G$ and $D_E$ can be as much as quadratic on $D_E$, i.e., $D_G=\varTheta (D_E^2)$. Figure 1 illustrates these ideas. Therefore, an $\mathcal{O}(D_E)$-time algorithm would be universally optimal for gathering, since $\varOmega (D_E)$ is the trivial time lower bound for robots to meet at a single point (or to position within a small area) starting from any arbitrary initial configuration.

Fig. 1.

An illustration of two initial configuration dependent parameters, $D_E$ (the Euclidean diameter) and $D_G$ (the visibility graph diameter), and the relation between them: (left) The diameter $D_E$ for an initial arbitrary configuration, (middle) The visibility graph G with diameter $D_G$ for the configuration of the left, and (right) An initial configuration showing the quadratic difference between $D_E$ and $D_G$ with $D_G = \varTheta (D_E^2)$.

Recently, Izumi et al. [17] presented an $\mathcal{O}(D_G)$-time algorithm for gathering on the plane in the fully synchronous setting under limited visibility with the condition that robots agree on one coordinate axis. They use the viewing range of 1 with an assumption that the visibility graph G is still connected even if the edges with the corresponding distance at least $1-\frac{1}{\sqrt{2}}$ are removed from it. The assumption on the visibility graph G in Izumi et al. [17] essentially means that the connectivity range is of radius $\frac{1}{\sqrt{2}}$ (different and in fact smaller than the viewing range of 1).

There is still a large gap between the $\mathcal{O}(D_G)$ bound of Izumi et al. [17] and the universally optimal $\mathcal{O}(D_E)$ bound, since $D_G$ can be quadratic on $D_E$ (Fig. 1). This work closes this gap under the same one axis agreement with a slightly modified viewing range of $\sqrt{10}$ and the square connectivity range¹ of $\sqrt{2}$ compared to the viewing range of 1 and the (circular) connectivity range of $\frac{1}{\sqrt{2}}$ in [17] (if we consider the viewing range of 1 similar to [17], we need the square connectivity range of $\frac{\sqrt{2}}{\sqrt{10}}$ and our algorithm again achieves $\mathcal{O}(D_E)$ runtime). The square connectivity range of distance c means that a robot is connected to all other robots inside or on the boundary of the (axis-aligned) square area with the (diagonal) distance from the robot to each corner of the square c. Therefore, if we have both the viewing and connectivity ranges of c, then the area they enclose differs if the connectivity range is “square”, otherwise they enclose the same area. Moreover, in contrast to [17] which works in the fully synchronous setting, our algorithm works in the asynchronous setting.

Contributions. We consider autonomous, anonymous, indistinguishable, oblivious, and silent point robots (also called swarms) as in the classic oblivious robots model [15]. Robots agree on the unit of distance measure. The viewing range is $\sqrt{10}$ – a robot can see all other robots within the fixed radius of at most distance $\sqrt{10}$. The square connectivity range is $\sqrt{2}$ – a robot is connected to all other robots inside or on the boundary of the (axis-aligned) $2\times 2$-sized square area whose center is the position of the robot (Definition 1). In a LCM cycle, a robot can move to any position inside or on the square area, including its four corners. The challenge here is that robot movements must not harm the swarm connectivity. As in Izumi et al. [17], we assume that robots agree on one coordinate axis (say North) but they may not agree on the other coordinate axis. Moreover, we assume that the robot setting is asynchronous – there is no notion of common time and robots perform their LCM cycles arbitrarily. Furthermore, we assume that the robot moves are rigid – a robot in motion in each cycle cannot be stopped (by an adversary) before it reaches its destination at that cycle.

In this paper, we prove the following result which, to our best knowledge, is the first algorithm for gathering that is universally (time) optimal for classic oblivious robots under limited visibility since the trivial time lower bound for gathering under limited visibility starting from any initial configuration of $N\ge 1$ robots is $\varOmega (D_E)$.

Theorem 1

For any initial connected configuration of $N\ge 1$ robots with the viewing range $\sqrt{10}$ and the square connectivity range $\sqrt{2}$ on a plane, gathering can be solved in $\mathcal{O}(D_E)$ time in the asynchronous setting, when robots agree on one coordinate axis.

Notice that, the visibility graph G must be connected, since gathering may not be solvable under limited visibility if G is not connected [15, 16]. Our selection of the viewing and (square) connectivity ranges, and the assumption of one-axis agreement play an important role in proving Theorem 1. For both the viewing and (circular or square) connectivity ranges of 1, we conjecture that there is no $\mathcal{O}(D_E)$-time algorithm for gathering of classic oblivious robots, even when robots agree on both the coordinate axes. For the viewing and (circular or square) connectivity ranges of constant ${>}1$, we conjecture that there is no $\mathcal{O}(D_E)$-time algorithm for gathering of classic oblivious robots, if robots do not agree on any coordinate axis.

Comparison to the Previous Runtime Results. In comparison to [8, 10, 11, 14, 18] (described above), our algorithm assumes one-axis agreement but runs in universally optimal $\mathcal{O}(D_E)$ time whereas all those algorithms run in non-optimal $\mathcal{O}(N)$ to $\mathcal{O}(N^2)$ time. [10, 11, 18] have both the viewing and (circular) connectivity ranges of 1 and [8, 14] has the square connectivity range of 1 and the viewing range of 20 (7). Our algorithm has the viewing range of $\sqrt{10}$ and the square connectivity range of $\sqrt{2}$. In comparison to Izumi et al. [17], our algorithm runs in $\mathcal{O}(D_E)$ time whereas their algorithm runs in $\mathcal{O}(D_G)$ time. In contrast to ours, they have the viewing range of 1 and the (circular) connectivity range of $\frac{1}{\sqrt{2}}$. Moreover, all the previous algorithms including Izumi et al. [17] work in the fully synchronous setting, except [11] which works in the one by one activation setting. Our algorithm works in the asynchronous setting. Furthermore, all previous algorithms assume that when two or more robots move to the same location they are merged to be only one robot. Our algorithm does not merge robots, i.e., even if robots located at the same position and activated at different time, the gathering progress is achieved through the (individual) moves of these robots.

Technique. Let L be the topmost horizontal line so that all the robots of any initial configuration I are either on the positions of line L or South from L. Let $L'$ be the line parallel to L at distance 1 South of L. The main idea behind the algorithm is to make robots of I on North of $L'$ move to the positions of $L'$ or South of $L'$ in $\mathcal{O}(1)$ epochs, even under the asynchronous setting, where an epoch is the time interval for all N robots to execute their LCM cycle at least once (formal definition is given in Sect. 2). To accomplish this, we classify the moves of robots into three categories: diagonal hops, horizontal hops, and vertical hops. We will show that if all the robots on North of $L'$ make diagonal or vertical hops, they reach $L'$ or South of $L'$ in 1 epoch. However, if those robots make a horizontal hop, then in 2 epochs, they reach positions of $L'$ or South of $L'$ through the subsequent vertical or diagonal hop.

Similarly, let $L_b$ be the bottommost horizontal line (parallel to L) so that the robots on I are either on $L_b$ or North of $L_b$. The main idea is to show that the robots on $L_b$ do not move South of $L_b$ forever. Specifically, we show that robots on $L_b$ wait for all the robots on North of $L_b$ so that the robots on North of $L_b$ meet the robots of $L_b$ at distance (at most) D South of $L_b$ with D being proportional to the horizontal diameter of the initial configuration I. This has been achieved by asking robots not to make any diagonal, horizontal, or vertical hop, if they see at least a robot on North at vertical distance 1 (or more) from their positions.

Other Related Work. The other related work to ours is [2, 3, 5,6,7, 9, 12, 13, 16, 17, 19, 21, 22]. We omit the discussion due to space constraints.

Roadmap. In Sect. 2 we detail the model and touch on some preliminaries. For simplicity in discussion, we first provide an $\mathcal{O}(D_E)$-time algorithm for robots on a grid agreeing on both the coordinate axes in Sect. 3. We then provide an $\mathcal{O}(D_E)$-algorithm for robots on a plane agreeing on both the coordinate axes in Sect. 4. In Sect. 5, we discuss how the algorithms of Sects. 3 and 4 can be modified to solve gathering when robots agree on only one axis. Finally, we conclude in Sect. 6. Many proofs, pseudocodes, and some figures and details are omitted due to space constraints.

2 Model and Preliminaries

Robots. We consider a distributed system of N robots (agents) from a set $\mathcal{Q}=\{r_0,r_1,\cdots ,r_{N-1}\}$. Each robot is a (dimensionless) point that can move in an infinite 2-dimensional real space $\mathbb {R}^2$. Throughout this paper we will use a point to refer to a robot as well as its position. We denote by $\mathsf{dist}(r_i,r_j)$ the distance between two robots $r_i,r_j\in \mathcal{Q}$. Each robot $r_i$ works under limited visibility and the viewing range² of each robot is $\sqrt{10}$, i.e., a robot $r_i$ can see, and be visible to, another robot $r_j$ if and only if $\mathsf{dist}(r_i,r_j)\le \sqrt{10}$. The connectivity range of each robot is $\sqrt{2}$ following square connectivity, i.e., two robots have an edge between them on G if one robot is inside the (axis-aligned) $2\times 2$-sized square area formed by the other robot being at its center. The robots agree on the unit of distance measure, i.e., the viewing and connectivity ranges of $\sqrt{10}$ and $\sqrt{2}$ are the same for each robot $r_i\in \mathcal{Q}$. The robots also agree on one coordinate axis, North (the assumption of robots agree on East is analogous).

Look-Compute-Move. Each robot $r_i$ is either active or inactive. When a robot $r_i$ becomes active, it performs the “Look-Compute-Move” cycle as follows: (i) Look: For each robot $r_j$ that is within the viewing range of $r_i$, $r_i$ can observe the position of $r_j$ on the plane. Robot $r_i$ also knows its own position; (ii) Compute: In any cycle, robot $r_i$ may perform an arbitrary computation using only the positions observed during the “look” portion of that cycle. This includes determination of a (possibly) new position for $r_i$ for the start of next cycle; and (iii) Move: At the end of the cycle, robot $r_i$ moves to its new position. In the fully synchronous setting ($\mathcal{FSYNC}$), every robot is active in every LCM cycle. In the semi-synchronous setting ($\mathcal{SSYNC}$), at least one robot is active, and over an infinite number of LCM cycles, every robot is active infinitely often. In the asynchronous setting ($\mathcal{ASYNC}$), there is no common notion of time and no assumption is made on the number and frequency of LCM cycles in which a robot can be active. The only guarantee is that every robot is active infinitely often. Complying with the $\mathcal{ASYNC}$ setting, we assume that a robot “wakes up” and performs its Look phase at an instant of time. We also assume that during the Move phase it moves in a straight line and stops only after reaching its destination point, i.e., the moves are rigid [15].

Runtime. For the $\mathcal{FSYNC}$ setting, time is measured in rounds. Since a robot in the $\mathcal{SSYNC}$ and $\mathcal{ASYNC}$ settings could stay inactive for an indeterminate interval of time, we bound a robot’s inactivity and introduce the idea of an epoch to measure runtime. An epoch is the smallest interval of time within which each robot is guaranteed to execute its LCM cycle at least once. Therefore, for the $\mathcal{FSYNC}$ setting, a round is an epoch. We will use the term “time” generally to mean rounds for the $\mathcal{FSYNC}$ setting and epochs for the $\mathcal{SSYNC}$ and $\mathcal{ASYNC}$ settings.

Square Area. Let $r_i\in \mathcal{Q}$ be a robot positioned at coordinate $(x_i,y_i)$. Let $L_i,L_i'$, respectively, be the horizontal and vertical lines passing through $r_i$. Since, $r_i$ knows North, $r_i$ can easily compute $L_i,L_i'$. The square area for $r_i$, denoted as $SQ(r_i)$, is an area of the plane enclosed by four lines $L_{i,t},L_{i,b},L_{i,l},L_{i,r}$ with $L_{i,t},L_{i,b}$ parallel to $L_i$ (perpendicular to $L_i'$) passing through coordinates $(x_i,y_i+1)$ and $(x_i,y_i-1)$, respectively, and $L_{i,l},L_{i,r}$ perpendicular to $L_i$ (parallel to $L_i'$) passing through coordinates $(x_i-1,y_i)$ and $(x_i+1,y_i)$, respectively. Notice that $SQ(r_i)$ is axis-aligned and both height and width of it is 2. We denote by $p_{tl},p_{bl},p_{br},p_{tr}$ the intersection points of lines $L_{i,t}$ and $L_{i,l}$, $L_{i,b}$ and $L_{i,l}$, $L_{i,b}$ and $L_{i,r}$, and $L_{i,t}$ and $L_{i,r}$, respectively. We can divide $SQ(r_i)$ to four quadrant squares $SQ_1(r_i), SQ_2(r_i), SQ_3(r_i), SQ_4(r_i)$ with both height and width 1. Let $SQ_1(r_i),SQ_2(r_i)$ be in North of $L_i$ and $SQ_3(r_i),SQ_4(r_i)$ be in South of $L_i$. Moreover, let $SQ_1(r_i),SQ_3(r_i)$ be in West of $L_i'$ and $SQ_2(r_i),SQ_4(r_i)$ be in East of $L_i'$. We say that positions of $L_i$ in $SQ(r_i)$ belong to $SQ_3(r_i)$ and $SQ_4(r_i)$. Figure in the right illustrates these ideas.

Unit Area. Let $r_j,r_k$, respectively, be the topmost and leftmost robots among the robots in $SQ(r_i)$. In some situations, both $r_j,r_k$ may be the same robot and this definition is still valid. Let $L_T$ be the horizontal line passing through $r_j$ and $L_L$ be the vertical line passing through $r_k$. Let $L_B$ be the horizontal line parallel to $L_T$ passing though distance 1 South of $L_T$. Similarly, let $L_R$ be the vertical line parallel to $L_L$ passing through distance 1 East of $L_L$. The unit area for $r_i$, denoted as $SQ_{unit}(r_i)$, is an area of the plane inside $SQ(r_i)$ enclosed by lines $L_L,L_T,L_R,L_B$. Note that $SQ_{unit}(r_i)$ is an (axis-aligned) unit square of both height and width 1. We denote by $p_{TL},p_{BL},p_{BR},p_{TR}$ the intersection points of lines $L_T$ and $L_L$, $L_B$ and $L_L$, $L_B$ and $L_R$, and $L_T$ and $L_R$, respectively. Figure in the right illustrates these ideas.

Visibility Graph and Gathering Configuration. We define the visibility graph of any initial configuration I and gathering configurations as follows.

Definition 1

(Initial Visibility Graph). The visibility graph $G(I)=(\mathcal{Q},E)$ of any arbitrary initial configuration I of robots is the graph such that, for any two distinct robots $r_i,r_j$, $(r_i,r_j)\in E$ if $r_j$ is positioned on or inside $SQ(r_i)$ (and vice-versa).

$SQ(*)$ provides connectivity for robots with square connectivity range $\sqrt{2}$. The gathering problem may not be solvable under limited visibility, if the initial visibility graph G(I) is not connected [15, 16]. Therefore, we assume that G(I) is connected at time $t=0$ throughout the paper. Moreover, any algorithm for gathering must maintain the connectivity of G(I) during its execution until a gathering configuration is reached. For clarity, we denote by $G_t(I)$ the visibility graph G(I) for any time $t\ge 0$.

Definition 2

(Ideal Gathering Configuration). An ideal gathering configuration is one where all robots are at a single point not known beforehand.

Definition 3

(Relaxed Gathering Configuration). A relaxed gathering configuration is one where all robots are in a horizontal segment of length 1 not known beforehand.

The relaxed gathering configuration (Definition 3) is inspired from the recent work of [8], where they modified the ideal gathering configuration (Definition 2) to solve gathering on a grid by locating all robots within a $2\times 2$-sized square area that is not known beforehand. Definition 3 helps us to circumvent the impossibility results on gathering to a point in the $\mathcal{ASYNC}$ setting [20], even when $N=2$, by gathering the robots in a unit horizontal line segment. Using our square connectivity range $\sqrt{2}$, the viewing range $\sqrt{10}$, and one-axis agreement, even when $N=2$, robots can reach in a unit length horizontal segment. The viewing range helps each robot $r_i$ to see whether there is a robot outside $SQ(r_i)$ and decide whether (at least) Definition 3 is reached. Under both axis agreement, our algorithms provide an ideal gathering configuration (Definition 2). Under one-axis agreement, our algorithms provide a relaxed gathering configuration (Definition 3). Since we focus on runtime, we do not explicitly characterize which configurations do not achieve Definition 2 under one-axis agreement, and simply prove that all the configurations (at least) attain Definition 3 in $\mathcal{O}(D_E)$ time.

3 $\mathcal{O}(D_E)$ Time Algorithm for the Grid

The Grid Model. We define the grid model which is a restriction imposed on the Euclidean plane. The motivation behind designing an algorithm for this model is that it is simple to understand and easy to analyze. We design and analyze an algorithm without the grid restriction in Sect. 4. In the grid model, a robot moves on a 2-dimensional grid and changes its position to one of its eight horizontal, vertical, or diagonal neighboring grid points. Throughout this section, we assume that robots agree on both the coordinate axes and each robot has the viewing range of 2 (measured in $L_1$-distance a.k.a. Manhattan distance). Moreover, each robot has the square connectivity range of 2 (if measured in $L_1$-distance), otherwise it is $\sqrt{2}$ (if measured in Euclidean distance). We say gathering is done when the robot configuration satisfies Definition 2.

The Algorithm. Depending on the positions of other robots within its viewing range, $r_i$ distinguishes diagonal, horizontal, and vertical hops, which we discuss separately below. A robot $r_i$ hops on one of its neighboring grid points based on which diagonal, horizontal or vertical pattern matches the snapshot it takes in the Look phase. Notice that since robots agree on North, $r_i$ never hops on any of the three neighboring grid points on North from its position, i.e., $r_i$ hops only to one of its 5 neighboring grid points on the same horizontal line $L_i$ or on South of $L_i$. We will show that this allows to achieve gathering progress in every epoch. Since robot moves are not instantaneous due to the $\mathcal{ASYNC}$ setting, a robot $r_i$ also does not move if it sees at least a robot on North of $L_i$ inside or on $SQ(r_i)$. This is crucial to guarantee that robots do not move South forever. Robot $r_i$ terminates when it sees no other robot inside or on $SQ(r_i)$ other than its position.

Diagonal Hops. Robot $r_i$ makes a diagonal hop, when it sees no robot in $SQ(r_i)$ on North of $L_i$ (including the positions of $L_i$) and either (i) $r_i$ sees no other robot in $SQ_3(r_i)$ (except at its position) and sees at least one robot on $L_{i,r}$ in South of $L_i$, or (ii) $r_i$ sees no other robot in $SQ_4(r_i)$ (except at its position) and sees at least one robot on $L_{i,l}$ in South of $L_i$. In case (i), $r_i$ hops on the grid point $p_{br}$, whereas in case (ii), on the grid point $p_{bl}$. A diagonal hop makes $r_i$ move $L_1$-distance of 2 although $r_i$ itself moves diagonally distance $\sqrt{2}$. The left two of Fig. 2 illustrate diagonal hops.

Horizontal Hops. A horizontal hop takes $r_i$ to its neighboring grid point on $L_i$ in East. Robot $r_i$ makes a horizontal hop, when it sees no robot in $SQ(r_i)$, except at least a robot $r_j$ on neighboring grid point on $L_i$ in East and possibly on $L_i$ between $r_i$ and $r_j$. Robot $r_i$ hops on that neighboring grid point (i.e., the position of $r_j$). The middle of Fig. 2 illustrates this horizontal hop.

Vertical Hops. A vertical hop always takes $r_i$ to its neighboring grid point vertically South from it. Robot $r_i$ makes a vertical hop, if either (i) it sees a robot $r_j$ on $L_i'$ in South of $L_i$ and no other robot in $SQ(r_i)$ on North of $L_i$ or (ii) it sees at least one robot each on $L_{i,l}$ and $L_{i,r}$ on or South of $L_i$ and no robot in $SQ(r_i)$ on North of $L_i$. The second from right of Fig. 2 illustrates case (i) and the right of Fig. 2 illustrates case (ii).

Fig. 2.

An illustration of diagonal (left two), horizontal (middle) and vertical hops (rest).

Analysis of the Algorithm. We first prove the correctness of the algorithm in the sense that the visibility graph $G_t(I)$ remains connected during execution. We then prove the progress of the algorithm, i.e., in every epoch, any connected initial configuration converges towards an ideal gathering configuration (Definition 2). Let I be any arbitrary initial configuration of robots in $\mathcal{Q}$ on a grid such that $G_0(I)$ is connected. Let SER(I) be the axis-aligned smallest enclosing rectangle for the robots in I. Let $D_Y, D_X$, respectively, be the height and width of SER(I). Let $L_{D_Y},\ldots ,L_{D_0}$ be the horizontal line segments of SER(I) at every 1 unit vertical distance with $L_{D_Y}$ being the topmost horizontal line segment and $L_{D_0}$ being the bottommost horizontal line segment. Similarly, let $L_{D_X},\ldots , L_{0}$ be the vertical line segments of SER(I) at every 1 unit horizontal distance with $L_{D_X}$ being the rightmost vertical line segment and $L_{0}$ being the leftmost vertical line segment. Let $L_Y'$ be the line parallel to $L_{D_0}$ at distance $\frac{D_X}{2}$ South of $L_{D_0}$. Figure 3 illustrates these definitions. Note that The algorithm for Euclidean Plane in both axis agreement (Sect. 4) chooses $L'_Y$ at distance $D_X$ South of $L_{D_0}$.

Lemma 1

Given any initial configuration I such that the visibility graph $G_0(I)$ is connected, the graph $G_t(I)$ at any time $t>0$ remains connected.

Lemma 2

All the robots on the line segment $L_{D_Y}$ of SER(I) move to the line segment $L_{D_{Y-1}}$ in at most 2 epochs.

Fig. 3.

SER(I) and the triangular area on South of it.

The following observation is immediate for vertical hops since a vertical hop by a robot takes it to its neighboring grid point vertically South of it. For a horizontal/diagonal hop, this is also true since a robot doing a horizontal/diagonal hop never finds its neighboring robot outside $L_{D_X}$ and $L_0$.

Observation 1

No robot of SER(I) moves to the positions outside of lines $L_0$ and $L_{D_X}$ during the execution.

Lemma 3

No robot of SER(I) reaches South of horizontal line $L_Y'$ (Fig. 3) during the execution.

Lemma 4

Both the viewing and square connectivity ranges of 2 is sufficient for gathering to a grid point (that is not known beforehand) on a grid under both axis agreement.

The analysis of this section proves the following main result.

Theorem 2

Given any connected configuration of $N\ge 1$ robots with both the viewing and square connectivity ranges of 2 on a grid, the robots can gather to a point in $\mathcal{O}(D_E)$ epochs in the $\mathcal{ASYNC}$ setting under both axis agreement.

Proof

We have from Lemma 1 that $G_t(I)$ remains connected during the execution. We have from Lemma 2 that all the robots at the topmost horizontal line $L_{D_Y}$ of SER(I) move to $L_{D_{Y-1}}$ in at most 2 epochs. After at most 2 epochs, $L_{D_{Y-1}}$ becomes $L_{D_{Y}}$, and Lemma 2 applies again to the robots of $L_{D_{Y-1}}$ which takes all the robots on $L_{D_{Y-1}}$ to $L_{D_{Y-2}}$ or South in next 2 epochs. This situation then continues. Therefore, all the robots in SER(I) move to line $L_{D_0}$ or South in at most $2 D_Y$ epochs. These robots will be in one grid point in at most next $D_X$ epochs, arguing similar to Lemma 2 and observing that for every 1 unit vertical hop of the robots on South of $L_{D_0}$, $D_X$ will decrease by 2, since $L_Y'$ is $D_X/2$ South of $L_{D_0}$. Therefore, the robots can gather in $\mathcal{O}(D_X+D_Y)$ epochs. We have that $\max \{D_X,D_Y\} \le D_E \le \sqrt{2} \cdot \max \{D_X,D_Y\}$ for SER(I) of any initial configuration I. Therefore, $D_X+D_Y \le 2\cdot \max \{D_X,D_Y\}$, and hence $\mathcal{O}(D_X+D_Y)=\mathcal{O}(2\cdot \max \{D_X,D_Y\})=\mathcal{O}(D_E)$. The algorithm terminates (Lemma 4) since if a robot $r_i$ sees no robot in $SQ(r_i)$ other than its current position, then all the robots of $\mathcal{Q}$ must be gathered in the current position of $r_i$ (due to the connectivity guarantee of Lemma 1).    $\square$

4 $\mathcal{O}(D_E)$ Time Algorithm for the Euclidean Plane

We discuss here how to solve gathering in a Euclidean plane, removing the restrictions on robot moves imposed on a grid. The viewing range is $\sqrt{10}$ and the square connectivity range is $\sqrt{2}$ (both measured in the Euclidean distance). The robots agree on both coordinate axes. We say gathering is done when the robot configuration satisfies the ideal gathering configuration (Definition 2).

The Algorithm. Depending on the positions of other robots in its viewing range, a robot $r_i$ can decide to hop on positions of one of its neighboring quadrants $SQ_3(r_i)$ or $SQ_4(r_i)$; we do not allow $r_i$ to move to positions North of $L_i$. In contrast to grid where robots always move either unit distance (horizontal and vertical hops) or distance 2 (diagonal hops), in the Euclidean plane, a robot may move with varying distance of at most 1 for horizontal and vertical hops and varying distance of at most $\sqrt{2}$ for diagonal hops. The main difference (with the grid) is on how robots match patterns to perform diagonal, horizontal, and vertical hops. In contrast to relatively simple matching of patterns on a grid, the matching patterns for the Euclidean plane are significantly complicated.

Overview of the Patterns. The idea is to resemble the patterns for the grid even in the Euclidean plane. For that we ask each robot $r_i$ to compute unit area $SQ_{unit}(r_i)$ as defined in Sect. 2. $SQ_{unit}(r_i)$ helps $r_i$ to decide whether to make a diagonal, horizontal, or vertical hop. If the robots in $SQ_{unit}(r_i)$ are not connected to any other robot outside of $SQ_{unit}(r_i)$ in West of $L_R$ (in East of $L_L$), then $r_i$ make a horizontal hop to East (West). If $r_i$ satisfies the conditions for a horizontal hop, except that there is a robot on point $p_{BR}$ (or $p_{BL}$) and the robots in $SQ_{unit}(r_i)$ are in a single diagonal line, then it makes a diagonal hop to $p_{BR}$ (or $p_{BL}$). If the robots in $SQ_{unit}(r_i)$ are not connected to any other robot outside of $SQ_{unit}(r_i)$ in North of $L_B$, but (at least) a robot in $SQ_{unit}(r_i)$ is connected to a robot on or South of $L_B$, then $r_i$ makes a vertical hop. In other words, if $r_i$ sees itself or at least a robot in $SQ_{unit}(r_i)$ is connected to a robot on North of $L_T$, it does not move. This guarantees that robots do not move South forever. Also, if $r_i$ sees at least one robot each on its both sides (East and West) at horizontal distance $\ge$2, then it makes a vertical hop. The termination is guaranteed by asking $r_i$ to check in every LCM cycle whether all robots in its viewing range are positioned in $SQ_{unit}(r_i)$ (that is, $r_i$ sees no robot outside $SQ_{unit}(r_i)$). When that is the case, $r_i$ and the remaining robots in $SQ_{unit}(r_i)$ run a special procedure to reach a single point (Definition 2) and terminate their computation. Reaching to a single point is facilitated for robots by both axis agreement.

Detailed Description of the Patterns. We provide details of the patterns below. Robot $r_i$ terminates when it sees no other robot in $SQ(r_i)$, except on its current position.

Diagonal Hops. Robot $r_i$ makes a diagonal hop in either of the following conditions:

• This case is similar to grid. If $r_i$ sees no other robot in $SQ(r_i)$ except at least a robot $r_j$ in $SQ_4(r_i)$ on the diagonal corner point $p_{br}$, $r_i$ hops to $p_{br}$. Robot $r_i$ moves distance exactly $\sqrt{2}$ if it performs this hop.

• Robot $r_i$ hops diagonally distance $\sqrt{2}-L_{ij}$ (where $L_{ij}$ is the distance between $r_i$ and $r_j$, the topmost robot at point $p_{TL}$ which is also the leftmost) to a point in $SQ_4(r_i)$, if the following conditions satisfy:

  • No robot in $SQ_{unit}(r_i)$ is connected to any other robot in North of $L_T$.

  • No robot in $SQ_{unit}(r_i)$ is connected to any other robot in West of $L_R$, except the robots in $SQ_{unit}(r_i)$.

  • All robots in $SQ_{unit}(r_i)$ are in its diagonal line that passes through $SQ_4(r_i)$.

  • There is at least a robot on the diagonal point $p_{BR}$ of $SQ_{unit}(r_i)$.

Figure 4 (left) illustrates this hop for $r_i$. The symmetric diagonal case moves $r_i$ to point $p_{BL}$ which is illustrated in Fig. 4 (middle).

Fig. 4.

An illustration of diagonal hops (left and middle) and a horizontal hop (right).

Remarks. If there is at least a robot on $L_R$ (but not on $L_B$, including point $p_{BR}$) of $SQ_{unit}(r_i)$, then $r_i$ makes a horizontal hop (described in the next paragraph), even though all the robots in $SQ(r_i)$ are in its diagonal line passing through $SQ_4(r_i)$. If there is at least a robot on $L_B$ between points $p_{BR}$ and $p_{BL}$, then $r_i$ makes a vertical hop (described later), irrespective of the robots on $L_R$. If any robot in $SQ_{unit}(r_i)$ is connected to any other robot on South of $L_B$ and West of $L_R$, $r_i$ also makes a vertical hop (described later), irrespective of the robots on $L_R$. The analogous conditions apply for the symmetric diagonal hop case shown in Fig. 4 (middle) for $r_i$.

Horizontal Hops. Robot $r_i$ makes a horizontal hop in the following conditions:

• This case is similar to the grid. If $r_i$ sees a robot $r_j$ in its East at distance 1 on line $L_i$ and there is no robot in $SQ(r_i)$, except the current position of $r_i$ and possibly on $L_i$ from $r_i$ up to $r_j$, $r_i$ hops to the position of $r_j$ (distance 1).

• Robot $r_i$ hops horizontally East on $L_i$ distance $1-L_{ik}$ ($L_{ik}$ is the distance between $r_i$ and $r_k$, the leftmost robot in $SQ(r_i)$), if all the following conditions satisfy (Fig. 4 (right) illustrates this hop for $r_i$):

  • No robot in $SQ_{unit}(r_i)$ is connected to any other robot in North of $L_T$.

  • No robot in $SQ_{unit}(r_i)$ is connected to any other robot on West of $L_R$, except the robots in $SQ_{unit}(r_i)$.

  • There is no robot on $L_B$ of $SQ_{unit}(r_i)$.

Since we ask robots to always move East in a horizontal hop, we do not have a symmetric case for horizontal hops under both axis agreement.

Fig. 5.

An illustration of vertical hops

Vertical Hops. If no robot in $SQ_{unit}(r_i)$ is connected to any other robot in North of $L_{i,t}$ (of $SQ(r_i)$), robot $r_i$ makes a vertical hop distance $1-L_{ij}$ (where $L_{ij}$ is the vertical distance from $r_i$ to line $L_T$) in either of the following conditions:

• Robot $r_i$ sees at least one robot at the intersection point of $L'_i$ and $L_B$.

• Robot $r_i$ sees at least one robot each in both East and West at horizontal distance $\ge$2. Figure 5 (middle) illustrates this case.

• Robot $r_i$ sees at least a robot on $L_B$ of $SQ_{unit}(r_i)$, no robot in $SQ_{unit}(r_i)$ is connected to any other robot in North of $L_B$ and West of $L_L$, and the diagonal hop is not satisfied for $r_i$. Figure 5 (left) illustrates this case.

• Robot $r_i$ sees at least one robot in $SQ_{unit}(r_i)$ that is connected to a robot in South of $L_B$ on or West of $L_R$ and no robot in $SQ_{unit}(r_i)$ is connected to any other robot in North of $L_B$ and West of $L_L$. Figure 5 (left) also illustrates this case.

• Let $SP_{unit}(r_i)$ be a unit area in West of $L_{i,l}$ and South of $L_B$ with $L_B$ being the topmost horizontal line $L_T$ of $SP_{unit}(r_i)$ and $L_{i,l}$ being the rightmost vertical line $L_R$ of $SP_{unit}(r_i)$. Robot $r_i$ sees at least a robot in $SQ_{unit}(r_i)$ is connected to a robot in North of $L_B$ and West of $L_L$, $r_i$ sees at least a robot in $SP_{unit}(r_i)$, and a horizontal hop is not satisfied. Figure 5 (right) illustrates this case.

Remarks. Robot $r_i$ also makes a vertical hop if the symmetric situations on last 3 conditions are satisfied. The above rules infer that the robots move only under certain situations. Robots do not move in all the remaining situations. This process repeats until all robots of $\mathcal{Q}$ are inside an (axis-aligned) $1\times 1$-sized square area so that special procedure for termination, as described in the next paragraph, can be applied.

The Termination Procedure. We will show in the analysis that the diagonal, horizontal, and vertical hops described above position all robots in $\mathcal{Q}$ in an (axis-aligned) $1\times 1$-sized square area, say SA. We now discuss how the robots reach to a point and terminate. Let $r_l,r_b,r_r$ be the leftmost, bottommost, and rightmost robots in SA. We have that the unit area $SQ_{unit}(r_i)$ of each robot $r_i$ that is in SA overlaps. Therefore, if all the robots in SA are in a single diagonal line, then $r_b$ does not move and all other robots in SA make a diagonal hop with destination the current position of $r_b$. Otherwise, robots first perform a horizontal hop as destination point the positions on the right vertical line $L_R$ of SA. The robots on $L_R$ do not move until all the robots in SA (the same for all robots) are positioned on $L_R$. After that, the robots (now on $L_R$) perform a vertical hop as destination the bottommost robot on $L_R$, which does not move.

Analysis of the Algorithm. We first prove correctness and then progress guarantee of the algorithm. We use SER(I) and other definitions as in Sect. 3.

Lemma 5

Given that $G_0(I)$ is connected, the visibility graph $G_t(I)$ at any time $t>0$ remains connected.

Lemma 6

All the robots on North of $L_{D_{Y-1}}$ in SER(I) move to the positions on $L_{D_{Y-1}}$ or South of $L_{D_{Y-1}}$ in at most 2 epochs.

The following observation is again immediate since the robots never make a horizontal hop to West and the robots making the horizontal hops never reach East of $L_{D_X}$.

Observation 2

No robot of SER(I) move outside of lines $L_0$ and $L_{D_X}$ during the execution.

Lemma 7

No robots of SER(I) reaches South of $L_{Y}'$ during the execution.

Observation 3

For every vertical hop of the robots in $\mathcal{Q}$ on South of $L_{D_0}$, $D_X$ decreases by (at least) 1.

We have the following observation after all the robots in the viewing range of a robot $r_i\in \mathcal{Q}$ are positioned in an (axis-aligned) $1\times 1$-sized square area SA.

Observation 4

The robots within an (axis-aligned) $1\times 1$-sized square area SA are positioned at a single point in at most 2 epochs.

Lemma 8

The viewing range of $\sqrt{10}$ is sufficient for gathering to a point (that is not known beforehand) on a plane under both axis agreement.

The analysis of this section proves the following main result.

Theorem 3

Given any connected configuration of $N\ge 1$ robots with the viewing range of $\sqrt{10}$ and the square connectivity range of $\sqrt{2}$ on a plane, the robots can gather to a point in $\mathcal{O}(D_E)$ epochs in the $\mathcal{ASYNC}$ setting under both axis agreement.

5 Gathering Under One-Axis Agreement

We discuss modifying the above algorithms when robots agree on only one axis.

Grid. We can prove the following theorem for the grid. The details are omitted.

Theorem 4

Given any connected configuration of $N\ge 1$ robots with the viewing range of 3 and the square connectivity range of 2 on a grid, the robots can gather in a unit length horizontal line segment (that is not known beforehand) in $\mathcal{O}(D_E)$ epochs in the $\mathcal{ASYNC}$ setting under one-axis agreement.

Euclidean Plane. We first discuss changes in the model of Sect. 4. We say gathering is done when the configuration satisfies the relaxed gathering configuration (Definition 3). The viewing and square connectivity ranges remain the same as in Sect. 4.

We now discuss changes in the algorithm. The change is on horizontal and vertical hops, and on termination. Instead of computing $SQ_{unit}(r_i)$ using $L_L$ and $L_T$ as reference lines, $SQ_{unit}(r_i)$ also needs to be computed using $L_R$ and $L_T$ as references. When $r_i$ sees no other robot in one side (say West) at distance >1 but in other side (East), it takes the topmost robot $r_j$ and leftmost robot $r_k$ in $SQ(r_i)$ to compute $SQ_{unit}(r_i)$ and for the symmetric case, it takes the topmost and rightmost robots in $SQ(r_i)$ as reference. This allows the robots to make horizontal hops in both directions (not necessarily only East under both axis agreement). Therefore, $r_i$ hops to West of $L_i$ if the conditions for horizontal hop defined in Sect. 4 are satisfied symmetrically for it to hop to West. Regarding vertical hop, the following changes are made in the last three conditions:

• Robot $r_i$ sees at least one other robot each on both sides of $L'_i$ on $L_B$ or South of $L_B$ which are connected to at least one robot of $SQ_{unit}(r_i)$.

• Robot $r_i$ sees at least one other robot on $L_B$ or South of $L_B$ (which is connected $SQ_{unit}(r_i)$) in one side of $L'_i$ (say East) and at least one other robot at horizontal distance $\ge$2 in other side (West) (and vice-versa).

• Robot $r_i$ sees other robot(s) on $L_B$ (or connected to other robot(s) in South of $L_B$) only in one side of $L'_i$, say East, then finds the leftmost robot $r_l$ on $L_B$ of $SQ_{unit}(r_i)$ ( or South of $L_B$ that is connected to $SQ_{unit}(r_i)$) and sees no robot in $SQ_{unit}(r_i)$ is connected to other robot in left (i.e. West) at horizontal distance $\ge$1 from $r_l$ (and vice-versa).

Regarding termination, $r_i$ terminates if all the robots it sees within its viewing range (including itself) are within a horizontal line segment of length (at most) 1. We will show in the analysis that, with these changes, the algorithm positions the robots in $\mathcal{Q}$ inside an axis-aligned $1\times 1$-sized square area SA in $\mathcal{O}(D_E)$ epochs.

We now discuss how the robots in SA reach a relaxed gathering configuration (Definition 3). Let $r_b$ be the bottommost robot in SA (if more than one, pick one arbitrarily). Let $L_B$ be the horizontal line passing through $r_b$. The robots on $L_B$ (including $r_b$) do not move. The other robots move vertically to the positions of $L_B$. The viewing range allows the robots to decide whether there are robots outside SA or not.

Theorem 5

Given any connected configuration of $N\ge 1$ robots with the viewing range of $\sqrt{10}$ and the square connectivity range of $\sqrt{2}$ on a plane, the robots can gather in a unit length horizontal line segment (that is not known beforehand) in $\mathcal{O}(D_E)$ epochs in the $\mathcal{ASYNC}$ setting under one-axis agreement.

Proof of Theorem 1: Theorem 5 proves Theorem 1.

6 Concluding Remarks

We have presented, to our knowledge, the first universally optimal $\mathcal{O}(D_E)$-time algorithm for gathering $N\ge 1$ classic oblivious robots in a plane in the $\mathcal{ASYNC}$ setting under limited visibility, improving significantly on the previous $\mathcal{O}(D_G)$-time algorithm of [17] that works in the $\mathcal{FSYNC}$ setting. Our result assumes the viewing range of $\sqrt{10}$, the square connectivity range of $\sqrt{2}$, and the agreement on one axis. This is in contrast to the viewing range of 1 and the (circular) connectivity range of $\frac{1}{\sqrt{2}}$ in [17] under the same one axis agreement. For future work, it will be interesting to relax our assumption of rigid moves to accommodate non-rigid moves.

It will also be interesting to reduce the gap between the connectivity and viewing ranges, without affecting time.