A Probabilistic Learning Algorithm for the Shortest Path Problem

Abstract

Ant colony optimization (ACO) has been shown effectiveness for solving combinatorial optimization problems. Inspired by the basic principles of ACO, this paper proposes a novel evolutionary algorithm, called probabilistic learning (PL). In the algorithm, a probability matrix is created based on weighted information of the population and a novel random search operator is proposed to adapt the PL to dynamic environments. The algorithm is tested on the shortest path problem (SPP) in both static and dynamic environments. Experimental results on a set of carefully designed 3D-problems show that the PL algorithm is effective for solve SPPs and outperforms several popular ACO variants.

1 Introduction

The shortest path problem (SPP) is a classical combinatorial optimization problem. In this paper, the problem is defined as follows. Given a graph of a set of nodes linked by directed edges, where each node is connected with eight neighbour nodes, the aim is to find the shortest path from a starting point to a destination point. It is a simple problem and has been widely applied in many applications, e.g., robot routing problem, the shortest path in games, the shortest traffic route, etc.

The Dijkstra algorithm is widely used to find the shortest path in a completely known environment. However, when the environment is partially known, unknown or changing, the Dijkstra algorithm seems unsuitable to solve this problem. To overcome these limitations, many heuristic approaches have been used to address this problem, such as ant colony optimization (ACO).

Inspired by ACO, this paper proposes a novel probabilistic algorithm, namely probabilistic learning (PL), for the SPP. A probabilistic matrix is created and updated according to weighted values of historical solutions. Each element in the matrix denotes the probability of an edge to be chosen. Different from ACO, PL neither follows the basic operations of ACO nor uses any geographical heuristic. An efficient random search operator is proposed to maintain the population diversity. The proposed algorithm is competitive in comparison with several ACO algorithms on the SPP.

The rest of this paper is organized as follows. Section 2 gives a brief review of related work. Section 3 describes the proposed algorithm in detail. Section 4 presents experimental results and discussions. Finally, conclusions and future work are discussed in Sect. 5.

2 Related Work

There are many research branches for combinatorial optimization problems. However, in this section, we mainly focus on the methods related to ACO. ACO simulates the foraging behavior of real ants for finding the shortest path from a food source to their nest by exploiting pheromone information. While walking, ants deposit pheromone chemicals, and follow, in probability, pheromone previously deposited by other ants.

Ant system (AS) [8] was the first ACO model proposed by Dorigo, and it has gained huge success. In order to simulate the foraging behavior, each ant chooses its next node by:

$$\begin{aligned} p_{ij}^k(t)=\left\{ \begin{array}{l}\frac{\left[ \tau _{ij}(t)\right] ^\alpha \left[ \eta _{ij}\right] ^\beta }{\sum _{l\in U}\left[ \tau _{ij}(t)\right] ^\alpha \left[ \eta _{ij}\right] ^\beta }\quad \; j\in U \\ 0\qquad \qquad \qquad \quad \quad j\not \in U, \end{array}\right. \end{aligned}$$

(1)

where $p_{ij}^k(t)$ means the possibility of ant k moves from node i to node j. If ant k has visited node j, $p_{ij}^k(t)$ will be 0; otherwise, the ant will probabilistically choose a candidate node. $\tau _{ij}$ means the pheromone intensity of edge (i,j). $\eta _{ij}$ means the visibility of edge (i,j), which equals to the reciprocal of the length of this edge. $\alpha$ is the weight of pheromone and $\beta$ is the weight of the visibility. After all ants reach the food point, the pheromone matrix is updated by:

$$\begin{aligned} \tau _{ij}\left( t+1\right) =\rho *\tau _{ij}\left( t\right) +\sum _{k=1}^m\Delta \tau _{ij}^k \left( t\right) , \end{aligned}$$

(2)

where m is the number of ants, and $\rho$ means the persistence of pheromone. After this update, all ants go back to the start point and repeat the above procedures until the algorithm stops.

AS has a strong ability in searching good solutions. However, it has shortcomings: the slow convergence speed and the stagnation issue. Inspired by the selection principle of genetic algorithms, an elitist AS (EAS) [2] was developed. Compared to AS, EAS takes an ant which performs best as an “elitist”, and it leaves more pheromone than other ants. As a result, ants are more likely to choose the elitist path.

The ant colony system (ACS) [7] was proposed based on Ant-Q (AS with Q-learning) [6]. ACS provides two ways to update global pheromone: the local online update and the global offline update. The local online update is used after every ant moves a step, which means the pheromone of the map changes synchronously. On the other hand, the global offline update is used when all ants reach the food point, then the best ant is chosen to update the global pheromone. ACS is quick and it can obtain good solutions, but it is not stable.

A rank-based AS (RAS) [1] was proposed by sorting ants based on route lengths. Like EAS, ants with high rank leave more pheromone than the others as follows. RAS is more likely to find a better solution than EAS, but its convergence speed is slower than EAS. A min-max AS (MMAS) [12] was proposed. The amount of the pheromone of each edge is constrained within a range. Also, like EAS, only the ant with best performance can leave pheromone on its route. The rules of the node selection and pheromone update are the same as in EAS, except that it keeps the pheromone level in a dynamic range. A best-worst AS (BWAS) [3] was proposed where it rewards the best ant and punishes the worst one. In each generation, BWAS increases the pheromone level on the best ant’s route and decreases the pheromone level of the worst route.

Recently, many other improvements for ACO have been proposed, such as ant colony system with a cooperative learning approach [7], a hybrid method combining ACO with beam search (Beam-ACO) [9], parallel ant colony optimization (PQACO) [15], a hybrid PS-ACO algorithm with the hybridization of the PSO [11], a novel two-stage hybrid swarm intelligence optimization algorithm [4], cooperative genetic ant systems [5], ACO with new fast opposite gradient search [10], advanced harmony search with ACO [16], and so on.

3 The Proposed Method

This section will introduce the PL algorithm in detail. Before the introduction of PL, we first describe the problem to be solved in this paper in a game scenario.

3.1 The Map for the SPP

Figure 1-a shows a game map, which is discretized into a grid shown in Fig. 1-b where each cross point in the grid is represented by a two dimensional integer coordinate (i, j). The color of the point stands for its height from the highest (red color) to the lowest (purple color). The yellow point at the left bottom corner is the home point, and the red point at the right top corner is the food point. The dotted path obtained is the shortest path from the home point to the food point. Figure 1-c shows a blue path, which constructed by an ant. Figure 1-d shows 3D ants moving on the map in the game, where an ant can only be placed on a cross point. Note that, an ant is only allowed to visit its 8-neighborhood points of the point where it is.

Fig. 1.

An example of a 3D problem, where the dotted path is the shortest path from the home point to the food source labelled by the yellow point at the left bottom corner and the red point at the right top corner, respectively. (Color figure online)

3.2 Probabilistic Learning

In this paper, a population consists of a set of solutions constructed by ants from the home point to the food point. This paper introduces a probability matrix (PM) to learn promising edges found by ants. The idea of the PM was initially proposed in [13] and recently updated in [14] for solving the travelling sales problem. Each item in the PM denotes the probability of each edge to be chosen during the construction of a path. In this paper, we build the PM using a different strategy used in [14] to adapt it to the SPP.

In the SPP, each ant can only visit its 8-neighborhood points and the ant is allowed to revisit a point. A randomly constructed path may contain many loops. We need to design a method to avoid these loops to obtain an effective path.

The Probabilistic Matrix. An element in the PM indicates the frequency of an edge visited by ants. Initially, ants randomly construct their paths since there is no information in the PM. Each ant keeps its historical best path so far and update it once the ant finds a better path. Correspondingly, the PM will be also updated.

The PM in fact reflects the learning process as the evolutionary process goes on: (1) The number of good edges in a particular solution increases; (2) The frequency of appearance of a particular good edge increases in the population.

To implement the above idea, we assume that the shorter the path, the better the solution. So we use the length of a solution to evaluate its fitness. The fitness of a solution is obtained by:

$$\begin{aligned} F_i = \frac{L^{max}-L^i+1}{L^{max}-L^{min}+1} \end{aligned}$$

(3)

where $F_i$ is the fitness of the ith solution, $L^{max}$ and $L^{min}$ are the maximum and the minimum length of all the solutions, respectively. We assign each ant i a weight $W_i$ based on its historical best solution as follow:

$$\begin{aligned} W_i = \frac{1}{1+\mathrm {e}^{-F_i}}, \end{aligned}$$

(4)

The higher value of the fitness, the higher value of the weight. Finally, we compute each element $p_{ij}$ of the matrix as follows:

$$\begin{aligned} p_{ij}=\sum _{k=1}^{PS}W_k*o_{ij}/\sum _{k=1}^{PS}W_k, o_{ij}=\left\{ \begin{array}{l}1,edge(i,j)\in best\_path^k\\ 0,else\end{array}\right. \end{aligned}$$

(5)

where $p_{ij}$ means the possibility of each ant moves from node i to node j, PS is the population size and $best\_route^k$ is the historical best path of ant k.

3.3 Probabilistic Learning Algorithm

The framework of the PL algorithm is presented in Algorithm 1. An archive population is utilized to store the historical best solution of each ant. For each generation, a solution is constructed from the home point to the food point either by the PM or by Algorithm 2 (introduced later) depending on a probability $\rho$. After all ants obtain a valid path, the PM will be updated according to each ant’s historical best solution.

Random Search Operator. Although an ant is able to construct a solution based on the PM, it cannot produce new edges. So we need to find an effective random search operator to maintain the population diversity. The aim is also to adapt PL to dynamic environments by using the diversity maintaining schemes as follows.

In this paper, we design two rules for an ant to efficiently construct a random path from the start point to the end point: (1) Each ant always head to the end point, which helps it avoid loops on its path. To achieve this, we suppose that each ant know the position of the end point; (2) The ant walks toward a fix direction for several steps unless it comes across a visited node, where a step means an ant moves to one of its 8-neighborhood points. A random direction is chosen from a set of neighbourhood nodes if $\overrightarrow{N_cN_e}\cdot \overrightarrow{N_cN_d} \ge 0$, where $N_c$, $N_e$, and $N_d$ are positions of the current, ending, and next nodes, respective. An ant sometime might not be able to move forward since all its neighborhood points have been visited. In this case, we allow the ant to reconstruct its path.

Using these rules, this paper introduces a new random search operator to construct an effective path. Algorithm 2 presents the procedures for constructing a new solution. It works as follows. Each ant re-starts from the start point. It randomly select a feasible direction which heads to the end point and selects a random step between 1 and the maximum number between the height and the width of a map. It will change its direction if the next point has been visited. The process is repeated until it reaches the end point.

Local Distance Matrix. Although we can construct an effective path by Algorithm 2, the path may not always get improved since it is randomly created. To fully use the information we get during the random searching process, this paper introduces a matrix for each ant to remember the current shortest distance from each point in the map to the end point, and we will update the matrix DM whenever a shorter path is found.

Adaptation of Parameter $\varvec{\rho }$. In the beginning of the search, all ants randomly construct solutions, and learning too much from the PM may not benefit the search. As the run goes on, the population will improve as the number of good edges increases, and it will be helpful to increase the probability of learning from the PM. In this paper, we adaptively adjust $\rho$ by the equation below:

$$\begin{aligned} \rho = \frac{S}{T}*\theta \end{aligned}$$

(6)

where S is the total number of the points of the best paths found so far by all ants and T is the total number of points which appear in all the historical best paths found by all ants. $\theta$ is used to set the lowest possibility of random search.

4 Experimental Studies

Performance comparison between the proposed algorithm and several ACO variants is conducted on a set of 3D problems in this section.

Fig. 2.

The 3D maps for all the problems

4.1 Test Problems

To test the performance of an algorithm in a game scenario, we have carefully designed a set of 3D maps to simulate real-world environments. Figure 2 shows 15 test problems. We divide these test problems into two groups: asymmetrical and symmetrical. The difficulty of a problem mainly depends on the number of curve segments and the degree of the curvature of curve segments on the shortest path. The asymmetrical problems P00 and P01 have only one global optimum. P01 is more difficult than P00 due to the steep terrain. The symmetrical problems (P03-P14) have more than one global optimum because of its symmetrical characteristics, and are more difficult than the problem in the fist group. These maps are defined in Table 1, where H and W are the height and width of a map, respectively.

Table 1. Test problems, where H and W are the height and width, respectively.

4.2 Parameter Settings

We set the parameters of ACO variants based on the suggestions of their authors for TSPs. Parameter settings of involved algorithms are as follows. (1) AS: $\alpha = 1.0$, $\beta =5.0$, $\rho =0.5$, $Q=100$, $\tau _{ij}\left( 0\right) = \frac{2}{W+H}$; (2) ACS: $\alpha = 1.0$, $\beta =2.0$, $\rho =0.1$, $Q=0.9$, $\tau _{ij}\left( 0\right) = \frac{2}{\left( W+H\right) *L^{hunger}}$, $L^{hunger}$ is the length of path constructed by hunger strategy, where we construct a path always by choosing the shortest edges; (3) MMAS: $\alpha = 1.0$, $\beta =2.0$,$\rho = 0.02$, $length=20$ (the length of the candidate list), $\lambda = 0.05$, $\tau _{max}^0 = \frac{1}{\rho *L^{hunger}}$, $\tau _{min}^0= \frac{\tau _{max}^0}{4.0*(W+H)}$where $\tau _{max0}$ and $\tau _{min0}$ is the initially min pheromone and the max pheromone respectively. For each iteration, $\tau _{max}^t = \frac{1}{\rho *L_{best}}$, where $L_{best}$ is the length of global best solution, $\tau _{min}^t= \frac{\tau _{max}^t*(1-\exp (\frac{\log (0.05)}{n}))*2}{\exp (\frac{\log (0.05)}{n})*(length+1)}$, where n is the number of points in the global best solution.

All algorithms terminate when the number of iterations is greater than $I_{max}$ or the population meets $L_{worst}-L_{best} \le$1e-5 $L_{best}$, $Len_{best}$ and $Len_{worst}$ are the current best and worst solutions, respectively. The relative error (RE), which is used to evaluate the performance of an algorithm, is defined as follows.

$$\begin{aligned} RE= (Dis(x_{best})-Dis(x^*))/Dis(x^*) \end{aligned}$$

(7)

where $x_{best}$ and $x^*$ are the best solution found by an algorithm and the global optimum, respectively. All results are averaged over 30 independent runs in this paper. To test the statistical significance between the results of algorithms, the Wilcoxon rank sum test is performed at the significance level $\alpha =0.05$ in this paper.

4.3 Experimental Results

Minimum Probability. In the PM, the possibility of an edge to be chosen is zero if it does not appear in any solution. To improve its global search ability, we set a lowest possibility of each edge to be selected.

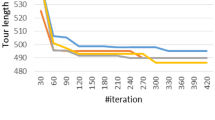
In this test, we set W = H = 50, $I_{max}$ = 1000, and PS = 500. If the possibility of an edge to be chosen is zero, then we use a minimum possibility $\lambda *W_{max}$, where $W_{max}$ is the weight of the best so far solution and $\lambda$ is a parameter to be tested. Figure 3 presents the effect of varying $\lambda$ on all the problems.

Fig. 3.

The effect of varying $\lambda$.

The experiment shows that as the value of $\lambda$ increases, the relative error also increases. The ants in PL will be more likely to perform random search as $\lambda$ increase since all neighbour nodes have similar possibilities. For example, when the $\lambda$ is small, e.g., between 0 and 4, its performance stays at almost the same level. In this paper, we set $\lambda$ = 0.2 to make sure PL can achieve a good result in a relatively short time on most problems.

Performance Comparison. In this subsection, to compare the global search capability with AS, ACS, and MMAS, we only use the probability matrix for PL. In this test, we set W = H = 50, PS = 500, and $I_{max}$ = 1000. Table 2 shows the performance comparison of all the algorithms, where Worst, Best, and Mean are the worst, the best, and the mean of RE over all runs. The Wilcoxons rank sum test is performed among algorithms on the best mean results on each problem, Y and N denote that the mean results of the best algorithm are significantly better than and statistically equivalent to other algorithms, respectively.

Table 2. Performance comparison of all the algorithms on SPP.

The Results show that PL outperforms ACS, AS, and MMAS on most problems. MMAS performs best on P07, P12, and P14 and ACS on P10 and P11. Although PL performs best on most problems, it could be improved in comparison with MMAS on hard problems P07, P12, and P14.

The Possibility to Learn from PM. The PM helps PL quickly find a solution, which often is a local optimum. The random search operator has a strong global search capability but it takes a long time to converge. In this subsection, we test the sensitivity of parameter $\theta$. Figure 4 presents the effect on varying $\theta$ on the performance of PL regarding the RE and the average number of iterations which PL takes. In this test, we set W = H = 500, PS = 50, and $I_{max}$ = 20000. The results show that the PL takes less number of iterations to converge as $\theta$ increases, but it more likely get stuck at local optima, and vice versa for decreasing $\theta$. From the results, the random search operator does help PL to improve the RE at the price of increasing the number of iterations. From the results, we suggest to take $\theta$ = 0.2.

Fig. 4.

The effect of varying parameter $\theta$.

Experiment on Dynamic SPP. In this subsection, we carry out experiments on dynamic SPP, where the food point changes to a random location on the map every a certain number of iterations $I_g$. Given the knowledge that a large value of $\theta$ helps PL achieve a fast convergence speed, we set $\theta =0.9$. The random search operator is enabled. In this test, we set W = H = 500 and PS = 50. The change interval $I_g$ varies from 5 to 100.

Table 3. Results of PL on dynamic SPP with different change frequencies.

Table 3 shows the results of PL on all problems with different change frequencies. From the results, we can have a common observation: the RE gets better as the change interval increases. It is reasonable since a greater change interval means a longer time for PL to search. PL achieves a good performance even in frequently changing environments. Take $I_g$ = 5 for example, where the food point changes every five iterations, PL is able to achieve a small RE on most problems, e.g., $RE<$ 1e−2. Thanks to the random search operator, the PL is able to maintain the population diversity during the runtime. On the other hand, the PM helps PL quickly find a reasonable solution. These two components make PL easily adapt to dynamic environments without using extra dynamism handling techniques.

Compared with ACOs, PL has only two parameters ($\lambda$ and $\theta$) to set and it outperforms the ACOs on most problems. To handle dynamic problems, ACO should reconstruct the pheromone matrix or use some strategies to update its matrix. While PL calculates its matrix based on the ants’ best solutions, which will change as the problem changes. Therefore, PL is more suitable to solve dynamic SPP than ACOs.

5 Conclusions

This paper proposes a probabilistic learning algorithm with a random search operator for solving the dynamic SPP. A set of 3D problems are also designed. PL shows competitive performance in comparison with several peer algorithm on static SPP and it also shows good performance on dynamic SPP. In the future, we will compare PL with other algorithm equipped with dynamism handling techniques.