Keywords

1 Introduction

Engineering design is typically characterised by several considerations, usually with conflicting requirements, which cannot be simplified down to a single objective. In such cases, more than one solution exists that fits the bill of the design problem. Hence, for these multi-objective problems, the Pareto frontier of the entire design space is the most valuable tool a designer can have, allowing the most appropriate design to be selected. The Pareto frontier is defined as the set of all solutions for which no other solution is better in all objectives [1]. A solution that lies on the Pareto frontier is known as Pareto-optimal or non-dominated. Therefore, Pareto sets give the trade-off relationships between the particular objectives in a multi-objective problem. However, in the “real-world” there also exists unavoidable design constraints. A common example being the stress in a structure constrained to not exceed its material limit value. Therefore, if an optimisation algorithm is to be used for real-world engineering design problems it must be able to handle multiple objectives and constraints.

Structural optimisation can trace its roots back over a century to the publication of a paper that derived the optimality criteria for the least weight layout of trusses [2]. Currently, structural optimisation can be divided into three primary categories: sizing [3, 4], shape [5, 6] and topology optimisation [7,8,9]. Of these categories, topology optimisation has the greatest potential for exploring superior optimised structures, since both changes in topology and shape are permitted. The first general theory of topology optimisation, known as layout theory, was formulated by Prager and Rozvany [10]; however, it was the seminal paper by Bendsøe and Kikuchi [7], which developed the first material distribution method, making topology optimisation applicable to real-world engineering problems. Nowadays, two methods, namely, Solid Isotropic Material with Penalisation (SIMP) [8, 11] and Bi-directional Evolutionary Structural optimisation (BESO) [9, 12, 13] have reached the stage of application in single-objective industrial problems [14]. This study is concerned with the latter, extending a recently proposed algorithm [15], known as Smart Normal Constraints BESO (SNC-BESO), to handle multiple constraints in multi-objective topology optimisation (MOTO) problems. Thus, realising the full potential of topology optimisation in real-world applications.

Typically, to facilitate the handling of multi-objective optimisation (MOO) problems, a scalarisation technique such as the weighted-sums method [16] or the \(\epsilon \)-constraint method [17], is employed. These methods combine all objectives to form a single function, known as the aggregate objective function, so that a MOO problem can be converted to a single-objective optimisation (SOO) problem. These methods are the most common approach found in the MOO literature, possibly owing to their simplicity and ease of application. However, there are three main difficulties associated with these types of methods. First, a satisfactory a priori selection of weights does not guarantee an acceptable final solution will be obtained [18]. Second, these methods are unable to capture solutions on the non-convex regions of the Pareto frontier [19, 20]. Finally, varying the weights consistently and continuously does not guarantee an even distribution of Pareto solutions and an accurate, complete representation of the Pareto set. Hence, these methods are suitable for obtaining Pareto solutions, but ill-suited for the creation of Pareto sets [21].

One popular method to obtain a comprehensive Pareto set is to use metaheuristic-based MOO techniques, such as a multi-objective genetic algorithm [22] or a multi-objective particle swarm optimisation [23], which are extensions of their SOO algorithms, respectively. Metaheuristic-based techniques have also been applied to multi-objective topology optimisation problems, see for example [24,25,26]. One advantage of these techniques is that they do not require design sensitivities, making their implementation simpler. However, for this same reason metaheuristic-based techniques are inefficient, and thus, cannot be applied to large scale problems that have thousands of design variables [27]. In the literature, metaheuristic-based approaches that are able to handle MOTO problems have been limited to approximately \(10^3\) design variables [28]. Conversely, topology optimisation problems are usually characterised by large-scale problems for which the number of design variables is in the order of \(10^3\)–\(10^6\), as each element or node in the discretised design domain is assigned as a design variable [29]. Consequently, additional techniques to reduce the number of design variables are required when metaheuristic-based approaches are applied to topology optimisation problems [30, 31]. Further, the complexity of these order reducing techniques becomes increasingly problematic as the MOTO problem becomes more complex. Therefore, making application of these methods to real-world design problems futile.

On the other hand, gradient-based topology optimisation methods, such as SIMP and BESO, can effectively and efficiently handle problems with design variables in the order of \(10^6\). A wide variety of objective functions have been used with gradient-based topology optimisation algorithms, diversifying their application to almost all fields of engineering and design [32, 33]. However, compared with the extensive research on SOO, there has been considerably less work concerned with topology optimisation for multi-objective problems. This gap in the literature is highlighted by the most recent review articles [13, 14, 27, 34] and textbooks [35,36,37] on topology optimisation, with only one or two references and no section dedicated to multi-objective problems. Recently, Sigmund and Maute identified the handling of multiple constraints as one of the main future challenges of topology optimisation [27]. The authors of this work feel that along with the handling of multiple constraints, multiple objectives should also be handled in topology optimisation algorithms for their continued use in real-world problems.

The Evolutionary Structural optimisation (ESO) method has been employed with the weighted sums method to incorporate multiple criteria into the ESO process [38, 39]. Proos et al. showed that this approach is able to produce a range of options, of Pareto attribute, for a multi-objective problem. However, the weighted sums method is unable to produce Pareto sets. Kim et al. [40] developed a multi-objective structural optimisation method for a three-dimensional (3D) thermal protection system using the ESO algorithm. They again used the weighted sums method with the objective of minimising maximum thermal stress and maximising the fundamental frequency. More recently, the Aggregative Gradient-based Multi-objective optimisation (AGMO) method was applied to a topology optimisation problem with a minimum compliance and volume objective [41]. However, the AGMO method can only be applied to topology optimisation problems with two objectives, and further, points located at a great distance from the Pareto frontier are updated along with points near the frontier, which is computationally inefficient. Moreover, AGMO requires an additional method to ensure diversity of the obtained Pareto-optimal solutions [42]. Sato et al. [43] recently coupled an adaptive weighted sums method with point selection schemes, namely a population-based approach, to a level-set based topology optimisation algorithm. They applied their method to compliance minimisation problems for multiple static load cases, providing insight into the relationship between the topology and the applied load. However, their method is unable to produce uniform Pareto-optimal solutions, and hence, Pareto-optimal solutions are sparse in certain areas, due to the use of the weighted sums approach. Furthermore, this renders the approach unsuitable for problems that have a non-convex Pareto frontier.

As outlined above, multi-objective optimisation methods that are suitable for MOTO problems with multiple constraints are yet to be developed. In this paper, the recently introduced SNC-BESO method [15], which was shown to produce smart Pareto sets in an efficient and effective manner, is therefore extended to also handle multiple constraints. The method is demonstrated on a number of examples having dynamic and static constraints. Hence, realising the full potential of gradient-based topology optimisation algorithms in real-world design problems.  

2 Methodology

In this section the SNC-BESO method, which is able to consider topology optimisation problems with multiple constraints as well as objectives, is briefly outlined. This section focuses on outlining the methods that enable the algorithm to consider multiple constraints, whilst finding the Pareto-set for a multi-objective topology optimisation problem. For a more in-depth description of the algorithm the interested reader is advised to seek out the recent publication by the authors [15].  

2.1 Smart Normal Constraints Method

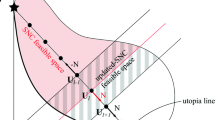
First, the variation of the smart normal constraints method used is defined. The SNC method can be divided into 7 steps, which will be described in this section using a bi-objective optimisation problem. Steps 2–7 are repeated until there are no more approximate regions of the Pareto surface that are capable of yielding a smart Pareto point.

Step 1: Generating the reference points

To approximate the Pareto frontier the anchor and anti-anchor points, the points in the feasible design space that correspond to the minimum and maximum value of one of the objectives respectively, must be found. The anchor point for the \(i^{th}\) objective is found by:

$$\begin{aligned} \mu ^{i*} = \left[ \mu _1(\mathbf{x}^{\mathbf{i}{*}}), \mu _2(\mathbf{x}^{\mathbf{i}{*}}), \dots , \mu _n(\mathbf{x}^{\mathbf{i}{*}})\right] ^T \end{aligned}$$
(1)

where \(\mu \) is the design objective vector and \(\mathbf {x^{i*}}\) is defined as the design variable vector that gives the minimum value of the \(i^{th}\) objective. The anti-anchor point for the \(i^{th}\) objective is found by:

$$\begin{aligned} \mu ^{i\circ } = \left[ \mu _1(\mathbf{x}^{\mathbf{i}\circ }), \mu _2(\mathbf{x}^{\mathbf{i}\circ }), \ldots , \mu _n(\mathbf{x}^{\mathbf{i}\circ }) \right] ^T \end{aligned}$$
(2)

where \(\mathbf{x}^{\mathbf{i}\circ }\) is the design variable vector that gives the maximum value for the \(i^{th}\) objective. The anchor and anti-anchor points are used as the vertices on the edges of the Pareto frontier approximation to guarantee convergence of the entire Pareto set [44].  

Step 2: Connecting the approximation points

The vertices found in the previous step are divided into approximation segments or planes (for more than two objectives) to approximate the Pareto frontier. The anchor points are connected to each other, creating the utopia lines. Therefore, a utopia line vector, \(N_j\), is found using the equation:

$$\begin{aligned} N_j = \mu ^{j*} - \mu ^{n*} \quad \quad \forall j \in (1, 2, \ldots , n-1) \end{aligned}$$
(3)

Hence, \(n-1\) utopia line vectors are defined, all of which point to the anchor point corresponding to the \(n^{th}\) dimension, \(\mu ^{n*}\).  

Step 3: Approximating the Pareto frontier

A set of evenly spaced approximation points are generated along each approximation line or plane, by the following relation:

$$\begin{aligned} S_i = \sum _{j=1}^n \alpha _i^j P_j \end{aligned}$$
(4)

where \(S_i\) is the \(i^{th}\) approximation point and \(P_j\) is the \(j^{th}\) approximation vertex. The non-dimensional parameter \(\alpha ^j_i\) is defined such that it satisfies the constraints given by:

$$\begin{aligned} 0 \le \alpha _i^j \le 1 \end{aligned}$$
(5)

and

$$\begin{aligned} \sum _{j=1}^n = \alpha _i^j = 1 \end{aligned}$$
(6)

\(\alpha ^j\) is varied from 0 to 1 with a fixed increment of \(\delta _j\) such that an even distribution of approximation points is obtained. Small increments, \(\delta _j\), will result in more approximation points. However, computations performed on the approximation points are relatively inexpensive, since more approximation points will not result in more function calls, as only one point is used per iteration. Therefore, contrary to the normal constraints (NC) method, the efficiency of this algorithm depends little on the value of \(\delta _j\).  

Step 4: Removing restricted approximation points

Unavoidably, some of the new solutions found will not add to the smart Pareto set. There may also be regions where the Pareto frontier is discontinuous and, therefore, solutions cannot exist. In Step 7 these restricted regions are recorded and avoided in further iterations. In this step the approximation points that lie within one smart distance (defined in next step) of already existing smart Pareto points are removed from further consideration.  

Step 5: Calculating the smart distance

In this step the smart distance between each approximation point and all approximation vertices is calculated. Mattson et al. [45] first introduced the idea of a smart Pareto set, based on the assumption that: “when the trade-off is significant a designer is willing to give up an insignificant amount in one objective to gain significantly in another”. Consequently, Mattson et al. [45] introduced the smart Pareto filter, which removes any duplicate Pareto solutions that fall inside a user defined shape, known as the Practically Insignificant Trade-off (PIT) region, surrounding each Pareto solution.

In the SNC method, the direct generation of a smart Pareto set is facilitated by the smart distance between points in the design space. The shape of the PIT region around a point is called a Lamé curve. Therefore, the PIT region is defined as the area that lies on or within the Lamé curve. All points inside the PIT region have a smart distance of \(s \le 1\) from the centre point. Hence, by definition all members of a smart Pareto set do not lie inside the PIT regions of any other members of the set, thus each will have a smart distance of \(s > 1\) with respect to all other members of the set. The smart distance between two points is found by:

$$\begin{aligned} s = \left\| {{\mathbf {Ad}}} \right\| _{p} \quad \quad \mathrm {for} \quad (0 \le p \le 2) \end{aligned}$$
(7)

where

$$\begin{aligned} \mathbf {A} = \left[ \begin{array}{lll} \frac{1}{a_1} &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \frac{1}{a_n} \end{array} \right] \quad \quad \mathrm {for} \quad (\mathbf {a} > \mathbf {0}) \end{aligned}$$
(8)

\(\mathbf {d}\) is a vector between the two points and \(||\mathbf {Ad}||_\mathbf{p}\) is the p-norm of the vector \(\mathbf {Ad}\), which follows that given by Rynne [46], in this case it is found by:

$$\begin{aligned} \left\| {{\mathbf {Ad}}} \right\| _{p} = \left( \sum _{i=1}^n | A_{i,i} d_i |^p \right) ^{\frac{1}{p}} \end{aligned}$$
(9)

The variables \(\mathbf {a}\) and p determine the distribution of the smart Pareto points. The values of \(a_i\) which make up the diagonal of the matrix \(\mathbf {A}\), correspond to the \(i^{th}\) objective and can be considered as the amount of change in the \(i^{th}\) objective necessary to constitute a significant difference between two points if all other objectives were to remain practically unchanged. Larger values of the matrix \(\mathbf {A}\) will thus result in fewer points in the smart Pareto set. The value of p determines the amount of curvature of the PIT region, and hence controls the degree of trade-off between objectives that is required in order for two points near each other to both be considered smart Pareto points. Since the values of \(\mathbf {a}\) and p are user-defined, it is therefore the user’s preferences that determine the distribution of the set. Hence, the SNC method is able to search the entire design space more efficiently and determine which approximation point is most likely to generate a new smart Pareto solution.  

Step 6: Generating the new Pareto point

The approximation point with the largest smart distance to its nearest known Pareto point is selected to construct a single objective optimisation (SOO) problem with two normal constraints, given by:

$$\begin{aligned} N_j \left( \mu (\mathbf {x}) - \mathbf{S}_{\mathbf{r}}\right) \le 0 \quad \forall j(1, 2, \ldots , n-1) \end{aligned}$$
(10)

and

$$\begin{aligned} -N_j \left( \mu (\mathbf {x}) - \mathbf{S}_{\mathbf{l}}\right) \le 0 \quad \forall j(1, 2, \ldots , n-1) \end{aligned}$$
(11)

where \(S_r\) and \(S_l\) are the approximation points on either side of the approximation point that is determined to be most likely to produce a smart Pareto solution. In this way the solution is guaranteed to fall at the intersection of the Pareto curve and the normal line, which intersects the approximation point most likely to produce a smart Pareto solution. Therefore, the new Pareto point is found by solving the SOO problem given by:

$$\begin{aligned} \begin{array}{ll} \mathrm {min}(\mathbf {x}) \quad &{} \mu _1(\mathbf {x}) \\ \text {subject to:} \quad &{} n \ge 2 \\ &{} \mathbf g (\mathbf x ) \le 0 \\ &{} \mathbf h (\mathbf x ) = 0 \\ &{} \mathbf x _l \le \mathbf x \le \mathbf x _u \\ &{} N_j(\mu (\mathbf x ) - S_{{r}_j})^T \le 0 \quad \forall j (1, 2, \ldots , n-1) \\ &{} -N_j(\mu (\mathbf x ) - S_{{l}_j})^T \le 0 \quad \forall j (1, 2, \ldots , n-1) \end{array} \end{aligned}$$
(12)

where \(\mathbf {g}\) and \(\mathbf {h}\) are inequality and equality constraints, respectively, and n is the dimension of the problem or number of objectives. Thus, for every approximation point that is considered likely to produce a smart Pareto solution, a corresponding point on the Pareto frontier is found. Once a new Pareto solution has been obtained the approximation points are updated. Consequently, the approximation points become closer to the Pareto front than the utopia line points that are obtained with the NC method. This usually results in fewer function calls per SOO for the SNC method compared to the NC method.  

Step 7: Confirming the new Pareto point belongs to the smart Pareto set

The new Pareto point, found in Step 6, may not lie on the smart Pareto set. Therefore, if this is the case, a restriction enabling the removal of future approximation points in these regions, which are known to be unable top produce smart Pareto points, must be added. In the literature it is generally accepted that three criteria: dominated, redundant and separated, can be formulated to test whether the new point lies inside the smart Pareto set [15, 47]. If the point meets one of these criteria, then it is not a smart Pareto point.

A dominated point may be produced by solving the SOO problem from Step 6 when there are local minima or maxima in the region defined by the two normal constraints. When using gradient-based algorithms, local optima can be perceived as global optima by the optimiser. A dominated solution is one which is locally optimal, but not globally optimal, since there exists one other solution where one of the objective functions can be improved in value, compared to the dominated point, without degrading the other objective values. Therefore, a solution is called Pareto-optimal if there does not exist another solution that dominates it.

A redundant point can be produced when the new solution falls within the PIT region of another, already present, Pareto point. This can occur because the true shape of the Pareto frontier is unknown, rather it is approximated by the already existing Pareto solutions that have been obtained. Therefore, by simply selecting an approximate point which does not lie inside the PIT of another Pareto point does not guarantee that the obtained Pareto point also won’t lie inside the PIT of another Pareto point.

A separated point is a point that is separated from the normal constraint lines or planes, which were used in the SOO problem that created it (Step 6). This separation indicates that there is a region in the design space in which all SOOs will converge to the same solution. This occurs because the Pareto frontier is discontinuous in this region. Using the normal constraint line that produced the separated point and a parallel normal constraint line that intersects the final solution, a restricted region can be created. This restricted region is kept for the remainder of the optimisation process, to avoid further generation of redundant points.  

2.2 Bi-direction Evolutionary Structural Optimisation

This work uses the Bi-directional Evolutionary Structural Optimisation (BESO) algorithm [9, 12] to solve the SOO problem in Step 6. In this section only the method used to extend the SNC-BESO algorithm to handle both multiple constraints will be described in detail. For further details on the BESO algorithm and the specific variation used here the reader should seek out the latest textbook [36] and the recent manuscript by the authors which introduced the SNC-BESO algorithm [15].

To solve a multi-constrained optimisation problem, Zuo et al. [48] proposed relaxing the problem using Lagrange multipliers. Thus, the constraints are treated as penalty terms in the calculation of the objective functions. Therefore, the sensitivity analysis becomes:

$$\begin{aligned} \alpha = \alpha _{\mathrm {objectives}} + \lambda \alpha _{\mathrm {constraint}} \end{aligned}$$
(13)

where \(\alpha \) is the sensitivity function, \(\lambda \) is a Lagrange multiplier and the subscripts objectives and constraint refers to the objectives and constraint values, respectively. The additional Lagrange multipliers are continuous in an infinite domain. Thus, it is computationally infeasible to search such a domain with a direct method. Instead \(\lambda \) can be defined through a scaling function of replacement factors \(\phi \) that range in a finite domain \(\left[ 0, 1\right) \), given by:

$$\begin{aligned} \lambda = \frac{\phi }{1 - \phi } \quad \quad \phi \in \left[ 0, 1\right) \end{aligned}$$
(14)

Hence, the Lagrange multipliers, \(\lambda \), are represented in the whole range by the replacement factors, \(\phi \), since \(\phi = 0 \implies \lambda = 0\) and \(\lim _{\phi \rightarrow 1} \lambda = \infty \). Thus, the Lagrange multiplier, and hence the penalty term due to the constraint, can be increased or decreased by increasing or decreasing the corresponding replacement factors. Therefore, in this manner any number of physical constraints can be handled by adding a penalty term to the sensitivity analysis.

However, there is another type of constraint, known as geometrical constraints, which can be handled even before the calculation of the sensitivity numbers. A common example in topology optimisation is a volume constraint, where the final structure must have a volume less than or equal to a pre-defined percentage of the design space. Another example is when certain areas of the design domain are non-designable, i.e. must remain solid or void. For these types of constraints no modification to the SNC-BESO algorithm is needed as it can already handle geometrical constraints [15].  

3 Results and Discussion

In this section the results of the SNC-BESO algorithm, with and without multiple constraints, are presented. First, a 2D plane stress problem taken from the literature of multi-objective topology optimisation [38] is solved. Only the weighted sums method was used to solve this kind of problem in topology optimisation, therefore a smart Pareto set could not be obtained. However, it is shown that by using the SNC-BESO method a smart Pareto set is found effectively and efficiently. Next, the same problem is solved, however with an added physical constraint on the \(2^{nd}\) natural frequency. This demonstrates the algorithms ability to not only handle multiple objectives, but multiple constraints as well. Hence, multiple objectives and multiple constraints, both physical and geometrical, are handled in the same problem, showing the ability of such a methods to be applied to real-world problems.  

3.1 Multiple Objective Topology Optimisation

Proos et al. [38] present a multiple objective topology optimisation problem, where a structure subjected to nine point loads, having a magnitude of 200N each, distributed over 0.09m is being designed. The structure is supported by two roller supports at the bottom two corners (Fig. 1). The design domain has dimensions \(0.8\,\times \,0.5\,\times \,0.01\) m for the length, height and width, respectively. The domain is discretised using \(80\,\times \,50\) four-node square elements (Fig. 1). The material properties defined for the design domain are: a Young’s modulus of \(E = 200\) GPa, a Poisson’s ratio of \(\nu = 0.3\) and a density of \(\rho = 7000\) kgm\(^{-3}\). Throughout the analysis 2D plane-stress conditions are assumed.

Fig. 1.
figure 1

Initial design domain [38]

Full size image

The design objectives for the topology optimisation problem are to minimise the mean compliance and to maximise the first natural frequency. For this problem, a volume constraint of \(V = 0.7\) is also applied. The multiple objective topology optimisation problem is solved using the SNC-BESO method. The amount of change in either objective that would constitute a significant difference between two Pareto points, if all other objectives remain practically unchanged, is set to \(5\%\). The amount of curvature of the PIT region is defined as \(p = 0.4\). The corresponding Pareto curve of the minimum mean compliance terms and first mode natural frequencies is presented in Fig. 2. The points marked (a)–(i) all correspond to the topologies shown in Fig. 3. The dashed lines represent the limits of both objectives, found by solving a single-objective topology optimisation problem for both objectives.

Fig. 2.
figure 2

Pareto frontier of the mean compliance and first mode natural frequency for the multiple objective topology optimisation problem found using the SNC-BESO method

Full size image

The points illustrated in Fig. 2 are evenly spaced along the Pareto front, with no points lying within the PIT of any other, thus making up a smart Pareto set. Furthermore, all the PIT regions intersect their neighbouring point’s PIT region in some location, demonstrating that no new designs can be found that would be of interest to the designer. Hence, the entire design space has been searched. This is a particularly important improvement over the previous methods used in multi-objective topology optimisation, since the designer has the minimum amount of information required to give all possibilities for the current design problem. Therefore, the SNC-BESO method used is able to access the entire design space, produce evenly distributed Pareto solutions and efficiently obtain a smart Pareto set, illustrating its ability to solve multi-objective optimisation problems in an efficient and effective manner.

In contrast, the work of Proos et al. [38] does not produce a smart Pareto set, showing the deficiencies of the weighted sums method. Moreover, evenly distributed weights are prescribed, but an even distribution of points is not obtained. Furthermore, the points are concentrated around the knee region of the Pareto curve, where larger areas of trade-off are observed. Proos et al. found that using the weighted sums method, for this particular problem, did not necessarily lead to a design that showed any improvement in one criteria leading to a clear trade-off with the others. Hence, increasing the weights of one objective did not always lead to an improvement in that objective with a corresponding reduction in the others. They found that the solution with a \(90\%\) stiffness weighting had a lower natural frequency than the solution produced with a stiffness weighting of \(100\%\). However, the mean compliance was lower for the solution with a stiffness weighting of \(100\%\). Thus, this solution was optimal in terms of being the stiffest design; the authors had found a local optimum, i.e. a dominated point was produced. These problems are not evident for the SNC-BESO method of this work.

Fig. 3.
figure 3

Topologoes of smart Pareto-set

Full size image

The final topologies (Fig. 3) found using the SNC-BESO method are not affected by numerical instabilities, such as mesh-dependency and checkerboarding. Each solution has clear holes, with a uniform mesh transition between the two anchor points. In contrast, the topologies illustrated in [38] contain some checkerboarding, with several small holes formed and elements connected at only two corners. This shows the benefits of implementing an updated BESO method compared to the ESO method. The mesh-independency filter employed in this work spreads the sensitivities across the entire design domain such that these instabilities do not occur. Furthermore, the topologies produced in this work (Fig. 3) are convergent, whereas the ESO method does not have a rigorous convergence criterion. The SNC-BESO method is thus better able to find smart Pareto sets of multi-objective topology optimisation problems.  

3.2 Multiple Objective Topology Optimisation with Multiple Constraints

The previous subsection solved a multiple objective topology optimisation problem from the literature, showing the improvements of the SNC-BESO algorithm over the current state of the art. However, as previously mentioned, in real world design problems often the designer must manage constraints as well as objectives. Therefore, in this subsection an additional physical constraint, where the difference between the first and second natural frequency must be greater than 400 Hz (i.e. \(\omega _{{n}_2} - \omega _{{n}_1} \ge 400\) Hz), is added to the problem formulation. Such a constraint is used to ensure that frequency coupling, where two natural frequencies come together resulting in a damping ratio of zero causing resonance, does not occur. Hence, the addition of such a constraint, along with the already present geometrical constraint, makes the problem a multiple objective as well as a multiple constraint problem.

The design objectives for this problem are again to minimise the mean compliance and to maximise the first natural frequency. Furthermore, the volume constraint is again set to \(V=0.7\). The multiple objective and constraint topology optimisation problem is solved using the SNC-BESO method. The amount of change in either objective that would constitute a significant difference between two Pareto points, if all other objectives remain practically unchanged, is set to \(5\%\). The amount of curvature of the PIT region is defined as \(p = 0.4\). The corresponding Pareto curve of the minimum mean compliance terms and first mode natural frequencies is presented in Fig. 4. The points marked (a)–(h) all correspond to the topologies shown in Fig. 5. The dashed lines represent the limits of both objectives, found by solving a single-objective topology optimisation problem for both objectives with the constraints.

Fig. 4.
figure 4

Pareto frontier of the mean compliance and first mode natural frequency for the multiple objective topology optimisation problem with a geometric and physical constraint found using the SNC-BESO method

Full size image
Fig. 5.
figure 5

Topologoes of smart Pareto-set with geometrical and physical constraint

Full size image

The points illustrated in Fig. 4 are spaced across the entire Pareto front, with no points lying within the PIT of any other, thus making up a smart Pareto set. The Pareto front (Fig. 4) is noticeably different from the one found for the problem without the additional physical constraint (Fig. 2). Namely, there is a discontinuity in the Pareto front between solutions (e) and (f). This discontinuity is due to the flatness of the Pareto front towards the right hand side (Fig. 4), where the structures with higher compliance values are found. The added physical constraint has resulted in a steep drop to almost the maximum fundamental frequency (solutions (a)–(e)) and then a flat region where large decreases in compliance result in only a small increase in the first natural frequency (solutions (f)–(h)). This is due to the reduction in the range of the first natural frequencies, \(675.9\,\mathrm {Hz} \le \omega _{{n}_1} \le 694.4\,\mathrm {Hz}\), for the multi-constrained problem compared to, \(675.9\,\mathrm {Hz} \le \omega _{{n}_1} \le 699.1\,\mathrm {Hz}\), for the initial problem. Furthermore, the range of compliance values has increased from: \(6.61(10^{-3})\,\mathrm {Nm} \le \mathrm {Compliance} \le 7.70(10^{-3})\,\mathrm {Nm}\) for the initial problem to: \(6.61(10^{-3})\,\mathrm {Nm} \le \mathrm {Compliance} \le 7.90(10^{-3})\,\mathrm {Nm}\) for the multi-constrained problem. Therefore, the added constraint has extended the range of compliance design, but put a restriction on the amount by which the first natural frequency can be maximised.

The final topologies (Fig. 5) found using the SNC-BESO method are again not affected by numerical instabilities, such as mesh-dependency and checkerboarding. Each solution has clear holes, with a uniform mesh transition between the two anchor points. Compared to the previous problem, the final topologies are all different except for solution (a). The effect of the added constraint can be clearly seen, especially towards the latter solutions (Fig. 5(f)–(h)). This added constraint is especially difficult for the optimiser, because increasing the gap between the first and second frequencies results in the structure where the load is applied being removed. This drastically increases the compliance of the structure, whose minimisation is also one of the objectives of the problem. This removal is easily seen by solutions (f) and (g) (Fig. 5). Therefore, the structure becomes less rounded and more triangular. Hence, the updated SNC-BESO method is thus able to find smart Pareto sets to multi-objective as well as multi-constrained topology optimisation problems.  

4 Conclusions

A recently developed multi-objective topology optimisation algorithm, known as SNC-BESO, which uses a variation of the smart normal constraints method combined with a bi-directional evolutionary structural optimisation algorithm, has been extended to also include multiple constraints (both physical and geometrical). The literature review showed that, thus far, topology optimisation methods have mainly focused on single-objective problems. Hence, reducing the applicability of topology optimisation algorithms to real-world problems. Two multiple objective topology optimisation problems were solved using the updated SNC-BESO method, the first was taken from the limited literature on multi-objective topology optimisation and the second was an extension of this first problem with an added physical constraint to make the problem contain both multiple objectives as well as constraints.

The first test case was purely a multi-objective problem with a stiffness and dynamic criterion. The same problem had previously been solved in the literature using a weighted sums ESO method [38]. The Pareto front determined by the SNC-BESO method was found to constitute a smart Pareto set, while the same cannot be said for the Pareto front found using the weighted sums method [38]. Hence, the SNC-BESO method is shown to be able to produce multi-objective topology optimisation problems in an efficient and effective manner.

The second problem has multiple constraints as well as objectives, having an added dynamic stability constraint. To the best of the author’s knowledge, such a problem has not yet been solved before using any method in the BESO literature. Again, the SNC-BESO method was shown to be able to produce a smart Pareto set covering the entire design domain. The added constraint resulted in a discontinuous Pareto front; however, the updated SNC-BESO algorithm was able to find solutions on either side of the discontinuity. This demonstrated that the recently developed SNC-BESO algorithm is able to handle multiple constraint problems along with multiple objectives and physics as demonstrated in an earlier work by the authors [15].

The work presented here adds to the literature on multi-objective topology optimisation, as well as multi-constrained topology optimisation, which is a limited field of research. This type of analysis is instrumental for further application of topology optimisation to industrial design problems, where the consideration of multiple objectives, physics and constraints is a very frequent requirement. Finally, it is left as future work to apply the updated SNC-BESO method to topology optimisation problems with more than two-objectives, thus demonstrating that this method is suitable for any dimension of multi-objective problem.