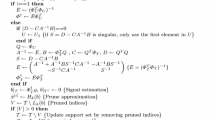Keywords

1 Introduction

Currently, the demand for wireless communication services has grown exponentially, this has generated some overcrowded band [1], because they are used by commercial systems. However, there are frequencies bands which are sub-used [2], like TV Bands, those band offer a great opportunity to solve this problem. Therefore, there are spectral holes that are permanent in some cases and in others, occur at certain times on some frequency bands; which implies a dilemma, because users from some services such as mobile, do not have enough spectrum to transmit, but on the other hand, some spectral bands are not completely used. This happens due to the current static spectrum allocation strategy, and consequently dynamic spectrum access (DSA) is proposed as a solution strategy.

So, the technology which can help to implement devices with DSA capabilities is Cognitive Radio. This technology allows changing the parameters of the devices and the network itself in order to establish an efficient communication in terms of radio resource use, but this communication must not interfere with the users who have a legal concession of the band. CR devices have 3 steps to work and do the dynamic channel’s assignment which are: Spectrum sensing, Radio Environment analysis and Transmission Parameters adjustment. Spectrum sensing is known as the CR enabler and it must be done continuously in the CR for giving key data such as traffic and noise statistics, channel state, White Spaces information, and so on, to finally do the transmission parameter adjustment, and doing so allowing the CR to adapt the environment

However, spectrum sensing is a task that involves significant challenges from the perspective of the computational resources required, and to implement this function using traditional methods such as the energy detector [3, 4], sensing per adapted filters [4, 5] sensed by cyclo-stationary characteristics [4, 6] and a wavelet detector [7, 8] among others, involves sampling the broadband spectrum at rates above the Nyquist rate; this is the reason why the new paradigm implemented called Compressive Sensing (CS) [9, 10] is so appealing; it provides an efficient way to sample and process sparse signals or signals that can be adequately approximated by sparse signals, in other words, those which can be approximated by an expansion in terms of a suitable base, that only has a few significant terms. Therefore, to solve the problems of spectrum sensing it is necessary to establish a set of methodological steps for the developing of sub-Nyquist sampling sensing in wideband signals. In addition, proposing an approximation with sensing algorithms for wideband signals is key to solve the sampling problem in rates below the Nyquist rate, and doing so improving the processing capacity requirements, which are proportional to the number of samples to process. In the same way, an alternative solution for solving this problem will be generated, which compared with the traditional spectrum techniques, it will allow to sense narrowband signals and wideband signals in sequential way.

Then, using the frequency domain sparse property of the wireless signals in outdoor scenarios [11], it is proposed a methodology for the use of CS in CR to solve spectrum sensing problem in wideband signals. The band of interest is divided into a finite number of spectral bands, in which the presence or absence of carriers through the reconstruction of the sampled spectrum is examined. The sampling process is performed with a random demodulator proposed in [11], and the reconstruction of the same for the identification the occupied bands by means of identifying the presence or absence of carrier is performed with the convex relaxation algorithm based on minimizing the norm \( \text{ }\ell_{1} \).

This paper is organized as follows: In Sect. 2 the reference framework is described, then in Sect. 3 the methodology based on the proposed steps is defined in Sect. 4 the results are shown, and finally in Sect. 5 the conclusions of the study are shown.

2 Reference Framework

In the compressive sensing paradigm [13], it is assumed that a signal \( z \in {\mathbb{R}}^{n} \) is formed by samples taken at the Nyquist rate; this signal, in turn, can be represented by an sparse approximation in a transformed domain, wherein, denoting by \( {\varvec{\Phi}} \) the matrix of size \( n \times n \) which represents the transformation between the original signal domain and the domain in which the signal is sparse, and assuming that in the transformed domain, the signal \( x \in {\mathbb{R}}^{n} \) is described as \( x = {\varvec{\Phi}}z \) and has significant components only, where k ≪ n and the remaining components are approximately zero. Therefore it is said that the signal \( x \in {\mathbb{R}}^{n} \) is k-sparse, which is represented as \( \left\| x \right\|_{0} \le k \), where the operator \( \left\| x \right\|_{p} \) denotes vector norm \( \ell_{p} \) of \( x \) when \( p = 0 \), and is not according with triangular inequality then \( \left\| x \right\|_{0} : = \left| {supp} \right| \) and represent cardinality of \( x \) vector support, and the \( \ell_{p} \) rule is defined as shown in Eq. 1.

$$ \left\| x \right\|_{p} = \left\{ {\begin{array}{*{20}l} {\quad \,\,\left| {supp\left( x \right)} \right|} \hfill & { para \,p = 0} \hfill \\ {\left( {\sum\nolimits_{i = 1}^{n} {\left| {x_{i} } \right|^{p} } } \right)^{{\frac{1}{p}}} } \hfill & {para\,p \in \left[ {1,\infty } \right)} \hfill \\ {\quad \,\,\hbox{max} {}_{i = 1,2,3, \ldots ,n}\left| {x_{i} } \right|} \hfill & { para\,p = \infty } \hfill \\ \end{array} } \right. $$
(1)

It may be interpreted manner not so precise, but highly illustrative, that compressive sensing allows sampling at the Nyquist rate followed by a sub-sampling performed by a matrix \( \varvec{A} \) of size \( m \times n \), where \( m\, < \,n \), therefore, the process of making m linear measurement by an acquisition system, can be represented mathematically as indicated by Eq. 2.

$$ y = \varvec{A}x $$
(2)

Where \( y \in {\mathbb{R}}^{m} \) is the measurements vector.

To ensure the recovery of only the original signal from the linear measurements \( y \), the sensing matrix \( \varvec{A} \) must satisfy, generally, the restricted isometry property (RIP) [13], which is illustrated in the following definition.

Definition 1.

A matrix \( \varvec{A} \) satisfies the restricted isometry property of order \( k \), if a \( \delta_{k} \in (0,1) \) such that

$$ (1 - \delta_{k} )\left\| x \right\|_{2}^{2} \le \left\| {\varvec{A}x} \right\|_{2}^{2} \le (1 + \delta_{k} )\left\| x \right\|_{2}^{2} $$
(3)

For all \( x \in S_{k} \), where \( S_{k} \) is the set of all k-sparse signals.

If a matrix \( \varvec{A} \) satisfies the restricted isometry property of order \( 2k \), then from Eq. 3 it can be interpreted that the matrix \( \varvec{A} \) preserves the distance of any pair of k-sparse vectors.

The problem of reconstructing the signal \( x \in {\mathbb{R}}^{n} \) from the measurement vector \( y \in {\mathbb{R}}^{m} \), can be done using algorithms based on convex relaxation which are a key focus of the sparse approach; they replace the combinatorial function \( \ell_{0} \) with the convex function \( \text{ }\ell_{1} \), which converts the combinatorial problem in a convex optimization problem [12], the \( \text{ }\ell_{1} \) norm is the convex function which is most approximated to the \( \ell_{0} \) function. The natural approach, from which the sparse approximation problem addressed, is to find the sparse solution \( y = \varvec{A}x \), by solving the optimization problem

$$ \min\nolimits_{x} \left\| x \right\|_{0} \quad subject \,to\,\,\,y = \varvec{A}x $$
(4)

However the problem posed in Eq. 4 is a combinatorial problem which in general is NP-Hard [13], and the simple fact of working with all media cardinality \( k \) becomes an intractable computational problem, by replacing the \( \ell_{0} \) norm with the \( \ell_{1} \) standard the problem becomes the one raised in Eq. 5.

$$ \min\nolimits_{x} \left\| x \right\|_{1} \quad subject \,to\,\,\,y = \varvec{A}x $$
(5)

When dealing with imperfectly sparse measurements (measurements contaminated by noise), the sensing model given by Eq. 6 is considered.

$$ y = \varvec{A}x + w $$
(6)

Where \( \varvec{A} \) is the sensing matrix of size \( m \times n \), \( y \in {\mathbb{R}}^{m} \) is the measurement vector and \( w \in {\mathbb{R}}^{m} \) is the noise vector, therefore, inputs from \( y \) are the measurements from \( x \) contaminated by noise, therefore the optimization problem of Eq. 5 becomes

$$ { \hbox{min} }_{x} \left\| x \right\|_{1} \quad subject\;to\;\left\| {\varvec{A}x\text{ - }y} \right\|_{2} \; \le \; \in $$
(7)

Or equivalently

$$ { \hbox{min} }_{x} \left( {\left\| x \right\|_{1} + \frac{\mu }{2}\left\| {\varvec{A}x - y} \right\|_{2}^{2} } \right) $$
(8)

The two programs are equivalent in the sense that the solution of a problem is also the solution of the other provided that the parameters \( \in \) and \( \mu \) are properly established; however, the correspondence between \( \in \) and \( \mu \) is not known beforehand; depending on the application and the information available, one of the two may be easier to obtain, which makes one of the two problems stated in Eqs. 7 and 8 preferred over the other. Properly selecting \( \in \) or \( \mu \) is a problem that is very important in practice, therefore, general principles for selection include:

  • Perform statistical assumptions about \( w \) and \( x \) and interpret Eqs. 7 or 8 as e.g. maximum a posteriori estimates.

  • Cross validation (perform reconstruction from a subset of the recovery action and validate on another subset of steps)

  • Find the best values of the parameters on a test data set and use these parameters on current data with appropriate adjustments to compensate for differences in scale, dynamic range, sparsity and noise.

3 Proposed Methodological Approach

Next, the methodological stages to be covered in the process of developing an efficient spectrum-sensing algorithm are defined by the particular functionality of the observation phase defined in the cognitive cycle proposed by Mitola [14]. In this phase of observation, the following can be defined as objectives associated with spectrum sensing: (1) Identification of Blank Spaces, (2) Identification of radio technology, modulation, coding or characteristics of the signal present in the channel; (3) Identification of the quality or condition of the channel; Considering these objectives, the proposed methodological stages are:

3.1 Pre-processing and Digitizing the RF Signal

At this stage, it must be decided that the alternative of digitizing the Radio Frequency (RF) signal present in the radio environment is more convenient according to the objectives set for the spectrum sensing operation. In this phase, the major challenges are presented in the aspects related to the hardware components required for the acquisition of the signal, such as Digital Analog Converters (ADC), Low Noise Filters and Amplifiers (LNA); with respect to the digitization process, in the scenario in which broadband spectrum sensing is sought, ideally, the CR should be supported by fully radio software hardware, in which the RF signal is directly digitized. However, there are fundamental physical limits to be exceeded according to the operating bandwidths, operating frequencies and number of bits required in the resolution of the conversion; in addition, it is relevant to consider in this scenario the number of measurements generated in the process of digitizing the RF signal since, depending on it, more or less processing capacities will be required in the later phases. As for the characteristics required in the filters, an important aspect is related to the bandwidths and low ripple of the passing band, small transition bands and levels in the attenuated band which involves complex and high-order filters that require components with important restrictions in their frequency response, finally with respect to the amplification of the received signal when it is broadband. The amplifier is required to operate in its linear region, which is a major challenge given the frequency response required by the amplifier components.

According to the aforementioned, it is important to decide which sampler to use according to the specific objective that is sought with the spectrum sensing, in this sense, the possibilities to consider are the Nyquist Sampling or the Sub-Nyquist Sampling. If the objectives of the spectrum sensing are (1) or (3) it is convenient to perform a sub-nyquist sampling because of the low computational complexity associated with the pre-processing stage associated with the selected sampler, this because in order to achieve these sensing targets do not require a perfect reconstruction of the signal; if the objective of the spectrum sensing is (2) It is advisable to perform a Nyquist sampling since perfect reconstruction of the signal is required. The above is shown in the decision diagram of the proposed methodological approach, which is illustrated in Fig. 1.

Fig. 1.
figure 1

Proposed methodological approach

Full size image

In this sense, since the objective of sensing is the identification of blanks, it is proposed to use sub-nyquist sampling based on compressive sensing, covering the stage of digitalization of signal by means of a dispersed representation of the multiband signal and obtaining sub samples -nyquist using the analog converter - information called Random Demodulator [10].

3.2 Extraction of Characteristics

Once digitized measurements of the RF signal present in the channel are taken, these measurements must be processed to obtain adequate representation for classification and identification purposes. This is a very delicate stage since the different spaces of characteristics lead to different representations of the signal. Therefore, the feature space used must be strictly related to the sensing objective.

Some of the characteristics related to the objectives associated to spectrum sensing are signal power, interference temperature, power spectral density, cycle - stationary, time - frequency distribution, eigenvalue distribution, signal covariance, etc. Each of them can be used to represent the signal according to the objective associated with spectrum sensing. For example, if the objective of the spectrum sensing is identification of blanks, it is possible to use characteristics such as signal strength, interference temperature, power spectral density, signal cycle distribution, distribution of the eigenvalues of the matrix channel, time - frequency distributions or signal correlation matrix. Nevertheless, if the purpose of the spectrum sensing is the identification of the radio technology of the primary user, modulation, coding or characteristics of the signal present in the channel, it is advisable to use characteristics such as power spectral density, signal cycle distribution or distributions time - frequency. Finally, if the objective of the spectrum sensing is the identification of the quality or state of the channel, it is most appropriate to make use of characteristics such as signal strength, interference temperature, power spectral density or time - frequency distributions.

This process does the Sub-Nyquist sampling of the signal \( x \in {\mathbb{R}}^{n} \), using a set of samples \( y \in {\mathbb{R}}^{m} \) where \( y = \varvec{A}x + w \) and the matrix \( \varvec{A} \) must satisfy RIP. Then, it is done the processing of the disperse signal in which the obtained samples \( y \in {\mathbb{R}}^{m} \) are used to recover the signal \( x \in {\mathbb{R}}^{n} \) using greedy search algorithms or convex programming algorithms [9].

3.3 Classification and Identification

Once it has been defined, which feature or feature sets are to be used for signal representation, it is necessary to establish where and how the decision process will be performed. For this, it is necessary to consider the most relevant aspects according to the objective of spectrum sensing and the particular problem to be addressed. From the present methodological proposal and according to the ways in which the spectrum sensing mentioned in Sect. 1 can be realized, three alternatives are seen for the decision-making process in CR.

  1. (1)

    Spectrum Sensing: In this alternative, each secondary user, individually, makes the decisions according to the established sensing objective, based on locally available measurements.

  2. (2)

    Cooperative Spectrum Sensing (Centralized): In this alternative, all secondary users who share a geographic area or radius of influence environment send the decisions taken locally to a central entity. Which exploits all available knowledge to make the decision in accordance with the goal of established senses.

  3. (3)

    Collaborative Spectrum Sensing (Distributed): In this alternative, all secondary users who share a geographic area or radius of influence environment send decisions made locally to all other collaborating members in the radio environment. Where each secondary user individually exploits all available knowledge, and makes decisions according to the goal of established senses.

For each alternative of spectrum sensing, it is necessary to define the rule or set of decision rules to be used, which is why, for the case of local spectrum sensing, the decision rule to be used par excellence is the rule of maximum a (MAP) [15], and for cooperative and collaborative spectrum sensing, the decision rules to be used may be rules of logical fusion [16] such as AND, OR or XOR, or Bayesian fusion rules [17]. There are other learning-based decision mechanisms such as Neural Networks [18], Vector Support Machines [19], Self-Organized Maps [20], Q-Learning [21] and Genetic Algorithms [22]. Leave to the discretion of the reader, as they are addressed in the learning phase defined in the cognitive cycle proposed by Mitola [14]. In general, the proposed methodological approach is summarized as illustrated in Fig. 1 at the end of the article.

4 Methodology Validation

Considering a single-antenna CR device that operates over a multiband (licenced) with a total bandwidth of \( B\; Hz \), which is divided into non-overlapping \( k \) sub-bands of equal bandwidth \( b \), equivalent to \( B/k \;Hz \) per channel, as shown in Fig. 2

Fig. 2.
figure 2

Wideband spectrum sensing scenario

Full size image

Assuming that the multiband signal samples are independent random variables that follow a normal distribution of zero mean and \( \sigma_{s} \) variance (\( {\mathcal{N}}(0,\sigma_{s} ) \)), a presumption that is valid for any multiband signal in which each carrier of a sub-band is modulated independently by data-streams; and that noise samples in each antenna are random variables normally distributed, independent, of zero mean and \( \sigma_{n} \) variance (\( {\mathcal{N}}(0,\sigma_{n} ) \)), la signal received in the antenna of the CR device can be expressed as indicated in Eq. (9).

$$ \varvec{x}_{j} \left( n \right) = \varvec{h}_{j} \varvec{s}_{j} \left( n \right) + \varvec{w}_{j} (n) $$
(9)

where \( \varvec{x}_{j} \left( n \right) \) is the \( n \)-th component of the signal received by the SU in the \( j \)-th sub-band with \( j = 1,2,..,k \), \( \varvec{h}_{j} \) represents the channel response in the \( j \)-th sub-band, \( \varvec{s}_{j} \left( n \right) \) is the \( n \)-th component of the signal transmitted by the \( j \)-th PU on the \( j \)-th sub-band and received by the SU antenna and \( \varvec{w}_{j} (n) \) is the \( n \)-th noise component in the \( j \)-th sub-band. The spectrum sensing problem in the \( j \)-th sub-band can be formulated as a statistical hypothesis testing problem in which a selection must be made between the hypothesis \( {\mathcal{H}}_{0,j} \) which indicates that the \( j \)-th sub-band is available, and hypothesis \( {\mathcal{H}}_{1,j} \) which indicates that the \( j \)-th sub-band is occupied; the aforementioned can be expressed according to Eq. (10).

$$ \left\{ {\begin{array}{*{20}l} {{\mathcal{H}}_{0,j} :\varvec{x}_{j} = \varvec{w}_{j} } \hfill \\ {{\mathcal{H}}_{1,j} : \varvec{x}_{j} = \varvec{h}_{j} \varvec{s}_{j} + \varvec{w}_{j} } \hfill \\ \end{array} } \right. $$
(10)

Where \( x_{j} \in {\mathbb{R}}^{p} \) is the vector of the signal received by the SU in the \( j \)-th sub-band, with \( p \) equal to the amount of samples taken per sub-band; \( w_{j} \in {\mathbb{R}}^{p} \) is the vector representing the white noise components present in the \( j \)-th sub-band; \( h_{j } \in [0,1] \) represents the channel response in the \( j \)-th sub-band; finally, \( s_{j} \in {\mathbb{R}}^{p} \) is the vector representing the signal transmitted by the \( j \)-th PU on the \( j \)-th sub-band. To develop the spectrum sensing we define the following stages.

A. SubNyquist Sampling

With the Random Demodulator (RD) [10] we performs Sub-Nyquist Sampling of multiband signal \( {\mathbf{x}}(t) \), it can be considered as a new type of sampling system, which can be used for the acquisition of sparse bandlimited signals. From sub-Nyquist sampling process, the obtained samples can be represented as:

$$ {\mathbf{y}} = {\mathbf{Ax}} $$
(11)

where \( {\mathbf{A}} \in {\mathbb{R}}^{m \times n} \) is the sensing matrix, \( {\mathbf{y}} \in {\mathbb{R}}^{m} \) the measurements vector and \( {\mathbf{x}} \in {\mathbb{R}}^{n} \) is the k-sparse vector that represents the multiband signal, therefore, \( {\mathbf{y}} \) entries are sub-Nyquist samples of \( {\mathbf{x}} \).

B. Characteristics Extraction

From (3) we can see that, by the calculation of the samples covariance matrix of \( {\mathbf{y}} \), results the following relation:

$$ {\mathbf{R}}_{{\mathbf{y}}} = {\mathbf{AR}}_{{\mathbf{x}}} {\mathbf{A}}^{{\mathbf{T}}} $$
(12)

where \( {\mathbf{R}}_{\varvec{x}} \in {\mathbb{R}}^{n \times n} \varvec{ } \) is the signal covariance matrix and \( {\mathbf{R}}_{\varvec{y}} \in {\mathbb{R}}^{m \times m} \) is the samples covariance matrix.

Therefore, it is possible from the samples covariance matrix to obtain the signal covariance matrix, and with it the performance of the wideband spectrum sensing operation identifying the energy in each of the \( k \) sub-bands.

To obtain the signal covariance matrix \( \varvec{R}_{\varvec{x}} \) from samples covariance matrix \( {\mathbf{R}}_{\varvec{y}} \), we must solve the optimization problem (13).

$$ {\mathbf{min}}\left\| {{\mathbf{R}}_{\varvec{x}} } \right\|_{{\mathbf{1}}} \,subject\,to\,{\mathbf{R}}_{\varvec{y}} = {\mathbf{AR}}_{{\mathbf{X}}} {\mathbf{A}}^{{\mathbf{T}}} $$
(13)

The proposed solution to (13) is a modification of the OMP (Orthogonal Matching Pursuit) algorithm [24] which does not work with vectors, and the Kronecker product is not used, instead it works directly in matrix form as illustrated in the next section.

C. Clasification and Identification

Identification of the occupation or not of each sub-band is done in two stages: (1) decide on the preliminary occupation or not in function of the energy present in each sub-band of the signal estimated in antenna. (2) Decide on the final occupation of the multiband according to the occupation average associated to the preliminary decisions obtained for each sub-band. The spectrum sensing function is possible to complete by identifying the values in the main diagonal of the estimated signal covariance matrix \( {\mathbf{R}}_{{\mathbf{x}}} \), doing \( diag({\mathbf{R}}_{{\mathbf{x}}} ) = \widehat{\varvec{X}}[f] \). Then, to perform energy detection for each sub-band (stage 1), the energy of the signal received is compared to a detection threshold, thus, deciding the occupation or not of a sub-band. Thereby, the energy present in each sub-band can be calculated according to Eq. (14).

$$ \upvarepsilon_{j} \left( f \right) = \left| {\varvec{h}_{j} } \right|^{2} \sum\nolimits_{{Sb_{j} }} {\left| {\widehat{\varvec{X}}[f]} \right|^{2} } $$
(14)

Where \( \upvarepsilon_{j} \) represents energy in the \( j \)-th sub-band over a sequence of \( N \) samples, \( Sb_{j} \) represents the \( j \)-th sub-band, \( \varvec{h}_{j} \) represents the channel response in the \( j \)-th sub-band, and \( \widehat{\varvec{X}}\left[ f \right] \) represents the signal estimated in the multiband. Then, if the energy in the \( j \)-th sub-band is higher than the \( {\mathcal{T}}_{h} (\upvarepsilon_{j} > {\mathcal{T}}_{{h_{j} }} ) \) decision threshold, the decision made is \( {\mathcal{H}}_{1,j} \) (occupied sub-band); on the contrary, the decision is \( {\mathcal{H}}_{0,j} \) (free sub-band - WS).

Detection probabilities, \( P_{{d_{j} }} \), miss detection probability, \( P_{{md_{j} }} , \) and false alarm probability, \( P_{{f_{j} }} \), in the \( j \)-th sub-band are defined as indicated in Eqs. (15), (16) and (17).

$$ P_{{d_{j} }} = P({\mathcal{H}}_{1,j} |{\mathcal{H}}_{1,j} ) $$
(15)
$$ P_{{md_{j} }} = P({\mathcal{H}}_{0,j} |{\mathcal{H}}_{1,j} ) = 1 - P_{{d_{j} }} $$
(16)
$$ P_{{f_{j} }} = P({\mathcal{H}}_{1,j} |{\mathcal{H}}_{0,j} ) $$
(17)

According to the central limit theorem [23], if the number of samples is sufficiently large (≥10 in practice), the test statistics (mean and variance) of \( \upvarepsilon_{j} \) associated to hypotheses \( {\mathcal{H}}_{0,j} \) and \( {\mathcal{H}}_{1,j} \) are normally distributed asymptotically and given by Eqs. (18) and (19).

$$ E(\upvarepsilon_{j} ) = \left\{ {\begin{array}{*{20}l} {2N\sigma_{nj}^{2} :{\mathcal{H}}_{0,j} } \hfill \\ {(SNR_{j} + N)\sigma_{{n_{j} }}^{2} :{\mathcal{H}}_{1,j} } \hfill \\ \end{array} } \right. $$
(18)
$$ Var(\upvarepsilon_{j} ) = \left\{ {\begin{array}{*{20}l} {2N\sigma_{nj}^{4} :{\mathcal{H}}_{0,j} } \hfill \\ {2(2SNR_{j} + N)\sigma_{{n_{j} }}^{4} :{\mathcal{H}}_{1,j} } \hfill \\ \end{array} } \right. $$
(19)

With \( \sigma_{{n_{j} }}^{2} \), noise energy is denoted in the \( j \)-th sub-band and \( SNR_{j} \) denotes the signal to noise ratio in the \( j \)-th sub-band.

Then, the detection probabilities and false alarm in the \( j \)-th sub-band can be expressed, as indicated in Eqs. (20) and (21).

$$ P_{{d_{j} }} = Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - E\left( {\upvarepsilon_{j} |{\mathcal{H}}_{1,j} } \right)}}{{\sqrt[2]{{Var\left( {\upvarepsilon_{j} |{\mathcal{H}}_{1,j} } \right)}}}}} \right] = Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - (SNR_{j} + N)\sigma_{{n_{j} }}^{2} }}{{\sqrt[2]{{2(2SNR_{j} + N)\sigma_{{n_{j} }}^{4} }}}}} \right] $$
(20)
$$ P_{{f_{j} }} = Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - E\left( {\upvarepsilon_{j} |{\mathcal{H}}_{0,j} } \right)}}{{\sqrt[2]{{Var\left( {\upvarepsilon_{j} |{\mathcal{H}}_{0,j} } \right)}}}}} \right] = Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - 2N\sigma_{{n_{j} }}^{2} }}{{\sqrt[2]{{2N\sigma_{{n_{j} }}^{4} }}}}} \right] $$
(21)

Where

$$ Q\left( x \right) = \frac{1}{{\sqrt {2\pi } }}\int_{x}^{\infty } {e^{{ - \frac{{t^{2} }}{2}}} dt} $$
(22)

Thereby, the decision threshold \( {\mathcal{T}}_{{h_{j} }} \) for a specific value of \( P_{{f_{j} }} \) is given by (23).

$$ {\mathcal{T}}_{{h_{j} }} = Q^{ - 1} \left( {P_{{f_{j} }} } \right)\sqrt[2]{{2N\sigma_{{n_{j} }}^{4} }} + 2N\sigma_{{n_{j} }}^{2} $$
(23)

Finally, the detection probabilities, \( P_{d} \), miss detection probability, \( P_{md} \), and false alarm probability, \( P_{f} , \) of the multiband are calculated according to Eqs. (24), (25), and (26).

$$ P_{d} = \frac{1}{K}\sum\nolimits_{j = 1}^{K} {\left\{ {Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - (SNR_{j} + N)\sigma_{{n_{j} }}^{2} }}{{\sqrt[2]{{2(2SNR_{j} + N)\sigma_{{n_{j} }}^{4} }}}}} \right]} \right\}} $$
(24)
$$ P_{md} = \frac{1}{K}\sum\nolimits_{j = 1}^{K} {\left\{ {1 - Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - (SNR_{j} + N)\sigma_{{n_{j} }}^{2} }}{{\sqrt[2]{{2(2SNR_{j} + N)\sigma_{{n_{j} }}^{4} }}}}} \right]} \right\}} $$
(25)
$$ P_{f} = \frac{1}{K}\sum\nolimits_{j = 1}^{K} {\left\{ {Q\left[ {\frac{{{\mathcal{T}}_{{h_{j} }} - 2N\sigma_{{n_{j} }}^{2} }}{{\sqrt[2]{{2N\sigma_{{n_{j} }}^{4} }}}}} \right]} \right\}} $$
(26)

5 Wideband Spectrum Sensing Algorithm

The idea is to reconstruct the covariance matrix, \( \varvec{R}_{\varvec{x}} \), from the representation of the covariance matrix, \( \varvec{R}_{\varvec{y}} , \) as the weighted sum of the lowest amount possible of external products of the columns of matrix \( \varvec{A} \). To perform the estimate of the covariance matrix of the signal it is important to calculate the \( K \) amount of significant components of the multiband signal that permit conducting a correct detection with probability above or equal to 0.95; this amount of significant components represents the amount of iterations the covariance estimation algorithm must perform. Experimental results permit establishing the relation existing between the number of significant components of the multiband signal and the bandwidth total of the multi-band \( B \), the bandwidth of each sub-band (channel) \( b \) and the sub-sampling \( n/m \) factor, as indicated in (27)

$$ K = \left( {\frac{n}{m}} \right)B/b $$
(27)

A. Covariance Estimation Algorithm

Let \( \varvec{X} \in \varvec{ }{\mathbb{R}}^{n} \) be the representation in the frequency domain of signal \( \varvec{x},\varvec{ } \) and \( {\varvec{\Psi}} \in \varvec{ }{\mathbb{R}}^{n \times n} \) the Fourier discrete transformation matrix, such that \( \varvec{X} = {\mathcal{F}}\left( \varvec{x} \right) = {\varvec{\Psi}}\varvec{x} \) where \( \varvec{X} \) presents only k ≪ n significant values (inputs different from zero); upon sampling \( \varvec{X} \) with the sampling matrix \( {\boldsymbol{\varphi }} \in \varvec{ }{\mathbb{R}}^{m \times n} \) where \( k < m < n \) to obtain \( \varvec{y} = {\boldsymbol{\varphi }}\varvec{X} = {\boldsymbol{\varphi }}{\varvec{\Psi}}\varvec{x} = \varvec{Ax} \); if \( {\boldsymbol{\varphi }} \) fulfills the restricted isometry property (RIP) in the \( k \) order [13] and has low coherence with \( {\varvec{\Psi}} \), then \( \varvec{X} \) may be effectively recovered from \( \varvec{y} \). To carry out the estimation process of the signal’s covariance matrix in the channel and solve the problem posed in Eq. (13), we need to use two auxiliary variables. The first of these \( (i,j) \) to avoid re-selecting external products, coordinates \( (i,j) \) keep the indices of the external products that can be selected. The second \( {\mathbf{R}} \in {\mathbb{R}}^{m \times n} \) to store the remainders produced upon removing the external products selected from \( \varvec{R}_{\varvec{y}} \). Initially, \( {\mathbf{R}} \) is equal to \( \varvec{R}_{\varvec{y}} \) and variable \( (i,j) \) starts with all the possible combinations of indices of external products of the columns of the sensing matrix \( \left( {\varvec{i},\varvec{j}} \right) \leftarrow \{ \left( {1,1} \right),\left( {1,2} \right), \ldots ,(n,n)\} \); then the external product is selected that best adapts to the remainder through \( (i_{t} ,j_{t} ) \leftarrow { \arg }\_\max_{{(i^{'} ,j^{'} ) \in \left( {\varvec{i},\varvec{j}} \right)}} \frac{{\left| {\left\langle {{\mathbf{R}},{\mathbf{P}}_{{i^{'} ,j^{'} }} } \right\rangle } \right|}}{{\left\| {{\mathbf{P}}_{{i^{'} ,j^{'} }} } \right\|_{2} }} \), excluding from the indices those corresponding to the external product selected and calculating the weights associated to each external product selected through least squares \( \hat{\varvec{u}} \leftarrow { \arg }\_\min_{\varvec{u}} \left\| {\varvec{R}_{\varvec{y}} - \sum\nolimits_{{t^{'} = 1}}^{t} {u_{{t^{'} }} {\mathbf{P}}_{{i^{'} ,j^{'} }} } } \right\|_{2} \); then the remainder is updated, according to the external products selected and associated weights \( {\mathbf{R}} \leftarrow \varvec{R}_{\varvec{y}} - \sum\nolimits_{{t^{'} = 1}}^{t} {\hat{u}_{{t^{'} }} {\mathbf{P}}_{{i^{'} ,j^{'} }} } \). The process is carried out on \( K \) occasions to obtain the estimated covariance matrix, \( \widehat{\varvec{R}}_{\varvec{x}} \), in which all its inputs are zero, except in the \( K \) inputs that correspond to the external products selected, inputs assigned the calculated weighted values.

B. Wideband Spectrum Sensing Algorithm

To implement the spectrum sensing function, the algorithm illustrated in Fig. 3 is proposed, where the input parameters of the proposed algorithm are: sensing matrix \( {\mathbf{A}} \), samples vector \( {\mathbf{y}} \), the total bandwidth of the multiband \( B \), the bandwidth of each sub-band \( b \), the size \( m \) of samples vector and sample size signal vector \( n \) at Nyquist rate (line 1). The proposed algorithm returns occupied and available sub-bands vector in the multiband denoted by \( \varvec{ch} \) (line 2); two auxiliary variables are used, \( \varvec{Psb} \) to store the energy per sub-band in all multiband (line 3) and \( \varvec{Pc} \) (line 4) which stores the energy of each signal component. The spectrum sensing process starts calculating the sub-bands that are in the multiband (line 7) and the amount of significant components of the multiband (line 8). Then, the signal covariance matrix \( {\mathbf{R}}_{\varvec{x}} \) is estimated by Covariance_Estimation function (line 9). Next, the main diagonal vector of \( {\mathbf{R}}_{\varvec{x}} \) is obtained (line 11) and it contains the estimated energy signal components. The sub-band energy is calculated (line 13), and finally the presence or absence of signal in each sub-band is estimated (lines 14 to 17).

Fig. 3.
figure 3

Compressive wideband spectrum sensing algorithm

Full size image

6 Performance Evaluation

In this section, the performance of the proposed algorithm is analyzed in a multiband signal scenario composed of six sub-bands (channels) of 3.3 MHz bandwidth each, which have a random occupation. To evaluate the performance of the proposed spectrum sensing algorithm, there are used as metrics the detection probability and Receiver Operating Characteristic compared to the metrics obtained from the sequential energy detection algorithm [25] and CS based algorithms [26,27,28,29]; the obtained results are shown in Figs. 4 and 5. In Fig. 4 the performance of the proposed algorithm is observed versus the performance of the other algorithms listed above; in the figure, it can be seen that the performance of the algorithms in [25,26,27,28,29] is lower than the performance achieved by the proposed algorithm. Figure 3 shows that the detection probability of the proposed algorithm is approximately equal to 1 for values of SNR greater than 0 dB, while other algorithms reach this detection probability for higher values of SNR.

Fig. 4.
figure 4

Compressive wideband spectrum sensing algorithm

Full size image
Fig. 5.
figure 5

ROC curves for SNR = 1 dB

Full size image

Figure 5 reveals that the best performance in terms of ROC curves corresponds to the algorithm proposed; this is because the area below the curve of the algorithm proposed is the biggest, indicating the capacity of the algorithm proposed to identify correctly the WS. As also noted in Fig. 5, the algorithm with the worst performance is that proposed by Sun [28], given that the ROC curve indicates a probability of 0.5 of correctly detecting the WS. Considering that the results illustrated in Fig. 5 correspond to the ROC curves of the five algorithms contrasted to an SNR of 1 dB, it is further evidence that the algorithm proposed improves significantly the performance of the other algorithms under low SNR conditions.

7 Conclusions

This article presents a methodological stages to perform spectrum sensing based on compressive sensing, where the validity of the proposal is demonstrated, at same time, is presented a bandwidth spectrum sensing algorithm based on CS, which allows successful signal recovery and identify occupied bands and white spaces reaching a superior performance than sequential energy detector.

The proposed algorithm presents superior performance at SNR values below 5 dB using sub-Nyquist sampling in comparison with sequential energy detector which uses Nyquist sampling rate, at SNR values above 5 dB performance is same.

Similarly, the success of the proposed model based on compressive sensing for spectrum sensing in Cognitive Radio systems, which it can be evidenced, that the proposed model successfully performs the operation of spectrum sensing, but it also makes evident the deficiency in the comprehensive sampling mechanism called a random modulator; the restriction that the ratio \( n/m \) be a whole number, makes the number of samples to be taken from the sparse signal be much higher than the estimated theoretical, in which the one proposed for the simulation scenario would be 36.