Statistical Inference for Incomplete Ranking Data: A Comparison of Two Likelihood-Based Estimators

Abstract

We consider the problem of statistical inference for ranking data, namely the problem of estimating a probability distribution on the permutation space. Since observed rankings could be incomplete in the sense of not comprising all choice alternatives, we propose to tackle the problem as one of learning from imprecise or coarse data. To this end, we associate an incomplete ranking with its set of consistent completions. We instantiate and compare two likelihood-based approaches that have been proposed in the literature for learning from set-valued data, the marginal and the so-called face-value likelihood. Concretely, we analyze a setting in which the underlying distribution is Plackett-Luce and observations are given in the form of pairwise comparisons.

1 Introduction

The study of rank data and related probabilistic models on the permutation space (symmetric group) has a long tradition in statistics, and corresponding methods for parameter estimation have been used in various fields of application, such as psychology and the social sciences [1]. More recently, applications in information retrieval (search engines) and machine learning (personalization, preference learning) have caused a renewed interest in the analysis of rankings and topics such as “learning-to-rank” [2]. Indeed, methods for learning and constructing preference models from explicit or implicit preference information and feedback are among the recent research trends in these disciplines [3].

In most applications, the rankings observed are incomplete or partial in the sense of including only a subset of the underlying choice alternatives, whereas no preferences are revealed about the remaining ones—pairwise comparisons can be seen as an important special case. In this paper, we therefore approach the problem of learning from ranking data from the point of view of statistical inference with imprecise data. The key idea is to consider an incomplete ranking as a set-valued observation, namely the set of all complete rankings consistent with the incomplete observation [4]. This approach is especially motivated by recent work on learning from imprecise, incomplete, or fuzzy data [5,6,7,8,9].

Thus, our paper can be seen as an application of general methods proposed in that field to the specific case of ranking data. This is arguably interesting for both sides, research on statistics with imprecise data and learning from ranking data: For the former, ranking data is an interesting test bed that may help understand, analyze, and compare methods for learning from imprecise data; for the latter, general approaches for learning from imprecise data may turn into new statistical methods for ranking.

In this paper, we compare two likelihood-based approaches for learning from imprecise data. More specifically, both approaches are used for inference about the so-called Plackett-Luce model, a parametric family of probability distributions on the permutation space.

2 Preliminaries and Notation

Let $\mathbb {S}_K$ denote the collection of rankings (permutations) over a set $U=\{a_1, \ldots , a_K\}$ of K items $a_k$, $k \in [K] = \{1, \ldots , K\}$. A complete ranking (a generic element of $\mathbb {S}_K$) is a bijection $\pi : [K] \longrightarrow [K]$, where $\pi (k)$ is the position of the kth item $a_k$ in the ranking. We denote by $\pi ^{-1}$ the ordering associated with a ranking, i.e., $\pi ^{-1}(j)$ is the index of the item on position j. We write rankings in brackets and orderings in parentheses; for example, $\pi =[2,4,3,1]$ and $\pi ^{-1} = (4,1,3,2)$ both denote the ranking $a_4 \succ a_1 \succ a_3 \succ a_2$.

For a possibly incomplete ranking, which includes only some of the items, we use the symbol $\tau$ (instead of $\pi$). If the kth item does not occur in a ranking, then $\tau (k)=~0$ by definition; otherwise, $\tau (k)$ is the rank of the kth item. In the corresponding ordering, the missing items do simply not occur. For example, the ranking $a_4 \succ a_1 \succ a_2$ would be encoded as $\tau =[2,3,0,1]$ and $\tau ^{-1} = (4,1,2)$, respectively. We let $I(\tau ) = \{ k \, : \, \tau (k) > 0 \} \subset [K]$ and denote the set of all rankings (complete or incomplete) by $\overline{\mathbb {S}}_K$.

An incomplete ranking $\tau$ can be associated with its set of consistent extensions $E(\tau ) \subset \mathbb {S}_K$, where

$$\begin{aligned} E(\tau ) = \Big \{ \pi \, : \, (\tau (i)-\tau (j))(\pi (i)- \pi (j)) \ge 0 \text { for all } i , j \in I(\tau ) \Big \} \end{aligned}$$

An important special case is an incomplete ranking $\tau _{i,j}$ in the form of a pairwise comparison $a_i\succ a_j$ (i.e., $\tau _{i,j}(i)=1$, $\tau _{i,j}(j)=2$, $\tau _{i,j}(k) = 0$ otherwise), which is associated with the set of extensions

$$\begin{aligned} E(\tau _{i,j}) = E(a_i \succ a_j) = \{\pi \in \mathbb {S}_K\,:\, \pi (i)<\pi (j)\} . \end{aligned}$$

Modeling an incomplete observation $\tau$ by the set of linear extensions $E(\tau )$ reflects the idea that $\tau$ has been produced from an underlying complete ranking $\pi$ by some “coarsening” or “imprecisiation” process, which essentially consists of omitting some of the items from the ranking. $E(\tau )$ then corresponds to the set of all possible candidates $\pi$, i.e., all complete rankings that are compatible with the observation $\tau$ if nothing is known about the coarsening, except that it does not change the relative order of any items.

Sometimes, more knowledge about the coarsening is available, or reasonable assumptions can be made. For example, it might be known that $\tau$ is a top-t ranking, which means that it consists of the items that occupy the first t positions in $\pi$.

3 Probabilistic Models

Statistical inference requires a probabilistic model of the underlying data generating process, which, in our case, essentially comes down to specifying a probability distribution on the permutation space. One of the most well-known probability distributions of that kind is the Plackett-Luce (PL) model [1].

3.1 The Plackett-Luce Model

The PL model is parametrized by a vector $\theta = (\theta _1, \theta _2, \ldots , \theta _K) \in \varTheta = \mathbb {R}_+^K$. Each $\theta _i$ can be interpreted as the weight or “strength” of the option $a_i$. The probability assigned by the PL model to a ranking represented by a permutation $\pi \in \mathbb {S}_K$ is given by

$$\begin{aligned} {\text {pl}}_\theta (\pi ) \, = \, \prod _{i=1}^K \frac{\theta _{\pi ^{-1}(i)}}{\theta _{\pi ^{-1}(i)} + \theta _{\pi ^{-1}(i+1)} + \cdots + \theta _{\pi ^{-1}(K)}} \end{aligned}$$

(1)

Obviously, the PL model is invariant toward multiplication of $\theta$ with a constant $c >0$, i.e., ${\text {pl}}_\theta (\pi ) = {\text {pl}}_{c \theta }(\pi )$ for all $\pi \in \mathbb {S}_K$ and $c > 0$. Consequently, $\theta$ can be normalized without loss of generality (and the number of degrees of freedom is only $K-1$ instead of K). Note that the most probable ranking, i.e., the mode of the PL distribution, is simply obtained by sorting the items in decreasing order of their weight:

$$\begin{aligned} \pi ^* = \mathop {\hbox {arg max}}\limits _{{\pi \in \mathbb {S}_K}} {\text {pl}}_\theta (\pi ) = \mathop {\hbox {arg sort}}\limits _{{k \in [K]}} \{ \theta _1, \ldots , \theta _K \} \, . \end{aligned}$$

(2)

As a convenient property of PL, let us mention that it allows for a very easy computation of marginals, because the marginal probability on a subset $U' = \{ a_{i_1}, \ldots , a_{i_J} \} \subset U$ of $J \le K$ items is again a PL model parametrized by $(\theta _{i_1}, \ldots , \theta _{i_J})$. Thus, for every $\tau \in \overline{\mathbb {S}}_K$ with $I(\tau ) = U'$,

$$\begin{aligned} {\text {pl}}_\theta (\tau ) = \sum _{\pi \in E(\tau )} {\text {pl}}_\theta (\pi ) = \prod _{j=1}^J \frac{\theta _{\tau ^{-1}(j)}}{\theta _{\tau ^{-1}(j)} + \theta _{\tau ^{-1}(j+1)} + \ldots + \theta _{\tau ^{-1}(J)}} \end{aligned}$$

(3)

In particular, this yields pairwise probabilities

$$\begin{aligned} {\text {pl}}_\theta (\tau _{i,j}) = {\text {pl}}_\theta (a_i \succ a_j) = \frac{\theta _i}{\theta _i + \theta _j} \, . \end{aligned}$$

This is the well-known Bradley-Terry model [1], a model for the pairwise comparison of alternatives. Obviously, the larger $\theta _i$ in comparison to $\theta _j$, the higher the probability that $a_i$ is chosen. The PL model can be seen as an extension of this principle to more than two items: the larger the parameter $\theta _i$ in (1) in comparison to the parameters $\theta _j$, $j \ne i$, the higher the probability that $a_i$ occupies a top rank.

3.2 A Stochastic Model of Coarsening

While (1) defines a probability for every complete ranking $\pi$, and hence a distribution $p:\, \mathbb {S}_K \longrightarrow [0,1]$, an extension of $p$ from $\mathbb {S}_K$ to $\overline{\mathbb {S}}_K$ is in principle offered by (3). One should note, however, that marginalization in the traditional sense is different from coarsening. In fact, (3) assumes the subset of items $U'$ to be fixed beforehand, prior to drawing a ranking at random. For example, focusing on two items $a_i$ and $a_j$, one may ask for the probability that $a_i$ will precede $a_j$ in the next ranking drawn at random according to $p$.

Recalling our idea of a coarsening process, it is more natural to consider the data generating process as a two step procedure:

$$\begin{aligned} p_{\theta , \lambda }(\tau , \pi ) = p_\theta (\pi ) \cdot p_\lambda (\tau \, | \,\pi ) \end{aligned}$$

(4)

According to this model, a complete ranking $\pi$ is generated first according to $p_\theta (\cdot )$, and this ranking is then turned into an incomplete ranking $\tau$ according to $p_\lambda (\cdot \, | \,\pi )$. Thus, the coarsening process is specified by a family of conditional probability distributions

$$\begin{aligned} \big \{ p_\lambda (\cdot \, | \,\pi ) \, : \, \pi \in \mathbb {S}_K , \, \lambda \in \varLambda \big \} , \end{aligned}$$

(5)

where $\lambda$ collects all parameters of these distributions; $p_{\theta , \lambda }(\tau , \pi )$ is the probability of producing the data $(\tau , \pi ) \in \overline{\mathbb {S}}_K \times \mathbb {S}_K$. Note, however, that $\pi$ is actually not observed.

4 Statistical Inference

As for the statistical inference about the process (4), our main interest concerns the “precise part”, i.e., the parameter $\theta$, whereas the coarsening is rather considered as a complication of the estimation. In other words, we are less interested in inference about $\lambda$ or, stated differently, we are interested in $\lambda$ only in so far as it helps to estimate $\theta$. In this regard, it should also be noted that inference about $\lambda$ will generally be difficult: Due to the sheer size of the family of distributions (5), $\lambda$ could be very high-dimensional. Besides, concrete model assumptions about the coarsening process may not be obvious.

Therefore, what we are mainly aiming for is an estimation technique that is efficient in the sense of circumventing direct inference about $\lambda$, and at the same time robust in the sense that it yields reasonably good results for a wide range of coarsening procedures, i.e., under very weak assumptions about the coarsening (or perhaps no assumptions at all). As a first step toward this goal, we look at two estimation principles that have recently been proposed in the literature, both being based on the principle of likelihood maximization.

In the following, the random variable X will denote the precise outcome of a single random experiment, i.e., a complete ranking $\pi$, whereas Y denotes the coarsening $\tau$. We assume to be given an i.i.d. sample of size N and let $\tau =(\tau _1, \ldots , \tau _N) \in (\overline{\mathbb {S}}_K)^N$ denote a sequence of N independent incomplete observations of Y.

4.1 The Marginal Likelihood

The perhaps most natural approach is to consider the marginal likelihood function (also called “visible likelihood” in [10]), i.e., the probability of the observed data Y given the parameters $\theta$ and $\lambda$:

$$\begin{aligned} L_V(\theta , \lambda )= p(\varvec{\tau }\, | \,\theta , \lambda )&= \prod _{i=1}^N p(Y=\tau _i \, | \,\theta , \lambda ) \nonumber \\&= \prod _{i=1}^N \sum _{\pi \in \mathbb {S}_K} p_\theta (\pi ) p_\lambda (\tau _i \, | \,\pi ) \end{aligned}$$

(6)

The maximum likelihood estimate (MLE) would then be given by

$$\begin{aligned} (\theta ^* , \lambda ^*) = \mathop {\hbox {arg max}}\limits _{(\theta , \lambda ) \in \varTheta \times \varLambda } L_V(\theta , \lambda ) \, , \end{aligned}$$

or, emphasizing inference about $\theta$, by

$$\begin{aligned} \theta ^* = \mathop {\hbox {arg max}}\limits _{\theta \in \varTheta } \mathop {\max }\limits _{\lambda \in \varLambda } L_V(\theta , \lambda ) \, . \end{aligned}$$

As can be seen, this approach requires assumptions about the parametrization of the coarsening, i.e., the parameter space $\varLambda$. Of course, since both $\mathbb {S}_K$ and $\overline{\mathbb {S}}_K$ are finite, these assumptions can be “vacuous” in the sense of allowing all possible distributions. Thus, the family (5) would be specified in a tabular form by letting

$$\begin{aligned} p_\lambda (\tau \, | \,\pi ) = \lambda _{\pi , \tau } \end{aligned}$$

(7)

for all $\tau \in \overline{\mathbb {S}}_K$ and $\pi \in E(\tau )$ (recall that $p_\lambda (\tau \, | \,\pi ) = 0$ for $\pi \notin E(\tau )$). In other words, $\varLambda$ is given by the set of all these parametrizations under the constraint that

$$\begin{aligned} \sum _{\tau \in \overline{\mathbb {S}}_K} \lambda _{\pi , \tau } = \sum _{\tau \in E(\tau )} \lambda _{\pi , \tau } = 1 \end{aligned}$$

for all $\pi \in \mathbb {S}_K$. We denote this parametrization by $\varLambda _{vac}$.

4.2 The Face-Value Likelihood

The face-value likelihood is expressed as follows [11, 12]:

$$\begin{aligned} L_F(\theta , \lambda )&= \prod _{i=1}^N P\big ( X\in E(\tau _i) \, | \,\theta ,\lambda \big ) \\&= \prod _{i=1}^N \sum _{\pi \in E(\tau _i)} p_\theta (\pi ) \nonumber \end{aligned}$$

(8)

Note that the face-value likelihood does actually not depend on $\lambda$, which means that we could in principle write $L_F(\theta )$ instead of $L_F(\theta , \lambda )$. Indeed, this approach does not explicitly account for the coarsening process, or at least does not consider the coarsening as a stochastic process. The only way of incorporating knowledge about this process is to replace the set of linear extensions, $E(\tau _i)$, with a smaller set of complete rankings associated with an incomplete observation $\tau _i$. This can be done if the coarsening is deterministic, like in the case of top-t selection.

5 Comparison of the Approaches

These two likelihood functions (6) and (8) coincide when the collection of possible values for Y forms a partition of the collection of permutations $\mathbb {S}_K$, since the events $Y=\tau _i$ and $X\in E(\tau _i)$ are then the same. But they do not coincide in the general case, where the event $Y=\tau _i$ implies but does not necessarily coincide with $X\in E(\tau _i)$.

In the following, we refer to the parameter estimation via maximization of (6) and (8) as MLM (marginal likelihood maximization) and FLM (face-value likelihood maximization), respectively.

5.1 Known Coarsening

A comparison between the marginal and face-value likelihood is arguable in the case where the coarsening is assumed to be known, because, as already said, the face-value likelihood is not able to exploit this knowledge (unless the coarsening is deterministic and forms a partition). Obviously, ignorance of the coarsening may lead to very poor estimates in general, as shown by the following example.

Let $K=3$ and $U=\{a_1, a_2, a_3\}$. To simplify notation, we denote a ranking $a_i \succ a_j \succ a_k$ inducing $\pi ^{-1}=(i, j, k)$ by $a_ia_ja_k$. We assume the PL model and suppose the coarsening to be specified by the following (deterministic) relation between complete rankings $\pi$ and incomplete observations $\tau$, which are all given in the form of pairwise comparisons:

$$\begin{aligned} \begin{array}{c | c c c c c c } &{} a_1\succ a_2 \ &{} \ a_2\succ a_1 \ &{} \ a_1\succ a_3 \ &{} \ a_3\succ a_1 \ &{} \ a_2\succ a_3 \ &{} \ a_3\succ a_2 \\ \hline a_1a_2a_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ a_1a_3a_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ a_2a_1a_3 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ a_2a_3a_1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ a_3a_1a_2 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ a_3a_2a_1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \end{aligned}$$

Denoting by $n_{i,j}$ the number of times $a_i \succ a_j$ has been observed, the face-value likelihood function reads as follows:

$$\begin{aligned} L_F(\varvec{\tau }; \theta )=\prod _{i=1}^3\prod _{j\ne i}\left( \frac{\theta _i}{\theta _i+\theta _j}\right) ^{n_{i , j}} \, . \end{aligned}$$

Let now $n_{ijk}$ denote the number of occurrences of the ranking $a_ia_ja_k$ in the sample. According to the above relation, we have the following:

$$\begin{aligned} n_{1,2}&=0 \\ n_{2,1}&=n_{213}+n_{231}+n_{321} \\ n_{1,2}&=0 \\ n_{1,3}&=n_{312} \\ n_{2,3}&=n_{123} \\ n_{3,2}&=n_{132} \end{aligned}$$

Therefore,

$$\begin{aligned} L_F(\theta ) =&\left( \frac{\theta _2}{\theta _1+\theta _2}\right) ^{n_{213}+n_{231}+n_{321}}\\&\times \left( \frac{\theta _3}{\theta _1+\theta _3}\right) ^{n_{312}} \times \left( \frac{\theta _2}{\theta _2+\theta _3}\right) ^{n_{123}} \times \left( \frac{\theta _3}{\theta _2+\theta _3}\right) ^{n_{132}}. \end{aligned}$$

For an arbitrary triplet $\theta = (\theta _1, \theta _2, \theta _2)$ with $\theta _1+\theta _2+\theta _3= 1$, we observe that

$$\begin{aligned} L_F(\theta _1, \theta _2, \theta _3) \le L_F\left( 0, \theta _2', \theta _3'\right) \, , \end{aligned}$$

where $\theta _2'= \frac{\theta _2}{\theta _2 + \theta _3}$ and $\theta _3'=\frac{\theta _3}{\theta _2 + \theta _3}.$ In fact,

$$\begin{aligned} L_F (0,\theta _2', \theta _3')=(\theta _2')^{n_{123}}\cdot (\theta _3')^{n_{132}} \, , \end{aligned}$$

and therefore

$$\begin{aligned} L_F(\theta )= \left[ \left( \frac{\theta _2}{\theta _1+\theta _2}\right) ^{n_{213}+n_{231}+n_{321}} \cdot \left( \frac{\theta _3}{\theta _1+\theta _3}\right) ^{n_{312}}\right] \times L_F (0,\theta _2', \theta _3') \, , \end{aligned}$$

which is clearly less than or equal to $L_F (0,\theta _2', \theta _3')$. Furthermore, according to Gibb’s inequality, the above likelihood value, $L_F (0,\theta _2', \theta _3')$, is maximized for

$$\begin{aligned} (\hat{\theta }_2', \hat{\theta }_3')=\left( \frac{n_{123}}{n_{123}+n_{132}}, \frac{n_{132}}{n_{123}+n_{132}}\right) \, . \end{aligned}$$

For instance, if we assume that the true distribution over $\mathbb {S}_3$ is PL with parameter $\theta =(\theta _1, \theta _2, \theta _3)=(0.99, 0.005, 0.005)$, then our estimation of $\theta$ based on the face-value likelihood function will be

$$\begin{aligned} \left( 0, \frac{n_{123}}{n_{123}+n_{132}}, \frac{n_{132}}{n_{123}+n_{132}}\right) \, , \end{aligned}$$

which tends to (0, 0.5, 0.5) as n tends to infinity.

5.2 Unknown Coarsening

The comparison between the two approaches appears to be more reasonable when the coarsening is assumed to be unknown. In that case, it might be fair to instantiate the marginal likelihood with the parametrization $\varLambda _{vac}$, because just like the face-value likelihood, it is then essentially ignorant about the coarsening. However, the estimation of the coarsening process under $\varLambda _{vac}$ is in general not practicable, simply because the number of parameters (7) is too large: One parameter $\lambda _{\pi , \tau }$ for each $\tau \in \overline{\mathbb {S}}_K$ and $\pi \in E(\tau )$ makes about $2^K K!$ parameters in total. Besides, $\varLambda _{vac}$ may cause problems of model identifiability. What we need, therefore, is a simplifying assumption on the coarsening.

5.2.1 Rank-Dependent Coarsening

The assumption we make here is a property we call rank-dependent coarsening. A coarsening procedure is rank-dependent if the incompletion is only acting on ranks (positions) but not on items. That is, the procedure randomly selects a subset of ranks and removes the items on these ranks, independently of the items themselves. In other words, an incomplete observation $\tau$ is obtained by projecting a complete ranking $\pi$ on a random subset of positions $A \in 2^{[K]}$, i.e., the family (5) of distributions $p_\lambda (\cdot \, | \,\pi )$ is specified by a single measure on $2^{[K]}$. Or, stated more formally,

$$\begin{aligned} p_\lambda \big ( \pi ^{-1}(A) \, | \,\pi ^{-1} \big ) = p_\lambda \big ( \sigma ^{-1}(A) \, | \,\sigma ^{-1} \big ) \end{aligned}$$

for all $\pi , \sigma \in \mathbb {S}^K$ and $A \subset [K]$, where $\pi ^{-1}(A)$ denotes the projection of the ordering $\pi ^{-1}$ to the positions in A.

In the following, we make an even stronger assumption and assume observations in the form of (rank-dependent) pairwise comparisons. In this case, the coarsening is specified by probabilities

$$\begin{aligned} \Big \{ \lambda _{i,j} \, | \,1 \le i< j \le K , \, \lambda _{i,j} \ge 0, \, \sum _{1 \le i < j \le K} \lambda _{i,j} = 1 \Big \} \, , \end{aligned}$$

where $\lambda _{i,j}$ denotes the probability that the ranks i and j are selected.

5.2.2 Likelihoods

Under the assumption of the PL model and rank-dependent pairwise comparisons as observations, the marginal likelihood for an observed set of pairwise comparisons $a_{i_n} \succ a_{j_n}$, $n \in [N]$, is given by

$$\begin{aligned} L_V(\theta , \lambda ) = \prod _{n=1}^N \sum _{\pi \in \mathbb {S}_K, \pi (i_n) < \pi (j_n)} \lambda _{\pi (i_n),\pi (j_n)} {\text {pl}}_\theta (\pi ) \, . \end{aligned}$$

(9)

The corresponding expression for the face-value likelihood is

$$\begin{aligned} L_F(\theta ) = \prod _{n=1}^N \frac{\theta _{i_n}}{\theta _{i_n} + \theta _{j_n}}= \prod _{i\ne j} \left( \frac{\theta _i}{\theta _i+\theta _j}\right) ^{n_{i,j}}, \, \end{aligned}$$

(10)

where $n_{i,j}$ denotes the number of times $a_i \succ a_j$ has been observed. This is the Bradely-Terry-Luce (BTL) model, which has been studied quite extensively in the literature [13].

Obviously, since the face-value likelihood is ignorant of the coarsening, we cannot expect the maximizer $\hat{\theta }$ of (10) to coincide with the true parameter $\theta$. Interestingly, however, in our experimental studies so far, these parameters have always been asymptotically comonotonic, which is enough to recover the most probable ranking (2). That is, the face-value likelihood seems to yield reasonably strong estimates

$$\begin{aligned} \hat{\pi } = \mathop {\hbox {arg sort}}\limits _{k \in [K]} \left\{ \hat{\theta }_1, \ldots , \hat{\theta }_K \right\} \, , \end{aligned}$$

(11)

for sufficiently large samples, although the parameter $\hat{\theta }$ itself might be biased. The question whether or not this comonotonicity holds in general is still open. Yet, we could prove an affirmative answer at least under an additional assumption.

Theorem 1

Suppose complete rankings to be generated by the PL model with parameters $\theta _1> \theta _2> \cdots > \theta _K$. Moreover, let the coarsening procedure be given by a rank-dependent selection of pairwise comparisons between items where $\lambda$ satisfies the following condition:

$$\begin{aligned} \lambda _{i,j}\ge \lambda _{i',j'}, \text { if } 1\le i\le i'<j'\le j\le K. \end{aligned}$$

Then, for an arbitrarily small $\epsilon >0$ there exists $N_\epsilon \in \mathbb {N}$ such that, for every $N\ge N_\epsilon$ the maximizer $\hat{\theta }$ of (10) satisfies

$$\begin{aligned} \hat{\theta }_1> \hat{\theta }_2> \cdots > \hat{\theta }_K \end{aligned}$$

with probability at least $1-\epsilon$.

The proof of Theorem 1 can be derived from Lemmas 1 to 6.

Lemma 1

Suppose complete rankings to be generated by the PL model with parameters $\theta _{i_1}> \theta _{i_2}> \cdots > \theta _{i_K}$. Given $i\ne j$, let $p_{i_k,i_l}=P(X\in E(a_{i_k}\succ a_{i_l}))=\frac{\theta _{i_k}}{\theta _{i_k}+\theta _{i_l}}$ denote the probability that $a_{i_k}$ is preferred to $a_{i_l}$. Then, the following inequalities hold:

$$\begin{aligned} p_{i_k,i_l}\ge p_{i_{k'},i_{l'}},\ \forall \, k\le k', l \ge l'. \end{aligned}$$

Proof

Straightforward, if we take into account that the mapping $f_c(x)=\frac{x}{x + c}$ is increasing on $\mathbb {R}_+$ for all $c>0$ while $g_c:(x)=\frac{c}{c + x}$ is decreasing on $\mathbb {R}_+$.

Definition 1

Consider a complete ranking $\pi \in \mathbb {S}_K$, and let us consider two indices $i\ne j$. We define the (i, j)-swap ranking, $\pi _{i,j}:[K]\rightarrow [K],$ as follows: $\pi _{i,j}(k)=\pi (k), \ \forall \, k\in [K]\setminus \{i,j\}$, $\pi _{i,j}(i)=\pi (j)$ and $\pi _{i,j}(j)=\pi (i)$.

Lemma 2

Suppose complete rankings to be generated by the PL model ${\text {pl}}_\theta$. Take $i,j\in [K]$ such that $\theta _i>\theta _j$ and $\pi \in \mathbb {S}_K.$ Then:

$$\begin{aligned} \pi (i)<\pi (j) \text { if and only if } {\text {pl}}_\theta (\pi )> {\text {pl}}_\theta (\pi _{i,j}). \end{aligned}$$

Proof

Let us take an arbitrary ranking $\pi \in \mathbb {S}_k$ satisfying the restriction $\pi (i)<\pi (j)$ We can write:

$$\begin{aligned} {\text {pl}}_\theta (\pi )&= C_{i,j} \cdot \frac{\theta _{\pi ^{-1}(\pi (i))}}{\sum _{s=\pi (i)}^{\pi (K)} \theta _{\pi ^{-1}(s)}} \cdot \frac{\theta _{\pi ^{-1}(\pi (j))}}{\sum _{s=\pi (j)}^{\pi (K)} \theta _{\pi ^{-1}(s)}}\\ {\text {pl}}_\theta (\pi _{i,j})&= C_{i,j}\cdot \frac{\theta _{\pi _{i,j}^{-1}(\pi _{i,j}(i))}}{\sum _{s=\pi _{i,j}(i)}^{\pi _{i,j}(K)} \theta _{\pi _{i,j}^{-1}(s)}} \cdot \frac{\theta _{\pi _{i,j}^{-1}(\pi _{i,j}(j))}}{\sum _{s=\pi _{i,j}(j)}^{\pi _{i,j}(K)} \theta _{\pi _{i,j}^{-1}(s)}}, \end{aligned}$$

where

$$\begin{aligned} C_{i,j}&= \prod _{r\not \in \{\pi (i),\pi (j)\}} \frac{\theta _{\pi ^{-1}(r)}}{\theta _{\pi ^{-1}(r)} + \theta _{\pi ^{-1}(r+1)} + \ldots + \theta _{\pi ^{-1}(K)}}\\&= \prod _{r\not \in \{\pi _{i,j}(i),\pi _{i,j}(j)\}} \frac{\theta _{\pi _{i,j}^{-1}(r)}}{\theta _{\pi _{i,j}^{-1}(r)} + \theta _{\pi _{i,j}^{-1}(r+1)} + \ldots + \theta _{\pi _{i,j}^{-1}(K)}}. \end{aligned}$$

According to the relation between $\pi$ and $\pi _{i,j}$, we can easily check the following equality:

$$\begin{aligned} {\sum _{s=\pi (i)}^{\pi (K)} \theta _{\pi ^{-1}(s)}} ={\sum _{s=\pi _{i,j}(j)}^{\pi _{i,j}(K)} \theta _{\pi _{i,j}^{-1}(s)}} \end{aligned}$$

(In fact, both $\theta _i$ and $\theta _j$ appear in both sums). Therefore, ${\text {pl}}_\theta (\pi )>{\text {pl}}_\theta (\pi _{i,j})$ if and only if ${\sum _{s=\pi (j)}^{\pi (K)} \theta _{\pi ^{-1}(s)}}<{\sum _{s=\pi _{i,j}(i)}^{\pi _{i,j}(K)} \theta _{\pi _{i,j}^{-1}(s)}}.$ Furthermore, we observe that:

$$\begin{aligned} {\sum _{s=\pi (j)}^{\pi (K)} \theta _{\pi ^{-1}(s)}}-{\sum _{s=\pi _{i,j}(i)}^{\pi _{i,j}(K)} \theta _{\pi _{i,j}^{-1}(s)}}=\theta _j-\theta _i, \end{aligned}$$

and therefore ${\text {pl}}_\theta (\pi )>{\text {pl}}_\theta (\pi _{i,j})$ if and only if $\theta _j<\theta _i$.

Lemma 3

If $a>a'$ and $b>b'$ then $ab+a'b'>ab'+a'b.$

Proof

Straightforward.

Lemma 4

Suppose that $\lambda _{k,l}\ge \lambda _{k',l'}$ for all $k,l,k',l'$ such that $k\le k'$, $l\ge l'$, $k< l$ $k'<l'$. Suppose complete rankings to be generated according to a distribution $p$ satisfying $p(\pi )>p(\pi _{i,j})$ for every $\pi \in E(a_i\succ a_j)$, for every pair $i<j$. Let $q_{i,j}=\sum _{\pi \in E(a_i>a_j)} p(\pi ) \lambda _{\pi (i), \pi (j)}$, for all $i\ne j$ denote the probability of observing that $a_i$ is preferred to $a_j$. Then

$$\begin{aligned} q_{i,j}>q_{i',j'}\text { if } i\le i' \text { and } j\ge j'. \end{aligned}$$

Proof

We will divide the proof into three cases.

• Let us first prove that $q_{i,j}>q_{j,i}$, for all $i<j$. By definition, we have:

  $$\begin{aligned} q_{i,j}=\sum _{\pi \in E(a_i>a_j)} p(\pi ) \lambda _{\pi (i), \pi (j)} \text { and } q_{j,i}=\sum _{\pi \in E(a_j>a_i)} p(\pi ) \lambda _{\pi (j), \pi (i)}. \end{aligned}$$

  Furthermore, $E(a_j\succ a_i)=\{\pi _{i,j}\,:\, \pi \in E(a_i\succ a_j)\}$ and thus we can alternatively write:

  $$\begin{aligned} q_{j,i}=\sum _{\pi \in E(a_i>a_j)} p(\pi _{i,j}) \lambda _{\pi _{i,j}(j), \pi _{i,j}(i)}=\sum _{\pi \in E(a_i>a_j)} p(\pi _{i,j}) \lambda _{\pi (i), \pi (j)}. \end{aligned}$$

  We easily deduce that $q_{i,j}>q_{j,i}, \ \forall \, i<j$ from the above hypotheses.

• Let us now prove that $q_{i,j}>q_{i+1, j},$ for all (i, j) with $i+1<j.$ By definition we have:

  $$\begin{aligned} q_{i,j}=\sum _{\pi \in E(a_i>a_j)} p(\pi ) \lambda _{\pi (i), \pi (j)}=\sum _{\pi \in \mathbb {S}_k} p(\pi ) \alpha _{\pi (i), \pi (j)}, \end{aligned}$$

  where $\alpha _{k,l}=\lambda _{k,l}$ for $k<l$ and $\alpha _{k,l}=0$ otherwise. We can alternatively write:

  $$\begin{aligned} q_{i,j}=\sum _{\pi \in E(a_i>a_{i+1})} p(\pi ) \alpha _{\pi (i), \pi (j)}+\sum _{\pi \in E(a_{i+1}>a_{i})} p(\pi ) \alpha _{\pi (i), \pi (j)}, \end{aligned}$$

  or, equivalently:

  $$\begin{aligned} q_{i,j}=\sum _{\pi \in E(a_i>a_{i+1})} [p(\pi ) \alpha _{\pi (i), \pi (j)}+ p(\pi _{i,i+1}) \alpha _{\pi (i+1), \pi (j)}]. \end{aligned}$$

  Analogously, we can write:

  $$\begin{aligned} q_{i+1,j}=\sum _{\pi \in E(a_i>a_{i+1})} [p(\pi ) \alpha _{\pi (i+1), \pi (j)}+ p(\pi _{i,i+1}) \alpha _{\pi (i), \pi (j)}]. \end{aligned}$$

  Now, according to the hypotheses, for every $\pi \in E(a_i\succ a_{i+1})$, $p(\pi )>p(\pi _{i,i+1})$ and $\alpha _{\pi (i), \pi (j)}>\alpha _{\pi (i+1), \pi (j)}.$ Then, we can easily deduce from Lemma 3 that $q_{i,j}>q_{i+1,j}$.

• It remains to prove that $q_{i,j}>q_{i, j-1}$ for all (i, j) with $i+1<j.$ The proof is analogous to the previous one.

Lemma 5

For every $i\ne j$ let $n_{i,j}$ the number of times $a_i\succ a_j$ is observed in a sample of size N. Given $\epsilon >0$ there exists $N_\epsilon \in \mathbb {N}$ such that for every $N\ge N_\epsilon$, the following equalities hold with probability at least $1-\epsilon$:

$$\begin{aligned} n_{i,j}\ge n_{i',j'}, \ \forall \, 1\le i\le i'<j' \le j\le K. \end{aligned}$$

Proof

This result is a direct consequence of the WLLN and Lemma 4.

Lemma 6

Consider the mapping $g: \mathscr {M}_K(\mathbb {R}_+)\times \mathscr {M}_K (\mathbb {R}_+)\rightarrow \mathbb {R}_+$ defined over the collections of pairs of K-square matrices of positive numbers as follows:

$$\begin{aligned} g(\mathbf {r}, \mathbf {s})=g((r_{i,j})_{i,j\in [K]}, (s_{i,j})_{i,j\in [K]})=\prod _{i\ne j} r_{i,j}^{s_{i,j}}. \end{aligned}$$

Suppose that the matrix $\mathbf {s}=(s_{i,j})_{i,j\in [K]}$ satisfies the following restriction:

$$\begin{aligned} s_{i,j}\ge s_{i',j'}, \text { if } i\le i', j\ge j'. \end{aligned}$$

Suppose that there exists $i^{*}\ne j^{*}$ such that $r_{i,j}\le r_{i',i'}$ for all $(i,j), (i',j')$ with:

$$\begin{aligned} i\le i', j\ge j', \ \{i,j\}\cap \{i^*,j^*\}\ne \emptyset \text { and } \{i',j'\}\cap \{i^*,j^*\}\ne \emptyset . \end{aligned}$$

Consider the matrix $\mathbf {r'}=(r'_{i,j})_{i\in {K}, j\in [K]}$ where: $r'_{i,j}=r_{\sigma (i), \sigma (j)}$, where $\sigma \in \mathbb {S}_K$ swaps $i^*$ and $j^*$, i.e., $\sigma (i^*)=j^*, \ \sigma (j^*)=i^*, \ \sigma (k)=k, \ \forall \, k\in [K]\setminus \{i^*,j^*\}$.

Then $g(\mathbf {r'}, \mathbf {s})\ge g(\mathbf {r},\mathbf {s}).$

Proof

It is easy to prove that, under the above conditions, the ratio $\frac{g(\mathbf {r'}, \mathbf {s})}{g(\mathbf {r},\mathbf {s})}$ is greater than 1.

5.2.3 Experiments

In order to compare the two approaches experimentally, synthetic data was produced by fixing parameters $\theta$ and $\lambda$ and drawing N samples at random according to (4). Then, estimations $\hat{\theta }$ and $\hat{\pi }$ were obtained for both likelihoods, i.e., by maximizing (9) and (10). As a baseline, we also included estimates of $\theta$ assuming the coarsening $\lambda$ to be known; to this end, (9) is maximized as a function of $\theta$ only. The three approaches are called MLM, FLM, and TLM, respectively.

The quality of estimates is measured both for the parameters and the induced rankings (11), in terms of the Euclidean distance between $\theta$ and $\hat{\theta }$, and in terms of the Kendall distance (relative number of pairwise inversions between items) between $\pi$ and $\hat{\pi }$. The expectations of the quality measures were approximated by averaging over 100 simulation runs.

Fig. 1

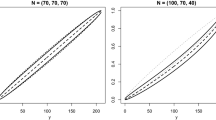
Euclidean distance of parameter estimate $\hat{\theta }$ (left column) and Kendall distance of predicted ranking $\hat{\pi }$ (right column) for three experimental settings: uniform selection of pairwise comparisons (top), top-2 selection (middle), and rank-proportional selection (bottom). Curves are plotted in solid lines for MLM, dashed for FLM, and dotted for TLM

Here, we present results for a series of experiments with parameters $K=4$, $\theta = (0.4, 0.3, 0.2, 0.1)$, and different assumptions on the coarsening:

• In the first experiment, we set $\lambda _{1,2}= \cdots = \lambda _{3,4}= 1/6$. Thus, pairwise comparisons are selected uniformly at random. In this case, the face-value likelihood coincides with the likelihood of $\theta$ assuming the coarsening to be known, so this setting is clearly in favor of FLM (which, as already said, also coincides with TLM). Indeed, as can be seen in Fig. 1 (top), FLM yields very accurate estimates that improve with an increasing sample size. Nevertheless, MLM is not much worse and performs more or less on a par.

• In the second experiment, $\lambda _{1,2}= 1$ and $\lambda _{1,3} = \lambda _{1,4} = \cdots = \lambda _{3,4}=0$. This corresponds to the top-2 setting, in which always the two items on the top of the ranking are observed. As expected, FLM now performs worse than MLM. As can be seen in Fig. 1 (middle, left), the parameter estimates of FLM are biased. Nevertheless, the estimation $\hat{\pi }$ is still decent (Fig. 1, middle, right) and continues to improve with increasing sample size.

• In the last experiment, items are selected with a probability inversely proportional their ranks: $\lambda _{i,j} \propto (8-i-j)$. Thus, pairs on better ranks are selected with a higher probability than pairs on lower ranks. The results are shown in Fig. 1 (bottom). As can be seen, FLM is again biased and performs worse than MLM. However, the bias and the difference in performance are much smaller than in the top-2 scenario. This is hardly surprising, given that the coarsening $\lambda$ in this experiment is less extreme than in the top-2 case. Instead, it is closer to the uniform coarsening of the first experiment, for which, as already said, FLM is the right likelihood.

6 Conclusion

This paper is meant as a first step toward learning from incomplete ranking data based on methods for learning from imprecise (set-valued) data. Needless to say, the scope of the paper is very limited, both in terms of the methods considered (inference based on the marginal and the face-value likelihood) and the setting analyzed (observation of pairwise comparisons based on the PL model with rank-dependent coarsening)—generalizations in both directions shall be considered in future work. Nevertheless, our results clearly reveal some important points:

• The arguably “correct” way of tackling the problem is complete inference about $(\theta , \lambda )$, i.e., about the complete data generating process, as done by MLM. While this approach will guarantee theoretically optimal results, it will not be practicable in general, unless the number of items is small or the parametrization of the coarsening process is simplified by very restrictive assumptions.

• Simplified estimation techniques such as FLM, which make incorrect assumptions about the coarsening or even ignore this process altogether, will generally lead to biased results.

• Yet, in the context of ranking data, one has to distinguish between the estimation of the parameter $\theta$, i.e., the identification of the model, and the prediction of a related ranking $\pi$ (typically the most probable ranking given $\theta$, i.e., the mode of the distribution). Indeed, the main interest often concerns $\pi$, while $\theta$ only serves an auxiliary purpose. As shown by the case of FLM, a biased estimation of $\theta$ does not exclude an accurate prediction of $\pi$, at least under certain assumptions on the coarsening process.

These observations suggest a natural direction for future work, namely the search for methods that achieve a reasonable compromise in the sense of being practicable and robust at the same time, where we consider a method robust if it guarantees a strong performance over a broad range of relevant coarsening procedures. Such methods should improve on techniques that ignore the coarsening, albeit at an acceptable increase in complexity.