Keywords

1 Introduction

With the increasing use of flexible structures in civil engineering, it has become important to develop strategies to reduce the vibrations experimented by them. Because of the large flexibility, the vibrations amplitudes can grow to unwanted values. This leaded to an extensive research into active, semi-active and passive vibration control methods, where the latter ones standout due to no need of external energy source and its robustness.

Among these strategies, the passive control with viscoelastic materials (VEM) has shown reasonable efficiency. These materials have low bearing properties with high dissipative capacity when subjected to cyclic shear deformations. That is the main reason that justifies the wide application of VEM in sandwich layers with stiff elastic materials working as a passive control system. This type of vibration control has experienced a growth in practical applications also due to some benefits related to cost-effectiveness [1,2,3].

The differences between the behavior of viscoelastic and other materials are basically due to its frequency dependent rheological properties. Because of this and due to the difficulties to establish models in time domain, time domain models are not as numerous as the frequency domain models. In view of the benefits that the time domain models may directly provide, such as the maximum displacement range, many researchers have been working on numerical methods to simulate the dynamical response of VEM in time domain.

Among the time-domain based methods for VEM, those that introduce extra dissipation coordinates or internal variables in a Finite Element Model have been applied in several applications, e.g. Golla-Hughes-McTavish (GHM) method [4, 5] and Anelastic Displacement Field model (ADF) [6, 7]. In recent years, time-domain models based on fractional derivative calculus [8,9,10] are attracting attention due to its advantages: the reduced computational memory consumption, precision on its results and easiness to curve fit experimental data.

Another advantage of fractional derivative (FD) models is its theoretical approach. That seems to be more suitable to model VEM than the GHM and ADF models. The actual mechanical behavior of a VEM is a function of its whole histories of stresses and strains experienced. In regard to this, it will be shown that the evaluation of fractional derivatives allows a direct approach to account these histories.

In this way, the present work presents a computational FD model and it is used to evaluate the behavior of viscoelastic sandwich beam. Comparisons between experimental and numerical results are also presented.

2 Viscoelastic Fractional Derivative Based Model

Traditionally, the behavior of linear viscoelastic materials may be represented by means of rheological models composed of linear elastic and linear viscous elements. These basic elements have their stress-strain relations well defined and they are given, respectively, by the following equations:

$$ \sigma (t) = E\varepsilon (t)\,{\rm and} $$
(1)
$$ \sigma (t) = \eta_{v} D\varepsilon (t), $$
(2)

where σ(t) and ε(t) are the stress and strain time dependent functions, E is the Young modulus, η ν is the viscosity and D is the first order derivative operator. Considering the concepts of fractional calculus one can write a general stress-strain relation as:

$$ \sigma (t) = pD^{\alpha } \varepsilon (t), $$
(3)

where σ(t) and ε(t) are the stress and strain time dependent functions, p is a proportionality factor, α is the derivative order, with α ϵ [0,1], and D α is the fractional derivative operator defined by Riemann-Liouville as:

$$ D^{\alpha } x\left( t \right) = \frac{{d^{\alpha } }}{{dt^{\alpha } }}x\left( t \right) = \frac{1}{{{{\Gamma }}(1 - \alpha )}}\frac{d}{dt}\mathop \smallint \nolimits_{0}^{t} \frac{x(s)}{{(t - s)^{\alpha } }}ds , $$
(4)

with Γ(t) being the gamma function.

In that way, when α = 0 Eq. (3) becomes the linear elastic model (σ(t) = pε(t)) and when α = 1 this equation becomes the linear viscous model (\( \sigma \left( t \right) = p\dot{\varepsilon } \left( t \right) \)), or dashpot element. Therefore, as soon as α assumes values on interval [0,1], one has a model with intermediary behavior. A graphical interpretation of these three elements can be seen in Fig. 1.

Fig. 1.
figure 1

Rheological elements used in viscoelasticity: (a) elastic, (b) dashpot and (c) fractional order elements

Full size image

Considering the Standard Linear Solid rheological model, or Zener model, and its mathematical representation given by:

$$ \sigma \left( t \right) + \tau \dot{\sigma }\left( t \right) = E_{0} \varepsilon \left( t \right) + \tau E_{\infty } \dot{\varepsilon }\left( t \right), $$
(5)

where τ is the relaxation time, E 0 is the relaxated Young modulus and E ∞ is the non-relaxated Young modulus. This model can be written using de fractional derivative operator, D α, in the following way:

$$ \sigma \left( t \right) + \tau^{\alpha } D^{\alpha } \sigma \left( t \right) = E_{0} \varepsilon \left( t \right) + \tau^{\alpha } E_{\infty } D^{\alpha } \varepsilon \left( t \right) $$
(6)

One challenge to implement a computational model with Eq. (6) is the numerical evaluation of fractional order derivatives. Diethelm et al. [11] present different ways to numerically evaluate the fractional derivatives. The Grünwald-Letnikov definition is the one that seems to be the most attractive one, since it is valid for any value of α and its easiness of computational implementation. The Grünwald-Letnikov definition is given by:

$$ D^{\alpha } x\left( t \right) \approx {{\Delta }}t^{ - \alpha } \mathop \sum \nolimits_{j = 0}^{{N_{t} }} A_{j + 1} x(t - j{{\Delta }}t), $$
(7)

where ∆t is the time step increment, N t is the number of time steps considered to evaluate the fractional and A j+1 the Grünwald coefficients given by:

$$ A_{j + 1} = \frac{j - \alpha - 1}{j}A_{j} , $$
(8)

with A 1 = 1.

For illustrative purposes Table 1 presents some values of Grünwald coefficients for four values of α. As can be seen, the Aj+1 coefficients take smaller values as j increases, when j = 99 the coefficients are lower than 10−3. Therefore, it can be said that the contribution of first time instants becomes smaller as j increases. In this context, the full history of x(t) need not to be computed.

Table 1. Grünwald coefficients for different values of α and j
Full size table

Analyzing Eq. (7), one can observe that the numerical evaluation of Dx α(t) depends on the functions history, x(t − j∆t). Therefore, in order to numerically evaluate the model defined by Eq. (6) it is necessary to evaluate the derivatives and store the stresses and strains histories, σ(t) and ε(t). In order to reduce the computational cost of the model, Glaucio et al. [12] introduce an internal variable, \( \bar{\varepsilon }\left( t \right) \), to eliminate the fractional derivative D α σ(t). This variable is defined by the following expression:

$$ \bar{\varepsilon }\left( t \right) = \varepsilon \left( t \right) - \frac{\sigma \left( t \right)}{{E_{\infty } }}. $$
(9)

Applying the Finite Element Method on Eqs. (6) and (9), one can show that is possible to write the following equation system for a discrete time instant t = n + 1:

$$ {\mathbf{M}}\ddot{\mathbf{q}}_{n + 1} + E_{0} \left( {1 + c\frac{{E_{\infty } - E_{0} }}{{E_{\infty } }}} \right){\mathbf{K}}_{v} {\mathbf{q}}_{n + 1} + cE_{\infty } {\mathbf{K}}_{v} \mathop \sum \nolimits_{j = 1}^{{N_{t} }} A_{j + 1} {\bar{\mathbf{q}}}_{n + 1 - j} = {\mathbf{F}}_{n + 1} , $$
(10)
$$ {\bar{\mathbf{q}}}_{{n + 1}} = \left( {1 - c} \right)\frac{{E_{{\infty}} - E_{0}}}{{E_{\infty } }}{\mathbf{q}}_{n + 1} - c\mathop \sum \nolimits_{{j = 1}}^{{N_{t} }} A_{j + 1} {\bar{\mathbf{q}}}_{n + 1 - j} , $$
(11)

where M is the mass matrix, K v is the geometrical contribution of stiffness, q is the displacement vector, \( {\bar{\mathbf{q}}} \) is an auxiliary displacement vector, F the force vector and \( c = \frac{{\tau^{\alpha } }}{{\tau^{\alpha } + {{\Delta }}t}} \).

3 Experimental Data

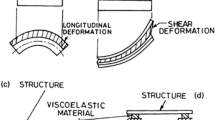
In order to evaluate the viscoelastic model, experimental data was taken from literature. Huang et al. [13] performed a wide laboratory study. In these laboratory studies, a set of thirty sandwich beams were tested. The beams layer configuration consists in two elastic layers (base beam and clamped restraining layer) and one viscoelastic layer, as can be seen at Fig. 2.

Fig. 2.
figure 2

An extract of the Finite Element mesh used to model the viscoelastic sandwich beams.

Full size image

From this set two sandwich beams were selected, here called SB-1 and SB-2. These beams have rectangular cross section and 290 mm length; the base beam has 1.91 mm height; the viscoelastic layer of SB-1 has 1.0 mm height and 1.96 mm on SB-2; and the elastic constraining layers has 0.5 and 1.96 mm height for SB-1 and SB-2 beams, respectively.

The elastic material was aluminium and the viscoelastic material used was ZN-1, developed by Aerospace Research Institute of Materials & Processing Technology (ARIMT). Some mechanical properties of these materials are listed in Table 2.

Table 2. Mechanical properties of beam materials.
Full size table

These beams were excited under the action of a hammer impact and the transversal accelerations were measured and at the free end section. The experimental measurements in terms of natural frequencies, F n , and damping ratios, ξ, for the first three vibration modes are presented in Table 3.

Table 3. Experimental results in terms of natural frequencies and damping ratios of SB-1 and SB-2 beams.
Full size table

Usually structural damping is in the order of 0.5% [14]. Analyzing the data from Table 3, one can see that this type of vibration control can improve significantly the damping ratios of original structures.

3.1 VEM Characterization

Huang et al. [13] present the results of VEM characterization test in terms of Young Modulus, \( E^{'} \left( \omega \right) \), and Loss Factor, η(ω), for frequencies between 5 and 600 Hz. After the values of Complex Modulus are experimentally determined, one can adjust the curves of the real part of the Complex Modulus and the loss factor for the points obtained experimentally. In the case of the presented fractional derivative formulation, they are given, in terms of Shear Modulus, by:

$$ E^{'} \left( \omega \right) = \frac{{E_{0} + \left( {E_{\infty } + E_{0} } \right)\left( {\omega \tau } \right)^{\alpha } \cos \left( {\pi \alpha /2} \right) + E_{\infty } \left( {\omega \tau } \right)^{2\alpha } }}{{1 + 2\left( {\omega \tau } \right)^{\alpha } \cos \left( {\pi \alpha /2} \right) + \left( {\omega \tau } \right)^{2\alpha } }}\;{{\rm and}} $$
(12)
$$ \eta \left( \omega \right) = \frac{{\left( {E_{\infty } + E_{0} } \right)\left( {\omega \tau } \right)^{\alpha } \sin \left( {\pi \alpha /2} \right)}}{{E_{0} + \left( {E_{\infty } + E_{0} } \right)\left( {\omega \tau } \right)^{\alpha } \cos \left( {\pi \alpha /2} \right) + E_{\infty } \left( {\omega \tau } \right)^{2\alpha } }}. $$
(13)

where ω is the system’s vibration frequency, defined in hertz.

Equations from (12) and (13) were used to determine the materials parameters. In this work, it was applied a Particle Swarm Optimization (PSO) algorithm based strategy [15] in order to curve fit the characterization equations.

Using the experimental data, the material parameters could be determined. These fitted values, defined in terms of Young modulus, are: E 0 = 1.9 × 105 Pa, E ∞ = 9.1318 × 108 Pa, τ = 2.1614 × 10−7 s and α = 0.59088. Figure 3 shows two graphics comparing the experimental values and the adjusted curves of \( E^{'} \left( \omega \right) \) and η(ω).

Fig. 3.
figure 3

Experimental values and fitted curves of \( E^{'} \left( \omega \right) \) and η(ω).

Full size image

4 Numerical Evaluation

In order to numerically simulate the dynamical behavior of the beams, the structures were discretized meshes as the ones stated by Barbosa and Farage [16]. Figure 4 presents an extract of the Finite Element mesh actually used to model SB-1 and SB-2 beams. This figure presents the Finite Element mesh and a representation of the beams layers overlapped. It also presents the dimensions of base beam, H bb , damping layer, H dp , and constraining layer, H cr .

Fig. 4.
figure 4

An extract of the finite element mesh used to model the viscoelastic sandwich beams.

Full size image

As can be seen, the elastic layers are modeled with Plane Frame elements and the damping layer with LST elements (quadratic triangular Finite Elements with 6 nodes). The elastic and damping layers are connected with rigid link elements in order to simulate the null line eccentricity of the elastic layers, e 1 and e 2. These elements are defined with plane frame elements with negligible mass and its Young modulus is 1000× the one of elastic layers. The final mesh was defined with 18240 LST elements and 2280 elements for each elastic layer; this mesh has 2079 nodes and 5346 dof. This configuration was achieved through a convergence analysis.

Once the mesh was defined, the value of the parameter N t could be determined through another convergence analysis. The adopted value is N t  = 402 for SB-1 beam and N t  = 355 for SB-2 beam. The time step during the simulations was ∆t = 10−4 s.

The models were simulated under the action of a hammer impact at 72.5 mm from cantilever and the transversal displacements were observed along the time, at same point. With the models given by Eqs. (8) and (9), the time response of the beams could be obtained. Natural frequencies and damping ratios were extracted by means of an automatic Stochastic Subspace Identification algorithm as proposed by Cabboi et al. [17].

5 Results

Tables 4 and 5 list the natural frequencies and damping ratios numerically obtained for the analyzed sandwich beams. They also present the errors between experimental and numerical results.

Table 4. Comparisons of numerical and experimental evaluations of SB-1 beam in terms of natural frequencies and damping ratios.
Full size table
Table 5. Comparisons of numerical and experimental evaluations of SB-2 beam in terms of natural frequencies and damping ratios
Full size table

6 Conclusions

This study evaluated a fractional derivative based model in order to establish a computational model to simulate viscoelastic materials acting as structural sandwich dampers. Based on experimental data available in literature, it was shown that this type of passive control significantly improve the damping rates, since the damping contribution of the elastic beams were close to zero and, after the damping treatment, the sandwich beams achieved significant values for damping ratio as shown in Table 3. As one can observe, beams with thicker viscoelastic layers present higher damping rate than those with thinner ones. Nevertheless, this behavior tends to vanish at high vibration modes.

Comparing the obtained responses of the computational FD viscoelastic model with of their experimental counterpart, it is possible to notice that natural frequencies identified with the numerical model have good agreement with the experimental counterpart for all tested beams. Despite the good agreement between the experimental characterization data and the fitted curves, the numerical model tends to under-evaluate ξ values for higher frequencies. Previous results [18] show that those differences are mostly due to the experimental dispersion observed in the VEM characterization data and in the damping ratios. Despite this, other factors such as: the methodology used on modal identification and the Finite Element discretization, also play a significant influence on numerical results.

Considering the difficulties on predicting damping ratios, the authors suggest that this model is accurate enough to be used to predict damping in current structures.