Upper Bounds Categorization for Constrained Two-Dimensional Guillotine Cutting

Abstract

In the two-dimensional cutting problem, a large rectangular sheet has to be dissected into smaller rectangular desired pieces. If limits exist on the number of extracted pieces, the problem is classified as constrained, with a wide range of applications. Most literature solving methods are based on ad hoc tree search strategies, with top-down or bottom-up approach. In both cases, lower and upper bounds are exploited, leading to branch and bound algorithms. We present a review of the upper bounds and identify a set of features for their categorization.

1 Problem Formulation and Solution Methods

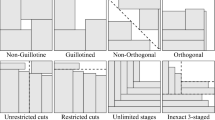
In the class of cutting and packing (C&P) problems, a strong interest has been shown in literature for the two-dimensional problems. Main applications are in the production of materials, for which the constraint of guillotine cuts is often needed.

We consider the problem where a large rectangular object (sheet or plate) has to be dissected to extract rectangular piece types, with guillotine cuts. According to [34], this problem is classified as guillotine variant of 2-dimensional rectangular SLOPP (Single Large Object Placement Problem), but it is often referred to as 2-Dimensional Cutting, or 2DC/TDC (e.g. in [12]). This problem is NP-hard [22].

In case of limited piece demands, the problem is constrained (C2DC), otherwise unconstrained (U2DC) if all demands are unlimited. According to the relation between profit and area of the pieces, the problem is weighted or unweighted. Most authors use a fixed orientation, i.e. with no chance to rotate pieces.

We treat the C2DC, both weighted and unweighted, with fixed orientation. In the following we formalize the problem and describe the existing methods to solve it. In Sect. 2 we present four classification criteria for related upper bounds. In Sect. 3 we match the upper bounds with a proper list of literature papers.

A rectangular sheet (L, W) and n piece types (t ₁,…, t _n ) are given. Each type t _i has dimensions (l _i , w _i ), demand d _i and profit π _i . We refer to the ratio π _i / (l _i · w _i ) as profitability. The problem is unweighted if π _i  = l _i · w _i for all i. The pieces cannot be rotated to (w _i , l _i ). A vector B = (b ₁,…, b _n ) represents a set of pieces with frequencies b _i and profit π(B) = b ₁ ·π ₁ + … + b _n ·π _n . It is a cutting pattern if its pieces can be extracted using guillotine cuts. It is feasible if b _i ≤ d _i for all i. All parameters are positive integers. The goal is to maximize π(B) over all feasible patterns.

1.1 Dynamic Programming Methods

The knapsack function [15] f _U gives the best profit in the unconstrained case for any rectangle (l, w). It is computed in recursion (1)–(2.a, 2.b, 2.c) as best among f _U,0 (one piece term), f _U,v or f _U,h (vertical/horizontal cut, i.e. horizontal/vertical merge).

$$f_{U} \left( {l,w} \right) = \hbox{max} \left\{ {f_{U,0} \left( {l,w} \right),f_{U,v} \left( {l,w} \right),f_{U,h} \left( {l,w} \right)} \right\},0 \le l \le L;0 \le w \le W$$

(1)

$$f_{U,0} \left( {l,w} \right) = \hbox{max} \{ 0;\pi_{i} :l_{i} \le l,w_{i} \le w\}$$

(2.a)

$$f_{U,v} \left( {l,w} \right) = \hbox{max} \left\{ {0;f_{U} \left( {x_{1} ,w} \right) + f_{U} \left( {x_{2} ,w} \right):0 < x_{1} \le x_{2} ,x_{1} + x_{2} = l} \right\}$$

(2.b)

$$f_{U,h} \left( {l,w} \right) = \hbox{max} \left\{ {0;f_{U} \left( {l,y_{1} } \right) + f_{U} \left( {l,y_{2} } \right):0 < y_{1} \le y_{2} ,y_{1} + y_{2} = w} \right\}$$

(2.c)

Two implementations exist. We refer to them as bottom-up and top-down respectively, as used in literature for the tree search solution methods. In the first case, an outer loop scrolls all couples (x ₂, y ₂) in increasing order (one line per time). Two independent inner loops, on x ₁ and y ₁ respectively, generate horizontal or vertical merging, with dimensions (x ₁ + x ₂, y ₂) or (x ₂, y ₁ + y ₂). This approach has been followed in [15] and in recent improvements [28, 29]. In the second case, the couples (l, w) scrolled at the outer loop represent the dimensions of a dissected rectangle, whereas x ₁ and y ₁ in the inner loops correspond to cut coordinates.

If demands are limited, the piece sets have to be considered. Let B ₀ = (d ₁, d ₂, …, d _n ) be the set with full demands d _i , and B a generic subset with frequencies b _i ≤ d _i .

Let f _C (l, w, B) be the best profit for a rectangle (l, w) with the available piece set B. The following recursion (3)–(4.a, 4.b, 4.c), similar to (1)–(2.a, 2.b, 2.c), allows to compute all f _C (l, w, B) values. In (4.b) and (4.c) the set B is partitioned between the two sub-rectangles generated by the vertical or the horizontal cut respectively.

$$\begin{aligned} f_{C} \left( {l,w,B} \right) & = \hbox{max} \left\{ {f_{C,0} \left( {l,w,B} \right),f_{C,v} \left( {l,w,B} \right),f_{C,h} \left( {l,w,B} \right)} \right\}, \\ & \quad 0 \le l \le L;0 \le w \le W;\phi \subseteq B \subseteq B_{0} \\ \end{aligned}$$

(3)

$$f_{C,0} \left( {l,w,B} \right) = \hbox{max} \left\{ {0;\pi_{i} :l_{i} \le l,w_{i} \le w,b_{i} \ge 1} \right\}$$

(4.a)

$$\begin{aligned} f_{C,v} \left( {l,w,B} \right) & = \hbox{max} \{ 0;f_{C} \left( {x_{1} ,w,B_{1} } \right) + f_{C} (x_{2} ,w,B - B_{1} ): \\ & \quad 0 < x_{1} \le x_{2} ,x_{1} + x_{2} = l,\phi \subseteq B_{1} \subseteq B\} \\ \end{aligned}$$

(4.b)

$$\begin{aligned} f_{C,h} \left( {l,w,B} \right) & = \hbox{max} \{ 0;f_{C} \left( {l,y_{1} ,B_{1} } \right) + f_{C} (l,y_{2} ,B - B_{1} ): \\ & \quad 0 < y_{1} \le y_{2} ,y_{1} + y_{2} = w,\phi \subseteq B_{1} \subseteq B\} \\ \end{aligned}$$

(4.c)

Dynamic programming on (3)–(4.a, 4.b, 4.c) is impracticable for the huge number of subsets. In relation (3) any frequency b _i can be reduced if bigger than $\left\lfloor {(l \cdot w)/(l_{i} \cdot w_{i} )} \right\rfloor$, as noticed in [9], but the ratio $\left\lfloor {l/l_{i} } \right\rfloor \cdot \left\lfloor {w/w_{i} } \right\rfloor$ is smaller and still correct as limit.

In [11] there is a top-down implementation of (3)–(4.a, 4.b, 4.c). The authors define the sum of two cutting patterns $B^{\prime } = \left( {b_{1}^{{\prime }} ,b_{2}^{{\prime }} , \ldots ,b_{n}^{{\prime }} } \right)$ and $B^{{\prime \prime }} = \left( {b_{1}^{{\prime \prime }} ,b_{2}^{{\prime \prime }} , \ldots ,b_{n}^{{\prime \prime }} } \right)$ as the pattern with frequencies $\hbox{min} \left\{ {d_{i} ,b_{i}^{{\prime }} + b_{i}^{{\prime \prime }} } \right\}$. They assign a set F(l, w) of best partial patterns to each couple (l, w). In the first inner loop, for example, for each x ₁ they add to F(l, w) all patterns from F(x ₁, w) ⊕ F(l−x ₁, w), defined as {B ₁ + B ₂: B ₁ ∈ F(x ₁, w), B ₂ ∈ F(l−x ₁, w)}, and then keep only the best patterns of F(l, w).

In [9] and [27] a different recursion is exploited, in a relaxed state space. Any piece set B = {b ₁, b ₂,…,b _n } is mapped to a number s(B) through the scalar product B × S. The mapping S = {s ₁, s ₂, … , s _n } has pre-fixed non-negative integers. The advantage is in the reduced size of the mapped space. An upper bound function f _S is then obtained with the recursion (5)–(6.a, 6.b, 6.c), i.e. f _C (l, w, B) ≤ f _S (l, w, s(B)) is valid.

$$\begin{aligned} f_{S} \left( {l,w,s} \right) & = \hbox{max} \{ f_{S,0} \left( {l,w,s} \right),f_{S,v} \left( {l,w,s} \right),f_{S,h} \left( {l,w,s} \right)\} , \\ & \quad 0 \le l \le L;0 \le w \le W;0 \le s \le s_{0} = B_{0} \times S \\ \end{aligned}$$

(5)

$$f_{S,0} \left( {l,w,s} \right) = \hbox{max} \{ 0;\pi_{i} :l_{i} \le l,w_{i} \le w,s_{i} \le s\}$$

(6.a)

$$\begin{aligned} f_{S,v} \left( {l,w,s} \right) & = \hbox{max} \{ 0;f_{S} \left( {x_{1} ,w,s_{1} } \right) + f_{S} (x_{2} ,w,s - s_{1} ):0 < x_{1} \le x_{2} , \\ & \quad x_{1} + x_{2} = l,0 \le s_{1} \le s\} \\ \end{aligned}$$

(6.b)

$$\begin{aligned} f_{S,h} \left( {l,w,s} \right) & = \hbox{max} \{ 0;f_{S} \left( {l,y_{1} ,s_{2} } \right) + f_{S} (l,y_{2} ,s - s_{1} ):0 < y_{1} \le y_{2} , \\ & \quad y_{1} + y_{2} = w,0 \le s_{1} \le s\} \\ \end{aligned}$$

(6.c)

1.2 Branch and Bound Methods

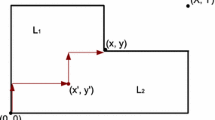
The first type of tree search is based on the top-down approach [8]. The root node contains the sheet as open rectangle. When a node N is chosen, its branching consists in selecting an open rectangle from N, and then a child node is generated for any possible guillotine cut to apply only on it. A special 0-cut makes the rectangle closed, i.e. only one piece can be extracted. Hence, any node N contains the rectangles generated by the sequence of guillotine cuts added from the root to N.

At any node, if (α ₁, β ₁) (α ₂, β ₂), … , (α _k , β _k ) are its open rectangles, an upper bound is computed by using the knapsack function but, for the set C of closed ones, the best matching pieces-rectangles is found, with value opt(C). The result is

$$f_{U} (\alpha_{1} ,\beta_{1} ) + f_{U} (\alpha_{2} ,\beta_{2} ) + \ldots + f_{U} (\alpha_{k} ,\beta_{k} ) + opt\left( C \right)$$

(7)

The first method with a bottom-up approach was heuristic [31, 33], later improved into an exact tree search by [32]. It merges the rectangles (builds) with a separating horizontal or vertical guillotine cut, starting by the pieces up to the sheet. The root node is a dummy node with an empty build. At the first level, n different nodes contain a rectangle equivalent to one piece of the corresponding type. Hence, the search starts with n non-branched (or open) nodes, and their set is denoted by O. Any node is identified with its build, i.e. a rectangle and a cutting pattern, and we use the symbol B also to denote the builds and related nodes.

At any step, a build B is chosen from O, in order to be branched, hence moved into the set C of closed nodes. The chosen build is combined with all builds from C (itself too) in two ways, i.e. vertical or horizontal. Each combination generates a new build, placed into O according to two conditions, otherwise it is dropped. First, it has to fit inside the sheet. Second, no demand has to be exceeded.

2 Upper Bounds Classification

We present four criteria to characterize the upper bounds in tree searches for C2DC, describing some details from topic literature papers. (a) the type of relaxation. Four types can be identified: unconstrained relaxation, state space relaxation, one-dimensional (or geometric) relaxation, non-guillotine relaxation. In geometric case, additional options are the continuous frequencies or the container relaxation. We avoid treating ILP relaxations, since just two ILP models exist, which allow to solve only small instances [14, 25]. (b) the kind of node for which the bound is computed: root or inner. In the first case the full sheet is available. In the second case there is a residual area, with non-rectangular shape for bottom-up, or separated parts for top-down. (c) the available piece set. Some upper bounds are pre-computed at the begin of the algorithm with all desired pieces, and we call them free. Other upper bounds are frequently computed using a residual subset of pieces. We refer to them as residual. (d) the geometric compatibility of piece types and demands with respect to available areas. We shall describe the options in combination to the ones selected for the three previous features.

The four criteria are not independent. For example, in the root node all upper bounds are free, the unconstrained relaxation implicitly integrates the geometric compatibility, the geometric relaxations imply the non-guillotine relaxation.

2.1 Geometric Relaxations

The first two relaxations have been presented in Sect. 1.1, with the knapsack function (unconstrained relaxation) and the state space relaxation. Two types of one-dimensional relaxation exist. We call the first 1D-area, since it considers only the area of both sheet and pieces [17, 20], by solving a knapsack problem. In the second, the pieces are split into slices [36, 37], hence we call it 1D-slice.

The slices are used to fill the available area, which can be broken into empty strips. The computation is simplified since only one pattern is used for equivalent strips. In particular, for any piece type t _i , the horizontal slice has length l’ _i,h  = l _i , width w’ _i,h  = 1, profit π’ _{i, h}  = π _i / w _i and demand d’ _i,h  = min{d _i , $\left\lfloor {L/l_{i} } \right\rfloor$}. The slice profits are fractional, hence a truncation $\left\lfloor \cdot \right\rfloor$ is applied on the overall bound, even when not explicit. This happens whenever continuous piece frequencies are used.

The best pattern is computed through a knapsack problem with capacity L. It is vertically replicated W times with no care about the limited demands d _i , hence in this phase the unconstrained relaxation is added. Vertical slices are similarly defined and used, and the minimum is selected between the two orientations.

The two relaxations do not dominate each other, since the 1D-slice considers the geometric limits on each axis, but it uses fractional frequencies and a partial unconstrained relaxation, which would be full if d’ _i,h is replaced by d’’ _i,h  = $\left\lfloor {L/l_{i} } \right\rfloor$. Also the 1D-area can be integrated with these relaxations on the frequencies.

2.1.1 Non-guillotine Relaxations

Geometric relaxations implicitly include the drop of the guillotine constraint, since it has no meaning when treating with one-dimensional pieces. However the non-guillotine relaxation can be independently considered and a better upper bound would be obtained by dropping only this constraint. Unfortunately the problem becomes more difficult. This kind of bounds is explicitly mentioned in [5, 11]. The former is addressed to the U2DC. In the latter the non-guillotine solutions from literature are manually imported, but only for the full sheet.

In literature two groups of upper bounds can be identified for the non-guillotine case, which turn out to be valid also for the guillotine case. The first group is based on geometric relaxations extending the 1D-slice and the 1D-area, often from proposals given in the context of different problems, as the Strip Packing and the Orthogonal Packing problems. In 1D-slice case, one-dimensional cutting stock problems raise (with strips as piece containers), for which ILP models exist in literature. In 1D-area case, piece dimensions are modified through smart strategies (e.g. dual feasible functions), leading to greater areas. However, all corresponding bounds have been mainly experienced to check if a set of pieces fits into a rectangle. Because of this different perspective, we shall not discuss further details, in particular about ILP models and relaxations, and we just underline that area increasing represents a powerful pre-processing but it does not affect the skeleton of our classification. The interested reader is addressed to [1, 3, 4, 13, 24].

The second group comes from relaxations (constraint removal, lagrangian, etc.) applied to ILP models of the full non-guillotine problem, but we pursue the choice to avoid using ILP models. The interested reader is addressed to [2, 6, 7].

2.2 Root Node and Inner Nodes

In the root node, the full sheet is considered, with no difference between top-down and bottom-up approaches, as for the upper bounds previously described.

In top-down case, for the inner nodes the model of upper bounds has been given in (7). In [20], for each open rectangle, the knapsack function and the 1D-area relaxation are used, selecting the minimum between the two corresponding sums.

In the bottom-up methods, for any inner node with a build B, an upper bound is given by π(B) + u(Γ), where u(Γ) is a bound for the best way to use the complementary residual surface Γ when B is placed on the bottom-left corner of the sheet.

No state space relaxation has been proposed for u(Γ). An upper bound with 1D-area relaxation can be computed straightly by using the area of Γ. For the 1D-slice relaxation, Γ can be divided in two parts [38] through a horizontal line along the top edge of B. The bottom-right part of Γ is filled by using shorter strips.

In [32], an upper bound with unconstrained relaxation is based on the backward recursion (8.a, 8.b)–(9.a, 9.b), where f _U is the knapsack function and B has dimensions (l, w).

$$V_{U} \left( {L,W} \right) = 0$$

(8.a)

$$V_{U} \left( {l,w} \right) = \hbox{max} \left\{ {v_{U} \left( {l,w} \right),h_{U} \left( {l,w} \right)} \right\},0 \le l \le L;0 \le w \le W$$

(8.b)

$$v_{U} \left( {l,w} \right) = \hbox{max} \{ 0;V_{U} \left( {l + x,w} \right) + f_{U} \left( {x,w} \right):0 < x \le L - l\}$$

(9.a)

$$h_{U} \left( {l,w} \right) = \hbox{max} \{ 0;V_{U} \left( {l,w + y} \right) + f_{U} \left( {l,y} \right):0 < y \le W - w\}$$

(9.b)

The value V _U (l, w) plays the role of u(Γ). Another bound from [32], dominated by V _U (l, w) but faster, is given by f _U (L−l, W) + f _U (L, W−w).

2.3 Free and Residual Upper Bounds

All upper bounds described above are free (all pieces available). In the inner nodes, residual upper bounds can be used, by taking into account only the residual available pieces. For unconstrained and state space relaxations there are no literature examples. For the 1D-area the bounds are based on reduced frequency limits.

For the 1D-slice relaxation, at the begin of the bottom-up algorithm in [36], the authors compute the best strips not only with the full piece set B ₀, but also with the n subsets where (only) one type is removed. In any node, also the bounds associated to types with no residual demands are selected, and the minimum is chosen.

In general, note that the free upper bounds are pre-computed at the begin of the algorithm, hence there is no need to be faster by using continuous frequencies, which are instead useful for the residual upper bounds, frequently computed.

2.4 Geometric Compatibility

In this section we present residual and free upper bounds from literature, based on one-dimensional relaxations, with focus on the options to filter piece types and piece demands, according to the geometric compatibility with respect to the available areas. Let T(α, β) be the subset containing the type indexes i for which l _i ≤ α and w _i ≤ β. We say that these pieces are compatible with the rectangle (α, β).

For unconstrained and state space relaxations, the restriction to the subsets T(α, β) is implicit, since the constraints l _i ≤ l and w _i ≤ w are used in (1) and in (6.a).

We shall first discuss the compatibility for residual 1D-area upper bounds, then for strips construction, and finally for some free 1D-area upper bounds.

2.4.1 Residual Upper Bounds with Compatibility

Two residual upper bounds related to the 1D-area relaxation exist, both for the bottom-up case. The first appeared in [10] with the sum of all residual piece profits, with no limits on the sum of their area, hence ignoring Γ, and we refer to that as container relaxation. However, the authors only use the piece types compatible with Γ . We denote this set by T _Γ . Hence, if b _i are the frequencies in B, u(Γ) is

$$\sum\nolimits_{{i \in T_{\Gamma } }} {\left( {d_{i} - b_{i} } \right) \cdot \pi_{i} }$$

(10)

In [32], if this expression is zero, then it is used in place of V _U (l, w).

For the second upper bound, continuous frequencies are used, but it is better that (10) since it takes into account the area of Γ as upper limit [18, 36]. For a given build B, the knapsack formulation with $b_{i}^{{\prime }}$ as variable frequencies is

$$\hbox{max} \sum\nolimits_{{i \in T_{\Gamma } }} {b_{i}^{{\prime }} \cdot \pi_{i} } \quad {\text{s}}.{\text{t}}. 0 \le b_{i}^{{\prime }} \le d_{i} - b_{i} ,\sum\nolimits_{{i \in T_{\Gamma } }} {b_{i}^{{\prime }} \cdot l_{i} \cdot w_{i} } \le A = area(\varGamma )$$

(11)

2.4.2 Strips with Compatible Pieces

A bound for 1D-slice relaxation originally appeared in a top-down approach for U2DC [37]. The best horizontal strip compatible with a rectangle (α, β) is

$$u_{h} (\alpha ,\beta ) = \hbox{max} \sum\nolimits_{i \in T} {\pi_{i,h}^{{\prime }} \cdot b_{i} } \quad {\text{s}}.{\text{t}}.\,\sum\nolimits_{i \in T} {l_{i} \cdot b_{i} } \le \alpha ;b_{i} \,{\text{integer}};b_{i} \ge 0$$

(12)

The authors compute (12) only for β equal to piece widths. A similar definition u _v (α, β) is valid for the vertical slices. The minimum is selected as upper bound.

In [21, 38] this bound is applied to the bottom-up (for U2DC), but it is just computed for the full sheet, and u _h (α, β) is replaced by u _h (α), with β = W in (12).

The bound was adapted to C2DC in [36] by adding constraints b _i ≤ d _i in (12). We refer to these strips as constrained strips. For a build with size (l, w), u(Γ) is given, for example with horizontal strips, by (13), which we refine later according to the discrete points. The authors also select the best residual bound (Sect. 2.3).

$$\left\lfloor {u_{h} (L - l) \cdot w + u_{h} \left( L \right) \cdot (W - w)} \right\rfloor$$

(13)

2.4.3 Free 1D-Area Upper Bounds

In the top-down approach of [20] the geometric compatibility is integrated to the 1D-area relaxation. For an open (α, β), an integer knapsack problem is solved:

$$\hbox{max} \sum\nolimits_{i \in T} {b_{i} \cdot \pi_{i} } {\text{ s}}.{\text{t}}.\sum\nolimits_{i \in T} {b_{i} \cdot l_{i} \cdot w_{i} } \le A = \alpha \cdot \beta ;b_{i} \,{\text{integer}};0 \le b_{i} \le c_{i} (\alpha ,\beta )$$

(14)

with capacity α·β, the piece types of T(α, β), and the upper limits c _i (α, β) = min{d _i , $\left\lfloor {\alpha /l_{i} } \right\rfloor \cdot \left\lfloor {\beta /w_{i} } \right\rfloor$} for the integer variable frequencies b _i . We refer to c _i as specific demands. When they are used we say there is full geometric compatibility.

For the bottom-up approach, the formulation given in [17] is equivalent to (14), but the constraint l _i ≤ α and w _i ≤ β should be replaced by l _i ≤ L−α or w _i ≤ W−β, as noticed also in [36]. In [18] an upper limit is defined for frequencies. We denote it by c _Γ,i (α, β). The authors set c _Γ,i (α, β) = 0 if l _i  > L−α and w _i  > W−β. When only the first condition is valid, they set c _Γ,i (α, β) = min{ d _i , $\left\lfloor {L \cdot \left( {W - \beta } \right)/\left( {l_{i} \cdot w_{i} } \right)} \right\rfloor$}, and similarly if only the second is satisfied. In all other cases, the total area of Γ is exploited, by setting c _Γ,i (α, β) = min{d _i , $\left\lfloor {area(\varGamma )/\left( {l_{i} \cdot w_{i} } \right)} \right\rfloor$}.

2.5 Mixed Upper Bounds

Upper bounds can be mixed by selecting the minimum. A better strategy, related to (1)–(2.a, 2.b, 2.c) and (8.a, 8.b)–(9.a, 9.b), integrates the unconstrained and the 1D-area relaxations. In [23], f _U (l, w) is replaced by f _U,m (l, w) = min{f _1D(l, w), f _U (l, w)}, where f _1D refers to a 1D-area relaxation. Hence, f _U,m can be smaller than f _U . The authors propagate any smaller value also to the bigger rectangles, since they use f _U,m in (1.b, 1.c) instead of f _U , so leading to reduced functions f _U,h,m and f _U,v,m .

A similar strategy appeared in [18], with different perspectives. First, the authors applied the mix to (8.a, 8.b)–(9.a, 9.b). Second, it is performed by replacing f _U (x, y) with min {f _1D(x, y), f _U (x, y)} in (9.a, 9.b). Hence, this mix only reduces the propagation of f _U .

2.6 Discrete Points

A way to improve a tree search approach is with the discretization of the cut coordinates by considering only the integer combinations of the piece dimensions [8, 16]. We denote the discrete points sets by D _X (lengths) and D _Y (widths).

The useful portion of a rectangle (l, w) has dimensions (〈l〉 _x , 〈w〉 _y ) and area 〈l〉 _x ·〈w〉 _y , where 〈l〉 _x  = max{x ∈ D _X : x ≤ l} and 〈w〉 _y  = max{y ∈ D _Y : y ≤ w}. These reductions imply smaller upper bounds for the 1D-slice and 1D-area relaxations.

No example exists for top-down methods. In the bottom-up case, the dimensions l and w of any build B are necessarily discrete points. The dimensions L−l and W−w of the complementary surface Γ are reduced to 〈L−l〉 _x and 〈W−w〉 _y in [35]. We denote the reduced surface by 〈Γ 〉 _d . A reduction of Γ through discrete points is also described in [18], before defining c _Γ,i , but no formulation was given.

For the 1D-slice relaxation, the reduction has no effect on the construction of the best strips but, for example, the replication of the horizontal ones is reduced on the y-axis. Hence, the following refined expression is used in [36] instead of (13)

$$\left\lfloor {u_{h} (L - l) \cdot \left( {W - \left\langle {W - w} \right\rangle_{y} } \right) + u_{h} \left( L \right) \cdot \left\langle {W - w} \right\rangle_{y} } \right\rfloor$$

(15)

where, in the second term, the factor (W−w) is replaced by 〈W−w〉 _y whereas, in the first term, the factor w has been increased with an equivalent gap.

3 Literature Categorization

We characterize the upper bounds used in a set of significant literature papers, by using our four criteria. Tables 1 and 2 refer to the top-down and bottom-up case respectively. Last column reports if a bound mixing is used. In some cases the mix involves bounds from other papers, as better detailed in an extended report on-line, accessible at opslab.dieti.unina.it and containing also formal formulations.

Table 1 Literature upper bounds for top-down algorithms

Table 2 Literature upper bounds for bottom-up algorithms