Keywords

1 Introduction

A great interest has always been devoted to model industrial processes managed by supply systems. Such an exigence has become higher due to the necessity of obtaining safe and fast processes that could avoid, in some way, unwished situations, such as bottlenecks, dead times, and so on.

Various mathematical models have been studied for this aim. Several approaches are continuous and mainly based on differential equations, see for instance [3, 9]. In these cases, supply chains are characterized by: parts dynamics described by conservation laws; Queues, that are in front of each supplier and are defined by ordinary differential equations. There are also other models, that focus on individual parts and deal with exponential queueing networks. A theoretical example is given in [8] for waiting lines, while various applications for manufacturing systems are in [4, 11], with emphasis on possible numerical approaches in [10]. In this direction, some variants have been studied, such as the “G-networks” (see [5, 6]), introduced by Gelenbe, motivated by analogies with neural networks, and interested by the simultaneous presence of positive customers, negative customers, signals and triggers. Positive customers are the common ones, who join a queue for a service, and they can be destroyed by a negative customer arriving at a non-empty queue. Triggers displace positive customers from a queue to another one, while a signal behaves either as a negative customer or a trigger. Exhaustive descriptions of G-networks are in [1, 2], where exact solutions are found in product form.

In this paper, focusing on some G-networks described in [7], we consider a queueing network, that models a supply system, characterized by either parts dynamics or control electrical signals in the working stations. Unfinished goods and control impulses, these last ones generated by a Control Station (CS), arrive, following two different and independent Poisson processes, at each node from outside the network. Parts are processed one by one at each node, and service times of the unfinished goods are exponentially distributed. After the working process, a part travels from a node to another one with fixed probabilities as either a good to process or a control signal, or leaves the network. The activation time of a control electrical signal is exponentially distributed. Activated impulses with fixed probabilities either move a good from the node they are activated to another one or destroy an unfinished good. For such a queueing network, the stationary state distribution is obtained in product form, and numerical results, also focusing on the ergodicity condition, are then computed. Notice that the queueing network analysed in this paper is a model of a system for car engines inside a real Italian company. The main advantage, with respect to the existing models in the scientific literature, is the extension of the G-networks by introducing phenomena that usually occur in the real industrial systems.

The paper is structured as follows. Section 2 describes the supply system and its mathematical formulation. Section 3 contains some numerical results. Conclusions end the paper in Sect. 4.

2 A Model for Supply Systems

Focus on a supply system, modelled via a queueing network with the following features:

  • Each node represents a working station, that receives raw material flows of either external type (flows from outside the network) or internal one (flows from nodes inside the network). Materials are processed one by one at each node, characterized by an own working frequency and an infinite buffer.

  • A Control Station (CS) provides each node some electrical control impulses that rule dynamics for the working stations.

  • Beside the control signals generated by the CS, each node has a set of non-active impulses, that have their own frequency action and are activated only if necessary. In particular, if a node has not goods to process (namely, it is empty), the activation of a control impulse has no effects, the impulse is disabled and is not activated anymore.

  • An unfinished good, once it has been processed in a node i, either leaves the network or moves to another node j. Inside node j, the good can be further manufactured, or behave like a control signal. In this last case the unfinished part can destroy a good, which is inside node j, or move the good itself to another node k.

From a mathematical point of view, the queueing network is identified by the couple \(\left( \mathscr {V}\text {, }\mathscr {E}\right) \), where \(\mathscr {V=} \left\{ 0,1,2,\ldots ,M\right\} \) and \(\mathscr {E}=\displaystyle \underset{i\in \mathscr {V} \text {, }j\in \mathscr {V}}{\mathscr {\bigcup }}\left\{ \varepsilon _{ij}\right\} \) represent, respectively, the set of nodes and arcs. Precisely, node 0 indicates the external of the network, while node i, \( i=1,\ldots ,M\), is a generic working station, which belongs to the queueing network; \(\varepsilon _{ij}\) is the arc that connects nodes i and j, \( i\in \mathscr {V}\), \(j\in \mathscr {V}\).

The queueing network has M working stations with infinite buffers. External arrival flows are independent Poisson processes. Precisely, the arrival rates of external unfinished goods and electrical control impulses, generated by the CS, at node i, \(i=1,...,M\), are, respectively, indicated by \(A_{0i}^{1}\) and \(A_{0i}^{2}\). Each node i has one server, hence goods are processed one by one with a frequency \(b_{i}^{1}\). An unfinished good, that leaves node i, moves to node j, \(j=1,\ldots ,M\), with: probability \( \gamma _{ij}^{1}\) as a part that has to be processed inside node j; probability \(\gamma _{ij}^{2}\) as a control impulse for node j. Finally, the unfinished part leaves the network with probability \(\gamma _{i0}=1-\sum \limits _{j=1}^{M}\left( \gamma _{ij}^{1}+\gamma _{ij}^{2}\right) \). Define the matrices \(\mathbf {G^{1}:=}\left( \gamma _{ij}^{1}\right) \) and \(\mathbf {G^{2}:=}\left( \gamma _{ij}^{2}\right) \). Then, \(\mathbf {G }=\mathbf {G^{1}}+\mathbf {G^{2}:=}\left( \gamma _{ij}^{1}+\gamma _{ij}^{2}\right) \) represents the transition matrix of a Markov chain for the dynamics of parts.

A control impulse is activated at a random instant of time t. An impulse, sent to node i, works in \(\left] t,t+\varDelta \right[ \) with probability \( b_{i}^{2}\left( k\right) \varDelta +o\left( \varDelta \right) \), provided that k non-activated signals are inside node i at the time instant t. When the activation period ends, a control impulse: with probability \(\xi _{ij}^{1}\) moves a good, that is inside node i, to node j with the aim of continuing the working process; with probability \(\xi _{ij}^{2}\) moves to node j an unfinished part, that belongs to node i, and the moved good behaves like a control impulse inside node j. Finally, \(\xi _{i0}=1-\sum \limits _{j=1}^{M}\left( \xi _{ij}^{1}+\xi _{ij}^{2}\right) \) is the probability that a control impulse destroys an unfinished part inside node i. When this event occurs, the control impulse ends its own action and is not activated inside node i anymore. Consider now the matrices \(\mathbf {H^{1}}:=\left( \xi _{ij}^{1}\right) \) and \(\mathbf {H^{2}}:=\left( \xi _{ij}^{2}\right) \). Then, the matrix \(\mathbf {H }=\mathbf {H^{1}}+\mathbf {H^{2}}:=\left( \xi _{ij}^{1}+\xi _{ij}^{2}\right) \) is the transition matrix of a Markov chain, that focuses on all possible dynamics for control impulses.

2.1 Equilibrium Equations and Stationary Probabilities

The just described system is modelled by a queueing network, represented by a homogeneous Markov process \(\left\{ Z\left( t\right) \text {, }t\ge 0\right\} \), with state space:

$$\begin{aligned} \zeta =\left\{ \left( \left( x_{1},y_{1}\right) ,\left( x_{2},y_{2}\right) ,\ldots ,\left( x_{M},y_{M}\right) \right) ,\text { }x_{i}\ge 0,\text { } y_{i}\ge 0,\text { }i=1,\ldots ,M\right\} . \end{aligned}$$

Notice that the state \(\left( \left( x_{1},y_{1}\right) ,\left( x_{2},y_{2}\right) ,\ldots ,\left( x_{M},y_{M}\right) \right) \) indicates that, for a defined instant of time, node i,  \(i=1,\ldots ,M,\) has \(x_{i}\) unfinished goods and \(y_{i}\) non-activated impulses. Define the quantities:

$$\begin{aligned} \mathbf {x}:=\left( x_{1},x_{2},\ldots ,x_{M}\right) ,\quad \mathbf {y}:=\left( y_{1},y_{2},\ldots ,y_{M}\right) , \end{aligned}$$
$$\begin{aligned} \left( \mathbf {x},\mathbf {y}\right) :=\left( \left( x_{1},y_{1}\right) ,\left( x_{2},y_{2}\right) ,\ldots ,\left( x_{M},y_{M}\right) \right) ,\quad A_{0}^{1}:=\sum _{i=1}^{M}A_{0i}^{1},\quad A_{0}^{2}:=\sum _{i=1}^{M}A_{0i}^{2}, \end{aligned}$$

and indicate by \(\mathbf {e}_{i}\) the vector, whose \(i-\)th component is 1 while the other ones are zero. Assume that \(\pi \left( \mathbf {x},\mathbf {y} \right) \) is the stationary probability of the state \(\left( \mathbf {x}, \mathbf {y}\right) \), namely the probability that the queueing network has, for large times, \(x_{i}\) unfinished goods and \(y_{i}\) non-activated impulses inside node i, \(\forall \) \(i=1,\ldots ,M\). If \(\pi \left( \mathbf {x},\mathbf {y} \right) \) exists, then the following Chapman-Kolmogorov equations system holds:

$$\begin{aligned} \pi \left( \mathbf {x},\mathbf {y}\right) \left( A_{0}^{1}+A_{0}^{2}+\sum _{i=1}^{M}b_{i}^{1}\left( 1-\gamma _{ii}^{1}\right) u\left( x_{i}\right) +\sum _{i=1}^{M}b_{i}^{2}\left( y_{i}\right) \right) =\sum _{i=1}^{M}\pi \left( \mathbf {x-e}_{i},\mathbf {y}\right) A_{0i}^{1}u\left( x_{i}\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\pi \left( \mathbf {x},\mathbf {y-e}_{i}\right) A_{0i}^{2}u\left( y_{i}\right) +\sum _{i=1}^{M}\pi \left( \mathbf {x+e}_{i}, \mathbf {y}\right) b_{i}^{1}\gamma _{i0}u\left( x_{i}+1\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\pi \left( \mathbf {x+e}_{i},\mathbf {y+e}_{i}\right) b_{i}^{2}\left( y_{i}+1\right) \xi _{i0}+\sum _{i=1}^{N}\pi \left( \mathbf {x}, \mathbf {y+e}_{i}\right) b_{i}^{2}\left( y_{i}+1\right) \left( 1-u\left( x_{i}\right) \right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\sum _{j=1\text {, }j\ne i}^{M}\pi \left( \mathbf {x+e}_{i} \mathbf {-e}_{j},\mathbf {y}\right) b_{i}^{1}\gamma _{ij}^{1}u\left( x_{i}+1\right) u\left( x_{j}\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\sum _{j=1}^{M}\pi \left( \mathbf {x+e}_{i},\mathbf {y-e} _{j}\right) b_{i}^{1}\gamma _{ij}^{2}u\left( x_{i}+1\right) u\left( y_{j}\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\sum _{j=1}^{M}\pi \left( \mathbf {x+e}_{i}\mathbf {-e}_{j}, \mathbf {y+e}_{i}\right) b_{i}^{2}\left( y_{i}+1\right) \xi _{ij}^{1}u\left( x_{j}\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\sum _{j=1\text {, }j\ne i}^{M}\pi \left( \mathbf {x+e}_{i}, \mathbf {y+e}_{i}\mathbf {-e}_{j}\right) b_{i}^{2}\left( y_{i}+1\right) \xi _{ij}^{2}u\left( y_{j}\right) + \end{aligned}$$
$$\begin{aligned} +\sum _{i=1}^{M}\pi \left( \mathbf {x+e}_{i},\mathbf {y}\right) b_{i}^{2}\left( y_{i}\right) \xi _{ii}^{2},\text { }\left( \mathbf {x},\mathbf {y}\right) \in \zeta , \end{aligned}$$
(1)

where \(b_{i}^{2}\left( 0\right) =0\) and \(u\left( x\right) \) is a unit Heavyside function. The system (1), that allows to get the steady state probability \(\pi \left( \mathbf {x},\mathbf {y}\right) \), has been obtained considering all transitions from/to the state \(\left( \mathbf {x}, \mathbf {y}\right) \) by balancing incoming and outgoing flows for such state (similar examples are in [7]).

Now, a general product-form solution for the equations system (1) is provided. Indicate by \(A_{i}^{1}\) and \(A_{i}^{2}\) the total steady state rates of arrival of goods and control electrical impulses, respectively, at node i, and define the quantities:

$$\begin{aligned} x_{i}^{2}:=A_{i}^{2}+b_{i}^{1},\quad \rho _{i}:=\frac{A_{i}^{1}}{x_{i}^{2}} ,\quad q_{i}^{2}\left( j\right) :=\frac{A_{i}^{2}}{b_{i}^{2}\left( j\right) } ,\quad i=1,\ldots ,M,\text { }j=1,\ldots ,M; \end{aligned}$$

Remark 1

Notice that \(\rho _{i}\) is the stationary probability that the queue of the working station i is busy.

The following traffic equations hold (see [1, 5,6,7] for further details):

$$\begin{aligned} A_{i}^{1}=A_{0i}^{1}+\sum _{j=1}^{M}\rho _{j}\left( b_{j}^{1}\gamma _{ji}^{1}+A_{j}^{2}\xi _{ji}^{1}\right) ,\quad i=1,\ldots ,M, \end{aligned}$$
(2)
$$\begin{aligned} A_{i}^{2}=A_{0i}^{2}+\sum _{j=1}^{M}\rho _{j}\left( b_{j}^{1}\gamma _{ji}^{2}+A_{j}^{2}\xi _{ji}^{2}\right) ,\quad i=1,\ldots ,M. \end{aligned}$$
(3)

We get the following theorems (for ideas of the proofs, see [7]):

Theorem 1

(Solution of traffic equations) If matrices \(\mathbf {G}\) and \(\mathbf {H}\) are irriducible, the solution \(\left\{ A_{i}^{1},A_{i}^{2}\right\} \), \( i=1,\ldots ,M,\) to equations (2) and (3) is unique.

Theorem 2

(Product-form solution for stationary probabilities) If matrices \(\mathbf {G} \) and \(\mathbf {H}\) are irreducible and the following conditions hold:

$$\begin{aligned} \rho _{i}<1,\quad \delta _{i}=\sum _{y_{i}=0}^{+\infty }\prod \limits _{j=1}^{y_{i}}q_{i}^{2}\left( j\right) <\infty ,\quad i=1,\ldots ,M, \end{aligned}$$

then the Markov process \(\left\{ Z\left( t\right) \text {, }t\ge 0\right\} \) is ergodic and its stationary distribution is represented in product form as:

$$\begin{aligned} \pi \left( \mathbf {x},\mathbf {y}\right) =\prod \limits _{i=1}^{M}\pi _{i}\left( x_{i},y_{i}\right) , \end{aligned}$$
$$\begin{aligned} \pi _{i}\left( x_{i},y_{i}\right) =\frac{\left( 1-\rho _{i}\right) \rho _{i}^{x_{i}}}{\delta _{i}}\prod \limits _{j=1}^{y_{i}}q_{i}^{2}\left( j\right) ,\text { }x_{i}\ge 0,\text { }y_{i}\ge 0,\text { }\forall i=1,\ldots ,M, \end{aligned}$$

and \(\prod \limits _{j=1}^{0}\equiv 1\).

3 Simulations

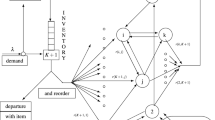
In this section, we describe some numerical results for a supply system, depicted in Fig. 1: there are five nodes (working stations). Each node is interested by external flows of goods, while only nodes 1 and 2 are characterized by electrical signals sent by the CS. Following some fixed probabilities, unfinished goods can move from node i to node \(i+1\), \( i=1,2,3,4\); from node 5, parts either leave the system or come back to node 1. For electrical impulses, the dynamics is the same of the unfinished goods. Notice that such system describes the different construction steps of car engines in a real Italian company. For privacy reasons, names and/or details about the real functionalities of each node are avoided.

Fig. 1
figure 1

Topology of the supply system

Full size image

Assume that: \(A_{0i}^{1}=20\) \(\forall \) \(i=1,\ldots ,5\), \(b_{1}^{1}=30\), \( b_{2}^{1}=b_{5}^{1}=40\), \(b_{3}^{1}=b_{4}^{1}=35\), where all such quantities are seen as number of parts per minute; \(A_{01}^{2}=A_{02}^{2}=5\), \( A_{03}^{2}=A_{04}^{2}=A_{05}^{2}=0\); \(b_{1}^{1}=30\), \(b_{2}^{1}=b_{5}^{1}=40\), \(b_{3}^{1}=b_{4}^{1}=35\); \(b_{1}^{2}=b_{2}^{2}=b_{3}^{2}=b_{4}^{2}=35\), \( b_{5}^{2}=30\), where such last quantities are intended as number of control signals per minute. As for matrices \(\mathbf {G}^{1}\), \(\mathbf {H}^{1}\), \( \mathbf {G}^{2}\) and \(\mathbf {H}^{2}\), they have zero elements with the following exceptions: \(\mathbf {G}^{1}\left( m,m+1\right) =\mathbf {H} ^{1}\left( m,m+1\right) =\mathbf {G}^{2}\left( m,m+1\right) =\mathbf {H} ^{2}\left( m,m+1\right) =0.5\) \(\forall \) \(m=1,\ldots ,4\); \(\mathbf {G}^{1}\left( 5,1\right) =\mathbf {H}^{1}\left( 5,1\right) =0.2.\)

Table 1 reports some values of the stationary probabilities for node 2. The choice of considering such node is due to the fact that it is inside the network and interested by both external parts and control signals rates. If the number of control impulses grows, \(\pi _{2}\left( x_{2},y_{2}\right) \) decreases. This occurs because controls in nodes determine variations of the ordinary parts dynamics, in terms either of movements to other nodes or possible destructions.

Table 1 Values of \(\pi _{2}\left( x_{2},y_{2}\right) \) for different values of \(x_{2}\) (columns) and \(y_{2}\) (rows)
Full size table

In order to analyze the behaviour of stationary probabilities versus the number of parts, we define the probability \(\widetilde{\pi _{i}}\left( x_{i}\right) :=\sum \limits _{y_{i}=0}^{+\infty }\pi _{i}\left( x_{i},y_{i}\right) \) that a node i, \(i=1,\ldots ,5,\) has \(x_{i}\) goods. In Table 2, we have some values of \(\widetilde{\pi _{1}}\) and \( \widetilde{\pi _{2}}\).

Table 2 \(\widetilde{\pi _{i}}\) for node i (columns), \(i=1,2\), assuming \(x_{j}\) unfinished goods (rows), \(j=1,2,3\)
Full size table

Notice that \(\widetilde{\pi _{i}}\left( x_{i}\right) \) grows when the number of parts decreases and, moreover, \(\widetilde{\pi _{2}}\left( x_{2}\right) > \widetilde{\pi _{1}}\left( x_{1}\right) \), indicating that node 2 tends to have more goods than node 1.

Further studies are done by computing the mean number of parts in the network, defined as:

$$\begin{aligned} N_{p}:=\sum \limits _{x_{i}=0}^{+\infty }x_{i}\left( \sum \limits _{y_{j}=0}^{+\infty }y_{j}\pi _{i}\left( x_{i},y_{j}\right) \right) . \end{aligned}$$

If we depict N versus \(A_{01}^{1}\) (Fig. 2, left) and versus \(A_{02}^{2}\) (Fig. 2, right), we get an idea of the ergodicity condition of the network process.

Fig. 2
figure 2

\(N_{p}\) versus \(A_{01}^{1}\) (left) and \(A_{02}^{2}\) (right)

Full size image

In particular, if the network is simulated with:

  • \(A_{01}^{1}\) variable and other parameters equal to the ones used before, node 1 becomes instable when \(A_{01}^{1}\simeq 27\), leading to the instability of the whole network;

  • \(A_{02}^{2}\) variable and other parameters equal to the ones used before, the network process is not ergodic anymore if \(A_{02}^{2}\ge 21\).

Similar phenomena occur by analyzing the behaviour of \(N_{p}\) vs \(A_{02}^{1}\) and versus \(A_{01}^{2}\).

4 Conclusions

In this paper, a queueing network, that models a real supply chain to assemble car engines, is described. For such a system, steady state probabilities have been computed in product form. Numerical tests have established that the control signals inside each node influence deeply the dynamics of the overall network.

Future work activities aim at applying the proposed model to scenarios, that involve other real supply systems in different contexts. In this direction, obvious modifications of the mathematical background foresee a fuzzy logic approach in order to obtain a robust optimization for the performances of the supply systems.