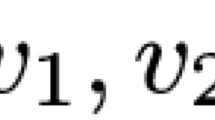Progressive Generation of Canonical Irredundant Sums of Products Using a SAT Solver

Abstract

We present an algorithm that progressively generates canonical irredundant Sums Of Products (SOPs) for completely- and incompletely-specified Boolean functions using a satisfiability (SAT) solver. The progressive generation allows for real time monitoring and early termination, as well as for generation of partial SOPs for incremental applications. On the other hand, canonicity brings independence of the original representation and often yields smaller and more regular SOPs that lead to smaller circuits after algebraic factoring. Also, canonicity is key in applications such as constraint solving and random assignment generation, which traditionally rely on methods based on Binary Decision Diagram (BDD). However, in contrast with BDDs, our algorithm can relax canonicity to improve speed and scalability. In general, our method is more scalable for benchmarks with many structurally isomorphic outputs. It also improves the quality of results up to 10%, in terms of the SOP size, compared to a state-of-the-art BDD-based method. Experiments with global circuit restructuring using SAT-based SOPs show that area-delay product can be improved up to 27%, compared to global restructuring using BDD-based SOPs.

1 Introduction

Minimization of the two-level Sum Of Products (SOP) representation is well-studied due to the wide use of SOPs. In the past, research in SOPs was motivated by mapping into Programmable Logic Arrays (PLAs); now SOPs are supported in many tools for logic optimization and are used for multi-level logic synthesis [3, 25], delay optimization [20], test generation [9], but they are also used for fuzzy modelling [10], data compression [1], photonic design automation [5], and in other areas.

These publications show that, contrary to the popular belief, research in SOP minimization and its applications is not outdated. As an example, a recent work uses SOPs for delay optimization in technology independent synthesis and technology mapping [20]. In this work, improved quality is achieved by enumerating different SOPs of the local functions of the nodes, factoring them, and finding circuit structures balanced for delay.

Another important application of SOP minimization, which is targeted and used as case-study in this paper, is global circuit restructuring. If a multi-level circuit structure for a Boolean function is not available, or if the circuit structure is with poor quality, then a new circuit structure with desirable properties, such as low area, short delay, good testability, or improved implicativity (if the circuit represents constraints in a SAT solver), should be derived. The best known and widely used method for global circuit restructuring is computing SOPs of the output functions in terms of inputs, factoring the multi-output SOPs and deriving a new circuit structure from the shared factored form. The main drawback of this method is the lack of scalability of the algorithm for SOP generation and minimization.

Starting with the Quine-McCluskey algorithm [16], many algorithms and heuristics for SOP generation and minimization have been developed. Prior research falls into two broad categories: BDD-based algorithms and ESPRESSO-style algorithms.

To generate an SOP for a given Boolean function, techniques based on Binary Decision Diagrams (BDDs), such as those of Minato-Moreale [18] and SCHERZO [6, 7], first build a BDD or a Zero-suppressed Decision Diagram (ZDD), then minimize the BDD/ZDD size by using some heuristic approach to obtain a smaller SOP, and finally convert the BDD/ZDD to an SOP. If building a BDD is feasible, then an SOP, even a suboptimal one, can be generated. However, for some circuits, the BDD construction suffers from the BDD memory explosion problem—the BDD size is exponential in the number of input variables—and thus, using BDDs is often impractical. Additional drawback is that BDDs are incompatible with incremental applications since they require building a BDD for the complete circuit before converting it to an SOP. Despite these issues, to our knowledge, the BDD-based method for SOP generation and minimization is used in most of the industrial tools, and therefore scalability improvements of it are highly desirable.

On the other hand, the ESPRESSO-style algorithms are inspired by the first version of ESPRESSO [3]. For example, the logic minimizer ESPRESSO-MV [26] is a faster and more efficient version of ESPRESSO. But, although these techniques avoid the memory explosion problem inherent in the use of BDDs, they still incur impractical runtimes for large Boolean functions and only minimize existing SOPs.

Alternatively, recent progress in the performance of Boolean satisfiability (SAT) solvers enabled using SAT in various domains of logic synthesis and verification despite their worst-case exponential runtime. Thus, it has become a trend to replace BDD-based methods with SAT-based ones. For example, this was done for model checking [17], functional dependency [11], functional decomposition [14, 15], and logic don’t-care-based optimization [19]. Existing methods for SOP generation using SAT solvers are based on enumeration of satisfying assignments [21]. On the other hand, Sapra et al. [27] proposed using a SAT solver to implement part of ESPRESSO’s procedures for SOP minimization in order to speed them up. But, since they largely follow the traditional ESPRESSO style of SOP minimization, they operate only on existing SOPs and do not consider generating a new SOP from a multi-level representation of the Boolean function. Moreover, its runtime and end results significantly depend on the SOP received as input. To the best of our knowledge, there is still no complete SAT-based method for SOP generation similar to the Irredundant Sum-of-Product (ISOP) algorithm for incompletely-specified functions using BDDs [18].

Accordingly, the main contribution of this paper is to propose a new engine for SOP generation and minimization that is completely based on SAT solvers. Our method generates the SOP progressively, building it cube by cube. We guarantee that the generated SOPs are irredundant, meaning that no literal and no cube can be deleted without changing the function. As we show in the result section, our algorithm generates SOPs with the size similar to that of the BDD-based method [18]. Interestingly, for some circuits, we generate smaller SOPs (up to 10%), which is useful in practical applications. For example, when a multi-level description of the circuit is built using an SOP produced by the proposed SAT-based method, the area-delay product of the resulting circuit, assuming unit-area and unit-delay model, often decreases (up to 27%), compared to global restructuring using BDDs.

Two main features characterize our SAT-based SOP generation and make it desirable in various domains.

First, we generate an SOP progressively, unlike BDD-based methods that attempt to construct a complete SOP at once. The progressive computation allows generation of a partial SOP for circuits whose complete SOP cannot be computed given the resource limits. The partial SOPs can be exploited by other applications that do not require the complete circuit functionality, but work with partially defined functions [4, 30]. Moreover, for circuits with large SOPs, the progressive generation allows us to predict whether it is feasible to build an SOP for a circuit, and to check if the SOP size is within the limits of the methods that are going to use it. For this, at any moment, we can retrieve the number of outputs for which the SOP is already computed, as well as the finished SOP portion of the currently processed output. We can also easily compute an estimate or a lower-bound of the percentage of covered minterms, considering uniform distribution of minterms in the space or considering the size of the truth table, respectively. In contrast, the termination time and the quality of results of the BDD-based methods are unpredictable since the complete BDD has to be built before converting it to an SOP.

Second, counter-intuitive as it may sound, we show that the SAT-based computation can generate canonical SOPs. To this end, we combine (1) an algorithm that, under a given variable order, generates consecutive SAT assignments in lexicographic order [24], considering each assignment as integer value, and (2) a deterministic algorithm that expands the received assignments into cubes. For a given function and a variable order, the assignments (i.e., the minterms) are always generated in the same order, and each assignment always results in the same cube. Thus, the resulting SOP is canonical—it is unique and independent of the input implementation of the function. The canonical nature of the resulting SOPs can be useful in those domains where previously only BDDs could be used. For example, applications as constraint solving [31] and random assignment generation [22] can benefit from the canonicity if we iterate repeated generation of random valuation of inputs and get the closest SAT assignment, as it is done in the proposed canonical SOP generation method. Also, the canonicity brings regularity in the SOPs, and thus the results after using algorithms for factoring [25] are in some cases better.

In the rest of the paper, we focus on completely-specified functions, but the given SAT-based formulation works for incompletely-specified functions without any changes. Indeed, after extracting the first cube and blocking it in the on-set of the function, the rest of the computation is performed for the incompletely-specified functions, even if the initial function was completely specified.

The rest of the paper is organized as follows. Section 2 gives background on Boolean functions, the SOP representation, and the satisfiability problem. Next, we describe our algorithm for SAT-based progressive generation of irredundant SOPs in Sect. 3. Section 4 gives our experimental setup and discusses the experimental results. Finally, we conclude and present ideas for future work in Sect. 5.

2 Background Information

In this section, we define the terminology associated with Boolean functions and the SOP representation, as well as with the satisfiability problem.

2.1 Boolean Functions

For a variable v, a positive literal represents the variable v, while the negative literal represents its negation $\bar {v}$. A cube, or a product, c, is a Boolean product (AND, ⋅) of literals, c = l ₁ ⋅⋯ ⋅ l _k . If a variable is not represented by a negative or a positive literal in a cube, then it is represented by a don’t-care ( −), meaning that it can take both values 0 and 1. A cube with i don’t-cares covers 2ⁱ minterms. A minterm is the smallest cube in which every variable is represented by either a negative or a positive literal.

Let f(X) : B ⁿ →{0, 1, −}, B ∈{0, 1}, be an incompletely-specified Boolean function of n variables X = {x ₁, …, x _n }. The terms function and circuit are used interchangeably in this paper. The support set of f is the subset of variables that determine the output value of the function f. The set of minterms for which f evaluates to 1 defines the on-set of f. Similarly, the minterms for which f evaluates to 0 and don’t-care define the off-set and the don’t-care-set, respectively. In a multi-output function F = {f ₁, …f _m }, each output f _i , 1 ≤ i ≤ m, has its own support set, on-set, off-set, and don’t-care-set associated with it.

For simplicity, we define the following terms for single-output functions, although our algorithm can handle multi-output functions. Any Boolean function can be represented as a two-level sum of products (SOP), which is a Boolean sum (OR, + ) of cubes, S = c ₁ + ⋯ + c _k . Assume that a Boolean function f is represented as an SOP. A cube is prime, if no literal can be removed from the cube without changing the value that the cube implies for f. A cube that is not prime can be expanded by substituting at least one literal with a don’t-care. The SOP is irredundant if each cube is prime and no cube can be deleted without changing the function.

A canonical representation is a unique representation for a function under certain conditions. For example, given a Boolean function and a fixed input variable order, a canonical SOP is an SOP independent of the original representation of the function given to the SAT solver, of the CNF algorithm, and of the used SAT solver. In a similar way, BDDs generate a canonical SOP that only depends on an input variable order [18].

2.2 Boolean Satisfiability

A disjunction (OR, + ) of literals forms a clause, t = l ₁ + ⋯ + l _k . A propositional formula is a logic expression defined over variables that take values in the set {0, 1}. To solve a SAT problem, a propositional formula is converted into its Conjunctive Normal Form (CNF) as a conjunction (AND, ⋅) of clauses, F = t ₁ ⋅⋯ ⋅ t _k . Algorithms such as the Tseitin transformation [29] convert a Boolean function into a set of CNF clauses.

A satisfiability (SAT) problem is a decision problem that takes a propositional formula in CNF form and returns that the formula is satisfiable (SAT) if there is an assignment of the variables from the formula for which the CNF evaluates to 1. Otherwise, the propositional formula is unsatisfiable (UNSAT). A program that solves SAT problems is called a SAT solver. SAT solvers provide a satisfying assignment when the problem is satisfiable.

Modern SAT solvers can determine the satisfiability of a problem under given assumptions. Assumptions are propositions that are given as input to the SAT solver for a specific single invocation of the SAT solver and have to be satisfied for the problem to be SAT.

Example 1

For the function $f(x_1, x_2, x_3)=(x_1+x_2)\bar {x}_3$, which is satisfiable for the following assignments of the inputs {(0, 1, 0), (1, 0, 0), (1, 1, 0)}, a SAT solver without assumptions can return any of the given assignments. But, if we give as input to the SAT solver the assumption x ₁ = 1, then it returns either (1, 0, 0) or (1, 1, 0), because those two assignments satisfy the given assumption.

A lexicographic satisfiability (LEXSAT) problem is a SAT problem that takes a propositional formula in CNF form and, given a variable order, returns a satisfying variable assignment whose integer value under the given variable order is minimum (maximum) among all satisfying assignments. The returned satisfying assignment is called a LEXSAT assignment. If the formula has no satisfying assignments, LEXSAT proves it unsatisfiable. There are several solutions for the LEXSAT problem [12, 23, 24]. For our work, we use an efficient algorithm for generating consecutive LEXSAT assignments [24].

Example 2

For the function f(x ₁, x ₂, x ₃) from Example 1, LEXSAT returns either the lexicographically smallest assignment (0, 1, 0) or the lexicographically greatest assignment (1, 1, 0), depending on the user preference.

3 SAT-Based SOP Generation

In this section, we describe our SAT-based algorithm that progressively generates an irredundant SOP for a single-output function. For multi-output circuits, each output is treated separately. In this paper, we focus on completely-specified functions, but the algorithm can be easily used for incompletely-specified functions by providing both the on-set and off-set as input to the algorithm. In the case of a completely-specified function one of them is derived by complementing the other.

The presented algorithm iteratively generates minterms, expands them into prime cubes, and adds these cubes to the SOP. The SAT-based heuristics for minterm generation and cube expansion are described in Sects. 3.1 and 3.2, respectively. Finally, to guarantee that the resulting SOP is irredundant, it is post-processed to remove redundant cubes, as described in Sect. 3.3. Additionally, Sect. 3.4 describes several techniques that reduce the runtime.

The algorithm can be implemented with one SAT solver parameterized to store both on-set and off-set. Alternatively, it can use two solvers, one for on-set and one for off-set. In our implementation of the algorithm, we use four different SAT solvers: for both on-set and off-set, one is used to generate satisfying assignments, the other to expand assignments to cubes. By employing four solvers, we ensure that assignment generation and expansion do not interact with each other during the SOP computation.

The procedures described in the following subsections assume that we are generating the on-set SOP. The same procedures are used to generate the off-set SOP, by substituting the on-set SAT solver with an off-set SAT solver and vice versa.

3.1 Generation of Minterms

In order to generate minterms for the on-set of a function f by using a SAT solver, we initialize a SAT solver with the CNF of f. Then, to discard the trivial case when the function has a constant on-set, we solve the SAT problem by asserting that f = 0. If the problem is UNSAT, then f is a constant, and we return an SOP with one constant cube. Otherwise, if the problem is SAT, we continue with the following methods for minterm generation. Figure 8.1 shows the flowchart of these methods, as well as their connection with the other methods of the SOP generation algorithm.

Fig. 8.1

Flowchart of the algorithm for minterm generation. Minterms are generated either as SAT or LEXSAT assignments. If the problem is SAT, the generated minterm is passed to the cube expansion algorithm to generate a cube that would cover the minterm. Once all minterms are covered by the generated cubes, the SAT problem becomes UNSAT, and the SOP is returned after removing the redundant cubes

Generation of a Non-canonical SOP

When the problem is SAT, an assignment for the inputs is returned for which the function evaluates to 1. From the assignment, we can generate a minterm for the function f in which the variables assigned to 0 and 1 are represented with the negative and positive literal, respectively. For example, for a function f(x, y, z), the assignment (1, 1, 0) implies the minterm $xy\bar {z}$. Once a minterm is obtained, we expand it into a cube using the heuristic procedure from Sect. 3.2. Next, we add the cube with its literals complemented to the SAT solver as a blocking clause, which is an additional clause that blocks known solutions of the SAT problem. This allows to generate a new minterm that is not covered by any of the previously generated cubes. While the problem is SAT, we iteratively obtain a minterm, expand it to a cube, and add the cube to both the SAT solver and the SOP. The unsatisfiability of the problem indicates that the generated SOP is complete and covers all on-set minterms.

Generation of a Canonical SOP

Generating minterms from satisfying assignments received from a SAT solver does not guarantee canonicity, since SAT solvers return minterms in a non-deterministic order that depends on the design of the solver and the CNF generated for the function. Thus, to ensure canonicity, we iteratively use a binary search-based LEXSAT algorithm, called BINARY [24], that generates minterms in a lexicographic order that is unique for a given variable order. The algorithm BINARY receives as input a potential assignment, which is the lexicographically smallest assignment that might be satisfying, that is either the last generated minterm or, initially, an assignment with all 0s. Then, BINARY tries to verify and fix the assignment of each variable defined with the potential assignment starting from the leftmost variables and moving to right. We also use the proposed methods for runtime improvement [24]: skip verifying the leading 1s, correcting the initial potential assignment, and profiling the success of the first SAT call. Similarly to the non-canonical SOPs, once we obtain a minterm, we expand it into a cube and add it to the SAT solver as a blocking clause.

Example 3

For example, assume that for the function f(x ₁, …, x ₈), the last generated minterm (1, 1, 0, 0, 0, 0, 0, 1) is received as an initial potential assignment. Since this minterm is covered by the last cube, this assignment is not satisfying, so we can increase its value for 1 to get the smallest assignment that might be satisfying (1, 1, 0, 0, 0, 0, 1, 0). Next, we can skip verifying the assignments x ₁ = 1 and x ₂ = 1, because the next lexicographically smallest assignment has to start with the same leading 1s. Thus, we should only check the assignments for x _i , for 3 ≤ i ≤ 8. Due to using binary search, with the first SAT call we assume half of the unfixed assignments, and we give to the on-set SAT solver the assumptions (x ₁, …, x ₅) = (1, 1, 0, 0, 0). Assume that the problem was satisfiable and the SAT solver returned the assignment (1, 1, 0, 0, 0, 0, 1, 1). This assignment proves that an on-set minterm with the assumed values exists, but moreover we can learn that the assignments from the potential minterm x ₆ = 0 and x ₇ = 1 are correct. Next, to check if the assignment for the last input x ₈ can be set to 0, we call the SAT solver with the assumptions (x ₁, …, x ₈) = (1, 1, 0, 0, 0, 0, 1, 0). If it returns SAT, we return the potential assignment as a minterm since all assignments are verified and fixed. Otherwise, we flip x ₈ to 1 to increase the potential assignment before returning it.

3.2 Expansion of Minterms into Cubes

In this subsection, we describe our SAT-based procedure that receives a minterm and transforms it into a prime cube by iteratively removing literals (i.e., substituting them with don’t-cares). For the on-set SOP, a literal can be removed, if after its removal all minterms covered by the cube do not overlap with the off-set. Figure 8.2 shows a flowchart of the algorithm.

Fig. 8.2

Flowchart of the algorithm for expansion of minterms into cubes. The algorithm for canonical expansion ensures that all generated cubes are prime. After a cube is generated, it is added as a blocking clause to the SAT solver used for minterm generation, and another minterm is generated

Canonical Expansion to Prime Cubes

The following deterministic algorithm expands a minterm into a cube by ensuring that, after removing each literal, the cube is covering only on-set minterms. Since the literals are removed always in the same order, which can be specified by the user, the algorithm is deterministic and produces canonical cubes if the given minterms are canonical. Thus, to remove a literal, first, we assume that the literal is removed from the cube, and an off-set SAT solver is run with assumptions for the remaining literals of the cube. If the problem is UNSAT, then no minterm covered by the cube belongs to the off-set, so we can extend the cube by removing this literal. On the other hand, if the problem is SAT, we cannot extend the cube, since the SAT solver found an off-set minterm that is covered by the extended cube.

Example 4

Assume that for the function in Fig. 8.3, we received the minterm $\bar {x}y\bar {z}t$. To remove the literal $\bar {x}$, we would call the off-set SAT solver with the assumptions (y, z, t) = (1, 0, 1). The SAT solver would return SAT, which means that $\bar {x}$ cannot be removed, because the cube $y\bar {z}t$ is covering the off-set minterm $xy\bar {z}t$. However, if we try to remove the literal $\bar {z}$ by calling the SAT solver with the assumptions (x, y, t) = (0, 1, 1), then we would receive UNSAT because there are no off-set minterms that satisfy these assumptions, so $\bar {z}$ can be removed to obtain the on-set cube c ₁.

Fig. 8.3

A Karnaugh map for the Boolean function $f(x,y,z,t)=\bar {x}yt+xyz+x\bar {y}t$ with its prime cubes c _i , where 1 ≤ i ≤ 5. The cubes c ₁, c ₂, and c ₃ are essential and they compose the minimum SOP of f

Greedy Canonical Cube Expansion

To minimize the overlapping of cubes, we propose to remove literals in two rounds. In the first round, they are removed greedily, after ensuring that multiple on-set minterms are covered by expanding each literal.

Example 5

Assume that for the function in Fig. 8.3, the cube c ₁ was computed and added to the on-set SAT solver as a blocking clause. Also, assume that as a second minterm xyzt is generated, which can be extended by removing one of the literals x, y or t. If we remove x, we will obtain the cube c ₄ that covers only one additional minterm with respect to the existing cube c ₁, but if we remove y or t, we will obtain c ₂ or c ₅, respectively, each of which covers two yet uncovered minterms.

In Example 5, our expansion procedure skips the opportunity to remove the literal x, and tries to expand other literals if possible. This greedy selection of literals decides to candidate a literal l _i for removal, if by removing it, the expanded cube covers more than one new minterm. To check if this condition is satisfied, we flip l _i and provide it, along with the remaining literals of the cube, as assumptions to an on-set SAT solver in which the already generated cubes are added as blocking clauses. If the problem is UNSAT, then we skip removing it temporarily. Otherwise, if the problem is SAT, then we consider this literal for removal since by removing it we cover more than one uncovered minterm. Once a literal is a candidate for removal, we run the algorithm for canonical expansion described above to ensure that it can be removed.

However, in this first round, we might skip some opportunities for expansion. Thus, in the second round, for each skipped literal, we execute the algorithm for canonical expansion. This guarantees that, after the second round, no literal can be further removed, which means that the cube is prime. Since, we always try to remove the literals in the same user specified order, this method generates a canonical SOP.

Fast Non-canonical Expansion

If generating a canonical SOP is not required, we can substitute the first round of expansion with a faster method to improve runtime: If in an off-set SAT solver we assume the values from the received on-set minterm, the problem is UNSAT and the SAT solver returns the set of literals used to prove unsatisfiability (procedure “analyse_final” in MiniSAT [8]). Since the returned literals are sufficient to prove unsatisfiability in an off-set SAT solver, they construct a cube that covers only on-set minterms, and we can remove literals that are not returned by the SAT solver. However, the set of remaining literals is not always minimal, and thus we run additionally the algorithm for canonical expansion as a second round to obtain a prime cube.

3.3 Removing Redundant Cubes

The cubes expanded with the methods from Sect. 3.2 are prime by construction. However, by progressively adding cubes to the SAT solver, as described in Sect. 3.1, we ensure that each cube is irredundant with respect to the preceding cubes, but not with respect to the whole set of cubes.

Example 6

For the function f from Fig. 8.3, assume that the cubes c ₁, c ₅, c ₂, and c ₃ are generated in the given order. The cube c ₅ is irredundant with respect to c ₁, since it additionally covers the minterms xyzt and $x\bar {y}zt$, but it is contained in the union of c ₂ and c ₃.

In order to produce an irredundant SOP, after generating all cubes, we iterate through the cubes to detect and remove redundant ones. First, we initialize a new SAT solver with clauses for all generated cubes and we assume that all cubes are required. Then, by using the assumption mechanism, for each cube c _i , we check if there is an assignment for which c _i evaluates to 1 while all the other irredundant cubes evaluate to 0. If the problem is SAT, the cube is irredundant and the SAT solver returns an assignment that corresponds to a minterm which is covered only by c _i . Otherwise, if the problem is UNSAT, then the cube is redundant, and thus it is removed from the SOP and is excluded when checking the redundancy of the following cubes. Since we always try to remove cubes in the order in which they were generated, this method is deterministic and maintains canonicity when canonical SOPs are generated.

Example 7

Considering the cubes from Example 6, to check whether c ₃ is redundant, we set c ₃ = 1 by assuming the values x = 1, y = 0 and t = 1. For the assumed values, the other cubes evaluate to c ₁ = 0, c ₂ = 0 and c ₅ = z. Setting z = 0 leads to c ₅ = 0. Thus, the problem is SAT and c ₃ is irredundant. The returned assignment (x, y, z, t) = (1, 0, 0, 1) defines a minterm $x\bar {y}\bar {z}t$ that is covered only by c ₃.

3.4 Improving the Runtime

In this subsection, we present four techniques that improve the runtime of the algorithm by allowing early termination and by treating some special cases.

Simultaneous On-Set and Off-Set Generation

Often, the SOP of the on-set and off-set differ in size. For example, a three-input function implementing an AND gate, f(x, y, z) = xyz, has an on-set SOP, f = S _on  = xyz with size 1, and an off-set SOP, $\bar {f}=S_{\mathtt {off}} = \bar {x}+\bar {y}+\bar {z}$ with size 3. Since we want to use the set with a smaller SOP, we simultaneously generate two SOPs, for both the on-set and off-set, by generating one cube at a time from each set, and we stop the generation when one SOP is complete. This way, if one of set is much smaller than the other, we can avoid the situation when the larger set of cubes has to be completely generated, before the smaller set is discovered.

Prioritizing Outputs with Large SOPs

Before generating SOPs for each output, we propose to sort outputs by size of their input supports. The outputs with larger supports are processed first since it is more likely that the SOP generation for these outputs will exceed resource limits, so we can determine if we should terminate the computation earlier.

Isomorphic Circuits

To benefit from the structure sharing among the circuit outputs, we implemented a method that decreases the runtime by detecting isomorphic outputs. For this, first, we divide the outputs into isomorphic classes. Two outputs are isomorphic and belong to the same class, if they implement an identical function using different inputs. Then, for each class, we generate an SOP only for one output, which is the class representative, and duplicate it for the others. In Sect. 4.2, we show that this allows effective generation of an SOP only for 16.5% of all combinatorial outputs and has a big influence on scalability.

CNF Sharing

Generating a CNF for each output is time consuming. Thus, to benefit from the logic sharing among the outputs, we can optionally share one CNF, which corresponds to the complete circuit. For this, we generate the CNF of the circuit, and then, for each output, we initialize the SAT solver only with the part of the CNF for the corresponding output. Besides improving the runtime, as Table 8.1 shows, this option sometimes leads to better results in terms of area-delay product after global restructuring.

Table 8.1 Number of benchmarks (out of the 71 used benchmarks) for which activating or deactivating an option for SATCLP results in the smallest SOP in terms of number of cubes (columns under “#Cubes”) or the best area-delay product (columns under “Area ⋅Delay”). If for one benchmark, an identical best result is obtained both when the option is activated and deactivated, then we count it as a tie

Exploiting Parallelism

There are several opportunities where computations are independent and can be parallelized. First, the computation of the on-set and off-set SOPs can be executed in parallel. Since now we compute sequentially one cube for each SOP interchangeably, it is expected that this would decrease the runtime by 2 ×. Second, instead of computing the SOP of each output one after the other, we can also compute each of them in parallel. Finally, for one SOP, we can compute cubes in parallel by generating minterms from different parts of the Boolean space. However, in this paper, all computations are done sequentially. Analyzing and exploiting the effect of parallelism is left for future work.

4 Experimental Results

In this section, we describe our experimental setup and compare the proposed SAT-based algorithm with a state-of-the-art BDD-based method.

4.1 Experimental Setup

We implemented the SAT-based algorithm described in Sect. 3 as a new command satclp in ABC [2]. ABC is an open-source tool for logic synthesis, technology mapping, and formal verification of logic circuits. ABC features an integrated SAT solver based on an early version of MiniSAT [8] that supports incremental SAT solving. Furthermore, ABC provides an implementation of the BDD-based method for SOP generation, namely the BDD construction for a multi-level circuit (command collapse) and the BDD-based ISOP computation [18] (command sop). For convenience, in this section, we refer to the SAT-based and BDD-based methods as SATCLP and BDDCLP, respectively. Finally, ABC allows us to analyze the area-delay results when the generated SOPs are used to build a new multi-level circuit structure. A multi-level network is generated using the fx command [25]. The network is next converted into an And-Inverter Graph (AIG) (command strash), which is an internal representation of ABC, and optimized with the dc2 command. The area and delay of the resulting AIGs are compared for different SOP generation methods.

To evaluate our algorithm, we use the ISCAS’89 benchmarks, a set of large MCNC benchmarks, a set of nine logic tables from the instruction decoder unit [28] denoted as LT-DEC, and a set of proprietary industrial benchmarks. The LT-DEC suite is well suited to demonstrate the factoring gains as circuit size increases [13]. The names of the LT-DEC benchmarks are given in the form “[N _PI ]/[N _PO ]”, where N _PI is the number of primary inputs and N _PO is the number of primary outputs. For the main experiments, we discard benchmarks for which the SOP size exceeds the built-in resource limits of the used commands, and thus, we use 30 (out of 32) benchmarks from the ISCAS’89 set, 15 (out of 20) benchmarks from the MCNC set, and 17 (out of 18) industrial benchmarks. With the discarded benchmarks, we demonstrate the generation of partial SOPs.

4.2 SAT-Based vs. BDD-Based SOP Generation

To analyze the performance of the algorithm presented in Sect. 3, we run both SATCLP and BDDCLP available in ABC. In this section, we present the results of these experiments.

Although the command collapse dynamically finds a good variable order for the BDD, changing the initial order of the primary inputs results in a different BDD structure, which leads to a different SOP. Thus, to obtain a good SOP, we generate five SOPs for BDDCLP by using five different initial orders of the primary inputs. Similarly, SATCLP generates different SOPs for different orders of the primary inputs, which define the order of removing literals from the cubes. We either use the pre-defined order from the benchmark file or order the inputs based on their number of fanouts (option “Order PI”), which currently works only for the combinational benchmarks. We can also, optionally, reverse the selected variable order (option “Reverse PI”). Moreover, we can enable generation of canonical SOPs (option “Canonical”), and for non-canonical SOPs we can enable generating one CNF for all outputs as described in Sect. 3.4 (option “Shared CNF”). Thus, by changing these four options, we generate 12 SOPs using SATCLP.

Generating multiple SOPs with each method results in SOPs that differ in size, where the SOP size is equal to the number of cubes that constitute the SOP. Figure 8.4 shows and compares the benchmarks for which the size of the smallest SOP generated by each method is different. Although SATCLP most often generates SOPs with almost the same size as those generated by BDDCLP, for some benchmarks it generates smaller SOPs (up to 10%). Since the results for SATCLP are obtained using several different options, Table 8.1 shows, under “#Cubes”, the number of benchmarks for which the smallest SOP is generated when a given option is deactivated or activated. We can notice that, for 34 benchmarks we get exclusively smaller SOP when generating canonical SOPs, and only for 7 benchmarks the non-canonical SOPs are smaller. Similarly, the SOP size increases for about 60% of the benchmarks if the CNF is shared or if the inputs are ordered by their number of fanouts.

Fig. 8.4

Size of the smallest SOPs generated by SATCLP compared to the smallest SOP generated by BDDCLP. Only the benchmarks for which the SOP size differs are shown. The gray line shows that, on average, SATCLP decreases the SOP size by 2.1%

Next, we compare the algorithms’ runtime. The reported runtime is average over three runs of the algorithm for SOP generation. For BDDCLP, we report the time required to execute the commands collapse and sop. For SATCLP, we report the time taken by our command satclp, which includes the time to generate isomorphic outputs, derive CNF, and initialize SAT solver instances, as well as the time for all SAT calls for minterm generation, cube expansion, and removing redundant cubes.

In terms of scalability, as Table 8.2 shows, the idea of filtering out structurally isomorphic outputs presented in Sect. 3.4 allows computing an SOP only for 16.5% of the combinational outputs, one for each isomorphic class, while for the other outputs we duplicate the generated SOP of the class representative. This reduces the runtime of our algorithm SATCLP, and for benchmarks rich in isomorphic outputs, the proposed method is significantly faster than BDDCLP. For example, from the public benchmarks, the maximum speedup is achieved for the benchmark s35932 from the ISCAS’89 set, for which we generate SOPs only for 10 out of 2048 combinational outputs and thus, on average, SATCLP requires 0.10 s, while BDDCLP requires 1.57 s. However, on average, our SATCLP is 7.5 × slower than BDDCLP for the public benchmarks. We have observed that the functions for expanding minterms into cubes are the bottleneck. For example, for the LT-DEC benchmarks, on average, 85% of the runtime is spent in this operation, while 8% is spent on minterm generation, 2% on removing redundant cubes, and 5% on other operations, such as dividing the outputs into classes, generating CNF, initializing SAT solver instances, etc.

Table 8.2 Comparison of the number of combinational outputs, which are primary outputs and latch inputs, in the used benchmarks and the number of isomorphic classes, which is equal to the number of calls of the SAT-based algorithm for SOP generation

On the other hand, Table 8.3 shows runtime results for a suite of proprietary industrial benchmarks. We can see that SATCLP is often faster than BDDCLP, especially for the benchmarks that have many isomorphic outputs, and is definitely more scalable, that is, it completes on some test-cases, for which BDDCLP fails. For example, for the non-canonical SOPs, on average, SATCLP decreases the runtime of SOP generation by 45.9%. For canonical SOPs, although SATCLP is 5.2 × slower than its non-canonical version and 2.9 × slower than BDDCLP, it successfully generates SOPs for 5 benchmarks, for which BDDCLP fails.

Table 8.3 Runtime results for the combinational industrial benchmarks when SOPs are generated with BDDCLP and SATCLP

We believe that the increased scalability of SATCLP is largely due to the fact that most of the industrial testcases have hundreds of inputs and outputs, which makes constructing global BDDs in the same manager problematic for all outputs at once. The algorithm SATCLP does not suffer from this limitation, because it computes the SOPs for one output at a time. It can be argued that the BDD-based computation can also be performed on the per-output basis. However, in this case, the BDD manager will inevitably find different variable orders for different outputs, which will increase the size of the resulting multi-level circuits when these SOPs are factored. In fact, factoring benefits from computing SOP with the same variable order that facilitates creating similar combinations of literals in different cubes, which in turn helps improve the quality of shared divisor extraction and factoring.

Finally, since we generate cubes progressively, unlike BDDCLP, we can build partial SOPs even for large circuits, and these can be used for incremental applications. Figure 8.5 shows the number of cubes composing the partial non-canonical SOPs for which a time limit for the runtime is set to t seconds, where t is an integer value such that 1 ≤ t ≤ 10. For functions with larger supports, we usually generate less cubes because more time is required for cube expansion. Only for the benchmark test14 we are not able to generate any cube in the first 6 s due to the large support set of the first processed output, which depends on 6246 inputs. For the other benchmarks, we generate thousands of cubes in just a few seconds. In this experiment, we are still generating both the on-set and the off-set SOP at the same time. However, in the incremental applications, we can generate just one of them, which would increase the number of generated cubes for a given time limit.

Fig. 8.5

The number of generated cubes for a partial SOP when the time limit is set between 1 and 10 s. The number of generated cubes depends on the size of the support set of the output with largest support set, which is given in brackets. For all benchmarks, the generated cubes belong to one output

4.3 Case-Study: SAT-Based SOPs for Generation of Multi-level Implementation

As explained in Sect. 4.2, we generate several SOPs with each method. The different SOPs result in multi-level networks with different area and delay. As Fig. 8.6 shows, for most benchmarks, our algorithm obtains Pareto-optimal solutions, compared to BDDCLP. To obtain these results, we isolate the best circuit implementations in terms of area-delay product as derived by each method. Table 8.1, with the columns “Area ⋅Delay”, shows the number of benchmarks with the smallest area-delay product generated when a given option was deactivated and activated. For 26 benchmarks we generate a circuit structure with smaller area-delay product when generating canonical SOPs, while for 28 benchmarks the non-canonical SOPs are a better option. Also, for most benchmarks it is best to generate an SOP by using the original ordering of primary inputs used in the benchmark file.

Fig. 8.6

The best results for each benchmark after a multi-level description is built from SOPs generated by our SAT-based algorithm, compared to using a BDD-based SOPs. For most benchmarks, we obtain Pareto optimal solutions

5 Conclusion

In this paper, we present a novel algorithm for progressive generation of irredundant canonical SOPs using heuristics based solely on SAT solving. Besides generating SOPs, the canonicity and the progressive generation make our heuristics desirable in many other areas where minterms or cubes are required, and for which the existing methods are either unscalable or impractical to use.

Regarding the quality of results, we show that for computing a complete SOP, on average, the SAT-based computation is as good as the BDD-based one. Moreover, the multi-level circuit structures derived using the SOPs generated by our approach are often better or Pareto-optimal.

Regarding the runtime, the proposed method is somewhat slower than the BDD-based method for most of the public benchmarks, but it is faster for circuits that are rich in isomorphic outputs. Thus, for the industrial benchmarks, our method is both faster and more scalable, and therefore it is a good candidate for global circuit restructuring at least in that particular industrial setting.

Besides the described opportunities for parallelization, the proposed method can also benefit from the ongoing improvement in modern SAT solvers. For example, recently we explored a new push/pop interface for assumptions used in the incremental SAT solving, which led to additional runtime improvements. As we show, for some circuits the results can improve by changing the variable order in which the cubes are expanded, but a careful study of this problem is required to improve further the quality of results.

In addition to runtime improvements, future work will focus on developing a dedicated SAT-based multi-output SOP computation, which computes cubes that are shared between several outputs. A recent publication [13] indicates that a significant improvement in quality (more than 10%) can be achieved by computing and factoring multi-output SOPs. We are not aware of a practical method for BDD-based multi-output SOP computation, so it is likely that SAT will be the only way to work with multiple outputs. Other directions of future work will include exploring the benefits of the progressive generation of canonical minterms and cubes in different areas. One such area is multi-level logic synthesis where incremental SAT-based decomposition methods can be developed based on partial SOPs computed for the output functions.