Order Reduction and Uniform Convergence of an Alternating Direction Method for Solving 2D Time Dependent Convection-Diffusion Problems

Abstract

In this work we solve efficiently 2D time dependent singularly perturbed problems. The fully discrete numerical scheme is constructed by using a two step discretization process, firstly in space, by using the classical upwind finite difference scheme on a special mesh of Shishkin type, and later on in time by using the fractional implicit Euler method. The method is uniformly convergent with respect to the diffusion parameter having first order in time and almost first order in space. We focus our interest on the analysis of the influence of general Dirichlet boundary conditions in the convergence of the algorithm. We propose a simple modification of the natural evaluations, which avoid the order reduction associated to those natural evaluations. Some numerical tests are shown in order to exhibit, from a practical of point of view, the robustness of the numerical method as well as the influence of the improved boundary conditions.

1 Introduction

Let us consider 2D time dependent convection-diffusion singularly perturbed problems defined by

$$\displaystyle{ \begin{array}{l} \mathcal{L}u \equiv \frac{\partial u} {\partial t} + \left (\mathcal{L}_{1,\varepsilon }(t) +\mathcal{ L}_{2,\varepsilon }(t)\right )u = f,\mbox{ in }\varOmega \times (0,T], \\ u(x,y,0) =\varphi (x,y),\mbox{ in }\varOmega, \\ u(x,y,t) = g(x,y,t),\mbox{ in }\partial \varOmega \times [0,T], \end{array} }$$

(1)

where Ω ≡ (0, 1)², and the spatial differential operators $\mathcal{L}_{i,\varepsilon },i = 1,2$ are given by

$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{1,\varepsilon }(t) \equiv -\varepsilon \frac{\partial ^{2}} {\partial x^{2}} + v_{1}(x,y,t) \frac{\partial } {\partial x} + k_{1}(x,y,t),{}\end{array}$$

(2)

$$\displaystyle\begin{array}{rcl}& & \mathcal{L}_{2,\varepsilon }(t) \equiv -\varepsilon \frac{\partial ^{2}} {\partial y^{2}} + v_{2}(x,y,t) \frac{\partial } {\partial y} + k_{2}(x,y,t), \\ \end{array}$$

respectively. We assume that the diffusion parameter ɛ, 0 < ɛ ≤ 1, can be very small with respect to the convective coefficients which will be considered strictly positive here, i.e., $v_{i}(x,y,t) \geq \overline{v} > 0$; also, the reaction terms satisfy k _i (x, y, t) ≥ 0,  i = 1, 2. We assume that sufficient smoothness and compatibility conditions between data hold so that the solution is four times derivable in space and twice in time (see [1, 3] for instance).

It is well known that, in general, when $\varepsilon \ll \overline{v}$, the solution of these problems presents a multiscale character even for smooth data, and the exact solution has regular boundary layers of size $\mathcal{O}(\varepsilon )$ at the sides x = 1 and y = 1 of the boundary of Ω (see [6–9]). In such case, the use of standard finite difference or finite element methods, defined on uniform meshes, is inappropriate because a large number (ɛ-dependent) of mesh points will be necessary to obtain accurate approximations. Then, the use of uniformly convergent methods is a much better choice, due to the rates of convergence and the associated error constants being independent of ɛ and, consequently, they are able to obtain reliable solutions using meshes with a reasonable number of mesh points independently of the value of ɛ. Here, we use a fitted mesh method (see [7, 9]), which concentrates appropriately the grid points in the boundary layer regions, to obtain a uniformly convergent scheme.

Similar 2D parabolic singularly perturbed problems are analyzed in many works. In [4, 5] the numerical algorithm was defined by using a two step process, discretizing firstly in time and secondly in space. In [1, 2] the technique discretizes first in space and later on integrates in time, via the implicit Euler method, the derived stiff initial value problems. The resulting numerical algorithm in [1, 2] must solve pentadiagonal linear systems at each time level; therefore, the computational cost of the algorithm is high. To reduce the computational cost, here we follow the same technique as in [1, 2], but now we use the fractional implicit Euler method to discretize in time; in this way, only tridiagonal systems have to be solved. We prove that the fully discrete scheme, which combines the fractional implicit Euler method, on a uniform mesh, and the classical upwind scheme, defined on a piecewise uniform Shishkin mesh, is uniformly convergent of first order in time and of almost first order in space.

We focus special attention to the influence of considering general time dependent Dirichlet boundary conditions. It is well known that, when using one step methods, a classical evaluation of the boundary conditions causes, in general, a reduction, both theoretically and numerically, in the order of convergence. This is the rationale for as to consider a different and very simple modification of these evaluations. We prove that the new evaluations of the boundary conditions retain the first order of consistency of the fractional implicit Euler method, without increasing the computational cost of the algorithm.

The paper is structured as follows: in Sect. 2, we introduce the spatial discretization of the continuous problem on a special nonuniform mesh of Shishkin type and we prove its almost first order uniform convergence. In Sect. 3 we introduce the time discretization and we prove the uniform convergence of the fully discrete method. Finally, in Sect. 4 some numerical results corroborating in practice the theoretical results are shown.

Henceforth, C denotes a generic positive constant independent of the diffusion parameter ɛ and also of the discretization parameters N and M.

2 Spatial Discretization

In this section we describe the spatial discretization chosen for (1). First we construct the mesh $\varOmega _{\overline{N}} \equiv I_{x,\varepsilon,N} \times I_{y,\varepsilon,N}$, as a tensor product of one dimensional piecewise uniform Shishkin meshes, I _x, ɛ, N = {0 = x ₀ < … < x _N = 1}, I _y, ɛ, N = {0 = y ₀ < … < y _N = 1}. We give the details of the construction of I _x, ɛ, N . Let us choose N as an even number. We define the transition parameter

$$\displaystyle{ \sigma _{x} =\min (1/2,m_{x}\varepsilon \ln N), }$$

(3)

where $m_{x} \geq 1/\overline{v}$; then, the piecewise uniform mesh has N∕2 + 1 points in [0, 1 −σ _x ] and [1 −σ _x , 1], and the mesh points are given by

$$\displaystyle{ x_{i} = \left \{\begin{array}{l} 2i(1 -\sigma _{x})/N,\ i = 0,\ldots,N/2, \\ 1 -\sigma _{x} + 2(i - N/2)\sigma _{x}/N,\ i = N/2 + 1,\ldots,N. \end{array} \right. }$$

(4)

In a similar way, defining the transition parameter

$$\displaystyle{ \sigma _{y} =\min (1/2,m_{y}\varepsilon \ln N), }$$

(5)

where $m_{y} \geq 1/\overline{v}$, we can construct the mesh I _y, ɛ, N .

Let us denote Ω _N the subgrid composed by all of the points of $\varOmega _{ \overline{N}}$ which are in the interior of Ω. Let us denote u _N (t) the semidiscrete approximations which we are going to define in Ω _N and let us denote $u_{\overline{N}}(t)$ the natural extension of u _N (t) to $\varOmega _{\overline{N}}$, by adding the corresponding evaluations of the boundary data. On these meshes, $\mathcal{L}_{i,\varepsilon,N},\ i = 1,2$, are the discretization differential operators of $\mathcal{L}_{i,\varepsilon },\ i = 1,2$, using the simple upwind finite difference scheme, which is given by

$$\displaystyle{ \begin{array}{l} \mathcal{L}_{1,\varepsilon,N}(t)u_{N}(t)(x_{i},y_{j}) \equiv l_{i-,\,j}u_{N}(t)(x_{i-1},y_{j}) + l_{i+,\,j}u_{N}(t)(x_{i+1},y_{j})+ \\ l_{i,\,j}^{1}u_{N}(t)(x_{i},y_{j}),\ \ i = 1,\ldots,N - 1,\ j = 0,\ldots,N,\end{array} }$$

(6)

where

$$\displaystyle\begin{array}{rcl} & l_{i-,\,j} = \frac{-\varepsilon } {h_{x,i}\tilde{h}_{x,i}} -\frac{v_{1}(x_{i},y_{j},t)} {h_{x,i}},\ \ & l_{i+,\,j} = \frac{-\varepsilon } {h_{x,i+1}\tilde{h}_{x,i}},{} \\ & l_{i,\,j}^{1} = -l_{i-,\,j} - l_{i+,\,j} + k_{1}(x_{i},y_{j},t),& \\ \end{array}$$

(7)

and analogously

$$\displaystyle{ \begin{array}{l} \mathcal{L}_{2,\varepsilon,N}(t)u_{N}(t)(x_{i},y_{j}) \equiv l_{i,\,j-}u_{N}(t)(x_{i},y_{j-1}) + l_{i,\,j+}u_{N}(t)(x_{i},y_{j+1})+ \\ l_{i,\,j}^{2}u_{N}(t)(x_{i},y_{j}),\ \ j = 1,\ldots,N - 1,\ i = 0,\ldots,N, \end{array} }$$

(8)

where

$$\displaystyle\begin{array}{rcl} & l_{i,\,j-} = \frac{-\varepsilon } {h_{y,\,j}\tilde{h}_{y,\,j}} -\frac{v_{2}(x_{i},y_{j},t)} {h_{y,\,j}},\ \ & l_{i,\,j+} = \frac{-\varepsilon } {h_{y,\,j+1}\tilde{h}_{y,\,j}},{} \\ & l_{i,\,j}^{2} = -l_{i,\,j-}- l_{i,\,j+} + k_{2}(x_{i},y_{j},t),& \\ \end{array}$$

(9)

with h _x, i = x _i − x _i−1,  i = 1, …, N,  h _y, j = y _j − y _j−1,  j = 1, …, N, $\tilde{h}_{x,i} = (h_{x,i} + h_{x,i+1})/2,\ i = 1,\ldots,N - 1,\ \tilde{h}_{y,\,j} = (h_{y,\,j} + h_{y,\,j+1})/2,\ j = 1,\ldots,N - 1$.

Let us denote [. ] _N , the restriction to Ω _N of any function defined in Ω. In [1], it was proven that it holds

$$\displaystyle{ \|[u(x,y,t)]_{N} - u_{N}(t)\|_{\varOmega _{N}} \leq CN^{-1}\ln N,\ \ \forall \ t \in (0,T], }$$

(10)

showing the almost first order of uniform convergence of the spatial discretization.

3 Time Discretization: Uniform Convergence

In this section we discretize in time, by means of the fractional implicit Euler method (see [4]), the stiff initial value problem

$$\displaystyle{ \begin{array}{l} u_{N}^{{\prime}}(t) + \left (\mathcal{L}_{1,\varepsilon,N}(t) +\mathcal{ L}_{2,\varepsilon,N}(t)\right )u_{\overline{N}}(t) = [f]_{N},\ \mbox{ in }\varOmega _{N}, \\ u_{\overline{N}}(t) = [g]_{\overline{N}},\ \mbox{ in }\varOmega _{\overline{N}}\setminus \varOmega _{N}, \\ u_{N}(0) = [\varphi ]_{N},\ \mbox{ in }\varOmega _{N},\end{array} }$$

(11)

Let τ ≡ T∕M be the time step, and let us consider the mesh $\bar{I}_{M} =\{ t_{m} = m\tau,\ m = 0,1,\ldots,M\}$. Let u _N ^m ≈ u _N (x, y, t _m ),  m = 0, 1, …, M. Then, the fully discrete method is given by

$$\displaystyle{ \begin{array}{l} (i)\mbox{ (initialize) } \\ u_{N}^{0} = [\varphi (x,y)]_{N},\mbox{ in }\varOmega _{N}. \\ u_{\overline{N}}^{0} = [g(x,y,0)]_{\overline{N}},\mbox{ in }\varOmega _{\overline{N}}\setminus \varOmega _{N}. \\ (ii)\mbox{ (first half step) } \\ (I +\tau \mathcal{ L}_{1,\varepsilon,N}(t_{m+1}))u_{\overline{N}}^{m+1/2} = u_{\overline{N}}^{m} +\tau f_{1,\overline{N}}^{m+1},\mbox{ in }\varOmega _{\overline{N}}\setminus \{0,1\} \times [0,1], \\ u_{\overline{N}}^{m+1/2} = g_{\overline{N}}^{m+1/2},\mbox{ in }\varOmega _{\overline{N}} \cap \{ 0,1\} \times [0,1]. \\ (iii)\mbox{ (second half step)} \\ (I +\tau \mathcal{ L}_{2,\varepsilon,N}(t_{m+1}))u_{\overline{N}}^{m+1} = u_{\overline{N}}^{m+1/2} +\tau f_{2,\overline{N}}^{m+1},\mbox{ in }\varOmega _{\overline{N}}\setminus [0,1] \times \{ 0,1\}, \\ u_{\overline{N}}^{m+1}(x,y) = g_{\overline{N}}^{m+1},\mbox{ in }\varOmega _{\overline{N}} \cap [0,1] \times \{ 0,1\}, \\ \qquad \ m = 0,\ldots,M - 1, \end{array} }$$

(12)

being $f = f_{1} + f_{2},f_{1,\overline{N}}^{m+1} = [\,f_{1}(x,y,t_{m+1})]_{\overline{N}},\ f_{2,\overline{N}}^{m+1} = [\,f_{2}(x,y,t_{m+1})]_{\overline{N}}.$

An important question in the numerical approximation of initial value problems is related with the evaluations of the boundary data. The most classical option for that is given by

$$\displaystyle{ \begin{array}{l} g_{\overline{N}}^{m+1/2} = [g(x,y,t_{m+1})]_{\overline{N}},\mbox{ in }\varOmega _{\overline{N}} \cap \{ 0,1\} \times [0,1], \\ g_{\overline{N}}^{m+1} = [g(x,y,t_{m+1})]_{\overline{N}},\mbox{ in }\varOmega _{\overline{N}} \cap [0,1] \times \{ 0,1\}. \end{array} }$$

(13)

Nevertheless, in general, this choice reduces the order of unconditional (independent of N) consistency to zero, and causes a sharp increase in the global error of the method. Then, we propose a different choice for the boundary data, given by

$$\displaystyle{ \begin{array}{l} g_{\overline{N}}^{m+1/2} = (I +\tau \mathcal{ L}_{2,\varepsilon,N}(t_{m+1})[g(x,y,t_{m+1})]_{\overline{N}} -\tau f_{2,\overline{N}}^{m+1},\mbox{ in }\varOmega _{\overline{N}} \cap \{ 0,1\} \times [0,1], \\ g_{\overline{N}}^{m+1} = [g(x,y,t_{m+1})]_{\overline{N}},\mbox{ in }\varOmega _{\overline{N}} \cap [0,1] \times \{ 0,1\}.\\ \end{array} }$$

(14)

Theorem 1

Under sufficient smoothness and compatibility conditions on data (see [ 3 ]), if we choose the boundary data given in ( 14 ), then the error in time satisfies

$$\displaystyle{ \Vert u_{N}(t_{m}) - u_{N}^{M}\ \Vert _{ \varOmega _{N}} \leq C\tau,\ \ \forall \ m = 1,\ldots,M, }$$

(15)

therefore, the time integration process ( 12 ) is uniformly and unconditionally convergent of first order; in other words, ( 15 ) is obtained independently of the size of ɛ and without restrictions between N and M.

Then, combining the uniform convergence of the spatial and time discretization, the main result follows.

Theorem 2

Under sufficient smoothness and compatibility conditions on data (see [ 3 ]), if we use the improved boundary data ( 14 ), then the global error given by

$$\displaystyle{E_{N,M} \equiv \max \limits _{1\leq m\leq M}\|[u(x,y,t_{m})]_{N} - u_{N}^{m}\|_{ \varOmega _{N}},}$$

satisfies

$$\displaystyle{E_{N,M} \leq C(N^{-1}\ln N + M^{-1}),}$$

and therefore the fully discrete method is uniformly convergent of first order in time and almost first order in space.

Remark 1

In [3], there are the full details of the proofs of the last two results.

4 Numerical Experiments

In this section we solve some test problems using our numerical algorithm. The first example is given by

$$\displaystyle{ \begin{array}{l} u_{t} -\varepsilon \varDelta u + u_{x} + u_{y} + (30t + xy)u = f(x,y,t),\ (x,y,t) \in \varOmega \times [0,1], \\ u(x,y,t) = g(x,y,t),\mbox{ in }\partial \varOmega \times [0,1] \\ u(x,y,0) =\varphi (x,y),\quad x,y \in [0,1], \end{array} }$$

(16)

where f(x, y, t), g(x, y, t) and φ(x, y) are chosen in such way that the exact solution is

$$\displaystyle{u(x,y,t) = (e^{-20t} - t)\left (\varPsi (x)\varPsi (y) - x^{2}y^{2}\right ),\ \mbox{ with }\varPsi (z) \equiv 1 - z -\frac{1 - e^{-\frac{1-z} {\varepsilon } }} {1 - e^{-\frac{1} {\varepsilon } }}.}$$

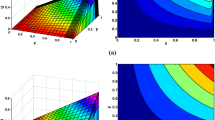
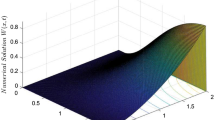
Figure 1 shows the solution at the final time t = 1; from it, we clearly see the boundary layers at x = 1 and y = 1.

Fig. 1

Numerical solution of example (16) for ɛ = 10⁻², N = M = 32, at the final time t = 1

In all tables corresponding to example (16), we take m _x = m _y = 1 to define the transition parameters of the meshes I _1,ɛ, N and I _2,ɛ, N respectively. In this example we decompose the right-hand side in the form f(x, y, t) = f ₁(x, y, t) + f ₂(x, y, t), where f ₂(x, y, t) = f(x, 0, t) + y( f(x, 1, t) − f(x, 0, t)) and f ₁(x, y, t) = f(x, y, t) − f ₂(x, y, t).

As the exact solution is known, the maximum global errors at the mesh points can be computed exactly by

$$\displaystyle{e_{N,M} =\max _{0\leq n\leq M}\max _{0\leq i\leq N}\max _{0\leq j\leq N}\vert U_{N}^{n} - u(x_{ i},y_{j},t_{n})\vert,}$$

and therefore the numerical orders of convergence are calculated by

$$\displaystyle{p = \log \left (e_{N,M}/e_{2N,2M}\right )/\log 2.}$$

From these values we calculate the uniform maximum errors by $emax^{N,M} = \max _{\varepsilon }e_{N,M}$, and from them, in a usual way, the corresponding numerical uniform orders of convergence are given by

$$\displaystyle{p^{uni} = \log \left (emax^{N,M}/emax^{2N,2M}\right )/\log 2.}$$

Tables 1 and 2 display the errors and the orders of convergence when natural and improved boundary conditions are used, respectively. From them, we observe the typical almost first order of uniform convergence (up to a logarithmic factor, in both cases; so, we can conclude that in this example the errors associated to the spatial discretization dominate in the global error.

Table 1 Maximum errors and orders of convergence for (16) with natural boundary conditions

Table 2 Maximum errors and orders of convergence for (16) with improved boundary conditions

To clarify the influence, in the numerical behavior of the method, of the two options for the boundary data considered here as well as the improvements provided by the non natural evaluations of the boundary conditions, we estimate the local errors in time. As the exact solution is known, such estimates are calculated as

$$\displaystyle{\tilde{e}_{N,M} =\max _{0\leq m\leq M}\max _{0\leq i\leq N}\max _{0\leq j\leq N}\vert \tilde{U} _{N}^{m} - u(x_{ i},y_{j},t_{m})\vert,}$$

where N must be chosen large enough in order to the contribution of the spatial discretization can be neglected and $\tilde{U} _{N}^{m}$ are the result of performing one step of our algorithm, but substituting U _N ^m−1 by [u(x _i , y _j , t _m−1] _N . From them, the quantities

$$\displaystyle{\tilde{p} = \log \left (\tilde{e}_{N,M}/\tilde{e}_{N,2M}\right )/\log 2,}$$

permit to estimate the numerical orders of consistency in time, given by $\tilde{p} - 1$.

Next tables show such estimated local errors and the values of $\tilde{p}$ corresponding to the two choices of the boundary data, taking N = 512 fixed. Table 3 displays the result when natural boundary conditions are used; from it the zero order of consistency of the algorithm can be observed. Table 4 displays the result when improved boundary conditions are used; here, we can appreciate the first order of consistency of the algorithm according to the theoretical results.

Table 3 Local errors and values of $\tilde{p}$ for (16) with natural boundary conditions, N = 512

Table 4 Local errors and values of $\tilde{p}$ for (16) with improved boundary conditions, N = 512

The second example that we consider is given by

$$\displaystyle\begin{array}{rcl} \begin{array}{l} u_{t} -\varepsilon \varDelta u + (1 + t + x + y)u_{x} + (1 + xyt^{2})u_{ y} + (30t + 10xye^{-t})u = \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad e^{t}\left (x + y + x^{2} + y^{2}\right ),\ (x,y,t) \in \varOmega \times [0,1], \\ u(x,y,t) = t\left (x + y + x^{2} + y^{2}\right ),\mbox{ in }\partial \varOmega \times [0,1] \\ u(x,y,0) = 0,\quad x,y \in [0,1].\end{array} & &{}\end{array}$$

(17)

In this case the exact solution is unknown. We take again m _x = m _y = 1 to define the piecewise uniform Shishkin mesh, and we decompose the source term in a different way; now we take f ₁(x, y, t) = f ₂(x, y, t) = f(x, y, t)∕2.

To approximate the maximum pointwise errors, we use a variant of the two-mesh principle. We calculate $\{\hat{u}^{N}\}$, the numerical solution on the mesh $\{(\hat{x}_{i},\hat{y}_{j},\hat{t}_{n})\}$ containing the original mesh points and its midpoints, i.e.,

$$\displaystyle{\begin{array}{c} \hat{x}_{2i} = x_{i},\ \ i = 0,\ldots,N,\quad \hat{x}_{2i+1} = (x_{i} + x_{i+1})/2,\ \ i = 0,\ldots,N - 1, \\ \hat{y}_{2j} = y_{j},\ \ j = 0,\ldots,N,\quad \hat{y}_{2j+1} = (y_{j} + y_{j+1})/2,\ \ j = 0,\ldots,N - 1, \\ \hat{t}_{2m} = t_{m},\ \ m = 0,\ldots,M,\quad \hat{t}_{2m+1} = (t_{m} + t_{m+1})/2,\ \ m = 0,\ldots,M - 1.\end{array} }$$

Then, we estimate the maximum errors at the mesh points of the coarse mesh as

$$\displaystyle{d_{i,\,j,N,M} =\max _{0\leq m\leq M}\max _{0\leq i,\,j\leq N}\vert u^{N}(x_{ i},y_{j},t_{m}) -\hat{ u}^{N}(x_{ i},y_{j},t_{m})\vert,}$$

the corresponding numerical orders of convergence are given by

$$\displaystyle{q = \log \left (d_{i,\,j,N,M}/d_{i,\,j,2N,2M}\right )/\log 2.}$$

The uniform maximum errors are estimated by $d^{N,M} = \max _{\varepsilon }d_{i,\,j,N,M}$; from them, as usual, we define the numerical uniform orders of convergence as

$$\displaystyle{q^{uni} = \log \left (d^{N,M}/d^{2N,2M}\right )/\log 2.}$$

Tables 5 and 6 display the errors and the orders of convergence when natural and improved boundary conditions are used, respectively. Again, it can be observed that, if the improved boundary conditions are used, the maximum errors present a much better behavior, according to the theoretical results.

Table 5 Maximum errors and orders of convergence for (17) with natural boundary conditions

Table 6 Maximum errors and orders of convergence for (17) with improved boundary conditions