1 Introduction

We present some elements of the theory of fuzzy sets. The concept of a fuzzy set was proposed by Zadeh (1965).

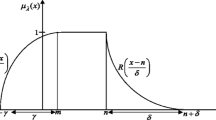
An interval fuzzy number \(\tilde{X}\) is a family of intervals of real numbers \([\tilde{X}]_\lambda \), where \(\lambda \in [0,1]\) such that: \(\lambda _1 < \lambda _2 \Rightarrow [\tilde{X}]_{\lambda _1} \subset [\tilde{X}]_{\lambda _2}\) and \(I\subseteq [0,1] \Rightarrow [\tilde{X}]_{\sup I} = \cap _{\lambda \in I} [\tilde{X}]_\lambda \). For a given \(\lambda \in [0,1]\), the interval \([\tilde{X}]_\lambda \) is called the \(\lambda \)-level of the fuzzy number \(\tilde{X}\). This interval will be denoted by \([\tilde{X}]_\lambda = [ \underline{x}(\lambda ), \overline{x}(\lambda )]\).

Dubois and Prade (1978) introduced the following useful definition of the class of L-R fuzzy numbers. A fuzzy number \(\tilde{X}\) is called an L-R fuzzy number, if its membership function is given by

$$\begin{aligned} \mu _X (x) = \left\{ \begin{array}{ccc} L\left( \frac{\underline{m} - x}{\alpha } \right) &{} \text{ for } &{} x < \underline{m} \\ 1 &{} \text{ for } &{} \underline{m} \le x \le \overline{m} \\ R\left( \frac{x-\overline{m}}{\beta } \right) &{} \text{ for } &{} x>\overline{m} \\ \end{array} \right. , \end{aligned}$$
(1)

where L(x) and R(x) are continuous non-increasing functions and \(x,\alpha ,\beta >0\).

The functions L(x) and R(x) are called the shape functions of the fuzzy numbers. The most commonly applied shape functions are \(\max \{ 0, 1-x^p\}\) and \(\exp (-x^p), x\in [0,\infty ), p\ge 1\). An interval fuzzy number for which \(L(x) = R(x) = \max \{ 0,1-x^p\}\) and \(\underline{m}=\overline{m}=m\) is called a triangular fuzzy number and will be denoted by \((m,\alpha ,\beta )\).

Let \(\tilde{X}\) and \(\tilde{Y}\) be two fuzzy numbers with membership functions given by \(\mu _X (x)\) and \(\mu _Y (y)\), respectively. Based on Zadeh’s extension principle (Zadeh 1965), the membership functions of the sum \(\tilde{Z}=\tilde{X}+\tilde{Y}\) and the product \(\tilde{V} = \tilde{X}\tilde{Y}\) are given by \(\mu _Z (z) = \sup _{z=x+y} \left( \min (\mu _X (x),\mu _Y (y))\right) \); \(\mu _V (v) = \sup _{v=xy} \left( \min (\mu _X (x),\mu _Y (y))\right) \).

Carlsson and Fullér (2001) defined the possibilistic expected value \(E(\tilde{X})\) and variance Var\((\tilde{X})\) of the fuzzy number \(\tilde{X}\) as follows:

$$\begin{aligned} E(\tilde{X})= & {} \int _0^1 \frac{1}{2} \left( \underline{x}(\lambda ) +\overline{x}(\lambda )\right) d\lambda \end{aligned}$$
(2)
$$\begin{aligned} \text{ Var }(\tilde{X})= & {} \int _0^1 \frac{1}{4} \left( \overline{x}(\lambda ) -\underline{x}(\lambda )\right) ^2 d\lambda . \end{aligned}$$
(3)

If \(\tilde{X}\) is a triangular fuzzy number \(\tilde{X} = (m,\alpha ,\beta )\), the possibilistic expected value and the possibilistic variance are given by

$$\begin{aligned} E(\tilde{X})= & {} m + \frac{\beta - \alpha }{4} \end{aligned}$$
(4)
$$\begin{aligned} \text{ Var }(\tilde{X})= & {} \frac{(\alpha + \beta )^2}{12}. \end{aligned}$$
(5)

The possibilistic expected value has the following properties, see Carlsson and Fullér (2001):

$$\begin{aligned} E(a\tilde{X})= & {} aE(\tilde{X}), \end{aligned}$$
(6)
$$\begin{aligned} E(\tilde{X}+\tilde{Y})= & {} E(\tilde{X}) + E(\tilde{Y}), \end{aligned}$$
(7)

where a is a real number.

2 Truncated Interval Fuzzy Number

We now introduce the concept of a truncated interval fuzzy number and the possibilistic expected value of such a number.

Definition 1

The interval fuzzy number \(\tilde{X}_S\) is called the truncation of the fuzzy number \(\tilde{X}\) (\([\tilde{X}]_\lambda \), where \(\lambda \in [0,1])\) on the crisp, closed (or semi-infinite) set \(S\in \mathbb {R}\), if the corresponding \(\lambda \)-levels are given by \([\tilde{X}_S]_\lambda = [\underline{x}(\lambda ),\overline{x}(\lambda )]\cap S = \left[ \underline{x_S}(\lambda ),\overline{x_S}(\lambda )\right] \).

Definition 2

The possibilistic expected value of a truncated fuzzy number \(\tilde{X}_S\) is given by

$$\begin{aligned} E(\tilde{X}_S) = E(\tilde{X}/\tilde{X}\in S) = \frac{1}{\lambda _{max}} \int _0^{\lambda _{max}} \frac{\underline{x_S}(\lambda ) + \overline{x_S}(\lambda )}{2} d\lambda \end{aligned}$$
(8)

where \(\lambda _{max} = \max _{\lambda } \{ \lambda : [\tilde{X}_S]_{\lambda } \ne \phi \}\).

For the triangular fuzzy number \((m,\alpha ,\beta )\) truncated on the set \(S=(-\infty ,x_0]\), where \(x_0 \le m\) and \(\mu (x_0) = \frac{x_0 - (m-\alpha )}{\alpha }\):

$$\begin{aligned} E(\tilde{X}/\tilde{X} \in (-\infty ,x_0]) = \frac{1}{2} (m+x_0)\mu (x_0 ) + \frac{\alpha }{4} \left( \mu ^2 (x_0) - 2\mu (x_0) \right) . \end{aligned}$$

For the triangular fuzzy number \((m,\alpha ,\beta )\) truncated on the set \(S=[x_0,\infty )\), where \(x_0 \ge m\) and \(\mu (x_0) = \frac{(m+\beta )-x_0}{\beta }\):

$$\begin{aligned} E(\tilde{X}/\tilde{X} \in [x_0 , \infty )) = \frac{1}{2} (m+x_0)\mu (x_0 ) - \frac{\beta }{4} \left( \mu ^2 (x_0) - 2\mu (x_0) \right) . \end{aligned}$$

For the triangular fuzzy number \((m,\alpha ,\beta )\) truncated on the set \(S=[x_0,\infty )\), where \(x_0 \le m\) and \(\mu (x_0) = \frac{x_0 - (m-\alpha )}{\alpha }\):

$$\begin{aligned} E(\tilde{X}/\tilde{X} \in [x_0 , \infty )) = \frac{1}{2} [m(3-2\mu (x_0))+x_0] + \frac{\beta - \alpha }{4} (2\mu ^2 (x_0) - 4\mu (x_0) +1) - \frac{\beta }{4} \left( \mu ^2 (x_0) - 2\mu (x_0) \right) . \end{aligned}$$

For the triangular fuzzy number \((m,\alpha ,\beta )\) truncated on the set \(S=(-\infty ,x_0 ]\), where \(x_0 \ge m\) and \(\mu (x_0) = \frac{(m+\beta )-x_0}{\beta }\):

$$\begin{aligned} E(\tilde{X}/\tilde{X} \in (-\infty , x_0 ]) = \frac{1}{2} [m(3-2\mu (x_0))+x_0] + \frac{\beta - \alpha }{4} (2\mu ^2 (x_0) - 4\mu (x_0) +1) + \frac{\alpha }{4}(\mu ^2(x_0)-2\mu (x_0)). \end{aligned}$$

3 Transportation Problem

The classical transportation problem involves transporting a uniform good from m suppliers to n customers. In a unit of time, supplier i can produce \(a_i\) units of the good and customer j demands \(b_j\) units. The unit cost of transporting a unit from supplier i to customer j is \(c_{ij}\). The parameters of this problem (the capacities \(a_i\), demands \(b_j\) and transportation costs \(c_{ij}\)) are all known constants. The objective is to select the transportation plan which minimizes the transportation costs while satisfying the demand of the customers, i.e.

$$\begin{aligned} \min \sum _{i=1}^m \sum _{j=1}^n c_{ij}x_{ij}, \end{aligned}$$
(9)

subject to the constraints

$$\begin{aligned} \sum _{j=1}^n x_{ij} \le a_i,&\text{ for } i = 1,2,\ldots m \nonumber \\ \sum _{i=i}^m x_{ij} \ge b_j,&\text{ for } j = 1,2,\ldots n \\ x_{ij} \ge 0,&\text{ for } i = 1,2,\ldots m, j = 1,2,\ldots n \nonumber \end{aligned}$$
(10)

The transportation problem given by (9)–(10) is a linear programming problem. When the capacities and demands are all integers, the algorithm proposed by Dantzig (1951) can be applied to find a solution where all the decision variables, the \(x_{ij}\), are integers.

In reality, it is often the case that the parameters of the transportation problem (capacities, demands and transportation costs) are not known precisely. Applying the concept of probability theory or fuzzy logic is an approach to modeling uncertainty. Such an approach was used in many works. Probabilistic transportation problems are NP-hard problems, see Chaudhuri et al. (2013). The fuzzy models proposed in this article are linear and quadratic models.

Chanas and Kuchta (1996) assumed that the unit costs of transportation are fuzzy numbers, while supply and demand are given by crisp numbers. The object is to minimize the total transportation cost. In the optimal solution, the amounts to be transported along each route are crisp numbers, while the total transportation cost is a fuzzy number. This article proposes a two criterion approach based on minimizing both the possibilistic expected total transport cost and the variance of this cost. Consequently the total cost of optimal solution has a small diversity, see Model I.

Chanas and Kuchta (1988), Gupta and Kumar (2012) assumed that supply and demand are given by fuzzy numbers. The solution is given by the set of real numbers which determine how many units of the good are transported from each supplier to each customer. However, assuming that the capacities or the demands are not precisely known leads to the possibility that the realized values of the capacities and demands are such that the decision maker cannot find an appropriate solution, since e.g. there is not enough supply to satisfy the actual demand.

Pandian and Natarajan (2010), Narayanamoorthy et al. (2013), Salajapan and Jayaraman (2014), Hussain and Jayaraman (2014) assumed that the unit costs of transportation as well as supply and demand are given by fuzzy numbers. In the optimal solution the amounts of transportation, together with the total transportation cost, are also fuzzy numbers. Rita and Vimatka (2009) assumed that transport costs are crisp, while supply and demand are given by fuzzy numbers. The loads to be transported along each route are also fuzzy numbers. In this case, it is not clear to the decision maker what the specific loads should be, thus this approach is impractical. In fact, these loads can even takes negative values. This article proposes a model which considers the costs incurred due to shortages when the supply and demand are given by fuzzy numbers, see Model II.

In this article, we propose two models of the fuzzy transportation problem:

  • Model I. Uncertainty regarding the transportation costs is modeled using fuzzy numbers and the decision is based on two criteria. The capacities and demands are known constants. The decision is based on two criteria (i) minimizing the possibilistic expected value of the total transportation costs and (ii) minimizing the possibilistic variance of these costs, since variance is a measure of risk (Sect. 4).

  • Model II. Uncertainty regarding all the parameters (transportation costs, capacities and demands) is modeled using fuzzy numbers. The decision is based on two criteria: (i) minimizing the possibilistic expected value of the total transportation costs and (ii) minimizing the possibilistic expected costs of the shortages. We interpret both excess production (i.e. insufficient demand) and unsatisfied demand as shortages. These shortages are determined by the concrete realizations of the supply and the demand (Sect. 5).

In both models transportation costs are not known precisely. The first model can be applied when the supply and demand are deterministic. The second model we could be applied when supply and demand not known precisely. The solutions of both models are given by the set of real numbers which determine how many units of the good are transported from each supplier to each customer. Such structure of solutions is useful for decision maker.

4 Transportation Problem with Fuzzy Costs

Define the unit transportation cost on the route from the i-th supplier to the j-th customer in the transportation problem given by (9)–(10) to be the triangular fuzzy number \(\tilde{C}_{ij} = (c_{ij},\alpha _{ij},\beta _{ij})\). According to Zadeh’s extension principle, it follows that the total transportation cost is given by the following fuzzy number:

$$\begin{aligned} \tilde{C} = \sum _{i=1}^m \sum _{j=1}^n \tilde{C}_{ij} x_{ij} = ( \sum _{i=1}^m \sum _{j=1}^n c_{ij} x_{ij} , \sum _{i=1}^m \sum _{j=1}^n \alpha _{ij} x_{ij} , \sum _{i=1}^m \sum _{j=1}^n \beta _{ij} x_{ij} ). \end{aligned}$$
(11)

Consider a transportation problem with the following objective functions:

  • Minimization of the possibilistic expected value of the total costs of transport \(F_1: \min E(\tilde{C})\).

  • Minimization of the possibilistic variance of the total costs of transport \(F_2: \min \text{ Var }(\tilde{C})\).

Using Eqs. (4) and (11), we can write criterion \(F_1\) in the following form:

$$\begin{aligned} F_1 : \min E(\tilde{C}) = \min \sum _{i=1}^m \sum _{j=1}^n E(\tilde{C}_{ij}) x_{ij} = \min \sum _{i=1}^m \sum _{j=1}^n \left( c_{ij} + \frac{\beta _{ij}-\alpha _{ij}}{4} \right) x_{ij} . \end{aligned}$$
(12)

It can be seen that the transportation problem based on the single optimality criterion \(F_1\) with the constraints given by (10) is a linear programming problem. Hence, in order to solve it, we can use the simplex algorithm or Dantzig’s algorithm (1951).

Now consider the problem in which the optimality criterion is the minimization of the variance of the total transportation costs. From Eqs. (5) and (11), we can write criterion \(F_2\) in the following form:

$$\begin{aligned} F_2 :\min \text{ Var }(\tilde{C}) = \min \frac{1}{12} (\sum _{i=1}^m \sum _{j=1}^n (\alpha _{ij}+\beta _{ij})x_{ij})^2 \end{aligned}$$
(13)

In this case, the objective function is quadratic. Hence, the transportation problem with objective function (13) and set of constraints given by (10) can be solved by quadratic programming.

Now consider the transportation problem with constraints given by (10) in which both \(F_1\) and \(F_2\) are used as optimality criteria. In order to solve such a problem, we can use e.g. the trade-off method. Assume that the decision maker wishes to find a transportation plan which minimizes the possibilistic variance of the total transportation costs while ensuring that the possibilistic expected costs of transportation are not greater than C. The measure of risk is defined to be the possibilistic variance of the total transportation costs. It follows that the appropriate transportation plan is the solution of the following optimization problem:

$$\begin{aligned} \min \frac{1}{12} (\sum _{i=1}^m \sum _{j=1}^n (\alpha _{ij}+\beta _{ij})x_{ij})^2 \end{aligned}$$
(14)

subject to the constraints

$$\begin{aligned}&\mathop {\sum }\nolimits _{i=1}^m \mathop {\sum }\nolimits _{j=1}^n \left( c_{ij} + \frac{\beta _{ij}-\alpha _{ij}}{4}\right) x_{ij} \le C&\nonumber \\&\mathop {\sum }\nolimits _{j=1}^n x_{ij} \le a_i, \text{ for } i = 1,2,\ldots m&\\&\mathop {\sum }\nolimits _{i=i}^m x_{ij} \ge b_j, \text{ for } j = 1,2,\ldots n&\nonumber \\&x_{ij} \ge 0, \text{ for } i = 1,2,\ldots m, j = 1,2,\ldots n&\nonumber \end{aligned}$$
(15)

A transportation problem formulated in this way has a quadratic objective function and a set of linear constraints.

Example 1. Consider the transportation problem with three suppliers and four customers defined by Liang et al. (2005). This problem was also analyzed in Kaur and Kumar (2011). In both of the articles, the authors assumed that the goal was to minimize the total transportation costs. The firm Dali, based in Taiwan, produces soft drinks and frozen foods. The firm wishes to extend its activities into the Chinese market. It plans to distribute its range of teas to four destinations: Taichung, Chiayi, Kaohsiung and Taipei. The production units are located in Changhua, Touliu and Hsinchu. The firm estimates the capacities of these units, together with the level of demand from the four destinations and the transportation costs (see Table 1). The transportation costs are given in the form of triangular fuzzy numbers, since they are not known precisely. There are a number of factors which determine these transportation costs, such as weather, road and technical conditions. In the original paper (Liang et al. 2005), supply and demand were given in the form of fuzzy numbers. Here, they are given as constants, which are assumed to be the most likely values.

Table 1. Unit transportation costs, supply and demand for Example 1
Full size table

The possibilistic expected value and variance of the unit transportation costs can be derived from Eqs. (4) and (5).

The optimal transportation plans based on each objective individually: minimize the possibilistic expected value of the total transportation costs (\(F_1\)) and minimize the possibilistic variance of the total transportation costs (\(F_2\)) are given in Table 2. The only parts of these solutions which coincide are the use of two transportation routes, between Changhua and Kaoshiung and between Hsinchu and Chiayi.

Table 2. Optimal solutions to the transportation problems based on the criteria \(F_1\) and \(F_2\) and the associated costs
Full size table

In the case of minimizing the expected value of the transportation costs, the total transportation costs are given by the triangular fuzzy number (352, 72.4, 30) [in thousands of $] with expected value $ 341.4 thou. and dispersion $ 29.6 thou. This is the same solution as the one obtained using the algorithms proposed by Kaur and Kumar (2011) and Liang et al. (2005). In the case of minimizing the variance of the transportation costs, the total transportation costs are given by the triangular fuzzy number (496, 51.8, 37.8) [in thousands of $] with expected value $ 492.5 thou. and dispersion $ 25.9 thou. The variance of the costs are somewhat smaller. However, the expected costs are $ 148.73 thou. greater. One advantage of this transportation plan lies in the fact that only five routes are used.

Now we consider the model of the transportation problem with objective functions (14) and set of constraints given by (15). Assume that the decision maker is interested in a transportation plan which minimizes the variance of the transportation costs given that the expected value of the total transportation costs is less than $ 360 thou. The optimal transportation plan for this problem is described in Table 2. The total transportation costs are given by the triangular fuzzy number (364, 68.4, 29.2) [in thousands of $], which has expected value $ 354.2 thou. and dispersion $ 28.67 thou.

5 Transportation Problem with Fuzzy Costs, Demand and Supply

Consider a fuzzy transportation problem in which all the parameters (the unit transportation costs, supply and demand) are all given by fuzzy numbers. Such problems are common in practice, especially in the case of goods which have seasonal demand (which commonly depends on the weather). Similarly, supply can also be uncertain. Given such a model, we consider the following objective functions: minimization of the possibilistic expected value of the total transportation costs, minimization of the sum of the possibilistic expected value of the total costs associated with shortages. The unit transportation costs are given by triangular fuzzy numbers of the form \(\tilde{C}_{ij} = (c_{ij},\alpha _{ij},\beta _{ij})\). In addition, let the capacities and demands be given by the set of triangular fuzzy numbers \(\tilde{A}_i = (a_i, \gamma _{i}, \delta _{i})\) for \(i=1,2,\ldots ,m\) and \(\tilde{B}_j = (b_j ,\epsilon _{j},\theta _{j})\) for \(j=1,2,\ldots ,n\). Let the unit cost of purchasing (producing) the good at the last moment at the i-th point of supply be \(PA_i\), \(i=1,2,\ldots ,m\) and the unit penalty for not delivering a product to the j-th customer be \(PB_j\), \(j=1,2,\ldots ,n\). In the case when \(PA_i = PB_j\) for all i and j, the objective is to minimize the possibilistic expected value of the sum of the shortage in supply and the shortage in demand. The appropriate model of a multicriteria fuzzy transportation problem is given by

$$\begin{aligned} F_1 : \! \!&\! \! \min E(\tilde{C}) = \min \sum _{i=1}^m \sum _{j=1}^n E(\tilde{C}_{ij})x_{ij} \end{aligned}$$
(16)
$$\begin{aligned} F_2 : \! \!&\! \! \min \left[ \sum _{i=1}^m PA_i \cdot \left[ \sum _{j=1}^n x_{ij}- E\left( \tilde{A}_i /\tilde{A}_i \in (-\infty ,\sum _{j=1}^n x_{ij} ]\right) \right. \right] + \\ \! \!&\! \! + \left. \sum _{j=1}^n PB_j \cdot \left[ E\left( \tilde{B}_j / \tilde{B}_j \in [\sum _{i=1}^m x_{ij}, \infty ) \right) -\sum _{i=1}^m x_{ij}\right] \right] \nonumber \end{aligned}$$
(17)

subject to the conditions

$$\begin{aligned} a_i - \gamma _i \le \sum _{j=1}^n x_{ij} \le a_i+\delta ,&\text{ for } i = 1,2,\ldots m \nonumber \\ b_j - \epsilon _j \le \sum _{i=i}^m x_{ij} \le b_j + \theta _j,&\text{ for } j = 1,2,\ldots n \\ x_{ij} \ge 0,&\text{ for } i = 1,2,\ldots m, j = 1,2,\ldots n \nonumber . \end{aligned}$$
(18)

Example 2. We return to the transportation problem considered in Example 1. However, supply and demand are assumed to be given by the following triangular fuzzy numbers: \(\tilde{A}_1 = (8, 0.8, 0.8), \tilde{A}_2 = (14, 2, 2), \tilde{A}_3 = (12, 1.8, 1.8), \tilde{B}_1 = (7, 0.8, 0.8)\), \(\tilde{B}_2 = (10, 1.4, 1.4), \tilde{B}_3 = (8, 1.5, 1.5), \tilde{B}_4 = (9, 1.2, 1.2)\), see Liang et al. (2005). The optimality function is taken to be combination (sum) of the two functions defined above, \(F = F_1 + F_2\), where \(PA_i =PB_j = 10000\). This means that the \(F_2\) criterion is to minimize the possibilistic expected shortage (in supply or demand). Optimal solution is:

$$\begin{aligned} x_{11}=4, x_{13}=3, x_{21}=2, x_{23}=2, x_{24}=8, x_{31}=1, x_{32}=9, x_{33}=2 \end{aligned}$$

The expected shortage is 3.73 thousand 12-packs, the transportation cost is the triangular fuzzy number (336, 63.6, 27) [in thou. $] and the possibilistic expected value of the transport costs are $ 326.85 thou. Lets now compare our solution with the solutions of this problem obtained by other methods: the generalized fuzzy methods (GFNWCM, GFLCM, GFVAM) proposed by Kaur and Kumar (2011) and the method proposed by Liang et al. (2005). The optimal solution obtained by each of this method is the same as our solution in the example 1 when the criterion function is minimization of the possibilistic expected value of transportation costs. The optimal transportation plan and fuzzy transportation cost are given in Table 2 in column 2. The possibilistic expected value of the transportation costs are $ 341.4 thou. the expected shortage is 2.375 thousand 12-packs. So the expected transport cost in the solution proposed by our method is smaller and the expected shortage is greater.

6 Conclusion

This article has presented two models of a multicriteria transportation problem. Under the first model, it is assumed that the unit transportation costs are fuzzy numbers. The two optimality criteria considered were: (a) minimization of the possibilistic expected value of the total transportation costs and (b) minimization of the possibilistic variance of the total transportation costs. Under the second model, all of the parameters of the problem are fuzzy numbers. The two optimality criteria considered here were: (a) minimization of the possibilistic expected value of the total transportation costs and (b) minimization of the expected costs resulting from shortages in supply and demand. The first model enables the derivation of transportation plans which achieve “stable” (minimum variance) costs. Applying the second model, we take into account both transportation costs as well as losses resulting from unsatisfied demand or excessive production. This approach uses the concept of truncated fuzzy numbers, as proposed in this article, as well as the possibilistic expected value. Two illustrative examples were given.