Abstract
We present the first internal calculi for Lewis’ conditional logics characterized by uniformity and reflexivity, including non-standard internal hypersequent calculi for a number of extensions of the logic \(\mathbb {V}\mathbb {T}\mathbb {U}\). These calculi allow for syntactic proofs of cut elimination and known connections to \(\mathsf {S5}\). We then introduce standard internal hypersequent calculi for all these logics, in which sequents are enriched by additional structures to encode plausibility formulas as well as diamond formulas. These calculi provide both a decision procedure for the respective logics and constructive countermodel extraction from a failed proof search attempt.
Supported by the Project TICAMORE ANR-16-CE91-0002-01, by the EU under Marie Skłodowska-Curie Grant Agreement No. [660047], and by the project “ExceptionOWL”, Università di Torino and Compagnia di San Paolo, call 2014 “Excellent (young) PI”.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Conditional logics have a long history going back, e.g., to the works of Stalnaker, Lewis, Nute, Chellas, Burgess, Pollock in the 60’s–70’s [3, 4, 13, 14, 18]. In his seminal works Lewis proposed a formalization of conditional logics to capture counterfactual and other hypothetical conditionals that cannot be accommodated by the material implication of classical logic [13]. Conditional logics have since found an interest in several fields of knowledge representation, from reasoning about prototypical properties and nonmonotonic reasoning [9] to modeling belief change. A successful attempt to relate conditional logic and belief update (as opposite to belief revision) was carried out by Grahne [8], who established a precise mapping between belief update operators and Lewis’ logic \(\mathbb {V}\mathbb {C}\mathbb {U}\). The relation is expressed by the so-called Ramsey’s Rule:
\(A \circ B \rightarrow C\) holds if and only if
holds
where the operator \(\circ \) is any update operator satisfying Katsuno and Mendelzon’s postulates. The relation means that C is entailed by “A updated by B” if and only if the conditional  is entailed by A. In this sense it can be said that the conditional
is entailed by A. In this sense it can be said that the conditional  expresses an hypothetical update of a piece of information A.
expresses an hypothetical update of a piece of information A.
The family of logics studied by Lewis in [13] is semantically characterized by sphere models, where each world x is equipped with a set of nested sets of worlds  . Each set in
. Each set in  is called a sphere: the intuition is that concerning x, worlds in inner spheres are more plausible than worlds belonging only to outer spheres. Lewis takes as primitive the comparative plausibility connective \(\preccurlyeq \), with a formula \(A \preccurlyeq B\) meaning “A is at least as plausible as B”. The conditional
is called a sphere: the intuition is that concerning x, worlds in inner spheres are more plausible than worlds belonging only to outer spheres. Lewis takes as primitive the comparative plausibility connective \(\preccurlyeq \), with a formula \(A \preccurlyeq B\) meaning “A is at least as plausible as B”. The conditional  is then defined as “A is impossible or \(A \wedge \lnot B\) is less plausible than A”. Vice versa, \(\preccurlyeq \) can be defined in terms of
is then defined as “A is impossible or \(A \wedge \lnot B\) is less plausible than A”. Vice versa, \(\preccurlyeq \) can be defined in terms of  .
.
In this paper we continue our proof-theoretic investigation of the family of Lewis’ logics, concentrating on the logics characterized by two properties: (i) Uniformity: all worlds have the same set of accessible worlds, where the worlds accessible from a world x are those belonging to any sphere  ; (ii) Total reflexivity: every world x belongs to some sphere
; (ii) Total reflexivity: every world x belongs to some sphere  . The basic logic is \(\mathbb {V}\mathbb {T}\mathbb {U}\); we will then consider some of its extensions, including the above mentioned \(\mathbb {V}\mathbb {C}\mathbb {U}\). It is worth mentioning that equivalent logics are those of Comparative Concept Similarity studied in the context of ontologies [17]. These logics contain a connective \(\leftleftarrows \), which allows to express, e.g.,
. The basic logic is \(\mathbb {V}\mathbb {T}\mathbb {U}\); we will then consider some of its extensions, including the above mentioned \(\mathbb {V}\mathbb {C}\mathbb {U}\). It is worth mentioning that equivalent logics are those of Comparative Concept Similarity studied in the context of ontologies [17]. These logics contain a connective \(\leftleftarrows \), which allows to express, e.g.,
asserting that “Picasso’s paintings are more similar to Braque’s paintings than to Giotto’s ones”. The semantics is provided in terms of Distance Space Models, defined as a set of worlds equipped with a distance function. It turns out that the basic logic of Comparative Concept Similarity coincides with Lewis’ logic \(\mathbb {V}\mathbb {W}\mathbb {U}\) and the one defined by “minspace” Distance Models coincides with \(\mathbb {V}\mathbb {C}\mathbb {U}\), so that Distance Space Models provide an alternative simple and natural semantics for conditional logics with uniformity [1, 17].
Here we investigate internal calculi for logics extending \(\mathbb {V}\mathbb {T}\mathbb {U}\), i.e., calculi where each configuration of a derivation corresponds to a formula of the corresponding logic, in contrast to external calculi which make use of extra-logical elements (such as labels, terms and relations on them). Ideally, we seek calculi with the following features: (i) they should be standard, i.e., each connective is handled by a finite set of rules with a finte and fixed set of premises; (ii) they should be modular, i.e., it should be possible to obtain calculi for stronger logics by adding independent rules to a base calculus; (iii) they should have good proof-theoretical properties, such as a syntactic proof of cut admissibility; finally (iv) they should provide a decision procedure for the respective logics. In our opinion requirement (i) is particularly important: a standard calculus provides a self-explanatory presentation of the logic, thus a kind of proof-theoretic semantics.
In previous work [7], we defined calculi with many of these properties for weaker logics of the Lewis’ family. For the logics with uniformity to the best of our knowledge no internal calculi are known; the only known external calculi for these adopt a hybrid language and a relational semantics [6]. We also consider logics with absoluteness, a property stronger than uniformity stating that all worlds have the same system of spheres. It is unlikely that sequents, even extended as in [7], are sufficient to capture logics with uniformity: Since modal logic \(\mathsf {S5}\) can be embedded into \(\mathbb {V}\mathbb {T}\mathbb {U}\), a sequent calculus for the latter would most probably also yield a sequent calculus for \(\mathsf {S5}\). The existence of such a calculus, however, would be very surprising. We therefore adopt the framework of hypersequents [2], where the basic objects are multisets of sequents.
We first provide a non-standard hypersequent calculus for \(\mathbb {V}\mathbb {T}\mathbb {U}\) and its extensions and syntactically prove cut-elimination and hence completeness. We then show that by translating \(\Box A\) as \(\bot \preccurlyeq \lnot A\) the calculi - restricted to such formulas - correspond to known hypersequent calculi for \(\mathsf {S5}\). Further, we construct standard calculi for all the logics by enriching the hypersequents with additional structural connectives encoding plausibility and “possible” formulas respectively. The obtained standard calculi provide decision procedures for the respective logics. Finally, we give a direct semantic completeness proof for the logics without absoluteness, by considering the invertible version of the rules and constructing a countermodel from a failed attempt at proof search. Thus, the calculi can also be used for countermodel generation, a task of independent interest.
2 Preliminaries
We consider the conditional logics of [13]. The set of conditional formulae is given by \( A {:}{:} = p \mid \bot \mid A \rightarrow A \mid A \preccurlyeq A \), where \(p \in \mathcal {V}\) is a propositional variable. We define the boolean connectives \(\wedge , \vee , \top \) in terms of \( \bot \) and \( \rightarrow \) as usual. Intuitively, a formula \(A \preccurlyeq B\) is interpreted as “A is at least as plausible as B”. Lewis’ counterfactual implication  is defined by
is defined by  , whereas the outer modality \(\Box \) is defined by \(\Box A \equiv (\bot \preccurlyeq \lnot A)\). The logics we consider are defined as follows:
, whereas the outer modality \(\Box \) is defined by \(\Box A \equiv (\bot \preccurlyeq \lnot A)\). The logics we consider are defined as follows:
Definition 1
A universal sphere model (or model) is a triple  , consisting of a non-empty set W of elements, called worlds, a mapping
, consisting of a non-empty set W of elements, called worlds, a mapping  , and a propositional valuation
, and a propositional valuation  . Elements of
. Elements of  are called spheres. We assume the following conditions:
are called spheres. We assume the following conditions:

The valuation  is extended to all formulae by: \([\![{\bot }]\!]= \emptyset \); \([\![{A \rightarrow B}]\!]= (W - [\![{A}]\!]) \cup [\![{B}]\!]\);
is extended to all formulae by: \([\![{\bot }]\!]= \emptyset \); \([\![{A \rightarrow B}]\!]= (W - [\![{A}]\!]) \cup [\![{B}]\!]\);  . We also write \(w \Vdash A\) instead of \(w \in [\![{A}]\!]\) as well as \( \alpha \Vdash ^{\forall }A \) for \( \forall x \in \alpha .\; x \Vdash A\) and \( \alpha \Vdash ^{\exists } A \) for \( \exists x \in \alpha .\; x \Vdash A \)
Footnote 1. Validity and satisfiability of formulae in a class of models are defined as usual. Conditional logic \(\mathbb {V}\mathbb {T}\mathbb {U}\) is the set of formulae valid in all universal sphere models.
. We also write \(w \Vdash A\) instead of \(w \in [\![{A}]\!]\) as well as \( \alpha \Vdash ^{\forall }A \) for \( \forall x \in \alpha .\; x \Vdash A\) and \( \alpha \Vdash ^{\exists } A \) for \( \exists x \in \alpha .\; x \Vdash A \)
Footnote 1. Validity and satisfiability of formulae in a class of models are defined as usual. Conditional logic \(\mathbb {V}\mathbb {T}\mathbb {U}\) is the set of formulae valid in all universal sphere models.
Extensions of \(\mathbb {V}\mathbb {T}\mathbb {U}\) are defined by additional conditions on the class of models, namely:
-
weak centering: for all
 we have \(w \in \alpha \);
we have \(w \in \alpha \); -
centering: for all \( w \in W\;\) we have
 ;
; -
absoluteness: for all \( w,v \in W\;\) we have
 .
.
Extensions of \(\mathbb {V}\mathbb {T}\mathbb {U}\) are denoted by concatenating letters for these properties: \(\mathbb {W}\) for weak centering, \(\mathbb {C}\) for centering, and \(\mathbb {A}\) for absoluteness. We consider the following systemsFootnote 2:

These logics can be characterized by axioms in a Hilbert-style system [13, Chap. 6]. The modal axioms in the language with only the comparative plausibility operator are given in Table 1 (\(\vee \) and \(\wedge \) bind stronger than \(\preccurlyeq \)). Propositional axioms and rules are standard.
3 Hypersequent Calculi
In this section we introduce calculi for \( \mathbb {V}\mathbb {T}\mathbb {U}\) and extensions. We call a calculus standard if (a) it has a finite number of rules and (b) each rule has a finite and fixed number of premisses. With respect to this definition, the calculi introduced in this section are non-standard, whereas the calculi we introduce in Sect. 6 are standard.
Our calculi are based on hypersequents, where as usual a sequent is a pair consisting of two multisets of formulae, written as \(\varGamma \Rightarrow \varDelta \).
Definition 2
A hypersequent is a non-empty multiset of sequents, written \(\varGamma _1 \Rightarrow \varDelta _1 \mid \ldots \mid \varGamma _n \Rightarrow \varDelta _n\), where \(n \ge 1\) is the cardinality of the multiset. The conditional formula interpretation of a hypersequent is
where \(\Box \) is the outer modality defined by \(\Box A \equiv (\bot \preccurlyeq \lnot A)\).
The rules of the calculi \(\mathsf {H}_{\mathcal {L}}\) extend the calculi from [12] to the hypersequent setting and are given in Fig. 1. These calculi are non-standard, meaning that the rules have an unbounded number of premisses. We abbreviate multisets of formulae \(A_k,\ldots , A_n\) to \(\varvec{[ A ]}_{k}^{n}\), and \(C_k\preccurlyeq D_k, \ldots , C_n \preccurlyeq D_n\) to \(\varvec{[ C \preccurlyeq D ]}_{k}^{n}\) with the convention that \(\varvec{[ A ]}_{k}^{n}\) is empty if \(k > n\). The crucial rule for uniformity is the rule \(\mathsf {trf}_m\). Intuitively it unpacks a number of comparative plausibility formulae behaving like boxed formulae on the left hand side of a component in the conclusion into a different component in the rightmost premiss, most clearly seen in the case of \(n = 1\). The leftmost set of premisses ensures that the comparative plausibility formulae indeed behave like boxed formulae. The rule \(\mathsf {T}_m\) is the local version of \(\mathsf {trf}_m\), and essentially captures total reflexivity.
Lemma 3
For \(\mathcal {L}\) any of the considered logics, the calculus \(\mathsf {H}_{\mathcal {L}}\) is sound for \(\mathcal {L}\).
Proof
This follows from validity of \(\Box A \rightarrow A\) in all the logics and the fact that the rules preserve soundness with respect to \(\iota \). The latter is shown for each rule by constructing a countermodel for one of the premisses from a countermodel for the conclusion, using that the sphere system is universal. For all the rules apart from \(\mathsf {trf},\mathsf {abs}_L,\mathsf {abs}_R,\mathsf {spl}\) this follows as in [12], using that \(\Box A \rightarrow \Box \Box A\) is valid. For \(\mathsf {abs}_L,\mathsf {abs}_R\) this follows straightforwardly from absoluteness, and for \(\mathsf {spl}\) this follows from the fact that frames for \(\mathbb {V}\mathbb {C}\mathbb {A}\) are degenerate in the sense that  for every world w (see footnote 2).
for every world w (see footnote 2).
For the rule \(\mathsf {trf}\), let  be a \(\mathbb {V}\mathbb {T}\mathbb {U}\) model, let \(w \in W\), and suppose that
be a \(\mathbb {V}\mathbb {T}\mathbb {U}\) model, let \(w \in W\), and suppose that
Then in particular \(\mathfrak {M},w \models \lnot \left( \iota (\mathcal {G}) \vee \Box \left( \bigwedge \varSigma \rightarrow \varPi \right) \vee \Box \left( \wedge \varOmega \rightarrow \varTheta \right) \right) \). Furthermore, suppose that for every \(k \le m\) we have
Then from the case \(k = 1\) of (2) we obtain \(\mathfrak {M},w \models \Box \lnot C_1\). From this together with (1) and the fact that for every  we have
we have  we then obtain \(\mathfrak {M},w \models \Box \lnot D_1\). Similarly, using the case \(k=2\) of (2) we get \(\mathfrak {M},w \models \Box \lnot D_2\) and continuing like this we get \(\mathfrak {M},w \models \Box \lnot D_1 \wedge \ldots \wedge \Box \lnot D_m\). Together with (1) this gives \( \mathfrak {M},w \models \lnot \iota (\mathcal {G}) \wedge \lozenge \left( \bigwedge \varSigma \wedge \lnot \bigvee \varPi \right) \wedge \lozenge \left( \wedge \varOmega \wedge \lnot \left( D_1\vee \ldots \vee D_m \vee \bigvee \varTheta \right) \right) \) and hence we have a countermodel for the remaining premiss. \(\square \)
we then obtain \(\mathfrak {M},w \models \Box \lnot D_1\). Similarly, using the case \(k=2\) of (2) we get \(\mathfrak {M},w \models \Box \lnot D_2\) and continuing like this we get \(\mathfrak {M},w \models \Box \lnot D_1 \wedge \ldots \wedge \Box \lnot D_m\). Together with (1) this gives \( \mathfrak {M},w \models \lnot \iota (\mathcal {G}) \wedge \lozenge \left( \bigwedge \varSigma \wedge \lnot \bigvee \varPi \right) \wedge \lozenge \left( \wedge \varOmega \wedge \lnot \left( D_1\vee \ldots \vee D_m \vee \bigvee \varTheta \right) \right) \) and hence we have a countermodel for the remaining premiss. \(\square \)
By induction on the formula complexity we straightforwardly obtain:
Lemma 4
For every formula A we have \(\mathsf {H}_{\mathcal {L}}\vdash \mathcal {G} \mid \varGamma , A \Rightarrow A, \varDelta \).
As usual, a rule is admissible in \(\mathsf {H}_{\mathcal {L}}\) if whenever the premisses are derivable in \(\mathsf {H}_{\mathcal {L}}\), then so is its conclusion. It is depth-preserving admissible, if the depth of the derivation of its conclusion is at most the maximal depth of the derivations of its premisses.
Lemma 5
The rules \(\mathsf {IW}, \mathsf {EW}, \mathsf {mrg}\) from Fig. 2 are depth-preserving admissible in \(\mathsf {H}_{\mathcal {L}}\).
Proof
By induction on the depth of the derivation in all cases. For \(\mathsf {mrg}\), if the last applied rule was \(\mathsf {trf}_m\), we might need to replace it with \(\mathsf {T}_m\). \(\square \)
Observe that from admissibility of \(\mathsf {mrg}\) using the internal contraction rules we also immediately obtain admissibility of the external contraction rules, i.e., contraction on hypersequent components. We first show completeness of the systems with the cut rule:

Cut-free completeness then will follow from cut elimination. In the following we write \(\mathsf {H}_{\mathcal {L}}\mathsf {cut}\) for the system \(\mathsf {H}_{\mathcal {L}}\) with the cut rule.
Lemma 6
(Completeness with cut). For \(\mathcal {L}\) one of the considered logics the calculus \(\mathsf {H}_{\mathcal {L}}\mathsf {cut}\) is complete for \(\mathcal {L}\), i.e., whenever \(A \in \mathcal {L}\), then \(\mathsf {H}_{\mathcal {L}}\mathsf {cut}\vdash \;\Rightarrow A\).
Proof
By deriving the axioms and using \(\mathsf {cut}\) to simulate modus ponens and the rule \((\mathsf {CPR})\). The interesting cases are the axioms \((\mathsf {U1}),(\mathsf {U2})\) for uniformity and \((\mathsf {A1}),(\mathsf {A2})\) for absoluteness. The derivation for \((\mathsf {U1})\) is as follows:

The derivations of the remaining axioms are similar, using the rules \(\mathsf {abs}_L,\mathsf {abs}_R\) in the case of absoluteness. \(\square \)
4 Cut Elimination
To obtain cut-free completeness for all systems we now give a syntactic proof of cut elimination. For this, in the presence of absoluteness we consider slightly extended calculi containing also versions of the rules \(W_{m,n}, R_C, R_W\) where absoluteness is built in:

Since these are derivable using the original version of the rule followed by applications of \(\mathsf {abs}_L,\mathsf {abs}_R\), cut elimination in the extended system entails cut elimination in the original system. As can be expected, due to the presence of contraction cut elimination in a hypersequent system is rather more involved than in the sequent case of [12]. Moreover, due to the form of the absoluteness rules we cannot simply apply the general results of [11], although the strategy for the cut elimination proof is the same: Intuitively, an application of the cut rule (shown before Lemma 6) with cut formula of maximal complexity is permuted up in the derivation of the left premiss, where applications of contraction are swallowed up in a more general induction hypothesis, until an occurrence of the cut formula is principal (Lemma 10). Then essentially the fact that contractions can be permuted above logical rules is used to obtain a single occurrence of the cut formula in the left premiss of the cut, and the cut is permuted up in the right premiss. Again, contractions are swallowed up by a generalised induction hypothesis, and once the cut formula becomes principal in the last applied rule, its complexity is reduced (Lemma 9). For technical reasons we also include the rule \(\mathsf {mrg}\) in the calculus when proving cut elimination. By Lemma 5 it is clear that all applications of this rule can then be eliminated in the cut-free system. In the following we write \(\mathsf {H}_{\mathcal {L}}^*\) for the system \(\mathsf {H}_{\mathcal {L}}\) with \(\mathsf {cut},\mathsf {mrg}\) and with the rules \(W_{m,n}^\mathsf {abs}, R_C^\mathsf {abs}, R_W^\mathsf {abs}\) where applicable, and abbreviate \(\underbrace{A,\ldots ,A}_{n\text {-times}}\) to \(A^n\).
Definition 7
The cut rank of a \(\mathsf {H}_{\mathcal {L}}^*\)-derivation \(\mathcal {D}\) is the maximal complexity of a cut formula occurring in \(\mathcal {D}\), written \(\rho (\mathcal {D})\). A rule is cut-rank preserving admissible in \(\mathsf {H}_{\mathcal {L}}^*\) if whenever its premiss(es) are derivable in \(\mathsf {H}_{\mathcal {L}}^*\) with cut-rank n, then so is its conclusion.
Lemma 8
The rules \(\mathsf {EW},\mathsf {IW}\) are depth- and cut-rank preserving admissible in \(\mathsf {H}_{\mathcal {L}}^*\).
Proof
Standard induction on the depth of the derivation. \(\square \)
Lemma 9
(Shift Right). Suppose that for \(k>0\) and \(n_1,\ldots , n_k > 0\) there are \(\mathsf {H}_{\mathcal {L}}^*\)-derivations \(\mathcal {D}_1\) and \(\mathcal {D}_2\) of \(\mathcal {G} \mid \varOmega \Rightarrow \varTheta , A\) and \(\mathcal {H} \mid A^{n_1},\varXi _1 \Rightarrow \varUpsilon _1 \mid \ldots \mid A^{n_k}, \varXi _k \Rightarrow \varUpsilon _k\) with \(\rho (\mathcal {D}_1) < |A| > \rho (\mathcal {D}_2)\) and such that the displayed occurrence of A is principal in the last rule application in \(\mathcal {D}_1\). Then there is a \(\mathsf {H}_{\mathcal {L}}^*\)-derivation \(\mathcal {D}\) with endhypersequent \( \mathcal {G} \mid \mathcal {H} \mid \varOmega , \varXi _1 \Rightarrow \varTheta , \varUpsilon _1 \mid \ldots \mid \varOmega , \varXi _k \Rightarrow \varTheta , \varUpsilon _k \) and \(\rho (\mathcal {D}) < |A|\).
Proof
By induction on the depth of \(\mathcal {D}_2\). If none of the displayed occurrences of A is principal in the last rule in \(\mathcal {D}_2\), we apply the induction hypothesis on the premiss(es) of that rule, followed by the same rule (and possibly structural rules). If at least one of the displayed occurrences is principal in the last rule in \(\mathcal {D}_2\), we distinguish cases according to the last applied rule in \(\mathcal {D}_1\), with subcases according to the last rule in \(\mathcal {D}_2\). For space reasons we only consider an exemplary case, the remaining cases are similar. Suppose the last rules in \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are \(R_{m,n+1}\) and \(\mathsf {trf}_s\) respectively, that A is the formula \(E \preccurlyeq F\) and that \(\mathcal {D}_1\) ends in:

First we apply the induction hypothesis to the conclusion of this and the premisses of \(\mathsf {trf}_s\) to eliminate all the occurrences of \(E \preccurlyeq F\) from the context. Hence we assume that the only occurrences of \(E \preccurlyeq F\) in the conclusion of \(\mathsf {trf}_s\) are principal and that \(\mathcal {D}_2\) ends in:

with \(E \preccurlyeq F\) not occurring in \(\varvec{[ G\preccurlyeq H ]}_{1}^{r}\). Cuts on the formulae E and F then yield:

Admissibility of internal weakening (Lemma 8) and an application of \(R_{m+s, n+t}\) then gives:
Iterating this process to eliminate the remaining occurrences of \(E \preccurlyeq F\) from \(\varvec{[ G \preccurlyeq H ]}_{r+1}^{s}\), followed by \(\mathsf {mrg}\) and applications of contraction then yields the desired sequent. \(\square \)
Lemma 10
(Shift Left). Suppose that for \(k>0\) and \(n_1,\ldots , n_k > 0\) there are \(\mathsf {H}_{\mathcal {L}}^*\)-derivations \(\mathcal {D}_1\) and \(\mathcal {D}_2\) of the hypersequents \(\mathcal {G} \mid \varOmega _1 \Rightarrow \varTheta _1, A^{n_1} \mid \ldots \mid \varOmega _k \Rightarrow \varTheta _k, A^{n_k}\) and \(\mathcal {H} \mid A,\varXi \Rightarrow \varUpsilon \) with \(\rho (\mathcal {D}_1) < |A| > \rho (\mathcal {D}_2)\). Then there is a \(\mathsf {H}_{\mathcal {L}}^*\)-derivation \(\mathcal {D}\) with endsequent \( \mathcal {G} \mid \mathcal {H} \mid \varOmega _1, \varXi \Rightarrow \varTheta _1, \varUpsilon \mid \ldots \mid \varOmega _k, \varXi \Rightarrow \varTheta _k, \varUpsilon \) and \(\rho (\mathcal {D}) < |A|\).
Proof
By induction on the depth of \(\mathcal {D}_1\). If none of the displayed occurrences of A is principal in the last rule in \(\mathcal {D}_1\) or the active formula of \(\mathsf {abs}_R\), we apply the induction hypothesis on the premiss(es) of the last rule in \(\mathcal {D}_1\) followed by the same rule and possibly admissibility of weakening and contraction. If one of the occurrences of A is active in \(\mathsf {abs}_R\), we use admissibility of \(\mathsf {EW}\) (Lemma 8) and \(\mathsf {abs}_L\) on \(\mathcal {D}_2\) to obtain \(\mathcal {H} \mid \varXi \Rightarrow \varUpsilon \mid A \Rightarrow \;\). Then the induction hypothesis on this and the premiss of \(\mathsf {abs}_R\) followed by \(\mathsf {mrg}\) and \(\mathsf {IW}\) yields the result. If an occurrence of A is principal in the last rule in \(\mathcal {D}_1\), we use the induction hypothesis to remove all the occurrences of A in the context of that rule. Then, in case this rule is \(R_{m,n},W_{m,n}, W_{m,n}^\mathsf {abs}\), we apply contraction in the premisses and apply the same rule, so that only one occurrence of A is principal. Now Lemma 9 yields the result. \(\square \)
Theorem 11
(Cut Elimination). Let \(\mathcal {L} \in \{ \mathbb {V}\mathbb {T}\mathbb {U}, \mathbb {V}\mathbb {W}\mathbb {U}, \mathbb {V}\mathbb {C}\mathbb {U}, \mathbb {V}\mathbb {T}\mathbb {A}, \mathbb {V}\mathbb {W}\mathbb {A}, \mathbb {V}\mathbb {C}\mathbb {A}\}\). If a hypersequent is derivable in \(\mathsf {H}_{\mathcal {L}}^*\), then it is derivable in \(\mathsf {H}_{\mathcal {L}}\).
Proof
First we eliminate all applications of \(\mathsf {cut}\) by induction on the tuples \(\langle \rho (\mathcal {D}), \sharp ( \mathcal {D} ) \rangle \) under the lexicographic ordering, where \(\sharp ( \mathcal {D} )\) is the number of applications of \(\mathsf {cut}\) in \(\mathcal {D}\) with cut formula of complexity \(\rho (\mathcal {D})\). Then applications of \(W_{m,n}^\mathsf {abs},R_C^\mathsf {abs},R_W^\mathsf {abs}\) are replaced with the \(W_{m,n},R_C, R_W\) and \(\mathsf {abs}_L,\mathsf {abs}_R\), and \(\mathsf {mrg}\) is eliminated using Lemma 5. It is straightforward to check that applications of \(W_{m,n}^\mathsf {abs}, R_C^\mathsf {abs}, R_W^\mathsf {abs}\) are only introduced in systems including the absoluteness rules. \(\square \)
Corollary 12
(Cut-free completeness). If \(A \in \mathcal {L}\), then \(\mathsf {H}_{\mathcal {L}}\vdash \;\Rightarrow A\).
5 Connections to Modal Logic
The constructed hypersequent calculi provide purely syntactical proofs of results from [13] connecting the conditional logics to, e.g., modal logic \(\mathsf {S5}\). We write \(\mathcal {L}^\Box \) for the modal fragment of a conditional logic \(\mathcal {L}\), i.e., the fragment where comparative plausibility formulae are restricted to the shape \((\bot \preccurlyeq \lnot A)\), and we write \(A^\Box \) for the result of replacing every subformula \(\bot \preccurlyeq \lnot B\) of A with \(\Box B\). The proofs use the fact that the hypersequent calculus \(\mathsf {H}_{\mathsf {S5}}\) with the propositional rules of Fig. 1, the structural rules and the rules

is cut-free complete for \(\mathsf {S5}\) [16], see also [11].
Lemma 13
If \(A^\Box \in \mathsf {S5}\), then \(A \in \mathcal {L}^\Box \) for each of the logics \(\mathcal {L}\) considered here.
Proof
By translating \(\mathsf {H}_{\mathsf {S5}}\)-derivations into \(\mathsf {H}_{\mathcal {L}}\)-derivations. E.g., \(\Box _L\) is translated into:

The translations of \(\Box _R,\mathsf {T}\) are similar, using \(R_{0,1}\) and \(\mathsf {T}_1\) respectively. \(\square \)
The backwards direction is similar, but translates into the calculus \(\mathsf {H}_{\mathsf {S5}}\) above with a form of Avron’s modal splitting rule from [2]:

It is straightforward to check that the resulting calculus is sound for \(\mathsf {S5}\).
Lemma 14
If \(\mathcal {L} \ne \mathbb {V}\mathbb {C}\mathbb {A}\) and \(A \in \mathcal {L}^\Box \), then \(A^\Box \in \mathsf {S5}\).
Proof
By translating derivations in \(\mathsf {H}_{\mathcal {L}}\) into derivations in \(\mathsf {H}_{\mathsf {S5}}\mathsf {cut}\) and applying cut elimination. In particular, an application of the rule \(R_{m,n}\)

is translated into

Here \(\mathrm {prop}\) uses derivability of the inversions of the propositional rules using cut. Similarly, applications of \(\mathsf {T}_m\) and \(\mathsf {trf}_m\) are translated using m applications of \(\Box _L\) and \(\mathsf {T}\) respectively. Applications of \(W_{m,n}\) and \(R_C\) are translated by \(\mathsf {T}\), and \(R_W\) is replaced with weakening, using that whenever \(\mathcal {G} \mid \varGamma \Rightarrow \varDelta , \bot \) is derivable in the system for \(\mathsf {S5}\), then so is \(\mathcal {G} \mid \varGamma \Rightarrow \varDelta \). Finally, \(\mathsf {abs}_L,\mathsf {abs}_R\) are replaced with the modalised splitting rule MS. \(\square \)
Theorem 15
[13, Sect. 6.3]. Let \(\mathcal {L} \ne \mathbb {V}\mathbb {C}\mathbb {A}\). Then \(A \in \mathcal {L}^\Box \) iff \(A^\Box \in \mathsf {S5}\).
The proof of the previous theorem is immediate from the preceeding lemmas. It is then also straightforward to derive the known collapses of the counterfactual implication  in \(\mathbb {V}\mathbb {W}\mathbb {A}\) and \(\mathbb {V}\mathbb {C}\mathbb {A}\). Recall that
in \(\mathbb {V}\mathbb {W}\mathbb {A}\) and \(\mathbb {V}\mathbb {C}\mathbb {A}\). Recall that  .
.
Proposition 16
-
1.
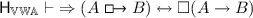
-
2.
\(\mathsf {H}_{\mathbb {V}\mathbb {C}\mathbb {A}} \vdash \;\Rightarrow A \leftrightarrow \Box A\)
-
3.
 and \(\mathsf {H}_{\mathbb {V}\mathbb {C}\mathbb {A}} \vdash \;\Rightarrow (A \preccurlyeq B) \leftrightarrow (B \rightarrow A)\).
and \(\mathsf {H}_{\mathbb {V}\mathbb {C}\mathbb {A}} \vdash \;\Rightarrow (A \preccurlyeq B) \leftrightarrow (B \rightarrow A)\).
6 Standard Calculi
To convert the non-standard calculi \(\mathsf {H}_{\mathcal {L}}\) into standard calculi, we consider an extended notion of sequents, where the succedent contains additional structural connectives. These sequents extend those of [7, 15] with a connective \(\left\langle . \right\rangle \) interpreting possible formulae.
Definition 17
A conditional block is a tuple \(\left[ \varSigma \vartriangleleft C \right] \) containing a multiset \(\varSigma \) of formulae and a single formula C. A transfer block is a multiset of formulae, written \(\left\langle \varTheta \right\rangle \). An extended sequent is a tuple \(\varGamma \Rightarrow \varDelta \) consisting of a multiset \(\varGamma \) of formulae and a multiset \(\varDelta \) containing formulae, conditional blocks, and transfer blocks. An extended hypersequent is a multiset containing extended sequents, written \(\varGamma _1 \Rightarrow \varDelta _1 \mid \ldots \mid \varGamma _n \Rightarrow \varDelta _n\).
The formula interpretation of an extended sequent is (all blocks shown explicitly):
The formula interpretation of an extended hypersequent is given by
The rules of the non-invertible calculi for \(\mathbb {V}\mathbb {T}\mathbb {U}\) and extensions are given in Fig. 3.
Theorem 18
(Soundness). If \(\mathsf {SH}_{\mathcal {L}}\vdash \mathcal {G}\), then \(\vdash _{\mathcal {L}} \iota _e(\mathcal {G})\), and if \(\mathsf {SH}_{\mathcal {L}} \vdash \;\Rightarrow A\), then \(A \in \mathcal {L}\).
Proof
As for Lemma 3, by showing that the rules preserve validity under \(\iota _e\) and using validity of \(\Box A \rightarrow A\). For the rules \(\preccurlyeq _L,\preccurlyeq _R, \mathsf {com}, \mathsf {jump}, \mathsf {W}, \mathsf {C}\) this is similar as in [7]. For rule \(\mathsf {T}\), if the interpretation of the conclusion is falsified in \(\mathfrak {M},w\), then there is a world  with \(\mathfrak {M}, v \Vdash \bigwedge \varGamma \wedge (A \preccurlyeq B) \wedge \lnot \bigvee \varDelta \wedge \Box \lnot \bigvee \varTheta \). If \([\![{B}]\!]= \emptyset \), then in particular \(\mathfrak {M}, v \Vdash \Box \lnot (\bigvee \varTheta \vee B)\), and the formula interpretation of the second premiss is falsified in \(\mathfrak {M},w\). Otherwise, from \(\mathfrak {M},v \Vdash A \preccurlyeq B\) we obtain a world
with \(\mathfrak {M}, v \Vdash \bigwedge \varGamma \wedge (A \preccurlyeq B) \wedge \lnot \bigvee \varDelta \wedge \Box \lnot \bigvee \varTheta \). If \([\![{B}]\!]= \emptyset \), then in particular \(\mathfrak {M}, v \Vdash \Box \lnot (\bigvee \varTheta \vee B)\), and the formula interpretation of the second premiss is falsified in \(\mathfrak {M},w\). Otherwise, from \(\mathfrak {M},v \Vdash A \preccurlyeq B\) we obtain a world  with \(\mathfrak {M},x \Vdash A\), and from \(\mathfrak {M},v \Vdash \Box \lnot \bigvee \varTheta \) we also get that \(\mathfrak {M},x \Vdash \lnot \bigvee \varTheta \). Hence the formula interpretation of the first premiss is falsified at \(\mathfrak {M},w\). The remaining cases are similar. \(\square \)
with \(\mathfrak {M},x \Vdash A\), and from \(\mathfrak {M},v \Vdash \Box \lnot \bigvee \varTheta \) we also get that \(\mathfrak {M},x \Vdash \lnot \bigvee \varTheta \). Hence the formula interpretation of the first premiss is falsified at \(\mathfrak {M},w\). The remaining cases are similar. \(\square \)
Theorem 19
(Completeness). If \(A \in \mathcal {L}\) then \(\mathsf {SH}_{\mathcal {L}} \vdash \;\Rightarrow A\).
Proof
By simulating derivations in \(\mathsf {H}_{\mathcal {L}}\). Most of the rules are simulated as in [7], except for the rules \(\mathsf {trf}_m, \mathsf {T}_m\). For \(\mathsf {T}_m\) the derivation is given in Fig. 4. The derivation of \(\mathsf {trf}_m\) only replaces \(\mathsf {jump}_T\) with \(\mathsf {jump}_U\). \(\square \)
7 Semantic Completeness via Invertible Calculi
An alternative completeness proof for the logics without absoluteness is given semantically by constructing a countermodel from a failed proof search. For this we consider the invertible versions \(\mathsf {SH}_{\mathcal {L}}^i\) of the calculi from Sect. 6, given in Fig. 5. Equivalence with the non-invertible calculi follows from admissibility of the structural rules, including the ones below, the proofs of which are standard by induction on the depth of the derivation:

Lemma 20
The rules \(\mathsf {IW},\mathsf {EW},\mathsf {CW},\mathsf {CIW},\mathsf {TW}\) are admissible in \(\mathsf {SH}_{\mathcal {L}}\).
Lemma 21
The rules \(\mathsf {ICL},\mathsf {ICR},\mathsf {Con}_B,\mathsf {Con}_S,\mathsf {mrg}\) are admissible in \(\mathsf {SH}_{\mathcal {L}}^i\).
From Lemmas 20 and 21 it immediately follows that:
Proposition 22
The invertible and non-invertible calculi are equivalent.
Definition 23
An extended hypersequent \(\mathcal {G}\) is \(\mathbb {V}\mathbb {T}\mathbb {U}\) -saturated if it satisfies all of the following conditions:
-
1.
(\(\preccurlyeq _R\)) if \(\varGamma \Rightarrow \varDelta , A \preccurlyeq B \in \mathcal {G}\), then \(\left[ \varSigma , A \vartriangleleft B \right] \in \varDelta \) for some \(\varSigma \);
-
2.
(\(\preccurlyeq _L\)) if \(\varGamma , C \preccurlyeq D \Rightarrow \varDelta , \left[ \varSigma \vartriangleleft A \right] \in \mathcal {G}\), then \(D \in \varSigma \) or \(\left[ \varSigma \vartriangleleft C \right] \in \varDelta \);
-
3.
(\(\mathsf {com}\)) if \(\varGamma \Rightarrow \varDelta , \left[ \varSigma \vartriangleleft A \right] , \left[ \varPi \vartriangleleft B \right] \in \mathcal {G}\), then \(\varSigma \subseteq \varPi \) or \(\varPi \subseteq \varSigma \);
-
4.
(\(\mathsf {jump}\)) if \(\varGamma \Rightarrow \varDelta , \left[ \varSigma \vartriangleleft A \right] \in \mathcal {G}\), then \(A, \varTheta \Rightarrow \varSigma , \varPi \in \mathcal {G}\) for some \(\varTheta ,\varPi \);
-
5.
(\(\mathsf {T}\)) if \(\varGamma , C \preccurlyeq D \Rightarrow \varDelta , \left\langle \varTheta \right\rangle \in \mathcal {G}\), then \(D \in \varTheta \) or \(C, \varSigma \Rightarrow \varTheta , \varPi \in \mathcal {G}\) for some \(\varSigma , \varPi \);
-
6.
(\(\mathsf {in}_{\mathsf {trf}}\)) if \(\varGamma \Rightarrow \varDelta \in \mathcal {G}\), then \(\left\langle \varTheta \right\rangle \in \varDelta \) for some \(\varTheta \);
-
7.
(\(\mathsf {jump}_U, \mathsf {jump}_T\)) if \(\varGamma \Rightarrow \varDelta , \left\langle \varTheta \right\rangle \in \mathcal {G}\) and \(\varSigma \Rightarrow \varPi \in \mathcal {G}\), then \(\varTheta \subseteq \varPi \);
-
8.
(\(\rightarrow _L\)) if \(\varGamma , A \rightarrow B \Rightarrow \varDelta \in \mathcal {G}\), then \(B \in \varGamma \) or \(A \in \varDelta \);
-
9.
(\(\rightarrow _R\)) if \(\varGamma \Rightarrow A \rightarrow B, \varDelta \in \mathcal {G}\), then \(A \in \varGamma \) and \(B \in \varDelta \);
It is \(\mathbb {V}\mathbb {W}\mathbb {U}\) -saturated (resp. \(\mathbb {V}\mathbb {C}\mathbb {U}\) -saturated) if it also satisfies (W) (resp. (C)) below:
-
1.
(\(\mathsf {W}\)) if \(\varGamma \Rightarrow \varDelta , \left[ \varSigma \vartriangleleft A \right] \in \mathcal {G}\), then \(\varSigma \subseteq \varDelta \);
-
2.
(\(\mathsf {C}\)) if \(\varGamma , C \preccurlyeq D \Rightarrow \varDelta \in \mathcal {G}\), then \(C\in \varGamma \) or \(D \in \varDelta \);
A \(\mathbb {V}\mathbb {T}\mathbb {U}\)-saturated extended hypersequent \(\mathcal {G}\) is called unprovable if it is not an instance of (init) or (\(\bot _L\)). We construct a countermodel from an unprovable \(\mathbb {V}\mathbb {T}\mathbb {U}\)-saturated extended hypersequent \(\mathcal {G} = \varGamma _1 \Rightarrow \varDelta _1 \mid \ldots \mid \varGamma _n \Rightarrow \varDelta _n\) as follows:
-
\(W := \{ 1, \ldots , n \}\)
-
\([\![{p}]\!]:= \{ i \le n : p \in \varGamma _i \}\)
The sphere systems  for \(i \le n\) are then defined as follows: Assume that \(\varGamma _i \Rightarrow \varDelta _i\) is
for \(i \le n\) are then defined as follows: Assume that \(\varGamma _i \Rightarrow \varDelta _i\) is
where \(\varDelta _i'\) contains no conditional blocks. First observe that due to saturation condition 3 we may assume w.l.o.g. that \(\varSigma _1 \subseteq \varSigma _2 \subseteq \ldots \subseteq \varSigma _k\). Moreover, by condition 4 for every \(j \le k\) there is a component \(\varGamma _{m_j} \Rightarrow \varDelta _{m_j}\in \mathcal {G}\) with \(A_j \in \varGamma _{m_j}\) and \(\varSigma _j \subseteq \varDelta _{m_j}\). Hence we set

Call the resulting structure \(\mathfrak {M}_{\mathcal {G}}\).
Lemma 24
For a \(\mathbb {V}\mathbb {T}\mathbb {U}\)-saturated hypersequent \(\mathcal {G}\) the structure \(\mathfrak {M}_{\mathcal {G}}\) is a \(\mathbb {V}\mathbb {T}\mathbb {U}\)-model.
Proof
Nesting of spheres is obvious from the fact that \( \{ m_k\} \subseteq \{ m_k, m_{k-1}\} \subseteq \ldots \subseteq \{ m_k, \ldots ,m_1\} \subseteq W\); reflexivity and uniformity follow from the fact that  . \(\square \)
. \(\square \)
Lemma 25
Let \(\mathcal {G} = \varGamma _1 \Rightarrow \varDelta _1 \mid \ldots \mid \varGamma _n \Rightarrow \varDelta _n\) be a \(\mathbb {V}\mathbb {T}\mathbb {U}\)-saturated hypersequent and let \(\mathfrak {M}_{\mathcal {G}}\) be define as above with world i associated to component \(\varGamma _i \Rightarrow \varDelta _i\). Then:
-
1.
given a formula A, if \(A\in \varGamma _i\) then \(\mathfrak {M}_{\mathcal {G}}, i \Vdash A\)
-
2.
given a formula A, if \(A\in \varDelta _i\) then \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash A\)
-
3.
given a block \(\left[ \varSigma \vartriangleleft C \right] \), if \(\left[ \varSigma \vartriangleleft C \right] \in \varDelta _i\), then \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash \bigvee _{B \in \varSigma } (B \preccurlyeq C)\)
-
4.
given a formula B, if \(\left\langle \varTheta ,B \right\rangle \in \varDelta _i\) for some \(\varTheta \), then \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash \Diamond B\)
Proof
We prove statements 1 and 2 by mutual induction on the complexity of A. The base case and the propositional case are straightforward, hence we consider \(A = E \preccurlyeq F\). Let \(i\in W\) be associated to \(\varGamma _i \Rightarrow \varDelta _i\) with \(\varDelta _i = \varDelta '_i, \left[ \varSigma _1 \vartriangleleft D_1 \right] , \ldots , \left[ \varSigma _k \vartriangleleft D_k \right] ,\left\langle \varTheta \right\rangle \), where \(\varDelta '_i\) contains no conditional block and \(\varSigma _1\subseteq \varSigma _2 \subseteq \ldots \subseteq \varSigma _k\).
-
Suppose \(E \preccurlyeq F\in \varGamma _i\). For
 , we have to show that \(\alpha \Vdash ^{\forall } \lnot F\) or \(\alpha \Vdash ^{\exists } E\).
, we have to show that \(\alpha \Vdash ^{\forall } \lnot F\) or \(\alpha \Vdash ^{\exists } E\).In case \(\alpha \ne W\) we have \(\alpha = \{ m_k,\ldots , m_{j}\}\) for some \(j\le k\) and each \(m_\ell \in \alpha \) comes from a block \(\left[ \varSigma _\ell \vartriangleleft D_\ell \right] \) and is associated to a component \(D_\ell ,\Lambda _\ell \Rightarrow \varPi _\ell , \varSigma _\ell \) of \(\mathcal {G}\). By saturation condition (\(\preccurlyeq _L\)), either \(F\in \varSigma _j\) or \(E = D_j\). In the former case with \(\varSigma _j \subseteq \varSigma _{j+1} \subseteq \ldots \varSigma _k\) and the induction hypothesis we have \(\mathfrak {M}_{\mathcal {G}}, m_\ell \not \Vdash F\), for \(\ell = j, \ldots , k\), showing that \(\alpha \Vdash ^{\forall } \lnot F\). If \(E = D_j\), by induction hypothesis on the component \(E,\Lambda _j \Rightarrow \varPi _j, \varSigma _j\), we get \(\mathfrak {M}_{\mathcal {G}}, m_j\Vdash E\), showing \(\alpha \Vdash ^{\exists } E\).
In case \(\alpha = W\), by saturation condition (T) either \(F\in \left\langle \varTheta \right\rangle \), or \(E, \Lambda \Rightarrow \varPi , \varTheta \in \mathcal {G}\) for some \(\Lambda ,\varPi \). In the latter case for the world j associated to the component \(E, \Lambda \Rightarrow \varPi , \varTheta \) by induction hypothesis on E we get \(\mathfrak {M}_{\mathcal {G}}, j \Vdash E\), whence \(W\Vdash ^{\exists } E\). In the former case we have \(F\in \left\langle \varTheta \right\rangle \). Any \(k\in W\) (including k=i) is associated to a component \(\varGamma _k \Rightarrow \varDelta _k\), but by saturation condition (jump\(_T\), jump\(_U\)) we have \(\varTheta \subseteq \varDelta _k\), whence \(F\in \varDelta _k\); by induction hypothesis on F we have \(\mathfrak {M}_{\mathcal {G}}, k \not \Vdash F\), showing \(W\Vdash ^{\forall } \lnot F\).
-
Suppose \(E \preccurlyeq F\in \varDelta _i\). Recall that
 with each \(m_\ell \) associated to a sequent \(D_\ell ,\Lambda _\ell \Rightarrow \varPi _\ell , \varSigma _\ell \in \mathcal {G}\) coming from a block \(\left[ \varSigma _\ell \vartriangleleft D_\ell \right] \in \varDelta _i\), for \(\ell = j, \ldots , k\). By saturation, there is \(j\le k\) with \(D_j = F\) and \(E\in \varSigma _j\). Consider \(m_j\) associated to the component \(F, \Lambda _j \Rightarrow \varSigma _j, \varPi \). By induction hypothesis we get \(\mathfrak {M}_{\mathcal {G}}, m_j \Vdash F\). Since \(\varSigma _j\subseteq \varSigma _{j+1} \subseteq \ldots \subseteq \varSigma _k\), we also get \(\mathfrak {M}_{\mathcal {G}}, m_\ell \not \Vdash E\), for \(\ell = j,\ldots ,k\). Thus for
with each \(m_\ell \) associated to a sequent \(D_\ell ,\Lambda _\ell \Rightarrow \varPi _\ell , \varSigma _\ell \in \mathcal {G}\) coming from a block \(\left[ \varSigma _\ell \vartriangleleft D_\ell \right] \in \varDelta _i\), for \(\ell = j, \ldots , k\). By saturation, there is \(j\le k\) with \(D_j = F\) and \(E\in \varSigma _j\). Consider \(m_j\) associated to the component \(F, \Lambda _j \Rightarrow \varSigma _j, \varPi \). By induction hypothesis we get \(\mathfrak {M}_{\mathcal {G}}, m_j \Vdash F\). Since \(\varSigma _j\subseteq \varSigma _{j+1} \subseteq \ldots \subseteq \varSigma _k\), we also get \(\mathfrak {M}_{\mathcal {G}}, m_\ell \not \Vdash E\), for \(\ell = j,\ldots ,k\). Thus for  we get \(\alpha \not \Vdash ^{\forall } \lnot F\) and \(\alpha \not \Vdash ^{\exists } E\), showing \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash E\preccurlyeq F\).
we get \(\alpha \not \Vdash ^{\forall } \lnot F\) and \(\alpha \not \Vdash ^{\exists } E\), showing \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash E\preccurlyeq F\).
The proof of 3 uses 2, recalling that a block is a disjunction of \(\preccurlyeq \)-formulas. The proof of 4 uses 2 with an argument as in the proof of 1 for the case of \(\alpha = W\) with \(B\in \left\langle \varTheta \right\rangle \). \(\square \)
The countermodel construction described above can be extended to \( \mathbb {V}\mathbb {W}\mathbb {U}\) and \( \mathbb {V}\mathbb {C}\mathbb {U}\) by modifying the definition of the model as follows. For \( \mathbb {V}\mathbb {W}\mathbb {U}\), let  . For \( \mathbb {V}\mathbb {C}\mathbb {U}\), we add \(\{i\}\) to
. For \( \mathbb {V}\mathbb {C}\mathbb {U}\), we add \(\{i\}\) to  for any i. The proof of Lemma 25 can be easily extended to both cases (statements 1 and 2), using the specific saturation conditions for these systems. We leave the details to the reader; the case of Absoluteness will be handled in future work. From Lemma 25 we obtain:
for any i. The proof of Lemma 25 can be easily extended to both cases (statements 1 and 2), using the specific saturation conditions for these systems. We leave the details to the reader; the case of Absoluteness will be handled in future work. From Lemma 25 we obtain:
Lemma 26
For \(\mathcal {L} \in \{ \mathbb {V}\mathbb {T}\mathbb {U}, \mathbb {V}\mathbb {W}\mathbb {U}, \mathbb {V}\mathbb {C}\mathbb {U}\}\) let \(\mathcal {G} = \varGamma _1 \Rightarrow \varDelta _1 \mid \ldots \mid \varGamma _n \Rightarrow \varDelta _n\) be a \(\mathcal {L}\)-saturated hypersequent and let \(\mathfrak {M}_{\mathcal {G}}\) be defined as above, then
-
for any \(i\in W\) associated to sequent \(\varGamma _i \Rightarrow \varDelta _i\) we have \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash \iota _e(\varGamma _i \Rightarrow \varDelta _i)\)
-
for any \(i\in W\) we have \(\mathfrak {M}_{\mathcal {G}}, i \not \Vdash \iota _e(\mathcal {G})\)
To use these results in a decision procedure, we consider local loop checking: rules are not applied if there is a premiss from which the conclusion is derivable using structural rules. Since these are all admissible in \(\mathsf {SH}_{\mathcal {L}}^i\), this does not jeopardise completeness.
Proposition 27
Backwards proof search with local loop checking terminates and every leaf of the resulting derivation is an axiom or a saturated sequent.
Proof
By Lemmas 20 and 21, we may assume that the proof search only considers duplication-free sequents, i.e., sequents containing duplicates neither of formulae nor of blocks. By the subformula property, the number of duplication-free sequents possibly relevant to a derivation of a sequent is bounded in the number of subformulae of that sequent, and hence backwards proof search for \(\mathcal {G}\) terminates. Furthermore, every leaf is either an axiom or a saturated sequent, since otherwise another rule could be applied. \(\square \)
Theorem 28
(Completeness). If \(\iota _{e}(\mathcal {G}) \in \mathcal {L}\), then \(\mathsf {SH}_{\mathcal {L}} \vdash \mathcal {G}\) for \(\mathcal {L} \in \{ \mathbb {V}\mathbb {T}\mathbb {U}, \mathbb {V}\mathbb {W}\mathbb {U}, \mathbb {V}\mathbb {C}\mathbb {U}\}\).
Proof
By Proposition 27 backwards proof search with root \(\mathcal {G}\) terminates and every leaf of it is an axiom or a saturated sequent. By invertibility of the rules each sequent \(\mathcal {G'}\) occurring as a leaf is valid. But then \(\mathcal {G'}\) must an axiom, since otherwise, by Lemma 26 we can bulid a countermodel \(\mathfrak {M}_{\mathcal {G'}}\) falsifying \(\iota _e(\mathcal {G'})\) and hence by monotonicity also \(\iota _e(\mathcal {G})\). \(\square \)
We note that Proposition 27 gives rise to a (non-optimal) co-NEXPTIME-decision procedure for validity: Since applying backwards proof search with local loop checking to an input sequent \(\;\Rightarrow G\) terminates and every leaf of the resulting derivation is an instance of \(\mathsf {init}\) or \(\bot _L\) or a saturated sequent, in order to check whether \(\;\Rightarrow G\) is derivable is suffices to non-determinstically choose a duplication-free \(\mathcal {L}\)-saturated extended hypersequent containing only subformulas of G and containing a component \(\varGamma \Rightarrow \varDelta , G\). If this is not possible, then backwards proof search will produce a proof of \(\;\Rightarrow G\). But if it is possible, then by Lemma 26 this hypersequent gives rise to a countermodel for G. Since the size of duplication-free extended hypersequents consisting of subformulae of G is bounded exponentially in the number of subformulae of G, this gives the co-NEXPTIME complexity bound. Of course it is known that the logics of this section are EXPTIME-complete [5].
8 Conclusion
In this work we have introduced to our knowledge the first internal hypersequent calculi for Lewis’ conditional logics with uniformity and reflexivity, both in non-standard and in standard form. While the former lend themselves to syntactic cut elimination, the latter are amenable to a semantic completeness proof via countermodel construction from a failed proof search and give rise to decision procedures for the considered logics.
While the treatment of these logics is an important step towards a comprehensive proof-theoretic treatment of the whole family of Lewis’ logics, many interesting questions are still open. In particular, we plan to extend the semantic completeness proof also to the logics with absoluteness. Further, by moving to the framework of grafted hypersequents [10] we expect to be able to extend our results to the logics \(\mathbb {V}\mathbb {U}\) and \(\mathbb {V}\mathbb {N}\mathbb {U}\). Concerning Lewis’ conditional logics, this would leave only the logics satisfying Stalnaker’s assumption [13] lacking a satisfactory internal proof system. Their proof-theoretic investigation will be subject of future research. Finally, we aim at providing complexity-optimal proof methods for the logics under consideration. In particular, for logics with absoluteness, one could make the blocks “global” to the whole hypersequent. We conjecture that such calculi could yield complexity-optimal decision procedures.
Notes
- 1.
Using this notation we thus have: \(x \Vdash A\preccurlyeq B \) iff for all
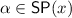 . \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \).
. \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \). - 2.
Observe that \( \mathbb {V}\mathbb {T}\mathbb {A}\)+weak centering collapses to S5, since in any model over a set of worlds W it must be for all \(w\in W\),
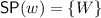 . Furthermore, \( \mathbb {V}\mathbb {T}\mathbb {A}\) + centering collapses to Classical Logic, as in any model the set of worlds must be a singleton \(\{w\}\) and
. Furthermore, \( \mathbb {V}\mathbb {T}\mathbb {A}\) + centering collapses to Classical Logic, as in any model the set of worlds must be a singleton \(\{w\}\) and 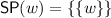 , so that \(A\preccurlyeq B\) is equivalent to the material implication \(B \rightarrow A\). See also Proposition 16 below..
, so that \(A\preccurlyeq B\) is equivalent to the material implication \(B \rightarrow A\). See also Proposition 16 below..
References
Alenda, R., Olivetti, N.: Preferential semantics for the logic of comparative similarity over triangular and metric models. In: Cerro, L.F., Herzig, A., Mengin, J. (eds.) JELIA 2012. LNCS (LNAI), vol. 7519, pp. 1–13. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33353-8_1
Avron, A.: The method of hypersequents in the proof theory of propositional non-classical logics. In: Hodges, W., Hyland, M., Steinhorn, C., Truss, J. (eds.) Logic: From Foundations to Applications. Clarendon Press, New York (1996)
Burgess, J.P.: Quick completeness proofs for some logics of conditionals. Notre Dame J. Formal Log. 22, 76–84 (1981)
Chellas, B.F.: Basic conditional logics. J. Philos. Log. 4, 133–153 (1975)
Friedman, N., Halpern, J.Y.: On the complexity of conditional logics. In: Doyle, J., Sandewall, E., Torasso, P. (eds.) KR 1994, pp. 202–213. Morgan Kaufmann (1994)
Giordano, L., Gliozzi, V., Olivetti, N., Schwind, C.: Tableau calculus for preference-based conditional logics: PCL and its extensions. ACM TOCL 10(3), 21:1–21:50 (2009)
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L.: Standard sequent calculi for Lewis’ logics of counterfactuals. In: Michael, L., Kakas, A. (eds.) JELIA 2016. LNCS, vol. 10021, pp. 272–287. Springer, Cham (2016). doi:10.1007/978-3-319-48758-8_18
Grahne, G.: Updates and counterfactuals. J. Log. Comput. 8(1), 87–117 (1998)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. 44(1–2), 167–207 (1990)
Kuznets, R., Lellmann, B.: Grafting hypersequents onto nested sequents. Log. J. IGPL 24, 375–423 (2016)
Lellmann, B.: Hypersequent rules with restricted contexts for propositional modal logics. Theoret. Comput. Sci. 656, 76–105 (2016)
Lellmann, B., Pattinson, D.: Sequent systems for Lewis’ conditional logics. In: Cerro, L.F., Herzig, A., Mengin, J. (eds.) JELIA 2012. LNCS, vol. 7519, pp. 320–332. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33353-8_25
Lewis, D.: Counterfactuals. Blackwell, London (1973)
Nute, D.: Topics in Conditional Logic. Reidel, Dordrecht (1980)
Olivetti, N., Pozzato, G.L.: A standard internal calculus for Lewis’ counterfactual logics. In: Nivelle, H. (ed.) TABLEAUX 2015. LNCS, vol. 9323, pp. 270–286. Springer, Cham (2015). doi:10.1007/978-3-319-24312-2_19
Restall, G.: Proofnets for S5: sequents and circuits for modal logic. In: Logic Colloquium 2005. Lecture Notes in Logic, vol. 28, pp. 151–172. Cambridge University Press (2007)
Sheremet, M., Tishkovsky, D., Wolter, F., Zakharyaschev, M.: A logic for concepts and similarity. J. Log. Comput. 17(3), 415–452 (2007)
Stalnaker, R.: A theory of conditionals. In: Rescher, N. (ed.) Studies in Logical Theory, pp. 98–112. Blackwell (1968)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L. (2017). Hypersequent Calculi for Lewis’ Conditional Logics with Uniformity and Reflexivity. In: Schmidt, R., Nalon, C. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2017. Lecture Notes in Computer Science(), vol 10501. Springer, Cham. https://doi.org/10.1007/978-3-319-66902-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-66902-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66901-4
Online ISBN: 978-3-319-66902-1
eBook Packages: Computer ScienceComputer Science (R0)





 holds
holds we have
we have  ;
; .
.

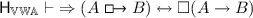
 and
and 


 , we have to show that
, we have to show that  with each
with each  we get
we get 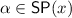 .
. 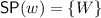 . Furthermore,
. Furthermore, 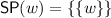 , so that
, so that