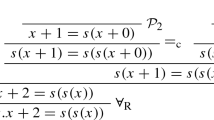Goal-Sensitive Reasoning with Disconnection Tableaux

Abstract

One of the challenges that has been outlined for instantiation-based theorem proving methods is their application in reasoning over theories with many axioms, as in tasks involving large ontologies or mathematical libraries. Goal-sensitive methods, which restrict inferences to those related to the goal to be refuted, tend to outperform other methods on large axiom sets especially. This paper presents a goal-sensitive adaptation of the disconnection tableau calculus, leveraging the advantages of goal-sensitivity in an instantiation-based, tableau-guided proof method. A proof of the method’s completeness follows its description, as well as a discussion of planned future work in this area.

1 Introduction

Instantiation-based automated reasoning methods combine the expressive power of first-order logic with existing propositional theorem-proving technology to solve difficult problems efficiently. These methods apply Herbrand’s theorem to show the unsatisfiability of a set of first-order clauses by reducing to ground instances of clauses. One of the application domains of such methods is reasoning over very large axiom sets, in which their performance is promising [5, 11]. Growing interest in this area suggests that more work should be done to improve the strength and efficiency of these methods.

Goal-sensitive methods, which restrict inferences to those related to a particular goal to be refuted, tend to perform better especially over large theories because of their ability to ignore potentially very large parts of the axiom set known to be satisfiable [14]. In methods without goal-sensitivity, to prove a theorem $\varphi$ from an axiom set T, it is possible that most inferences do not involve $\varphi$ at all. It is desirable to have methods which are first-order and goal-sensitive [12].

The disconnection calculus was developed in [2], and its tableau format was elaborated on and presented more rigorously in [8] as the disconnection tableau calculus. Instead of interleaving instance generation with a separate propositional procedure, the disconnection tableau calculus uses a tableau as a data structure for guiding its search so that unsatisfiability detection is integrated into the instance generation procedure. In this paper, the disconnection tableau calculus is shown to be incapable of goal-sensitive reasoning as-is, and an adapted form of the calculus, referred to as the goal-sensitive disconnection tableau calculus or GSDC, is introduced which makes this kind of reasoning possible.

In Sect. 2 an explanation of terminology and background information is provided, along with an overview of the disconnection tableau calculus. In Sect. 3 the goal-sensitive adaptation to the calculus is presented, and Sect. 4 provides a proof of this adaptation’s completeness. Section 5 concludes and provides a description of future work.

2 Preliminaries and Background

Definitions of terms and basic notions used in this paper are explained here for clarification. An overview of the basic disconnection tableau method follows.

2.1 Terminology

A first-order language $\mathcal {L}$ with function symbols is assumed. As usual, a literal is an atom or a negated atom. Literals L and $\lnot L$ are complementary. The set of ground atoms over $\mathcal {L}$ is the Herbrand base of $\mathcal {L}$; the set of ground terms over $\mathcal {L}$ is its Herbrand universe. A Herbrand interpretation is a set of literals containing exactly one of A or $\lnot A$, for each atom A in the Herbrand base.

A clause is a disjunction of literals, often written as a set containing those literals. In this paper, the clauses in a clause set S are assumed to be pairwise variable-disjoint.

A substitution $\sigma$ is a finite set $\{t_1 / x_1, t_2 / x_2, \ldots , t_n / x_n\}$, where the $x_i$ are distinct variables and the $t_i$ are terms such that $t_i \ne x_i$ for any $i=1,\ldots , n$. Applying $\sigma$ to an expression E means to simultaneously replace each occurrence of $x_i$ in E with the corresponding $t_i$ for each $i=1, \ldots , n$. The expression resulting from applying $\sigma$ to E is written as $E\sigma$ and is called an instance of E. Given a clause set S, its Herbrand set $S^*$ consists of all ground instances of clauses in S with terms from the Herbrand universe.

For substitutions $\sigma$ and $\tau$, their composition $\sigma \tau$ is a substitution which, when applied to an expression E, has the same result as first applying $\sigma$ to E, and then applying $\tau$. This is expressed by the identity $E(\sigma \tau )=(E\sigma )\tau$. If there exists a substitution $\tau '$ such that $\tau =\sigma \tau '$, then $\sigma$ is said to be more general than $\tau$. The substitution $\sigma$ is a unifier of expressions $E_1$ and $E_2$ if $E_1\sigma =E_2\sigma$. If such a substitution exists, $E_1$ and $E_2$ are said to be unifiable. A most general unifier or mgu is a unifier which is more general than any other unifier.

The definitions and notions more specific to the disconnection tableau calculus itself are provided below. A description of the method follows these definitions.

A literal occurrence is a pair $\langle {L}, {C} \rangle$ such that L is a literal and C is a clause in which it appears. When convenient, $\langle {L}, {C} \rangle$ may be written as $L_C$. For a substitution $\sigma$, let $\langle {L}, {C} \rangle \sigma$ (and $L_C \sigma$) denote the literal occurrence $\langle {L\sigma }, {C\sigma } \rangle$.

A connection or link is a pair of literal occurrences $\ell =\{L_C, K_D\}$ such that C and D are variable-disjoint and there exists a mgu $\sigma$ of L and $\lnot K$. A clause $C\sigma$ is called a linking instance of C with respect to $\ell$.

A path through a clause set S is a function $\pi$ mapping each clause $C\in S$ to a single literal $L\in C$. A path may be represented by the set of literal occurrences $P=\{L_C~|~L=\pi (C)\}$. The set of clauses of P, written $\text {Cl}(P)$, is the domain of the function $\pi$; the set of literals of P, written $\text {Lit}(P)$, is the image of $\pi$. A path is complementary if there exist literal occurrences $L_C, \lnot L_{D} \in P$. A path which is not complementary is open or consistent. The following proposition from [9] emphasizes the use of this notion of path.

Proposition 1

If S is a clause set and P is an open path through the Herbrand set $S^*$, then the set of literals of P is a model for S.

A tableau is a downward tree in which every non-root node N is labeled with a literal occurrence. Specifically, for a clause set S, a tableau for S is a tree in which the children $N_1,\ldots , N_m$ of each node N are labeled with $\langle {L_1}, {C} \rangle , \langle {L_2}, {C} \rangle , \ldots ,$ $\langle {L_m}, {C} \rangle$, respectively, for $C=L_1\vee L_2\vee \cdots \vee L_m$ an instance of a clause in S. A branch of a tableau is a maximal sequence $\{N_1, N_2, \ldots \}$ of nodes in T such that $N_1$ is a child of the root node, and $N_{i+1}$ is a child of $N_i$ for all $i\ge 1$. A branch B has an associated path $P_B$, which can be represented by the set of literal occurrences labeling the nodes on B.

2.2 Disconnection Tableau Calculus

Here the basic calculus of the disconnection tableau method is described. Construction of a tableau for a clause set S begins with respect to an input path $P_S$ through S called the initial path. The initial path remains fixed during construction of the tableau for S. The calculus consists of the following linking rule: given $P_S$ and a tableau branch B such that $P_S\cup P_B$ contains a pair of literal occurrences $L_C$ and $K_D$ forming a link $\ell$ with mgu $\sigma$,

• 1. expand B with a variable-disjoint renaming of a linking instance of one of the clauses with respect to $\ell$, say $C\sigma$, and

• 2. below the node labeled $L\sigma$, expand the branch with a variable-disjoint renaming of a linking instance of $D\sigma$ with respect to $\ell$.

That is, a clause linking step is performed and the coupled linking instances are attached below the leaf node N of the current tableau branch B. For each branch B, the links which can be used to expand B by the linking rule are those belonging to $P_S\cup P_B$; in this way the initial path acts as a prefix shared by all branches in the tableau. Requiring that the attached linking instances be variable-disjoint maintains that all clauses on the tableau are pairwise variable-disjoint. After being used to expand B, a link need not be used any more on B below the node N, “disconnecting” the connected literals. Additionally, disconnection tableaux are generally required to be variant-free; that is, links which would expand the tableau with a clause which could be obtained by a renaming of a clause already on the tableau are not considered. A branch is saturated if there exist no links to expand it in a variant-free manner.

The normal tableau closure condition of requiring two complementary literals on the same branch is not sufficient, so a modified notion of closure is typically used. A branch B is closed with respect to a term t, or t -closed, if its associated path $P_B$ becomes complementary when all variables occurring in the literals on B are replaced with t. A branch is $\forall$ -closed if it is t-closed for any term t. In other words, a branch is $\forall$-closed if it contains literals $L, \lnot K$ such that $L\theta =K\theta$ for a substitution $\theta$ identifying all variables. Both closure conditions can be used for disconnection tableaux, but as in [8] the weaker notion of $\forall$-closure is used here, since then the results in this paper will hold automatically for t-closure as well. As a result a tableau is said to be closed if all its branches are $\forall$-closed; a tableau is saturated if it is closed or if it contains a saturated branch. An example closed disconnection tableau is shown in Fig. 1.

Fig. 1.

Example closed disconnection tableau. The literals contained in the initial path are underlined.

Disconnection tableaux for a clause set S, with chosen initial path $P_S$, are defined as the elements of any sequence $\mathcal {T}_0, \mathcal {T}_1,\ldots$, where $\mathcal {T}_0$ is the tableau consisting of only the root node, and any $\mathcal {T}_i$, for $i>0$, can be obtained from $\mathcal {T}_{i-1}$ by an application of the linking rule. The disconnection tableau calculus is sound and complete for any choice of initial path: a clause set S is unsatisfiable if and only if for any initial path $P_S$, there is a finite closed disconnection tableau for S with $P_S$.

As described, the disconnection tableau calculus is non-deterministic and requires an inference strategy for guiding tableau construction by making choices concerning the initial path, the next branch chosen for expansion, and the next linking step to be performed on that branch. An inference strategy which always results in a saturated tableau is called systematic or fair. A more thorough description of the disconnection tableau calculus and inference strategies can be found in [9].

3 Goal-Sensitivity

The notion of goal-sensitivity in theorem proving originated from resolution with set of support [15], a strategy appearing as a feature of contemporary theorem provers which use the given-clause loop [10]. Goal-sensitivity has been used in the context of equational reasoning [3] and as part of a set of criteria for analyzing theorem proving methods [13]. A recent formulation of goal-sensitivity was given in [4], which is used here and summarized below.

The clause set S is assumed to comprise a collection of assumptions, known to be consistent among themselves, and a collection of clauses generated from the negation $\lnot \varphi$ of a conjectured formula $\varphi$. As such the clause set is taken to be $S=T\cup G$, where $T\cap G = \emptyset$. The set G consists of clauses generated from $\lnot \varphi$, referred to as goal clauses, while the set T is the collection of assumptions.

The central notion of goal-sensitivity is relevance. Initially, only clauses in G are considered relevant. An inference is considered relevant if at least one of its hypotheses is relevant; clauses that result from the application of a relevant inference are relevant as well. A theorem proving strategy is goal-sensitive if it only performs relevant inferences. In other words, a method is goal-sensitive if all inferences involve clauses in, or deduced from, the clauses generated from the negated conjecture $\lnot \varphi$.

Define a literal to be relevant if it belongs to a relevant clause, a literal occurrence to be relevant if its clause is relevant, and a link to be relevant if it contains a relevant literal occurrence.

3.1 Disconnection Tableau Calculus Is Not Goal-Sensitive

Even inference strategies for the disconnection tableau calculus that prioritize the selection of relevant links will require in some cases non-relevant links to be expanded. As an immediate example, if the initial path does not include any literals complementary to the specified goal literal, there will be no relevant links for selection. However, making sure that relevant links exist on the initial path is not enough to ensure goal-sensitivity.

Example 1

Consider the input clause set given in Fig. 2, with the single goal clause $G=\{\lnot R(a)\}$. Let the initial path P be the one selecting the leftmost literal in each clause, indicated by the underlined literals. Then there are two links on this path: $\ell _1 = \{\underline{R(x)}\vee \lnot Q(x), \underline{\lnot R(a)}\}$, and $\ell _2 = \{\underline{\lnot P(x)}\vee Q(x), \underline{P(a)}\}$.

Again, the goal clause here is $\lnot R(a)$, indicated by the boxed clause. Only $\ell _1$ is relevant initially, so we select it to expand the tableau. After this step, the left branch is closed, leaving only the right branch open. The only link on $P_S\cup P_B$ is $\ell _2$, which is not relevant. However, expansion of $\ell _2$ closes the tableau, showing the unsatisfiability of the clause set.

Fig. 2.

Example in which non-relevant links must be expanded to close the tableau. The goal clause is indicated by the box.

Notice that in Example 1 above, had the initial path included Q(x) then a relevant link $\ell _3=\{\lnot P(x) \vee \underline{Q(x)}, \lnot Q(a)\}$ would have been present on B, and goal-sensitive construction of the tableau would have been possible. To reason with disconnection tableaux in a goal-sensitive manner, particular literal occurrences in $T=S\setminus G$ must be available for linking. The next section describes a method for finding these literal occurrences during tableau construction.

4 Goal-Sensitive Disconnection Tableau Calculus

The typical input to the disconnection tableau calculus is a clause set S and an initial path $P_S$ through S. In the previous section it is shown that $P_S$ can be chosen so that non-relevant linking steps must be performed to close the tableau. As a result, the goal-sensitive disconnection tableau calculus or GSDC requires a new notion of path.

Definition 1

(Multipath). A multipath over a clause set S is a relation $\pi \subseteq S\times \bigcup S$ such that $\pi (C, L)$ implies $L\in C$.

Here, $\bigcup S$ refers to the set of all literals occurring in clauses in S; that is,

$$\begin{aligned} \bigcup S := \bigcup _{C\in S} \{L~|~L\in C\}. \end{aligned}$$

Similar to paths, a multipath $\pi$ over S may be represented by a set of literal occurrences $P=\{L_C~|~\pi (C,L)\}$. The terms set of literals and set of clauses for paths are defined similarly for multipaths. Whereas a path is defined as a function from S to $\bigcup S$, a multipath is simply a relation. As a result, multipaths differ from paths in two ways: first, there may be multiple literal occurrences from the same clause on a multipath, and second, not every clause in S need have a specified literal occurrence.

The GSDC takes as input a clause set $S=T\cup G$, where T is known to be consistent and G is the set of goal clauses as before. Instead of starting with an input, fixed initial path, a multipath is dynamically constructed over the consistent set of assumptions during tableau construction. The GSDC consists of two rules, the first of which is usual linking rule from the disconnection tableau calculus, where the initial path $P_S$ over S has been replaced with a multipath P over T. The second is the following rule to add new literal occurrences to the multipath P over T to expand a branch B:

Definition 2

(Multipath-add rule). If no relevant links exist on $P\cup P_B$, then for each $L_C \in P_B$, do the following:

• for each $D\in T$, if there exists $K \in D$ such that $\{L_C, K_D\}$ is a link which has not been used on B, add $K_D$ to P.

The multipath P over T takes the place of the initial path in the usual disconnection calculus in that it acts as a common prefix of all branches. Each open branch B is expanded by application of the linking rule to a relevant link. If none exist for an open branch B, the multipath-add rule is applied to find links which have not yet been used on B, if they exist.

At the beginning of tableau construction, P consists of only the literal occurrences in T which form a link with some clause in G; this is referred to as the initial multipath. As a result, the literal occurrences added to P by the multipath-add rule for a branch B are those which form new relevant links, making these available for expanding B by applying the linking rule.

Tableaux for the GSDC are defined in a similar manner to disconnection tableaux, except that the fixed initial path $P_S$ over S has been replaced with a dynamically constructed multipath.

Definition 3

(Goal-sensitive disconnection tableau sequence). A goal-sensitive disconnection tableau sequence is defined as any sequence

$$\begin{aligned} (\mathcal {T}_0,P_0), (\mathcal {T}_1, P_1),(\mathcal {T}_2,P_2), \ldots \end{aligned}$$

such that $\mathcal {T}_0$ is the tableau which consists of only the root node, $P_0$ is the initial multipath, and for $i>0$, either

• $\mathcal {T}_i$ is obtained from $(\mathcal {T}_{i-1},P_{i-1})$ by an application of the linking rule and $P_i=P_{i-1}$, or

• $\mathcal {T}_i=\mathcal {T}_{i-1}$ and $P_i$ is obtained from $P_{i-1}$ by an application of the multipath-add rule.

Any tableau $\mathcal {T}_i$ in the sequence above is called a goal-sensitive disconnection tableau for S.

The branch and tableau closure condition used here for the GSDC is $\forall$-closure, as for the usual disconnection tableau calculus. However, an altered definition of saturation is used. The GSDC expand a branches in a tableau until it closes, or until there are no links to expand it further, even after applying the multipath-add rule.

Definition 4

(Relevance-saturation). A branch B is relevance-saturated if it cannot be expanded in a variant-free manner by an application of the multipath-add rule followed by an application of the linking rule. A tableau is relevance-saturated if it is closed, or if one of its branches is relevance-saturated.

Like the usual disconnection tableau calculus, an inference strategy is needed for branch and link selection.

Definition 5

(Revelance-fairness). An inference strategy is relevance-fair if it always results in a relevance-saturated tableau.

This method is sound and complete when guided by a relevance-fair inference strategy. Its soundness follows from the soundness of the usual disconnection tableau calculus, as any closed tableau constructed by the GSDC is simply a closed disconnection tableau. Its completeness is shown in the following section. The remainder of this section provides examples of tableaux constructed with the GSDC.

Example 2

Consider the clause set from Example 1, with initial satisfiable set $T=\{\lnot P(x)\vee Q(x), R(y)\vee \lnot Q(y), P(a)\}$ and goal clause $G=\lnot R(a)$. There are two links $\ell _1$ and $\ell _2$ as defined in Example 1. The multipath P initially contains just the literal occurrence $\langle R(y), R(y)\vee \lnot Q(y)\rangle$.

The linking rule expands the tableau with $\ell _1$, the only relevant link. As before, the left branch closes, leaving the right branch B open. Since there are no relevant links on $P\cup P_B$, and B is open, the multipath-add rule is applied, setting $P=\{\underline{R(y)}\vee \lnot Q(y), \lnot P(x)\vee \underline{Q(x)}\}$. The updated branch B now contains the unused, relevant link $\ell =\{\lnot P(x) \vee \underline{Q(x)},\lnot Q(a)\}$. Expanding $\ell$ closes the tableau.

The following example illustrates the importance of the multipath definition allowing multiple literals from a single clause to be present on P.

Fig. 3.

Example tableau in which multiple literals from a single clause must be added to the multipath.

Example 3

Let the $S=T\cup G$ be given as in Fig. 2. Since two links are possible between the top clause and the goal, but only one will lead to a tableau closure, it is important to include multiple literal occurrences for this clause in the multipath.

The following example shows the advantage of goal-sensitivity; that links between clauses not related to the goal need not be considered.

Example 4

Let $S=T\cup G$ be given as in Fig. 3. After expanding the only relevant link, the multipath-add rule searches for other literals to link with $\lnot Q(a)$. However, since none are present in T, the branch becomes relevance-saturated, and tableau construction ends, showing satisfiability of the clause set S (Fig. 4).

Fig. 4.

Example in which tableau construction terminates early on a satisfiable clause set S because no relevant links can be made.

4.1 Completeness

The aim of this section is to show the completeness of the GSDC; that is, that whenever $S=T\cup G$ is unsatisfiable, for a consistent clause set T, the GSDC constructs a closed tableau. The main idea is that when a branch in a goal-sensitive disconnection tableau for S is relevance-saturated, an instance-preserving enumeration [8] of that branch can be combined with a model for T to construct a model for S.

Given a set P of literal occurrences, an instance-preserving enumeration of P is a sequence $\ell _1, \ell _2, \ell _3, \ldots$ in which exactly the elements of P appear in a particular order. Specifically, for $\ell _i=L_C$ and $\ell _j=K_{D}$, whenever C is a proper instance of D it holds that $i>j$. To any instance-preserving enumeration E of P is associated its Herbrand path $P^*$ through $S^*$, the Herbrand set of $\text {Cl}(P)$, as follows: $L_C\in P^*$ if and only if there exists $\ell _m=K_D$ in E such that C is an instance of D, and there does not exist $\ell _n=K'_{D'}$ in E, with $n>m$, such that C is an instance of $D'$.

The main conclusion of this section will follow from the lemma below.

Lemma 1

Let B be a relevance-saturated branch in a tableau for $S=T\cup G$, where T is a satisfiable clause set. Let $P'$ be a consistent Herbrand path for T, and $P_B$ the path associated with B. Then the set of literals I of

$$\begin{aligned} P=P^*_B\cup \{L_C\in P'~|~C\in \left( Cl (S)\setminus Cl (P_B)\right) \} \end{aligned}$$

is a partial Herbrand model for S.

Proof

We show that P is a consistent Herbrand path through $S^*$. Suppose not; that is, that there exist complementary literal occurrences $L_C$ and $\lnot L_D$ in P. Because B is open, the path $P_B$ is consistent, so it must be that not both $L_C$ and $\lnot L_D$ belong to $P^*_B$. Because $P'$ is consistent and $(P\setminus P^*_B)\subseteq P'$, it must be that not both $L_C$ and $\lnot L_D$ belong to $P\setminus P^*_B$ either. Without loss of generality, then, assume $L_C\in P^*_B$ and $\lnot L_D\in P\setminus P^*_B$. Then in the tableau $L_C$ is a node on branch B, so $L_C$ is relevant. Since B is open, the multipath-add rule would have added $\lnot L_D$ to the multipath over T, and then $\ell =\{L_C, \lnot L_D\}$ would have been a relevant link on B. This contradicts the assumption that $\lnot L_D\in P\setminus P^*_B$; that is, that $D \not \in \text {Cl}(P_B)$.

Since P is a consistent Herbrand path through $S^*$, then by proposition 1, P is a partial Herbrand model for S.

The main result of this section follows as a result of this lemma.

Proposition 2

If $S=T\cup G$ is an unsatisfiable clause set, T is a satisfiable clause set, and f is a relevance-fair strategy, then the tableau for S and f is a $\forall$-closed disconnection tableau for S.

Proof

Let $\mathcal {T}$ be the tableau for S and f and suppose that $\mathcal {T}$ had an open branch B. Since f is a fair strategy, then B would be relevance-saturated. Therefore by Lemma 1, S would be satisfiable.

5 Discussion and Conclusion

In this paper the GSDC was presented, an adaptation of the disconnection tableau calculus that allows for goal-sensitive reasoning. A proof of completeness was given along with examples of the method in use. The GSDC is an automated reasoning method that is both instantiation-based and goal-sensitive, a combination which could have practical use in areas such as formal software verification that handle very large axiom sets.

The usual disconnection tableau calculus benefits from well-chosen initial paths in that they can lead to significantly shorter proofs, but the GSDC as presented simply initializes the multipath using the set of literal occurrences which form links with the goal. However, the multipath-add rule ensures that relevant links are found, and the method is complete, regardless of the way the initial multipath is specified. In other words, a well-chosen multipath for initializing tableau construction can lead to shorter proofs in the GSDC as well, while remaining goal-sensitive.

The mechanics and notions employed by the GSDC as described are similar to those of previous methods, including hyper tableaux [1], and as such the first planned follow-up to this work is a detailed qualitative comparison. In addition, an experimental evaluation of the GSDC is needed. An implementation of the disconnection tableau calculus was developed as the disconnection calculus theorem prover or DCTP [7], and so an initial planned follow-up to this work is to implement the GSDC as an extension of the DCTP and evaluate its performance. As a future research direction, we are interested in adapting other instantiation-based methods to be goal-sensitive as well, including the Inst-Gen method [6].