Keywords

1 Introduction

It seems that the question whether technologies could be used in mathematics education is long behind us. This undoubtedly includes the teaching and learning of linear algebra content. While historically some questions regarding the role of digital and non-digital resources in linear algebra instruction have been addressed, many remain unanswered. To give a sense of the scope of the remaining questions, consider the following. What makes the use of a particular digital resource efficient? What are the ideal qualities of technology-based materials for the teaching and learning linear algebra and how can we measure these qualities? What are the advantages of one type of software over another, for example, a Computer Algebra System (CAS) versus a Dynamic Geometry System (DGS)? When and how should each be applied? How can we best disseminate research-based materials and sustain investigations about their values? Which new forms of digital support may increase the motivation, communication and collaboration in a linear algebra course, e.g. flipped or inverted linear algebra classroom? These questions are still present and of significance in the current debates. Rather than try to answer any one of these questions in detail, this chapter presents a way to frame an examination of these types of questions.

This chapter builds on the discussions on the teaching and learning linear algebra in two relatively different groups at the 13th International Congress on Mathematical Education (ICME13). Firstly, the topic study group (TSG43) about the uses of technology in upper secondary mathematics education focused on the implementation of technologies from cognitive and epistemological perspectives, as well as accessibility to and the roles of emerging technologies. It also studied interrelations between technology and specific mathematical contents. Secondly, one of the key issues proposed within the discussion group (DG) for Teaching Linear Algebra at the ICME13 was the incorporation of technology specifically in the teaching of this subject. This chapter aspires to establish connections between the perspectives deliberated within these groups. It describes a diversity of technologies that can be used as a supplement to traditional educational media. The chapter begins by considering how the development of particular students’ competencies for linear algebra may be fostered by appropriate technology-based environments such as CAS or DGS. The aim of the chapter is to suggest a model for multiple representations of concepts that are important when designing efficient (digitally based) environments in order to support the development of particular students’ competencies in linear algebra .

2 Theoretical Background

Discussions about technology utilization in university linear algebra courses started with considerations of how “super calculators” or “commercial systems for both numeric and symbolic computation” (Carlson, Johnson, Lay, & Porter, 1993, p. 45) may be relevant for the content related knowledge of mathematics. In the last twenty years, the discussions have continued by also considering the role of technology for didactical purposes. For example, Day and Kalman (1999) point out that computers could be efficient not only for “eliminating computational drudgery”, but also for providing interactive “environments for actively exploring properties of mathematical structures and objects” (Day & Kalman, 1999, p. 12). Rapid intensification of digitalization in general also parallels new educational trends. Curricula have been re-oriented towards learning outcomes and competencies. Similar to the principles and standards (NCTM, 2000) in the USA, there are six general competencies for tertiary level of mathematics in Germany (the numeration is used only for easier reading):

  1. (K1)

    bringing forward arguments and proofs,

  2. (K2)

    problem solving,

  3. (K3)

    mathematical modeling,

  4. (K4)

    representing mathematical concepts,

  5. (K5)

    interacting with symbols, formal and technical elements of mathematics and

  6. (K6)

    communicating mathematically (Kultusministerkonferenz, 2012, pp. 14–17).

Each of them is relevant for, and meets the goals of the teaching of linear algebra . Though there are certainly no firm boundaries between them, the development of one or more of them may be supported by meaningful implementation of digital resources deployed during the teaching and learning processes. This could be done through interactive explorations in modeling and problem solving, by promoting understanding through the use of multiple representations or by reducing systematic procedures when handling large data sets. Such students’ competencies and the possible effects of technology on their development are the focus of this chapter. An overview of the theoretical background precedes this description.

Investigating complex phenomena like mathematics education in the presence of technology is challenging because of the fast pace of technological change and the lack of specific theories for studying the teaching and learning a particular mathematical content, e.g. linear algebra , with digital aids. This has been explored in recent literature (e.g. Donevska-Todorova & Trgalova, 2017; Turgut & Drijvers, 2017). This also appears as a new issue in the call for topic-working group 17 at the 10th conference of the European Society for Research in Mathematics Education (CERME 10). A recent review (Drijvers et al., 2016) considered whether digital technology improves students’ learning of a particular mathematical content (e.g. geometry) through quantitative studies, and why it may be the case through qualitative studies focusing on the teacher as an important factor. Another survey paper (Sinclair et al., 2016) stated seven ‘threads’ of contributions which affect the teaching and learning geometry with technologies at different levels of education including pre- and post compulsory. A question that comes out of this research is if these ‘threads’ might also refer to the teaching and learning other mathematical domains including linear algebra . I focus on two of the min particular.

The first ‘thread’, “developments and trends in the use of theories” (Sinclair et al., 2016, p. 1) relates to whether the use of general theories about the teaching and learning mathematics with digital equipment is adequate for a specific mathematical domain such as geometry, or linear algebra . In the absence of a particular theoretical framework or apparatus for investigating the teaching and learning linear algebra with digital resources, this chapter suggests connecting suitable theoretical frameworks. In order to give the reader a sense of what is meant by a later categorization, a possible network that may consider three groups of theoretical frameworks is:

  1. (1)

    general theories on mathematics education,

  2. (2)

    theories on technologies in mathematics education and

  3. (3)

    specific theories for the teaching and learning linear algebra (with or without technological support).

The suggested groups of theories are certainly global and do not exclude other. Nonetheless, they refer to the works of the TSG43 and the DG at the ICME13 and are here meant to serve as examples. Exploited theoretical frameworks from each of the groups have to be adjusted and linked for achieving the goals of the research of teaching and learning linear algebra . General theoretical frameworks (1) which may be useful in the sense of competencies may be the construct concept image-concept definition (Tall & Vinner, 1981), regarding the competency K1. Further, the three worlds of mathematical thinking (Tall, 2004) or the action-process-object-schema (APOS) theory (Dubinsky & McDonald, 2001) is relevant for studying the development of the competency K4. These frames directly relate to the above consideration (‘thread’) about the underrepresentation of defining (K1)—versus overemphasis of representing (K4) issues in technology-enhanced environments. This already shows a natural bridge between the general theories (1) and the theories associated to digital media (2).

Further on, the theory of semiotic mediation (Bartolini & Mariotti, 2008), also used within the ICME13-TSG43, may be exploited for investigating exact effects of particular tools (drag/drop, touch/move, hide/show, slide, zoom in/zoom out) on the learning linear algebra (e.g. distinguishing scalar from vector operations, or referring geometric meaning to algebraic concepts, etc.). Studying historical and epistemological developments of the concepts in linear algebra is relevant for designing technology-based teaching/learning environments and increasing their semiotic potential for didactical purposes. Taking the multifaceted nature of concepts in linear algebra such as analytic-arithmetic or synthetic-geometric, into consideration may contribute the creation of environments to foster development of multiple representations (K4). I come to this point in Sect. 3.3. Another theoretical framework specific for technology-rich settings is instrumental genesis (Trouche, 2005), which has a potential to facilitate arrangement of instruction of linear algebra , among other, and to provide relevant data at interpersonal, classroom, resource or institutional level of a multiple-level data analysis of communication and collaboration competencies (K6).

Finally, specific theories for the teaching and learning linear algebra (3) as the one referring to students’ difficulties with the unifying and general theory of linear algebra and the obstacle of formalism (Dorier, 2000), multiple modes of description (Hillel, 2000) and multiple modes of thinking (Sierpinska, 2000) may also be valuable in the teaching of technology supported instruction. I elaborate these issues more in detail also in Sect. 3.3 in relation to the competencies K1, K4 and K5.

Looking back to the survey the ‘thread’ “advances in the understanding of the teaching and learning of definitions” (Sinclair et al., 2016, p. 2) in geometry supported with technology , may as well refer the insufficient number of studies directly addressing key mathematical issues as defining concepts in linear algebra . This issue about the defining mathematical concepts is in particular relevant for developing a competency of formal proving (K1). Further, depending on the way concepts in linear algebra are defined, e.g. analytically or geometrically, their representations may also vary, which affects the development of the competency K4. Finally, each definition of concepts in linear algebra uses a particular symbolic and formal mathematical language that directly influences the growth of the competency K5. I investigate the possibilities to strengthen mutual development of these competencies and, based on chosen theories from (1) to (3), suggest a model that I consider important when teaching or creating teaching/learning trajectories or environments for concepts in linear algebra (in Sect. 3.3).

  • Research question

Drawing upon the theoretical concerns above, including (1)–(3), the main research question that arises is: how could the development of students’ competencies in linear algebra be facilitated by technology usage in instruction and learning?

By collecting, comparing, contrasting and synthesizing data for digital environments suitable for gaining competencies in linear algebra , I provide insights to each of the competencies briefly (in Sects. 3.1, 3.2 and 3.4), however set my focus on the competencies K1, K4 and K5 (in Sect. 3.3).

3 Content Specific and Process Oriented Competencies in Linear Algebra

This section offers some insights in some of the previously mentioned content specific (or subject matter) and process oriented competencies for a tertiary level mathematics K1–K6 with reference to linear algebra .

3.1 Defining, Proving and Understanding

The inverse treatment of axiomatic properties for defining, at tertiary level of linear algebra , on the one hand and describing concepts, at upper secondary level of linear algebra , on the other hand, signalizes possible obstacle for learning (Donevska-Todorova, 2017b, p. 2). Sometimes concepts and their properties remain to occur as separate mathematical objects in the students’ minds (Donevska-Todorova, 2017b, p. 6). For example, while associativity is a defining property of vector spaces at university level linear algebra , it is perceived as a characteristic of the operation addition of vectors that are previously defined as classes of parallel arrows with same length and orientation in upper high school. Although, there exist some studies, which have considered descriptive (a posteriori) defining of concepts after exploring properties with DGS (in addition to other media), in author’s knowledge there are no studies on students’ deeper understanding of the need for axioms and definitions for avoiding infinite regress and circularity (de Villiers, 1998). The dependence of the development of deep conceptual understanding on the definitions of concepts has seldom been in focus (e.g. Donevska-Todorova, 2015; Hannah, Stewart, & Thomas, 2016). Based on semi-structured clinical interviews with participating students in a linear algebra class, Bagley, Rasmussen, and Zandieh (2015, p. 36) have found that all participating students think that “the result of composition of a function and its inverse should be 1”. In a linear algebra context, functions appear as linear transformations from one vector space into another, preserving axiomatic properties as addition and scalar multiplication, but such function conceptions have also rarely been directly examined. An exemplary study about transformations in a Cabri-based environment has been undertaken by Dreyfus, Hillel & Sierpinska, 1998. Another exemplary study (Donevska-Todorova, 2016), points out students’ difficulties about the introduction and understanding of linear, bi-linear and multi-linear transformations on a real vector space which have been discovered in pre-service teachers when working on discussing questions and multiple-solution tasks. Many abstract mathematical concepts, function (in this context linear transformation) among them, can be understood either operationally, as processes, or structurally as objects but the operational and the structural aspects do not replace, rather complement each other (Bagley, Rasmussen, & Zandieh, 2015, p. 37). Yet, there are studies, which have discovered students’ predominant possession of procedural versus conceptual understanding for example for concepts as determinants and suggest that this discrepancy may be overcome with a possible technology-based environment for a semiotic mediation (Donevska-Todorova, 2016, p. 10). The problem of defining concepts in linear algebra is certainly further related to argumentation and proving. Students’ abilities for proving have been examined, e.g. that a set is a subspace of a vector space (Britton & Henderson, 2009, p. 963) however insufficiently from the aspect of technology facilitation.

The competency about defining concepts, possibly with technological assistance in visualizing and representing axiomatic properties, is connected to two other of the above-mentioned competencies (K4 translations between multiple representations and K5 symbolic language and formal nature of linear algebra ). I will revisit this point in Sect. 3.3.

3.2 Computation, Symbol Manipulation and Programming

The historical evolution of technological devices starting with hand-held calculators through graphical calculators to powerful CAS shows a quick ongoing expansion. This growth has many possibilities and challenges for the teaching and learning of linear algebra . A common agreement among researchers is that the usage of CAS should be an integral part of mathematical instructions (e.g. Janetzko, 2016). Development of competencies for programming besides those for computing or symbol manipulation (K5) may be supported by CAS because of their embedded powerful apparatus (e.g. Díaz et al., 2011). Manual solutions of systems of linear equations (SLE), e.g., by the Gaussian elimination method, are meaningful both at school and university level. In particular, understanding the meaning of the solutions sets, the structure and the algorithm are among the most important learning goals. On the one hand, exercise and assessment tasks are usually suited to lead towards achieving these goals without a technological support. On the other hand, engagement in algorithm development and computer programming may contribute in the development of spatial reasoning and coding capabilities (e.g. Francis, Khan, & Davis, 2016) or development of undergraduate students’ proficiency, as a combination of fluency and confidence, in a pillar of scientific inquiry having form of simulation, optimization and modeling (Buteau, Muller, Marshall, Sacristán, & Mgombelo, 2016). When solving SLE with large number of equations and unknowns e.g. by students in economic studies, interpretations, rather than calculations of results is worth more. However, by implementing CAS calculators for checking answers or performing single step direct calculations to compute, for example a determinant, or an inverse of a matrix, Stewart and Thomas (2004) have found that even enthusiastic students require sustained attention in a technology-based learning environment. The efficiency in calculating inverse or exponential matrices of large dimension (over a hundred), eigenvectors and eigenvalues of matrices with real and complex entries have made CAS become an integral part of contemporary mathematics (Caridade, Encinas, Martín‐Vaquero, & Queiruga‐Dios, 2015). Digital image processing by the use of CAS in a Mathematic Virtual Laboratory (MVL) developed on a Moodle platform has been suggested for making some linear algebra concepts, as matrix operations and their properties, more concrete and clearer to geological and industrial engineering students by Caridade et al. (2015). The authors also envision possibility for similar resourceful usage in high school mathematics. MATLAB,Footnote 1 for example, is often perceived and recommended as one of the most natural CAS for linear algebra as it has been developed purposely for matrix operations (Dios, Martínez, Encinas, & Encinas, 2012; Jin & Bi, 2011). Its usage in instruction is however not straightforward for the reason that, students have to be familiar with the programming language in advance. A linguistic perception of mathematics includes syntactical, semantical and pragmatic aspects of the algebraic language and it can easily be handled by a CAS, nevertheless, students have difficulty to understand what a CAS does and how its output is to be interpreted (Oldenburg, 2016). Some difficulties of engineering students when CAS are sporadically used may be overcome by a user interface, called CATO, for different CASs written in Java as Mathematica,Footnote 2 MaximaFootnote 3 or the mathematical toolbox of MATLAB (Janetzko, 2016).

The roles of CAS may also be observed as “multiply-linked graphical, numerical, and symbolic manipulation utilities” (Heid & Edwards, 2001, p. 128). Powerful technology-based mathematics packages as Mathematica or MapleFootnote 4 enable rich approaches for teaching and learning undergraduate linear algebra . Their capabilities for performing exhausting calculations and symbolic manipulations, e.g. solutions of (large) SLE or matrix multiplication, may transform or even replace some classroom activities. In particular, their relevance for graphical, in addition to the numerical and symbolic representations is connected to the competencies (K4).

3.3 Visualization, Representation, Exploration and Generalization

Students’ difficulties with a priory visualizations have already been noticed and reported in research and an overemphasis of the visual potential of technologies in improving conceptual understanding per se, is considered as a naïve attitude (Lagrange, Artigue, Laborde, & Trouche, 2001, p. 7). Yet, it seems that a careful implementation of an appropriate DGS with an integrated algebra in it, rather than a CAS environment, may be helpful for visualizing and multiple-representing concepts in linear algebra . While a pure synthetic-geometric approach may be quite challenging the students to apprehend, building linear algebra on a coherent multi-domain base, e.g. geometry, functional calculus and modern axiomatic may be more beneficial. In this sense, appropriate DGE for concepts in linear algebra may be of help and I try to elaborate how.

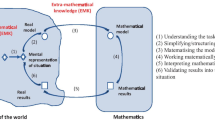
DGS have the potential for dynamic and simultaneous changes of multiple representations. In continuation, I prefer a usage of rigorous terminology that is specific to the research field of teaching and learning linear algebra . Namely, instead of considering the “algebraic, geometrical and abstract presentation” (e.g. Fig. 1 in Konyalioglu, Isik, Kaplan, Hizarci, & Durkaya, 2011, p. 4042), I use the vocabulary different modes of description (Hillel, 2000) and modes of thought (Sierpinska, 2000). Besides, a triple of distant components of linear algebra concepts, the relations between which are not identified (Fig. 1) seems a bit problematic.

Fig. 1
figure 1

Abstract, algebraic, and geometric presentations of concepts in linear algebra on Fig. 1 in Konyalioglu et al. (2011, p. 4042), Copyright (2018), with permission from Elsevier

Full size image

The authors also suggest a teaching approach according to these components by considering the “geometric presentation” for dimensions less than or equal to three, while the “algebraic presentation” for dimensions greater that three (Konyalioglu et al., 2011, p. 4042). In my opinion, there seems to be no reason why not considering the algebraic one also for dimensions less than or equal to three. Moreover, the order: first, algebraic definition, second geometric meaning and third, abstract representation (Konyalioglu et al., 2011, p. 4043) does not necessarily need to take place in the teaching of linear algebra even in high school. On the contrary, beginning with a geometrical context may foster students to deep intuitive thinking, motivate explorations and therefore contribute to the development of alternative competencies . Furthermore, the teaching of linear algebra at the university level goes along with the nature of mathematics as a science, so the concepts are introduced by definitions through the abstract mode of description. Abstract concepts gain their meaning in contexts and both the algebraic and the geometric modes allow such concretizations. Therefore, a severe order in the introduction of the concepts, as suggested by the authors above, is not a necessity. Similarly, to this view, Dray and Manogue (2008) have suggested a geometric introduction for an exemplary concept, the dot product of vectors, which may continue with arithmetic-algebraic and culminate with analytic-structural aspects. This seems to be a more natural sequence due to the primarily geometric introduction of vectors in physics, lower-secondary mathematics and upper-secondary linear algebra and because of the vector-input and scalar-output of the dot product. For empirical results with this sequencing for the introduction of the dot product in a dynamic geometry environment, see Donevska-Todorova (2015).

3.3.1 A Nested Model of the Three Modes of Thinking of Concepts in Linear Algebra

In contrast to the triple presentation of distant constituents of concepts in linear algebra given above (Fig. 1) and because of a doctoral study (Donevska-Todorova, 2017a), I would rather suggest a nested model for presenting the modes of thinking. I actually situate the algebraic and the geometric modes of description (Hillel, 2000) and corresponding analytic-arithmetic and synthetic-geometric modes of thinking (Sierpinska, 2000) as nested constituents of the analytic-structural mode (Fig. 2). The prior two allow concretization of the abstractness of the concepts.

Fig. 2
figure 2

Nested model of the three modes of thinking and description of concepts in linear algebra

Full size image

How does the nested model (Fig. 2) refer to the theoretical considerations (1)–(3) and the competencies K1 to K6 in Sect. 2 exactly? In other words, how does the nested model help in the analysis towards answering the posed research question? I try to explain this through its nodes and arrows.

Starting form (1) general theories about mathematics education, the model allows a development of a wider and deeper concept image for the concept definition (Tall & Vinner, 1981) of a particular concept in linear algebra . For example, the node analytic-arithmetic mode thinking in the model refers to thinking of vectors in as ordered n-tuples, while the node geometric mode refers to vectors as equivalent classes of arrows that are equal in length, orientation and direction. These two nodes show how vectors as elements of vector spaces in an analytic-structural mode of thinking perceive their concretization in a context (e.g. in R 2 or R 3). Perceiving these three different concept definitions of a single concept (e.g. vectors) is enabled through different modes of description (Hillel, 2000) which, likewise the corresponding modes of thinking (Sierpinska, 2000) belong to (3) specific theories for the teaching and learning linear algebra .

Due to the importance of precise definitions of concepts in linear algebra , based on which argumentations and formal proofs develop (competency K1), it may be worthy to further utilize the nested model when aiming to also advance the competency for multiple representing and symbol manipulating (modes of description and language) of concepts (K4 and K5).

Looking at the nested model again, the arrows represent the relations and interplays between the nodes. For example, translations from the geometric into the arithmetic-analytic mode of thinking or the other way around, like visualization from the arithmetic-analytic to the geometric mode of thinking and even generalization of concepts from 2D and 3D to nD may take place simultaneously (Fig. 2). In particularly, this may come into focus in a DGE, which brings us to the use of (2) theories about technologies in mathematics education.

Switching from one mode of thinking into another and vice versa may significantly be stimulated, e.g. by the dragging tool in a DGE. Such devices could serve as instruments of semiotic mediation (Bussi & Mariotti, 2008) in exploring multiple modes of description. A digital simultaneous multiple-dynamic manipulation, in contrast to single-static paper-pencil control could be achieved e.g.by means of sliders which facilitate numerical variations. The numerical dependences represented by sliders allow transparency of the difference between scalars and vectors which is typical for the content of linear algebra , e.g. for the teaching and learning of linear combinations of vectors, linear (in)dependence of vectors, vector spaces, linear transformations, bi- and multi-linear forms, etc. What makes a DGS toll a specific instrument of semiotic mediation could deeply be observed by the Vigotskian perspective for the transformation form inter- to intra-personal mental processes (Falcade, Laborde, & Mariotti, 2007). Further on, geometric, and simultaneously arithmetic-algebraic dependences could also be examined by the dragging facilities of points or vectors and there already exist DGEs for such purposes. For example, a recursive exploration space (Hegedus, Dalton, & Moreno-Armella, 2007) can mediate a mental concept formation and therefore participate in development of mathematical cognition (e.g. the concept of dot product of vectors in Donevska-Todorova, 2017b). Students co-act with the environment by exchanging their roles in switching from one into another mode of description and thinking which modifies (though not negates) the paper, as a frozen (Hegedus, Dalton, & Moreno-Armella, 2007) into the DGE as a fluid medium for thinking of mathematical concepts (Donevska-Todorova, 2017b). This study shows that the challenge of supporting the learning of abstract concepts or even completely abstract structures, e.g. vector space or subspace, by the DGS has by now been approached to a certain degree by interactive dynamic artifacts for one or more of their defining axiomatic properties.

3.4 Communication and Collaboration

A Spanish group of authors has been looking at generic, content-independent competencies like team-working, self-learning, critical thinking, problem solving and technical communication with the use of CAS Derive (García López, García Mazario, & Villa Cuenca, 2011) and CAS Maxima in a later study (García, García, Del Rey, Rodríguez, & De La Villa, 2014). They have concluded that both CAS have allowed not only improvement of students’ academic performance but also increase of students’ motivation, satisfaction, self-confidence and team working. Bulgarian scholars have examined a combined, traditional and CAS-based environment for an acquisition of competencies in higher education and have concluded that it is helpful for action competencies related to emotional, social and value-related components (Varbanova & Durcheva, 2016, p. 54).

Although communication and collaboration among students and instructors in a technology-enhanced environment may be fostered and researched in relation to CAS or DGS, the next subsection offers insights to possibilities for development of these competencies (K6) from a bit different aspect.

3.4.1 Cyber Learning, Communication and Collaboration

One of the oldest functions of technology is the collection of data required for teaching and learning processes. New Web 2.0 and 3.0 technologies allow for the exchange of collected data, as well as time and place independent communication and collaboration. Nevertheless, a first reaction to the teaching and learning of a specific mathematical content, including linear algebra , through social networks for example, is a dose of skepticism. Social media may involve inaccurate information, biased comments and unreceptive responses, yet an effortless search shows that hundreds of groups called “Linear algebra” or similar, already exist and have thousands of members on Facebook and Twitter. It is predictable that the number of such groups will continue to grow. Research Gate, the largest academic social network (Matthews, 2016), is another type of virtual resource that may or may not serve teaching and learning beyond research purposes. There are also numerous online forums and blogs, specifically related to linear algebra , YouTube tutorials and courses with over millions of views (e.g. thirty four videos of the MIT OpenCourseWare, Linear Algebra , Strang, 2005). Virtual teaching and learning environments, for example, online classrooms, flipped classrooms, wikis (e.g. GeoGebra Wiki and Wikispaces) could also be part of the repertoire for organizing linear algebra courses. An inverted or flipped classroom used as a “one-time class design to teach a single topic, as a way to design a recurring series of workshops, and as a way of designing an entire linear algebra course” (Talbert, 2014, p. 361). Love et al. (2014) found that students in a flipped linear algebra classroom had “a more significant increase between the sequential exams compared to the students in a traditional lecture section, while performing similarly in a final exam” (Love et al., 2014, p. 317) and expressed conceptual understanding and joy (Love et al., 2014, p. 323). A teaching and learning platform for linear algebra for engineers, created according to the blended-learning-concept, has significantly improved students’ performance (Roegner & Seiler, 2012). The participating students in the project had direct access to an online-script with visualizations, individualized homework problems with an interactive training environment and automatic corrections. The sustainability, further expansion, and dissemination of these projects, as well as the development of other such platforms remain ongoing.

These plentiful and diverse educational innovations have the potential to become a part of quality teaching and (in)formal learning of linear algebra after careful research and documentation has been undertaken. There is still a lack of satisfactory evidence that these innovative forms of instruction and learning guarantee development of subject matter competencies . Even development of other non-content specific competencies such as networked debating, blogging, and chatting, as well as socio-cultural and anthropological aspects of formal and informal education in a pure context of teaching and learning linear algebra need to be further examined and documented. In the era of global digitalization, computer technologies have high social legitimacy, but their educational legitimacy, remains an open research question.

4 Discussion and Challenges Ahead

Alongside the evolution of technologies and the enlargement of classroom accessibility, critical research suggests cautious implementation. Even in the late 90s, Guin and Trouche (1998) pointed out complexities in teaching and learning situations which are brought by implementation of calculators. The above analysis shows that the learning and understanding of the abstract nature of linear algebra through axioms, definitions, theorems and structures does not become straightforward by a simple use of a CAS or a DGS. Though a rigorous systematization regarding the research question would be difficult to establish, an attempt to show which digital tool may facilitate the development of which competency and how it may be researched is proposed in Table 1.

Table 1 Technological tools for facilitating development of competencies in linear algebra
Full size table

The initial ideas illustrated in Table 1 must be considered with some flexibility. For example, a CAS environment may also be helpful for visualization and representation, (K4), though the DGS with embedded algebraic features is seen as having more potential for this purpose due to mutual dependence and invariant properties which can be simultaneously investigated (are not always brought by the software a priory but are additionally designed). This shows that a whole linear algebra course does not necessarily have to be designed in a single, either CAS or DGS environment. It could be the case that combining different technological tools for facilitating the learning of particular concepts in a single course may also be useful.

What has been considered as “smarter technologies, like computer software or symbolic calculators [and] emerging technologies (Internet, etc.)” (Lagrange et al., 2001, p. 3) fifteen years ago may seem history now. New emerging technological devices such as touch and multi-touch (iPads, iPhones, etc.) open new questions for further investigations.

5 Conclusion

This chapter has surveyed current literature on both technology-facilitated teaching and the learning of linear algebra , taking the discussions in two ICME13 working groups as starting viewpoints. The analysis focused on whether and how technology-enhanced environments could facilitate the development of students’ competency in linear algebra . From this analysis and regarding the research question, it seems that CAS are more suitable for the development of competencies such as symbol manipulation and programming (K5) (in Sect. 3.2) and DGS are better for competencies such as visualization, representation, exploration, and generalization (K4) (in Sect. 3.3). Both types of environments may be appropriate for defining, proving and understanding (K1) (Table 1). In order to show how a digitally based environment may be considered for fostering K1, K4 and K5, I have suggested a nested model (Fig. 2). This model presents all three modes of description and thinking that I consider important in instruction and in the design of tasks or teaching environments. It is a visual presentation showing that the modes are not dispersed one from another, rather connected. In particular, specifically designed technologically-based environments may enable easier and more efficient shifts between the modes, facilitating the development of competencies for defining, representing and understanding concepts in linear algebra .