Resource Allocation with Multiple QoS Constraints in OFDMA-Based Cloud Radio Access Network

Abstract

Due to the spread of mobile Internet and development of many new multimedia applications, there are much different quality-of-service (QoS) requirements of users in fifth generation (5G) communication system. In this paper, we consider two types of users with different QoS requirements in OFDMA based cloud radio access network (C-RAN). One type QoS requirements of users are joint bit error rate (BER) and data rate (type I users), and the other type is the data rate (type II users). We formulate the resource allocation problem in OFDMA-based C-RAN, the problem is maximal weighted sum rate for type II users subject to the QoS requirements of type I users and the fronthaul capacity constraint. Since the formulated problem is a non-convex problem, two subproblems are reformulated firstly, and then based on the CPLEX package, time-sharing and alternating methods, we proposed an iterative algorithm. Simulation results confirm that the proposed algorithm can achieve good performance.

1 Introduction

Cloud radio access network (C-RAN) can provide significant enhancement in data rate to support broadband applications [1, 2]. It is anticipated that wireless communication systems will support more than 1000 times todays traffic volume by 2020 [2]. Besides, the number of mobile devices with diverse quality-of-service (QoS) requirements is increased. For example, video services need high speed data rate to guarantee with best effort for QoS requirement. However, voice services need low latency and low delay jitter. Therefore, how to satisfy the different QoS requirements of users is a significant problem in C-RAN.

In wireless communication networks, there are various QoS requirements (such as rate, delay, bit error rate (BER) and energy efficiency) for different users. To meet the multiple QoS requirements of users, resource allocation has attracted considerable attention in recent years. Matalgah et al. proposed a subchannel and power allocation algorithm to maximize the sum capacity subject to fairness parameters and QoS requirements constraints [3]. Considering the QoS requirements are interference tolerance and data rate, a resource allocation policy was proposed to obtain the maximal sum rate [4]. A resource allocation policy was proposed for different QoS guarantee, fair transmission and high data rate in OFDMA to get maximal sum data rate [5]. An optimal power allocation strategy was investigated maximize effective capacity subject to joint statistical delay and energy efficiency requirements [6].

All the previous works considered the maximal sum rate of all users subject to the different QoS requirements. However, since the resources are limited, we need guarantee the basic services firstly. If the resources are remaining, other services can be guaranteed. For example, voice services are the basic services in wireless networks, and we need guarantee them firstly. But for video services, we can meet their QoS requirements when the resources are remaining. Therefore, how to allocate resources to meet different QoS requirements of users is an urgent problem.

In this paper, we consider two types of users with different QoS requirements to share resources in OFDMA based C-RAN. We focus on the weighted sum rate maximization problem of the users whose QoS requirement is data rate, and the constraints are the other users whose QoS requirements, such as BER and data rate, should be guaranteed. Since the problem is non-convex, two subproblems are reformulated firstly. And then we use CPLEX package, time-sharing and alternating methods to solve these two subproblems. Based the solution of these two subproblems, we proposed an iterative algorithm. Numerical results show that the proposed algorithm can achieve good performance.

Fig. 1.

System model

2 System Model

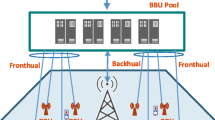
In this paper, we consider the downlink transmission in OFDMA-based C-RAN, as shown in Fig. 1. This system consists L remote radio heads (RRHs), which are connected to the baseband unit (BBU) pool via a fronthaul link with capacity of $C_{f}$. The transmission power for each RRH is P. Let B denote the bandwidth of each RRH, which is divided into K subcarriers. The set of subcarriers are denoted as $\varOmega = \{1,2\,...\,K\}$ and the bandwidth of each subcarrier is B/K. Each RRH can reuse all the subcarriers, we ignore all interference in this system. $N_{0}$ is the power spectral density (PSD) of the white Gaussian noise. In this system, there are two types of users with different QoS requirements. One type QoS requirements of users are joint BER and data rate (type I users), the other type is the data rate (type II users). For different QoS requirements users, each RRH divides the available power P and subcarriers $\varOmega$ into two parts. Let $P_{I}$ and $\varOmega _{I}$ be the power and subcarriers to the type I users; respectively $P_{II} = P - P_{I}$, $\varOmega _{II} = \varOmega \setminus \varOmega _{I}$ are the power and subcarriers to the type II users. In each RRH, the set of type I users is $\mathcal {M}=\{1,...,M\}$, and the set of type II users is $\mathcal {N}=\{1,...,N\}$. Each user is served by one RRH.

For the type I users, each RRH supports T classes of services, denoted by the set $\mathcal {T}=\{1,...,T\}$. Let $M_{t}$ be the number of users belonged to the class t and the $1^{st}$ user to the $M_{1}^{th}$ user belong to class 1, the $(M_{1}+1)^{th}$ user to the $(M_{1}+M_{2})^{th}$ user belong to class 2, and so on [7, 8]. To satisfy the QoS requirements, $t^{th}$ class users need a target BER of $P_{e}^{t}$ and a constant data rate of $D_{t}$ bits/OFDM symbol. $c_{m,i}$ denotes the number of bits to be modulated onto one OFDM symbol on the ith subcarrier by the mth user. In this system, we consider M-ary Quadrature Amplitude Modulation (QAM), where $C=2^{c_{m,i}}$ is the constellation size, as $c_{m,i} = \{2,4,6\}$, $C =\{4,16,64\}$. $c_{m,i}=0$ means that no bit is transmitted on the ith subcarrier for the mth user. We denote $p_{m,i}$ and $\tau _{m,i}$ as the power and subcarriers allocated to the type I users by each RRH, where $p_{m,i}$ is the power allocated to user m over the i subcarrier. $\tau _{m,i}$ is a binary indicator, if subcarrier i allocated to user m, $\tau _{m,i} = 1$, otherwise $\tau _{m,i} = 0$. Then $\sum _{m=1}^{M} \sum _{i\in \varOmega _{I}}p_{m,i}\doteq P_{I}$. And, $\sum _{m=1}^{M} \tau _{m,i} \le 1$, $i \in \varOmega _{I}$, it means one subcarrier only be allocated to one user. $h_{m,i}$ is the channel gain that user m experiences on subcarrier i.

For the type II users, we denote $p_{n,j}$ and $\tau _{n,j}$ as the power and subcarriers allocated to the type II users by each RRH. $h_{n,j}$ is the channel gain that user n experiences on subcarrier j.

3 Problem Formulation

In this section, we allocate the power and subcarriers to maximize the weighted sum rate of type II users with the constraints of the QoS of type I users and the fronthaul capacity.

For the type II users, the rate $R_{n}$ achieved by user n in each RRH can be express as

$$\begin{aligned} R_{n} = \sum _{j\in \varOmega _{II}} \tau _{n,j}\frac{B}{K}\log _{2}\left( 1+\frac{p_{n,j}}{N_{0}\frac{B}{K}}\right) . \end{aligned}$$

(1)

The fronthaul capacity constraint of RRHs in this system can be expressed as

$$\begin{aligned} LB \log _{2}\left( 1+\frac{P}{N_{0}B}\right) \le C_{f}. \end{aligned}$$

(2)

In this paper, we allocate the power and subcarriers to maximize the weighted sum rate of the type II users with the constraints of the QoS requirements of type I users and the fronthaul capacity, the QoS requirements including the BER and data rate for type I users. Then, this problem is formulated as

$$\begin{aligned} (\mathbf P1 )&~~\max _{\{p_{n,j}, \tau _{n,j}\}} L\sum _{n=1}^{N}\omega _{n}R_{n} \end{aligned}$$

(3a)

$$\begin{aligned} \mathrm {s.t}&~~\sum _{i\in \varOmega _{I}}\tau _{m,i}c_{m,i} = D_{1}, ~~m=1,2,...,M_{1},\nonumber \\&~~ \sum _{i\in \varOmega _{I}}\tau _{m,i}c_{m,i} = D_{2}, ~~m=M_{1}+1, ~~ M_{1}+2,... M_{1}+M_{2},\nonumber \\&~~ ...\nonumber \\&~~ \sum _{i\in \varOmega _{I}}\tau _{m,i}c_{m,i} = D_{t}, ~~m=M_{T-1}+1, ~~ M_{T-1}+2,... M_{T-1}+M_{T} ,\end{aligned}$$

(3b)

$$\begin{aligned}&~~ \sum _{m=1}^{M}\tau _{m,i}\le 1, \tau _{m,i}\in \{0,1\},~~i\in \varOmega _{I} , \sum _{n=1}^{N}\tau _{n,j}\le 1,\tau _{n,j}\in \{0,1\},~j\in \varOmega _{II} ,\end{aligned}$$

(3c)

$$\begin{aligned}&~~LB \log _{2}\left( 1+\frac{P}{N_{0}B}\right) \le C_{f} ,\end{aligned}$$

(3d)

$$\begin{aligned}&~~ \sum _{t=1}^{T}\sum _{m=1}^{M} \sum _{i\in \varOmega _{I}}p_{m,i}^{t}\doteq P_{I},\end{aligned}$$

(3e)

$$\begin{aligned}&~~P_{I}+P_{II}\le P,~~\varOmega _{I}+\varOmega _{II}\subseteq \varOmega , \end{aligned}$$

(3f)

where $\omega _{n}$ is the weight of user n, and it expresses the priority of user n. $p_{m,i}^{t}$ is the power allocated to user m over the i subcarrier for t class of service. Constraint (3b) guarantees the transmission rate of type I users. Constraint (3c) means one subcarrier only shared by one user. Constraint (3d) is the fronthaul capacity constraint. Constraint (3e) is the power allocated to type I users. Constraint (3f) is the system subcarriers and power constraints. This problem is a mixed-integer nonlinear programming (MINLP) problem, so it can not be solved by classical convex optimization methods [9].

4 Resource Allocation Algorithm

The problem (P1) is to maximize the weighted sum rate of type II users subject to the QoS requirements of type I users and the fronthaul capacity. Because the resources are limited, for the type I users, we only need allocate minimum resources to guarantee their minimum QoS requirements, and the remaining resources are all allocated to type II users. In order to solve this problem, firstly, we use CPLEX package to obtain the minimum resources for type I users. And then, we use time-sharing and alternating methods to allocate resources for type II users.

4.1 Resource Allocation for Type I Users

In this subsection, we formulate a subproblem to minimize the transmission power of type I users while satisfying the QoS requirements of type I users for all classes of services.

For the type I users, according to [10], we denote $f_{t}(c)$ as the required received power for class t users in a subcarrier for reliable reception of c information bits/symbol

$$\begin{aligned} f_{t}(c) = \frac{N_{0}B}{3K}\left[ Q^{-1}(\frac{P_{e}^{t}}{4})\right] ^{2}(2^{c}-1), \end{aligned}$$

(4)

where $Q^{-1}(x)$ is inverse function.

In order to satisfy the QoS requirements of each type I user, the allocated power to ith subcarrier by the mth user of class t is

$$\begin{aligned} \begin{aligned} p_{m,i}^{t}= f_{t}(c_{m,i})/h_{m,i}^{2}=\frac{N_{0}B}{3K}\left[ Q^{-1}(\frac{P_{e}^{t}}{4})\right] ^{2}(2^{c_{m,i}}-1)/h_{m,i}^{2}. \end{aligned} \end{aligned}$$

(5)

Inspired by [7, 8], we notice that the term $2^{c_{m,i}}$ can only take discrete values of $2^{2}$, $2^{4}$ and $2^{6}$. Therefore $f_{t}(c_{m,i})\tau _{m,i}$ can be replaced by

$$\begin{aligned} q_{t}(g_{m,i}^{s}) = 3\rho _{t}g_{m,i}^{1}+15\rho _{t}g_{m,i}^{2}+63\rho _{t}g_{m,i}^{3}, \end{aligned}$$

(6)

with additional constraints

$$\begin{aligned} \sum _{s=1}^{3}g_{m,i}^{s}\le 1, m = 1,2...,M,i\in \varOmega _{I}, \end{aligned}$$

(7)

where $g_{m,i}^{s} \in \{0,1\}$ are the three new binary variables, where $s =1,2,3$. Equation (7) means the selected modulation mode.

$$\begin{aligned} \rho _{t} = \frac{N_{0}B}{3K}\left[ Q^{-1}(\frac{P_{e}^{t}}{4})\right] ^{2}. \end{aligned}$$

(8)

According to the above analysis, the minimal transmission power of type I users problem can be formulated as

$$\begin{aligned} (\mathbf P2 )&~~\min _{g_{m,i}^{s}} L\sum _{t=1}^{T}\sum _{m=1}^{M}\sum _{i\in \varOmega _{I}}\frac{q_{t}(g_{m,i}^{s})}{h_{m,i}^{2}}\end{aligned}$$

(9a)

$$\begin{aligned} \mathrm {s.t}&~~\sum _{i\in \varOmega _{I}}r_{m,i} = D_{1},~~ m=1,2,...,M_{1},\nonumber \\&~~ \sum _{i\in \varOmega _{I}}r_{m,i} = D_{2}, ~~m=M_{1}+1, ~~ M_{1}+2,... M_{1}+M_{2},\nonumber \\&~~ ...\nonumber \\&~~ \sum _{i\in \varOmega _{I}}r_{m,i} = D_{t}, ~~m=M_{T-1}+1, ~~ M_{T-1}+2,... M_{T-1}+M_{T},\end{aligned}$$

(9b)

$$\begin{aligned}&~~ r_{m,i} = 2g_{m,i}^{1}+4g_{m,i}^{2}+6g_{m,i}^{3},~~ m=1,...,M,i\in \varOmega _{I},\end{aligned}$$

(9c)

$$\begin{aligned}&q_{t}(g_{m,i}^{s}) = 3\rho _{t}g_{m,i}^{1}+15\rho _{t}g_{m,i}^{2}+63\rho _{t}g_{m,i}^{3},~~ m=1,...,M, i\in \varOmega _{I},\end{aligned}$$

(9d)

$$\begin{aligned}&~~ \rho _{t} = \frac{N_{0}B}{3K}\left[ Q^{-1}(\frac{P_{e}^{t}}{4})\right] ^{2},~~ t =1,2...,T,\end{aligned}$$

(9e)

$$\begin{aligned}&~~ \sum _{s=1}^{3}g_{m,i}^{s}\le 1,~~ m=1,...,M,i\in \varOmega _{I},\end{aligned}$$

(9f)

$$\begin{aligned}&~~ g_{m,i}^{s} \in \{0,1\},~~ s =1,2,3. \end{aligned}$$

(9g)

Constraint (9b) and (9c) guarantee the transmission rate of type I users. Constraint (9d), (9e), (9f) and (9g) are the relationship between BER and transmission power.

Problem (P2) is a standard binary linear programming (BLP), therefore we can use standard packages such as CPLEX [11] to solve it.

4.2 Resource Allocation for Type II Users

By using CPLEX package, we can obtain the power $P_{I}$ and subcarriers $\varOmega _{I}$ which are allocated to type I users. After that, the remaining resources are all allocated to type II users. The maximal weighted sum rate of type II users problem can be formulated as

$$\begin{aligned} (\mathbf P3 )&~~\max _{\{p_{n,j}, \tau _{n,j}\}} L \sum _{n=1}^{N}\omega _{n}R_{n}\end{aligned}$$

(10a)

$$\begin{aligned} \mathrm {s.t}&\sum _{n=1}^{N}\tau _{n,j}\le 1,~~ \tau _{n,j}\in \{0,1\}, j\in \varOmega _{II}, \end{aligned}$$

(10b)

$$\begin{aligned}&\sum _{n=1}^{N}\sum _{j\in \varOmega _{II}} \tau _{n,j} p_{n,j}\le P - P_{I},\end{aligned}$$

(10c)

$$\begin{aligned}&\varOmega _{I}+\varOmega _{II}\subseteq \varOmega ,\end{aligned}$$

(10d)

$$\begin{aligned}&LB_{II} \log _{2}\left( 1+\frac{P}{N_{0}B_{II}}\right) \le C_{f}-C_{I}, \end{aligned}$$

(10e)

where $B_{II}$ is the bandwith allocated to type II users by each RRH. And $C_{I}$ is the transmission capacity of type I users and it can be get from problem (P2). Constraint (10b) means one subcarrier only shared by one user. Constraint (10c) and (10d) are the system power and subcarriers constraints. Constraint (10e) is the fronthaul capacity constraint.

4.3 Resource Allocation for Type II Users Without Fronthaul Constraint

For convenience, we denote problem (P3) without fronthaul constraint (2) as problem (P3-1), which is a MINLP problem. In this subsection, we use time-sharing and alternating methods to solve this problem [12].

Problem (P3-1) with Time-Sharing: For constraint (10b), we relax it firstly,

$$\begin{aligned} \sum _{n=1}^{N}\tau _{n,j}\le 1, \tau _{n,j}\in [0,1],~~ j\in \varOmega _{II}. \end{aligned}$$

(11)

And then, we use alternating method to solve problem (P3-1) with time-sharing by considering two problems: one for tuning the allocated power for given time-share values and the other for tuning time-share values for given fixed power allocation.

Proposition 1

For given fixed allocated time-share values, the optimal power allocation is

$$\begin{aligned} p_{n,j} = \max \left( \frac{L\omega _{n}\frac{B}{K}}{\lambda _{n}\ln 2}-N_{0}\frac{B}{K},0\right) , \end{aligned}$$

(12)

where $\lambda _{n}$ are the Lagrange multipliers.

Proof

Due to the limited pages, we can easily get (12) by using the dual decomposition method [9].    $\square$

The power allocation $p_{n,j}$ is instantaneous power. The average power used by the user on this subcarrier is $q_{n,j} = p_{n,j}\tau _{n,j}$. Now, we fix the average power $q_{n,j}$ to tune time-share values.

For given fixed allocated average power, the optimal time-share variables are the solutions of the following optimization problem

$$\begin{aligned} \tau _{n,j} = \arg \max _{\tau _{n,j}} L\sum _{n=1}^{N}\sum _{j\in \varOmega _{II}}\omega _{n}\tau _{n,j}\frac{B}{K}\log _{2}\left( 1+\frac{q_{n,j}}{N_{0}\frac{B}{K}\tau _{n,j}}\right) , \end{aligned}$$

(13)

subject to the constraints (10d) and (11).

Proposition 2

For given fixed allocated power, the time-share values of (13) can be found by solving the following equations

$$\begin{aligned} u_{n}(y) = L\omega _{n}\frac{B}{K}\left( \log _{2}(1+y)-\frac{y}{\ln 2(1+y)}\right) = \beta _{n},~~y = \frac{q_{n,j}}{N_{0}\frac{B}{K}\tau _{n,j}}, \end{aligned}$$

(14)

where $u_{n}(y)$ is the utility function of user n and $\beta _{n}$ are the Lagrange multipliers.

Proof

Due to the limited pages, we can easily get (14) by using the dual decomposition method [9].    $\square$

Equation(14) means that for any given subcarrier the optimal time-share values should balance the utility function of the users. We propose an iterative algorithm to obtain the optimal time-share values.

For a given subcarrier j, set initial time-share values and calculate the time-share values for the fixed values of $q_{n,j}^{\bar{l}}$

$$\begin{aligned} \tau _{n,j}^{(\bar{t}+1)}=\frac{u_{n,j}^{\bar{t}}\tau _{n,j}^{\bar{t}}}{\Sigma _{n=1}^{N} u_{n,j}^{\bar{t}}\tau _{n,j}^{\bar{t}}},~~u_{n,j}^{\bar{t}}=u_{n}\left( \frac{q_{n,j}^{\bar{l}}}{N_{0}\frac{B}{K}\tau _{n,j}^{\bar{l}}}\right) . \end{aligned}$$

(15)

Proposition 3

For large enough number of iterations on $\bar{t}$, (15) will converge to the time-share optimal solution.

Proof

Equation (15) allocates new time-share proportional to the next utility function of users. Therefore, users with larger/smaller utilities will get more/less time-share values. It will make the overall utility increase every step. Moreover, there exists a fixed point corresponding to the balanced utilities. Hence, by increasing the number of iterations Eq. (15) will converge to its fixed point.    $\square$

4.4 Resource Allocation for Type II Users with Fronthaul Constraint

From the previous subsection, we get the resource allocation for type II users without fronthaul constraint. We define the optimal objective value of problem (P3-1) as $R_{II w/f}$ and define the optimal objective value of problem (P3) as $R_{II}^{*}$. Then, $R_{II}^{*}$ can be found as

$$\begin{aligned} R_{II}^{*}= {\left\{ \begin{array}{ll} R_{II w/f} &{}\qquad if ~ R_{II w/f}\le C_{f}-C_{I}\\ C_{f}-C_{I} &{}\qquad if~ R_{II w/f}\ge C_{f}-C_{I}. \end{array}\right. } \end{aligned}$$

(16)

4.5 Proposed Iterative Algorithm

According to the above analysis, we propose an algorithm to calculate problem (P1). The algorithm is presented as Algorithm 1.

5 Results and Discussions

In this section, simulations are made to confirm our analysis. The number of RRH is 1 and RRH transmission power is 5 w. The fronthaul capacity is 70 Mbps. The bandwidth is set 8 MHz and it is divided into 16 subcarriers. The bandwith of each subcarrier is 512 kHz. There are 2 type I users of two different service classes, i.e. $M_{1}=M_{2}=1$, which data rates are $D_{1}=6$, $D_{2}=8$ bits/OFDM symbol and the target BER values are $P_{e}^{1}= 10^{-2}$, $P_{e}^{2}= 10^{-4}$. The PSD level $N_{0}$ is $4\times 10^{-10}$ W/Hz.

5.1 Resource Allocation for Type I Users

In order to obtain the maximal weighted sum rate of type II users, we only need allocate minimum resources to type I users to guarantee theirs QoS requirements. The problem (P2) is to minimize the transmission power with satisfying the data rate and BER for type I users. To understand subcarrier and bit allocation for type I users. We give one allocated result at one snapshot of channel gain in Table 1. From this table, we can see the subcarrier allocation and constellation selection on each subcarrier for each user with every constraints fulfilled.

Table 1. Subcarrier and bit allocation at minimized transmit power. When $M_{1}=M_{2}=1$, $N=16$, $D_{1}=6,~D_{2}=8$ bits/OFDM symbol, $P_{e}^{1}=10^{-2},~P_{e}^{2}=10^{-4}$.

5.2 Resource Allocation for Type II Users

We compare the following algorithms with our proposed algorithm:

• Average power algorithm: A solution where subcarrier is optimal but power is allocated to each user averagely in each subcarrier at one snapshot.

• Average subcarrier algorithm: A solution where power allocation is optimal but subcarrier is allocated to each user averagely at one snapshot.

Fig. 2.

Weighted sum rate versus number of type II users under different resource allocation policies

Figure 2 illustrates the weighted sum rate versus number of type II users under different resource allocation policies. For the proposed algorithm, it can be seen that with the number of type II users increases, the weighted sum rate increases, which is because of the multiuser diversity. However, when the number of type II users reaches 5, the weighted sum rate can not increase, which is because that the resources are limited. For the average subcarrier algorithm, it can be seen that with the number of type II users increases, the weighted sum rate decreases. We can explain as follows: when the number of type II users increases, the number of deep fading users also increases, and these deep fading users occupy more subcarriers. And the power is allocated to the users who has been allocated subcarriers. Therefore, with the number of type II users increases, the weighted sum rate decreases. The average power algorithm has the same trend with the proposed algorithm, that is because all users are allocated power in these two algorithms.

Fig. 3.

Weighted sum rate versus number of type II users under different BER of type I users

Fig. 4.

Weighted sum rate versus number of type II users under different data rate of type I users

Figure 3 illustrates weighted sum rate versus number of type II users under different BER of type I users. From this figure we can see that with the BER value of type I users decreases, the weighted sum rate of type II users decreases. This is because when the BER value of type I users decreases, the RRH needs to allocate more power to type I users, so the weighted sum rate of type II users becomes low.

Figure 4 illustrates weighted sum rate versus number of type II users under different data rate of type I users. From this figure we can see that with the data rate of type I users increases, the weighted sum rate of type II users decreases. It is because that as the data rate of type I users increases, the RRH needs to allocate more subcarriers to type I users, so the weighted sum rate of type II users becomes low.

6 Conclusion

In this paper, we investigated the weighted sum rate maximization of type II users with joint QoS requirements of type I users and fronthaul capacity constraints in OFDMA-based C-RAN. To deal with the optimization problem, a MINLP problem was formulated. Because it is a non-convex problem, two subproblems were reformulated firstly. And then based on CPLEX package, time-sharing and alternating methods, an iterative algorithm was proposed. Simulation results have demonstrated that the proposed algorithm can achieve good performance.