High Order Semi-Lagrangian Particle Methods

Abstract

Semi-lagrangian (or remeshed) particle methods are conservative particle methods where the particles are remeshed at each time-step. The numerical analysis of these methods show that their accuracy is governed by the regularity and moment properties of the remeshing kernel and that their stability is guaranteed by a lagrangian condition which does not rely on the grid size. Turbulent transport and more generally advection dominated flows are applications where these features make them appealing tools. The adaptivity of the method and its ability to capture fine scales at minimal cost can be further reinforced by remeshing particles on adapted grids, in particular through wavelet-based multi-resolution analysis.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Accuracy Issues in Particle Methods

Particle methods are not in general associated with the concept of high accuracy. They are instead viewed as numerical models, able to reproduce qualitative features of advection dominated phenomena even with few particles, in particular in situations with strongly unsteady dynamics. Examples of early applications of particle methods which illustrate these capabilities in flow simulations are transition to turbulence in wall bounded flows [23] or the study of vortex reconnection [25]. Free surface or compressible flows are other examples where particle methods can give an intuitive qualitative understanding of the flow dynamics in situations where Direct Numerical Simulations with classical discretization methods would require prohibitive computational resources. This is in particular true for applications in computer graphics [17] or in astrophysics [12, 20].

The numerical analysis of particle methods allows to understand the accuracy issues that these methods face. Particle methods are based on the concept that Dirac masses give exact weak solutions to advection equations written in conservation form. For simple linear advection equations, the approximations of exact solutions by particles, measured on distribution spaces, therefore only relies on quadrature estimates for initial conditions and right hand sides. A typical error estimate for the solution U of an advection equation reads

$$\displaystyle{\|(\mathbf{U} -\mathbf{U}_{h})(\cdot,t)\|_{W^{-m,p}} \leq C_{1}\exp (C_{2}T)\,h^{m}}$$

for t ≤ T, where h is the initial inter-particle spacing, m is the order of the quadrature rule using particle initial locations as quadrature points, C ₁ and C ₂ are positive constants depending on the flow regularity, and W ^−m, p is the dual of W ^m, q, with 1∕p + 1∕q = 1. When one wishes to recover smooth quantities U _h ^ε from the Dirac masses carried by the particles, one needs to pay for the regularization involved in the process and a typical error estimate becomes:

$$\displaystyle{\|(\mathbf{U} -\mathbf{U}_{h}^{\epsilon })(\cdot,t)\|_{ L^{p}} \leq C(\,\epsilon ^{r} + h^{m}/\epsilon ^{m}),}$$

where r is the approximation order of the regularization used to mollify the particles (the reference [6] provide detailed proofs of the above estimates in the context of vortex methods).

This estimate immediately shows the dilemma of particle methods: the regularization size must be small, and controls the overall accuracy of the method, but it must contain enough particles so that the term h ^m∕ε ^m does not compromise the convergence of the method. This constraint is even more stringent if particles are involved in additional terms of the model, in particular pressure gradient terms (in compressible flows) or diffusion terms. In the later case error terms of the form h ^m∕ε ^m+2 arise. In any case, proper convergence would require, on top of ε → 0, that h∕ε → 0, the so-called overlapping condition. This condition is in practice difficult to satisfy, in particular for 3D flows. Instead, a constant ratio h∕ε is most often chosen in refinement studies.

On the other hand, even if the overlapping condition is not satisfied, particle methods still enjoy conservation properties and some kind of adaptivity which goes with the belief that “particles go where they are needed”. This belief is however often more a hand-waving argument than a reasonable assumption based on solid grounds. Figure 1 shows very simple examples which illustrate the shortcomings of particle methods in the simulation of 2D inviscid vortex flows. In this case the 2D Euler incompressible Euler equations in vorticity form

$$\displaystyle{{ \partial \omega \over \partial t} + \mbox{ div}\ (\mathbf{u}\omega ) = 0}$$

are discretized by particles of vorticity. In the left picture, a typical particle distribution is shown for an initial vorticity field with support in an ellipse. This figure shows that particles tend to align along directions related to the flow strain, creating gaps in the vorticity support. The right picture corresponds to an axisymmetric initial vorticity field, leading to a stationary solution. In this example ω ₀(x) = (1 − | x |²)³. Error curves, in the energy norm for the particle velocities, corresponding to h = h ₀ = 0. 1 and h = h ₀∕2 are plotted, with a constant ratio h∕ε. This figure shows that, despite the smoothness of the solution, the expected initial gain in accuracy is almost completely lost after a short time due to the distortion of the particle distribution.

Fig. 1

Simulation with a grid-free vortex particle methods [7]. Left picture: particle distribution in the simulation of an elliptical vortex patch. Right picture: error curves for a stationary axisymmetric vortex. Solid line h = 0. 005, dashed line h = 0. 01. ε∕h = 1. 5

Whenever point-wise values are required with some accuracy (for instance to recover satisfactory spectra in turbulent flows or local pressure or vorticity values on an obstacle) the overlapping condition cannot be ignored.

2 Remeshing and Semi-Lagrangian Particles

Although several methods have been considered to overcome the lack of overlapping of particles while keeping their grid-free nature, particle remeshing is to our knowledge the only tool which so far allowed to deliver in a clear-cut way accurate results for complex two and three-dimensional dynamics, in particular in incompressible flows. Remeshing was already used in early simulations for some specific flow topology, like vortex sheets [15] or filaments [19], but its first systematic use goes probably back to [13, 14], where pioneering results where obtained for flow past a cylinder at challenging Reynolds numbers and for the problem of axisymmetrization of elliptical vortices. The first numerical comparisons of these methods with spectral methods in 3D turbulent flows were performed in [9].

Remeshing consists of redistributing particle masses on nearby grid points, in a way that conserves as many moments of the particles as possible. The number of moments, and hence the accuracy, dictates the size of the remeshing kernel. Conserving the 3 first moments (including mass) in some sense guarantees that remeshing has not a diffusive net effect. This has been considered as a minimal requirement in the references already cited and in all following works.

The remeshing frequency can be a point of debate. However there are two aspects to consider. On the one hand remeshing a particle distribution which has already been highly distorted is likely to produce numerical noise. On the other hand, the time scale on which particles are distorted is the same as the one on which the particle advection should be discretized, namely 1∕ | ∇a | _∞ , where a is the advecting velocity field. It is therefore natural to remesh particles every few time-steps and numerical truncation errors coming from remeshing must be accounted for in the numerical analysis. Recently [10] particle methods have been analyzed from this point of view - in other words as semi-lagrangian methods.

To describe the method and discuss its accuracy, let us consider the 1D model linear advection problem - which is somehow the engine of particle methods in all applications:

$$\displaystyle{ \theta _{t} + (a\theta )_{x} = 0,x \in \mathbf{R},t> 0, }$$

(1)

where a is a given smooth velocity field. A particle method where particles are remeshed at each time step can be recast as

$$\displaystyle{ \theta _{i}^{n+1} =\sum \theta _{ j}^{n}\,\varGamma \left ({x_{j}^{\,n+1} - x_{ i} \over \varDelta x} \right ),i \in \mathbf{Z}^{d},n \geq 0. }$$

(2)

In the above equation Δx is the grid size on which particles are remeshed (assuming a regular grid), x _j are the grid points and Γ is the remeshing interpolating kernel. x _j ⁿ⁺¹ is the result of the advection at time t _n+1 of the particle located at x _j at time t _n .

Note that to generalize the method to several dimensions one may use similar formulas with remeshing kernels obtained by tensor products of 1D kernels (this is the traditional way) or, following [18], one can alternate the advection steps in successive directions, with classical recipes to increase the accuracy of the splitting involved in this process. This later method is economical when one uses high order kernels (with large supports) as, in 3D, its computational cost scales like O(3M) instead of O(M ³) for a kernel involving M points in each direction.

The moment conservation properties mentioned earlier to be satisfied by the remeshing kernel Γ can be expressed as

$$\displaystyle{ \sum _{k\in \mathbf{Z}}(x - k)^{\alpha }\varGamma (x-k) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\mbox{ if }\alpha = 0\\ 0\quad &\mbox{ if } 1 \leq \alpha \leq p \end{array} \right.,\,x \in \mathbf{R}, }$$

(3)

for a given value of p ≥ 1. An additional requirement is that Γ is globally in W ^r+1, ∞ and of class C ^∞ in each integer interval (in practice Γ is a polynomial in these intervals), and satisfies the interpolation property: Γ(i − j) = δ _ij . In the simple case of an Euler explicit scheme to advect particles, x _j ⁿ⁺¹ = x _j + a(x _j , t _n )Δt and when the time step satisfies the condition

$$\displaystyle{ \varDelta t <\vert a'\vert _{L^{\infty }}^{-1}, }$$

(4)

on can prove [10] that the consistency error of the semi-lagrangian method is bounded by O(Δt + Δx ^β) where β = min( p, r). Using higher order Runge-Kutta schemes increase the time accuracy, as expected. Moreover, at least for kernels of order up to 4, under appropriate decay properties for the kernel Γ one can prove for a large class of kernels the stability of the method under the sole assumption (4).

Let us give a sketch of the consistency proof for the case r = p = 1 if a is only a function of x and the Euler scheme is used to advance particles. We start from (2) and assume that θ _j ⁿ = θ(x _j , t _n ) where θ is the exact smooth solution to the advection equation and we want to prove that θ _i ⁿ⁺¹ = θ(x _i , t _n+1) + O(Δt ² + Δx ²).

We write j = i + k and, in (2),

$$\displaystyle{\theta _{j}^{n} =\theta _{ i}^{n} + k\varDelta x\,\theta _{ x}(x_{i},t_{n}) + O(\varDelta x^{2}).}$$

Particle advection with the Euler scheme gives

$$\displaystyle{x_{j}^{\,n+1} = x_{ j} + a_{j}\varDelta t = x_{i} + k\varDelta x + a_{i}\varDelta t + [a(x_{i} + k\varDelta x) - a(x_{i})]}$$

and thus

$$\displaystyle\begin{array}{rcl} \varGamma \left ({x_{j}^{\,n+1} - x_{i} \over \varDelta x} \right )& =& \varGamma \left (k +\lambda _{i} +\nu [a(x_{i} + k\varDelta x) - a(x_{i})]\right ) {}\\ & =& \varGamma (k +\lambda _{i}) + k\varDelta t\,a'(x_{i})\,\varGamma '(k +\lambda _{i}) + O(\varDelta x^{2}), {}\\ \end{array}$$

where we have used the notations

$$\displaystyle{\nu =\varDelta t/\varDelta x\;,\;\;\lambda _{i} = a_{i}\nu.}$$

We thus obtain

$$\displaystyle\begin{array}{rcl} \theta _{i}^{n+1} =\sum _{ k}\left [\theta (x_{i},t_{n}) + k\varDelta x\,\theta _{x}(x_{i},t_{n}) + O(\varDelta x^{2})\right ] {}\\ \left [\varGamma (k +\lambda _{i}) + k\varDelta t\,a'(x_{i})\,\varGamma '(k +\lambda _{i}) + O(\varDelta x^{2})\right ]. {}\\ \end{array}$$

The moment properties of order 0 and 1 yield

$$\displaystyle{\sum _{k}k\,\varGamma (k +\lambda _{i}) = -\lambda _{i}\;\;,\;\;\sum _{k}k\,\varGamma '(k +\lambda _{i}) = -1.}$$

We therefore have

$$\displaystyle\begin{array}{rcl} \theta _{i}^{n+1}& =& \theta (x_{ i},t_{n}) -\varDelta t\,a(x_{i})\,\theta _{x}(x_{i},t_{n}) -\varDelta t\,a'(x_{i})\,\theta (x_{i},t_{n}) + O(\varDelta t^{2} +\varDelta x^{2}) {}\\ \mbox{ }& =& \theta (x_{i},t_{n}) -\varDelta t(a\,\theta )_{x}(x_{i},t_{n}) + O(\varDelta t^{2} +\varDelta x^{2}) {}\\ \end{array}$$

and, by (1),

$$\displaystyle{\theta _{i}^{n+1} =\theta (x_{ i},t_{n+1}) + O(\varDelta t^{2} +\varDelta x^{2})}$$

which proves our claim.

In the general consistency result mentioned above, one can also check that the order of spatial accuracy is p whenever one can ensure that after the advection step each grid cell contains exactly one particle. [10] contains explicit expressions of kernels of order up to 6, denoted by Λ _p, r where p and r measure the moment and regularity properties of the kernel. It also contains a number of refinement studies which suggests that in practice for a kernel Λ _p, r the observed order of accuracy is between min( p, r) and p. Figure 2 shows the results of a typical refinement study on a 2D level set benchmark. This case consists of a level set function corresponding to a disk of radius 0. 15 centered at (0. 5, 0. 15) in the periodic box [0, 1]². The velocity field is given by

$$\displaystyle{ \mathbf{a}(x_{1},x_{2},t) = f(t)\left (-\sin ^{2}(\pi x_{ 1})\sin (2\pi x_{2}),\sin (2\pi x_{1})\sin ^{2}(\pi x_{ 2})\right ), }$$

(5)

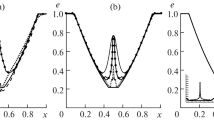
with f(t) = cos(πt∕12). This field produces a strong filamentation of the solution culminating at t = 6 then drives the solution back to its initial state at t = 12, where numerical errors can be recorded. The actual convergence rate observed in this example for the kernels Λ _2,1, Λ _4,2 and Λ _6,4 are respectively 1. 87, 3. 17 and 5. 92.

Fig. 2

Refinement study for the flow (5). CFL value is equal to 12. Black-circle curve : kernel Λ _2,1; red-square : kernel Λ _4,2; blue-triangle : kernel Λ _6,4; dashed lines indicate slopes corresponding to second and fourth order convergence

It is interesting to note that several authors have recently advocated the use of particle methods to correct dissipative effects of finite-difference of finite-volume level set methods. Roughly speaking the idea is to seed particles at sub-grid levels near the interface and use these particles to rectify the location of the interface (see [17] for instance). However [10] shows that, both in 2D and 3D, plain semi-lagrangian particle methods, with appropriate remeshing kernels (second order is actually enough) deliver better results with fewer points and larger time-steps.

The possibility of combining high accuracy with stability non constrained by the grid size makes semi-lagrangian particle methods appealing tools for turbulent transport. In [16] this was exploited to investigate universal scaling laws for passive scalars advected in turbulent flows. In this study the accuracy of particle methods was first compared to classical spectral methods. Figure 3 shows a typical comparison of scalar spectra and of the pdf of the scalar dissipation for a turbulent flow. In this experiment a second order kernel was used for the particle method. These results, and several other diagnostics, indicate that except for the very tail of the spectra most of the scales are well captured by the particle method with the same resolution as for the spectral method. A factor 1. 2 between the grids was found sufficient to resolve satisfactorily the scalar also in the dissipative range. In the case of high Schmidt numbers (ratio between flow viscosity and scalar diffusivity) even with this requirement for slightly increased resolution, the gain in CPU time over the spectral method resulting from the use of large time steps in the particle method reached a factor 80.

Fig. 3

Comparison of spectral and particle methods in a turbulent flow with a Schmidt number equal to 50 [16]. Top picture: spectra of the scalar variance. Bottom picture: pdf of the scalar dissipation. Red curves: spectral method with 1024³ points; green curves: particle method with 1024³ points; blue curves: particle method with 1280³ points

3 Adaptive Semi-Lagrangian Particles

Remeshing particles somehow detracts particle methods from self adaptivity (however illusive that notion might be, as we have seen). To restore some kind of adaptivity in the method it is natural to rely on the grid on which particles are remeshed. Like for grid-based methods, one may envision several ways of doing so. One way is to assume a priori that grid refinement is desirable in some parts of the flow, typically zones which are close to fixed boundaries. Another way is to adapt the grid to the smoothness of the solution itself.

3.1 Semi-Lagrangian Particle Methods on Non-Uniform Grids

In that case we assume that a non-uniform grid (the physical space) is obtained by a predefined mapping from a cartesian uniform grid (the reference space). The method works as follows [8]. At each time step, particles are pushed in the physical space, then mapped in the reference space. In this space regular remeshing formulas are used on cartesian grids, and particle locations are meshed back to the physical space. Figure  4 is an illustration of this method in the context of 2D vortex particle methods for the simulation of the rebound of a vortex dipole impinging on a wall. In this example the grid is stretched in both directions in an exponential manner with respect to the distance to the wall. Applications in 3D flows of similar technics can for instance be found in [21].

Fig. 4

Vortex dipole impinging on a wall [8]. Top pictures: results at two successive times with remeshing on an exponentially stretched grid. Bottom pictures: results with uniform grids at the later time for the coarsest (left) and finest (right) grids. Only a small percentage of the active particles are shown by dots

3.2 Particle Methods with Adaptive Mesh Refinement

Particle remeshing also enables to incorporate Adaptive Mesh Refinement (AMR) finite difference techniques [2] to adapt the particle discretization to the solution itself. Bergdorf et al. [3] describes how to define, move and remesh patches of particles at different resolution in a consistent way. Figure 5 illustrates how the method allows to capture filaments ejected by an elliptical vortex in a 2D inviscid flow. In this example the refinement was based on the vorticity gradients. We do not enter more into the details of this method as we believe that it is outperformed by the more recent wavelet-based method described below.

Fig. 5

Blocks of refined particles in an AMR implementation of particle methods for the simulation of an elliptical vortex [3]

3.3 Wavelet-Based Multi-Level Particle Methods

The concept of multi-resolution semi-lagrangian particle methods was recently pushed further in [4], using wavelet tools. The idea of combining particle and wavelet methods can actually already been found in [1]. In this reference wavelet served as particle shapes in a grid-free method. The method however did not find practical ways to address the issue of interacting and recombining wavelets. In [4] instead, because particles are remeshed at every time-step on regular grids, particle methods can inherit concepts and techniques used in the context of finite-difference methods (see for instance [24]). Nonetheless the semi-lagrangian character of the method introduces original and interesting features. To describe the method and understand how it works, let us consider again the 1D advection equation on the real line, first with constant velocity then in the general case. The multi-dimensional case and the application to incompressible flows will be next outlined.

We consider Eq. (1). The method is based on the following classical wavelet decomposition, in the framework of interpolating bi-orthogonal wavelets [5]:

$$\displaystyle{ \theta (x) =\sum _{j}c_{k}^{0}\phi _{ j}^{0}(x) +\sum _{ j}\sum _{l=l_{0}}^{L-1}d_{ j}^{l}\psi _{ k}^{l}(x) }$$

(6)

where l ₀ (resp. l = L) corresponds to the coarsest (resp. finest) level. In the above equation ϕ _j ^l and ψ _j ^l are respectively the scaling and wavelet (or detail) basis functions, centered around the grid point x _j ^l = jΔx _l , where $\varDelta x_{l} = 2^{L_{0}-l}\varDelta x_{0}$ is the grid size at level l. This decomposition allows to define the solution at the different scales :

$$\displaystyle{ \theta _{l}(x) =\sum _{j}c_{j}^{l}\,\phi _{ j}^{l}(x). }$$

(7)

Scale and detail coefficients are related between successive levels through classical filtering operations:

$$\displaystyle{ c_{i}^{l} =\sum _{ j}\tilde{h}(2i-j)c_{j}^{l+1},d_{ i}^{l} =\sum _{ j}\tilde{g}(2i-j)c_{j}^{l+1},c_{ i}^{l+1} =\sum _{ j}[h(2j-i)c_{j}^{l}+g(2j-i)d_{ j}^{l}] }$$

(8)

where the filter functions g, h, $\tilde{g}$, $\tilde{h}$ depend on the particular wavelet system chosen.

Let us now describe one time-step of the algorithm, first for a constant velocity value. The methods advances the solution scale by scale in the following manner. Assume at time t _n = nΔt the solution is known on grid points belonging to the nested grids (x _j ^l) _j, l . For each level l ∈ [L ₀, L]

• a wavelet analysis selects grid points which correspond to detail coefficients d _j ^l above a given threshold

• particles are initialized on these grid points with, for grid values, the corresponding scale parameters c _j ^l

• particles are pushed and remeshed on the grid (x _k ^l) _k .

For the remeshing step above to be consistent one needs to ensure that active particles are always surrounded by “enough” particles carrying consistent values of θ _l . This is done in a way similar to what would be done in a finite-difference method by creating ghost particles in the neighborhood of the active particles. The values of the solution assigned at time t _n to these grid points is obtained by interpolation from θ _l−1. In order to make sure that only relevant values at level l are retained at the end of the iteration, a tag value equal to 0 is assigned to the ghost particles while the value 1 is assigned to the active particles. These tag values are pushed and remeshed along with the particles. After remeshing, only particles with tag values different from 0 are retained.

Finally, when all active particles have been moved and remeshed at all scales, values of the function at a given scale are updated by values at the next scale on even points when available.

Figure 6 illustrates the method in the case of a translating top-hat profile. The remeshing kernel is Λ _2,1 which for a constant velocity corresponds to a second order method. The scaling function is a piecewise linear function and the detail coefficients correspond to central finite-differences of the second derivatives. In the left picture we compare, after the time needed to travel 15 times the width of the top-hat, the results obtained with uniform one-level resolution at Δx ₀ = 0. 01 and Δx ₁ = 0. 005 and the wavelet-based method using these two levels. For the two-level case, only the coarse resolution is showed together with active particles at the higher resolution. One can see that all solutions exhibit overshoots, as expected from a second order method, but the two-level solution limits the overshoot even at the coarse level and is very close to the higher resolution solution. The number of active particles, shown on the right picture of the figure, increases to respond to the oscillations created by the remeshing, then stabilizes.

Fig. 6

Advection of top-hat profile in a uniform field by a 2-level particle method. Left picture: black curve: result for uniform coarse resolution; blue curve: result at the coarsest level for a 2-level method; red squares active particle at the fine level. Right picture: number of active particles as a function of time

Let us now consider the case of a non uniform velocity. In this case, scales are not advected in an independent fashion but interact as a result of compression and dilatation. To allow fine scales to appear from coarse scales, there are two options. The first one is similar to what would be done in a finite difference method [24]. It consists of considering for each scale at the beginning of each step additional ghost particles at the level immediately above on which values of solutions are interpolated from the coarse scale. Another option, simpler and more specific to particle methods, is to remesh each scale on a scale twice smaller. At the end of the time-step, the value of the solution on this smaller scale is chosen to be either the result of the remeshing either of the coarse grid or the fine grid, depending on the value of the flag described earlier.

It is important to note that, in both options, the time scale on which the scale l + 1 appears from scale l is governed by 1∕ | a′ | _∞ which is consistent with the maximum time step allowed for the particle method. In other words for time steps corresponding to large CFL numbers, only scale l + 1 can appear form scale l if the condition (4) is satisfied. Figure 7 illustrates the method for two scales for an initial condition consisting on a sine wave advected in a velocity given by a(x) = 1 + cos(2πx). As the wave travels to the right it is subject to successive compressions/amplification and dilatation/damping. As a result, the number of active particles oscillates (right picture). The left picture shows that the adaptive method allows to recover the high resolution results.

Fig. 7

Multilevel particle method in a compression/dilatation flow. See Fig. 6 for captions

To go beyond the 1d toy problem just considered, there are again two options. One is to use the same ideas but to rely on multidimensional tensor product wavelets, with the added complexity that one grid point is associated to several wavelets. This is the option followed in [4]. The other one, presumably simpler and which only uses 1D wavelets, would be to split advection into three successive directional advections, along the lines of [18].

In vortex flows, where these methods have been primarily applied, an additional work is to compute velocities created by multi-level vortices. The solution chosen in [4] is to use a fast multipole method, where each particle associated to the value of the solution and the associated grid size is accounted for in the Biot Savart law. The left picture of Fig. 8 illustrates the method for the flow around swimming fishes [11]. The power of the method is here fully apparent. The complex geometries and the associated boundary conditions are dealt with by a penalization method an the nested multi-level cartesian grids allow to capture at a minimal cost the fine vortices created by the swimmers, despite the low accuracy of the penalization method. This method has been implemented for both 2D and 3D geometries [22]. It has been in particular applied in combination with optimization technics to determine efficient swimming strategies [11].

Fig. 8

Multi-level vorticity particle method with penalization around complex geometries. Top figure: 2D calculation around multiple fishes. Bottom picture: 3D vorticity passed a wind turbine (from [22])

4 Conclusion

Particle methods with particle remeshing at each time-step can be analyzed as semi-lagrangian conservative methods. The accuracy of the method is governed by moment and regularity properties of the remeshing kernel and high order kernels can be derived in a systematic fashion. Adaptivity in the method can be reinforced in particular by using wavelet-based multi-resolution analysis. In any case, the semi-lagrangian nature of the method allows to use time-steps which are not constrained by the grid size. In many applications this can lead to substantial computational savings.