hp-Version Discontinuous Galerkin Approximations of the Elastodynamics Equation

Abstract

In this paper we extend the results contained in Antonietti et al. (J Sci Comput 68(1):143-170, 2016) and consider the problem of approximating the elastodynamics equation by means of hp-version discontinuous Galerkin methods. For the resulting semi-discretized schemes we derive stability bounds as well as hp error estimates in the energy and L ²-norms. Our theoretical estimates are verified through three dimensional numerical experiments.

1 Introduction

The present paper deals with the numerical modeling through the (linear) elastodynamics equation of seismic wave propagation phenomena in complex, three-dimensional media. Currently, the numerical methods mostly employed to tackle seismic wave propagation include finite differences, pseudo-spectral, spectral element, and high–order/spectral element discontinuous (DG) Galerkin techniques. In particular Spectral Element methods, firstly introduced for fluid dynamics problems in the seminal paper [28], have become one of the most effective and powerful approaches for solving three-dimensional seismic wave propagation problems in strongly heterogeneous media thanks to their geometrical flexibility and high order accuracy, which made them well suited to correctly approximate the wave field. We refer to [14, 20, 22, 25, 35] for the first development of Spectral Element methods for the elastodynamics equation, and, for example, to [21, 23, 36, 39] for its application in computational seismology. In recent years, displacement-based high–order/spectral element discontinuous Galerkin methods have also been developed for linear and nonlinear (visco) elastic wave propagation problems, mainly because the discretization parameters, i.e. the mesh-size and/or the polynomial approximation degree, can be naturally tailored to the region of interests; see e.g. [3–6, 12, 24, 26, 31–33]. Additionally, high–order/spectral element DG methods feature very low dispersion and dissipation errors. A dispersion/dissipation analysis based on the approach of [1] for DG approximations of elastic wave propagation problems has been carried out in [3, 11] and [4], respectively, on two-dimensional quadrilateral/triangular meshes: the extension to three-dimensions has been addressed recently in [15]. Another interesting feature is their being embarrassingly parallel and therefore naturally oriented towards high performance parallel computing. DG methods are thus very well suited to deal with i) the intrinsic multi-scale nature of seismic wave propagation problems, involving a relative broad range of wavelengths; ii) the complexity of the geometrical constraints. The aim of this paper is to extend to the hp-version the theoretical analysis developed in [5] as well as to prove approximation bounds in the L ² norm. For the sake of brevity, here we focus only on displacement DG formulation, but the present analysis can be extended also to displacement-stress formulations. We show that, also in the hp-version setting, stability and approximation properties hold without the need to introduce an extra term that penalizes the time derivative of the displacement besides the displacement itself, as considered in previous works [31–33]. Our semidiscrete analysis represents an intermediate but essential step towards the analysis of stability of the fully discrete scheme resulting after time integration.

The remaining part of manuscript is organized as follows. In Sect. 2 we introduce the model problem and its hp-version discontinuous Galerkin approximation. The stability analysis is presented in Sect. 3, whereas in Sect. 4 we present the hp−version a priori error estimates in both the energy and L ² norms. Three-dimensional numerical experiments verifying the theory are presented in Sect. 5.

2 Problem Statement and its hp-Version Discontinuous Galerkin Approximation

Let Ω ⊂ R ^d, d = 2, 3, be an open, bounded convex region with Lipschitz boundary ∂Ω. Throughout the paper, [H ^m(Ω)]^d and [H ^m(Ω)]_sym ^d×d denote the standard Sobolev spaces of vector–valued and symmetric tensor-valued functions defined over Ω, respectively, and (⋅ , ⋅ ) _Ω denote the standard inner product in any of the spaces [L ²(Ω)]^d or [L ²(Ω)]_sym ^d×d. For given T > 0 and f = f(x, t) ∈ L ²((0, T]; [L ²(Ω)]^d), we consider the problem of approximating the variational formulation of the linear elastodynamics equation with homogeneous Dirichlet boundary conditions: for all t ∈ (0, T] find u = u(t) ∈ V ≡ [H ₀ ¹(Ω)]^d such that:

$$\displaystyle{ (\rho \mathbf{u}_{tt},\mathbf{v})_{\varOmega } + (\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{u}),\boldsymbol{\varepsilon }(\mathbf{v}))_{\varOmega } = (\mathbf{f},\mathbf{v})_{\varOmega }\qquad \qquad \forall \,\mathbf{v} \in \mathbf{V}, }$$

(1)

subjected to the (regular enough) initial conditions u ₀ and u ₁. Here, $\mathbf{u}:\varOmega \times [0,T]\longrightarrow \mathbb{R}^{d}$ is the displacement vector field and $\boldsymbol{\varepsilon }(\mathbf{u}):\varOmega \longrightarrow \mathbb{R}_{\mathrm{sym}}^{d\times d}$ is the symmetric gradient. Moreover, ρ is the mass density, which is supposed to be a strictly positive and uniformly bounded function, and $\mathcal{D} = \mathcal{D}(x): \mathbb{R}_{\mathrm{sym}}^{d\times d}\longrightarrow \mathbb{R}_{\mathrm{sym}}^{d\times d}$ is the inverse of the compliance tensor defined as $\mathcal{D}\boldsymbol{\tau } = 2\mu \boldsymbol{\tau } +\lambda \mathrm{ tr}(\boldsymbol{\tau })\mathbb{I}\quad \forall \,\boldsymbol{\tau } \in \mathbb{R}_{\mathrm{sym}}^{d\times d}$. $\mathbb{I} \in \mathbb{R}^{d\times d}$ and tr(⋅ ) are the identity and trace operators, respectively, and λ, μ ∈ L ^∞(Ω), λ, μ > 0, being the Lamé parameters.

Henceforth, C denotes a generic positive constant independent of the discretization parameters, but that can depend on the physical quantities ρ, $\mathcal{D}$ as well as on the final observation time T. Moreover, $x\lesssim y$ and $x\gtrsim y$ will signify x ≤ Cy and x ≥ Cy, respectively, with C as before.

2.1 Mesh, Trace Operators, and Discrete Spaces

We consider a sequence $\left \{\mathcal{T}_{h}\right \}_{h}$ of shape-regular (not-necessarily matching) partitions of Ω into disjoint open elements K such that $\overline{\varOmega } = \cup _{K\in \mathcal{T}_{h}}\overline{K}$, where each $K \in \mathcal{T}_{h}$ is the affine image of a fixed master element $\widehat{K}$, i.e., $K = F_{K}(\widehat{K})$, $\widehat{K}$ being either the open unit d-simplex or the open unit hypercube in $\mathbb{R}^{d}$, d = 2, 3. An interior face (for d = 2, “face” means “edge”) of $\mathcal{T}_{h}$ is defined as the (non–empty) interior of $\partial \overline{K}^{+} \cap \partial \overline{K}^{-}$, where K ^± are two adjacent elements of $\mathcal{T}_{h}$. Similarly, a boundary face of $\mathcal{T}_{h}$ is defined as the (non-empty) interior of $\partial \overline{K} \cap \overline{\varOmega }$, where K is a boundary element of $\mathcal{T}_{h}$. We collect the interior and boundary faces in the sets $\mathcal{F}_{h}^{I}$ and $\mathcal{F}_{h}^{B}$, respectively, and define $\mathcal{F}_{h} = \mathcal{F}_{h}^{I} \cup \mathcal{F}_{h}^{B}$. We also assume the following mesh-regularity: i) for any $K \in \mathcal{T}_{h}$ and for all $F \in \mathcal{F}_{h}$, F ⊂ ∂K, $h_{K}\lesssim h_{F}$; ii) for any pair of elements $K^{\pm }\in \mathcal{T}_{h}$ sharing a (d − 1)–dimensional face $h_{K^{-}}\lesssim h_{K^{+}}\lesssim h_{K^{-}}$: cf. [16, 29] for example.

Next, we introduce suitable trace operators, cf. [8]. Let F be an interior face shared by two elements K ^± of $\mathcal{T}_{h}$, and let n ^± denote the normal unit vectors on F pointing outward K ^±, respectively. For (regular enough) vector-valued and symmetric tensor-valued functions v and $\boldsymbol{\tau }$, respectively, we define the weighted average and jump operators as

$$\displaystyle{ \begin{array}{llllll} &\{\mathbf{v}\}_{\delta } =\delta \mathbf{v}^{+} + (1-\delta )\mathbf{v}^{-}, &\{\boldsymbol{\tau }\}_{\delta } & =\delta \boldsymbol{\tau }^{+} + (1-\delta )\boldsymbol{\tau }^{-}, &&\delta \in [0,1], \\ &[\![\mathbf{v}]\!] = \mathbf{v}^{+} \odot \mathbf{n}^{+} + \mathbf{v}^{-}\odot \mathbf{n}^{-},&[\![\boldsymbol{\tau }]\!]& = \boldsymbol{\tau }^{+}\,\mathbf{n}^{+} + \boldsymbol{\tau }^{-}\,\mathbf{n}^{-},&&\end{array} }$$

(2)

where v ^± and $\boldsymbol{\tau }^{\pm }$ denote the traces of v and $\boldsymbol{\tau }$ on F taken within the interior of K ^±, respectively, and where v ⊙ n = (vn ^T + nv ^T)∕2. Notice that [​[v]​] is a symmetric tensor-valued function. On a boundary face $F \in \mathcal{F}_{h}^{B}$, we set analogously

$$\displaystyle{ \begin{array}{c} \{\mathbf{v}\}_{\delta } = \mathbf{v},\qquad \{\boldsymbol{\tau }\}_{\delta } = \boldsymbol{\tau },\qquad [\![\mathbf{v}]\!] = \mathbf{v} \odot \mathbf{n},\qquad [\![\boldsymbol{\tau }]\!] = \boldsymbol{\tau }\mathbf{n}. \end{array} }$$

(3)

When δ = 1∕2, we drop the subindex and simply write {⋅ }.

Finally, to any element $K \in \mathcal{T}_{h}$ we assign a polynomial approximation degree p _K ≥ 1, and define the hp-discontinuous finite element space

$$\displaystyle{ \mathbf{V}_{hp} =\{ \mathbf{u} \in [L^{2}(\varOmega )]^{d}\:\ \mathbf{u} \circ F_{ K} \in [\mathbb{M}^{p_{K} }(\widehat{K})]^{d}\quad \forall \ K \in \mathcal{T}_{ h}\}, }$$

where $\mathbb{M}^{p_{K}}(\widehat{K})$ is either the space $\mathbb{P}^{p_{K}}(\widehat{K})$ of polynomials of degree at most p _K on $\widehat{K}$, if $\widehat{K}$ is the reference d-simplex, or the space $\mathbb{Q}^{p_{K}}(\widehat{K})$ of tensor–product polynomials on $\widehat{K}$ of degree p _K in each coordinate direction, if $\widehat{K}$ is the unit reference hypercube in $\mathbb{R}^{d}$. In the following we also assume that the following local bounded variation holds: $p_{K^{-}}\lesssim p_{K^{+}}\lesssim p_{K^{-}}$ for any pair of elements $K^{\pm }\in \mathcal{T}_{h}$ sharing a (d − 1)–dimensional face, cf. [29] for example.

Given a face $F \in \mathcal{F}_{h}$ of an element $K \in \mathcal{T}_{h}$, i.e., F ⊂ ∂K the following inverse inequality holds:

$$\displaystyle{ \begin{array}{c} \|v\|_{L^{2}(F)}^{2}\lesssim \frac{p_{K}^{2}} {h_{K}} \|v\|_{L^{2}(K)}^{2}\qquad \forall v \in \mathbb{M}^{p_{K}}(K), \end{array} }$$

cf. [34]. Finally, we recall the following interpolation estimates, cf. [9].

Lemma 1

For any real number s _K ≥ 0 and for any function $\mathbf{v} \in [H^{s_{K}}(K)]^{d}$ , $K \in \mathcal{T}_{h}$ , there exists Π _h v ∈ V _hp such that

$$\displaystyle{ \begin{array}{rlll} \sum \limits _{K\in \mathcal{T}_{h}}\|\mathbf{v} -\varPi _{hp}\mathbf{v}\|_{H^{r}(K)} & \lesssim \sum \limits _{K\in \mathcal{T}_{h}}\frac{h_{K}^{\min (s_{K},p_{K}+1)-r}} {p_{K}^{s_{K}-r}} \|\mathbf{v}\|_{H^{s_{K}}(K)} & & \forall r,\,0 \leq r \leq s, \\ \sum \limits _{K\in \mathcal{T}_{h}}\|D^{\xi }(\mathbf{v} -\varPi _{hp}\mathbf{v})\|_{L^{2}(\partial K)} & \lesssim \sum \limits _{K\in \mathcal{T}_{h}}\frac{h_{K}^{\min (s_{K},p_{K}+1)-\left \vert \xi \right \vert -1/2}} {p_{K}^{s_{K}-\left \vert \xi \right \vert -1/2}} \|\mathbf{v}\|_{H^{s_{K}}(K)} & & \forall \xi,\,0 \leq \left \vert \xi \right \vert \leq k, \end{array} }$$

(4)

where $\xi \in \mathbb{N}_{0}^{d}$ is a multi-index of length $\left \vert \xi \right \vert$ . Here, the second inequality holds provided s _K > 1∕2 and k is the largest non-negative integer strictly less than s − 1∕2.

2.2 Semi-Discrete and Fully-Discrete Formulations

We are now ready to state the semi-discrete weak formulation: For any time t ∈ (0, T], find u ^h = u ^h(t) ∈ V _hp such that

$$\displaystyle{ (\rho \mathbf{u}_{tt}^{h},\mathbf{v})_{\mathcal{ T}_{h}} + \mathcal{A}(\mathbf{u}^{h},\mathbf{v}) = (\mathbf{f},\mathbf{v})_{\mathcal{ T}_{h}}\quad \forall \,\mathbf{v} \in \mathbf{V}_{hp}, }$$

(5)

subjected to the initial conditions u ₀ ^h and u ₁ ^h, being u ₀ ^h, u ₁ ^h ∈ V _hp suitable approximations in V _hp of the initial data u ₀, u ₁, respectively. The bilinear form $\mathcal{A}(\cdot,\cdot ):$ $\mathbf{V}_{hp} \times \mathbf{V}_{hp}\longrightarrow \mathbb{R}$ in (16) is given by

$$\displaystyle\begin{array}{rcl} \mathcal{A}(\mathbf{w},\mathbf{v}) = (\boldsymbol{\varepsilon }(\mathbf{w}),\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{v}))_{\mathcal{T}_{h}}& -& \langle \{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{w})\}_{\delta },[\![\mathbf{v}]\!]\rangle _{\mathcal{F}_{h}} \\ & & \qquad -\langle [\![\mathbf{w}]\!],\{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{v})\}_{\delta }\rangle _{\mathcal{F}_{h}} +\langle \sigma [\![\mathbf{w}]\!],[\![\mathbf{v}]\!]\rangle _{\mathcal{F}_{h}},{}\end{array}$$

(6)

where we have used the shorthand notation $(\mathbf{w},\mathbf{v})_{\mathcal{T}_{h}} =\sum _{K\in \mathcal{T}_{h}}(\mathbf{w},\mathbf{v})_{K}$ and $(\mathbf{w},\mathbf{v})_{\mathcal{F}_{h}} =\sum _{F\in \mathcal{F}_{h}}(\mathbf{w},\mathbf{v})_{F}$. The above method corresponds to the family of Interior Penalty (IP) methods: for δ = 1∕2, we get the Symmetric Interior Penalty (SIP) method [7, 41], whereas for δ ≠ 1∕2 we obtain the weighted SIP method of Stenberg, [38]. In (6) the stabilization function $\sigma \in L^{\infty }(\mathcal{F}_{h})$ is defined facewise as

$$\displaystyle{ \sigma =\sigma (x) = \left \{\begin{array}{llll} &\alpha \{\mathcal{D}\}\frac{\max (p_{K^{+}}^{2},p_{ K^{-}}^{2})} {\min (h_{K^{+}},h_{K^{-}})} & & \mathrm{if}\,x \in \partial \overline{K^{+}} \cap \partial \overline{K^{-}}, \\ &\alpha \{\mathcal{D}\}\frac{p_{K}^{2}} {h_{K}} & & \mathrm{if}\,x \in \partial \overline{K} \cap \partial \varOmega, \end{array} \right. }$$

(7)

By defining $[H^{s}(\mathcal{T}_{h})]^{d}$ as the space of elementwise [H ^s(K)]^d functions, s ≥ 0, and endowing the V _hp and $\mathbf{V}_{hp} + [H^{2}(\mathcal{T}_{h})]^{d}$ spaces with the (mesh-dependent) norms

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{v}\|_{\mathrm{DG}}^{2} =\| \mathcal{D}^{1/2}\boldsymbol{\varepsilon }(\mathbf{v})\|_{L^{2}(\mathcal{T}_{h})}^{2} +\|\sigma ^{1/2}[\![\mathbf{v}]\!]\|_{L^{2}(\mathcal{F}_{h})}^{2} & & \forall \mathbf{v} \in \mathbf{V}_{hp}, \\ &\|\!\vert \mathbf{v}\vert \!\|_{\mathrm{DG}}^{2} =\| \mathbf{v}\|_{\mathrm{DG}}^{2} +\|\sigma ^{-1/2}\{\boldsymbol{\varepsilon }(\mathbf{v})\}\|_{L^{2}(\mathcal{F}_{h})}^{2} & & \forall \mathbf{v} \in \mathbf{V}_{hp} + [H^{2}(\mathcal{T}_{h})]^{d}, \end{array} }$$

(8)

respectively, with $\|\mathbf{w}\|_{L^{2}(\mathcal{T}_{h})} = \sqrt{(\mathbf{v}, \mathbf{v} )_{\mathcal{T} _{h }}}$ and $\|\mathbf{w}\|_{L^{2}(\mathcal{F}_{h})} = \sqrt{(\mathbf{v}, \mathbf{v} )_{\mathcal{F} _{h }}}$, with standard arguments it is easy to prove the following result.

Lemma 2

The bilinear form $\mathcal{A}(\cdot,\cdot ): \mathbf{V}_{hp} \times \mathbf{V}_{hp}\longrightarrow \mathbb{R}$ defined as in  (6) satisfies

$$\displaystyle{ \begin{array}{lllll} &\left \vert \mathcal{A}(\mathbf{w},\mathbf{v})\right \vert \lesssim \|\mathbf{v}\|_{\mathrm{DG}}\|\mathbf{w}\|_{\mathrm{DG}},&\mathcal{A}(\mathbf{v},\mathbf{v})\gtrsim \|\mathbf{v}\|_{\mathrm{DG}}^{2} & & \forall \mathbf{w},\mathbf{v} \in \mathbf{V}_{hp},\\ \end{array} }$$

(9)

where the second estimates holds provided that the penalty parameter α is chosen large enough, cf. (7). Moreover,

$$\displaystyle{ \begin{array}{llll} &\left \vert \mathcal{A}(\mathbf{w},\mathbf{v})\right \vert \lesssim \|\!\vert \mathbf{v}\vert \!\|_{\mathrm{DG}}\|\!\vert \mathbf{w}\vert \!\|_{\mathrm{DG}},&&\forall \mathbf{w},\mathbf{v} \in \mathbf{V}_{hp} + [H^{2}(\mathcal{T}_{h})]^{d}. \end{array} }$$

We remark that a sharp estimate on the minimum value α so that the second estimate in (9) holds can be obtained based on employing the results of [2].

The semi-discrete algebraic formulation of problem (16) reads as

$$\displaystyle{ \mathbf{M}\ddot{\mathbf{U}}(t) + \mathbf{A}\mathbf{U}(t) = \mathbf{F}(t), }$$

(10)

supplemented with initial conditions U(0) = U ⁰ and $\dot{\mathbf{U}}(0) = \mathbf{V}^{0}$. The vector U = U(t) contains, for any time t, the expansion coefficients of u _h (t) ∈ V _hp in a chosen basis. Analogously, M and A are the matrix representations of the mass and stiffness bilinear forms, respectively. By fixing a time-step Δt > 0 and denoting by U ⁱ ≈ U(t _i ) the approximation of U at time t _i = iΔt, we discretize (10) by the leap-frog method

$$\displaystyle{ \begin{array}{rlll} \mathbf{M}\mathbf{U}^{n+1} & = (2\mathbf{M} -\varDelta t^{2}\mathbf{A})\mathbf{U}^{n} -\mathbf{M}\mathbf{U}^{n-1} +\varDelta t^{2}\mathbf{F}^{n},&&n = 1,\ldots. \end{array} }$$

with $\mathbf{M}\mathbf{U}^{1} = (\mathbf{M} -\frac{\varDelta t^{2}} {2} \mathbf{A})\mathbf{U}^{0} +\varDelta t\mathbf{M}\mathbf{V}^{0} + \frac{\varDelta t^{2}} {2} \mathbf{F}^{0}$.

3 Stability of the Semi-Discrete Formulation

We now prove stability in the following natural energy norm induced by the DG methods described in the previous section:

$$\displaystyle{ \begin{array}{llllll} &\|\mathbf{v}\|_{\mathrm{E}}^{2} =\|\rho ^{1/2}\mathbf{v}_{t}\|_{0,\mathcal{T}_{h}}^{2} +\| \mathbf{v}\|_{\mathrm{DG}}^{2} & & \forall \mathbf{v} = \mathbf{v}(t) \in C^{2}([0,T];\mathbf{V}_{hp})&&\forall \in [0,T]. \end{array} }$$

(11)

First, we recall the following classical result, cf. [30, pag. 28].

Lemma 3

Let ξ ∈ L ²(0, T) a positive function and η ∈ C ⁰(0, T) a non-negative function such that

$$\displaystyle{ \begin{array}{llll} &\eta ^{2}(t) \leq C +\int _{ 0}^{t}\xi (\tau )\eta (\tau )\,d\tau &&\forall t \in (0,T) \end{array} }$$

with C a non-negative constant. Then,

$$\displaystyle{ \begin{array}{llll} &\eta (t) \leq \sqrt{C} + \frac{1} {2}\int _{0}^{t}\xi (\tau )\,d\tau &&\forall t \in (0,T) \end{array} }$$

For the forthcoming analysis we will assume that the (possible) discontinuities of the piecewise constant stiffness tensor $\mathcal{D}$ are aligned with the mesh partition $\mathcal{T}_{h}$.

Proposition 1

Let u ^h ∈ C ²((0, T]; V _hp ) be the approximate solution obtained with the SIP(δ) method  (16), for a sufficiently large penalty parameter α, cf. (7). Then,

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{u}^{h}(t)\|_{\mathrm{E}}^{2}\lesssim \|\mathbf{u}^{h}(0)\|_{\mathrm{E}} +\int _{ 0}^{t}\|\mathbf{f}(\tau )\|_{L^{2}(\varOmega )}\,d\tau &&0 <t \leq T. \end{array} }$$

Proof

We take v = u _t ^h ∈ V _hp in (16) to obtain

$$\displaystyle{ \frac{1} {2} \frac{d} {dt}\left (\|\mathbf{u}^{h}\|_{ \mathrm{E}}^{2} - 2\langle \{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{u}^{h})\}_{\delta },[\![\mathbf{u}^{h}]\!]\rangle _{\mathcal{ F}_{h}}\right ) = (\mathbf{f},\mathbf{u}_{t}^{h})_{\mathcal{ T}_{h}}. }$$

(12)

Integrating in time between 0 and t leads to

$$\displaystyle\begin{array}{rcl} & & \|\mathbf{u}^{h}\|_{ \mathrm{E}}^{2} - 2\langle \{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{u}^{h})\}_{\delta },[\![\mathbf{u}^{h}]\!]\rangle _{\mathcal{ F}_{h}} =\| \mathbf{u}_{0}^{h}\|_{ \mathrm{E}}^{2} - 2\langle \{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{u}^{h}(0))\}_{\delta },[\![\mathbf{u}^{h}(0)]\!]\rangle _{\mathcal{ F}_{h}} \\ & & \qquad \qquad \qquad \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad + 2\int _{0}^{t}(\mathbf{f},\mathbf{u}_{\tau }^{h})_{\mathcal{ T}_{h}}\,d\tau. {}\end{array}$$

(13)

We first observe that, for any $F \in \mathcal{F}_{h}$, and any w, v ∈ V _hp , the Cauchy-Schwarz inequality gives

$$\displaystyle{ \begin{array}{rl} \sum \limits _{F\in \mathcal{F}_{h}}\left \vert \langle \{\mathcal{D}\varepsilon (\mathbf{w})\}_{\delta },[\![\mathbf{v}]\!]\rangle _{F}\right \vert &\leq \|\sigma ^{-1/2}\{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{w})\}\|_{0,\mathcal{F}_{h}}\|\sigma ^{1/2}[\![\mathbf{v}]\!]\|_{0,\mathcal{F}_{h}} \\ & \lesssim \frac{1} {\sqrt{\alpha }}\|\mathcal{D}^{1/2}\boldsymbol{\varepsilon }(\mathbf{w})\|_{ 0,\mathcal{T}_{h}}\|\sigma ^{1/2}[\![\mathbf{v}]\!]\|_{ 0,\mathcal{F}_{h}} \\ & \leq \frac{1} {\sqrt{\alpha }}\|\mathbf{w}\|_{\mathrm{DG}}\|\mathbf{v}\|_{\mathrm{DG}} \leq \frac{1} {\sqrt{\alpha }}\|\mathbf{w}\|_{\mathrm{E}}\|\mathbf{v}\|_{\mathrm{E}}, \end{array} }$$

where in the second step we have employed the definition (7) of the penalty function σ, the local bounded variation property of the discretization parameters, together with the trace-inverse inequality (2.1). From the Young inequality, we obtain

$$\displaystyle{ \|\mathbf{u}^{h}\|_{ \mathrm{E}}^{2} - 2\langle \{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{u}^{h})\}_{\delta },[\![\mathbf{u}^{h}]\!]\rangle _{\mathcal{ F}_{h}}\gtrsim \|\mathbf{u}^{h}\|_{ \mathrm{E}}^{2}\,, }$$

provided that the penalty parameter α is chosen sufficiently large. This leads to

$$\displaystyle{ \|\mathbf{u}^{h}\|_{ \mathrm{E}}^{2}\lesssim \|\mathbf{u}^{h}(0)\|_{\mathrm{ E}}^{2} +\int _{ 0}^{t}(\mathbf{f},\mathbf{u}_{\tau }^{h})_{\mathcal{ T}_{h}}\,d\tau. }$$

Next, we observe that, from the Cauchy-Schwarz inequality we have

$$\displaystyle{ \int _{0}^{t}(\mathbf{f},\mathbf{u}_{\tau }^{h})_{\mathcal{ T}_{h}}\,d\tau \leq \int _{0}^{t}\|\mathbf{f}\|_{\mathcal{ T}_{h},0}\|\rho ^{1/2}\mathbf{u}_{\tau }^{h}\|_{ \mathcal{T}_{h},0} \leq \int _{0}^{t}\|\mathbf{f}\|_{\mathcal{ T}_{h},0}\|\mathbf{u}^{h}\|_{ \mathrm{E}}\,d\tau, }$$

which leads to

$$\displaystyle{ \|\mathbf{u}^{h}(t)\|_{\mathrm{ E}}^{2}\lesssim \|\mathbf{u}^{h}(0)\|_{\mathrm{ E}}^{2} +\int _{ 0}^{t}\|\mathbf{f}\|_{\mathcal{ T}_{h},0}\|\mathbf{u}^{h}\|_{ \mathrm{E}}\,d\tau. }$$

The theorem follows by Lemma 3.

4 Error Analysis of the Semi-Discrete Formulation

Before stating the main result of this section, we recall some preliminary results that will be needed for the forthcoming analysis.

Lemma 4

For any $\mathbf{v} \in [H^{s_{K}}(K)]^{d}$ , s _K ≥ 0, $K \in \mathcal{T}_{h}$ , there exists Π _hp v ∈ V _hp s.t.

$$\displaystyle\begin{array}{rcl} \|\!\vert \mathbf{v} -\varPi _{hp}\mathbf{v}\vert \!\|_{\mathrm{DG}}^{2}\lesssim \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \|\mathbf{v}\|_{H^{s_{K}}(K)}^{2}.& &{}\end{array}$$

(14)

Moreover, if $\mathbf{v},\mathbf{v}_{t} \in [H^{s_{K}}(K)]^{d}$ , for any $K \in \mathcal{T}_{h}$ , then

$$\displaystyle{ \|\mathbf{v} -\varPi _{hp}\mathbf{v}\|_{\mathrm{E}}^{2}\lesssim \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \left (\|\mathbf{v}_{t}\|_{H^{s_{K}}(K)}^{2} +\| \mathbf{v}\|_{ H^{s_{K}}(K)}^{2}\right ). }$$

(15)

Proof

We only show (15), as (14) is a particular case. Recalling the definition of the energy norm ∥⋅ ∥_E and employing the estimates of Lemma 1 we obtain

$$\displaystyle\begin{array}{rcl} \|\rho ^{1/2}(\mathbf{v}_{ t} -\varPi _{hp}\mathbf{v}_{t})\|_{0,\mathcal{T}_{h}}^{2}& \lesssim & \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)}} {p_{K}^{2s_{K}}} \|\mathbf{v}_{t}\|_{H^{s_{K}}(K)}^{2}, {}\\ \|\mathcal{D}^{1/2}\boldsymbol{\varepsilon }(\mathbf{v} -\varPi _{ hp}\mathbf{v})\|_{L^{2}(\mathcal{T}_{h})}^{2}& \lesssim & \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-2}} \|\mathbf{v}\|_{H^{s_{K}}(K)}^{2}, {}\\ \|\sigma ^{1/2}[\![\mathbf{v} -\varPi _{ hp}\mathbf{v}]\!]\|_{L^{2}(\mathcal{F}_{h})}^{2}& \lesssim & \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \|\mathbf{v}\|_{H^{s_{K}}(K)}^{2}, {}\\ \end{array}$$

that is

$$\displaystyle\begin{array}{rcl} \|\mathbf{v} -\varPi _{hp}\mathbf{v}\|_{\mathrm{E}}^{2}& \lesssim & \sum _{ K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \left (\frac{h_{K}^{2}} {p_{K}^{3}} \|\mathbf{v}_{t}\|_{H^{s_{K}}(K)}^{2} + \frac{1} {p_{K}}\|\mathbf{v}\|_{H^{s_{K}}(K)}^{2} +\| \mathbf{v}\|_{ H^{s_{K}}(K)}^{2}\right ) {}\\ & \lesssim & \sum _{K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} (\|\mathbf{v}_{t}\|_{H^{s}(K)}^{2} +\| \mathbf{v}\|_{ H^{s_{K}}(K)}^{2}), {}\\ \end{array}$$

where the last step follows by observing that $\frac{h_{K}^{2}} {p_{K}^{3}} <1$ and $\frac{1} {p_{K}} <1$ for any $K \in \mathcal{T}_{h}$.

4.1 Error Estimates in the Energy Norm

In this section we present a priori error estimates in the natural energy norm. Assuming that the exact solution u is regular enough, i.e., $\mathbf{u}\vert _{K} \in [H^{s_{K}}(K)]^{d}$ for any $K \in \mathcal{T}_{h}$, with s _K ≥ 2, with standard arguments it is also possible to show that formulation (16) is strongly consistent, i.e.,

$$\displaystyle{ (\rho \mathbf{u}_{tt},\mathbf{v})_{\mathcal{T}_{h}} + \mathcal{A}(\mathbf{u},\mathbf{v}) = (\mathbf{f},\mathbf{v})_{\mathcal{T}_{h}}\quad \forall \,\mathbf{v} \in \mathbf{V}_{hp}. }$$

(16)

From the above identity, we can obtain the following relation for the error e = u − u ^h

$$\displaystyle{ (\rho \mathbf{e}_{tt},\mathbf{v})_{\mathcal{T}_{h}} + \mathcal{A}(\mathbf{e},\mathbf{v}) = \mathbf{0}\quad \forall \,\mathbf{v} \in \mathbf{V}_{hp}, }$$

(17)

which serves as the basis for the forthcoming error estimates.

Theorem 1 (A-Priori Error Estimate in the Energy Norm)

Let u be the exact solution of problem  (1) and let u ^h be its approximation based on employing the semidiscrete DG formulation given in  (16), with a penalty parameter α chosen large enough, cf. (7). If, for any time t ∈ [0, T], the exact solution u(t) and its two first temporal derivatives belong $[H^{s_{K}}(K)]^{d}$ , $K \in \mathcal{T}_{h}$ , s _K ≥ 2, then

$$\displaystyle\begin{array}{rcl} & & \sup _{t\in (0,T]}\|\mathbf{e}(t)\|_{\mathrm{E}}^{2}\lesssim \sup _{ t\in (0,T]}\left \{\sum _{K\in \mathcal{T}_{h}}\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \left (\|\mathbf{u}_{t}(t)\|_{H^{s_{K}}(K)}^{2} +\| \mathbf{u}(t)\|_{ H^{s_{K}}(K)}^{2}\right )\right \} {}\\ & & \qquad \quad +\int _{ 0}^{T}\sum _{ K\in \mathcal{T}_{h}}\left \{\frac{h_{K}^{2\min (s_{K},p_{K}+1)-2}} {p_{K}^{2s_{K}-3}} \left (\|\mathbf{u}_{tt}(\tau )\|_{H^{s_{K}}(K)}^{2} +\| \mathbf{u}_{ t}(\tau )\|_{H^{s_{K}}(K)}^{2}\right )\right \}\,d\tau \;. {}\\ \end{array}$$

Before reporting the proof of Theorem 1 we recall the integration by parts formula

$$\displaystyle{ \int _{0}^{t}(\mathbf{w},\mathbf{v}_{\tau })_{ {\ast}}d\tau = (\mathbf{w}(t),\mathbf{v}(t))_{{\ast}}- (\mathbf{w}(0),\mathbf{v}(0))_{{\ast}}-\int _{0}^{t}(\mathbf{w}_{\tau },\mathbf{v})_{ {\ast}}d\tau, }$$

(18)

that holds for w, v regular enough and for any scalar product (⋅ , ⋅ )_∗

Proof

Let Π _hp u ∈ V _hp be the interpolant defined as in Lemma 4. By decomposing the error as e = e ^π − e ^h, with e ^π = u −Π _hp u and e ^h = u ^h −Π _hp u, (17) becomes:

$$\displaystyle{ (\rho \mathbf{e}_{tt}^{h},\mathbf{v})_{\mathcal{ T}_{h}} + \mathcal{A}(\mathbf{e}^{h},\mathbf{v}) = (\rho \mathbf{e}_{ tt}^{\pi },\mathbf{v})_{\mathcal{ T}_{h}} + \mathcal{A}(\mathbf{e}^{\pi },\mathbf{v})\quad \forall \,\mathbf{v} \in \mathbf{V}_{ hp}. }$$

By taking v = e ^h in the above identity, we have

$$\displaystyle{ \frac{1} {2} \frac{d} {dt}\left (\|\mathbf{e}^{h}\|_{ \mathrm{E}}^{2} - 2\langle [\![\mathbf{e}^{h}]\!],\{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{e}^{h})\}_{\delta }\rangle _{\mathcal{ F}_{h}}\right ) = (\rho \mathbf{e}_{tt}^{\pi },\mathbf{e}_{ t}^{h})_{\mathcal{ T}_{h}} + \mathcal{A}(\mathbf{e}^{\pi },\mathbf{e}_{ t}^{h})\;. }$$

(19)

Reasoning as in the proof of Theorem 1, we have

$$\displaystyle{ \begin{array}{c} \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2} - 2\langle [\![\mathbf{e}^{h}]\!],\{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{e}^{h})\}_{\delta }\rangle _{\mathcal{F}_{h}}\gtrsim \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2},\end{array} }$$

provided that the penalty parameter α is chosen large enough; cf. (7). Integrating (19) in time between 0 and t and using that e ^h(0) = u ^h(0) − u ^π(0) = 0, we get

$$\displaystyle{ \begin{array}{rl} \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2} & \lesssim \int _{0}^{t}(\rho \mathbf{e}_{tt}^{\pi },\mathbf{e}_{t}^{h})_{\mathcal{T}_{h}}\,d\tau +\int _{ 0}^{t}\mathcal{A}(\mathbf{e}^{\pi },\mathbf{e}_{t}^{h})\,d\tau \\ &\lesssim \,\int _{0}^{t}\|\mathbf{e}_{t}^{\pi }\|_{\mathrm{E}}\|\mathbf{e}^{h}\|_{\mathrm{E}}\,d\tau + \mathcal{A}(\mathbf{e}^{\pi },\mathbf{e}^{h}) -\int _{0}^{t}\mathcal{A}(\mathbf{e}_{t}^{\pi },\mathbf{e}^{h})\,d\tau \\ &\lesssim \,\int _{0}^{t}\|\mathbf{e}_{t}^{\pi }\|_{\mathrm{E}}\|\mathbf{e}^{h}\|_{\mathrm{E}}\,d\tau +\|\! \vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}\|\mathbf{e}^{h}\|_{\mathrm{DG}} +\int _{ 0}^{t}\|\!\vert \mathbf{e}_{t}^{\pi }\vert \!\|_{\mathrm{DG}}\|\mathbf{e}^{h}\|_{\mathrm{DG}}\,d\tau,\\ \end{array} }$$

(20)

where the second step follows based on employing the Cauchy-Schwarz inequality together with integration by parts formula (18) with w = e ^π, v = e ^h and $(\cdot,\cdot )_{{\ast}} = \mathcal{A}(\cdot,\cdot )$, whereas the third one follows from Lemma (8). From the Young inequality

$$\displaystyle{ \|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}\|\mathbf{e}^{h}\|_{ \mathrm{DG}} \leq \frac{1} {\epsilon } \|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}^{2} +\epsilon \| \mathbf{e}^{h}\|_{ \mathrm{DG}}^{2} \leq \frac{1} {\epsilon } \|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}^{2} +\epsilon \| \mathbf{e}^{h}\|_{ \mathrm{E}}^{2}, }$$

we can suitably choose ε and rewrite (25) as

$$\displaystyle{ \begin{array}{rl} \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2} & \lesssim \, +\|\! \vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}^{2} +\int _{ 0}^{t}(\|\!\vert \mathbf{e}_{t}^{\pi }\vert \!\|_{\mathrm{DG}} +\| \mathbf{e}_{t}^{\pi }\|_{\mathrm{E}})\|\mathbf{e}^{h}\|_{\mathrm{DG}}\,d\tau.\\ \end{array} }$$

(21)

Applying Gronwall’s Lemma 3 we get

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{e}^{h}(t)\|_{\mathrm{E}}\lesssim \sup _{t\in [0,T]}\|\!\vert \mathbf{e}^{\pi }(t)\vert \!\|_{\mathrm{DG}}^{2} +\int _{ 0}^{t}\|\mathbf{e}_{t}^{\pi }(\tau )\|_{\mathrm{E}}\,d\tau &&\quad \forall t \in (0,T].\end{array} }$$

Finally, from the Cauchy-Schwarz inequality and the above bound, and taking the supremum over t ∈ (0, T]

$$\displaystyle\begin{array}{rcl} \sup _{t\in (0,T]}\|\mathbf{e}(t)\|_{\mathrm{E}}^{2}\lesssim \sup _{ t\in (0,T]}\left \{\|\mathbf{e}^{\pi }(t)\|_{\mathrm{ E}}^{2} +\|\! \vert \mathbf{e}^{\pi }(t)\vert \!\|_{\mathrm{ DG}}^{2}\right \} +\int _{ 0}^{T}\|\mathbf{e}_{ t}^{\pi }(\tau )\|_{\mathrm{ E}}^{2}\,d\tau \;.& & {}\\ \end{array}$$

The proof is completed by applying Lemma 4.

Remark 1

If the mesh size is quasi uniform, i.e. $h =\max _{K\in \mathcal{T}_{K}}h_{K} \approx h_{K}$ for any $K \in \mathcal{T}_{h}$, the polynomial approximation degree is uniform, i.e. p _K = p for any $K \in \mathcal{T}_{h}$, and the exact solution satisfies u | _K , u _t | _K , u _tt | _K ∈ [H ^s(K)]^d for any $K \in \mathcal{T}_{h}$ and for any t ∈ [0, T], with s ≥ p + 1, the error estimate of Theorem 1 becomes

$$\displaystyle\begin{array}{rcl} & & \sup _{t\in (0,T]}\|\mathbf{e}(t)\|_{\mathrm{E}}^{2}\lesssim \frac{h^{2p}} {p^{2s-3}}\sup _{t\in (0,T]}\left \{\|\mathbf{u}_{t}(t)\|_{H^{s}(\varOmega )}^{2} +\| \mathbf{u}(t)\|_{ H^{s}(\varOmega )}^{2}\right \} {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad + \frac{h^{2p}} {p^{2s-3}}\int _{0}^{T}\left \{\|\mathbf{u}_{ tt}(\tau )\|_{H^{s}(\varOmega )}^{2} +\| \mathbf{u}_{ t}(\tau )\|_{H^{s}(\varOmega )}^{2}\right \}\,d\tau \;. {}\\ \end{array}$$

The above bounds are optimal in h and suboptimal in p by a factor p ^1∕2; see, e.g., [19, 29] for analogous bounds for stationary (scalar) second order elliptic problems. Optimal error estimates with respect to the polynomial approximation degree can be shown either using the projector of [17] provided the solution belongs to a suitable augmented space, or whenever a continuous interpolant can be built; cf. [37].

4.2 Error Estimates in the L ² Norm

In this section we present a priori error estimates in the L ² norm. We follow the approach of [13] for second order hyperbolic equations, and introduce, for a regular enough vector-valued function w, the elliptic-projection operator Π w defined as

$$\displaystyle{ \begin{array}{llll} &\mathcal{A}(\varPi \mathbf{w},\mathbf{v}) = \mathcal{A}(\mathbf{w},\mathbf{v})&&\forall \mathbf{v} \in \mathbf{V}_{hp}. \end{array} }$$

(22)

We immediately have

$$\displaystyle{ \begin{array}{rl} \|\mathbf{u} -\varPi \mathbf{u}\|_{\mathrm{DG}} & \leq \|\mathbf{u} -\varPi _{hp}\mathbf{u}\|_{\mathrm{DG}} +\|\varPi _{hp}\mathbf{u} -\varPi \mathbf{u}\|_{\mathrm{DG}}\lesssim \|\!\vert \varPi _{hp}\mathbf{u} -\mathbf{u}\vert \!\|_{\mathrm{DG}}, \end{array} }$$

(23)

where Π _hp is the interpolant of Lemma 4, and where the second step follows from Lemma 2 and the definition (22)

$$\displaystyle{ \begin{array}{rl} \|\varPi _{hp}\mathbf{u} -\varPi \mathbf{u}\|_{\mathrm{DG}}^{2} & \lesssim \mathcal{A}(\varPi _{hp}\mathbf{u} -\varPi \mathbf{u},\varPi _{hp}\mathbf{u} -\varPi \mathbf{u}) = \mathcal{A}(\varPi _{hp}\mathbf{u} -\mathbf{u},\varPi _{hp}\mathbf{u} -\varPi \mathbf{u}) \\ &\lesssim \|\!\vert \varPi _{hp}\mathbf{u} -\mathbf{u}\vert \!\|_{\mathrm{DG}}\|\varPi _{hp}\mathbf{u} -\varPi \mathbf{u}\|_{\mathrm{DG}}. \end{array} }$$

We also recall the following Poincaré–Friedrichs inequality valid for piecewise vector–valued H ¹ functions

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{v}\|_{L^{2}(\mathcal{T}_{h})}^{2}\lesssim \sum \limits _{K\in \mathcal{T}_{h}}\|\nabla \mathbf{v}\|_{L^{2}(K)}^{2} +\sum \limits _{F\in \mathcal{F}_{h}} \frac{1} {h_{F}}\|[\![\mathbf{v}]\!]\|_{L^{2}(F)}^{2} & & \forall \mathbf{v} \in [H^{1}(\mathcal{T}_{h})]^{d}, \end{array} }$$

cf. [10]. Using that $\sum _{K\in \mathcal{T}_{h}}\|\nabla \mathbf{v}\|_{L^{2}(K)} \leq \|\varepsilon (\mathbf{v})\|_{L^{2}(\mathcal{T}_{h})}$, and from the definition of the DG norm and of the stabilization function (12), it immediately follows

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{v}\|_{L^{2}(\mathcal{T}_{h})}^{2}\lesssim \|\mathbf{v}\|_{\mathrm{DG}} & & \forall \mathbf{v} \in [H^{1}(\mathcal{T}_{h})]^{d}. \end{array} }$$

(24)

Theorem 2 (A-Priori Error Estimate in the L ² Norm)

Under the Assumptions of Theorem  1 , it holds

$$\displaystyle\begin{array}{rcl} & & \sup _{t\in (0,T]}\|\mathbf{e}(t)\|_{L^{2}(\varOmega )}^{2}\lesssim \sup _{ t\in (0,T]}\left \{\frac{h^{2\min (s,p+1)}} {p^{2s-2}} \left (\|\mathbf{u}_{t}(t)\|_{H^{s}(\varOmega )}^{2} +\| \mathbf{u}(t)\|_{ H^{s}(\varOmega )}^{2}\right )\right \} {}\\ & & \qquad \qquad \qquad \qquad +\int _{ 0}^{T}\left \{\frac{h^{2\min (s,p+1)}} {p^{2s-2}} \left (\|\mathbf{u}_{tt}(\tau )\|_{H^{s}(\varOmega )}^{2} +\| \mathbf{u}_{ t}(\tau )\|_{H^{s}(\varOmega )}^{2}\right )\right \}\,d\tau \;. {}\\ \end{array}$$

with $h =\max _{K\in \mathcal{T}_{h}}h_{K}$ , $p =\min _{K\in \mathcal{T}_{h}}p_{K}$ and $s =\min _{K\in \mathcal{T}_{h}}s_{K}$ .

Proof

As in the proof of Theorem 1 we decompose the error as e = e ^π − e ^h, where now e ^π = u ^h −Π u and e ^h = u −Π u, Π u being the elliptic projector defined in (22). With the above decomposition, the error equation (17) becomes:

$$\displaystyle{ (\rho \mathbf{e}_{tt}^{h},\mathbf{v})_{\mathcal{ T}_{h}} + \mathcal{A}(\mathbf{e}^{h},\mathbf{v}) = (\rho \mathbf{e}_{ tt}^{\pi },\mathbf{v})_{\mathcal{ T}_{h}}\quad \forall \,\mathbf{v} \in \mathbf{V}_{hp}. }$$

By taking v = e ^h in the above identity and reasoning as in the proof of Theorem 1, we have

$$\displaystyle{ \begin{array}{c} \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2} - 2\langle [\![\mathbf{e}^{h}]\!],\{\mathcal{D}\boldsymbol{\varepsilon }(\mathbf{e}^{h})\}_{\delta }\rangle _{\mathcal{F}_{h}}\gtrsim \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2},\end{array} }$$

provided that the penalty parameter α is chosen large enough; cf. (7). Therefore, integrating in time between 0 and t and using that e ^h(0) = u ^h(0) − u ^π(0) = 0, we get

$$\displaystyle{ \begin{array}{lll} \|\mathbf{e}^{h}\|_{\mathrm{E}}^{2} & \lesssim \int _{0}^{t}(\rho \mathbf{e}_{tt}^{\pi },\mathbf{e}_{t}^{h})_{\mathcal{T}_{h}}\,d\tau &\lesssim \,\int _{0}^{t}\|\mathbf{e}_{tt}^{\pi }\|_{L^{2}(\varOmega )}\|\mathbf{e}^{h}\|_{\mathrm{E}}\,d\tau \end{array} }$$

(25)

where the second step follows based on employing the Cauchy-Schwarz inequality. Applying Gronwall’s Lemma 3 we get

$$\displaystyle{ \begin{array}{llll} &\|\mathbf{e}^{h}(t)\|_{\mathrm{E}}\lesssim \int _{0}^{t}\|\mathbf{e}_{tt}^{\pi }(\tau )\|_{L^{2}(\varOmega )}\,d\tau &&\quad \forall t \in (0,T].\end{array} }$$

Next, from the Cauchy-Schwarz inequality, the above bound and the Poincaré–Friedrichs inequality (24), we immediately get

$$\displaystyle\begin{array}{rcl} \|\mathbf{u} -\mathbf{u}^{h}\|_{ L^{2}(\mathcal{T}_{h})}& \lesssim & \|\mathbf{e}^{\pi }\|_{ L^{2}(\mathcal{T}_{h})} +\| \mathbf{e}^{h}\|_{ L^{2}(\mathcal{T}_{h})}\lesssim \|\mathbf{e}^{\pi }\|_{ L^{2}(\mathcal{T}_{h})} +\| \mathbf{e}^{h}\|_{ \mathrm{DG}} {}\\ & \leq & \|\mathbf{e}^{\pi }\|_{L^{2}(\mathcal{T}_{h})} +\| \mathbf{e}^{h}\|_{ \mathrm{E}}\lesssim \|\mathbf{e}^{\pi }\|_{ L^{2}(\mathcal{T}_{h})} +\int _{ 0}^{t}\|\mathbf{e}_{ tt}^{\pi }(\tau )\|_{ L^{2}(\varOmega )}\,d\tau. {}\\ \end{array}$$

The estimate of the terms on the right hand sides is based on employing a duality argument; cf [13]. Let $\boldsymbol{\xi }$ be the solution of the problem

$$\displaystyle{ \begin{array}{llll} &\nabla \cdot \sigma (\boldsymbol{\xi }) = \mathbf{e}^{\pi }\quad \mathrm{in}\,\varOmega,&&\boldsymbol{\xi } =\boldsymbol{ 0}\quad \mathrm{on}\,\partial \varOmega. \end{array} }$$

As Ω is convex, the above problem is well-posed and its unique solution $\boldsymbol{\xi }\in [H^{2}(\varOmega )]^{d}$ and satisfies $\|\boldsymbol{\xi }\|_{H^{2}(\varOmega )}\lesssim \|\mathbf{e}^{\pi }\|_{L^{2}(\varOmega )}$. Moreover, it holds

$$\displaystyle{ \begin{array}{c} \|\mathbf{e}^{\pi }\|_{L^{2}(\varOmega )}^{2} = (\mathbf{e}^{\pi },\mathbf{e}^{\pi })_{L^{2}(\varOmega )} = \mathcal{A}(\boldsymbol{\xi },\mathbf{e}^{\pi }) = \mathcal{A}(\boldsymbol{\xi }-\boldsymbol{\xi }^{\pi },\mathbf{e}^{\pi })\lesssim \|\!\vert \boldsymbol{\xi }-\boldsymbol{\xi }^{\pi }\vert \!\|_{\mathrm{DG}}\|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}} \end{array} }$$

where $\boldsymbol{\xi }^{\pi } \in \mathbf{V}_{hp}$ is the interpolant of Lemma 4, and where the last steps follows from Lemma 2. Employing the interpolation estimates of Lemma 4 we have

$$\displaystyle{ \|\mathbf{e}^{\pi }\|_{L^{2}(\varOmega )}^{2}\lesssim \frac{h} {p^{1/2}}\|\boldsymbol{\xi }\|_{H^{2}(\varOmega )}\|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}\lesssim \frac{h} {p^{1/2}}\|\mathbf{e}^{\pi }\|_{L^{2}(\varOmega )}\|\!\vert \mathbf{e}^{\pi }\vert \!\|_{\mathrm{DG}}, }$$

where $h =\max _{K\in \mathcal{T}_{h}}h_{K}$ and $p =\min _{K\in \mathcal{T}_{h}}p_{K}$. The proof is completed by employing the error bounds of Theorem 1.

5 Numerical Results

The results of this section have been obtained with SPEED (http://speed.mox.polimi.it/), an open source Fortran code developed at Politecnico di Milano by the Laboratory for Modeling and Scientific Computing MOX of the Department of Mathematics and the Department of Civil and Environmental Engineering. SPEED is specifically designed for the simulation of seismic waves propagation problems, including both the ground motion induced by large scale earthquakes and soil-structure interaction in urban areas; see, e.g., [27]. Throughout the section we have set Δt = 10⁻⁵ so that the temporal component of the error is negligible compared to the spatial one.

In the first example we consider an elastic wave propagation problem in Ω = (0, 1)³, with ρ = λ = μ = 1. The source term f and the initial data are chosen so that the exact solution of problem (1) is given by

$$\displaystyle{\mathbf{u}_{\mathrm{ex}}(x,y,z,t) =\sin (3\pi t)\left [\begin{array}{c} -\sin ^{2}(\pi x)\sin (2\pi y)\sin (2\pi z) \\ \sin ^{2}(\pi y)\sin (2\pi x)\sin (2\pi z) \\ \sin ^{2}(\pi z)\sin (2\pi x)\sin (2\pi y) \end{array} \right ].}$$

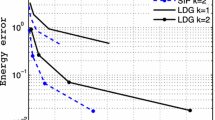
We first we consider both a tetrahedral and a hexahedral grid with mesh size h = 0. 5 and let p varies from 2 to 8. In Fig. 1a we report the error computed in the energy norm ∥⋅ ∥_E at t = T = 0. 05 and as a function of the polynomial degree. As expected, an exponential convergence is observed. For the sake of comparison Fig. 1a also reports the corresponding computed errors obtained with a conforming Spectral Element method on the same tetrahedral grid. Next, we investigate the behavior of the error as a function of the grid size h for different polynomial degrees. We consider a sequence of uniformly refined tetrahedral grids starting from an initial decomposition of size h ₀ = 0. 5. In Fig. 1b we report the computed errors measured in energy norm ∥⋅ ∥_E at the final observation time t = T versus the grid size for p = 2, 3, 4. As expected, the results confirm a convergence rate of order p.

Fig. 1

Example 1. (a) Computed errors versus p: computed errors measured in the energy norm ∥⋅ ∥_E at t = T = 0. 05 versus the polynomial degree p for a tetrahedral mesh (DG-Tet) and a hexahedral grid (DG-Hex). The results are also compared with the corresponding one based on employing conforming Spectral Element method on the same tetahedral grid (SE-Tet). (b) Computed errors versus h: computed errors measured in the energy norm ∥⋅ ∥_E at t = T versus the mesh size for p = 2, 3, 4. The dashed lines denote the expected slopes of the error curves

In the second test we consider a plane wave propagating along the vertical direction in a layered elastic half-space Ω = (0, 100) × (0, 100) × (−300, 0) m, see Fig. 2 (left). In Table 1 we report the depth and the material properties of the half-space Ω ₁ and the layer Ω ₂. The source plane wave is polarized in the x direction and its time dependency is given by a unit amplitude Ricker wave with peak frequency at 1 Hz. A dumping term proportional to 2ρξ u _t + 2ξ ² u, with ξ as in Table 1, is also added to the equation to take into account viscoelastic effects. The subdomains Ω ₁ and Ω ₂ are discretized with a hexahedral and a tetrahedral mesh, respectively, and the computational grids are built in order to have at least five grid points per wavelength, with p = 4 in both Ω ₁ and Ω ₂. Finally, we impose absorbing boundary conditions on the bottom surface, a free surface condition on the top surface, and homogeneous Dirichlet conditions for the y and z component of the displacement on the remaining boundaries. In Fig. 2 (right) we report the computed solution which is also compared with a reference semi-analytical solution u _TH based on the Thomson-Haskell propagation matrix method, cf. [18, 40]. More precisely, Fig. 2 (right) shows the time history of the x component of the displacement u _x recorded at the point R = (50, 50, 0) m. Finally, in Fig. 3 we report four snapshots of the deformed computational domain when invested by the plane wave. Two relevant physical effects can be observed: i) the wave field is amplified at the top of the domain due to the free surface condition; ii) reflections of the wave field take place inside the layer Ω ₂ characterized by a softer material with respect to the half space Ω ₁.

Table 1 Example 2. Material properties

Fig. 2

Example 2. Left: Computational domain Ω = Ω ₁ ∪Ω ₂. The elastic wave propagates from the bottom of Ω ₁ to the top surface of Ω ₂. Right: Computed time history of the x component of the displacement u _x recorded at R = (50, 50, 0) m. The results are compared with a reference semi-analytical solution u _TH obtained with the Thomson-Haskell propagation matrix method

Fig. 3

Example 2. Snapshots of the x-component of the displacement u _x .The deformed domain (colored) is compared with the non distorted one (black line)