Pitch Angle Active Disturbance Rejection Control with Model Compensation for Underwater Glider

Abstract

Underwater glider is a strong coupling and nonlinear system. Most current methods neglect the influences from the buoyancy adjustment system to pitch angle so that there always a large overshoot in the pitch angle control loop. In order to improve the control accuracy for pitch angle, a model compensation (MC) based on the Active disturbance rejection control (ADRC) was proposed in this paper. The Extended State Observer (ESO) estimated system comprehensive disturbances and avoided the influences from the perturbation by giving disturbance compensation. ADRC obtained segmental models through system modeling, estimation and physical sensors measurement. The estimation pressure of ESO was greatly reduced and the estimation precision was improved significantly. Simulations in the MATLAB indicated that MC-ADRC have a good control precision and low overshoot with settling time for glider systems. It reduced 4.5% overshoot and dropped the settling time to 90 s for pitch angle control than the traditional ADRC.

1 Introduction

Underwater glider has broad applications in marine scientific research environmental monitoring, which is significant for coastal environmental observation worldwide [1, 2]. Applying slight change to its buoyancy and converting vertical motion to horizontal motion through matching the wings, its forward motion can be driven with low electric consumption as well as super-long voyage and high endurance. The most mature gliders including: Slocum [3], Seaglider [4], Spray [5] and Petrel [6].

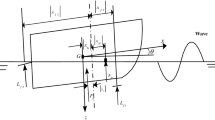
The most effective control method for pitch angle is that a moveable weight such as battery packs called pitch angle adjustment mechanism. Battery packs positions determine the pitch angle for glider. In addition, by changing its buoyancy through a variable volume oil sac called buoyancy adjustment mechanism, an underwater glider can move up and down in the horizontal plane, Fig. 1. The oil sac is located in the central axis of the head of the glider and the battery packs is seated in the latter half the cabin.

Fig. 1.

Structure of glider. 1. External oil capsule. 2. Plunger pump. 3. Internal oil capsule. 4. Battery pack. 5. Mid-bin. 6. Pitching adjustment mechanism. 7. Rolling adjustment mechanism. 8. Antenna. 9. Dome 10. Control module 11. Rear-bin. 12. Fore-bin. 13. High-pressure valve.

Zigzag motion trajectory decides the pitch angle control is very important for the glider [7]. However, there always exists a strong coupling in pitch angle control loop. The pitch angle is not only controlled by the positions of the battery packs, but also it is susceptible towards to multiple parameters such as the oil sac volume and external disturbances from ocean currents. The coupled relationship makes actuators act frequently which consumes added energy during the pitch angle control process.

Some algorithms have been proposed in the past to improve the control effect, such as the linear quadratic regulator (LQR) [8] and the classical proportional, integral, and derivative (PID) [9, 10]. However, these algorithms are based on linear equations. The controller performances would be weak when system state far from the equilibrium point, let alone there exist strong parameter perturbations and disturbances.

Active Disturbance Rejection Control (ADRC), which was proposed by Chinese scholar, Han Jingqing [11]. It voids large overshoot by arranging the transition process through Tracking Differentiator (TD) and optimizes the control instruction. It observes the system uncertainty and disturbance total sum through the Extended State Observer (ESO). By designing the Nonlinear State Error Feedback (NLSEF) and combing the observation of the ESO for the system status and unknown disturbance, the linearization of the dynamic compensation is sequentially realized. The best characteristic of ADRC is that it does not need any mathematical models of the controlled object. Despite this, it would be difficult to paly advantages if ADRC doesn’t make full use of the controlled object model in some complicated systems. For the glider, there are many coupled factors such as the battery packs position, buoyancy, velocity, etc. All of these factors are taken for perturbation terms and they are variable during glide motion. It is a heavy burden for ESO to estimate these perturbation terms.

For this reason, the model compensation ADRC (MC-ADRC) was proposed in this paper. By estimating parameters $\alpha$ and ${m_b}$ for compensation model, the ESO needn’t to estimate the total disturbances but only need to estimate the parameters that are not compensated. The ESO estimation pressure was reduced largely and the ADRC would have a higher control precision and stronger anti-interference ability.

This paper was organized as follows. Section 2 established the kinetic equations for the glider that considered pitch angle disturbance from the buoyancy adjustment mechanism. Section 3 introduced the ADRC based on the model compensation. Section 4 described the results of simulation in the MATLAB platform. In the Sect. 5, the experimental results were discussed and Sect. 6 concluded the paper.

2 Modelling of Underwater Glider

The general popular glider kinetic model was derived by the Gaver JG [12]. However, it did not consider that the variable buoyancy ${m_b}$ has an impact on pitch angle when the positions of ${m_b}$ is inconsistent with buoyancy centre. This paper deduced kinetic model based on the influence from the variable buoyancy for the pitch angle control.

2.1 Coordinate Frame Definition

Inertial coordinate $E - \xi \eta \zeta$, body coordinate $O{ - }xyz$ was showed in Fig. 2. Other parameters were descripted in literature [12].

Fig. 2.

Glider coordinate and force definition.

2.2 Glider Kinetic Equations

Glider is balanced with gravity $G$, buoyancy $F$, water resistance $D$, lift force $L$, and viscous moment ${M_{DL}}$. In the vertical plane, the glider moves with translational velocity $({v_1},0,{v_3})$ relative to the inertial coordinate $E - \xi \eta \zeta$. The variables were described as follows:

$$ {\bf{B}} = \left[\begin{array}{c} x \\ 0 \\ z \\ \end{array}\right],\,V = \left[ \begin{array}{c} {v_1} \\ 0 \\ {v_3} \\ \end{array} \right],\,\varvec{\Omega}= \left[ \begin{array}{c} 0 \\ {{\varvec{\Omega}_2}} \\ 0 \\ \end{array} \right],\,{r_p} = \left[ \begin{array}{c} {{r_{p1}}} \\ 0 \\ {const} \\ \end{array} \right],\,{U_p} = \left[ \begin{array}{c} {{u_{p1}}} \\ 0 \\ 0 \\ \end{array} \right],\,{r_b} = \left[ \begin{array}{c} {const} \\ 0 \\ 0 \\ \end{array} \right],\,{P_b} = \left[ \begin{array}{c} {{P_{p1}}} \\ 0 \\ {{P_{b3}}} \\ \end{array} \right]. $$

$V$ is the velocity and $\varvec{\Omega}$ denotes the pitch angle. ${\bf{B}}$ denotes the glider position in inertial coordinates and ${u_{p1}}$ is the input variable. The battery packs position vector ${r_{p3}} = 0$. For buoyancy adjustment mechanism: ${r_{b1}} = const$ and ${r_{b3}} = 0$. The motion equations can be simplified as follows based on the constraint conditions above:

$$ \dot x = {v_1}\cos \theta + {v_3}\sin \theta $$

(1)

$$ \dot z = {v_1}\sin \theta + {v_3}\cos \theta $$

(2)

$$ {\dot v_1} = \frac{1}{m_1}\left[ { - {m_3}{v_3}{\varvec{\Omega}_2} - {P_{p3}}{\varvec{\Omega}_2} - {m_0}g\sin \theta + L\sin \alpha - D\cos \alpha - {u_{p1}}} \right] $$

(3)

$$ {\dot v_3} = \frac{1}{m_1}\left[ {{m_1}{v_1}{\varvec{\Omega}_2} + {P_{p3}}{\varvec{\Omega}_2} + {P_{b1}}{\varvec{\Omega}_2} + {m_0}g\cos \theta - L\cos \alpha - D\sin \alpha } \right] $$

(4)

$\alpha$ represents the angle of attack(AOA). $\chi$ is the path angle and $\chi = \theta + \alpha$.

According to the $\ddot \theta = \dot{\varvec{\Omega}}_2$, it is easy to obtain the pitch angle control equation:

$$ \eqalign{ & \dot {\varvec{\Omega}}_2 = \frac{1}{J_2}[({m_3} - {m_1}){v_1}{v_3} - ({r_{p1}}{P_{p1}} + {r_{p3}}{P_{p3}})\dot \theta - {r_{b1}}{P_{b1}}\dot \theta - {m_p}g({r_{p1}}\cos \theta + {r_{p3}}\sin \theta ) \cr & - {m_b}g{r_{b1}}\cos \theta + {M_{DL}} - {r_{p3}}{u_{p1}}] \cr} $$

(5)

Where ${m_i}$ denotes the $i$ th diagonal element of $M$, ${m_0}$ represents the excess mass. ${P_p}$ and ${P_b}$ are the linear moment of the ${m_p}$ and ${m_b}$ in body coordinates. ${C_D}$, ${C_L}$ and ${C_M}$ are the standard aerodynamic drag, lift and moment coefficients by $A$, the maximum glider cross sectional area, and $\rho$ is the fluid density. ${K_{D0}}$, ${K_{L0}}$, ${K_{M0}}$, ${K_D}$, ${K_L}$ and ${K_M}$ are hydrodynamic parameters.

The general and optimal pitch angle of the glider ranges from −30° to +30° [13]. Considering the overshoot of the adjustment, we unfolded $\sin \theta$ and $\cos \theta$ range from −40° to 0° (descend phase) and 0° to +40° (ascend phase) according to the Taylor formula $\sin \theta \approx {a_1} + {b_1}\theta + {c_1}{\theta^2}$ and $\cos \theta \approx {a_2} + {b_2}\theta + {c_2}{\theta^2}$. Where $a$, $b$ and $c$ are the coefficients of the fitting curves, Table 1.

Table 1. Coefficients of the fitting curves for $\sin \theta$ and $\cos \theta$.

Eliminated the high order terms and transformed Eq. (5) as a standard equation $\ddot \theta = f(\theta ,\dot \theta ,w) + bu$, where $w$ is the disturbances and $u$ is the inputs variable, parameter $b$ is the coefficient.

$$ \ddot \theta = \frac{1}{J_2}\left[ \eqalign{ & - ({r_{p1}}{P_{p1}} + {r_{p3}}{P_{p3}} + {r_{b1}}{P_{b1}})\dot \theta - ({b_2}{m_p}g + {{\text{b}}_ 1}{m_p}g{r_{p3}} + {b_2}{m_b}g{r_{b1}})\theta - ({a_2}{m_p}g{r_{p1}} \cr & + {a_ 1}{m_p}g{r_{p3}} + {a_2}{m_b}g{r_{b1}}) + ({m_3} - {m_1}){v_1}{v_3} + {M_{DL}} - {r_{p3}}{u_{p1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr} \right] $$

(6)

It is obvious that the pitch angle control system is nonlinear and influenced by both of the battery packs position ${r_p}$, the oil sac volume ${m_b}$ and the glider velocity $v$.

3 ADRC for Pitch Angle Control

3.1 ADRC Principle

ADRC absorbs the kernel from classic PID controller that the adjustment is based on the feedback error, and it references a state observation theory as well as constructs a new controller by nonlinear combinations.

3.2 ADRC Design

The additive perturbation and the external disturbances of the system are attributed to the general disturbances in pitch angle control. The ESO estimates the general perturbations and compensates in form of the feedforward. Considering two order nonlinear object as follows:

$$ \left\{ \begin{array}{l} {\ddot x = f(x,\dot x) + w(t) + bu(t)} \hfill \\ {y = x(t)} \hfill \\ \end{array} \right. $$

Tracking Differentiator.

TD has the function of extracting the continuous signal and its differential signal. The input signal is ${v_0}(t)$ and output signals are ${v_1}(t)$ and ${v_2}(t)$. Signal ${v_1}(t)$ tracks the signal ${v_0}(t)$ and ${v_2} = {\dot v_1}$.

$$ \left\{ \begin{array}{l} {e = {v_1} - {v_0}} \hfill \\ {{{\dot v}_1} = {v_2}} \hfill \\ {{{\dot v}_2} = {f_{han}}(e,{v_2},{r_0},{h_0})} \hfill \\ \end{array} \right. $$

Parameter ${r_0}$ denotes the speed factor and ${h_0}$ denotes the filter factor; function $f_{han}$ represents the optimal control which is defined as follows:

$$ {f_{han}}(e,v,r,h) = \left\{ \begin{array}{l} { - rsign(a),\left| a \right| > d} \hfill \\ { - ra/d,\;\;\;\;\;\left| a \right| \leq d} \hfill \\ \end{array} \right. $$

Where $d = rh$, ${d_0} = hd$, $y = e + hv$, ${a_0} = \sqrt {{d^2} + 8r\left| y \right|}$,

$$ a = \left\{ \begin{array}{l} {v + sign(y)({a_0} - d)/2,\left| y \right| > {d_0}} \hfill \\ {v + y/h,\quad \quad \quad \quad \quad{\kern 1pt} \left| y \right| \leq {d_0}} \hfill \\ \end{array} \right. $$

Extended State Observer

$$ \left\{ \begin{array}{l} {e = {z_1} - x} \hfill \\ {{{\dot z}_1} = {z_2} - {\beta_{01}}e} \hfill \\ {{{\dot z}_2} = {z_3} - {\beta_{02}}{f_{al}}(e,0.5,h) + {b_0}u} \hfill \\ {{{\dot z}_3} = - {\beta_{03}}{f_{al}}(e,0.25,h)} \hfill \\ \end{array} \right. $$

Parameter $u$ is the input variable. ${z_1}$ is the estimation for the output state variable and ${z_2}$ is the speed estimation for output. Parameter $h$ represents the sampling step and ${\beta_{01}}$, ${\beta_{02}}$, ${\beta_{03}}$ are controller parameters. Let nonlinear function:

$$ {f_{al}}(e,\alpha ,\delta ) = \left\{ \begin{array}{l} {e/{\delta^{1 - \alpha }},\quad \,\;\;\left| e \right| \leq \delta } \hfill \\ {\left| e \right|\alpha sign(e),\left| e \right| > \delta } \hfill \\ \end{array} \right. $$

Each state tracks their status variable that was extended, ${z_1}(t) \to x(t)$, ${z_2}(t) \to \dot x(t)$, ${z_3}(t) \to \ddot x(t) \to f(x,\dot x,w)$.

Non-Linear State Error Feedback.

NLSEF makes good use of the past, present and future information for errors. The state estimation output ${z_i}$ from ESO was assumed as the state feedback variable in the ADRC. It is compared with the output ${v_i}$ from TD. The error amount ${e_i} = {v_i} - {z_i}$ constitutes the nonlinear combination for system error feedback.

$$ \left\{ \begin{array}{l} {{e_1} = {v_1} - {z_1}} \hfill \\ {{e_2} = {v_2} - {z_2}} \hfill \\ {{u_0} = {\beta_{11}}{f_{al}}({e_1},0.5,{h_1}) + {\beta_{12}}{f_{al}}({e_2},1.5,{h_1})} \hfill \\ \end{array} \right. $$

Parameter ${\beta_{11}}$ and ${\beta_{12}}$ are gain coefficients.

Disturbances Compensation

$$ u = {u_0} - {z_3}/{b_0} $$

Parameter ${b_0}$ represents the compensation coefficient.

The control law brings a disturbance compensation control in time for the system. The disturbances cannot make the system go bad in that case.

3.3 MC-ADRC for Glider

ADRC is a control method that doesn’t depend on the model of the controlled object. However, the ADRC may decrease the estimators for uncertainties by importing the model compensation. The model compensation could reduce the estimation pressures for ESO, and it improves the dynamic control performances.

From the structure of ADRC, the state estimation of the three orders ESO is used for estimating both of the parameter changes from the model and the external disturbances. When the object model changes acutely or the external disturbances are oversized. The ESO should have a good tracking performance, which means that the parameter ${z_3}$ have a very high estimation precision. The best way to improve tracking performance for ESO is that to decrease the estimators for ${z_3}$ as much as possible. That means the observed pressure of ESO from uncertainties would be reduced substantially by means of substituting known models into the observation function.

Suppose that $f(x,\dot x) = {f_1}(x,\dot x) + {f_2}(x,\dot x)$, where ${f_1}( \cdot )$ and ${f_2}( \cdot )$ denote the known and unknown model respectively. On the basis of the ESO, let ${x_3} = {f_2}(x,\dot x,w)$, so the ${z_3} \to {f_2}(x,\dot x, \cdots ,{x^{(n - 1)}},t) + w(t)$. The ESO observation equations were transformed as following forms:

$$ \left\{ \begin{array}{l} {{{\dot z}_1} = {z_2} - {\beta_{01}}e} \hfill \\ {{{\dot z}_2} = {z_3} - {\beta_{02}}{f_{al}}(e,0.5,h) + {f_1}(x,\dot x) + {b_0}u} \hfill \\ {{{\dot z}_3} = - {\beta_{03}}{f_{al}}(e,0.25,h)} \hfill \\ \end{array} \right. $$

The system was approximated as the “Integrator Series Mode”. The feedback compensation is $u(t) = {u_0}(t) - [{z_3} + {f_1}(x,\dot x)]/b$.

In the ESO, ${z_3}$ is the estimation value for generalized disturbances and it has many parameters estimation missions including $\theta$, $\dot \theta$, ${r_p}$, ${m_b}$, ${v_1}$ and ${v_3}$. It can be seen that the system has proposed exorbitant requirements for ESO when the parameters ${m_b}$, $\theta$ and $v$ changes tempestuously. In another words, ${z_3}$ must possesses a strong tracking and observation abilities.

Rewrite the pitch angle control equation: $\ddot \theta = {f_1}( \cdot ) + {f_2}( \cdot ) + bu$.

Function ${f_1}( \cdot )$ is the given model that can be estimated. Function ${f_2}( \cdot )$ is the unknown model in the pitch angle control loop.

The ESO estimation equation can be written as: ${z_3} = {f_2}( \cdot ) + (b - {b_0})u$.

According to the structural characteristics of the glider, parameters $\theta$ and $\dot \theta$ can be measured by the Micro Inertial Measurement Unit (MIMU) named MTi sensor. Battery packs position can be measured by the film potentiometer. Due to the $\alpha$, the horizontal component ${v_1}$ and vertical component ${v_3}$ of the velocity $V$ cannot be acquired accurately according to the pitch angle $\theta$.

Toward to the control equation, the input is: $bu = - {r_{p3}}{u_{p1}}$.

Where ${f_1}( \cdot ) = - ({r_{p1}}{P_{p1}} + {r_{p3}}{P_{p3}})\dot \theta - ({b_2}{m_p}g + {{\text{b}}_ 1}{m_p}g{r_{p3}})\theta - ({a_2}{m_p}g{r_{p1}} + {a_ 1}{m_p}g{r_{p3}})$ and ${f_2}( \cdot ) = - {r_{b1}}{P_{b1}}\dot \theta - {b_2}{m_b}g{r_{b1}}\theta - {a_2}{m_b}g{r_{b1}} + ({m_3} - {m_1}){v_1}{v_3} + {M_{DL}}$.

On the basis of the ESO, the estimator is equal to zero if these four conditions are established: (1). Parameter ${z_1}$ is able to track pitch angle $\theta$ commendably. (2) Parameter ${m_b}$ can be measured accurately. (3). Velocity ${v_1}$ and ${v_3}$ could be estimated precisely based on the pitch angle $\theta$. (4). $b = {b_0}$. Off course, the conditions above are strict. In fact, even if the $b \ne {b_0}$ or there are some estimate errors in conditions (1), (2) and (3). What need estimated of the ${z_3}$ is only $(b{ - }{b_0})u$ left. It is much smaller than before. The observation burden and the disturbances of the ESO have been reduced greatly which would have a great improvement for estimation precision. The diagram of pitch angle control based on MC-ADRC shows in Fig. 3.

Fig. 3.

Pitch angle control based on MC-ADRC for glider diagram.

3.4 Parameters Estimation for MC-ADRC

Parameter Estimation for $\alpha$ and $v$.

The external surface of the glider is asymmetric in the vertical direction. The $\alpha$ always exists as well as it is difficult to acquire.

Traditional methods for calculating velocity $V$ as follows: obtaining the vertical velocity component ${v_3}$ via depth pressure sensor. $\chi \approx \theta$ is established by supposing that $\alpha$ is small enough. In that case, the horizontal velocity component ${v_1} \approx {v_3}$ and we believe $V \approx V'$ in some way, Fig. 4. In fact, this assumption is not exactly right.

Fig. 4.

AOA and velocity decomposition in the vertical plane.

When motion of the glider is balanced, it is easy to obtain the torque equilibrium equation according to the kinetic equation of the glider.

The expression of the $\alpha$ is: $\alpha = \frac{{{C_{D0}} + {C_{D1}}{\alpha^2}}}{{({a_w} + {a_h})\tan (\theta + \alpha )}}$

${C_{D0}}$ and ${C_{D1}}$ are the coefficients determining the total (i.e., sum of drag from both the hull and the wings) parasite drag and induced drag, respectively. Where ${a_h}$ and ${a_w}$ are the lift-slope coefficients for the hull and wings.

It can be seen that the $\alpha$ is only related to the pitch angle $\theta$. We get the accurate velocity $V$ through the pitch angle $\theta$ which is measured by the high-precision MTi sensor. The velocity disturbance in the ESO would be eliminated consequently.

Estimation for Parameter ${m_b}$.

The glider buoyancy adjustment mechanism was divided into external oil sac and the internal oil storage tank. The internal oil tank was designed as the inerratic bellows structure and it was installed a cable displacement sensor VXY30. The cable displacement sensor captured a variable quantity when the net buoyancy ${m_b}$ changed.

Measurement for Parameter $\theta$, $\dot \theta$ and ${r_p}$.

Pith angle $\theta$ can be measured by the MTi-10 sensor. Its internal low-power signal processor provides drift-free 3D orientation as well as calibrated 3D acceleration, 3D rate of turn (rate gyro) and 3D earth-magnetic field data. Depended by the MTi, we get the precise pitch angle $\theta$ in an easy way. The pitch angular velocity is the differential signal of pitch angle $\theta$ which is defined as $\dot \theta = \frac{d\theta }{dt}$.

Battery packs position ${r_{p1}}$ can be measured by the ThinPot film potentiometer. The battery packs were fixed at the sliding rail with servo motor. The motor drives battery packs and film potentiometer shuttling back and forth, the position signal ${r_{p1}}$ of the battery packs could be obtained precisely.

4 Simulations Test in MATLAB

For testing the effects of the MC-ADRC algorithm, four groups of comparison experiments were simulated in the MATLAB platform. This control method was contrasted with the traditional ADRC. Control conditions for these four comparison tests as follows: Stabilizing the glider at a certain velocity $V$ and changing the battery packs position ${r_{p1}}$ independently, observing the results and regulation processes of the pitch angle $\theta$ between ADRC and MC-ADRC. The initial pitch angle is −26° and desired pitch angle is −34°.

• I. (1) ADRC algorithm: with no model compensation, $\alpha$ (as well as the $v$) or ${m_b}$. (2) MC-ADRC: parameter $\alpha$ was estimated accurately in compensation model but parameter ${m_b}$ wasn’t compensated.

• II. (1) ADRC algorithm: with no model compensation, any $\alpha$ or ${m_b}$. (2) MC-ADRC: parameter ${m_b}$ was estimated accurately but parameter $\alpha$ wasn’t compensated.

• III. (1) ADRC algorithm: with no model compensation, $\alpha$ or ${m_b}$. (2) MC-ADRC: both of the parameter ${m_b}$ and $\alpha$ were estimated precisely.

• IV. (1) ADRC algorithm: with no model compensation for $\alpha$ or ${m_b}$. (2) MC-ADRC: both of the parameter ${m_b}$ and $\alpha$ were estimated precisely. In this comparison test, we added a disturbance in the adjustment for pitch angle. More specifically, we changed the buoyancy from 400 ml to 300 ml when the pitch changed from −26° to −34°. In that case, the control process was encountered a strong disturbance.

4.1 ADRC Parameters Tuning [14]

Parameters ${r_0}$, ${h_0}$, ${\beta_{01}}$, ${\beta_{02}}$, ${\beta_{03}}$ and ${h_1}$ are related to the sampling step length in the ADRC. They can be determined as follows: ${r_0} = 0.001/{h^2}$, ${h_0} = 5h$, ${\beta_{01}} = 1/h$, ${\beta_{02}} = 1/(3{h^2})$, ${\beta_{03}} = 1/(32{h^3})$, ${h_1} = 10h$. In addition, gain coefficient ${\beta_{11}}$ and ${\beta_{12}}$ are equal to the proportional differential gains of PID controller; compensation coefficient ${b_0}$ corresponds to the integral gain. Combining to the simulation experiences, let ${\beta_{11}}$ = 2, ${\beta_{12}}$ = 0.9 and ${b_0}$ = 0.4.

4.2 Simulation Results

The comparison results shows in Fig. 5. The ADRC and MC-ADRC intervened at 180 s in the four control processes above. The disturbance of the variable buoyancy intervened between the 180 s and 200 s.

Fig. 5.

Adjustment processes comparisons between the ADRC and the MC-ADRC algorithms. (a). AOA $\alpha$ estimated but buoyancy ${m_b}$ was unknown; (b). Buoyancy ${m_b}$ was estimated but AOA $\alpha$ was unknown; (c). Both of the buoyancy ${m_b}$ and AOA $\alpha$ were estimated; (d). Buoyancy ${m_b}$ and AOA $\alpha$ were estimated and there existed a buoyancy disturbance.

Notably, the MC-ADRC controller has good performances. In the Fig. 5(a) with test I, the MC-ADRC has a 110 s settling time and 5.3% overshoot; yet, the ADRC controller’s performances were 160 s and 6.5%. Regarding to the Fig. 5(b) with test II, the performances of MC-ADRC and ADRC were 80 s vs. 160 s and 3.5% vs. 6.5%. For Fig. 5(c), the settling time and overshoot were reduced to 70 s and 2.0% in the test III. For comparison test with disturbance in Fig. 5(d) for test IV, the performances contrast was very obvious. MC-ADRC has a shorter settling time 105 s and a small overshoot 4.1%. However, the ADRC have a large overshoot process, the settling time was up to 190 s and the overshoot was reached 8.6%.

5 Discussions

Table 2 shows control performances comparison between ADRC and MC-ADRC algorithms. Where ${M_P}$ denotes the overshoot and ${t_s}$ represents the settling time in the pitch angle control process.

Table 2. Performances comparison between the ADRC and MC-ADRC algorithms.

It is very clear that the MC-ADRC has good control effects than the ADRC, no matter for the settling time or the overshoot. The former three groups of comparison tests (I, II and III) show that the model compensation method have improved the performances for ADRC significantly. Above all, the more models we know about the system, the better control performances we will obtain. Experiment IV shows that the MC-ADRC has excellent control performances for external disturbances. It reduced overshoot and settling time distinctly in pitch angle control.

6 Conclusions

A new approach to control pitch angle of an underwater glider using model compensation based on the ADRC has been demonstrated. The parameter estimation and parameter measurement methods were putted forward to acquire the compensation model in this paper. For the MC-ADRC method, the more parameters we know in the control model, the better control performances we would obtain. Simulation tests in the MATLAB proved its feasibility and high efficiency: the MC-ADRC algorithm has good control precision and low overshoot with settling time in pitch angle control for glider system. In the future, the MC-ADRC algorithm will be applied to our actual glider system.