Keywords

1 Introduction

Beaches, i.e. the low-lying coasts formed on unconsolidated sediments, are generally under erosion [1,2,3]. These significant on their own right ecosystems are critical components of the coastal zone, as they provide very important ecosystem services, such as flood protection to the valuable coastal assets/infrastructure they front [4] as well as substantial socio-economic benefits as they form the pillar of the ever-increasing coastal tourism [5]. Therefore, the long- and short-term beach morphological evolution (morphodynamics) and/or erosion and its controls have important implications for the sustainable development of the coastal zone.

Beach morphodynamics is controlled by complex forcing-response processes that operate at various spatio-temporal scales [6]. An important determinant of the current and future beach morphological evolution is the shoreline position. This is generally characterized by high spatio-temporal variability, mainly controlled by complex interactions between the beach morphology and sediments and the incident waves. Such interactions can lead to large localized shoreline position changesas well as an overall short- and long-term shoreline retreat (beach erosion) particularly under increasing sea levels and changing storminess [7, 8]. However, the study of these changes through traditional morphodynamic modeling (e.g. [7, 9, 10]) is subject to limitations arising from the: (a) high non-linearities involved in the shoreline re-alignment phenomenon due to complex nearshore hydrodynamical, sedimentological and morphological processes, and (b) high computational costs involved.

To address the above problem, we propose to use a novel neuro-fuzzy network (NFN), designed to model shoreline realignment on the basis of a small number of environmental variables that are based on high frequency observations of the shoreline position and the nearshore hydrodynamics. NFNs attempt to offset the approximate reasoning of fuzzy systems through the learning mechanisms and connectionist structures of neural networks [11,12,13,14]. The proposed network comprises three modules. The first module is a network representation of a standard fuzzy model. The second module is a competitive learning network structure, which generates a set of initial values for the fuzzy rule base antecedent parts. These values are then used to assist to a particle swarm optimization-based learning procedure that finally carries out the network’s optimal parameter estimation. The model is trained and tested at Kamari beach (Santorini), one of the most touristic beaches of the Aegean Archipelago.

The material is organized as follows. Section 2 describes the experimental setup and the data acquisition process. Section 3 presents the analytical structure of the proposed neuro-fuzzy network. The simulation study is given in Sect. 4. Finally, the paper concludes in Sect. 5.

2 Experimental Setup and Raw Data Extraction

Kamari beach is a microtidal beach, located at the island of Santorini (Fig. 1). The southern section of beach (length of about 600 m) forms on coarse sediments, which along the shoreline have mean grain sizes of 2.2–9.5 mm and in the nearshore seabed mean sizes of 0.17–1.39 mm. The beach has a SE orientation and could be exposed to energetic wave conditions.

Fig. 1.
figure 1

(a)–(c) Location of Kamari beach in Santorini, Greece. (d) Bathymetric map of the studied beach part showing also the 30 cross-shore sections and the location of the deployed RBR pressure sensor; and (e) example of a detected shoreline plotted on the corresponding TIMEX image showing also the reference line (the blue line located above the shoreline) used to define the output parameter in the experiments. (Color figure online)

Full size image

The experimental methodology consists of the collection/analysis of (a) beach topographic data and (b) time series of shoreline position and contemporaneous nearshore wave activity during a two-week period at the end of December 2016 (16-31/12/2016).

More specifically, nearshore bathymetric data were obtained through a single beam digital echo-sounder (Hi-Target HD 370) and a Differential GPS (Topcon Hipper RTK-DGPS) deployed from an inflatable boat, whereasland topographic data were obtained through a RTK-DGPS survey at the beginning of the examined period (16/12/2016). From these data, 30 cross-shore (perpendicular to the shoreline) profiles were extracted with a spacing of 20 m (Fig. 1(d)). For each of these cross-shore sections, the wet beach slope (\( W_{S} \)), a critical morphological variable of beach morphodynamics [7, 9], has been estimated forming the first input variable of the proposed network. A pressure sensor (RBRvirtuoso) deployed offshore at about 9 m water depth of the beach (Fig. 1(d)) provided high frequency (4 Hz) nearshore wave data, during 10 min bursts each hour, from which hourly values of significant wave height (\( H_{S} \)), peak wave period (\( T_{P} \)), wave energy (E) and tidal elevations (\( T_{S} \)) were estimated. In addition, mean wave directions during these bursts were estimated from video records obtained from the coastal video system deployed in the area to monitor in high frequency the shoreline position (see below). Wave directions were expressed with regard to the North-South (denoted as \( W_{NS} \)) and East-West (denoted as \( W_{EW} \)) vector components. All the above hydrodynamic characteristics control shoreline position as they impose direct effects on beach morphodynamics [15], and form the remainder of the network’s input variables. Based on the above nomenclature, the input variables taken into account are described as: \( x_{1} = W_{S} ,\,\,x_{2} = \,H_{s} ,\,\,x_{3} = T_{p} ,\,\,x_{4} = E,\,\,x_{5} = T_{s} ,\,x_{6} = \,W_{NS} \), and \( x_{7} = W_{EW} \).

An autonomous coastal video monitoring system was installed at the beach (at the (0,0) point shown in Fig. 1(e)) to monitor shoreline position. The system, which allows automatic and low-cost monitoring of key beach features, comprised a station PC and two fixed Vivotek IP8362 video cameras (center of view elevation of about 22 m above mean sea level), operating at a sampling rate of 5 frames per secondand in hourly 10-minute bursts. Images were corrected for lens distortion and georectified and projected on real-world coordinates using standard photogrammetric methods and ground control points (GCPs) collected during the dedicated RTK-DGPS survey. Shoreline detection was performed during post-processing, using an automated coastal feature detector that records the mean shoreline position over each 10-minute burst on the basis of the obtained TIMEX images (Fig. 1(e)); TIMEX images are the time-averages of the 3000 snapshots collected in each burst defined on the red–green–blue (RGB) colour model. A detailed description of the system and the automated procedure developed to extract the shoreline from the TIMEX imagery can be found in [10]. On the basis of this information, the network’s output variable (y) (for each of the 30 cross-shore profiles and each burst) was defined as the distance between the video extracted shoreline position and a reference line (see Fig. 1(e)); this variable expresses the shoreline position change (re-alignment).

To summarize, the experimental setup generated \( n = 3480 \) input-output data symbolized as \( \varvec{x}_{k} = \left[ {\begin{array}{*{20}c} {x_{k1} } & {x_{k2} } & {x_{k3} } & {x_{k4} } & {x_{k5} } & {x_{k6} } & {x_{k7} } \\ \end{array} } \right]^{T} \), and \( y_{k} \in {\text{R}} \). These data are elaborated by the neuro-fuzzy network in order to model the shoreline realignment during the period of the experiment.

3 The Proposed Neuro-Fuzzy Network

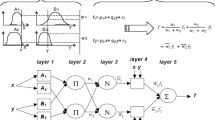
The proposed network comprises three modules (see Fig. 2) namely: (a) the Takagi-Sugeno-Kang (TSK) fuzzy network, (b) the competitive learning network, and (c) the particle swarm optimization (PSO). In what follows, it is assumed that there are \( n \) input-output data pairs \( \left. {\left\{ {\varvec{x}_{k} ;\,y_{k} } \right\}} \right|_{k = 1}^{n} \) with \( \varvec{x}_{k} \in {\text{R}}^{p} \) and \( y_{k} \in {\text{R}} \).

Fig. 2.
figure 2

The structure of the TSK neuro-fuzzy network.

Full size image

3.1 TSK Fuzzy Network

The typical TSK fuzzy model establishes the input-output relations in terms of \( c \) fuzzy rules written as:

$$ R_{\ell } :\,\,If\,\,x_{1} \,\,is\,\,A_{\ell 1} \,\,and\,\, \ldots .\,\,and\,\,x_{p} \,\,\,is\,\,\,A_{\ell p} \,\,\,then\,\,y\,\,is\,\,w_{\ell } (\varvec{x}),\,\,\,\,\,\left( {1 \le \ell \le c} \right) $$
(1)

where, \( A_{\ell j} \) are Gaussian fuzzy sets:

$$ A_{\ell j} (x_{j} ) = \exp \left( { - \left( {{{\left( {x_{j} - v_{\ell j} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{j} - v_{\ell j} } \right)} {\sigma_{\ell j} }}} \right. \kern-0pt} {\sigma_{\ell j} }}} \right)^{2} } \right) $$
(2)

and

$$ w_{\ell } \left( \varvec{x} \right) = a_{\ell 0} + a_{\ell 1} x_{1} + \ldots + a_{\ell p} x_{p} $$
(3)

with \( v_{\ell j} \) and \( \sigma_{\ell j} \) being the fuzzy set centers and widths, and \( a_{\ell j} \in {\text{R}} \). The proposed network representation of a TSK fuzzy model is illustrated in Fig. 2.

There are four layers involved in the inference process. Layer 1 is the input layer. Layer 2 calculates the rule firing degrees as indicated next,

$$ g_{\ell } \left( \varvec{x} \right) = \prod\limits_{j = 1}^{p} {A_{\ell j} (x_{j} )} = \exp \left( { - \sum\limits_{j = 1}^{p} {\left( {{{\left( {x_{j} - v_{\ell j} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{j} - v_{\ell j} } \right)} {\left( {\sigma_{\ell j} } \right)}}} \right. \kern-0pt} {\left( {\sigma_{\ell j} } \right)}}} \right)^{2} } } \right) $$
(4)

In Layer 3, the fuzzy basis functions are calculated as follows:

$$ h_{\ell } \left( \varvec{x} \right) = {{g_{\ell } \left( \varvec{x} \right)} \mathord{\left/ {\vphantom {{g_{\ell } \left( \varvec{x} \right)} {\sum\limits_{i = 1}^{c} {g_{i} \left( \varvec{x} \right)} }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{c} {g_{i} \left( \varvec{x} \right)} }} $$
(5)

Finally, Layer 4 estimates the output of the network:

$$ \hat{y} = \sum\limits_{\ell = 1}^{c} {h_{\ell } \left( \varvec{x} \right)\,w_{\ell } \left( \varvec{x} \right)} $$
(6)

3.2 Competitive Learning Network

The motivation of using the competitive learning network (CLN) is to facilitate the evolutionary process of the PSO algorithm. To do so, the CLN elaborates the input-output data and generates a set of parameter values for the rule antecedent parts. To provide an accurate initialization of the learning mechanism, the above values are then codified in the best position of the PSO algorithm (see Sect. 3.3). The structure of CLN (see Fig. 2) includes a hidden layer that comprises \( c \) nodes, the activation functions of which are given as,

$$ \mu_{\ell } \left( {\varvec{x}_{k} } \right) = \left[ {\sum\limits_{i = 1}^{c} {\left( {\frac{{\left\| {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right\|}}{{\left\| {\varvec{x}_{k} - {\varvec{\upupsilon}}_{i} } \right\|}}} \right)}^{{\frac{2}{m - 1}}} } \right]^{ - 1} ,\,\,\,\,\,\,\,\,\,\,\left( {1 \le \ell \le c;\,\,1 \le k \le n} \right) $$
(7)

where \( m > 1 \), and \( {\varvec{\upupsilon}}_{\ell } \, = \left[ {\upsilon_{\ell 1} ,\,\,\upsilon_{\ell 2} ,\,\, \ldots \,\,\upsilon_{\ell p} } \right]^{T} \in {\text{R}}^{p} \) are the codewords obtained by the competitive learning process. In this sense the set \( \varvec{U} = \left\{ {{\varvec{\upupsilon}}_{1} ,\,{\varvec{\upupsilon}}_{2} ,\, \ldots ,\,{\varvec{\upupsilon}}_{c} } \right\} \) is realized as the set of the center elements of the partition of the data set \( \varvec{X} = \left\{ {\varvec{x}_{1} ,\,\varvec{x}_{2} ,\, \ldots ,\,\varvec{x}_{n} } \right\} \) into \( c \) clusters. The CLN falls in the realm of batch learning vector quantization (BLVQ) introduced by Kohonen in [16]. The objective of the CLN is to provide an estimation of the \( {\varvec{\upupsilon}}_{\ell } \,\left( {1 \le \ell \le c} \right) \) by minimizing the following distortion function [16,17,18],

$$ D = \frac{1}{n}\sum\limits_{k = 1}^{n} {\mathop {\hbox{min} }\limits_{1 \le \ell \le c} \left\{ {\left\| {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right\|^{2} } \right\}} $$
(8)

Assume that we are given a partition of the data set \( \varvec{X} \) into \( c \) clusters with centers (i.e. codewords) \( \varvec{U} = \left\{ {{\varvec{\upupsilon}}_{1} ,\,{\varvec{\upupsilon}}_{2} ,\, \ldots ,\,{\varvec{\upupsilon}}_{c} } \right\} \). Then, the mean of the set \( \varvec{U} \) is evaluated as,

$$ {\tilde{\mathbf{\upsilon }}} = \frac{1}{c}\sum\limits_{\ell = 1}^{c} {{\varvec{\upupsilon}}_{\ell } } $$
(9)

In addition, we define the \( p \times \left( {c + 1} \right) \) matrix

$$ \varvec{B} = \left[ {\begin{array}{*{20}c} {\varvec{b}_{1} } & {\varvec{b}_{2} } & \ldots & {\varvec{b}_{c} } & {\varvec{b}_{c + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{\upupsilon}}_{1} } & {{\varvec{\upupsilon}}_{2} } & \ldots & {{\varvec{\upupsilon}}_{c} } & {{\tilde{\mathbf{\upsilon }}}} \\ \end{array} } \right] $$
(10)

The codeword positions are directly affected by the distribution of the clusters across the feature space [17, 18]. An optimal cluster distribution should possess well separated and compact clusters. These two properties depend on the relative positions of the codewords [18, 19]. To quantify the effect the codeword relative positions impose on the quality of the partition, we view each codeword as the center of a multidimensional fuzzy set, the elements of which are the rest of the codewords. In this direction, the membership degree of the codeword \( \varvec{b}_{\ell } = {\varvec{\upupsilon}}_{\ell } \) in the cluster with center the codeword \( \varvec{b}_{i} = {\varvec{\upupsilon}}_{i} \) is defined as [18]

$$ u_{i\ell } = \left[ {\sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne \ell \end{subarray} }^{c + 1} {\left( {\frac{{\left\| {\varvec{b}_{\ell } - \varvec{b}_{i} } \right\|}}{{\left\| {\varvec{b}_{\ell } - \varvec{b}_{l} } \right\|}}} \right)}^{{\frac{2}{m - 1}}} } \right]^{ - 1} ,\,\,\,\,\,\,\,\,\,\,\left( {1 \le \ell \le c;\,\,1 \le i \le c} \right) $$
(11)

where \( m \in \left( {1,\,\infty } \right) \) is the fuzziness parameter. Note that the indices \( \ell \) and \( i \) are not assigned the value \( c + 1 \), which corresponds to the position \( \varvec{b}_{c + 1} = {\tilde{\mathbf{\upsilon }}} \). If the quantity \( {\tilde{\mathbf{\upsilon }}} \) was not taken into account, then in case there were only two codewords (i.e. \( c = 2 \)) the function in \( u_{i\ell } \) would not work properly because it would give one in all cases. Therefore the presence of \( \varvec{b}_{c + 1} = {\tilde{\mathbf{\upsilon }}} \) is important. Next, for each \( \varvec{x}_{k} \) the closest codeword \( {\varvec{\upupsilon}}_{{i_{k} }} = \varvec{b}_{{i_{k} }} \) is detected

$$ \left\| {\varvec{x}_{k} - {\varvec{\upupsilon}}_{{i_{k} }} } \right\| = \mathop {\hbox{min} }\limits_{1 \le \ell \le c} \left\{ {\left\| {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right\|} \right\} $$
(12)

To this end, the codewords are updated by the subsequent learning rule,

$$ {\varvec{\upupsilon}}_{\ell }^{t + 1} = {\varvec{\upupsilon}}_{\ell }^{t} + \eta \,f_{{i_{k} ,\,\ell }}^{t} \,\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell }^{t} } \right) $$
(13)

where \( t \) is the iteration number, \( \eta > 0 \) is the learning rate, and \( \,f_{{i_{k} ,\,\ell }} \) is the neighborhood function:

$$ \,f_{{i_{k} ,\,\ell \,}} = \left\{ \begin{aligned} \,\,\,\,1\,\,\,,\,\,\,if\,\ell = i_{k} \,\, \hfill \\ u_{{i_{k} ,\,\ell }} ,\,\,otherwise \hfill \\ \end{aligned} \right. $$
(14)

with \( i_{k} \in \left\{ {1,\,2,\, \ldots ,\,c} \right\} \), \( 1 \le \ell \le c \), and \( u_{{i_{k} ,\,\ell }} \) is calculated in (11). The function \( \,f_{{i_{k} ,\,\ell }} \) gives the relative excitation degree of each codeword having as reference point the winning codeword and the relative positions of the rest of the codewords. For a more detailed analysis of the properties of the function \( \,f_{{i_{k} ,\,\ell }} \) the interested reader is referred to [18]. As easily seen, the learning rule in Eq. (13) constitutes an on-line process. In a similar way to the BLVQ [16], we can produce a batch mechanism by employing the subsequent expectation measure:

$$ E\left[ {\,f_{{i_{k} ,\,\ell }}^{t} \,\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell }^{t} } \right)} \right] = 0\,\,\,\,as\,\,\,t \to \infty $$
(15)

The condition in (15) enables us to modify the codeword updating rule as,

$$ {\varvec{\upupsilon}}_{\ell }^{t + 1} = {{\sum\limits_{k = 1}^{n} {\,f_{{i_{k} ,\,\ell }}^{t} \,\varvec{x}_{k} } } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{n} {\,f_{{i_{k} ,\,\ell }}^{t} \,\varvec{x}_{k} } } {\sum\limits_{k = 1}^{n} {\,f_{{i_{k} ,\,\ell }}^{t} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{n} {\,f_{{i_{k} ,\,\ell }}^{t} } }} $$
(16)

The above CLN appears to be less sensitive to initialization when compare to the BLVQ. This remark is justified by the fact that, based on the functions in (11) and (14), a specific codeword moves towards its new position considering the relative positions of the rest of codewords. Thus, before obtaining the new partition, the algorithm takes into account the overall current partition and forces all codewords to be more competitive. Therefore, in a single iteration all of the codewords are moving in an attempt to win as much as training vectors they can. This behavior enables the whole updating process to avoid undesired local minima.

Based on the nomenclature given in Eqs. (1)–(6), to extract initial values for the rule antecedents, the fuzzy set centers are determined by projecting the codewords \( {\varvec{\upupsilon}}_{\ell } \,\,\,(1 \le \ell \le c) \) on each dimension:

$$ v_{\ell j} = \upsilon_{\ell j} \,,\,\,\,\,\,\,\,\,\left( {1 \le \ell \le c;\,1 \le j \le p} \right)\, $$
(17)

while the corresponding fuzzy set widths by the next relation

$$ \sigma_{\ell j} = \left( {Diag\left( {\varvec{FC}_{\ell } } \right)} \right)^{1/2} $$
(18)

where \( \varvec{FC}_{\ell } \) is the fuzzy covariance matrix [20], which based on Eq. (7) is

$$ \varvec{FC}_{\ell } = {{\sum\limits_{k = 1}^{n} {\left( {\mu_{\ell } \left( {\varvec{x}_{k} } \right)} \right)^{m} \,\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right)\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right)^{T} \,} } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{n} {\left( {\mu_{\ell } \left( {\varvec{x}_{k} } \right)} \right)^{m} \,\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right)\left( {\varvec{x}_{k} - {\varvec{\upupsilon}}_{\ell } } \right)^{T} \,} } {\sum\limits_{k = 1}^{n} {\left( {\mu_{\ell } \left( {\varvec{x}_{k} } \right)} \right)^{m} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{n} {\left( {\mu_{\ell } \left( {\varvec{x}_{k} } \right)} \right)^{m} } }} $$
(19)

3.3 Particle Swarm Optimization

The particle swarm optimization (PSO) elaborates on a population of \( N \) particles \( \varvec{p}_{i} \in {\text{R}}^{q} \) [21,22,23]. Each particle is assigned a velocity \( \varvec{h}_{i} \in R^{q} \) \( \left( {1 \le i \le N} \right) \). The positions with the best values of the objective function obtained so far by the ith particle and by all particles are respectively denoted as \( \varvec{p}_{i}^{best} \) and \( \varvec{p}_{best} \). The velocity is updated as

$$ \varvec{h}_{i} \left( {t + 1} \right) = \,\omega \,\varvec{h}_{i} \left( t \right)\, + \varphi_{1} \,\varvec{U}\left( {0,\,1} \right)\, \otimes \,\left( {\varvec{p}_{i}^{best} \left( t \right) - \varvec{p}_{i} \left( t \right)} \right)\, + \,\varphi_{2} \,\varvec{U}\left( {0,\,1} \right) \otimes \,\left( {\varvec{p}_{best} \left( t \right) - \varvec{p}_{i} \left( t \right)} \right) $$
(20)

where \( \otimes \) is the point-wise vector multiplication; \( \varvec{U}\left( {0,\,\,1} \right) \) is a vector with elements randomly generated in [0, 1]; \( \omega ,\,\varphi_{1} \), and \( \varphi_{2} \) are positive constant numbers called the inertia, cognitive and social parameter, respectively. The position of each particle is:

$$ \varvec{p}_{i} (t + 1) = \varvec{p}_{i} (t) + \varvec{h}_{i} (t + 1) $$
(21)

In our case, to implement the PSO, each particle codifies the antecedent parameters, i.e. the fuzzy set centers and widths. Therefore, the dimension of the particles’ search space is equal to \( q = 2\,c\,p \) (i.e. \( \varvec{p}_{i} \in {\text{R}}^{q} ,\,\,i = 1,\,2,\, \ldots ,\,N \)). All particles are randomly initialized. In addition, the values of the antecedent parameters that were calculated in Eqs. (17) and (18) are codified in the best overall position \( \varvec{p}_{best} \), which is expected to guide more efficiently the particles in their search for optimal parameter estimation. On the other hand, there are \( c\left( {p + 1} \right) \) consequent parameters, described as

$$ \varvec{a} = \left[ {a_{10} ,\,a_{11} , \ldots ,\,a_{1p} ,\,a_{20} ,\,a_{21} , \ldots ,\,a_{2p} ,\, \ldots ,\,a_{c0} ,\,a_{c1} ,\, \ldots ,\,a_{cp} } \right]^{T} $$
(22)

The estimation of these parameters is carried out in terms of ridge regression [24]. To do so, we employ the following matrices:

$$ \Lambda = \left[ {\begin{array}{*{20}c} {\varLambda_{1} } & {\varLambda_{2} } & \ldots & {\varLambda_{n} } \\ \end{array} } \right]^{T} $$
(23)
$$ \varLambda_{k} = \left[ {\begin{array}{*{20}c} {\varvec{\lambda}_{k1} } & {\varvec{\lambda}_{k2} } & \ldots & {\varvec{\lambda}_{kc} } \\ \end{array} \,\,} \right]{\kern 1pt} \,\,\,\,\,\,\left( {1 \le k \le n} \right) $$
(24)
$$ \varvec{\lambda}_{k\ell } = \left[ {\begin{array}{*{20}c} {h_{\ell } \left( {\varvec{x}_{k} } \right)} & {h_{\ell } \left( {\varvec{x}_{k} } \right)\,x_{k1} \,} & \ldots & {h_{\ell } \left( {\varvec{x}_{k} } \right)\,x_{kp} } \\ \end{array} } \right]\,\,\,\,\,\left( {1 \le \ell \le c} \right) $$
(25)

Note that the dimensionality of matrix \( \Lambda \) is \( n \times c\left( {p + 1} \right) \). The objective of ridge regression is to minimize the following error function [24]:

$$ E = \left\| {\Lambda \varvec{a} - Y} \right\|^{2} + \left\| {\Gamma a} \right\|^{2} $$
(26)

where \( Y = \left[ {y_{1} ,\,y_{2} ,\, \ldots ,\,y_{n} } \right]^{T} \), \( \Gamma = \beta \,I \) with \( \beta > 0 \), and \( I \) the \( c\left( {p + 1} \right) \times c\left( {p + 1} \right) \) identity matrix. The parameter \( \beta \) is called regularization parameter and, in this paper, its value is adjusted manually. The solution to the above problem reads as [24],

$$ \tilde{\varvec{a}} = \left( {\Lambda ^{T}\Lambda +\Gamma ^{T}\Gamma } \right)^{ - 1}\Lambda ^{T} Y $$
(27)

4 Simulation Study and Discussion

Based on the analysis described in Sect. 2, the data set includes \( n = 3480 \) input-output data pairs (corresponding to 30 beach cross-sections) of the form \( \left. {\left\{ {\varvec{x}_{k} ;\,y_{k} } \right\}} \right|_{k = 1}^{n} \) with \( \varvec{x}_{k} = \left[ {\begin{array}{*{20}c} {x_{k1} } & {x_{k2} } & \ldots & {x_{k7} } \\ \end{array} } \right]^{T} \) and \( y_{k} \in \varvec{\Re } \). The data set was divided into a training set consisting of the 60% of the original data, and a testing set consisting of the remainder 40%. Parameter setting for the proposed methodology is as follows: \( m = 2 \), and \( \beta = 20 \). For the PSO we set \( \varphi_{1} = \varphi_{2} = 2 \), the parameter \( \omega \) was randomly selected in \( \left[ {0.5,\,\,1} \right] \), and the population size was \( N = 20 \).

For comparison, two more neural networks were designed and implemented. The first is a radial basis function neural network (RBFNN). The parameters of the basis functions were estimated in terms of the input-output fuzzy clustering algorithm developed in [20], while the connection weights were calculated by the orthogonal least squares method. The second is a feedforward neural network (FFNN), the activation functions of which read as:

$$ f(x) = \tanh \frac{x}{2} $$
(28)

To train the FFNN we used the PSO algorithm (see previous Section) with the above parameter setting. All networks were implemented using the Matlab software.

The performance index used in the simulations was the root mean square error:

$$ RMSE = \sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {\left| {y_{k} - \hat{y}_{k} } \right|^{2} } } $$
(29)

For the three networks, we considered various numbers of rules/nodes, whereas for each number of rules/nodes we run 10 different initializations. The results are shown in Table 1. The proposed network appears to have the best performance compared with the other two networks. The best result for both the training and testing data sets is obtained by the proposed network for a number of rules equal to \( c = 10 \).

Table 1. RMSEs and the corresponding standard deviations for the three networks with respect to various numbers of rule/nodes
Full size table

The number of rules plays an important role for the validity of the method since as it increases the RMSE decreases. The results reported in Table 1 are visualized also in Fig. 3. There are some interesting observations related to this figure. First, the superiority of the proposed method is clear, in comparison with the other two tested networks. Second, the behavior of the FFNN and the RBFNN appears to be similar, but with the latter achieving better performance in both the training and testing data. Third, in all networks, the general tendency is a decrease (as expected) of the RMSEs as the number of rules/nodes increases.

Fig. 3.
figure 3

Mean values of the RMSE as a function of the number of rules/nodes for the training and testing data.

Full size image

With regard to the effectiveness of the proposed network to model shoreline re-alignment, the following should be noted. The RMSEs found, although smaller than those of the other tested networks is still considered high, being between 7.2–7.7 m, depending on the number of rules/nodes. However, it should be noted that the variability of the shoreline position of the Kamari beach was indeed high during the 15-day period of observations, showing, in some cross-sections, differences between the minimum and maximum cross-shore shoreline position in excess of 15 m and a standard deviation of up to 8 m. Therefore, it seems that the obtained high RMSEs reflect the high spatio-temporal variability of the Kamari shoreline position observed during the period of observations; thus, the proposed network could model/predict the shoreline re-alignment to accuracy similar to that of the actual variability of the beach.

The results suggest that in order to improve the proposed model effectiveness in the case of beaches the shorelines of which are characterised by high spatio-temporal variability, there should be some changes in the input variables. First, another input variable might be introduced that can define the ‘antecedent’ cross-shore position of the shoreline; a good guess should be the average shoreline position of the previous 24 h for each tested cross-section that could be easily defined from the video imagery. It is thought that the inclusion of such a parameter will improve the behavior of the proposed model. Secondly, as the tidal range at the Kamari beach was found to be rather small (<0.08 m), it may be that nearshore total water level during energetic events is controlled mostly by the storm-induced level increases. In this case, it makes sense for an input variable reflecting this process (i.e. the total nearshore water level) to be used instead of the tidal elevation (\( T_{S} \)). Generally, the encouraging results of the modelling exercise suggest that the proposed neural network, after a fine-tuning of the input variables, can be used to model the shoreline re-alignment of beaches characterised by highly variable morphodynamics, on the basis of a small number of environmental variables.

5 Summary and Conclusions

In the present contribution we present a systematic methodology that uses a sophisticated experimental setup and a novel neuro-fuzzy network to model and predict the phenomenon of shoreline realignment at a highly touristic beach (Kamari, Santorini). A set of morphological and wave variables were identified that can affect shoreline realignment, which together with records of hourly shoreline positions obtained using a coastal video imagery system, were used to generate the network’s input-output training data. The proposed network consists of three modules. The main task of the first module is to provide the inference mechanism of a typical fuzzy system represented as network structure. The second module constitutes a competitive learning network able to provide an initial partition of the input feature space. This partition is used to extract a set of values for the fuzzy rule antecedent parameters that are codified in the overall best position of a PSO approach. Then, the PSO runs properly and optimizes the network’s parameters. In each step of the iterative implementation of the PSO algorithm, the fuzzy rule consequent parameters are evaluated using ridge regression. Simulation experiments were carried and the results were compared with those by two other neural networks: a radial basis function neural network and a feedforward neural network. The comparison showed that the proposed network performs better in all cases. Regarding the effectiveness of the proposed network to model shoreline re-alignment, the RMSE found (7.2–7.7 m, depending on the number of rules/modes), reflects the high variability of the shoreline position of the Kamari beach during the period of observations: the RMSE is of a similar order to the standard deviation (up to 8 m) of the cross-shore shoreline position. The results are encouraging and the effectiveness of the proposed network could be further improved by changes (fine-tuning) of the input variables.