Dynamics and Control of Spiral and Scroll Waves

Abstract

Excitable systems can sustain different kinds of wave forms like target patterns, two-dimensional spiral waves or their three-dimensional counterparts, the scroll waves . The dynamics of these excitation patterns and their responses to different kinds of internal and external perturbations are being looked into. These waves interact with neighboring vortices, that could lead to either attraction or repulsion and sometimes even their merging. Thermal gradients and electric fields can be used to control the motion of spiral and scroll waves. Scroll waves anchor to unexcitable heterogeneities and external field gradients can be used to unpin them from such obstacles. Our experiments with the Belousov–Zhabotinsky reaction are explained on the basis of numerical simulations using the Barkley model.

1 Introduction

Spiral and scroll wave activities are often encountered in different kinds of excitable media, like slime molds, viz. Dictyostelium discoideum [1], the nervous [2], retinal [3] and cardiac tissues [4, 5], catalytic [6] and precipitation chemical processes [7], etc. These waves have a higher frequency and shorter wavelength than the plane waves or target waves in the same medium [8]. Hence, once formed, they take over the entire excitable space, casting aside any target waves that may have been present. In a system such as the heart, this gives rise to arrhythmia, or fast and irregular heartbeats. This means that the heart cannot pump enough blood to the organs [9]. The situation may further worsen when there is spiral breakup or turbulence, as that is reflected in a medical condition called Fibrillation, which when occurring in the ventricles of the heart (VF) can cause immediate cardiac arrest and death. The understanding of such phenomenon requires a complete knowledge of the dynamics of these wave forms. Further, in order to find measures of cure, one needs to be able to control these waves. Current methods of defibrillation employ a strong and quick electric pulse that aims at erasing all wave forms and depends on the pacemaker cells of the heart to restart the supply of the regular waves. But such strong electric shock can create scars in the cardiac tissues which will act as seeds of future fibrillation. Milder methods of control of spiral and scroll waves are hence sought after. The heart is a complicated biological organ, and experiments on a live heart are neither easy nor cost-effective to be carried out on a regular basis. Another excitable system which shows similar kinds of wave forms is the Belousov–Zhabotinsky (BZ) reaction [10, 11]. This is an oscillatory redox reaction that can sustain spiral and scroll waves in an unstirred medium. Though there are several mismatches between the two systems: the heart is highly heterogeneous and the conduction velocity of the cardiac waves are around 0.2–0.5 m s$^{-1}$, whereas the BZ system is mostly homogenous and its waves have a typical velocity in the range of 0.01–0.1 mm s$^{-1}$; nevertheless, the exact nature of the waves that they sustain, makes the BZ system one of the simplest laboratory models for the study of spiral and scroll waves.

Through this contribution we try to summarize the results of some experimental research of spiral and scroll waves, specifically in the BZ system. Our main focus is on the methods employed for controlling the dynamics of these waveforms. We explore how vortices interact with each other, anchor to unexcitable obstacles, and how they respond to external stimuli. Simple numerical simulations used to explain the experimental findings are also discussed.

2 Spiral and Scroll Waves in the BZ System

In the last couple of decades, several studies have employed the BZ system to understand spiral and scroll wave dynamics [12]. The BZ system constitutes the oxidation of an organic acid by sodium bromate, in the presence of sulphuric acid. Ferroin as well as some ruthenium or cerium complex can act as a catalyst in the reaction that can show a change of color when stirred. In unstirred layers of BZ solution, the system can sustain two-dimensional (2D) spiral and three-dimensional (3D) scroll waves (Fig. 1). A typical BZ reaction in 2D constitutes a 2 mm layer of agarose gel with the required concentrations of the reagents. A gel is used to rule out convection effects. A 3D BZ system involves two gel layers (of 4 mm each) placed one above the other.

Fig. 1

a Spiral and b scroll waves in the Ferroin catalyzed BZ system. The initial concentrations of reactants in the 0.8% (w/v) agarose gel layers are, $[\text {NaBrO}_3]=0.04$ M, $[\text {CH}_2(\text {COOH})_2]=0.04$ M, $[\text {H}_2\text {SO}_4]=0.16$ M, and [Fe(o-phen)$_3$]SO$_4 = 0.5$ mM

In a typical experiment, the reaction is carried out in a flat reaction chamber (like a petri dish) that is illuminated from below by a white light source and viewed from the top. In recent times, a charge coupled device camera connected to a personal computer is frequently used to take snapshots of the experiment and record the data. The images are later analyzed by using different computational techniques, and the variation of the intensity studied to make observations on the dynamics of the wave forms. Tomographic techniques are also used by some groups to analyze the 3D scroll waves [13]. This enables one to get a three-dimensional view of the entire scroll as opposed to the top view. The latter gives an intensity profile that is basically the sum of intensities of every layer in the 3D object, more like a projection image.

Numerical studies of spiral and scroll waves are also very beneficial to understand the dynamics of the tips and the filaments. There are several mathematical models that mimic reaction diffusion systems. The simplest and most versatile amongst them is the Barkley model [14]. This is purely a mathematical model of an activator—inhibitor system that supports the formation of spiral and scroll waves (Fig. 2).

$$\begin{aligned} \frac{\partial u}{\partial t}= & {} {1 \over \epsilon } \left\{ u(1-u)\left( u-{{v+b}\over {a}}\right) \right\} - \nabla J_u,\end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial v}{\partial t}= & {} u - v - \nabla J_v. \end{aligned}$$

(2)

where u and v are the concentrations of the activator and inhibitor respectively, $\epsilon$, a and b are system parameters of the system, $J_u$ and $J_v$ are the fluxes of the ions. In the presence of diffusion, the fluxes are given by, $J_u= -D_u \nabla u$ and $J_v= -D_v \nabla v$, where $D_u$ and $D_v$ are the translational diffusion coefficients of u and v respectively.

Fig. 2

Numerical simulation of the Barkley model showing formation of a spiral in two dimensions (a) and a scroll in three dimensions (b). Parameter values taken are $a = 1.1$, $b = 0.84$, and $\epsilon = 0.02$. $D_u = 1.0$, $D_v = 1.0$. Zero flux boundary condition is set for each diffusing species along all the boundaries

The Oregonator model, which has been derived from the simplified kinetics of the BZ system, is also widely used in the theoretical study of these systems.

Fig. 3

a–c Various tip trajectories of spiral waves in the experimental BZ system. d A three-dimensional scroll wave obtained by simulation of the Barkley model. The filament, which is traced in blue, is identified at regions where $u = 0.5$ and $v = a/2-b$. Other parameters same as in Fig. 2

A two-dimensional spiral wave has a singularity, its tip. The trajectories of spiral tips are very interesting, and several attempts have been made to study them. Oftentimes the tip traces out trajectories that are aesthetically pleasing (Fig. 3a). The trajectory could be circular (Fig. 3b) or a meandering one (Fig. 3c). Meandering trajectories could be epicycloid or hypocycloid in nature [15].

Fig. 4

Time evolution of the filament of a scroll ring. The filament shrinks with time. a Filaments from four snapshots of an experiment with the BZ system, superposed on each other. Each snapshot is 15 min apart. b Filaments of a simulation involving a scroll ring in the Barkley model

The three-dimensional scroll waves also have a one-dimensional singularity. This is the filament of the scroll (Fig. 3d). The filament is that geometry around which the vortex rotates [16]. The ends of the filament will either close in on itself or touch the boundaries. Filaments are geometrical entities that follow the curvature dependent motion, according as

$$\begin{aligned} \frac{\text {d}{} \mathbf s }{\text {d}t} = \alpha \kappa \hat{\mathbf{N }} + \beta \kappa \hat{\mathbf{B }}, \end{aligned}$$

(3)

where $\alpha$ is the filament tension, $\beta$ the translational drift coefficient, $\kappa$ the local curvature, $\hat{\mathbf{N }}$ the unit normal vector, and $\hat{\mathbf{B }}$ the unit binormal vector of the curve. It has been shown that the filament of a scroll wave in the BZ reaction has positive filament tension $\alpha >0$, meaning a round scroll ring will always shrink (Fig. 4). Also $\beta \sim 0$ in an appreciable concentration range, choosing which would ascertain that there is no movement in the $z-$direction. Alternatively, negative filament tension paves the way for interesting situations like spiral wave turbulence.

3 Interaction of Spiral and Scroll Waves

Spiral waves of same frequency and wavelength will coexist side by side in a homogenously excitable system. Spiral waves generally occur in pairs. In a homogeneous environment, the two tips rotate with the same frequency and hence the mutual distance between them does not change with time. But if the excitability of one of the two tips of the spiral pair can be changed, then the faster arm will perturb the slower arm, and the two tips will move away from each other (Fig. 5).

Fig. 5

Faster arm (lower) of a spiral pair pushing away the slower arm in experiments involving a thin layer of the BZ system. a 15 min and b 100 min after initiation of spiral

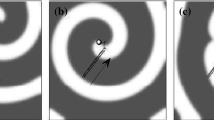
Again a spiral arm may act as a defect when it is forced by a high-frequency wave train that may be originating from a target source or another fast moving spiral (Fig. 6) [17].

Fig. 6

a–c Drift of a spiral defect in a BZ system. The time between subsequent snapshots is 200s. The arrows indicate the position of the defect at every instant. d Trapping of a defect by three forcing waves. The snapshot is from a later stage of the experiment, after the trapping of the defect. The trajectory of the defect has been superscribed in white

Depending on the relative frequencies of the spiral wave and the forcing wave, the direction of drift may vary. Two or three forcing waves can allow the positioning of the spiral at a specific point in space (Fig. 6d).

Scroll waves may interact with each other if they are close enough [18]. Depending on their mutual orientation, two scroll rings can push each other away and rupture on touching the system boundary, or they can reconnect to form a single, large ring (Fig. 7). Reconnection only occurs when the filaments lie within one core length of each other (Fig. 8). The reconnected filament has highly extended lifetimes, which could have serious implications in systems where they occur.

Fig. 7

Schematic representation of filament interaction [18]. Small black arrows denote the motion of the constituent spirals around the points of nearest approach of the filaments. a Reconnection of vortex filaments. The nearest approaching spirals have opposite sense of rotation. b Repulsion of filaments and possible rupture at the boundary. Here the nearest spirals have same sense of rotation

Fig. 8

a–d Reconnection of scroll wave filaments in the BZ system. Snapshots of a pair of coplanar scroll waves at a 7 min, b 21 min, c 35 min, and d 49 min after scroll-wave initiation. e Reconnection as a function of inter-filament distance Z$_{0}$, and ring diameter, d$_{0}$. Reconnected filaments are marked as full (red) circles and nonreconnected ones as open (blue) circles

4 Influence of External Gradients

Reaction-diffusion systems react to external field gradients. Noise, electromagnetic fields and thermal gradients can bring about instability in a stable system [19]. The ions in the BZ system are also expected to be directly affected by the application of such external fields. The flux in these cases get modified due to the presence of the gradients. In the presence of an electric field, the flux for a species u is of the form:

$$\begin{aligned} J_u= -D_u \nabla u + D_u z_u u E \end{aligned}$$

(4)

where $z_u$ is the charge on u, and E the electric field or electric potential gradient. The flux in the presence of a thermal gradient takes the form [20]:

$$\begin{aligned} J_u= -D_u \nabla u - D_{T_u} u (1-r_u) \nabla T \end{aligned}$$

(5)

where $D_{T_u}= (D_u S_{T_0})/ (1+k_s u)$, is the thermal diffusion coefficient of species u, $r_u$ is its relative concentration given by, $r_u = u/(u+v)$, and $\nabla T$ is the thermal gradient between two sides of the reaction vessel and a constant for a reaction. The flux of species v also gets similarly modified in the presence of external gradients.

Spiral waves meander away from their point of initiation under the influence of electrical and thermal gradients [21] (Fig. 9a). Scroll waves on the other hand try to align themselves perpendicular to the direction of the gradient [22, 23] (Fig. 9b, c). It was found that the reoriented scroll ring later moves in the direction of the hot end (thermal gradient) or the positive electrode (electric potential gradient) .

Fig. 9

a Movement of a spiral under the influence of an electric field (1.5 V cm$^{-1}$, positive electrode on the left). The snapshot has been taken 10 min after the field has been applied, and the tip trajectory has been superposed on it to show the path the spiral has traced. b–c Reorientation of a scroll ring under a thermal gradient ($\nabla \text {T} = 1\,^{\circ }\text {C cm}^{-1}$, right to left). The two snapshots have been taken b just before and c 26 min after applying the gradient

This observation can be further extended to control the position of spiral and scroll waves. A scroll ring can be made to traverse in a particular direction by employing moving or multiple gradients (Fig. 10) [24].

Fig. 10

Trajectory of a scroll ring under a moving electric potential. The field strength is 1.5 V cm$^{-1}$, and the position of the electrodes are changed after every 1 h. The continuous bold line in every box shows the trajectory for the current position of the electrodes, while broken lines denote past trajectory. Open circle in a denotes the initial position of the center of the scroll ring and 5 in d is the final position of the ring center. For any orientation of the gradient, it is observed that the scroll ring moves in the direction of the positive electrode

Fig. 11

Pinning of scroll waves. Snapshots (a, c, e) and corresponding time-space plots (b, d, f) of three experiments. a, b freely collapsing scroll; c, d vortex pinned to glass beads of 1 mm radius; e, f scroll ring pinned to a rubber O-ring of diameter 6.0 mm and thickness 2.0 mm. The time-space plots have been constructed by plotting intensity profiles with time, along the straight black lines seen in the corresponding snapshot. These plots (time going left to right) span time intervals of 120 min (b), 210 min (d) and 183 min (f)

5 Pinning of Scroll Waves to Unexcitable Obstacles

The breakage of a plane wave due to some unexcitable obstacle, in conducive conditions of excitability, can lead to the formation of spiral and scroll waves. Again, such unexcitable obstacles can also act as anchors to these wave forms. Pinning is a phenomenon which can be seen in the BZ reaction, where spiral waves and scroll waves get attached to glass beads and rubber rings (Fig. 11). Once pinned, the filament tends to be stabilized and no longer shrinks like a free filament. This increases the lifetime of the scroll rings infinitely [25, 26]. In the cardiac tissue, scroll waves may get pinned to scar tissues and other heterogeneous anomalies. The elongated lifetimes of these pinned vortices will be further detrimental to cardiac health. Hence, along with the control of free scroll waves, the mechanism of pinning and possible ways of unpinning of scroll waves are topics of major concern.

Fig. 12

a–b Electric field controlled unpinning of scroll ring in an experimental BZ system. The two snapshots are taken just before (a) and 23 min after (b) the application of electric field (1.5 V cm$^{-1}$). c—f Filament dynamics of unpinning under a thermal gradient (right to left) for different orientations of inert obstacles. Results of two sets of simulation for the Barkley model: interbead axis parallel to the gradient vector in (c, d) and perpendicular in (e, f). The curves (red) in the center of the cube are the filaments, the spheres (blue) are the pinning obstacles, and the curves (blue) along with the circles (purple) at the bottom of the box are the two-dimensional projections of the filament and the obstacle

6 Unpinning of Scroll Waves by External Gradients

In the earlier sections we have seen that spiral and scroll waves can be controlled by external field gradients. It is hence worthwhile to speculate if such external gradients could be successful in unpinning the waves anchored to inhomogeneous obstacles. Further studies showed that thermal [27] and electric potential [28] gradeints were able to unpin stable scroll rings attached to beads, in the BZ system (Fig. 12).

7 Discussion and Future Direction

The study of 2D spiral waves and 3D scroll waves in the homogeneous BZ system has led to an appreciable understanding of their dynamics. Activity of free and pinned waves, and their modified dynamics under the influence of neighboring sources of excitation waves and external field gradients have been well studied. It has been shown that such external fields can be used to control them and position them in space. Further studies aiming at the annihilation of trapped defects needs to be carried out. However, the real challenge lies in extending our knowledge to the control of such waves in biological systems, like the cardiac tissues. For this, we have to understand better the effect of irregular heterogeneities and other complexities present in such excitable systems. Once we are successful in bridging this gap and a correlation has been established between the waveforms in the BZ system and the heart, it may be possible to design medical gadgets that will pave the way for better treatment of conditions like VT and VF that results from these waves.