Modeling of Material Flow Problems

Abstract

In this article we discuss the description of modern manufacturing or production problems using continuous models. Instead of a detailed description of the production process, a mathematical formulation is used based on transport equations. The challenge is to derive novel and nonstandard approaches that allow to incorporate detailed nonlinear dynamic behavior, which is currently not possible with the widely applied linear or mixed integer linear approaches. Starting from discrete event simulations as a basic description we explore the relation between the product density and the flow of parts (also known as clearing function). Data-fitting procedures help to identify the underlying parameters. We show the relationships between discrete event simulations, queuing models and transport model-based methods, and present several applications.

1 Introduction and Literature Overview

Manufacturing systems are studied in the literature on either a discrete level (using time recursions) or on a macroscopic level (using a continuum description based on differential equations for transport processes). In recent years, continuous or fluid-like models have been particularly introduced to model high-volume production [3–5, 10–13, 17, 21]. Those dynamics are often inspired by discrete event simulations (DES), see [9]. In the current work we aim on bridging the discrete and continuous level by presenting a suitable hierarchy of models with reasonable transitions.

An approach is proposed similar to gas dynamics. In physics, discrete events and discrete parts are considered as fundamental units used to describe microscopic phenomena. Those time-dependent individual dynamics are typically governed by ordinary differential equations. They provide an accurate description of the underlying process. At the same time, the system as a whole shows pattern formation such as jams in traffic flow, flocking in swarming behavior or shock waves in aerodynamics. A similar approach for production processes is considered. Here, the detailed dynamic is the description of the production process of individual parts. However, often there is only interest in the global phenomena of the system like overloads, queuing or mean production rates. We may argue that there are different scales also present in production. Therefore, a similar approach as in gas dynamics is suitable in order to understand the pattern formation in production.

The individual dynamics are described by a discrete event simulation (DES) in production processes. DES is a stochastic simulation tool for individual parts. The corresponding continuous equations are fluid-like models. On a different scale the latter describe production flow in an aggregate way leading to coarse-grained models. Due to the reduced dimension they are expected to be computationally efficient. Typically, there is only one conserved quantity in production being the total number of produced items. Therefore, the proposed continuous models are conservation laws for the product density ρ(x, t) at production stage x ∈ [0, 1] and time t ≥ 0. Here, the flux function f is usually called clearing function. Starting with Graves [19] and Karmarkar [23] monotone, concave clearing functions have been proposed. They are now used in production engineering, see for example [7, 8, 25]. Other approaches to derive clearing functions are mean field limit considerations [3, 5], comparisons with observed behavior [6] or queuing theory under steady-state assumptions. Examples for all these possible options can be found in Sect. 2 (Fig. 1).

Fig. 1

Different ways to derive a clearing function f

In the case of a single unlimited buffer, Poisson processes for the arrival of products and a Poisson process for the production time lead to $f = \frac{\mu W} {1+W},$ where W = ∫ ₀ ¹ ρ(x, t)dx is the (total) Work in Progress (WIP), see for example [20], and μ is the maximal production rate. In queuing theory this is known as an M/M/1 queue, see also the discussion in Sect. 2. We may use ρ and W equivalently whenever ρ is constant in x due to a production stage of at most x = 1. In [25] a clearing function for an M/G/1 queue (here service times obey general distributions) is proposed including parameters that may adjusted to given data. The resulting clearing function is again a steady-state consideration and in general for models based on product flow no transient clearing function model has been derived yet [26]. It has been observed that in different production periods different clearing functions may be suitable. We refer to [2, 13, 24] for an overview.

We also propose different approaches using (real) data to establish the clearing function, i.e., the fundamental relation between f and ρ. We present new continuous models based on realistic data in order to predict production behavior. As already mentioned non-stationary queuing theory predicts that there is no fixed functional relationship between product density and flux [26]. Therefore we are concerned with the detailed data-fitted modeling of the flux function f and its application to conservation laws of the form

$$\displaystyle{ \partial _{t}\rho (x,t) + \partial _{x}\,f(\rho (x,t)) = 0. }$$

(1)

The model (1) is based on the assumption that the amount of products and the number of production stages justifies a continuous model. A prototype of a production process consists of a machine with associate buffer and no limit on the storage capacity. As we will see in Sect. 2 there are several ways to establish the fundamental relation between ρ and f. Such a relation is required to obtain a closed model by Eq. (1).

2 Data-Driven Differential Equations for Production

2.1 Mean Field Limit Approach

The following model was originally introduced by Armbruster et al. [5] in 2006. It was the starting point for the description of a high-volume multi-stage production line by partial differential equations. Detailed explanations and reasonable extensions regarding this model can be found in [13, 16, 17]. The key modeling idea was and is still today to use a discrete description, a so-called discrete event simulation (DES), for the small scale effects and a continuous model to describe large scale phenomena. It can be really shown that both approaches lead to the same results in case of mass production. In the following we present the main ingredients of these models since they are the basic framework for all further considerations.

Discrete event simulations models (DES) provide a powerful tool for an accurate description of the underlying production process. The main idea of these models is to track parts through the whole production process so that information on all part arrival times is fully available. These times obey internal production and order policies but can be given in the case of a first come-first serve policy in a straightforward manner.

In the sequel, we assume that the amount of parts is conserved, i.e. no parts are lost or gained during the production process. The parts have to undergo different production steps where there is the possibility to store parts inbetween. For the first consideration the inventories or buffers have infinite size. Parameters defined by production are the processing velocity and a maximal capacity for each entity.

To derive a discrete model we consider the particular situation of a serial production line consisting of M _P production units. The output of one unit is directly fed into the next one, i.e. machine m ships all parts to the next machine m + 1 as in Fig. 2.

Fig. 2

A serial production line

Every machine is characterized by the processing time T(m) and the maximal capacity μ(m) measured in parts per unit time. The processing time T(m) is the time which is needed to finish a single production step. In this first attempt, the production line should be reliable, i.e. sudden shut-downs of machines are ignored for the moment. However, since machines have possibly different capacities, it may happen that parts have to wait until the next operations can be performed. Therefore, inventories or buffers are installed between production units.

The evolution of parts through the system is now determined by the computation of arrival times. We define the arrival time of part n at the buffer of machine m as a _n ^m. The total amount of parts in the system is denoted by N _P . After successful production, the leaving time e _n ^m denotes when part n leaves machines m and arrives at machine m + 1, see Fig. 2.

The computation of arrival times a _n ^m obviously depends on the current buffer load, i.e. either the buffer is empty or filled. If the buffer is empty, part n is immediately passed into production. Once the part is released for production, the leaving time e _n ^m can be determined by adding the processing time T(m). In the other case the part has to wait. If N parts arrive at the same time t at the machine having an empty buffer, the model (2) yields the departure time of the ith part as T(m) + (i − 1)∕μ(m), i = 1, …, N. Hence, within a unit length of time the machine produces μ(m) parts. Therefore, a buffer will be build up if the inflow per unit time exceeds μ(m). This buffer may grow to infinity if the inflow to system exceeds μ(m) for all times.

We end up with a time recursion for the computation of all arrival times:

$$\displaystyle{ e_{n}^{m} =\max \big\{ a_{ n}^{m} + T(m),\,e_{ n-1}^{m} + \frac{1} {\mu (m)}\big\}\quad m = 0,1,\ldots,\quad n \geq 1. }$$

(2)

As evaluation measures for (2) we use curves of cumulative counts, so-called Newell-curves, as already successfully applied in traffic engineering, see [27]. The idea of Newell-curves U(m, t) is to count all parts that have been arrived at machine m up to any fixed time t:

$$\displaystyle\begin{array}{rcl} U(m,t) =\sum _{ n=0}^{N}H(t - e_{ n}^{m}),\quad m = 0,\ldots,M_{ P},\quad t> 0,& &{}\end{array}$$

(3)

where H(⋅ ) is the Heaviside function

$$\displaystyle\begin{array}{rcl} H(t - e_{n}^{m}) = \left \{\begin{array}{rcrcl} 0,\quad \mbox{ if }t <e_{n}^{m} \\ 1,\quad \mbox{ if }t \geq e_{n}^{m} \end{array} \right..& & {}\\ \end{array}$$

Hence, the Newell-curve U(m, t) provides the total number of parts passing from machine m − 1 to machine m up to time t. The difference of two consecutive Newell-curves is the number of parts actually processed in unit m including the parts in the buffer as well. This difference is known as Work In Progress (WIP) and is denoted by W(m, t):

$$\displaystyle{ W(m,t) = U(m,t) - U(m + 1,t),\quad m = 0,\ldots,M_{P} - 1. }$$

(4)

Although DES models reflect the most accurate way of modeling a time-varying production process, the computational complexity highly depends on the number of parts being considered. An alternative simulation approach might be continuous equations. These kind of equations arise whenever the relationship between changing quantities (modeled by functions) and their rates of change (expressed as derivatives) is known. For the special scenario depicted above, a continuous model can be directly derived from the DES, see [5] for a detailed proof. The idea is to investigate the continuum limit (M _P , N _P → ∞) and to analyze in which sense an approximate density and flux satisfy a conservation law for the part density.

The continuous model describes the evolution of the part density ρ(x, t) at x in time t. The space variable x can be interpreted as the degree of completion. For instance, x ∈ [0, 1] does not represent a physical position but rather the degree of completion or stage of production. The manufacturing system has a prescribed inflow λ(t) over time t at x = 0 and an outflow at x = 1 of finished products. The density ρ(x, t) is transported with velocity v(x) if the flow of parts is less than the maximal capacity μ(x), i.e., ρ satisfies the transport equation or mass conservation law

$$\displaystyle{ \partial _{t}\rho (x,t) + \partial _{x}\,f(\rho (x,t)) = 0,\quad \rho (x,0) =\rho _{0}(x), }$$

(5)

where the relation between flux and density is given by

$$\displaystyle\begin{array}{rcl} f(\rho (x,t)) =\min \{ v(x)\rho (x,t),\,\mu (x)\},& &{}\end{array}$$

(6)

and ρ ₀(x) describes the initial state of the line, see also Fig. 3. This relation is also known as clearing function in the production literature.

Fig. 3

Example of a clearing function given by Eq. (6)

Equation (5) is the continuous analogue to Eq. (4) and hence the Work In Progress (WIP) the discrete representation of the part density ρ(x, t). The main difficulty is that the flux function (6) can become discontinuous due to the assumption that processors may have different maximal capacities. For instance, if machine x _m has higher capacity than machine x _m+1, i.e. μ(x _m ) > μ(x _m+1), δ-distributions occur in the density at his point since mass has to be conserved. Obviously, the limiting density will be a distribution and not a classical function. This corresponds to the fact having buffers in front of machines.

Finally, we present computational results for the discrete (2) and the continuous model (5). We consider a production line consisting of two processors, i.e. M _P = 2. The capacities and processing times of the two machines are μ ₁ = 2, T ₁ = 1 and μ ₂ = 1, T ₂ = 1. The discrete model (2)–(4) can be straightforward implemented using

$$\displaystyle{ \lambda (\tau (0,n)) = \frac{1} {\tau (0,n + 1) -\tau (0,n)} }$$

(7)

$$\displaystyle{ \tau (m + 1,0) =\tau (m,0) + T(m). }$$

(8)

as initial conditions. Here, the function λ denotes the total inflow into the system, see Fig. 4. Furthermore, we discretize the system (5) in space m and time i using an Upwind-scheme for the conservation law:

$$\displaystyle\begin{array}{rcl} \rho (x_{m},t_{i+1}) =\rho (x_{m},t_{i}) - \frac{\varDelta t} {\varDelta x}(\,f(x_{m+1},t_{i}) - f(x_{m},t_{i})),\quad m = 0,1,2,& & \\ f(x_{m},t_{n}) = \left \{\begin{array}{lcrcl} \min \{\mu (x_{m}),v(x_{m})\rho (x_{m},t_{i})\}\quad m = 1,2 \\ \lambda (t_{i}),\quad m = 0. \end{array} \right.& &{}\end{array}$$

(9)

The time steps Δt are constant and satisfy the CFL condition Δt ≤ Δx∕v. We assume an empty line in the beginning, i.e. $\rho _{x_{m},0} = 0$, and a randomly disturbed initial profile λ(t) such that the maximum capacity of the machines is exceeded, see upper part of Fig. 4. We compute the arrival times according to (7). Both machines have length one and are divided into ten cells. We compare the WIP from the recursion (2) and the discretized conservation law (9). Figure 4 also shows the corresponding WIP of each machine in the production line. The red line is computed from the time recursion for the transition times while the blue dots are computed from the conservation law. The WIP of machine one is computed as ∫ ₀ ¹ ρ(x, t) dx. 

Fig. 4

Inflow profile λ(t) prescribed as initial data (above) and work in progress versus part density (below)

2.2 Observed Behavior and Phenomenological Approach

In this section we illustrate a phenomenological approach to modeling with macroscopic equations. The goal is to derive equations based on observations of DES simulations. This approach can be employed when the detailed description of the DES equations and its setup is not available.

To exemplify, we consider experiments conducted by Gossens [15] using the χ (or Chi) language during her Master-Thesis at TU Eindhoven. The data for the DES description was collected in semiconductor production with limited storage capacity. From the DES simulation several interesting observations have been obtained. A single production line with exponentially distributed interarrival times for the inflow has been considered, cf. Fig. 2. It has been assumed that the processing rate is μ(x) but with the crucial difference that the storage capacities buffers are limited by a quantity ρ _max > 0. The following scenario has been taken from the semiconductor factory and analyzed numerically using a DES simulator. In above case the χ Simulator developed by Beek and Rooda at TU Eindhoven has been used. The description of the experiments and simulations are summarized as follows:

• 1. A production line of M _P = 100 stations and time horizon of T = 11, 000 is considered.

• 2. We start with an initially empty factory, where the arrival rate is

  $$\displaystyle{ \min \limits _{t\in [0,T]}\lambda (t) <\min \limits _{x\in [0,M_{P}]}\mu (x). }$$

  The inflow is ramped up until a steady state formation of the part density within the factory is achieved.

• 3. After the system runs in steady state there is a shutdown μ(M _P ) = 0 of the last machine immediately leading to a bottleneck situation. Buffers of downstream machines are filled step by step since production is blocked by the unavailable last machine. Due to the finite size of the buffers the production process stops at some time t ₀. 

• 4. At time t ₁ the last machine is again operational at same capacity as before. The production starts again. The congestion is slowly moving and buffer sizes are reduced until the system approaches its steady state.

We are interested in a continuous equation having the same wave pattern as observed in the DES simulation, see Fig. 7. A suggestion has been proposed in [6] and [22]. In [6] a conservation law has been derived taking into account limited capacities of buffers and non-homogeneous steady state behavior starting from observations only. Since parts are still conserved during production a conservation law similar to (5) has been proposed. However, the design of the clearing function is more involved due to the maximum part density ρ _max characterizing the buffer limits. The key difference to the previous model is that the production might be interrupted and jams may occur. The latter move backwards within the production line. In particular, the observation described in step 2 motivates therefore a non-monotone and discontinuous clearing function. We introduce a discontinuity at ρ _max such that information propagates extremely fast towards the downstream machines. The final relation is given by Eq. (10)

$$\displaystyle{ f(\rho,x) = \left \{\begin{array}{ll} \frac{\mu \rho } {1+\rho +k\rho (1-x)} & \mbox{ for }\rho <\rho _{\max } \\ 0 &\mbox{ for }\rho \geq \rho _{\max } \end{array} \right. }$$

(10)

with k > 0 being the decay rate of the processing capacity along x. An example is depicted in Fig. 6.

The discontinuous clearing function involves several numerical challenges due to the high speed of wave propagation. The simplest remedy is to smooth the function (10). Unfortunately, this implies severe restrictions to the time step size Δt. An alternative is the embedding of the clearing function into a second order model [18, 22].

For the experiments we parameterize the workstations by x ∈ [0, 1] and a maximal density of ρ _max = 1. The production capacity is constant μ(x) = 2 for all x and k = 0. 7. We start with an empty factory at time t = 0 and a constant arrival rate λ(t) < μ(x) at x = 0.

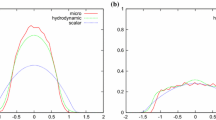
The computed results cover the essential scenarios ramp up, blocking and release as described in Fig. 5. Apparently, the system behavior reproduced by a continuous model is obtained at lower computational costs compared to the DES. We want to stress that the model (10) is not derived in a rigorous way as done in Sect. 2.1, but is solely based on observations. It is unclear for now if a rigorous derivation is possible (Figs. 6 and 7).

Fig. 5

Computational results for the discontinuous flux function from a χ-simulation for λ(t) < μ(x), cf. Fig. 3.6 in [15]. We observe the following phenomena from left to the right: shutdown of the last machine and congestion—release of production draining after the last machine has been repaired. The figure shows snapshots of averaged WIP profiles

Fig. 6

Example of a clearing function given by Eq. (10)

Fig. 7

Computational results for the discontinuous clearing function (10) used for a comparison with Fig. 6. The pictures are from reference [18]

2.3 Data-Fitted Simulated Clearing Functions

In this section we propose a general method to derive clearing functions based on a DES simulation using real factory data. As discussed previously non-stationary queuing theory predicts that there is no fixed functional relationship between product density and flux [26]. However, transient clearing functions have been proposed starting with the work of [1] and [28] to incorporate dynamic effects. We proceed in this spirit in order to obtain a coarse-grained model of transport type (1).

To exemplify we use data from a mid-size German manufacturing company. The available data are order and release data of the major single production step. The layout is precisely as in a theoretical queuing model, i.e., we have a buffer where parts arrive and a machine applying a manufacturing step. Available is production data for 1 year (2012). Mathematically, a probability distribution for the interarrival times is computed from the data. Further, a probability distribution for the production times is computed from the data. Here, we use as sample interval single days. The resulting probability distributions based only on the available data are depicted in Fig. 8. We observe a strong possibly exponential decay of the probability of high interarrival times. A similar observation is true for the production times. The discrete probability distribution is interpolated. This allows to have an arbitrary amount of data points available for later DES simulations. The sampled data are indicated by black dots in Fig. 9.

Fig. 8

Probability distribution of number of parts per day from a German manufacturing plant. Left: inter-arrival times, right: production times

Fig. 9

Probability distribution of number of parts resampled from real data depicted in Fig. 8. In black are simulated points, in blue available data points. Left: interarrival times, right: production times

Theoretically, now different approaches are possible. On the one hand we may fit an exponential probability distribution function Φ _r (x) = rexp(−rx)H(x) of mean $\frac{1} {r}$ to each discrete resampled probability distribution. This leads to a Poisson distributed interarrival process of a certain (fitted) rate (called λ) and a Poisson distributed production process of a data fitted rate μ. Then, the setup is precisely as in an M/M/1 queuing model with the well-established relation between WIP W and flux f ≡ λ as

$$\displaystyle{ f = \frac{\mu W} {1 + W}. }$$

This relation is obtained also when simulating a DES with interarrival process given by Φ _λ and a production process described by Φ _μ . We have the advantage of deriving a single explicit formula closing Eq. (1). However, the data-fitting happens prior to simulating the dynamics.

In the second approach we reverse the procedure. We first apply a DES simulation sampling from the interpolated probability distributions. Then, we record the WIP and flux of several DES simulation. Note that for a DES simulation is not required to have exponentially distributed times. However, we do not expect a closed formula since the probability distributions are not exponentially distributed and therefore the process is not necessarily Poisson. The resulting WIP and flux values for 2000 simulations of the interpolated data is shown in Fig. 10. Clearly, we observe a spread of the data across the diagram related to the fact that the underlying interarrival and production probabilities are obtained from interpolated data. However, the data suggests an empirical clearing function f = f(W). Several choices are possible. We depict in Fig. 11 a clearing function fitted to the mean of the data for any fixed WIP. This relation can not be expressed explicitly in a functional form. However, it also provides a closure relation for Eq. (1). In order to use this relation in a predictive model we would need to table the fitted clearing function. However, the computational effort is very small compared with a DES simulation. For example, here we require to table 50 pairs of WIP and flux in order to describe the closure relation. Within the second approach the averaging therefore happens after the DES simulation leading to a more detailed WIP flux relation. It is interesting to note that with the presented results the WIP flux relation would not be monotone any more. This allows therefore to also obtain a more complex flow pattern predicted by Eq. (1).

Fig. 10

WIP-flux relations for the DES simulated data. 2000 simulations are performed. The interarrival and production probabilities are interpolated from the existing data of the German company

Fig. 11

WIP-flux relations for the DES simulated data. The final clearing function f is shown in red. In green color we show the underlying simulation results from 2000 simulations. The interarrival and production probabilities are interpolated from the existing data of the German company

We also mention a different approach presented in [14]. In Fig. 11 we observe that the simulation averages (depicted as red dots) WIP flux relation resembles for small values of the WIP a shape similar to

$$\displaystyle{ f(\mu,W) = \frac{\mu W} {1 + W}. }$$

(11)

However, the value of μ is not necessarily equal to the value obtained in the first approach.

Furthermore, the simulation averages do not cover well the spread of the data. In [14] we propose to combine Eq. (1) with Eq. (11). This leads to an additional unknown μ = μ(x, t) in the system. We need to prescribe a model for this quantity in order to close the system. To this end we note that μ resembles a production rate. This rate is supposedly known when parts arrive (stating a release date). However, this rate might change for the new parts. Hence, it is reasonable to assume that μ is a quantity that is moved with the product flow. The equation describing this observation is given by

$$\displaystyle{ \partial _{t}\mu (x,t) + v(x,t)\partial _{x}\mu (x,t) = 0. }$$

(12)

Herein, v is the velocity of the moving parts of density ρ which is given by

$$\displaystyle{ \rho (x,t)v(x,t) = \frac{\mu (x,t)\rho (x,t)} {1 +\rho (x,t)} =: f(\mu (x,t),\rho (x,t)). }$$

(13)

Summarizing, the full model proposed in [14] is given by Eqs. (1), (12) and (13). Among the properties of the system are hyperbolicity except at zero production density. The eigenvalues are at most v(x, t). Therefore, there is only a finite speed of propagation of information bounded by the speed of the produced parts. This coincides with the expected behavior of a production line. The clearing functions of the extended model form a family of functions of the type (11) for a fixed value of μ. This allows to capture the spread in the data more efficiently.

Summarizing, several possibilities to extend classical M/M/1 queuing theory to time dynamic models of continuous type exist. Depending on the quality of the available data as well as the possible spread in the resulting DES simulation several approaches exit. We focus on the presentation of continuous models thereby neglecting detailed dynamics.

3 Outlook

We have presented recent approaches on modeling production flows using continuous partial differential equations. Compared with classical modeling approaches as DES, queuing theory or mixed-integer modeling, the differential equations allow for a reduced computational complexity as well as efficient and structure preserving optimization and control approaches. However rigorous derivations of models based on differential equations are only possible for simplistic models of production scenarios. In case of more complex problems two other approaches have been presented. The approach based on the observed behavior has so far been able to capture the main effects of production lines with limited buffers. The approach based on available data of interarrival and production times has led to a second-order model. The theory of a rigorous justification based on the underlying product dynamics is still its infancy for both cases. Future work may include progress in the mean field limits, the extension of the models towards control and optimization problems as well as the extension towards large scale production networks. In all fields there are challenging mathematical as well as computational problems. The derived equations resemble to some extended fluid dynamical equations and one may adapt those methods here. However, hyperbolic transport properties are fundamentally different from fluid dynamics and require adapted and different theoretical and numerical treatment.