Discrete Cosserat Rod Models Based on the Difference Geometry of Framed Curves for Interactive Simulation of Flexible Cables

Abstract

For software tools currently used in industry for computer aided design (CAD), digital mock-up and virtual assembly there is an increasing demand to handle not only rigid geometries, but to provide also capabilities for realistic simulations of large deformations of slender flexible structures in real time (i.e.: at interactive rates). The theory of Cosserat rods provides a framework to perform physically correct simulations of arbitrarily large spatial deformations of such structures by stretching, bending and twisting. The kinematics of Cosserat rods is described by the differential geometry of framed curves, with the differential invariants of rod configurations corresponding to the strain measures of the mechanical theory. We utilize ideas from the discrete differential geometry of framed curves in combination with the variational framework of Lagrangian mechanics to construct discrete Cosserat rod models that behave qualitatively correct for rather coarse discretizations, provide a fast computational performance at moderate accuracy, and thus are suitable for interactive simulations. This geometry based discretization approach for flexible 1D structures has industrial applications in design and digital validation. We illustrate this with some application examples from automotive industry.

1 Introduction

Standard software tools currently used in industry for CAD, digital mock-up and virtual assembly can only handle rigid geometries. However, there is an increasing demand for a realistic, yet easy-to-use simulation of large deformations of slender flexible structures, preferably in real time (i.e.: at interactive rates). Typical examples of such structures from automotive industry are tubes, hoses, single cables, or wiring harnesses collecting many cables within a compound structure (see Fig. 1).

Fig. 1

Overview of the system of cables installed in a car (left), and simulation model of a wiring harness in the IPS Cable Simulation software (right)

The theory of Cosserat rods [1, 26, 29] provides a framework for structural models that are suitable for physically correct simulations of deformations of slender flexible objects by stretching, bending and twisting. Due to the slenderness of the geometry—i.e.: typical cross section diameters d are small relative to typical lengths L of the considered structures, such that d∕L ≪ 1 holds—such deformations may possibly imply large spatial displacements and rotations, while the local strains always remain small. Cosserat rod models, also denoted as geometrically exact models due to the possibility of a kinematically exact treatment of large rigid body motions, are particularly well suited to handle such large deformations.

In computational mechanics, such models are usually discretized via nonlinear finite elements [13]. This approach is taylored to provide very accurate simulation results. However, due to their algorithmic and algebraic complexity, discrete models constructed via nonlinear FE are technically complicated and in general computationally far too demanding for doing fast simulations compatible with rendering at 25 Hz (at least), simultaneous to an interactive modification of the boundary conditions by the user, either via the graphical user interface of a desktop computer, or via a data glove (or similar devices) within an augmented reality (AR) environment, unless such simulations are executed on highly performant computer hardware, using many processors with multiple cores, and highly parallelized algorithms. Therefore, if one aims at interactive simulations on ordinary desktop computers available to a broader range of users, the development of a different approach is required.

The kinematics of Cosserat rods is closely related to the differential geometry of framed curves [3, 7], with the differential invariants of rod configurations corresponding to the strain measures of the mechanical theory [1]. We propose to utilize ideas from the discrete differential geometry of framed curves [2, 5, 27, 30] to construct the discrete kinematics of Cosserat rod models in a way that preserves the essential geometric properties independent of the coarseness of the discretization.

Different from a nonlinear FE approach aiming at weak solutions of the mechanical equilibrium equations [34], we consider Cosserat rod models within the variational framework of Lagrangian mechanics in terms of the kinetic and elastic energy of the rod [16, 20, 21]. In particular, as the elastic energy density of a rod is given as a quadratic form in the strain measures, we obtain the discrete elastic energy by an approach which we denote as geometric finite differences, providing a discretization of the strain measures that preserves their essential geometric properties, in combination with simple quadrature rule to approximate the integrated energy density. Due to the geometric discretization of the strains, discrete rod models constructed according to our discrete Lagrangian mechanics approach behave qualitatively correct even for very coarse discretizations, provide an ultrafast computational performance at moderate accuracy, and thus are suitable for interactive simulations.

In our article, we introduce the basic ideas of our geometry based discretization approach for flexible slender structures as sketched above. The mathematical backbone of our construction of discrete Cosserat rod models is provided by the difference geometry of framed curves in the spirit of Sauer’s approach [27] to discrete Frénet curve theory. We present an extension of Sauer’s ideas to construct the basic constituents of the discrete geometry of Cosserat curves in Euclidian space, including proper definitions of discrete curvatures, discrete generalized Frénet equations with geometrically exact solutions in terms of finite rotations, all summarized in the formulation of a principal theorem of discrete Cosserat curve theory. On this basis, the construction of discrete Cosserat rod models formulated in terms of discrete elastic energy functions, defined as quadratic forms of the invariants of discrete Cosserat curves, can be obtained in a straightforward manner.

Our discrete formulation of geometrically exact rods turns out to be particularly useful for a seamless integration into a CAE software environment as IPS Cable Simulation. As the models and algorithms are formulated in terms of elementary concepts of computational geometry, one can achieve the computational performance necessary for a true interaction of the user with the software in real time, which is a key feature in practical applications. We illustrate this aspect by presenting some typical application examples of assembly simulations of cables performed in automotive industry for design and digital validation purposes.

2 Notational Conventions

In this section we collect a few facts of linear algebra to introduce some notational conventions inspired by the ones given in [1, 14, 25].

2.1 Euclidian Point Space $\mathcal{E}^{3}$ and Its Vector Space $\mathbb{E}^{3}$

We denote three-dimensional Euclidian point space by $\mathcal{E}^{3}$, its associated Euclidian vector space by $\mathbb{E}^{3}$ and use bracket notation 〈⋅ , ⋅ 〉 to denote its scalar product. All vectors $\mathbf{w} \in \mathbb{E}^{3}$ are written in boldface roman letters. By definition, they provide parallel displacements $q = p + \mathbf{w}$ of points $p,q \in \mathcal{ E}^{3}$. This explains the operation $+:\mathcal{ E}^{3} \times \mathbb{E}^{3} \rightarrow \mathcal{ E}^{3}$ on Euclidian space $\left (\mathcal{E}^{3}, \mathbb{E}^{3},+\right )$ in a memnonic way, and likewise introduces the difference $q - p = \mathbf{w}$ of points as a proper operation. The distance of points in $\mathcal{E}^{3}$ is measured by the length $\|\mathbf{w}\| = \sqrt{\langle \mathbf{w}, \mathbf{w}\rangle } =:\| q - p\|$ of their displacement vectors. A fixed cartesian coordinate frame of $\mathbb{E}^{3}$ is defined by choosing a fixed origin $\mathcal{O} = \mathbf{0}$ and a fixed right-handed orthonormal triple $(\mathbf{e}_{1},\mathbf{e}_{2},\mathbf{e}_{3})$ of basis vectors. Any vector quantity may be decomposed with respect to the fixed basis $\{\mathbf{e}_{k}\}_{k=1,2,3}$ in the form $\mathbf{w} =\sum _{ k=1}^{3}w_{k}\mathbf{e}_{k}$, where the real numbers $w_{k} =\langle \mathbf{w},\mathbf{e}_{k}\rangle$ denote the cartesian components of $\mathbf{w} \in \mathbb{E}^{3}$. The position vector $\mathbf{x}(\,p)$ of a point $p \in \mathcal{ E}^{3}$ is given by $p =\mathcal{ O} + \mathbf{x}(\,p)$, with its cartesian components $x_{k}(\,p) =\langle \mathbf{x}(\,p),\mathbf{e}_{k}\rangle$.

2.2 Linear Mappings in $\mathbb{E}^{3}$

We denote linear mappings $\mathsf{A}: \mathbb{E}^{3} \rightarrow \mathbb{E}^{3}$ within Euclidian vector space by upper case upright serifless letters and use dot notation $\mathbf{w}\mapsto \mathsf{A} \cdot \mathbf{w}$ to indicate their operation on vectors. The composition $(\mathsf{A} \cdot \mathsf{B}) \cdot \mathbf{w} = \mathsf{A} \cdot (\mathsf{B} \cdot \mathbf{w})$ of linear mappings is written in the same style. The identity I maps all vectors onto themselves.

A linear mapping is completely determined by its values $\mathbf{v_{k}} = \mathsf{A} \cdot \mathbf{e}_{k}$ on the fixed basis and may be written in invariant form as a sum¹ $\mathsf{A} =\sum _{ k=1}^{3}\mathbf{v}_{k} \otimes \mathbf{e}_{k} \equiv \mathbf{v}_{k} \otimes \mathbf{e}_{k}$ of tensor products defined as $(\mathbf{a} \otimes \mathbf{b}) \cdot \mathbf{w} =\langle \mathbf{b},\mathbf{w}\rangle \,\mathbf{a}$. The corresponding representation of the identity in terms of the fixed basis is given by $\mathsf{I} = \mathbf{e}_{k} \otimes \mathbf{e}_{k}$. Occasionally we use the notation $\mathsf{A} = (\mathbf{v}_{1},\mathbf{v}_{2},\mathbf{v}_{3})$, which identifies the linear mapping A with the triple of vectors obtained as images of the fixed basis.

The determinant det(A) of a linear mapping is an invariant and equals the determinant of its representing matrix w.r.t. an arbitrary basis. The cross product $\mathbf{u}\,\times \,\mathbf{v}$ of vectors may be defined invariantly via the identity $\langle \mathbf{u} \times \mathbf{v},\mathbf{w}\rangle =\det ((\mathbf{u},\mathbf{v},\mathbf{w})) = [\mathbf{u},\mathbf{v},\mathbf{w}]$ which is required to hold for arbitrary vectors, and likewise explains their scalar valued triple product. The identity $\tilde{\mathsf{u}} \cdot \mathbf{v} = \mathbf{u} \times \mathbf{v}$ establishes the one-to-one correspondence between vectors $\mathbf{u}$ and skew-symmetric mappings $\tilde{\mathsf{u}} = -\tilde{\mathsf{u}}^{T}$, represented by tilde notation.

2.3 Orthogonal Mappings

Linear mappings that preserve length are denoted as orthogonal: for orthogonal mappings R the identity $\|\mathbf{w}\| =\| \mathsf{R} \cdot \mathbf{w}\|$ must holds for all vectors $\mathbf{w} \in \mathbb{E}^{3}$. This implies the orthonormality $\langle \mathbf{a}_{i},\mathbf{a}_{j}\rangle =\delta _{ij}$ of the column vectors $\mathbf{a}_{k} = \mathsf{R} \cdot \mathbf{e}_{k}$ of an orthogonal mapping. This characteristic property may be equivalently formulated in a more compact form by the identities R ^T = R ⁻¹ or R ^T ⋅ R = I = R ⋅ R ^T which hold by definition for any orthogonal mapping. Orthogonal mappings R that preserve the orientation of the fixed basis are characterized by det(R) = 1 and denoted as proper orthogonal. The orthogonal and proper orthogonal linear mappings on $\mathbb{E}^{3}$ form Lie groups O(3) and SO(3) respectively. Their Lie algebra is the set $\mathfrak{s}\mathfrak{o}(3) \simeq \mathbb{R}^{3} \simeq \mathbb{E}^{3}$ of skew-symmetric linear mappings.

2.4 Quaternions

Following ch. 7 of [11], we denote Hamilton’s algebra of quaternions by $\mathbb{H}$. We identify the orthonormal basis $\{\mathbf{i},\mathbf{j},\mathbf{k}\}$ of $\mathfrak{I}\mathbb{H} \simeq \mathbb{E}^{3}$ with the fixed basis $\{\mathbf{e}_{1},\mathbf{e}_{2},\mathbf{e}_{3}\}$ of $\mathbb{E}^{3}$. Denoting the base vector of $\mathfrak{R}\mathbb{H} \simeq \mathbb{R}$ as $\mathbf{e}_{0} = 1$, we may represent arbitrary quaternions invariantly as² $\mathsf{q} = q + \mathbf{q}$, with scalar part $q = \mathfrak{R}(\mathsf{q}) \in \mathbb{E}^{1} \simeq \mathbb{R}$ and vector part $\mathbf{q} = \mathfrak{I}(\mathsf{q}) \in \mathbb{E}^{3} \simeq \mathbb{R}^{3}$. The product of two arbitrary quaternions p and q is given by the formula: $\mathsf{p} \circ \mathsf{q} = pq -\langle \mathbf{p},\mathbf{q}\rangle + p\mathbf{q} + q\mathbf{p} + \mathbf{p} \times \mathbf{q}$. Using the notation $\mathsf{q}^{{\ast}} = q -\mathbf{q}$ for conjugate quaternions, the scalar product $\langle \,\,,\,\rangle _{\mathbb{H}}$ of $\mathbb{H} \simeq \mathbb{E}^{4}$ may be obtained by $\langle \mathsf{p},\mathsf{q}\rangle _{\mathbb{H}} = \frac{1} {2}(\mathsf{p} \circ \mathsf{q}^{{\ast}} + \mathsf{q} \circ \mathsf{p}^{{\ast}}) = pq +\langle \mathbf{p},\mathbf{q}\rangle$, such that $\vert \mathsf{q}\vert = \sqrt{\mathsf{q} ^{{\ast} } \circ \mathsf{q}} = \sqrt{q^{2 } + \mathbf{q} ^{2}}$ yields the modulus of a quaternion. All non-zero quaternions have a unique inverse q ⁻¹ = q ^∗∕ | q |², such that q ∘q ⁻¹ = 1 = q ⁻¹ ∘q holds. Quaternions $\mathsf{q} = \mathbf{q}$ with a scalar part $\mathfrak{R}(\mathsf{q}) = 0$ are called pure (or vector) quaternions and identified with vectors in $\mathbb{E}^{3}$. As the product of two vector quaternions is given by the simplified formula $\mathbf{p} \circ \mathbf{q} = -\langle \mathbf{p},\mathbf{q}\rangle + \mathbf{p} \times \mathbf{q}$, their scalar and cross products in $\mathbb{E}^{3}$ may be written in terms of quaternion products as: $\langle \mathbf{p},\mathbf{q}\rangle = -\frac{1} {2}(\mathbf{p} \circ \mathbf{q} + \mathbf{q} \circ \mathbf{p})$, and $\mathbf{p} \times \mathbf{q} = \frac{1} {2}(\mathbf{p} \circ \mathbf{q} -\mathbf{q} \circ \mathbf{p})$.

Proper rotations R ∈ SO(3) may be represented by unimodular (or rotational) quaternions $\hat{\mathsf{q}} = q + \mathbf{q}$, satisfying $\vert \hat{\mathsf{q}}\vert ^{2} = q^{2} + \mathbf{q}^{2} = 1$ and therefore located on the unit sphere $S^{3} \subset \mathbb{E}^{4}$, by means of the Euler map $\hat{\mathsf{q}}\mapsto \mathsf{R} = \mathfrak{E}(\hat{\mathsf{q}})$ implicitly defined via its operation on vectors $\mathbf{v} \in \mathbb{E}^{3} \simeq \mathfrak{I}\mathbb{H}$ as: $\mathsf{R}(\hat{\mathsf{q}}) \cdot \mathbf{v} =\hat{ \mathsf{q}} \circ \mathbf{v} \circ \hat{\mathsf{q}}^{{\ast}}$. Thus, the pair $\pm \hat{\mathsf{q}}$ represents the same proper rotation $\mathsf{R}(\hat{\mathsf{q}}) = \mathsf{R}(-\hat{\mathsf{q}})$, consistent with the fact that S ³ ≃ SU(2) yields a double covering of SO(3). The definition of $\mathfrak{E}(\hat{\mathsf{q}})$ implies the formulas $\mathsf{R}(\hat{\mathsf{p}}) \cdot \mathsf{R}(\hat{\mathsf{q}}) = \mathsf{R}(\hat{\mathsf{p}} \circ \hat{\mathsf{q}})$ for the composition of rotations and $\mathsf{R}(\hat{\mathsf{q}})^{T} = \mathsf{R}(\hat{\mathsf{q}}^{{\ast}})$ for the inverse rotation, as R(1) = I holds. According to Euler, each proper rotation may be represented as $\mathsf{R} =\exp (\vartheta \,\tilde{\mathsf{u}})$, i.e.: a rotation by an angle ϑ around an axis determined by the unit vector $\hat{\mathbf{u}}$, with uniquely determined ϑ ∈ (0, 2π) and $\hat{\mathbf{u}} \in S^{2}$ for R ≠ I. The corresponding rotational quaternion is given by $\hat{\mathsf{q}} =\exp (\vartheta /2\,\hat{\mathbf{u}}) =\cos (\vartheta /2) +\sin (\vartheta /2)\,\hat{\mathbf{u}}$, such that $\exp (\vartheta \,\tilde{\mathsf{u}}) = \mathfrak{E}(\pm \exp (\vartheta /2\,\hat{\mathbf{u}}))$ holds identically.

2.5 Geometric Curves in Euclidian Space

We regard geometric curves as simple arcs [30] corresponding to smooth, one-dimensional connected submanifolds.³ Thus, the mapping $\mathcal{C} \ni p\mapsto \xi (\,p) \in \mathbb{R}$ of the points p on a geometric curve $\mathcal{C} \subset \mathcal{ E}^{3}$ to their real coordinates ξ is (at least once) differentiable and invertible, and the inverse mapping ξ ↦ p(ξ) from open intervals in $\mathbb{R}$ into $\mathcal{E}^{3}$ provides a local parametrization of the curve. By joining the open intervals of local parametrizations, we obtain a larger one $(a,b) \subset \mathbb{R}$ corresponding to a global parametrization $\phi: [a,b] \rightarrow \mathcal{ C}$ of the geometric curve, such that (a, b) ∋ ξ ↦ p = ϕ(ξ) yields all interior points of $\mathcal{C}$, and the two boundary points of $\mathcal{C}$ are given by ϕ(a) and ϕ(b). The position vectors $\mathbf{x}(\,p) \in \mathbb{E}^{3}$ of curve points are then given by a parameter curve $\xi \mapsto \mathbf{r}(\xi ):= \mathbf{x}(\phi (\xi ))$ in $\mathbb{E}^{3}$.

3 Framed Curves and Cosserat Rods

The theory of Continuum Mechanics of solid bodies [14, 31] provides proper physical models to simulate deformations of flexible parts. A continuum-mechanical model of a material body consists of three main constituents: kinematics, equilibrium equations and constitutive laws. Summarized briefly, the general programme of continuum mechanics aims at determining equilibrium configurations of a body subject to certain boundary conditions, such that all external forces acting on the body are in equilibrium with the internal ones (resulting from deformations of its shape) and inertial effects, making use of constitutive laws that relate local changes of shape, measured in terms of strains, to stresses that encode information on the corresponding local forces.

The theoretical framework provided by Continuum Mechanics as sketched above is a rather complex one, in particular if one is interested to model large (finite) deformations of parts w.r.t. their shape in an undeformed state, in contrast to infinitesimally small ones that can be treated by the well known standard models and numerical methods of Linear Elasticity. This seems to be discouraging in view of our goal to simulate large deformations of cables and tube-like parts fast enough to permit interactive action for the users with the simulation model. Fortunately the slender geometry of the parts considered provides the possibility to reduce the continuum model analytically to an object which is well known (and likewise well understood) in classical differential geometry, namely: a framed curve.

3.1 Basic Differential Geometry of Framed Parameter Curves

More precisely, we consider so called Cosserat curves, consisting of [1]

• a space curve $\mathbf{r}(s)$ corresponding to the centerline of the rod, and

• a moving frame $\mathsf{R}(s) = \mathbf{a}^{(\,j)}(s) \otimes \mathbf{e}_{j}$ of orthonormal directors,

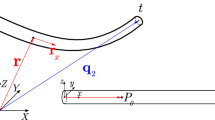
where the pair $\{\mathbf{a}^{(1)}(s),\mathbf{a}^{(2)}(s)\}$ spans the local cross section of the rod at the position $\mathbf{r}(s)$, such that $\mathbf{a}^{(3)} = \mathbf{a}^{(1)} \times \mathbf{a}^{(2)}$ equals the unit length cross section normal vector, as sketched in Fig. 2.

Fig. 2

Centerline curve $\mathbf{r}(s)$ and attached moving frame $\mathsf{R}(s) = \mathbf{a}^{(k)}(s) \otimes \mathbf{e}_{k}$ of a Cosserat curve, describing the geometry of the configurations of a prismatic rod in Euclidian space. The volumetric geometry is generated by sliding the cross section spanned by the frame directors $\{\mathbf{a}^{(1)},\mathbf{a}^{(2)}\}$ along the centerline. The position vectors of the material points in the rod volume are parametrized by: $\mathbf{x} = \mathbf{r}(s) +\xi _{\alpha }\,\mathbf{a}^{(\alpha )}(s)$

As $\mathbf{r}(s) \in \mathbb{E}^{3}$ and R(s) ∈ SO(3), a Cosserat curve may be interpreted as a parameter curve in the manifold $\mathbb{E}^{3} \times \mathsf{SO}(3)$ of rigid body configurations in Euclidian space. The curve parameter s is usually assumed to correspond to the arc length of $\mathbf{r}(s)$, such that the tangent vector $\mathbf{t}(s) = \mathbf{r}'(s)$ has unit length. The frame R(s) is called adapted to the curve if $\mathbf{a}^{(3)}(s) = \mathbf{t}(s)$ holds. While in the setting of classical differential geometry of framed curves mainly adapted frames are considered, non-adapted frames are of primary interest in the kinematical theory of geometrically exact rods, where adapted frames merely occur as a special case, recoverable from a kinematically more general Cosserat curve by the Euler–Bernoulli constraint $\mathbf{r}'(s) = \mathbf{a}^{(3)}(s)$, enforcing cross sections to remain orthogonal to the tangent vector of an inextensible centerline curve.

3.1.1 Frénet Curves and Ribbons

The most well known adapted frame in elementary differential geometry of space curves is the Frénet frame $(\mathbf{a}^{(1)},\mathbf{a}^{(2)},\mathbf{a}^{(3)}) = (\mathbf{n},\mathbf{b},\mathbf{t})$, consisting of the principal normal and binormal vectors defined as $\mathbf{n}(s):= \mathbf{t}'(s)/\kappa (s)$ and $\mathbf{b}(s):= \mathbf{t}(s) \times \mathbf{n}(s)$ on intervals of non-zero Frénet curvature $\kappa (s):=\| \mathbf{t}'(s)\|$. More general, one may consider parameter curves on oriented surfaces patches, with the (likewise adapted) Darboux frame of the curve defined by the curve tangent $\mathbf{t}$ and the unit length normal vector field $\mathbf{N}$ of the surface at the curve points. This leads to the notion of a ribbon (or surface strip), defined as a surface patch of infinitesimally small width around a curve $\mathbf{r}(s)$, oriented by a unit vector $\mathbf{N}(s)$ orthogonal to the tangent vector $\mathbf{t}(s)$ of the curve, with an adapted frame given by: $(\mathbf{a}^{(1)},\mathbf{a}^{(2)},\mathbf{a}^{(3)}) = (\mathbf{N},\mathbf{t} \times \mathbf{N},\mathbf{t})$.

From a slightly different point of view, one may consider an arbitrary frame field R(s), given as a parameter curve in SO(3), and recover its corresponding space curve by integration: $\mathbf{r}'(s) = \mathbf{a}^{(3)}(s)\; \Leftrightarrow \;\mathbf{r}(s) = \mathbf{r}_{0} +\int _{ 0}^{s}\mathbf{a}^{(3)}(\zeta )\,d\zeta$. The evolution of the adapted frame of a ribbon along its curve is determined by the generalized Frénet equations $\partial _{s}\mathbf{a}^{(k)}(s) =\pmb{\kappa } (s) \times \mathbf{a}^{(k)}(s)$. The curvatures ϰ ^(k)(s) are defined as the components of the Darboux vector $\pmb{\kappa }=\varkappa ^{(\,j)}\,\mathbf{a}^{(\,j)} = \frac{1} {2}\mathbf{a}^{(\,j)} \times \partial _{ s}\mathbf{a}^{(\,j)} =\kappa \, \mathbf{b} +\varkappa ^{(3)}\,\mathbf{t}$ w.r.t. the directors of the moving frame. If they are given as continuous functions of arc length, they provide a complete set of differential invariants that determine the geometry of a ribbon up to a global rigid body motion.

3.1.2 Cosserat Curves and Quaternion Frames

Cosserat curves may be considered as natural generalizations of ribbons by omitting the requirement of an adaption of the frame to the curve. In the context of the kinematics of geometrically exact rods one proceeds even one step further by considering regular curves that are not necessarily parametrized by arc length: If one resolves the tangent vector $\mathbf{r}'(\zeta )$ w.r.t. the directors of the moving frame $\mathsf{R}(\zeta ) = \mathbf{a}^{(k)}(\zeta ) \otimes \mathbf{e}_{k}$, then the components $\varGamma ^{(k)}(\zeta ):=\langle \mathbf{a}^{(k)}(\zeta ),\mathbf{r}'(\zeta )\rangle$ of the tangent vector, together with the curvatures K ^(k)(ζ), which are implicitly given by the frame equations $\partial _{\zeta }\mathbf{a}^{(k)} =\pmb{\kappa } \times \mathbf{a}^{(k)}$ and associated Darboux vector $\pmb{\kappa }(\zeta ) = K^{(\,j)}(\zeta )\,\mathbf{a}^{(\,j)}(\zeta )$, provide a complete set of differential invariants that determine a Cosserat curve up to a global rigid body motion.

The proof of this statement, which constitutes the principal theorem of the differential geometry of Cosserat curves, may be obtained by a straightforward adaption of the corresponding one for ribbons (see [1]): For given curvature functions K ^( j)(ζ), the frame equations become a system of linear ODEs for the frame directors that can be integrated for an arbitrary initial value R ₀ ∈ SO(3) according to the theory of ordinary differential equations. Due to the special algebraic structure of the frame equations, the scalar products of the frame directors are conserved (i.e.: $\langle \mathbf{a}^{(i)}(\zeta ),\mathbf{a}^{(\,j)}(\zeta )\rangle =\delta _{ij}$), such that the solution $\mathsf{R}(\zeta ) = \mathbf{a}^{(\,j)}(\zeta ) \otimes \mathbf{e}_{j}$ always remains in SO(3). For given $\pmb{\varGamma }(\zeta ):=\varGamma ^{(\,j)}(\zeta )\,\mathbf{e}_{j}$ and known R(ζ), the tangent vector $\mathbf{r}'(\zeta ) =\varGamma ^{(\,j)}(\zeta )\,\mathbf{a}^{(\,j)}(\zeta ) = \mathsf{R}(\zeta ) \cdot \pmb{\varGamma } (\zeta )$ can then be considered as a known function that can subsequently be integrated, which finally yields the space curve $\mathbf{r}(\zeta ) = \mathbf{r}_{0} +\int _{ 0}^{\zeta }\mathsf{R}(\xi ) \cdot \pmb{\varGamma } (\xi )\,d\xi$ for an arbitrarily chosen initial value $\mathbf{r}_{0}$.

Note that as $\|\mathbf{r}'(\zeta )\| =\|\pmb{\varGamma } (\zeta )\|$ holds, the differential of arc length is given by $ds =\|\pmb{\varGamma } (\zeta )\|\,d\zeta$, such that one may always reparametrize a regular Cosserat curve by its arc length function s(ζ), with a corresponding rescaling of the curvatures according to: $\varkappa ^{(k)}(s) = K^{(k)}(\zeta )/\|\pmb{\varGamma }(\zeta )\|$. For curves parametrized by arc length $\varGamma ^{(k)}(s) =\langle \mathbf{a}^{(k)}(s),\mathbf{t}(s)\rangle$ are the direction cosines of the tangent vector w.r.t. the local frame axes. Ribbons consisting of regular curves parametrized by arc length with adapted frames correspond to the special case of constant $\pmb{\varGamma }_{0} = (0,0,1)^{T} \equiv \mathbf{e}_{3}$. Frénet curves may in turn be considered as special cases of ribbons, with their Darboux vector given by $\pmb{\kappa }\,=\,\kappa \, \mathbf{b} +\tau \, \mathbf{t}$.

The formulation of Cosserat rod models as presented in [20] is based on quaternionic Cosserat curves, where the moving frame R(s) is represented equivalently by a moving unimodular (rotational) quaternion field $\hat{\mathsf{q}}(s)$, characterized by the identity $\mathsf{R}(s) \cdot \mathbf{v} =\hat{ \mathsf{q}}(s) \circ \mathbf{v} \circ \hat{\mathsf{q}}^{{\ast}}(s)$ holding for arbitrary vectors $\mathbf{v} \in \mathbb{E}^{3} \simeq \mathfrak{I}\mathbb{H}$. The generalized Frénet equations can be written equivalently in terms of a derivative equation $\mathsf{R}'(s) = \mathsf{R}(s) \cdot \tilde{\mathsf{K}}(s)$ for the moving frame, using the skew matrix $\tilde{\mathsf{K}} \in \mathfrak{s}\mathfrak{o}(3)$ associated to the material Darboux vector $\mathbf{K}(s) = K^{(\,j)}(s)\,\mathbf{e}_{j} = \mathsf{R}^{T}(s) \cdot \pmb{\kappa } (s)$.

The corresponding derivative equation for the equivalent quaternion frame is then given by $\hat{\mathsf{q}}'(s) = \frac{1} {2}\pmb{\kappa }(s) \circ \hat{\mathsf{q}}(s) = \frac{1} {2}\hat{\mathsf{q}}(s) \circ \mathbf{K}(s)$. As $\mathfrak{R}(\mathbf{K}) = 0 = \mathfrak{R}(\pmb{\kappa })$, any solution of this ODE has constant modulus. In particular $\vert \hat{\mathsf{q}}(s)\vert \equiv 1$ holds for any solution of the frame equation starting from an initial value $\hat{\mathsf{q}}_{0} \in S^{3}$. The recovery formula for the centerline by integration in terms of a solution $\hat{\mathsf{q}}(s)$ of the quaternionic frame equation—determined by the given curvature vector $\mathbf{K}(s)$ and initial value $\hat{\mathsf{q}}_{0}$—and given $\pmb{\varGamma }(s)$ may then be reformulated in terms of quaternionic quantities as: $\mathbf{r}(s) = \mathbf{r}_{0} +\int _{ 0}^{s}\hat{\mathsf{q}}(\zeta ) \circ \pmb{\varGamma } (\zeta ) \circ \hat{\mathsf{q}}^{{\ast}}(\zeta )\,d\zeta$. This implies an equivalent formulation of the principal theorem for quaternionic Cosserat curves, which are likewise determined by given functions $\mathbf{K}(s)$ and $\pmb{\varGamma }(s)$ up to a global rigid body motion.

3.2 Elastic Energy of a Cosserat Rod

Static equilibria of deformed elastic structures can be computed as minima of their elastic energy, subject to the assumed boundary conditions. As we intend to model slender flexible structures as elastic Cosserat rods, we need to specify a corresponding elastic energy function. For linear elastic material behaviour, the elastic (stored) energy function of a 3D body is a quadratic form of its Green–Lagrange strain tensor $\mathsf{E} = \frac{1} {2}(\mathsf{F}^{T} \cdot \mathsf{F} -\mathsf{I})$, where $\mathsf{F} =\mathrm{ d}\varPhi (\mathbf{X})$ is the deformation gradient computed as the derivative of the positions $\mathbf{x} =\varPhi (\mathbf{X})$ of the material points in the deformed body volume w.r.t. their positions $\mathbf{X}$ in the undeformed body (see [14] for details).

If one computes the deformation gradient and Green–Lagrange strain tensors for the deformed configurations $\mathbf{x} = \mathbf{r}(s) +\xi _{\alpha }\,\mathbf{a}^{(\alpha )}(s)$ of a Cosserat rod w.r.t. its undeformed reference configuration $\mathbf{X} = \mathbf{r}_{0}(s) +\xi _{\alpha }\,\mathbf{a}_{0}^{(\alpha )}(s)$ given by a smooth regular curve $\mathbf{r}_{0}(s)$ parametrized by arc length and its adapted frame $\mathsf{R}_{0}(s) = \mathbf{a}_{0}^{(k)}(s) \otimes \mathbf{e}_{k}$ with $\mathbf{r}_{0}^{{\prime}}(s) = \mathbf{a}_{0}^{(k)}(s)$, one obtains [22] an exact closed form expression for E which depends on the differences $\mathbf{K}(s) -\mathbf{K}_{0}(s)$ and $\pmb{\varGamma }(s) -\pmb{\varGamma }_{0}$ (with $\pmb{\varGamma }_{0} = (0,0,1)^{T}$) of the invariants of the framed curve in their deformed and undeformed configurations.

For slender rod geometries, one may always assume that the local strains remain small, although the deformations of the rod configuration correspond to large (finite) rotations and displacements in space. In this case one may approximate the exact expression for E by taking only the leading order terms in the differences of the invariants into account. The resulting approximated energy density can then be integrated analytically over the cross section coordinates (ξ ₁, ξ ₂) in closed form, which finally yields [22] the elastic energy $\mathcal{W}_{el}$ of a Cosserat rod as a quadratic functional in the differences $\mathbf{K} -\mathbf{K}_{0}$ and $\pmb{\varGamma }-\pmb{\varGamma }_{0}$ of the invariants, given by the sum $\mathcal{W}_{el} =\mathcal{ W}_{es} +\mathcal{ W}_{bt}$ of the two integrals

$$\displaystyle\begin{array}{rcl} \mathcal{W}_{es}& =& \frac{1} {2}\int _{0}^{L}ds\,\,[EA]\,\left (\varGamma ^{(3)}(s) - 1\right )^{2}\; +\; [GA_{\alpha }]\,\varGamma ^{(\alpha )}(s)^{2}\;,{}\end{array}$$

(1)

$$\displaystyle\begin{array}{rcl} \mathcal{W}_{bt}& =& \frac{1} {2}\int _{0}^{L}ds\,\,[EI_{\alpha }]\,\left (K^{(\alpha )}(s) - K_{ 0}^{(\alpha )}(s)\right )^{2}\; +\; [GJ]\,\left (K^{(3)}(s) - K_{ 0}^{(3)}(s)\right )^{2}\;.\qquad {}\end{array}$$

(2)

The first term (1) represents the elastic energy related to rod deformations by longitudinal extension combined with transverse shearing, the second term (2) accounts for the elastic energy stored in bending and torsional deformations of the rod.

The parameters [EA], [GA _α ], [EI _α ] and [GJ] quantify the effective stiffness properties of the local cross section of the rod related to the respective deformation mode. They may be constants, or vary along the rod as functions of s. In the simple case of a homogeneous and isotropic material characterized by the elastic moduli E and G, they are given as products of the moduli and geometric quantities (i.e.: area A, area moments I _α , polar moment J) of the cross section.

To discretize the energy integrals (1) and (2) we need a discrete model of framed curves with discrete versions of their invariants $\mathbf{K}$ and $\pmb{\varGamma }$.

4 The Difference Geometry of Framed Curves

In this section we inductively develop our approach to construct the discrete kinematics of geometrically exact rod models by “geometric finite differences”. We use concepts and results of the differential geometry of framed curves in three-dimensional Euclidian space, and introduce ideas from Discrete Differential Geometry (DDG) ⁴ to construct their discrete counterparts in a particular way, such that essential properties of the continuum theory are preserved in the discrete setting.

Below we consider basic concepts of the elementary differential geometry of parameter curves in Euclidian space, as presented in standard texts (e.g. do Carmo’s book [9]), from the geometric viewpoint emphasized throughout Blaschke’s books [3, 4], and outline some essential ideas how to transfer the continuous concepts to the discrete setting, following and extending ideas of Sauer [27].

4.1 Discrete Arc Length and Edge Tangent Vectors

The mutual distance of points on a smooth curve can be measured by unbending the curve to a straight line, such that the distance of the same points on the straightened curve equals their Euclidian distance in space.

This procedure of continuously “unrolling” a smooth curve to the real axis can be understood most easily for the simplified case of a discrete approximation of the curve by a polygonal arc, given by a sequence of curve points p _j = ϕ(ξ _j ) obtained from a given discretization a =: ξ ₀ < ξ ₁ < … < ξ _n : = b of the parameter interval with position vectors $\mathbf{r}_{j}:= \mathbf{r}(\xi _{j}) \equiv \mathbf{x}(\,p_{j})$. The corresponding polygonal arc is the piecewise linear curve in $\mathcal{E}^{3}$ defined as the union $\mathcal{P}_{n}[\,p_{0},\ldots,p_{n}]:= \cup _{j=1}^{n}[\,p_{j-1},p_{j}]$ of edges $[\,p_{j-1},p_{j}]\,:=\,\{ p \in \mathcal{ E}^{3}\vert p = p_{j-1} +\lambda (\,p_{j} - p_{j-1}),\,0 \leq \lambda \leq 1\}$ that are spanned by pairs of adjacent points (vertices) p _j−1 and $p_{j} = p_{j-1} + \mathbf{l}_{j-\frac{1} {2} }$, linked by edge vectors $\mathbf{l}_{j-\frac{1} {2} }:= p_{j} - p_{j-1} = \mathbf{r}_{j} -\mathbf{r}_{j-1}$ of length $\ell_{j-\frac{1} {2} }:=\| \mathbf{l}_{j-\frac{1} {2} }\| =\| \mathbf{r}_{j} -\mathbf{r}_{j-1}\|$.

Then, the distance of any pair ( p _k , p _l ) of vertices (with k < l), measured along the path of the polygonal arc $\mathcal{P}_{n}$, is given by the sum $\sum _{j=k+1}^{l}\ell_{j-\frac{1} {2} }$ of edge lengths in between, which equals the Euclidian distance of ( p _k , p _l ) if the polygonal arc is straightened out to a line. If the discretization is refined, the polygonal arc $\mathcal{P}_{n}$ approximates the curve $\mathcal{C}$ with increasing accuracy, provided the curve is sufficiently smooth (i.e.: at least Lipschitz continuous). According to the (approximate) identity

$$\displaystyle{\sum _{j=k+1}^{l}\ell_{ j-\frac{1} {2} }\; =\;\sum _{ j=k+1}^{l}\left \|\frac{\mathbf{r}_{j} -\mathbf{r}_{j-1}} {\xi _{j} -\xi _{j-1}} \right \|\,(\xi _{j} -\xi _{j-1})\; \approx \;\sum _{j=k+1}^{l}\left \|\mathbf{r}'(\xi _{ j-1/2})\right \|\,(\xi _{j} -\xi _{j-1})\;,}$$

the sum of edge lengths may be interpreted as a discrete approximation of the continuous integral $\int _{\xi _{ k}}^{\xi _{l}}\|\mathbf{r}'(\xi )\|\,d\xi \, =\,\sum _{ j=k+1}^{l}\int _{ \xi _{j-1}}^{\xi _{j}}\|\mathbf{r}'(\xi )\|\,d\xi$ by evaluating the integral over the intervals [ξ _j−1, ξ _j ] of length h _j−1∕2: = ξ _j −ξ _j−1 approximately by the midpoint rule according to $\int _{\xi _{ j-1}}^{\xi _{j}}\|\mathbf{r}'(\xi )\|\,d\xi \, \approx \,\|\mathbf{r}'(\xi _{ j-1/2})\|\,h_{j-1/2} + O(h_{j-1/2}^{3})$, and approximating the derivative $\mathbf{r}'(\xi )$ at the midpoints $\xi _{j-1/2}:= \frac{1} {2}(\xi _{j-1} +\xi _{j})$ by a central finite difference as $\mathbf{r}'(\xi _{j-1/2}) \approx (\mathbf{r}_{j} -\mathbf{r}_{j-1})/h_{j-1/2} + O(h_{j-1/2}^{2})$.

Likewise, the position vector $\mathbf{r}_{j-1/2}:= \frac{1} {2}(\mathbf{r}_{j-1} + \mathbf{r}_{j}) \equiv \mathbf{x}(\bar{p}_{j-1/2})$ of the edge center approximates the position vector $\mathbf{r}(\xi _{j-1/2})$ at the midpoint of the parameter interval with second order accuracy. Thus, considering the polygonal approximation of a curve naturally leads to the concept of edge based tangent vectors $\mathbf{l}_{j-1/2}/h_{j-1/2}$, with unit length edge tangent vectors given by $\mathbf{t}_{j-1/2}:= \mathbf{l}_{j-1/2}/\ell_{j-1/2}$, both located at edge centers. Requiring that consecutive vertices p _j and p _j+1 must not coincide, which in turn implies non–zero edge vectors (i.e.: $\|\mathbf{l}_{j+1/2}\| > 0 \Leftrightarrow p_{j}\neq p_{j+1}$) and unit vectors $\mathbf{t}_{j-1/2}$ well defined for all edges, corresponds to the definition of discrete regularity of a polygonal arc (see Fig. 3).

Fig. 3

Polygonal arc $\mathcal{P}_{n}[\,p_{0},\ldots,p_{n}]$ approximating a smooth regular geometric curve $\mathcal{C}$: The vertices $p_{j} \in \mathcal{ C}$ define the edges [ p _j−1, p _j ] of length ℓ _j−1∕2 > 0, with unit length tangent vectors $\mathbf{t}_{j-1/2} = (\,p_{j} - p_{j-1})/\ell_{j-1/2}$ located at edge centers $\bar{p}_{j-1/2}$

While the mapping k ↦ p _k of integer indices to vertex points in Euclidian space may be interpreted as a discrete geometric curve that induces a corresponding mapping $k\mapsto \mathbf{r}_{k} \equiv \mathbf{x}(\,p_{k})$ of indices to position vectors, a discrete parameter curve is defined by the mapping $\xi _{k}\mapsto \mathbf{r}(\xi _{k})$ induced by a discretization of the domain of a smooth parameter curve. Therefore, the discrete counterpart of arc length parametrisation corresponds to the case h _k−1∕2 = ℓ _k−1∕2 of grid constants equal to edge lengths, with discrete arc length parameters defined as ς _k : = ς ₀ + ∑ _{j = 1} ^k ℓ _j−1∕2, marking the vertex positions of the polygonal arc straightened out parallel to the real axis. The main concepts introduced in this section may be summarized as follows:

A discrete geometric curve is a mapping $\mathbb{Z} \ni j\mapsto p_{j} \in \mathcal{ E}^{3}$ of integer indices to points in Euclidian space. The discrete curve is regular iff p _j ≠ p _j−1 holds for all vertex pairs ( p _j−1, p _j ). A discrete regular geometric curve has well defined unit tangent vectors $\mathbf{t}_{j-1/2} = (\,p_{j} - p_{j-1})/\ell_{j-1/2}$ on all edges (see Fig. 3).

4.2 The Difference Geometry of Discrete Cosserat Curves

Our discussion of discrete regular geometric curves with edge centered unit tangent vectors indicates the path to introduce Cosserat curves in the discrete setting:

A discrete Cosserat curve is defined as a polygonal arc $\mathcal{P}_{n}[\,p_{0},\ldots,p_{n}]$ corresponding to a regular discrete geometric curve, augmented by a set {R _j−1∕2} _{j = 1, …, n} of orthonormal frames $\mathsf{SO(3)} \ni \mathsf{R}_{j-1/2} = \mathbf{a}_{j-1/2}^{(k)} \otimes \mathbf{e}_{k}$ located at edge centers $\bar{p}_{j-1/2}$. The frames are represented by rotational quaternions as $\mathsf{R}_{j-1/2} = \mathfrak{E}(\hat{\mathsf{q}}_{j-1/2})$ in terms of the Euler map $\mathfrak{E}: S^{3} \rightarrow \mathsf{SO(3)}$ implicitly defined via its operation $\mathfrak{E}(\hat{\mathsf{q}})\mathbf{v} =\hat{ \mathsf{q}} \circ \mathbf{v} \circ \hat{\mathsf{q}}^{{\ast}}$ on vectors, with frame directors given by: $\mathbf{a}_{j-1/2}^{(k)} = \mathsf{R}_{j-1/2} \cdot \mathbf{e}_{k} =\hat{ \mathsf{q}}_{j-1/2} \circ \mathbf{e}_{k} \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}$ (see Fig. 4).

Fig. 4

Polygonal arc $\mathcal{P}_{n}[\,p_{0},\ldots,p_{n}]$ and edge based quaternionic frames $\hat{\mathsf{q}}_{j-1/2} \equiv \mathsf{R}_{j-1/2} = \mathfrak{E}(\hat{\mathsf{q}}_{j-1/2})$ of a discrete Cosserat curve. In general, the frames are not adapted to the edges of $\mathcal{P}_{n}$, i.e.: $\mathbf{a}_{j-1/2}^{(3)}\neq \mathbf{t}_{j-1/2}$. A discrete ribbon is a special case of a discrete Cosserat curve with adapted frames

4.2.1 Curvature Angles and Discrete Curvatures

For each pair of frames R _j±1∕2, there is a unique spatial difference rotation ⁵ connecting these frames as R _j+1∕2 = w _j ⋅ R _j−1∕2. According to Euler’s theorem, this rotation w _j = R _j+1∕2 ⋅ R _j−1∕2 ^T can be written as $\mathsf{w}_{j} =\exp (\vartheta _{j}\,\tilde{\mathsf{u}}_{j})$, i.e.: a rotation by an angle ϑ _j around the axis given by the unit vector $\hat{\mathbf{u}}_{j}$. The corresponding rotational quaternion connects the quaternion frames via $\hat{\mathsf{q}}_{j+1/2} =\hat{ \mathsf{w}}_{j} \circ \hat{\mathsf{q}}_{j-1/2}$ and is given by:

$$\displaystyle{ \hat{\mathsf{q}}_{j+1/2} \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}\; =:\;\hat{ \mathsf{w}}_{ j}\; =\;\cos (\vartheta _{j}/2) +\sin (\vartheta _{j}/2)\,\hat{\mathbf{u}}_{j}\; =\;\exp (\vartheta _{j}/2\,\hat{\mathbf{u}}_{j})\;. }$$

The material difference rotation given by W _j : = R _j−1∕2 ^T ⋅ R _j+1∕2 may be obtained from the spatial one by a pull back rotation with either of the frames R _j±1∕2, i.e.: W _j = R _j±1∕2 ^T ⋅ w _j ⋅ R _j±1∕2, and can be written as a rotation $\mathsf{W}_{j} =\exp (\vartheta _{j}\,\tilde{\mathsf{U}}_{j})$ by the angle ϑ _j about the back rotated axis⁶ $\hat{\mathbf{U}}_{j}:= \mathsf{R}_{j\pm 1/2}^{T} \cdot \hat{\mathbf{u}}_{j}$. In terms of rotational quaternions, the equivalent relations for $\hat{\mathsf{W}}_{j} =\hat{ \mathsf{q}}_{j\pm 1/2}^{{\ast}}\circ \hat{\mathsf{w}}_{j} \circ \hat{\mathsf{q}}_{j\pm 1/2}$ read:

$$\displaystyle{ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}\circ \hat{\mathsf{q}}_{ j+1/2}\; =:\;\hat{ \mathsf{W}}_{j}\; =\;\cos (\vartheta _{j}/2) +\sin (\vartheta _{j}/2)\,\hat{\mathbf{U}}_{j}\; =\;\exp (\vartheta _{j}/2\,\hat{\mathbf{U}}_{j})\;. }$$

Extraction of the material rotation vector $\vartheta _{j}\,\hat{\mathbf{U}}_{j}\, =\, 2\log (\hat{\mathsf{W}}_{j})$ from the quaternionic difference rotation $\hat{\mathsf{W}}_{j}$ then leads to the following definition of curvature angles:

$$\displaystyle{ \psi _{j}^{(k)}\;:=\;\langle \mathbf{e}_{ k},2\log (\hat{\mathsf{W}}_{j})\rangle \; =\;\vartheta _{j}\,\langle \mathbf{e}_{k},\hat{\mathbf{U}}_{j}\rangle \;\, \Leftrightarrow \;\vartheta _{j}\,\hat{\mathbf{U}}_{j}\; =\;\psi _{ j}^{(k)}\,\mathbf{e}_{ k}\;. }$$

(3)

As $\hat{\mathbf{U}}_{j}:= \mathsf{R}_{j\pm 1/2}^{T} \cdot \hat{\mathbf{u}}_{j}$ and $\mathbf{a}_{j\pm 1/2}^{(k)} = \mathsf{R}_{j\pm 1/2} \cdot \mathbf{e}_{k}$ hold, one obtains the angles ψ _j ^(k) equivalently by decomposing $\vartheta _{j}\,\hat{\mathbf{u}}_{j}\, =\, 2\log (\hat{\mathsf{w}}_{j})$ w.r.t. the frame directors, i.e.: $\psi _{j}^{(k)} =\langle \mathbf{a}_{j\pm 1/2}^{(k)},2\log (\hat{\mathsf{w}}_{j})\rangle =\vartheta _{j}\langle \mathbf{a}_{j\pm 1/2}^{(k)},\hat{\mathbf{u}}_{j}\rangle$. The set $\{\vartheta _{j}\hat{\mathbf{U}}_{j}\}_{j=1,\ldots,n}$ of material rotation vectors (or equivalently: the set {ψ _j ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3} of curvature angles) corresponds to the discrete data of the set of quaternion frames $\{\hat{\mathsf{q}}_{j-1/2}\}_{j=1,\ldots,n}$ of a discrete Cosserat curve. The frames can be reconstructed iteratively by the material difference rotations as $\hat{\mathsf{q}}_{j-1/2}\mapsto \hat{\mathsf{q}}_{j+1/2} =\hat{ \mathsf{q}}_{j-1/2} \circ \exp (\vartheta _{j}/2\,\hat{\mathbf{U}}_{j})$, or likewise equivalently by spatial ones according to the algorithm

$$\displaystyle{ \hat{\mathsf{q}}_{j-1/2}\, \rightarrow \,\hat{\mathsf{w}}_{j} =\hat{ \mathsf{q}}_{j-1/2} \circ \exp (\vartheta _{j}/2\,\hat{\mathbf{U}}_{j}) \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}\,\rightarrow \,\hat{\mathsf{q}}_{ j+1/2} =\hat{ \mathsf{w}}_{j} \circ \hat{\mathsf{q}}_{j-1/2}\;, }$$

(4)

for j = 1, …, n − 1, starting at $\hat{\mathsf{q}}_{1/2}$ chosen as initial value, and proceeding edgewise in ascending order.

Discrete material curvatures K _j ^(k) can then be defined by dividing the curvature angles by the discrete arc length distance Δς _j between the edge centers $\bar{p}_{j\pm 1/2}$:

$$\displaystyle{ K_{j}^{(k)}\;:=\; \frac{\psi _{j}^{(k)}} {\varDelta \varsigma _{j}} \; =\;\varDelta \varsigma _{ j}^{-1}\,\langle \mathbf{e}_{ k},2\log (\hat{\mathsf{W}}_{j})\rangle \; =\; \frac{\vartheta _{j}} {\varDelta \varsigma _{j}}\,\langle \mathbf{e}_{k},\hat{\mathbf{U}}_{j}\rangle \;. }$$

(5)

If the discrete Cosserat curve approximates a smooth one, the vector $\mathbf{K}_{j} = K_{j}^{(k)}\,\mathbf{e}_{k}$ of discrete material curvatures converges to the material Darboux vector $\mathbf{K}(\,p_{j})$ in the limit Δς _j → 0. In this case, the curvature angles can be interpreted as integrated values, approximating the integrals $\int _{p_{j-1/2}}^{p_{j+1/2} }\langle \mathbf{e}_{k},2\hat{\mathsf{q}}^{{\ast}}\circ \mathrm{ d}\hat{\mathsf{q}}_{p}\rangle \approx \psi _{j}^{(k)}$ of the curvature 1–form $\mathbf{t}(\,p)\mapsto 2\hat{\mathsf{q}}^{{\ast}}(\,p) \circ \mathrm{ d}\hat{\mathsf{q}}_{p}(\mathbf{t}(\,p)) = \mathbf{K}(\,p)$, and the discrete curvatures K _j ^(k) = ψ _j ^(k)∕Δς _j with $\varDelta \varsigma _{j} \approx \int _{p_{j-1/2}}^{p_{j+1/2} }ds$ correspond to approximate integral averages.

Alternative discrete curvature expressions that approximate $\mathbf{K}(\,p_{j}) \approx \mathbf{K}_{j}$ according to the relations ϑ _j ≈ 2sin(ϑ _j ∕2) ≈ 2tan(ϑ _j ∕2) valid for small angles can be obtained directly from the imaginary and real parts $\mathfrak{I}(\hat{\mathsf{W}}_{j}) =\sin (\vartheta _{j}/2)\,\hat{\mathbf{U}}_{j}$ and $\mathfrak{R}(\hat{\mathsf{W}}_{j}) =\cos (\vartheta _{j}/2)$ of the material difference rotation. The simplest examples are: $\varDelta \varsigma _{j}\mathbf{K}_{j} \approx 2\mathfrak{I}(\hat{\mathsf{W}}_{j}) = 2\sin (\vartheta _{j}/2)\,\hat{\mathbf{U}}_{j}$ and $\varDelta \varsigma _{j}\mathbf{K}_{j} \approx 2\mathfrak{I}(\hat{\mathsf{W}}_{j})/\mathfrak{R}(\hat{\mathsf{W}}_{j}) = 2\tan (\vartheta _{j}/2)\,\hat{\mathbf{U}}_{j}$. A particularly interesting variant, which appears within the derivation of discrete derivative equations for quaternionic frames, is given by:

$$\displaystyle{ \varDelta \varsigma _{j}\,\mathbf{K}_{j}\; \approx \; 4\,\mathfrak{I}(\hat{\mathsf{W}}_{j})\;/\;(1 + \mathfrak{R}(\hat{\mathsf{W}}_{j}))\; =\; 4\,\tan (\vartheta _{j}/4)\,\hat{\mathbf{U}}_{j}\;. }$$

(6)

4.2.2 Material Edge Components, Edge Tangent Cosines and Shear Angles

The second set of data of a discrete Cosserat curve is given by the components

$$\displaystyle{ \ell_{j-1/2}^{(k)}\;:=\;\langle \mathbf{a}_{ j-1/2}^{(k)},\mathbf{l}_{ j-1/2}\rangle \; =\;\ell _{j-1/2}\,\langle \mathbf{a}_{j-1/2}^{(k)},\mathbf{t}_{ j-1/2}\rangle }$$

(7)

of the edge vectors $\mathbf{l}_{j-1/2} =\ell _{j-1/2}\,\mathbf{t}_{j-1/2}$ w.r.t. the local frame, which we denote as material edge components. The squared edge lengths can be obtained as the sum ℓ _j−1∕2 ² = ∑ _{k = 1} ³(ℓ _j−1∕2 ^(k))² of the squared material edges components. Considering {ℓ _j−1∕2 ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3} as given data, the edge lengths ℓ _j−1∕2 and the discrete arc length parameters ς _k = ς ₀ + ∑ _{j = 1} ^k ℓ _j−1∕2 can be computed from these.

According to (7) the components ℓ _j−1∕2 ^(k) are given as products of the edge lengths and the edge tangent cosines

$$\displaystyle{ \varGamma _{j-1/2}^{(k)}\;:=\; \frac{\ell_{j-1/2}^{(k)}} {\ell_{j-1/2}} \; =\;\langle \mathbf{a}_{j-1/2}^{(k)},\mathbf{t}_{ j-1/2}\rangle \; =\;\langle \mathbf{e}_{k},\hat{\mathsf{q}}_{j-1/2}^{{\ast}}\circ \mathbf{t}_{ j-1/2} \circ \hat{\mathsf{q}}_{j-1/2}\rangle \;. }$$

(8)

The shear angles γ _j−1∕2 ^(k) = arccos(Γ _j−1∕2 ^(k)) measure the angles enclosed by the edge vector and the frame axes. The edge tangent cosines (8) converge to the direction cosines $\langle \mathbf{a}^{(k)}(\,p),\mathbf{t}(\,p)\rangle$ of the unit tangent vector $\mathbf{t}(\,p)$ w.r.t. the frame directors $\mathbf{a}^{(k)}(\,p)$ at p = p _j−1∕2 in the limit ℓ _j−1∕2 → 0.

The set { p _j } _{j = 0, …, n} of vertices of the polygonal arc $\mathcal{P}$ can be obtained by summation of the edge vectors $\mathbf{l}_{j-1/2}$ according to $p_{j} = p_{0} +\sum _{ i=1}^{j}\mathbf{l}_{i-1/2}$, starting from an arbitrarily chosen initial value $p_{0} \in \mathcal{ E}^{3}$. As $\mathbf{l}_{j-1/2} =\langle \mathbf{a}_{j-1/2}^{(k)},\mathbf{l}_{j-1/2}\rangle \,\mathbf{a}_{j-1/2}^{(k)} =\ell_{ j-1/2}^{(k)}\,\mathbf{a}_{j-1/2}^{(k)}$ and $\mathbf{a}_{j-1/2}^{(k)} =\hat{ \mathsf{q}}_{j-1/2} \circ \mathbf{e}_{k} \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}$, the sum for the computation of the vertices from edge vectors may be rewritten in the form

$$\displaystyle{ p_{j}\, -\, p_{0}\; =\;\sum _{ i=1}^{j}\ell_{ i-1/2}\,\mathbf{t}_{i-1/2}\; =\;\sum _{ i=1}^{j}\ell_{ i-1/2}^{(k)}\,\hat{\mathsf{q}}_{ i-1/2} \circ \mathbf{e}_{k} \circ \hat{\mathsf{q}}_{i-1/2}^{{\ast}} }$$

(9)

as an expression in terms of known quantities.

The sum (9) yields a discrete approximation of the integral $p_{j} - p_{0} =\int _{ p_{0}}^{p_{j}}dp$ with $dp = \mathbf{t}(\,p)\,ds$, which can be rewritten equivalently as $\int _{p_{0}}^{p_{j}}\hat{\mathsf{q}} \circ \pmb{\varGamma }\circ \hat{\mathsf{q}}^{{\ast}}\,ds$ in terms of the quaternion frame $\hat{\mathsf{q}}(\,p)$ and $\pmb{\varGamma }(\,p) = \mathsf{R}^{T}(\,p) \cdot \mathbf{t}(\,p) =\hat{ \mathsf{q}}^{{\ast}}(\,p) \circ \mathbf{t}(\,p) \circ \hat{\mathsf{q}}(\,p)$. The second sum term in (9) corresponds to an approximation of the integrals $\int _{p_{i-1}}^{p_{i}}\hat{\mathsf{q}} \circ \pmb{\varGamma }\circ \hat{\mathsf{q}}^{{\ast}}\,ds$ by the midpoint rule as $\ell_{i-1/2}\,\hat{\mathsf{q}}_{i-1/2} \circ \pmb{\varGamma }_{i-1/2} \circ \hat{\mathsf{q}}_{i-1/2}^{{\ast}}$, with $\pmb{\varGamma }_{i-1/2}\,:=\,\varGamma _{ i-1/2}^{(k)}\,\mathbf{e}_{k}$. The discrete integration formula provided by (9) is equivalent to the difference equation

$$\displaystyle{ (\,p_{j} - p_{j-1})/\ell_{j-1/2}\; =\;\hat{ \mathsf{q}}_{j-1/2} \circ \pmb{\varGamma }_{j-1/2} \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}} }$$

(10)

discretizing the derivative equation $dp =\hat{ \mathsf{q}} \circ \pmb{\varGamma }\circ \hat{\mathsf{q}}^{{\ast}}\,ds$.

4.2.3 Discrete Generalized Frénet Equations

The directors $\mathbf{a}_{j\pm 1/2}^{(k)}$ of adjacent frames $\mathsf{R}_{j\pm 1/2} = \mathbf{a}_{j\pm 1/2}^{(k)} \otimes \mathbf{e}_{k}$ are connected by spatial difference rotations $\mathsf{w}_{j} =\exp (\vartheta _{j}\,\tilde{\mathsf{u}}_{j}) =\mathrm{ cay}(\tan (\vartheta _{j}/2)\,\tilde{\mathsf{u}}_{j})$ and satisfy the equations $\mathbf{a}_{j+1/2}^{(k)} = \mathsf{w}_{j} \cdot \mathbf{a}_{j-1/2}^{(k)}$, which may be rewritten equivalently as:

$$\displaystyle{ \mathbf{a}_{j+1/2}^{(k)}\, -\,\mathbf{a}_{ j-1/2}^{(k)}\; =\; 2\tan (\vartheta _{ j}/2)\,\hat{\mathbf{u}}_{j} \times \frac{1} {2}\,(\mathbf{a}_{j-1/2}^{(k)}\, +\, \mathbf{a}_{ j+1/2}^{(k)})\;. }$$

(11)

Divided by Δς _j , this coupled system of difference equations corresponds to a geometric FD discretization of the generalized Frénet equations $\mathrm{d}\mathbf{a}_{p}^{(k)} =\pmb{\kappa } \times \mathbf{a}^{(k)}$ satisfied by the frame directors of a Cosserat curve.

According to (5) the FD approximation of the material Darboux vector at p _j is given by $\mathbf{K}_{j} = (\vartheta _{j}/\varDelta \varsigma _{j})\,\hat{\mathbf{U}}_{j} \approx \mathbf{K}(\,p_{j})$. The corresponding spatial Darboux vector then results from a forward rotation according to $\pmb{\kappa }_{j} = \mathsf{R}_{j\pm 1/2} \cdot \mathbf{K}_{j}$ and is therefore given by: $\pmb{\kappa }_{j} = (\vartheta _{j}/\varDelta \varsigma _{j})\,\hat{\mathbf{u}}_{j} \approx \pmb{\kappa } (\,p_{j})$. The discrete spatial Darboux vector identified from (11) equals $\varDelta \varsigma _{j}^{-1}2\tan (\vartheta _{j}/2)\,\hat{\mathbf{u}}_{j} \approx \pmb{\kappa }_{j}$, which provides an alternative consistent FD approximation of $\pmb{\kappa }(\,p_{j})$ that coincides with $\pmb{\kappa }_{j}$ in the limit Δς _j → 0.

4.2.3.1 Averaged Frame Director Expansion of the Discrete Spatial Darboux Vector

For R _j±1∕2 ∈ SO(3) the matrix R _j−1∕2 +R _j+1∕2 = R _j−1∕2 ⋅ (I +W _j ) is regular if the eigenvalues of W _j are different from − 1, which is always the case for curvature angles | ψ _j ^(k) | < π. Then the averaged frame directors $\bar{\mathbf{a}}_{j}^{(k)}\,:=\, \frac{1} {2}\,(\mathbf{a}_{j-1/2}^{(k)}\, +\, \mathbf{a}_{ j+1/2}^{(k)})$ associated to vertex p _j , which appear on the r.h.s. of (11), are linearly independent and form a basis of $\mathbb{E}^{3}$. Although they do not form an orthonormal frame, they become orthonormal in the limit Δς _j → 0, as $\lim _{\varDelta \varsigma _{j}\rightarrow 0}\bar{\mathbf{a}}_{j}^{(k)} = \mathbf{a}^{(k)}(\,p_{j})$ holds. The discrete generalized Frénet equations (11) can be rewritten with greater formal similarity to their continuous counterpart by expanding the spatial Darboux vector $\pmb{\kappa }_{j} \sim \hat{\mathbf{u}}_{j}$ w.r.t. the dual basis vectors $\bar{\mathbf{b}}_{j}^{(k)}$ implicitly defined as $\langle \bar{\mathbf{b}}_{j}^{(k)},\bar{\mathbf{a}}_{j}^{(l)}\rangle =\delta _{kl}$ and explicitly given by $\bar{\mathbf{b}}_{j}^{(k)} = (\bar{\mathbf{a}}_{j}^{(l)} \times \bar{\mathbf{a}}_{j}^{(m)})/\langle \bar{\mathbf{a}}_{j}^{(1)} \times \bar{\mathbf{a}}_{j}^{(2)},\bar{\mathbf{a}}_{j}^{(3)}\rangle$ for cyclic permutations (klm) of (123). By construction $\lim _{\varDelta \varsigma _{ j}\rightarrow 0}\bar{\mathbf{b}}_{j}^{(k)} = \mathbf{a}^{(k)}(\,p_{ j})$ holds. The representation $\pmb{\kappa }(\,p_{j})\; \approx \;\varDelta \varsigma _{j}^{-1}\,2\tan (\vartheta _{j}/2)\,\langle \bar{\mathbf{b}}_{j}^{(k)},\hat{\mathbf{u}}_{j}\rangle \;\bar{\mathbf{a}}_{j}^{(k)}$ of the discrete spatial Darboux vector is obtained by using the identity $\hat{\mathbf{u}}_{j} =\langle \bar{ \mathbf{b}}_{j}^{(k)},\hat{\mathbf{u}}_{j}\rangle \,\bar{\mathbf{a}}_{j}^{(k)}$ and implies the corresponding approximation $K^{(k)}(\,p_{j})\, \approx \,\varDelta \varsigma _{j}^{-1}\,2\tan (\vartheta _{j}/2)\,\langle \bar{\mathbf{b}}_{j}^{(k)},\hat{\mathbf{u}}_{j}\rangle$ of the material curvatures at the vertices. Inserting this expansion into (11) leads to the equivalent reformulation

$$\displaystyle{ \mathbf{a}_{j+1/2}^{(k)}\, -\,\mathbf{a}_{ j-1/2}^{(k)}\; =\; 2\tan (\vartheta _{ j}/2)\,\left [\langle \bar{\mathbf{b}}_{j}^{(m)},\hat{\mathbf{u}}_{ j}\rangle \,\bar{\mathbf{a}}_{j}^{(m)}\; -\;\langle \bar{\mathbf{b}}_{ j}^{(l)},\hat{\mathbf{u}}_{ j}\rangle \,\bar{\mathbf{a}}_{j}^{(l)}\right ] }$$

of these equations for cyclic permutations (klm) of (123), as the Darboux vector component $\sim \bar{\mathbf{a}}_{j}^{(k)}$ is canceled due to the cross product. Dividing both sides of this FD equation for $\mathbf{a}_{j\pm 1/2}^{(k)}$ by Δς _j and taking the limit Δς _j → 0 yields the well known form $\mathrm{d}\mathbf{a}_{p}^{(k)} =\pmb{\kappa } \times \mathbf{a}^{(k)} = K^{(m)}\mathbf{a}^{(m)} - K^{(l)}\mathbf{a}^{(l)}$ of the generalized Frénet equations of the continuum theory of framed curves.

4.2.3.2 Discrete Derivative Equations for Quaternion Frames

An analogous discretisation of the derivative equation $\mathrm{d}\hat{\mathsf{q}}_{p} = \frac{1} {2}\pmb{\kappa } \circ \hat{\mathsf{q}}$ for the quaternion frames can be obtained from the Cayley transform⁷ and its inverse

$$\displaystyle{\mathbf{q}\mapsto \hat{\mathsf{p}}\, =\,\mathrm{ cay}(\mathbf{q})\, =\, \frac{1 + \mathbf{q}} {1 -\mathbf{q}}\;\,,\;\;\hat{\mathsf{p}}\mapsto \mathbf{q} =\mathrm{ cay}^{-1}(\hat{\mathsf{p}})\, =\, \frac{\hat{\mathsf{p}} - 1} {\hat{\mathsf{p}} + 1}}$$

mapping vectors to rotational quaternions and vice versa. For $\hat{\mathsf{p}} =\cos (\alpha ) +\sin (\alpha )\,\hat{\mathbf{e}} =\exp (\alpha \,\hat{\mathbf{e}})$ one obtains $\mathbf{q} =\mathrm{ cay}^{-1}(\hat{\mathsf{p}}) =\tan (\alpha /2)\,\hat{\mathbf{e}}$, such that $\exp (\alpha \,\hat{\mathbf{e}}) =\mathrm{ cay}(\tan (\alpha /2)\,\hat{\mathbf{e}})$ holds. Applied to the rotation $\hat{\mathsf{w}}_{j} =\exp (\vartheta _{j}/2\,\hat{\mathbf{u}}_{j}) =\hat{ \mathsf{q}}_{j+1/2} \circ \hat{\mathsf{q}}_{j-1/2}^{{\ast}}$ connecting adjacent quaternions frames this yields the desired result:

$$\displaystyle{ \hat{\mathsf{q}}_{j+1/2}\, -\,\hat{\mathsf{q}}_{j-1/2}\; =\; \frac{1} {2}\,\left [4\tan \left (\frac{\vartheta _{j}} {4}\right )\,\hat{\mathbf{u}}_{j}\right ]\, \circ \,\frac{1} {2}(\hat{\mathsf{q}}_{j-1/2}\, +\,\hat{ \mathsf{q}}_{j+1/2})\;. }$$

(12)

Starting from $\hat{\mathsf{q}}_{j+1/2} =\hat{ \mathsf{q}}_{j-1/2} \circ \hat{\mathsf{W}}_{j}$ with $\hat{\mathsf{W}}_{j} =\exp (\vartheta _{j}/2\,\hat{\mathbf{U}}_{j})$ one obtains the equivalent difference equation

$$\displaystyle{ 2\,(\hat{\mathsf{q}}_{j+1/2}\, -\,\hat{\mathsf{q}}_{j-1/2})\; =\; \frac{1} {2}(\hat{\mathsf{q}}_{j-1/2}\, +\,\hat{ \mathsf{q}}_{j+1/2})\, \circ \,\left [4\tan \left (\frac{\vartheta _{j}} {4}\right )\,\hat{\mathbf{U}}_{j}\right ]\;, }$$

(13)

which provides a geometric FD discretization of the equivalent form $\mathrm{d}\hat{\mathsf{q}}_{p} = \frac{1} {2}\hat{\mathsf{q}} \circ \mathbf{K}$ of the derivative equation for the quaternion frames in terms of the material Darboux vector $\mathbf{K} =\hat{ \mathsf{q}}^{{\ast}}\circ \pmb{\kappa }\circ \hat{\mathsf{q}}$. The FD approximation of the material Darboux vector $\mathbf{K}(\,p_{j})$ implied in (13) is the one already mentioned in (6). The FD formula for the spatial Darboux vector $\pmb{\kappa }$ results from a forward rotation $\hat{\mathbf{u}}_{j} =\hat{ \mathsf{q}}_{j\pm 1/2} \circ \hat{\mathbf{U}}_{j} \circ \hat{\mathsf{q}}_{j\pm 1/2}^{{\ast}}$ of the material rotation axis to the spatial one. The discrete derivative equations (12) and (13) are the equivalent quaternionic counterparts of the discrete generalized Frénet equations (11).

4.2.4 The Principal Theorem for Discrete Cosserat Curves

At this point, we have obtained all ingredients necessary for the statement and constructive proof of the principal theorem of discrete Cosserat curve theory.

The basic data of a discrete Cosserat curve, consisting of a polygonal arc $\mathcal{P}_{n}[\,p_{0},\ldots,p_{n}]$ and the set $\{\hat{\mathsf{q}}_{j-1/2}\}_{j=1,\ldots,n}$ of quaternion frames representing orthonormal frames $\mathsf{R}_{j-1/2} = \mathfrak{E}(\hat{\mathsf{q}}_{j-1/2})$ located at edge centers $\bar{p}_{j-1/2}$, are:

• the set {ψ _j ^(k)} _{j = 1, …, n−1} ^{k = 1, 2, 3} of curvature angles, and

• the set {ℓ _j−1∕2 ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3} of material edge components.

The essential parts of the discrete integration procedure, resulting in a reconstruction of a discrete Cosserat curve from its basic data and chosen initial conditions, have already been outlined in the previous paragraphs of this section and is summarized compactly in the following algorithm:

• 1. A rotational quaternion $\hat{\mathsf{q}}_{0} \in S^{3}$ representing an orthonormal frame $\mathsf{R}_{0} = \mathfrak{E}(\hat{\mathsf{q}}_{0}) \in \mathsf{SO(3)}$ and a point $p_{0} \in \mathcal{ E}^{3}$ are selected as arbitrarily chosen initial values.

• 2. Starting from $\hat{\mathsf{q}}_{1/2}:=\hat{ \mathsf{q}}_{0}$, the quaternion frames are generated iteratively from the material rotation vectors $\vartheta _{j}\,\hat{\mathbf{U}}_{j} =\psi _{ j}^{(k)}\,\mathbf{e}_{k}$ defined by the given curvature angles via sequential rotations

  $$\displaystyle{\hat{\mathsf{q}}_{j+1/2}\, =\,\hat{ \mathsf{q}}_{j-1/2} \circ \exp (\vartheta _{j}/2\,\hat{\mathbf{U}}_{j})\;\,\mathrm{for}\;\,j = 1,\ldots,n - 1}$$

  according to (4). The sequence $\{\hat{\mathsf{q}}_{j-1/2}\}_{j=1,\ldots,n}$ is an exact solution of the discrete derivative equations [ (12), (13)] uniquely determined by its initial value.

• 3. Starting from p ₀, the vertices are obtained iteratively by summation as

  $$\displaystyle{p_{j}\; =\; p_{0}\; +\;\sum _{ i=1}^{j}\ell_{ i-1/2}^{(k)}\,\hat{\mathsf{q}}_{ i-1/2} \circ \mathbf{e}_{k} \circ \hat{\mathsf{q}}_{i-1/2}^{{\ast}}\;\,\mathrm{for}\;\,j = 1,\ldots,n}$$

  according to (9) from the known quaternion frames and the given material edge components. The sequence { p _j } _{j = 0, …, n} is an exact solution of the discrete derivative equations (10) uniquely determined by its initial value p ₀.

This algorithm provides a constructive proof of the principal theorem for discrete Cosserat curves, which may be formulated as follows:

For given discrete data consisting of the sets of curvature angles {ψ _j ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3} and material edge components {ℓ _j−1∕2 ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3}, the solutions of the discrete derivative equations (10) and (12), (13) determine the quaternion frames $\{\hat{\mathsf{q}}_{j-1/2}\}_{j=1,\ldots,n}$ and the vertices { p _j } _{j = 0, …, n} of a discrete Cosserat curve up to an overall rigid body motion in $\mathcal{E}^{3}$.

5 Discrete Elastic Energy of Quaternionic Cosserat Rods

We discretize the continuum model of an elastic Cosserat rod by approximating its elastic energy integrals (1) and (2) by suitable quadrature rules, making use of the discrete curvatures {K _j ^(k)} _{j = 1, …, n−1} ^{k = 1, 2, 3} and extensional and shearing strains {Γ _j−1∕2 ^(k)} _{j = 1, …, n} ^{k = 1, 2, 3} defined in the previous Sects. 4.2.1 and 4.2.2. Here we briefly outline this approach described in detail in our article in [20].

We start with a discretization 0 =: s ₀ < s ₁ < … < s _n : = L of the interval domain [0, L] of the arc length parameter s of the reference curve $\mathbf{r}_{0}(s)$ into subintervals [s _j−1, s _j ] of length h _j−1∕2: = s _j − s _j−1. The distance between interval midpoints $s_{j\pm 1/2} = \frac{1} {2}(s_{j} + s_{j\pm 1})$ is given by $\varDelta s_{j}:= s_{j+1/2} - s_{j-1/2} =\bar{ h}_{j}$, where $\bar{h}_{j}:= \frac{1} {2}(h_{j-1/2} + h_{j+1/2})$ is the average of the grid constants h _j±1∕2 adjacent to s _j .

5.1 Discrete Extensional and Shear Energy

As the discrete extensional and shear strains Γ _j−1∕2 ^(k) are edge based quantities, an approximation of the energy integral (1) by midpoint quadrature is the natural choice to obtain a discrete version of $\mathcal{W}_{es}$. The pull back of the strains to the reference configuration is obtained by a rescaling with the factors $\ell_{j-1/2}/h_{j-1/2} \approx \|\mathbf{r}'(s_{j-1/2})\|$, according to

$$\displaystyle{ \bar{\varGamma }_{j-1/2}^{(k)}\;:=\; \frac{\ell_{j-1/2}} {h_{j-1/2}}\,\varGamma _{j-1/2}^{(k)}\; =\;\langle \mathbf{l}_{ j-1/2},\mathbf{a}_{j-1/2}^{(k)}\rangle /h_{ j-1/2}\; =\;\langle \bar{\pmb{\varGamma }} _{j-1/2},\mathbf{e}_{k}\rangle \;, }$$

(14)

where $\bar{\pmb{\varGamma }}_{j-1/2}:=\hat{ \mathsf{q}}_{j-1/2}^{{\ast}}\circ (\mathbf{l}_{j-1/2}/h_{j-1/2}) \circ \hat{\mathsf{q}}_{j-1/2}$ is the material vector obtained from rotating the discrete edge tangent vector $\mathbf{l}_{j-1/2}/h_{j-1/2}$ back to the local frame. The discrete approximation of $\mathcal{W}_{es}$ can be written in compact form as

$$\displaystyle{ \mathcal{W}_{es}\; \approx \;\mathcal{ W}_{es}^{(D)}\;:=\; \frac{1} {2}\sum _{j=1}^{n}h_{ j-1/2}\,\langle \varDelta \bar{\pmb{\varGamma }}_{j-1/2},\mathsf{C}_{es} \cdot \varDelta \bar{\pmb{\varGamma }}_{j-1/2}\rangle \;, }$$

(15)

where $\varDelta \bar{\pmb{\varGamma }}_{j-1/2}:=\bar{\pmb{\varGamma }} _{j-1/2} -\pmb{\varGamma }_{0}$ with $\pmb{\varGamma }_{0} = (0,0,1)^{T}$, and the shear and extensional stiffness parameters collected in the diagonal matrix C _es : = diag([GA ₁], [GA ₂], [EA]).

The condition of vanishing discrete transverse shear strains $\bar{\varGamma }_{j-1/2}^{(\alpha )} \equiv 0$ implies $\bar{\varGamma }_{j-1/2}^{(3)} =\ell _{j-1/2}/h_{j-1/2}$, such that (14) reduces to the extensional energy

$$\displaystyle{\mathcal{W}_{ext}^{(D)}\;:=\; \frac{1} {2}\sum _{j=1}^{n}h_{ j-1/2}\,[EA]\,\left (\ell_{j-1/2}/h_{j-1/2} - 1\right )^{2}}$$

of a discrete extensible Kirchhoff rod model [21], which approximates its continuum counterpart given by $\mathcal{W}_{ext}\,:=\, \frac{1} {2}\int _{0}^{L}ds\,[EA]\,(\|\mathbf{r}'(s)\| - 1)^{2}$. Additionally imposing the inextensibility condition ℓ _j−1∕2 ≡ h _j−1∕2 on the edges implies $\mathcal{W}_{ext}^{(D)} \equiv 0 \equiv \mathcal{ W}_{es}^{(D)}$.

5.2 Discrete Bending and Torsion Energy

The discrete curvatures K _j ^(k) are vertex based quantities, such that a discrete approximation of $\mathcal{W}_{es}$ can be obtained from the energy integral (2) by (non-equidistant) trapezoidal quadrature. The pull back of the curvatures originally defined w.r.t. discrete arc length to the reference configuration implies a rescaling by the factor $\varDelta \varsigma _{j}/\varDelta s_{j} \approx \|\mathbf{r}'(s_{j})\|$, i.e.: $\bar{K}_{j}^{(k)}:= (\varDelta \varsigma _{j}/\varDelta s_{j})\,K_{j}^{(k)}$, equivalent to the definition

$$\displaystyle{ \bar{K}_{j}^{(k)}\;:=\;\langle \bar{ \mathbf{K}}_{ j},\mathbf{e}_{k}\rangle \;,\;\;\bar{\mathbf{K}}_{j}\;:=\; (\varDelta s_{j})^{-1}\,2\log \hat{\mathsf{W}}_{ j}\; =\; (\vartheta _{j}/\varDelta s_{j})\,\hat{\mathbf{U}}_{j}\; =\;\bar{ K}_{j}^{(k)}\,\mathbf{e}_{ k} }$$

(16)

of discrete pulled back material curvatures. The discrete approximation of $\mathcal{W}_{bt}$ can then be written in compactly as

$$\displaystyle{ \mathcal{W}_{bt}\; \approx \;\mathcal{ W}_{bt}^{(D)}\;:=\; \frac{1} {2}\sum _{j=0}^{n}\varDelta s_{ j}\,\langle \varDelta \bar{\mathbf{K}}_{j},\mathsf{C}_{bt} \cdot \varDelta \bar{\mathbf{K}}_{j}\rangle \;, }$$

(17)

with the curvature differences $\varDelta \bar{\mathbf{K}}_{j}:=\bar{ \mathbf{K}}_{j} -\mathbf{K_{0}}_{j}$ between the deformed and reference configurations, the diagonal matrix C _bt : = diag([EI ₁], [EI ₂], [GJ]) of bending and torsional stiffness parameters, and the grid constants of the half-edges near the boundary defined as Δs ₀: = h _1∕2∕2 and Δs _n : = h _n−1∕2∕2.

5.3 Boundary Conditions

The definition of material curvature vectors $\bar{\mathbf{K}}_{0}$ and $\bar{\mathbf{K}}_{n}$ at the boundary vertices is a new element in the discrete model that did not have to be considered in the theory of discrete Cosserat curves up to this point. These discrete curvatures are defined in the deformed configuration in terms of the material difference rotations $\hat{\mathsf{W}}_{0}:=\hat{ \mathsf{q}}_{0}^{{\ast}}\circ \hat{\mathsf{q}}_{1/2}$ and $\hat{\mathsf{W}}_{n}:=\hat{ \mathsf{q}}_{n-1/2}^{{\ast}}\circ \hat{\mathsf{q}}_{n}$ connecting the boundary frames $\hat{\mathsf{q}}_{0}$ and $\hat{\mathsf{q}}_{n}$ to the frames on the adjacent edges, with analogous definitions for the boundary curvatures of the reference configuration.

The boundary frames of both configurations are determined by boundary conditions imposed on the discrete rod model, which have to be formulated as separate conditions, or can directly be built into the discrete energy $\mathcal{W}_{bt}^{(D)}$. Likewise, boundary conditions on the vertices p ₀ and p _n influence the discrete energy $\mathcal{W}_{es}^{(D)}$.

5.4 Discrete Equilibrium Equations

With the boundary conditions built into the respective terms of the discrete energies (15) and (17), the total discrete elastic energy given by

$$\displaystyle{ \mathcal{W}_{el}^{(D)}(\mathcal{X}_{ f})\;:=\;\mathcal{ W}_{es}^{(D)}(\mathcal{X}_{ f})\; +\;\mathcal{ W}_{bt}^{(D)}(\mathcal{X}_{ f}) }$$

(18)

become functions of the free vertex positions $\{\mathbf{r}_{j}\}$ and quaternion frames $\{\hat{\mathsf{q}}_{j-1/2}\}$ collected in the set $\mathcal{X}_{f}:=\{ \mathbf{r}_{j}\} \cup \{\hat{\mathsf{q}}_{j-1/2}\}$ of free variables.

Static equilibrium configurations of a discrete Cosserat rod subject to given boundary conditions can be obtained by minimizing the discrete elastic energy of the rod. The discrete equilibrium equations

$$\displaystyle{ \nabla _{\mathcal{X}_{f}}\,\mathcal{W}_{el}^{(D)}(\mathcal{X}_{ f})\; =\; 0\;\; \Leftrightarrow \;\; \frac{\partial \mathcal{W}_{el}^{(D)}} {\partial \mathbf{r}_{j}} (\mathcal{X}_{f})\; =\; \mathbf{0}\;\,,\;\; \frac{\partial \mathcal{W}_{el}^{(D)}} {\partial \hat{\mathsf{q}}_{j-1/2}} (\mathcal{X}_{f})\; =\; \mathbf{0} }$$

(19)

provide a necessary condition for such energy minima. The discrete equilibrium equations (18) is a coupled nonlinear system of algebraic equation, which can be solved numerically by Newton’s method. Alternatively, one can find approximate equilibrium configurations by energy minimization, using nonlinear conjugate gradients or Quasi-Newton type optimization methods like BFGS.

The system (18) is actually a special case of the dynamic equilibrium equations for a semi–discrete model of time dependent discrete quaternionic Cosserat rods [20], which are obtained as the (abstractly written) Euler–Lagrange equations

$$\displaystyle{\partial _{t}\,\left (\nabla _{\partial _{t}\mathcal{X}_{f}}\,\mathcal{L}^{(D)}(\mathcal{X}_{ f},\partial _{t}\mathcal{X}_{f})\right )\; -\;\nabla _{\mathcal{X}_{f}}\,\mathcal{L}^{(D)}(\mathcal{X}_{ f},\partial _{t}\mathcal{X}_{f})\; =\; 0}$$

for the Lagrangian function $\mathcal{L}^{(D)}(\mathcal{X}_{f},\partial _{t}\mathcal{X}_{f})\,:=\,\mathcal{ T}_{kin}^{(D)}(\mathcal{X}_{f},\partial _{t}\mathcal{X}_{f})\, -\,\mathcal{ W}_{el}^{(D)}(\mathcal{X}_{f})$ defined as the difference of the kinetic and potential energy according to the general concepts of Lagrangian mechanics (see [18, 20] for further details).

5.5 The Geometric Nature of the Discrete Elastic Energy

Up to this point, the various steps to obtain a discrete energy function from a continuum functional and to determine equilibrium configurations as energy minima did not involve any specific aspects of the discrete geometry of the underlying model: The energy integrals are discretized by standard quadrature rules, the discrete equilibrium equations result from the gradient of the discrete energy w.r.t. the free variables, and the numerical solution of the equations is done by Newton or Quasi–Newton methods.

The essential ingredient to this procedure is provided by the fact that the curvatures and strains are well defined for arbitrarily large deformations, completely independent of the coarseness of the discretization. The discrete curvatures increase with increasing values of the angles, up to the very limit of degenerate configurations. The energy vanishes exactly only in the reference configuration and does not possess any “artificial” minima otherwise.

Not all discretizations share these important properties. For example, a finite element approach using linear interpolation of nodal SO(3) frames yields discrete curvatures $\sim \sin (\vartheta _{j})\,\hat{\mathbf{u}}_{j}$ (see the discussion in Remark 8 of [16]), which becomes extremal at ϑ _j = ±π∕2 and then decreases in modulus for larger values of ϑ _j , up to the value zero taken in the degenerate case ϑ _j = ±π. For coarse discretizations, it can easily happen that bending or torsion angles | ϑ _j | ≈ π∕2 occur. A model based on this discretization of curvature would obviously produce unphysical results, as zig-zag type configurations with angles π∕2 ≤ | ϑ _j | ≤ π become energetically favourable.

The discussion of this example illustrates that our efforts to construct a proper discrete theory of framed curves by geometric finite differences yields the essential contribution to a rod model required to behave qualitatively correct even for very coarse discretizations. In this sense, one can state that our discrete Cosserat rod model inherits its structural stability from its underlying kinematic model of discrete Cosserat curves, completely independent of the coarseness of the discretization, and therefore displaying qualitatively correct physical behaviour at arbitrarily coarse discretizations.

5.6 Academic Test Examples

We conclude this section on discrete models of elastic Cosserat rods by showing some typical results obtained in two well known academic benchmark examples that illustrate the behaviour of our discrete Cosserat rod model in certain boundary value problems that are also relevant for our practical applications, and also show an illustrative comparison of a simulation with a corresponding laboratory experiment.

Figure 5 shows the performance of a recent implementation [19] of our discrete rod model in classical examples for inextensible rods due to Euler [12] and Kirchhoff [17] that are analytically solvable in closed form by Kirchhoff’s kinetic analogy (see Art. 260, 262 and 270 in Ch. XIX of [23] and Dill [8] for details and historical remarks).

Fig. 5

(a) Plane bending of a clamped cantilever beam loaded by a vertical end force, with analytical solution curves given by Euler’s Elastica model. (b) Bending moment (left), transverse shear force (middle), and tension force (right) as a function of arc length for the clamped cantilever beam example shown in (a): the values obtained from the discrete model with coarser (5 points) and finer (20 points) discretization approximate the analytical solution (blue curves) obtained from Euler’s Elastica model. (c) Two helical configurations with smaller and larger pitch angle of a steel string in space, modeled as an inextensible Kirchhoff rod, with analytical solutions given by Kirchhoff’s constant curvature helices, matched by discrete constant curvature solutions of the same boundary value problem with coarser (top) and finer (bottom) discretization

The coarse discretization in the Elastica example with only four edges has been deliberately fixed to equidistant edge lengths to induce visible differences between the discrete and the analytical solutions in configurations at larger deflections. However, these differences remain rather small, although an equidistant discretization is certainly not optimal in this example. Even on the level of kinetic quantities (i.e.: forces and moments), the “coarse” discrete solution captures the trend of the analytical curves of the bending moment and the tension force not only qualitatively, but displays a quantitative agreement with the corresponding analytical values that could hardly be expected. Nevertheless, the slight S–shaped variation of the analytical curve for the transverse shear force is captured only very roughly. For a finer equidistant discretization with 20 edges both the kinematic as well as the kinetic quantities of the analytical solution are captured almost perfectly.

The example of the Kirchhoff helix shows that equally positive results can be obtained for spatial deformations involving a combination of bending and torsion of the rod. In the classical form of Kirchhoff’s problem for helical equilibrium configurations of elastic rods, the latter are shown to result from special combinations of the material components of forces and moments applied at both ends of the rod, which determines the solution up to an overall rigid body motion. The solution shown in Fig. 5 results from a slightly different variant of the boundary value problem, where the vertices and frames at both ends were clamped and varied along the known analytical solution of the continuum problem. Here, only the configuration data are shown, perfectly matching the analytical centerline curves for both the coarser (10 edges) and finer (50 edges) discretization. The plots of the kinetic quantities, which are all straight horizontal lines corresponding to constant material components of the forces and moments relative to the local frames, all captured accurately by the discrete solution, are omitted here.

The laboratory experiment [10] shown in Fig. 6 is conceptually similar to the Kirchhoff helix example with clamped ends, but more general, as it involves non-constant torsion and bending, which is closer to realistic cases encountered in assembly simulation. Although the real cable that has been used as a specimen in the experiment clearly displayed viscoplastic material properties measured for larger local deformations, on top of the basic elastic constitutive behaviour that dominates in the regime of small local strains, the computation of equilibrium configurations performed with the discrete Cosserat rod model in the software IPS Cable Simulation properly captures the complex spatial deformation behaviour of the cable in the real experiment if appropriately averaged effective elastic cable properties are used.

Fig. 6

Spatial configurations of a clamped cable after twisting and axial displacement of the clamped ends. Left: Laboratory experiment; Right: Results in IPS Cable Simulation

Concerning the computing times we would like to remark that already a decade ago it was possible to simulate the entire deformation sequences of the two examples discussed in this section (as well as others, see [21]) on a standard desktop computer within the range of milliseconds. This provides the basis for true real time interaction with the simulation model by an interactive change of the boundary conditions, or likewise a change of model parameters, like e.g. the length and stiffness parameters of the rod. Also immediate adaptions of the (in general: non-equidistant) discretization in reaction to external constraints induced by various types of clips or contact with rigid geometries in the environment can be handled algorithmically in a very efficient manner.

6 Application Examples from Vehicle Industry

The software package IPS Cable Simulation contains different variants of discrete Cosserat models, augmented by numerous productivity features that are useful for a variety of applications in industry, like enhanced CAD, digital mock-up, or the simulation of assembly (or disassembly) processes on desktop computers as well as in virtual (VR) or augmented (AR) reality environments. In IPS Cable Simulation the rod models have been enhanced w.r.t. a variety of different elements, such that external constraints induced by various types of clips, restricting spatial motions of one to six of the local rigid body d.o.f. of the rod, frictionless contact interaction with rigid geometries in the environment, or self contact and contact with other rods can be handled efficiently.

The user can interact with the discrete elastic rod model of a cable or hose e.g. by grabbing one of its ends with the mouse (or more sophisticated VAR devices), or likewise a clip attached at some intermediate location, and change its position and orientation in space interactively. These changes are captured by the user interface and translated by the software into a sequential change of boundary conditions. This sequence is then passed to the simulation model, which computes corresponding deformation sequences by solving the mechanical equilibrium equations sufficiently fast for rendering deformed configuration at interactive rates (i.e.: 25 GHz or faster).

The seamless integration of discrete Cosserat rod models into the IPS software is supported by their formulation in terms of elementary geometric quantities (i.e.: vertex positions and orthonormal frames) that can be handled highly efficient by the computational geometry methods and algorithms already implemented in IPS. As an example, frames translated along polygonal paths in space are fundamental objects in rigid body path planning, which historically has been one of the core capabilities of the IPS software.

6.1 Representative Application Examples from Automotive Industry

In what follows, we present some examples, all taken from joint projects with Audi AG, to illustrate the typical usage of our discrete rod models integrated in the IPS software in automotive industry. Of course, simple screenshots from the software as the ones shown here are not able to convey the user experience in interactive operation with the software in a realistic way, and even the more detailed information provided by video⁸ sequences of the software in operation at real application cases can hardly be more than a substitute. Nevertheless, the principle way of usage of the simulation software and the benefits obtained in industrial applications should become clear from our descriptive exposition.

Figure 7 shows some screenshots taken from the simulation of the assembly sequence of various clips and connectors to be mounted at a head up display. The numbers indicate the assembly sequence, and the arrows point out the direction of the movement of the various clips and plugs towards their final mounting positions. The engineer working with the simulation software would typically grab individual clips, plugs or connectors with the mouse and perform the assembly operation for all on the virtual model sequentially, just as it would later be done by the worker in the real process. In this way, the engineer can validate if it is possibly to assemble all cables without mutual crossing, and if the cable lengths are sufficient to avoid extensional straining and sharp bending at clips. If not, the length of a cable can be changed interactively to its optimal length. Also, the function of various clip types as well as their positioning can be checked and varied to avoid infavourable configurations. The two pictures to the right of Fig. 7 show such a variation of the position and the type of a clip to lower the level of strain in the cable. Note that the assembly of the connector labeled as No. 3 requires a clockwise rotation by 90^∘ for plug-in. The effect of torsional straining of the attached cable can be computed in terms of the torsional moment acting on the cable in its mounted configuration, in combination with the bending strains that are simultaneously acting. The combined level of stresses and strains can be assessed by St. Venant type stress functions that superpose forces and moments of the rod model into local 3D stress tensor values, which can be evaluated e.g. in terms of von Mises stress values.

Fig. 7

Left: Assembly sequence of various clips and connectors to be mounted at head-up display. Right: Variation of the position and the type of a clip to lower the level of strain in the cable

Figure 8 displays another issue discovered and solved during the digital validation of the functionality of the same head up display: The originally suggested design of one of the plastic parts in the kinematic mechanism was done in a compact way to assure its mechanical stability with a minimal amount of plastic material, with a rather sharp rectangular kink at its upper right corner. Despite the slight rounding at its corner, the simulation of the operation of the whole mechanism including the cables showed that during sequential moving out and in of the display the cable had to slide across the corner, with a sudden change of its configuration due to buckling. The whole situation turned out to be rather sensitive to small changes in the cable length. All in all, it became clear that the initial design was not robust enough, and the increased bending strains occurring in the cable in its configuration hooked up at the corner of the plastic part might later cause damage due to the frequent repetitive loading. Therefore the design of the plastic part had to be changed. The picture to the right of Fig. 8 shows the final design solution: The vertical edge at the respective corner was bent upwards and elongated, such that the sharp right angle is eliminated, and the edge functions as a rail on which the cable can slide in a stable way during the forward and backward operation of the kinematic mechanism. Clearly, the simulation of the whole system with the physically correct deformation of flexible cables in contact with the rigid geometries in its environment provided the essential insights leading to an improved design. With this software, the functionality of the whole system of the headup display with all cables connected can be simulated and validated digitally in an early design phase. Traditionally, one would manufacture hardware prototypes of the simulated design to perform a physical validation. However, the possibility of simulation with physically correct models allows for functional validation without physical prototypes.

Fig. 8

Redesign of a plastic part in the kinematic mechanism of the same head-up display. Left: Former design with a sharp corner, where the cable may get hooked, which might cause damage. Right: Improved design, where the cable can slide along reproducibly always in the same stable way, such that potential damage due to hook-up or clamping of the cable is avoided

The third example shown in Fig. 9 addresses the optimization of the length of a flexible grommet to avoid damage during the repeated opening and closing operation of the hatchback and has been discussed in detail in [15], introducing a (at that time) new method of comparative durability assessment based on the prediction of local stresses during quasi-static deformation sequences of flexible cables or hoses. In this case, the grommet joining the chassis and hatchback, which conducts various cables inside, becomes substantially deformed during the opening and closing of the hatchback, such that bending and torsional strain occur at a considerable level. The issue could be resolved in a simulation study by an elongation of the length of the grommet tube, which lowers the level of strains, but still avoids unwanted clamping at the nearby hinge.

Fig. 9

Optimization of the length of a flexible grommet to avoid damage during the repeated opening and closing operation of the hatchback. Left: Design variant with a shorter length and higher bending strains. Middle: Alternative elongated design variant, showing lower bending strains in the shut state of the hatchback

7 Conclusion

Software tools used in industry for design and digital validation require a seamless integration of efficient models that are able to handle the simulation of large spatial deformations of slender elastic structures like cables and hoses by bending, twisting and extension at interactive rates.

In our article, we presented the construction of discrete elastic rod models of Cosserat type within the framework of Lagrangian mechanics on the kinematic basis of discrete models of framed curves in Euclidian space. We obtain discrete framed curves from their continuum counterparts by a discretization method we denote as geometric finite differences, which can be regarded as an extension of Sauer’s “difference geometry” approach to Frénet curves. These discrete Cosserat curves, which consist of polygonal arcs augmented by orthonormal frames located at edge centers and represented by rotational quaternions, provide a family of discrete kinematical models that qualitatively capture all essential features of Cosserat curves in the continuum, independent of the coarseness of the discretization.

As a consequence, the discrete bending and twisting curvatures as well as the discrete extensional and transverse shear strains obtained from the difference geometry of Cosserat curves yield discrete approximations of the elastic energy of continuum Cosserat rods that model the deformation behaviour of slender elastic structures physically correct for arbitrarily coarse discretizations. As the basic kinematical constituents of our discrete Cosserat rod models are vertex positions and orthonormal frames, i.e.: elementary geometric quantities that can be handled very efficiently by methods and algorithms of computational geometry, they can be integrated in a computationally efficient and seamless way in geometry-oriented software packages, with enhancements to support the interaction with the CAD geometries in the environment, as well as user interaction in real time.

Our application examples from automotive industry illustrate the principle way of usage to solve practical tasks in design and digital validation with the software IPS Cable Simulation. As an outlook, we would like to mention that by the same approach we are able to integrate fully dynamical models of cables that account for inertial and viscous effects into our software environment as well as in other CAE software packages for multibody system dynamics simulations [28]. Moreover, our geometric discretization approach may likewise be applied to obtain discrete models of flexible surfaces (see [32, 33] for basic research work).