Keywords

1 Introduction

The multi-state system (MSS) was firstly proposed by Barlow and Wu, it has been proved that lots of industrial systems are typical MSS, such as electrical power system, pipe transmission system, production and manufacturing system, aerospace system, etc. [1, 5, 9]. Those systems can define the multi-state characteristics of components accurately by analyzing the system failure process and the effect of the change of component performance to the system performance and reliability. Four types of methods can be used for reliability analysis of MSS, including multi-state fault tree method [24], Markov process method [6, 7], Monte-Carlo simulation (MCS) method [14, 31] and universal generation function (UGF) method [4]. The MSS plays a critical role in the reliability analysis and assessment of complex systems and also has extensive application foreground.

The uncertainty caused by lack of data and scarcity of information is one of the most important issues in MSS reliability analysis. When the system state performances and state probabilities cannot be exactly defined and obtained, sometimes the bounds of system states and state probabilities cannot be exactly defined and obtained, so the probability-based methods are no longer applicable for this kind of system. In this situation, the bounds of system states and state probabilities can be expressed by some other data forms, such as linguistic variables. Then some non-probabilistic methods are developed, such as Dempster-Shafer evidence theory (DSET) [27], fuzzy theory [13], probability-box [10, 26], interval theory [17], possibility theory [8], Bayesian method [22, 23], etc. The DS evidence theory has a flexible axiomatic system to describe uncertainty, and also has an independent frame to process uncertainty in system [18, 25]. It has been widely used for uncertainty modeling, quantification, reasoning and management in engineering [3, 29, 30].

There are many researches on Bayesian network (BN) based on evidence theory. Simon et al. [20, 21] analyzed reliability of complex system with epistemic uncertainty by using BN, where evidence theory is used to quantify system uncertainty. Then the evidential networks also have been used for the reliability and performance evaluation of system with imprecise knowledge [19]. Zhao et al. [28] studied the influence of incomplete original parameters and subjective parameters on the reliability of distribution system by using BN and evidence theory. Sallak et al. [16] has developed the combination method of BN and evidence theory for reliability analysis of multi-state system (MSS). It has shown that evidence theory can handle the imprecise information in system, and it can get more useful information than interval analysis method.

This chapter introduces a multi-state BN method for reliability analysis of complex system with CCFGs based on evidence theory. The remainder of this chapter is organized as follows: Firstly, the node definition and BN reasoning of multi-state BN under evidence theory are introduced in Sect. 2. Then, in Sect. 3, when the multiple CCF groups (CCFGs) are considered in complex redundant system, a modified β factor parametric model is introduced to model the CCF in system. This comprehensive method is used to analyze the reliability of an example system and a feeding control system of CNC heavy-duty horizontal lathe (HDHL) in Sect. 4. Finally, some conclusions are presented in Sect. 5.

2 Multi-state Bayesian Network Under Evidence Theory

2.1 The Node Definition of Multi-state Bayesian Network Under Evidence Theory

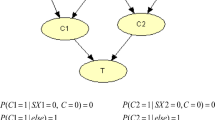
For a sample BN with three nodes which is shown in Fig. 1, assume that the nodes \(x_{1}\) and \(x_{2}\) are three state nodes, the state space is \(\Lambda = \{ 0,1,2\}\). Let \(x_{i} = 0,1,2\) represent the reliable state, partial failure state and complete failure state of the corresponding component. When the epistemic uncertainty exists in system, an added state \(x_{i} = [0,1,2]\) is defined to represent the uncertain state of node \(x_{i}\). Then the frame of discernment \(D = \{ 0,1,2,[0,1,2]\}\) is defined under evidence theory, and the basic probability assignment (BPA) is \(m:2^{D} \to [0,1]\). Its power set can be expressed as

Fig. 1
figure 1

A sample multi-state BN

Full size image
$$2^{D} = \left\{ {m\left( {x = \varnothing} \right) = 0;m\left( {x = 0} \right);m\left( {x = 1} \right);} \right.\left. {m\left( {x = 2} \right);m\left( {x = \left[ {0,1,2} \right]} \right)} \right\}.$$
(1)

For an event \(A:\{ x = 0\}\) on the frame of discernment D, and \(B \subseteq A\), the belief function of event A is

$$Bel\left( A \right) = \sum\limits_{B \subseteq A} {m\left( A \right)} = m\left( {x = 0} \right).$$
(2)

The (2) represents the belief degree of event \(A:x = 0\). It’s the lower bound of belief interval when the probability of uncertain information is not counting in the BPA [21]. Based on the definition of plausibility function, the plausibility function of event A can be gotten by

$$Pl\left( A \right) = \sum\limits_{B \cap A \ne \varnothing} {m\left( B \right)} = m\left\{ {x = 0} \right\} + m\left\{ {x = \left[ {0,1,2} \right]} \right\}.$$
(3)

Then the interval probability of event A can be calculated by (2) and (3), and it can be expressed as \([P](A) = [Bel(A),Pl(A)]\). Similarly, the interval probabilities of other nonempty events under the frame of discernment D can be computed.

When the corresponding components of nodes \(x_{1}\) and \(x_{2}\) are parallel or series, the conditional probability table (CPT) of node y under evidence theory can be derived. Then the belief reliability of node \(y:Bel(y = 0)\) can be computed by BN reasoning and

$$Bel\left( {y = 0} \right) = \sum\limits_{{x_{1} ,x_{2} }} {Bel\left( {y = 0\left| {x_{1} ,x_{2} } \right.} \right)} Bel\left( {x_{1} } \right)Bel\left( {x_{2} } \right).$$
(4)

The plausibility reliability \(Pl(y = 0)\) is

$$Pl\left( {y = 0} \right) = \sum\limits_{{x_{1} ,x_{2} }} {Pl\left( {y = 0\left| {x_{1} ,x_{2} } \right.} \right)} Pl\left( {x_{1} } \right)Pl\left( {x_{2} } \right).$$
(5)

The practical reliability of node \(y:P(y = 0)\) will belongs to interval \([Bel(y = 0),Pl(y = 0)]\).

2.2 The Multi-state Bayesian Network Reasoning Under Evidence Theory

For a multi-state BN with n root nodes, which can be denoted as \(x_{1} ,x_{2} , \ldots ,x_{n}\). Assume that the state number of node \(x_{i}\) and leaf node y are \(l_{i}\) and \(l_{y}\). The relation between the state probability of leaf node y and root nodes can be expressed as

$$P\left( {y = y^{j} \left| {x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right.} \right) = \frac{{P\left( {y = y^{j} ,x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right)}}{{P\left( {x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right)}},$$
(6)

where \(1 \le j \le l_{y} ,1 \le i \le n\) and \(1 \le k_{i} \le l_{i}\). Suppose that the interval probability of node \(x_{i}\) at state \(k_{i}\) is

$$\left[ P \right]\left( {x_{i} = x_{i}^{{k_{i} }} } \right) = \left[ {Bel\left( {x_{i}^{{k_{i} }} } \right),Pl\left( {x_{i}^{{k_{i} }} } \right)} \right],$$
(7)

where \(Bel(x_{i}^{{k_{i} }} )\) and \(Pl(x_{i}^{{k_{i} }} )\) can be calculated by the CPTs of nodes \(x_{i}\).

The conditional probability of node y of BN under evidence theory is

$$\left[ P \right]\left( {y = y^{j} \left| {x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right.} \right) = \left[ {Bel\left( {y^{j} } \right),Pl\left( {y^{j} } \right)} \right].$$
(8)

The mid-value of conditional probability is chosen as the static conditional probability of this node [21], that is

$$P\left( {y = y^{j} \left| {x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right.} \right) = \frac{{\left[ {Bel\left( {y^{j} } \right) + Pl\left( {y^{j} } \right)} \right]}}{2}.$$
(9)

Similarly, the static conditional probability of root node \(x_{i}\) on state \(x_{i}^{{k_{i} }}\) is

$$P\left( {x_{i} = x_{i}^{{k_{i} }} } \right) = \frac{{\left[ {Bel\left( {x_{i}^{{k_{i} }} } \right) + Pl\left( {x_{i}^{{k_{i} }} } \right)} \right]}}{2}.$$
(10)

The probability of node y on j-th state can be gotten by

$$P\left( {y = y^{j} } \right) = P\left( {y = y^{j} \left| {x_{1} = x_{1}^{{k_{1} }} , \ldots ,x_{n} = x_{n}^{{k_{n} }} } \right.} \right)P\left( {x_{1} = x_{1}^{{k_{1} }} } \right) \cdots P\left( {x_{n} = x_{n}^{{k_{n} }} } \right).$$
(11)

For a BN with n root nodes \(x_{i} (i = 1,2, \ldots ,n)\), m non-leaf nodes \(y_{j} (j = 1,2, \ldots ,m)\) and leaf node T. Based on the former reasoning method, the probability of leaf node \(T = T_{v}\) can be expressed as

$$\left[ P \right]\left( {T = T_{v} } \right) = \left[ {Bel\left( {T = T_{v} } \right),Pl\left( {T = T_{v} } \right)} \right],$$
(12)

where the lower bound \(Bel(T = T_{v} )\) is the belief probability and can be calculated by

$$\begin{aligned} Bel\left( {T = T_{v} } \right) & = \sum\limits_{{x_{1} , \ldots ,x_{n} ,y_{1} , \ldots ,y_{m} }} {Bel\left( {x_{1} , \ldots ,x_{n} ,y_{1} , \ldots ,y_{m} ,T = T_{v} } \right)} \\ & = \sum\limits_{\pi \left( T \right)} {Bel\left( {T = T_{v} \left| {\pi \left( T \right)} \right.} \right)} \prod\limits_{j = 1}^{m} {\sum\limits_{{\pi \left( {y_{1} } \right)}} {Bel\left( {y_{j} \left| {\pi \left( {y_{j} } \right)} \right.} \right)} } \prod\limits_{i = 1}^{n} {Bel\left( {x_{i}^{{k_{i} }} } \right)} \\ & = \sum\limits_{\pi \left( T \right)} {Bel\left( {T = T_{v} \left| {\pi \left( T \right)} \right.} \right)\sum\limits_{{\pi \left( {y_{1} } \right)}} {Bel\left( {y_{1} \left| {\pi \left( {y_{1} } \right)} \right.} \right)} } \times \cdots \\ & \quad \times \sum\limits_{{\pi \left( {y_{m} } \right)}} {Bel\left( {y_{m} \left| {\pi \left( {y_{m} } \right)} \right.} \right)} \times \cdots \times Bel\left( {x_{1} = x_{{1,k_{1} }} } \right) \times \cdots \times Bel\left( {x_{n} = x_{{n,k_{n} }} } \right). \\ \end{aligned}$$
(13)

The upper bound \(Pl(T = T_{v} )\) is the plausibility probability and can be computed by

$$\begin{aligned} Pl\left( {T = T_{v} } \right) & = \sum\limits_{{x_{1} , \ldots ,x_{n} ,y_{1} , \ldots ,y_{m} }} {Pl\left( {x_{1} , \ldots ,x_{n} ,y_{1} , \ldots ,y_{m} ,T = T_{v} } \right)} \\ & = \sum\limits_{\pi \left( T \right)} {Pl\left( {T = T_{v} \left| {\pi \left( T \right)} \right.} \right)} \prod\limits_{j = 1}^{m} {\sum\limits_{{\pi \left( {y_{1} } \right)}} {Pl\left( {y_{j} \left| {\pi \left( {y_{j} } \right)} \right.} \right)} } \prod\limits_{i = 1}^{n} {Pl\left( {x_{i}^{{k_{i} }} } \right)} \\ & = \sum\limits_{\pi \left( T \right)} {Pl\left( {T = T_{v} \left| {\pi \left( T \right)} \right.} \right)\sum\limits_{{\pi \left( {y_{1} } \right)}} {Pl\left( {y_{1} \left| {\pi \left( {y_{1} } \right)} \right.} \right)} } \times \cdots \\ & \quad \times \sum\limits_{{\pi \left( {y_{m} } \right)}} {Pl\left( {y_{m} \left| {\pi \left( {y_{m} } \right)} \right.} \right)} \times \cdots \times Pl\left( {x_{1} = x_{{1,k_{1} }} } \right) \times \cdots \times Pl\left( {x_{n} = x_{{n,k_{n} }} } \right). \\ \end{aligned}$$
(14)

The probability of leaf node can be obtained by the former forward reasoning of BN, and the posterior probability of root nodes can be gotten by backward reasoning. When \(T = T_{v}\), the posterior probability of root node \(x_{i} = x_{{i,k_{i} }}\) can be computed by

$$\left[ P \right]\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right) = \left[ {\begin{array}{*{20}l} {\hbox{min} \left( {Bel\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right),Pl\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right)} \right),} \hfill \\ {\hbox{max} \left( {Bel\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right),Pl\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right)} \right)} \hfill \\ \end{array} } \right],$$
(15)

where

$$Bel\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right) = \frac{{Bel\left( {x_{i} = x_{{i,k_{i} }} ,T = T_{v} } \right)}}{{Bel\left( {T = T_{v} } \right)}},$$
(16)
$$Pl\left( {x_{i} = x_{{i,k_{i} }} \left| {T = T_{v} } \right.} \right) = \frac{{Pl\left( {x_{i} = x_{{i,k_{i} }} ,T = T_{v} } \right)}}{{Pl\left( {T = T_{v} } \right)}},$$
(17)

where \(Bel(x_{i} = x_{{i,k_{i} }} ,T = T_{v} )\) and \(Pl(x_{i} = x_{{i,k_{i} }} ,T = T_{v} )\) are the belief and plausibility joint probability of root nodes and leaf node. The root nodes and leaf node of BN reflect the fault causes and fault state properties of system. Therefore, the system state probability can be computed by forward reasoning of BN, which can also realize a quantitative description of system fault states. The backward reasoning of BN can get the posterior probability of fault causes based on system failure state, and also can implement the system failure prediction and judgment, which has certain guiding significance for the reliability improvement of system.

3 Reliability Modeling of System with Multiple CCFGs

3.1 A Modified β Factor Model for CCFGs

Considering the dependent failure caused by interior component physical interactions and human interactions in system, the beta factor parametric model has been widely used for such cases [15]. Assume that P t is the total failure probability of a component; it can be expanded into an independent contribution P ind and a dependent contribution P ccf , which are functions of time t respectively. When the component is assumed to follow the exponential distribution, λ t , λ ind and λ ccf are the failure rates of entire system, independent part, and the dependent part respectively. Then the parameter β can be defined as the fraction of the total failure probability attributable to dependent failures [11, 15], and it can be mathematically described as

$$\beta = \frac{{P_{ccf} }}{{P_{t} }} = \frac{{P_{ccf} }}{{P_{ind} + P_{ccf} }} = \frac{{(1 - \exp ( - \lambda_{ccf} \cdot t))}}{{(1 - \exp ( - \lambda_{t} \cdot t))}} = \frac{{(1 - \exp ( - \lambda_{ccf} \cdot t))}}{{(1 - \exp ( - \lambda_{ind} \cdot t)){ + }(1 - \exp ( - \lambda_{ccf} \cdot t))}}.$$
(18)

The value of β-factor can be obtained by the direct use of field data and experts’ experience [11, 12, 15].

In order to present how the beta factor model works, a simple deduction is performed for single component within the FTA model. For a parallel system with two identical components A 1 and A 2, and \(P(A_{1} ) = P(A_{2} ) = P_{A}\), the failure probability of system P sys can be computed as:

$$P_{sys} = P\left( {A_{1} } \right)P\left( {A_{2} } \right) = P_{A}^{2}$$
(19)

For the basic component A, as shown in Fig. 2, the failure probability of A can be divided into two proportions: independent part and CCF part, and it can be expressed as

Fig. 2
figure 2

FTA explicit modeling method for component with CCF

Full size image
$$P_{A} = P_{A\_ind} + P_{A\_ccf}$$
(20)

Adding the CCF part, the failure probability is

$$P_{A\_ccf} = \beta P_{A}$$
(21)

By using the former explicit modeling method, the failure probabilities of component A 1 and A 2 are both divided into independent part and CCF part. Then based on the standard β-factor model and (18), the probability of CCF part can be obtained and \(P_{{A_{1} \_ccf}} = P_{{A_{2} \_ccf}} = \beta P_{A}\). The two components parallel system also can be further expressed as Fig. 3a. The system failure event Sys can be simplified by using Boolean algebra operation rules and expressed as

Fig. 3
figure 3

FT modeling and simplification of two components parallel system with common cause events

Full size image
$$\begin{aligned} Sys & = A_{1} A_{2} = \left( {A_{1} \_ind + A_{1} \_ccf} \right)\left( {A_{2} \_ind + A_{2} \_ccf} \right) \\ & = \left( {A_{1} \_ind + A\_ccf} \right)\left( {A_{2} \_ind + A\_ccf} \right) \\ & = A_{1} \_ind \cdot A_{2} \_ind + A\_ccf \cdot \left( {A\_ccf + A_{1} \_ind + A_{2} \_ind} \right) \\ & = A_{1} \_ind \cdot A_{2} \_ind + \underbrace {A\_ccf \cdot A\_ccf}_{A\_ccf} + \underbrace {{A\_ccf \cdot A_{1} \_ind}}_{0} + \underbrace {{A\_ccf \cdot A_{2} \_ind}}_{0} \\ & = A_{1} \_ind \cdot A_{2} \_ind + A\_ccf \\ \end{aligned}$$
(22)

Finally, the system with consideration of CCF can be simplified and shown as Fig. 3b.

Then the failure probability of system can be obtained by (22) and

$$\begin{aligned} P\left( {Sys} \right) & = P\left( {A_{1} \_ind \cdot A_{2} \_ind + A\_ccf} \right) \\ & = P\left( {A_{1} \_ind} \right) \cdot P\left( {A_{2} \_ind} \right) + P\left( {A\_ccf} \right) \\ & = \left( {1 - \beta } \right)P\left( A \right) \cdot \left( {1 - \beta } \right)P\left( A \right) + \beta P\left( A \right) \\ \end{aligned}$$
(23)

When a single component fails simultaneously within multiple CCFGs [2, 12], a modified beta factor parametric model is used to express the coupling mechanism. The explicit modeling of component A with multiple CCFGs is shown in Fig. 4.

Fig. 4
figure 4

Explicit modeling of multiple CCFGs within FT

Full size image

The failure probability of component A is then given as

$$\begin{aligned} P\left( A \right) & = P\left( {A\_ind} \right) + P\left( {A\_ccf} \right) \\ & = P\left( {A\_ind} \right) + P\left( {A\_CCFG_{1} \cup \cdots \cup A\_CCFG_{k} } \right) \\ & = P\left( {A\_ind} \right) + P\left( {A\_CCFG_{1} } \right) + \cdots P\left( {A\_CCFG_{k} } \right) \\ \end{aligned}$$
(24)

In this way, the failure probability of component A is divided into CCF parts and independent part as follow

$$\begin{aligned} P_{A\_ccf} & = P_{{A\_CCFG_{1} }} + P_{{A\_CCFG_{2} }} + \cdots + P_{{A\_CCFG_{k} }} \\ & = \beta_{1} P_{A} + \beta_{2} P_{A} + \cdots + \beta_{k} P_{A} = P_{A} \sum\limits_{i = 1}^{k} {\beta_{i} } \\ \end{aligned}$$
(25)
$$P_{A\_ind} = (1 - \sum\limits_{i = 1}^{k} {\beta_{i} } )P_{A}$$
(26)

3.2 Model Limitation and Solution

Because the beta factors are obtained by expert judgments, there exists the limitation of this modified beta factor parametric model for \(\left( {\beta_{1} + \beta_{2} + \cdots + \beta_{k} } \right) > 1\). In this case, the failure probability of CCF part is bigger than the probability of total components. To cope with this limitation in this model, a proportional reduction factor (PRF) method [2, 12] is applied in this chapter. The PRF factor is defined as

$${\text{PRF}} = \frac{1}{{\sum\nolimits_{j = 1}^{k} {\beta_{j} } }}$$
(27)

Then a set of new reduced beta factor are generated as

$${\varvec{\upbeta}} = \left[ {\beta_{1}^{{\prime }} ,\beta_{2}^{{\prime }} , \ldots ,\beta_{k}^{{\prime }} } \right] = {\text{PRF}}\left[ {\beta_{1} ,\beta_{2} , \ldots ,\beta_{k} } \right].$$
(28)

In this way, the failure probability of CCF parts and independent part are rewritten as

$$P_{A\_ccf} = P_{A} \sum\limits_{i = 1}^{k} {\beta_{k}^{{\prime }} }$$
(29)
$$P_{A\_ind} = (1 - \sum\limits_{i = 1}^{k} {\beta_{k}^{{\prime }} } )P_{A} = 0$$
(30)

The essence of the PRF method is an equilibrium process of the accumulated common cause parts on β factor, which has weaken the contradiction of the common cause part beyond the total failure probability to some extent. And the PRF method is just one of the methods which can be used to solve this kind of logical contradiction; any other method capable of dealing with such contradictions may be applicable.

3.3 The Bayesian Network Node with CCFGs

When CCFs is considered in system reliability modeling, the failure of system can be divided into independent part and CCF part. The independent part means the fail of system caused by a single cause, and the CCF part represents the simultaneous failure of multiple components which caused by a common coupling mechanism, then those components constitute a CCFG. Component A exists in multiple CCFGs, \(\left( {CCFG_{1} ,CCFG_{2} , \ldots ,CCFG_{k} } \right)\). By using the fault tree explicit modeling of multiple CCFGs in Sect. 3.2, the fault tree can be translated into BN, as shown in Fig. 5.

Fig. 5
figure 5

BN node with CCFGs

Full size image

When the independent failure probability of node A is \(P(A_{ind} )\), the corresponding \(\beta\) factors of common cause nodes are \(\beta_{1} ,\beta_{2} , \ldots ,\beta_{k}\). When \((\beta_{1} + \beta_{2} + \cdots + \beta_{k} ) < 1\), the failure probability of node A can be calculated by (23)–(27) and

$$\begin{aligned} P^{\prime}\left( A \right) & = P\left( {A_{ind} } \right) + P\left( {A_{ccf} } \right) \\ & = P\left( {A_{ind} } \right) + \frac{{\sum\nolimits_{i = 1}^{k} {\beta_{i} } }}{{1 - \sum\nolimits_{i = 1}^{k} {\beta_{i} } }}P\left( {A_{ind} } \right) = \frac{1}{{1 - \sum\nolimits_{i = 1}^{k} {\beta_{i} } }}P\left( {A_{ind} } \right) \\ \end{aligned}$$
(31)

When the sum of \(\beta\) factors are larger than 1, that is \((\beta_{1} + \beta_{2} + \cdots + \beta_{k} ) > 1\), by using the PRF method in Sect. 3.2, the failure probability of node A can be computed by (27)–(30) and

$$P^{{\prime }} \left( A \right) = P_{A\_ccf}^{{^{{\prime }} }} + P_{A\_ind}^{{\prime }} = P_{A} \sum\limits_{i = 1}^{k} {\beta_{i}^{{\prime }} } + 0 = P_{A} \cdot PRF \cdot \sum\limits_{i = 1}^{k} {\beta_{i} }$$
(32)

4 Reliability Analysis of Feeding Control System for CNC HDHLs with Multiple CCFGs

4.1 Fault Tree Modeling of Feeding Control System

The DL series horizontal lathes are computer numerical control (CNC) types and have the following work axes: X axis of tool head lateral movement, Z axis of tool head longitudinal movement, U 1 axis of left gang tool movement and U 2 axis of right gang tool movement. The functional block diagram of the electrical control and drive system for such DL series horizontal lathes is shown in Fig. 6. The feeding control system include 3 subsystems: X, Z, as well as U 1 and U 2 axes feeding control systems. A signal generated by 611D-type servo driven module (Mo) is transmitted through electric wire (Ew) to control the motor (Mt) in X axis feeding control system. There exists a speed feedback device (Sf). The grating scales (Gr) feedback the straightness of X axis to Mo to adjust the feed speed and direction. The electrical control of Z, U 1 and U 2 axes is almost the same as that of X axis, excepting the difference introduced in Sect. 1. Although U 1 and U 2 axes share a 611D-type servo driven module, they have different current relays (Re).

Fig. 6
figure 6

Functional block diagram of electrical control and drive system for the DL series CNC HDHL

Full size image

Based on the function analysis and failure mechanism analysis of feeding control system, the “functional failure of feeding control system” has been chosen as the top event in FTA, and the fault tree of feeding control system is built and shown in Fig. 7.

Fig. 7
figure 7

Fault tree model of the feeding control system

Full size image

The meanings of the notations in Fig. 7 are as following: T denotes the functional failure of feeding control system; XF, ZF, U 1 F and U 2 F are the functional failures of X, Z, U 1 and U 2 axes feeding control systems. The basic components of each axes feeding control system include Gr, Sf, Ew, Mo, Mt and Re. Therefore, in the fault tree model, the failure events of basic components are noted by two parts: the code of axes and the code of each component. For example, X Ew represents the Ew failure of X axis feeding control system, and the other notations follow the similar interpretations.

4.2 The BN Modeling and CCFGs Fusion

From Fig. 7, the different subsystems of feeding control system have several identical or similar components, an external shock or interior component physical interactions may cause the failure of those components simultaneously. So when considering the CCF caused by human interactions, system function correlation and environment, the following common cause events or CCFGs will exist in system.

  1. (1)

    \(C^{MO} = \{ X^{MO} ,Z^{MO} ,U^{MO} \}\), which means the motors of different subsystems fail at the same time by one influence factor. Based on expert experience, the common cause factor \(\beta^{MO} = 0.1\).

  2. (2)

    \(C^{GR} = \{ X^{GR} ,Z^{GR} ,U_{1}^{GR} ,U_{2}^{GR} \} ,C^{SF} = \{ X^{SF} ,Z^{SF} ,U_{1}^{SF} ,U_{2}^{SF} \}\) and \(\beta^{GR} = 0.2,\beta^{SF} = 0.15\).

  3. (3)

    \(C^{EW} = \{ X^{EW} ,Z^{EW} \} ,C^{RE} = \{ X^{RE} ,Z^{RE} \}\) and \(\beta^{EW} = \beta^{RE} = 0.15\).

  4. (4)

    When \(X^{MT}\) exists in multiple CCFGs, and expressed as \(CCFG_{1}^{MT} = \{ X^{MT} ,Z^{MT} \} ,\{ X^{MT} ,U_{1}^{MT} \} ,\{ X^{MT} ,U_{2}^{MT} \}\), \(\{ Z^{MT} ,U_{1}^{MT} \}\), \(\{ Z^{MT} ,U_{2}^{MT} \}\), \(\{ U_{1}^{MT} ,U_{2}^{MT} \}\); \(CCFG_{2}^{MT} = \{ X^{MT} ,Z^{MT} ,U_{1}^{MT} \}\), \(\{ X^{MT} ,Z^{MT} ,U_{2}^{MT} \}\), \(\{ Z^{MT} ,U_{1}^{MT} ,U_{2}^{MT} \}\) and \(CCFG_{3}^{MT} = \{ X^{MT} ,Z^{MT} ,U_{1}^{MT} ,U_{2}^{MT} \}\). The corresponding common cause factors of two components, three components and four components failure simultaneously are \(\beta_{1}^{MT} = 0.25,\beta_{2}^{MT} = 0.2\) and \(\beta_{3}^{MT} = 0.15\).

The failure rates and failure probabilities of system components at \(t = 3000{\text{ h}}\) are listed in Table 1. Based on the transformation method of fault tree to BN and the modified β factor model, the fault tree of feeding control system can be transformed to BN and decomposed by explicit modeling method. When CCFs are considered, the root nodes of BN can be decomposed into independent parts and common cause parts. Then the system BN with consideration of CCFGs can be gotten as Fig. 8.

Table 1 The failure rates and failure probabilities of components
Full size table
Fig. 8
figure 8

The system BN with consideration of CCF

Full size image

The BN of Fig. 10 is the same as system BN structure without considering CCF, the difference is the redefinition of the probabilities of root nodes, then CCF of each components can be taken into consideration. The failure probabilities of components in Table 1 are independent probabilities, then the root nodes’ actual failure probabilities can be updated by modified β factor model.

For component A which is not included in multiple CCFGs, the updated failure probabilities of this kind of basic components can be calculated by (31) and \(P^{{\prime }} (EW) = 0.0021,P^{{\prime }} (RE) = 0.0071\), \(P^{{\prime }} (GR) = 0.0075,P^{{\prime }} (SF) = 0.0018\), \(P^{{\prime }} (MO) = 0.0007\). For component MT which is included in multiple CCFGs, the failure probability of MT can be computed by (31) since it does not meet the limitation that the sum of β factors of different CCFGs is larger than 1, then

$$\begin{aligned} P^{\prime}\left( {MT} \right) & = P\left( {MT_{ind} } \right) + P\left( {MT_{ccf} } \right) \\ & = P\left( {MT_{ind} } \right) + P\left( {\left( {CCFG_{1}^{MT} } \right)} \right) + P\left( {\left( {CCFG_{2}^{MT} } \right)} \right) + P\left( {\left( {CCFG_{3}^{MT} } \right)} \right) \\ & = P\left( {MT_{ind} } \right) + \left( {\frac{{\sum\nolimits_{i = 1}^{3} {\beta_{i}^{MT} } }}{{1 - \sum\nolimits_{i = 1}^{3} {\beta_{i}^{MT} } }}} \right)P\left( {MT_{ind} } \right) = \frac{1}{{1 - \sum\nolimits_{i = 1}^{3} {\beta_{i}^{MT} } }}P\left( {MT_{ind} } \right) \\ \end{aligned}$$
(33)

Because \((\beta_{1}^{MT} + \beta_{2}^{MT} + \beta_{3}^{MT} ) < 1\), the logical contradiction of modified β factor model is inexistence here. So, the failure probability of this kind of components with consideration of CCFs can be calculated directly, and \(P^{{\prime }} (MT) = 0.0520\).

4.3 Reliability Analysis of Feeding Control System by Using DSET Based BN

As the main power take-off components of horizontal lathe, the work state of motors will affect the processing efficiency directly. Therefore, in this chapter, there exists an intermediate state between the perfect work state and failure state of the motors of DL series horizontal lathes, called derating working state. So the state space of motors can be expressed as \(\{ 0,1,2\}\), where, 0 is the perfect working state, 1 is the derating working state and 2 represents failure state. The other components of system are all considered as two-state component. Due to the complexity of system structure and the coupling relation between components, only a little reliability data are available, an uncertain state [0 ,1, 2] is induced to the state space to represent the uncertainty of system. Assume that the life of all components obey exponential distribution, the basic components state probabilities of feeding control system can be obtained by literature research and experts experience and listed in Table 2.

Table 2 The state probabilities of components at t = \(3 0 0 0\,{\text{h}}\) with CCF
Full size table

By using the BN node definition and probability reasoning method introduced in Sects. 2.1 and 2.2, the conditional probability table (CPT) of non-leaf nodes of BN in Fig. 8 can be gotten. Table 3 is the CPT of non-leaf nodes XF, ZF, U 1 F and U 2 F. Then the system BN model under evidence theory can be shown as Fig. 9, and the CPT of leaf node T is shown in Table 4. By using the multi-state BN reasoning method under Evidence theory in Sect. 2, the belief probabilities and plausibility probabilities of non-leaf nodes \(XF,ZF,U_{1} F\) and \(U_{2} F\) can be obtained and listed in Table 5.

Table 3 The CPT of non-leaf nodes under evidence theory
Full size table
Fig. 9
figure 9

System BN model under evidence theory

Full size image
Table 4 The CPT of leaf node T under evidence theory
Full size table
Table 5 The state belief and plausibility probabilities of non-leaf nodes of BN
Full size table

The belief and plausibility probabilities of leaf node T can be calculated by (13) and (14), and

$$\begin{aligned} Bel\left( {T = 0} \right) & = P\left( {T\_Bel = 0} \right) = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Bel\left( {XF,ZF,U_{1} F,U_{2} F,T = 0} \right)} \\ & = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Bel\left( {T = 0\left| {XF,ZF,U_{1} F,U_{2} F} \right.} \right)} \prod\limits_{i = 1}^{n} {Bel\left( {x_{i}^{{k_{i} }} } \right)} \\ & = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Bel\left( {T = 0\left| {XF,ZF,U_{1} F,U_{2} F} \right.} \right)} Bel\left( {XF} \right) \\ & \cdot Bel\left( {ZF} \right)Bel\left( {U_{1} F} \right)Bel\left( {U_{2} F} \right) \\ \end{aligned}$$
(34)
$$\begin{aligned} Pl\left( {T = 0} \right) & = P\left( {T\_Pl = 0} \right) = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Pl\left( {XF,ZF,U_{1} F,U_{2} F,T = 0} \right)} \\ & = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Pl\left( {T = 0\left| {XF,ZF,U_{1} F,U_{2} F} \right.} \right)} \prod\limits_{i = 1}^{n} {Pl\left( {x_{i}^{{k_{i} }} } \right)} \\ & = \sum\limits_{{XF,ZF,U_{1} F,U_{2} F}} {Pl\left( {T = 0\left| {XF,ZF,U_{1} F,U_{2} F} \right.} \right)} \\ & \cdot Pl\left( {XF} \right)Pl\left( {ZF} \right)Pl\left( {U_{1} F} \right)Pl\left( {U_{2} F} \right) \\ \end{aligned}$$
(35)

Then the state belief probabilities and plausibility probabilities of leaf node T under epistemic uncertainty can be calculated, and the results of system state probabilities when considering the influence of CCFs and without CCFs are listed in Table 6. In order to illustrate the influence of epistemic uncertainty to system, the uncertain state of component MT is classified as perfect work state 0. Then the state probabilities of system at t = 3000 h are calculated and listed in Table 6.

Table 6 The state probabilities of leaf node T
Full size table

Based on the previous assumption, the lifetime of components obey exponential distribution, and the derating work state is regarded as perfect working state. From the belief and plausibility probability of feeding control system at state 2 in Table 6, it has shown that the failure probability interval and failure rate interval of system at t = 3000 h is [0.232005, 0.280306] and [8.7991 ×10−5, 1.0964 ×10-4]/h respectively when consider the influence of epistemic uncertainty and CCFGs. When the CCFGs are ignored, the system failure probability interval will be [0.119782, 0.161703], and failure rate interval is [4.2529 ×10-5, 5.8794 ×10-5]/h. The contrast curves of system reliability with consideration of CCF are also obtained and shown in Fig. 10. From Fig. 10 we know that when the influence of uncertainty is ignored, the failure probability and failure rate of system are 0.238282 and 9.072629 ×10-5/h. And when the CCF and uncertainty are both ignored, the corresponding failure probability and failure rate of feeding control system are 0.122977 and 4.374068 ×10-5/h. Finally, the contrast curves of system reliability with epistemic uncertainty are shown in Fig. 11.

Fig. 10
figure 10

The contrast curves of the influence of epistemic uncertainty and CCFGs to system reliability

Full size image
Fig. 11
figure 11

The contrast curves of the influence of CCFGs to system reliability without considering epistemic uncertainty

Full size image

Based on the system function analysis and failure mechanism analysis, this section built an fault tree model of the feeding control system of a DL series horizontal lathe. The evidence theory is introduced to quantify the epistemic uncertainty caused by lack of data and information in this system, and BN model is combined to realize the system reliability indexes calculation. A modified β factor model is used to model the CCFGs existed in system. From Table 6 and Fig. 10, when the influence of epistemic uncertainty to system is considered, system reliability interval at t = 3000 h will be [0.808964, 0.838640] without consider CCFs, and when the influence of CCFs is also considered, the reliability interval will be [0.706706, 0.733514]. This shows that CCFs has evident effect on system reliability. The system state probabilities in Table 6 when the epistemic uncertainty is ignored are between the corresponding belief probabilities and plausibility probabilities, which verify the accuracy of results. This chapter provides an effective method for reliability analysis of complex system under epistemic uncertainty and CCFGs.

5 Conclusions

This chapter introduces a reliability analysis method for complex MSS with epistemic uncertainty based on BN and evidence theory. The epistemic uncertainty of system is quantified through adding an uncertain state of root nodes in multi-state BN, and then the state space is constructed. The belief function and plausibility function are defined under evidence theory. Based on the BN forward reasoning, the system reliability and failure probability can be computed. The case study has confirmed the feasibility of this comprehensive method, and realized a quantitative analysis of system failure state. The backward reasoning can get the posterior probability of failure causes based on the system failure state, and provide guidance for prediction of system failure types.

CCF is an important failure mode in complex systems, so the reliability analysis of MSS with consideration of both epistemic uncertainty and CCF are also studied in this chapter. When CCFGs exist in system, a modified β factor model is introduced and integrated with evidence theory based BN, and realize the state expression and probability reasoning for complex system with epistemic uncertainty and CCFGs. The reliability analysis of the feeding control system of DL series HDHLs by this method has shown that, the proposed comprehensive method has high computing efficiency and strong practical value.