Keywords

1 Introduction

The introduction of teaching innovations is a central feature of mathematics teacher education programmes. Watson and Mason (2007) report innovations in such programmes that engage prospective and practicing teachers in using research to design, analyse, try out and reflect on the use of tasks with learners. An emerging research area is the exploitation of realistic contexts in mathematics teacher education and the modelling process (e.g. Doerr 2007; Daher and Shahbari 2015). The workplace has not yet been such a context for many research studies, but those that exist indicate potential benefits for teachers of linking the workplace to education. For instance, Nicol (2002) found that a teacher education programme including visits to workplace sites helped prospective teachers keep mathematics contextualised when designing student activities. To this end, Triantafillou et al. (2016) studied how practicing teachers integrated workplace activity into mathematics teaching identifying facilitating or hindering factors. Approaches of this type introduce new sites of activity that challenge teachers to move within and between different practices, involving them in crossing boundaries created by different contexts (Akkerman and Bakker 2011). A key challenge then is to support teachers make links between these contexts and address their professional learning . Research focusing on the use of mathematics in the workplace indicates that school mathematics practices and workplace practices differ substantially (Hoyles et al. 2010). Nevertheless, the workplace context has potential for offering authentic situations that provoke problem-solving and modelling (Wake 2014).

Our study is inspired by the philosophy of the MaSciL project,Footnote 1 which provides the context for introducing innovative teaching approaches to teachers. Project MaScil aims to promote the integration of inquiry-based learning (IBL) and the world of work (WoW) into teacher education and professional development. The actions taken to achieve these goals included task design based on non-routine workplace situations, the development of communities of teachers and teachers’ engagement in designing, implementing and reflecting on mathematics teaching. In this chapter, we use the Activity Theory (ΑΤ) and the construct of boundary crossing to study the process of teachers’ professional learning when they are challenged to link mathematics teaching to the workplace through modelling.

2 Theoretical Considerations

In this section, we first discuss our perspective on the relation between workplace and modelling and then provide a short description of the main constructs we use from AT and boundary crossing.

2.1 Workplace and Modelling

Workplace contexts offer rich situations for mathematical modelling . Kaiser et al. (2013) describe a variety of modelling activities that have been designed and used in upper secondary mathematics classrooms on the basis of realistic everyday and workplace contexts. Professionals in workplace settings are involved in modelling, problem-solving and mathematical processes especially in situations where instruments and technological devices break down (Pozzi et al. 1998). Trial and error, logical exclusion, reasoning and justification, visual inspection and self-monitoring are some examples of processes that are central in workplace mathematical activity (Triantafillou and Potari 2010). In these processes, professionals’ actions are mediated by a number of conventions and inscriptions (Noss 2002). Although the variety of processes and tools used and developed in a workplace are essential elements of the modelling process, transforming authentic workplace situations in the classroom for engaging students in mathematical modelling is a complex process. Wake (2015) considers, from an epistemological point of view, the differences between modelling in the workplace and modelling in the mathematics classroom. He points out that in the workplace, a focus on context often deprives the visibility of the underlying mathematics, while the opposite occurs in school. Thus, in the modelling cycle , the initial stage of developing a model of the reality is crucial, and it requires a particular attention to mathematics teaching. Wake (2015) elaborates further how to facilitate the coupling of reality and mathematics in classroom contexts by suggesting that learners need support to develop critically and mathematically informed models of complex realities, to construct and deconstruct real and mathematical models of complex situations and to understand how the structure of models of workplace realities relate to the models of their mathematical counterparts. This perspective is also in the philosophy of MaSciL where teachers are encouraged to attribute to their students the role of the professional who faces a complex reality. In our study, we are interested in the interplay between workplace and mathematics teaching in the teachers’ attempt to integrate workplace into their didactical designs, classroom implementations and reflection s. The chapter is primarily focused on the teachers’ moves horizontally back and forth in workplace situations or contexts so as to see how they can be represented mathematically (horizontal mathematisation). Existing research in mathematics teacher education and modelling shows that, although teachers’ understanding of mathematical modelling can evolve through designing, implementing and reflecting on modelling activities, the link between mathematical modelling and ‘real-life’ contexts in teachers’ work requires more research (Anhalt and Cortez 2016).

2.2 Activity Theory and Boundary Crossing

The activity system is a basic concept of AT in Engeström’s (2001) approach. It is collective and tool-mediated, and it needs a motive and an object. Individual and group actions are studied and interpreted against the background of entire activity systems. Activity systems are transformed through contradictions when a new element comes from the outside. Transformations of activity systems are related to interventions that take place and describe phenomena of developmental character. In our study, the focus is on developments in teachers’ mathematics teaching in the context of teacher education. Under Engestrom’s (1999) perspective, teachers’ professional learning can be seen as expansive learning emerging “as practitioners struggle through developmental transformations in their activity systems” (p. 7). This learning approach entails a re-conceptualisation of development as a horizontal movement across borders.

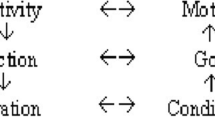
Figure 26.1 shows a representation of a third-generation activity in the form of two interacting activity systems. The two triangles indicate the basic dimensions of the second-generation AT with elements: the subject and the object of the activity that is constructed through the mediation of tools, the community in which the subject participates and its rules and the division of labour. Object 1 moves from an unreflected and situational given goal to a collectively meaningful object constructed by the activity system (object 2) and to a potentially shared or jointly constructed object (object 3). In the present study, we distinguish two activity systems: the system of mathematics teaching in which the teachers have been involved and the system of the workplace supported by the MaSciL philosophy.

Fig. 26.1
figure 1

Interacting activity systems (Engeström 2001, p. 136)

Full size image

The third-generation of AT considers learning emerging in dynamic movements between interacting activity systems. This draws our attention to the metaphor of boundary crossing (Suchman 1994). We adopt the view of Akkerman and Bakker (2011) for boundaries as “sociocultural differences that give rise to discontinuities in action and interaction” (p. 139). People who cross boundaries are often called boundary crossers , while a boundary object is a single object that has different meanings in several intersecting worlds but retains a common essence. Boundary crossing has been conceived as the efforts of individuals or groups at boundaries to establish or restore continuity in action or interaction across practices (cf. Bakker and Akkerman 2014). Boundary crossing between activity systems has been seen as a way to address learning through four learning mechanisms: identification, coordination, reflection and transformation (Akkerman and Bakker 2011). These mechanisms concern the different ways in which learning can occur when people interact with, move across and participate in different practices:

  1. 1.

    Identification: Boundary crossing can lead to a renewed insight into what the different practices concern.

  2. 2.

    Coordination: Boundary crossing can also lead to establishing minimal routine exchanges between two practices so as to facilitate transitions.

  3. 3.

    Reflection: Reflection involves going deeper into the specificities of two practices and learning to consider one practice by taking on the perspective of the other practice.

  4. 4.

    Transformation. Transformation leads to changes in practices or even the creation of a new practice that stands between the established ones.

Little attention has been given to how boundary crossing can be embedded into mathematics teacher education as a way to study teachers’ professional learning at the boundaries of multiple practices except for the Wake et al. (2016) study. In the present study, we analyse the interaction of two activity systems focussing more closely on boundary crossing between these systems in order to study the teachers’ professional learning in relation to integrating workplace contexts into mathematics teaching.

3 Methodology

3.1 The Participants

The study participants were mathematics teachers following a masters course that is part of a 2-year masters programme in mathematics education at the University of Athens. Experienced and novice mathematics teachers participated in the course. The experienced teachers came from lower and upper secondary schools, and their teaching experience ranged from 2 to 20 years. The novice teachers were mainly offering private tuition to students to help them with school mathematics. During two academic years (2013–2015), we (as teacher educators) introduced the workplace as a context for task design in the spirit of MaSciL. We encouraged teachers to use MaSciL classroom tasks or develop their own as part of their teacher education activities. Twenty teachers (13 novice and 7 experienced) worked in groups of two to four with MaSciL tasks or others in the same spirit.

3.2 The Course and Tasks

The course lasted 13 weeks with weekly sessions of 4 h. The main goals were to support teachers to link research findings and actual teaching, exploit different resources (e.g. digital tools, videos) in their didactical designs and explore the role of context and tools in students’ conceptual understanding . In the course, we initially introduced IBL and WoW (e.g. by presenting research findings from the corresponding literature) and engaged teachers in the cycle of design-implementation-analysis-reflection. This cycle began with selecting a MaSciL task or designing an IBL task connected to the WoW. Then participating teachers were asked to read research papers in mathematics education related to IBL, WoW and students’ understanding of specific mathematics concepts related to the task. After this, teachers used the task in the classroom and analysed students’ modelling process with an emphasis on the role of the workplace context and tools. Finally, teachers reflected on task design and use in teaching and linked emergent issues with existing research. Teachers’ designs were discussed during the course and the analysis of the interventions , and teachers’ reflections were presented in the final course session.

Here our focus is on one teacher group. It consisted of two experienced teachers (Elie and Natasa) and one novice (Manos) who designed the task Fuel Station in the context of the course. In this task, the students take the role of a worker (Giorgos) who supervises a fuel supply company’s filling of cylindrical tanks with petrol at a fuel station (Fig. 26.2). In this scenario, an employee from the fuel delivery company fills an empty petrol tank and claims that the amount needed to fill that tank was 7000 l. This is the value that also appears on the supply company’s counter. Giorgos must then verify whether this amount is correct by immersing a scaled (in cm) stick from the top of the tank and taking a measure corresponding to the liquid level. The students explore how Giorgos can do the calculation.

Fig. 26.2
figure 2

The cylindrical tank at the fuel station

Full size image

3.3 Data Collection and Analysis

The data consisted of (1) teachers’ written accounts/journals in which they described their design rationales and implementation experiences, (2) produced artefacts (worksheets, microworlds, etc.), (3) teachers’ PowerPoint presentations, (4) selected videos of discussions that took place in the courses and (5) selected teacher interviews. For the analysis, we adopted first a broad, data-grounded approach (Strauss and Corbin 1998) focussed on the group’s actions and goals related to each activity system. At a second level, we looked for emerging interactions of these systems and of their objects taking into account boundary crossing and the corresponding learning mechanisms.

4 Results

4.1 The Two Activity Systems

In Table 26.1, we present an analysis of the two activity systems in which the teacher educators intentionally encouraged the teachers to engage.

Table 26.1 Analysis of the activity systems of mathematics teaching and the workplace
Full size table

4.2 Boundary Crossing in the Group

The teachers referred mainly to the elements of the activity system of the workplace . The group’s attention was primarily on the ways that an authentic situation could be transformed into a school task. Manos proposed the initial idea for Fuel Station, as he had been working part-time at a fuel station at the time. As he put it in his interview:

I knew that the exact amount of fuel in the station is measured through the use of a scaled stick and ready-made table of values providing the output given the input … We needed to find ways to connect this reality to the school mathematics…Our intention was to see if a design based on an authentic practice would work in a 9th grade class. (Manos’s interview)

The teachers decided to implement their task in lower secondary schools where the group’s practicing teachers were working at that time. Thus, an additional challenge to be addressed was how to connect the authenticity of the situation to students’ prior knowledge . For this, they first analysed task potential to support the connection to the workplace and explored the mathematics underlying the filling of a cylindrical tank (i.e. in terms of functional dependency). The teachers simplified the real context by engaging students in a task where they had to explore how the volume of a cylindrical tank in a vertical position changes in relation to its height. They expected this real model was easier for the students to mathematize as they had the relevant mathematical knowledge (e.g. calculation of volume of a cylinder, proportional relations). Then, they challenged the students to consider the same problem when the cylindrical tank was horizontal as in the authentic situation . For this they simulated the situation using digital tools (i.e. GeoGebra files) to allow students’ experimentation with the real phenomenon . In this context, students were able to change tank height with a slider, while the tool gave the corresponding volume values. Students had to choose pairs of height-volume values from the screen and insert into a table on their worksheet. Then, still working with paper and pencil, they placed the corresponding points in a co-ordinate system and sketched a graph describing the functional relation. In a subsequent task, the graph was automatically provided by the software, and students compared it with their own. Figure 26.3 shows the graph in relation to the variation of petrol height in GeoGebra for a given radius and length of cylindrical tank.

Fig. 26.3
figure 3

The mathematical model in GeoGebra

Full size image

Reference to the workplace activity dominated the group’s reflections and discussions during the design process. Manos, acting as boundary crosser between workplace and teaching , challenged the others’ views regarding workplace practices and possible connections to school mathematics. Emerging tensions concerned the different goals underlying workplace actions and those in the school classroom and the difficulty of students’ and teachers’ familiarity with the authentic context . In their attempts to connect the mathematics within fuel stations to school-based mathematics, the teachers recognised a need to find detailed information about the original workers’ practices and the difficulty of conceptualising the specificities of the situation. Further, they appreciated the role of personal workplace experience in the design process, as Manos noted: “If I did not have the experience of working in the fuel station, the activity would not have been successful…It is important to be close to the workplace, to know the subject of the work very well” (Manos’s interview). The teachers also recognised the complexity of adapting the problem for the school level by including and excluding real context elements (e.g. excluding reference to physics or chemistry inherent in the situation). Additionally, they appreciated the importance of engaging students in solving workplace problems by use of school mathematics. In their initial attempts to couple school mathematics and reality in the modelling process , they provided a simplified situation model (vertical cylinder) that allowed students to work with known mathematics. Then, a model closer to the authentic situation (horizontal cylinder) brought a new iteration of modelling. This time, the dynamic manipulation of parameters involved in the problem (length, height and radius) supported students in approaching the mathematical model experimentally in close relation to reality.

For this group, boundary crossing was characterised by contradictions between activity systems leading to adaptations of the didactic tools (e.g. tasks) from the activity system of the workplace to that of mathematics teaching. In the reflection phase of their activity, the teachers referred to the role of the workplace in their teaching as can be seen in this excerpt:

The calculations (i.e., in the table used by workers) have been carried out taking into account elements of physics and chemistry. We chose not to include these elements in the activity. We were interested in the mathematical part. Thus, we did not say anything about the table during the implementation. We just informed the students that checking the volume of fuel in the stations is carried out through the sticks. Therefore, we introduced authenticity and workplace practice in our design without revealing all the tools used in the workplace. We wanted the challenge – namely the tools through which the employee can find out the volume – to emerge through school mathematics. (Manos’s interview)

Here the teachers used the ready-made table of values as a boundary object intersecting the world of the workplace and teaching. In the workplace, the table is used as a black box to carry out calculations in a routine way. In contrast, the teachers considered the table in the classroom as a mathematical representation. They engaged students in calculating the requested values through mathematical practices involving different function representations (i.e. graph, table). There was a dominance of mathematics teaching over the workplace, since contradictions were resolved by the rules of the dominant activity system and not according to reality . This seems related to teachers’ familiarity with school mathematics, limited experiences in integrating the workplace into mathematics teaching and construction of the mathematical model requiring knowledge beyond lower secondary. However, the analysis indicated that the teachers constructed a hybrid situation where school mathematics appears to play a complementary role to workplace mathematics.

4.3 Teachers’ Professional Learning

The analysis above focussed on the interactions and the corresponding contradictions among the activity systems of workplace and teaching. The teachers’ starting point in the group was Manos’s work experience at a fuel station. Although the teachers’ engagement in exploring the connection between workplace practices and school mathematics was primarily characterised by contradictions, they were able to progressively make links between activity in the workplace and mathematics teaching and enrich students’ modelling experiences. It seems that the object of the teachers’ activity was re-conceptualised and expanded, as it was more focussed on the ways that innovative workplace practices could be linked to school mathematics and integrated into classroom teaching. With regard to teachers’ learning, the analysis showed that different kinds of learning processes were at stake at the boundary crossings between classroom teaching and workplace . Identification was evident when the teachers recognised the intersecting practices of the workplace and classroom teaching. Coordination took place through their recognition of the need to keep a balance between the authenticity of the workplace and the mathematical inquiry in the classroom. Reflection was indicated by the fact that the teachers looked differently at workplace practices by taking into account the ways by which these practices can be exploited in mathematics teaching. Regarding transformation, the analysis indicated the emergence of hybrid practices (i.e. teaching characterised by a merging of workplace practices and school practices) in the hope of being better shaped in the future.

5 Conclusions

In this chapter, we asked if and how novice and experienced teachers were able to integrate innovative practices such as the workplace into mathematics teaching. In the course, we stimulated boundary crossing in the hope of propelling transformation, in the form of practice integration. The results show that the teachers experienced tensions or contradictions in integrating the workplace into teaching. Mathematics teaching practices dominated workplace practices and school mathematics complemented workplace-related mathematics. The coupling of reality and mathematics that Wake (2015) considers important in integrating workplace into mathematics teaching was approached by teachers through simplification of the authentic situation and the simulation of it with the use of digital tools . However, the boundary crossing from one context to the other was facilitated by a boundary crosser (Manos) who supported further elaboration of the real context and offered insights on how to integrate authentic workplace artefacts into the group’s didactical designs. Concerning their professional learning, we identified all learning types in teachers’ activity. Identification, coordination and reflection were evident in teachers’ attempts to keep a balance between elements of workplace in teaching. Transformation was indicated by teachers’ attempts to bring together the objects in the different activity systems, leading to the integration of these practices into a whole. From a methodological perspective, we have exemplified the potential of AT and boundary crossing taking into account the complexity of teacher education and other professional settings.