1 INTRODUCTION

Recently, flexible manipulators have become increasingly popular because of their unique features and versatility relative to traditional rigid manipulators. Flexible manipulators are advised to be less rigid due to the use of lightweight materials, making them safer to operate with human operators. Plus, perform multiple tasks with faster movement, lower energy consumption and higher resilience. The major application fields of this type of manipulator are scientific investigations such as modern industry, medical surgery, and space exploration. However, we should also handle the inherent complexities associated with using lightweight structures. Distributed structural flexibility and robotic linkage cause a tip vibration, which generates a quite complex dynamic model, making the control task even more arduous [1].

A flexible manipulator is part of the underactuated systems in which the number of generalized coordinates is greater compared to the output variables specifying the desired path. The flexible manipulator’s mathematical model is a distributed parameters model, to achieve enough high accuracy; several elastic modes are needed here. In addition, the inherent nonminimum phase behavior and the parametric variation (payload mass, structural damping coefficients, etc.) can prevent the system to reach simultaneously high performance and excellent robustness [2].

In the case of two-link flexible manipulator, the complexity of the problem rises, especially when the flexible arm lifts payloads since both the coupling between the two links and the payload variation significantly affects the dynamic behavior.

The control aim is to develop control laws that lead to asymptotic tracking of the desired trajectories and suppress unwanted elastic deformations. Therefore it’s necessary to develop a precise model which is able to characterize the dynamic behavior of the entire system.

In the literature, the finite element method and the assumed modes method (FEM and AMM) are the most studied methods for modeling flexible manipulators:

— De Luca [3] and De Luca and Siciliano [4] derived a multilink dynamic model using AMM without torsion effects.

— Subudhi and Morris [5] proposed a systematic method to generate the dynamic model of an n-link manipulator. Both rigid and flexible movements are described by the bihomogeneous transformation matrices.

— Khairudin et al. [6] reported the dynamic modeling and discretization of a two-link flexible manipulator with structural damping, hub inertia and payload, the dynamic of the whole system was derived using the combined Euler–Lagrange formalism and the assumed modes technique.

The assumed eigenmodes of the link deflections have a significant impact on the precision of the dynamic model derived from the analytical expression. Flexible manipulators have been often modeled using the finite element technique, which divides the structure into smaller elements and treats each element as an independent continuous member of the link [7, 8]. The dynamic of the entire system is obtained by assembling the dynamic of each element through a polynomial interpolation function. The FE method provides a precise model with a high number of elements.

To reach the control objectives, various control schemes were suggested in the literature.

An energy-based control design approach is proposed in [9], which results in a Hamiltonian structure, Compared with other similar schemes in the literature, the experimental results showed some acceptable results.

The work [10] developed a terminal sliding mode control (TSMC) for a two-link flexible arm without common feedback, The proposed controller ensures a zero tracking error in a finite time although the influence of external perturbations.

In [11], a composite learning sliding mode control of a two-link flexible manipulator is presented, the adaptive scheme is developed using a new neural network update law and a disturbance observer, and simulation results confirm the design concept that compound-learning can successfully complete the estimation task. In [12] a fractional order sliding mode control of a single link flexible manipulator was developed. The main advantage of this controller is the combination of both fractional-order control and sliding mode control’s robustness. Theoretical analysis and simulation results demonstrate that the proposed controller can eliminate tip vibration and improve tracking performance.

Work [13] presents an adaptive passive controller for a one-link flexible manipulator with a parametric variation. This controller includes the passivity-based approach and an adjustment mechanism that ensures online parameter estimation. Simulations illustrate the theoretical results and show that the controller implements asymptotic trajectory tracking and suppresses comfortably tip vibrations; Yatim et al. [21] proposes the use of a genetic algorithm to actively manage the vibration of a flexible manipulator. A novel intelligent optimizer known as the genetic algorithm with parameter exchanger (GAPE) was used to adapt the PID controller. The performance of PID and common genetic algorithms were examined. The findings demonstrate that PID-GAPE offers superior results in vibration attenuation; Meng et al. [23] deals with motion planning and adaptive neural tracking control of an uncertain two-link rigid flexible manipulator, in order to reach its position control via motion planning and adaptive tracking approach. Virtual damping and online trajectories correction techniques are used in motion planning to determine the motion trajectories for the manipulator’s two connections. In addition to ensuring that the two connections can attain the appropriate angles, the designed trajectories also have the capacity to reduce vibration. The simulation results show that the motion planning and tracking controllers perform better than other control strategies, and they also validate the effectiveness of the suggested control approach.

The main contribution of this work is to derive an accurate dynamic model for a two-link flexible manipulator using the assumed modes method and to design a passivity-based controller with the aim to reach asymptotic trajectory tracking and suppress residual flexible vibrations. The overall stability is demonstrated using Lyapunov’s theory. In passive system the stored energy is greater than the energy that is supplied, the difference is even lost through dissipation [14].

This paper’s remaining sections are assembled as follows. The flexible manipulator’s dynamic model based on the beam’s theory and Lagrangian formalism is presented in Section 2, the passivity-based control approach and the stability analysis using the Lyapunov theory are presented in Section 3. Simulation results are given in Section 4. The conclusion is presented in Section 5.

2 MATHEMATICAL MODELING

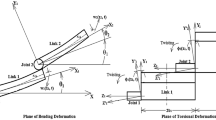
In this section, we consider a planar manipulator with two links, independent motor drives each link as seen in Fig. 1, the inertial coordinate frame is denoted \({{X}_{0}}{{Y}_{{0~}}}\), the ith link rigid body coordinate frame is denoted \({{X}_{i}}{{Y}_{i}}\) and the motion coordinate frame is \(\widehat {{{X}_{i}}}\widehat {{{X}_{i}}}\). The ith link length is \({{L}_{i}}\) with uniform mass density \(~{{\rho }_{i}}\). The first motor clamps the first link at the rotor, and the second motor is clamped at the first link tip. The two links individual Young modulus and area moment of inertia are denoted E and I respectively; \({{w}_{i}}\left( {{{x}_{i}},t} \right)~\) is the horizontal part of the displacement vector; \({{\theta }_{1}}~,{{\theta }_{2}}\) are the angular coordinates. The second link end-point is linked to an inertial payload mass \({{M}_{p}}\) with moment of inertia \({{J}_{p}}\) [6]. Each link of the flexible manipulator is modeled as Euler–Bernoulli beam, for simplicity, we put the following hypothesis [6]:

Fig. 1.
figure 1

A planar manipulator with two flexible links.

Full size image

— Each link length \({{L}_{i}}\) is much longer than its width.

— The impacts of rotary inertia and shear strain are neglected.

— Each link has a lower deflection than its length.

— The flexible arm only moves on the horizontal plane.

— The impacts of coulomb friction and reduction gear backlash are neglected.

2.1 Kinematics

This section focuses on the description of kinematics for a serial two-link flexible manipulator. Ai is the rotation matrix from \({{X}_{{i - 1}}}{{Y}_{{i - 1}}}\) to \({{X}_{i}}{{Y}_{i}}\) it can be written as [6]:

$${{A}_{i}} = \left( {\begin{array}{*{20}{c}} {\cos {\kern 1pt} {{\theta }_{i}}}&{ - \sin {\kern 1pt} {{\theta }_{i}}} \\ {\sin {\kern 1pt} {{\theta }_{i}}}&{~~~\cos {\kern 1pt} {{\theta }_{i}}} \end{array}} \right).$$
(1)

The matrix of elastic homogenous transformation Ei caused by the ith link deflection is given by

$${{E}_{i}} = \left( {\begin{array}{*{20}{c}} 1&{ - \left. {\frac{{\partial {{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}}}} \right|{{x}_{i}} = {{L}_{i}}} \\ {\left. {\frac{{\partial {{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}}}} \right|{{x}_{i}} = {{L}_{i}}}&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&{ - w_{{ie}}^{'}} \\ {w_{{ie}}^{'}}&1 \end{array}} \right),$$
(2)

where \({{L}_{i}},~{{w}_{i}}\left( {{{x}_{i}},t} \right)\) are the ith link length and elastic deflection respectively at a spatial location \({{x}_{i}}\). The total transformation matrix \({{T}_{i}}\) transforming coordinates from \({{X}_{0}}{{Y}_{{0~}}}\) to \({{X}_{i}}{{Y}_{i}}\) follows a recursion as expressed below

$${{T}_{i}} = {{T}_{{i - 1}}}{{E}_{{i - 1}}}{{A}_{i}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }_{{i1}}}{{A}_{i}},\,\,\,\,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }_{0}} = I,$$
(3)

where \(I\) is an identity matrix.

Let \(~r_{i}^{i} = \left\{ {\begin{array}{*{20}{c}} {{{x}_{i}}} \\ {{{w}_{i}}\left( {{{x}_{i}},t} \right)} \end{array}} \right\}\) be the position vector describing an arbitrary point along the ith deflected link with respect to its local coordinate frame \(\left( {{{X}_{i}}{{Y}_{{i~}}}} \right)\) and \(r_{i}^{0}\) be the same point referring to \(r_{i}^{i}\). The position of the origin of \(~{{X}_{{i + 1}}}{{Y}_{{i + 1}}}\) with respect to \({{X}_{i}}{{Y}_{i}}\) is given by

$$~p_{{i + 1}}^{i} = r_{i}^{i}({{L}_{i}}),$$
(4)

and \(p_{i}^{0}\) is its absolute position regarding to \({{X}_{0}}{{Y}_{0}}\), using the total transformation matrix, \(r_{i}^{0}\) and \(p_{i}^{0}\) can be expressed as

$$\begin{gathered} r_{i}^{0} = p_{i}^{0} + {{T}_{i}}r_{i}^{i}, \\ p_{{i + 1}}^{i} = p_{i}^{0} + {{T}_{i}}p_{{i + 1}}^{i}. \\ \end{gathered} $$
(5)

The rigid body frame (\({{X}_{i}},{{Y}_{i}}\)) has the absolute angular velocity as

$${{\dot {\alpha }}_{i}} = \mathop \sum \limits_{j = 1}^n {{\theta }_{j}} + \mathop \sum \limits_{k = 1}^{n - 1} \dot {w}_{{ke}}^{'},$$
(6)

where n the link number, prime and dot is are the first derivatives with respect to spatial variable x and time, the linear absolute velocity of an arm point is determined by

$$\dot {r}_{i}^{0}({{x}_{i}}) = \dot {p}_{i}^{0} + {{\dot {T}}_{i}}r_{i}^{i}({{x}_{i}}) + {{\dot {T}}_{i}}\dot {r}_{i}^{i}({{x}_{i}}),$$
(7)

where \(\dot {p}_{i}^{0}\) can be determined by using Eqs. (4) and (5) along with

$$\dot {p}_{{i + 1}}^{i} = \dot {r}_{i}^{i}({{L}_{i}}).$$
(8)

As the links are considered to be inextensible, \({{\dot {x}}_{i}} - 0\) so \(\dot {r}_{i}^{i} = \left\{ {\begin{array}{*{20}{c}} 0 \\ {{{{\dot {w}}}_{i}}\left( {{{x}_{i}},t} \right)} \end{array}} \right\}\).

From Eq. (3), the time derivative of the total transformation matrix \({{\dot {T}}_{i}}~\) can be recursively computed as follows:

$${{\dot {T}}_{i}} = {{\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }\limits^\centerdot }_{{i - 1}}}{{A}_{i}} + {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }_{{i - 1}}}{{A}_{i}}.$$
(9)

2.2 Dynamics

The flexible manipulator equation of motion is derived using the Euler–Lagrange formalism, the kinematic formulation must be used to calculate the overall energies involved with the manipulator system. The manipulator’s total kinetic energy is provided by

$$T = \mathop \sum \limits_{i = 1}^2 {{T}_{{hi}}} + \mathop \sum \limits_{i = 1}^2 {{T}_{{Li}}} + {{T}_{{pl}}},$$
(10)

where \(~{{T}_{{hi}}}\), \({{T}_{{Li}}}\), and \({{T}_{{pl}}}~\) are consequently, the kinetic energies related to hubs, links and payload, respectively. The rigid body’s kinetic energy situated at the hub i of mass \({{m}_{{hi~}}}\) and moment of inertia \({{J}_{{hi}}}\) is

$${{T}_{{hi}}} = \frac{1}{2}{{m}_{{hi}}}\dot {r}_{i}^{T}{{\dot {r}}_{i}} + \frac{1}{2}{{J}_{{hi}}}\dot {\alpha }_{i}^{2}$$
(11)

with \({{\dot {\alpha }}_{i}}\) as in Eq. (6), the kinetic energy for the link \(i\) is

$${{T}_{{Li{{\;}}}}} = \frac{1}{2}{{\rho }_{i}}\mathop \smallint \limits_0^{{{L}_{i}}} {{\left( {r_{i}^{0}} \right)}^{T}}\left( {{{x}_{i}}} \right)r_{i}^{0}\left( {{{x}_{i}}} \right)dx,$$
(12)

where \(r_{i}^{0}\) is the velocity vector.

The payload situated at the second link’s tip with mass \({{M}_{p}}\) and moment of inertia \({{J}_{p}}\) has the following expression of kinetic energy

$${{T}_{{pl{{\;}}}}} = \frac{1}{2}{{M}_{{p~}}}\dot {p}_{{n + 1}}^{T}{{\dot {p}}_{{n + 1}}}\frac{\pi }{4}\frac{1}{2}~{{J}_{p}}{{\left( {{{{\dot {\alpha }}}_{2}} + \dot {w}_{{2e}}^{'}} \right)}^{2}}.$$
(13)

To solve Eqs. (11)–(13), the following identities are used

$$\begin{gathered} A_{i}^{T}{{{\dot {A}}}_{i}} = S{{{\dot {\theta }}}_{i}}, \\ A_{i}^{T}{{A}_{i}} = E_{i}^{T}{{E}_{i}} = S_{i}^{T}{{S}_{i}} = I, \\ E_{i}^{T}{{{\dot {E}}}_{i}} = \left( {I\dot {w}_{{ei}}^{'} + S} \right){{{\dot {w}}}_{{ie}}}, \\ \end{gathered} $$
(14)

where S is an antisymmetric matrix \(~S = \left( {\begin{array}{*{20}{c}} 0&{ - 1} \\ 1&{~~0} \end{array}} \right).\)

By ignoring the impacts of gravity, the system’s total potential energy caused by the deformation of the ith link can be expressed as

$$~U = \mathop \sum \limits_{i = 1}^2 {{U}_{i}} = \mathop \sum \limits_{i = 1}^2 \mathop \smallint \limits_0^{Li} \left( {EI{{)}_{i}}({{x}_{i}}} \right){{\left[ {\frac{{{{d}^{2}}{{w}_{i}}\left( {{{x}_{i}}} \right)}}{{d{{x}_{i}}^{2}}}} \right]}^{2}}~d{{x}_{i}},$$
(15)

where\(~{{\left( {EI} \right)}_{i}}\) is the flexural stiffness and Ui is the elastic energy held in the ith link.

2.3 Assumed Modes Method

The two links are considered as Euler–Bernoulli beams with \({{w}_{i}}({{x}_{i}},t)\) deformations, each deformation satisfy the ith link partial differential equation [6]:

$${{(EI)}_{i}}{{\;}}\frac{{{{\partial }^{4}}{{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}^{4}}} + {{\rho }_{i}}\frac{{{{\partial }^{2}}{{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{t}^{2}}}} = 0,\,\,\,\,i = 1,{{\;}}2.$$
(16)

In order to solve this equation, proper boundary conditions are applied at the base and at the end of each link. The boundary conditions of a clamped-mass manipulator are

$$\begin{gathered} {{\left. {{{w}_{i}}\left( {{{x}_{i}},t} \right)} \right|}_{{{{x}_{i}} = 0}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}}}} \right|}_{{{{x}_{i}} = 0}}} = 0, \\ {{\left. {{{{(EI)}}_{i}}\frac{{{{\partial }^{2}}{{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}^{2}}}} \right|}_{{{{x}_{i}} = Li}}} = - {{J}_{{Li}}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {~{{{\left. {\frac{{\partial {{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}}}} \right|}}_{{{{x}_{i}} = 0}}}} \right) - ~{{M}_{{Di}}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {{{{\left. {{{w}_{i}}\left( {{{x}_{i}},t} \right)} \right|}}_{{{{x}_{i}} = Li}}}~} \right), \\ {{\left. {{{{(EI)}}_{i}}\frac{{{{\partial }^{3}}{{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}^{3}}}} \right|}_{{{{x}_{i}} = Li}}} = {{M}_{{Li}}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {{{{\left. {{{w}_{i}}\left( {{{x}_{i}},t} \right)} \right|}}_{{{{x}_{i}} = Li}}}{{\;}}} \right) + {{M}_{{Di}}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {{{\;}}{{{\left. {\frac{{\partial {{w}_{i}}\left( {{{x}_{i}},t} \right)}}{{\partial {{x}_{i}}}}} \right|}}_{{{{x}_{i}} = 0}}}} \right), \\ \end{gathered} $$
(17)

where \({{M}_{{Di}}}\) is the contribution of masses of distal links, \({{M}_{{Li}}}\), \({{J}_{{Li}}}\) are the effective mass and moment of inertia at the end of the ith link. A finite-dimensional expression of the link deflection \({{w}_{i}}\left( {{{x}_{i}},t} \right)~\) formulated as

$${{w}_{i}}\left( {{{x}_{i}},t} \right) = \mathop \sum \limits_{j = 1}^{{{m}_{i}}} {{\phi }_{{ij}}}\left( {{{x}_{i}}} \right){{q}_{{ij}}}\left( t \right),$$
(18)

where \({{q}_{{ij}}}\left( t \right)\) and \({{\phi }_{{ij}}}\left( {{{x}_{i}}} \right)~\) are the jth modal displacement and the jth mode shape function for the ithlink, which satisfy the geometric boundary conditions given in (17).

The solution of Eqs. (16) and (18) gives

$${{q}_{{ij}}}\left( t \right) = {\text{exp}}\left( {{{\omega }_{{ij}}}t} \right)$$
(19)

and

$${{\phi }_{{ij}}}({{x}_{i}}) = {{m}_{i}}\left[ {\cos ({{\beta }_{{ij}}}{{x}_{i}}) - \cosh ({{\beta }_{{ij}}}{{x}_{i}}) + {{\gamma }_{{ij}}}\sinh ({{\beta }_{{ij}}}{{x}_{i}}) - \cosh ({{\beta }_{{ij}}}{{x}_{i}})} \right],$$
(20)

where \({{m}_{i}}\) is the mass of the link \(i\) and \({{\gamma }_{{ij}}}\) is given as

$${{\gamma }_{{ij}}} = \frac{{\sin {\kern 1pt} {{\beta }_{{ij}}} - \sinh {\kern 1pt} {{\beta }_{{ij}}} + \frac{{{{M}_{{Li}}}{{\beta }_{{ij}}}}}{{{{\rho }_{i}}}}\left( {\cos {\kern 1pt} {{\beta }_{{ij}}} - \cosh {\kern 1pt} {{\beta }_{{ij}}}} \right)}}{{\cos {\kern 1pt} {{\beta }_{{ij}}} - \cosh {\kern 1pt} {{\beta }_{{ij}}} - \frac{{{{M}_{{Li}}}{{\beta }_{{ij}}}}}{{{{\rho }_{i}}}}\left( {\sin {\kern 1pt} {{\beta }_{{ij}}} - \sinh {\kern 1pt} {{\beta }_{{ij}}}} \right)}}$$

and \({{\beta }_{{ij}}}\) is the solution of the following equation:

$$\begin{gathered} 1 + \cosh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\cos {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}} - \frac{{{{M}_{{Li}}}{{\beta }_{{ij}}}}}{{{{\rho }_{i}}}}\left( {\sin {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\cosh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}} - \cos {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\sinh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}} \right) \\ - \,\,\frac{{{{J}_{{Li}}}{{\beta }_{{ij}}}^{3}}}{{{{\rho }_{i}}}}\left( {\sin {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\cosh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}} + \cos {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\sinh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}} \right) \\ + \,\,\frac{{{{M}_{{Li}}}{{J}_{{Li}}}\beta _{{ij}}^{4}}}{{\rho _{i}^{4}}}(1 - \cos {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}\cosh {\kern 1pt} {{\beta }_{{ij}}}{{L}_{i}}) = 0. \\ \end{gathered} $$
(21)

Afterwards, the natural frequency for the jth mode and ith link, \({{\omega }_{{ij}}}\) determined from the following expression [36]:

$${{\omega }_{{ij}}} = \beta _{{ij}}^{2}\sqrt {~\frac{{{{{\left( {EI} \right)}}_{i}}}}{{{{\rho }_{i}}}}} .$$
(22)

The effectiveness masses at the end of each link are set as

$$\begin{gathered} {{M}_{{L1}}} = {{m}_{2}} + {{m}_{{h2}}} + {{M}_{p}}, \\ {{M}_{{L2}}} = {{M}_{p}}, \\ {{M}_{{D1}}} = \left( {{{m}_{2}}\frac{{{{L}_{2}}}}{2} + {{M}_{p}}{{L}_{2}}\cos {\kern 1pt} {{\theta }_{2}}} \right), \\ {{M}_{{D2}}} = 0 \\ \end{gathered} $$
(23)

and the effective inertia of each link

$$\begin{gathered} ~{{J}_{{L1}}} = {{J}_{{02}}} + {{J}_{{h2}}} + {{J}_{p}} + {{M}_{p}}{{L}^{2}}, \\ {{J}_{{L2}}} = {{J}_{p}}. \\ \end{gathered} $$
(24)

2.4 Euler–Lagrange Formalism

The equation of motion is derived using the Euler–Lagrange formalism as follows [15]:

$$L = T - U~ = \frac{1}{2}{{\dot {Q}}^{T}}M\left( Q \right)\dot {Q}{{\;}} - \frac{1}{2}{{Q}^{T}}KQ,$$
(25)
$$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{{\dot {Q}}}_{i}}}}} \right) - \frac{{\partial L}}{{\partial {{Q}_{i}}}} = {{\tau }_{i}},\,\,\,\,~i = 1,n,$$
(26)

where

Q = \(\left[ {{{\theta }_{1}},~{{\theta }_{2}},~{{q}_{{11}}},{{q}_{{12}}},{{q}_{{21}}},{{q}_{{22}}}} \right]{{~}^{T}} = {{\left[ {\theta ~~~q} \right]}^{T}}\) is the generalized coordinates vector;

\({{\tau }_{i}} = {{\left[ {\begin{array}{*{20}{l}} {{{\tau }_{{1~}}}}&{{{\tau }_{2}}}&0&0&0&0 \end{array}} \right]}^{T}} = {{\left[ {\tau ~~~0} \right]}^{T}}\) refers to the system’s applied torque vector;

\({{m}_{i}}\) is the number of the flexible modes adopted for the ith link, in our case two modes for each link are required \({{m}_{1}} = {{m}_{2}} = 2\).

The dynamic model of a two-link flexible manipulator has the following compact form

$$M\left( Q \right)\ddot {Q} + C\left( {Q,\dot {Q}} \right)\dot {Q} + g\left( Q \right) = {{\tau }_{i}},$$
(27)

where Q, \(\dot {Q}\ddot {Q}\) are n-dimensional vectors representing joint displacements, velocities and accelerations, respectively \(~n = {{m}_{1}} + {{m}_{2}} + 2;\) where

— M (Q) \( \in {{\mathcal{R}}^{{n{\text{xn}}}}}\) is the inertia matrix of the system;

— \(K\) \( \in {{\mathcal{R}}^{{n{\text{xn}}}}}\) is the stiffness matrix of the system,

$$K = {\text{diag}}\left\{ {0,\,\,0,\,\,{{m}_{1}}\omega _{{11}}^{2},\,\,~{{m}_{1}}\omega _{{12}}^{2},\,\,~{{m}_{2}}\omega _{{21}}^{2},\,\,~{{m}_{2}}\omega _{{22}}^{2}} \right\};$$

— \(C\left( {Q,\dot {Q}} \right)\dot {Q} \in {{\mathcal{R}}^{n}}\) is the Coriolis and centripetal forces vector;

— \(g\) is the gravity vector \(g = KQ\).

3 PASSIVITY-BASED CONTROLLER DESIGN

The dynamics of a two-link flexible manipulator can be written as

$$M\left( Q \right)\ddot {Q} + C\left( {Q,\dot {Q}} \right)\dot {Q} + g\left( Q \right) = {{\tau }_{i}}.$$
(28)

Let us define the desired trajectory vector which includes the desired rigid and flexible coordinates.

\({{Q}_{d}} = {{[{{\theta }_{d}},{{\;}}{{q}_{d}}{{\;}}]}^{T}},\) and its successive derivatives \({{\dot {Q}}_{d}} - [{{\dot {\theta }}_{d}},{{\dot {q}}_{d}}],\,\,\,\,{{\ddot {Q}}_{d}} - [{{\ddot {\theta }}_{d}},{{\ddot {q}}_{d}}].\)

The control aim is to optimize the manipulator’s applied torque (28) so that the trajectory of the system \(Q\) follows nearly the intended trajectory \(~{{Q}_{d}}\).

Let us define the displacement error vector \({{e}_{q}}\) by

$${{e}_{Q}} = Q - {{Q}_{d}} = \left( {\begin{array}{*{20}{c}} {{{e}_{r}}} \\ {{{e}_{f}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\theta - {{\theta }_{d}}} \\ {q - {{q}_{d}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\theta - {{\theta }_{d}}} \\ q \end{array}} \right),$$
(29)

\({{q}_{d}}\) is set to zero to suppress vibrations.

In order to eliminate steady state position errors, we restrict them to lie on the following sliding surface

$$s = {{\dot {e}}_{Q}} + \Lambda {{e}_{Q}} = 0$$
(30)

with an adjustable diagonal positive gain matrix Λ.

The storage function with the coordinate \(s\) is defined as [16]:

$$H - \frac{1}{2}{{s}^{T}}M\left( Q \right)s.$$
(31)

Differentiating

$$\dot {H} = {{s}^{T}}M(Q)\dot {s} + \frac{1}{2}{{s}^{T}}\dot {M}\left( Q \right)s,$$
(32)
$$\dot {H} = {{s}^{T}}\left( {M{{{\ddot {e}}}_{Q}} + M\Lambda {{e}_{Q}} + \frac{1}{2}\dot {M}s} \right),$$
(33)
$$\dot {H} = {{s}^{T}}\left( {M\ddot {q} - M{{{\ddot {q}}}_{d}} + M\Lambda {{e}_{Q}} + \frac{1}{2}\dot {M}s} \right).$$
(34)

Then, substituting \(M\ddot {q}\) from the system dynamics equation (28)

$$M\ddot {q} = {{\tau }_{i}} - C\dot {Q} - g = {{\tau }_{i}} - C\left( {s + {{{\dot {Q}}}_{d}} - \Lambda {{e}_{Q}}} \right) - g.$$
(35)

Yields

$$\dot {H} = {{s}^{T}}\left( {{{\tau }_{i}} - C\dot {Q} - g - M{{{\ddot {q}}}_{d}} + M\Lambda {{e}_{Q}} + \frac{1}{2}\dot {M}s} \right),$$
(36)
$$\dot {H} = {{s}^{T}}\left( {{{\tau }_{i}} - {{\;}}M{{{\ddot {Q}}}_{d}} + M\Lambda {{e}_{Q}} - C{{{\dot {Q}}}_{d}} + C\Lambda {{e}_{Q}} - g + \frac{1}{2}(\dot {M}s - 2C)s} \right).$$
(37)

Using skew symmetry property, we obtain

$$\dot {H} = {{s}^{T}}\left( {{{\tau }_{i}} - {{\;}}M{{{\ddot {Q}}}_{d}} + M\Lambda {{e}_{Q}} - C{{{\dot {Q}}}_{d}} + C\Lambda {{e}_{Q}} - g} \right).$$
(38)

Let us introduce a virtual “reference trajectory”

$$v = {{\dot {Q}}_{d}} - \Lambda {{e}_{q}},$$
(39)
$$\dot {H} = {{s}^{T}}({{\tau }_{i}} - M\dot {v} - Cv - g).$$
(40)

We choose the following control law [17]

$${{\tau }_{i}} = M\left( Q \right)\dot {v} + C\left( {Q,\dot {Q}} \right)v + g\left( Q \right) + u.$$
(41)

Then, substituting (41) into (28) and (40) yields

$$M\left( Q \right)\dot {s} + C\left( {Q,\dot {Q}} \right)s = u,$$
(42)
$$~\dot {H} = {{s}^{T}}u.$$
(43)

Equation (43) means the passivity of the closed-loop manipulator dynamics (28) from the input torque \(u~~{\text{to the output }}s{{\;}}\) with respect to the storage function defined in Eq. (31).

We can set the new control law as [16]:

$$u = - {{K}_{v}}s = - {{K}_{v}}({{\dot {e}}_{Q}} + \Lambda {{e}_{Q}}),$$
(44)

with \({{K}_{v}}~\) is a diagonal positive gain matrix.

The final control law is given as

$${{\tau }_{i}} = M\left( Q \right)\dot {v} + C\left( {Q,\dot {Q}} \right)v + g\left( Q \right) - {{K}_{v}}s.$$
(45)

3.1 Global Stability Proof

Define the candidate Lyapunov function

$$V = \frac{1}{2}{{s}^{T}}M\left( Q \right)s + e_{Q}^{T}\Lambda {{K}_{v}}{{e}_{Q}}.$$
(46)

Then, its time derivative along the trajectories of (42) with (44) satisfies

$$\begin{gathered} \dot {V} = {{s}^{T}}(\ddot {Q})\dot {s} + \frac{1}{2}{{s}^{T}}\dot {M}(Q)s + 2e_{Q}^{T}\Lambda {{K}_{v}}{{{\dot {e}}}_{Q}} \\ = {{s}^{T}}\left( { - C(Q,\dot {Q})s + u} \right) + \frac{1}{2}{{s}^{T}}\dot {M}(Q)s + 2e_{Q}^{T}\Lambda {{K}_{v}}{{{\dot {e}}}_{Q}} \\ = \frac{1}{2}{{s}^{T}}\left( {\dot {M}(Q) - 2C(Q,\dot {Q})} \right)s - {{s}^{T}}{{K}_{v}}s + 2e_{Q}^{T}\Lambda {{K}_{v}}{{{\dot {e}}}_{Q}} \\ = - {{\left( {{{{\dot {e}}}_{Q}} + \Lambda {{e}_{Q}}} \right)}^{T}}{{K}_{v}}\left( {{{{\dot {e}}}_{Q}} + \Lambda {{e}_{Q}}} \right) + 2e_{Q}^{T}\Lambda {{K}_{v}}{{{\dot {e}}}_{Q}} \\ = - \dot {e}_{Q}^{T}{{K}_{v}}{{{\dot {e}}}_{Q}} - e_{Q}^{T}\Lambda {{K}_{v}}{{e}_{Q}} < 0. \\ \end{gathered} $$
(47)

According to the Lyapunov stability theorem, equation (47) implies that the origin \(~{{e}_{Q}} = {{\dot {e}}_{Q}} = 0~\) is asymptotically stable. The controller defined by Eq. (45) is asymptotically stable and guarantees steady-state convergence for the rigid angles and elastic deflections.

4 SIMULATION RESULTS

In this section, simulation results are presented with a fourth-order Runge–Kutta method in the Matlab/Simulink environment to show the trajectory tracking using the suggested passivity-based controller.

The reference trajectory is a polynomial function of fifth order which satisfies

$${{\theta }_{d}} = \left\{ \begin{gathered} \frac{\pi }{3}\left[ {5{{{\left( {\frac{t}{{{{t}_{f}}}}} \right)}}^{3}} - \frac{{15}}{2}{{{\left( {\frac{t}{{{{t}_{f}}}}} \right)}}^{4}} + 3{{{\left( {\frac{t}{{{{t}_{f}}}}} \right)}}^{5}}} \right] \hfill \\ \frac{\pi }{6}\,\,{\text{if}}\,\,t \geqslant {{t}_{f}} \hfill \\ \end{gathered} \right.\,\,{\text{if}}\,\,{{\;}}0 \leqslant t \leqslant {{t}_{f}} = 3s.$$
(48)

The proposed controller parameters are obtained with fine tuning using trial and error method as follows:

$$\begin{gathered} {{K}_{v}} = {\text{diag}}\left[ {600,{{\;}}600,{{\;}}100,{{\;}}2,{{\;}}0.5{{\;}},0.5} \right], \\ L = {\text{diag}}\left[ {500,{{\;}}400,{{\;}}250,{{\;}}300,{{\;}}350,{{\;}}300} \right]. \\ \end{gathered} $$
(49)

The system physical parameters are listed in Table 1 [17].

Table 1.   Physical parameters of the flexible arm
Full size table

Figures 2–5 show the tracking performances of the system.

Fig. 2.
figure 2

Trajectory tracking for the first link.

Full size image
Fig. 3.
figure 3

Trajectory tracking for the second link.

Full size image
Fig. 4.
figure 4

Position error for the first link.

Full size image
Fig. 5.
figure 5

Position error for the second link.

Full size image

As shown in the figures above, the rigid angles accurately followed the desired trajectory, after which the maximum tracking error achieved was only \(0.035\,\,{\text{deg}}\). After that, it gradually converges to zero. This indicates that the intended trajectory is attained with actually no tracking error.

Figures 6 and 7 show the necessary control torque inputs for trajectory tracking, until the final position is reached, control inputs converge to a minimum value, we can conclude that the desired trajectory is attained with minimal control effort.

Fig. 6.
figure 6

Control torque for the first link.

Full size image
Fig. 7.
figure 7

Control torque for the second link.

Full size image

Figure 8 shows the tip deflection, we can remark that the maximum value is \(15 \times {{10}^{{ - 4}}}m\). Besides, the tip vibrations are damped out within \(2.5s\) before the flexible link reaches the final position.

Fig. 8.
figure 8

Tip elastic deflection.

Full size image

In order to show the effectiveness of the proposed controller, a comparative study between the passivity based controller (PBC) and the backstopping controller (BSC) [17] is conducted. The flexible manipulator is subjected to an external perturbation (payload mass).

Figures 9 and 10 show the tip deflection and the position error of the second link for a change in the payload mass, we can remark that the PBC show better performances compared to the BSC in terms of positioning and vibration damping. This means that the proposed controller provides improved robustness against the external perturbations (payload change) compared to the BSC controller. However, if we apply a high change in the payload mass the performances of both controllers deteriorate more and more, hence the necessity to extend this approach to the adaptive version.

Fig. 9.
figure 9

Position error of the second link for Mp = 0.2 Kg.

Full size image
Fig. 10.
figure 10

Tip deflection for Mp = 0.2 Kg.

Full size image

5 CONCLUSIONS

In this paper, we develop an accurate modeling approach using Lagrangian formalism with the assumed modes method for a two-link flexible manipulator including structural elasticity and payload mass. To achieve the control goal, we design a passivity-based controller to ensure good trajectory tracking and suppress the elastic vibrations at the tip. Passive systems are a class of dynamical systems which illustrate the importance of energy exchange with the environment. The proposed controller uses this property to achieve asymptotic trajectory tracking with efficient tip vibration damping. It requires a perfect knowledge of the physical parameters with moderate external disturbances, which is often not the case in practice, hence the need for the adaptive controller [13] to estimate the unknown disturbances and system uncertainties. Simulation results show an excellent performance of the proposed controller when all system parameters are accurately known.