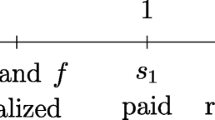Managerial Compensation, Investment Decisions, and Truthfully Reporting

Abstract

This paper provides a formal analysis of investment decisions with special emphasis to mechanisms which induce managers to reveal their knowledge truthfully. In a one-period context ‘knowledge’ usually means the profit ratio. In a multi-period setting ‘knowledge’ is referred to the (multivariate) cash flow stream or the (univariate) net present value. Both situations are analysed in the paper. We start with the basic case ‘one firm, one manager’ and continue with the case ‘divisional firm, division managers’. With respect to the first case, we criticise two approaches (Rogerson, JPolE 105(4):770–795, 1997; Reichelstein, RAS 2(2):157–180, 1997) and develop a solution based on extended incentive contracts. To tackle the second case, we analyse pros and cons of Groves schemes.

1 Introduction

Investment planning is often characterized by asymmetric information. Managers are frequently better informed about the technology and market opportunities than the corporate headquarters. Therefore, incentive mechanisms are needed to limit the scope of opportunistic managers. When selecting and implementing investment projects, managers shall act according to the corporate objectives. In particular, they shall report the profitability of investment opportunities truthfully ahead of investment decision making.

Incentive mechanisms discussed in the literature are—with only few exceptions—based on one-period models. On the other hand, typical investment projects span a multi-period planning horizon T (for example, 10 years). What is more, a real dynamic model should also consider e.g. changes in the economic environment, the development of other (later starting) projects, whether interactions between projects exist etc. As soon as stochastics and different risk attitudes are taken into account, the risk of misspecification increases and practicality decreases.

This paper strives to study a compromise between the overly restrictive one-period models and the complex multi-period models. This compromise is based on

• the examination of investment projects by the (deterministic or stochastic) net present value (NPV ) and

• the remuneration of managers by payments in the periods t = 1 to t = T proportional to residual income (RI _t ).

The last point is of particular interest from a practical point of view. Many incentive mechanisms determine managers’ compensation depending on the realized NPV or the deviation between the actual NPV and $\widehat{\mathit{NPV }}$, i.e. the NPV reported to central management at date t = 0. Both, the NPV as well as its deviation from $\widehat{\mathit{NPV }}$, cannot be evaluated without major dissent until date t = T (for example, in 10 years). A remuneration only at the planning horizon t = T without interim payments at dates t = 1, 2, …, T is problematic in practise. It seems reasonable (cf. Sect. 2.2) to make these interim payments proportional to residual income RI _t . However, the ongoing determination of project-specific RI _t involves high requirements to be met by the accounting system.

Section 2 sums up the foundations of NPV from the perspectives of money market and utility theory as well as the interrelations of net present value and residual income. In Sect. 3, the case ‘one firm, one manager’ is treated. Special attention is paid to the problem of the impatient manager, i.e. when the duration of the manager’s contract is shorter than that of her proposed projects. Section 4 analyses incentives within a divisionalized company in which the various divisional managers compete for the scarce resource investment capital. Section 5 concludes. All proofs are in the Appendix.

2 Net Present Value, Utility Theory, and Residual Income

2.1 Money Market Invariance

The task under consideration is to examine an investment opportunity that generates the cash flow stream c = (c ₀, c ₁, …, c _T ). Here, c ₁, …, c _T are cash flows at dates 1, …, T and c ₀ < 0 is the initial net investment due at date t = 0, cf. Fig. 1.

Fig. 1

Cash flow stream. Own representation

When c is risky, one may strive to evaluate it by means of a (scalar) certainty equivalent CE(c). The latter will, in general, depend on the date 0, 1, …, T of evaluation. We, however, restrict our considerations to date 0 as this is usually the date of evaluation in the context of investment accounting. Furthermore, if a perfect money market exists, the decision maker has the opportunity to transform the risky cash flow stream c, for instance by borrowing or lending certain amounts z _t (with t = 0, 1, …, T − 1) at rate r for one period each. When doing so, she can transform c into

$$\displaystyle{ \mathbf{c} + \mathbf{z} = (c_{0} - z_{0},c_{1} + qz_{0} - z_{1},c_{2} + qz_{1} - z_{2},\ldots,c_{T} + qz_{T-1})\,, }$$

(1)

where q = 1 + r and z = (−z ₀, qz ₀ − z ₁, …, qz _T−1). Since z is non-stochastic and already projectable at date 0, it seems natural to demand that both cash flow streams, c as well as c + z, should be assigned the same value, i.e.

$$\displaystyle{ \mathit{CE}(\mathbf{c}) = \mathit{CE}(\mathbf{c} + \mathbf{z}) }$$

(2)

for all c and z. Multiattributive utility functions u(x) (where x = (x ₀, x ₁, …, x _T ) is the vector of attributes) that suffice this condition are termed money market invariant. The respective certainty equivalent CE(c) is then characterized by the indifference c ∼ (CE(c), 0, …, 0). Theorem 5.1 clarifies the structure of multiattributive utility functions that are money market invariant in this sense.

Theorem 5.1

A multiattributive utility function u(x) is money market invariant in the sense of condition ( 2 ) if and only if it evaluates x on the basis of the net present value NPV (x) = ∑ _{t = 0} ^T x _t ⋅ γ  ^t (with γ = q ⁻¹ ) only, i.e. iff

$$\displaystyle{ u(\mathbf{x}) = u(\mathit{NPV }(\mathbf{x}),0,\ldots,0) }$$

(3)

holds true. Then, u(x) de facto simplifies to an uniattributive utility function u ₀(x) that evaluates payments x due at date 0, i.e. u ₀(x) = u(x, 0, …, 0).

The proof can be found in the Appendix (section “Proof of Theorem 5.1”).

2.2 Net Present Value and Residual Income

The well-known Theorem by Preinreich (1937) and Lücke (1955) captures the interrelation of cash flows and residual incomes. As this interrelation is fundamentally important for our considerations, we sketch the Preinreich-Lücke Theorem in the following. Given the cash flow stream c ₀, c ₁, …, c _T with c ₀ < 0, the residual income in period t is defined by

$$\displaystyle{ \mathit{RI}_{t} = \mathit{NI}_{t} - r \cdot \mathit{EC}_{t-1}\,. }$$

(4)

Here, NI _t = c _t − d _t ⋅  | c ₀ | denotes the net income in period t, where d _t is the depreciation factor relevant in period t. Further, r is the cost of equity , and EC _t−1 is the equity capital in the preceding period t − 1. The latter resembles the difference of net incomes and cash flows cumulated up to period t − 1, i.e. EC _t−1 = (NI ₁ + … + NI _t−1) − (c ₀ + c ₁ + … + c _t−1) for t > 1 (otherwise, EC ₋₁ = 0 and EC ₀ = −c ₀, respectively). In period 0, RI ₀ = 0 holds true. We are now able to formulate the Preinreich/Lücke Theorem 5.2.

Theorem 5.2

Given the total sum of net incomes NI ₁ + … + NI _T equals the total sum of cash flows c ₀ + c ₁ + … + c _T (and, hence, EC _T = 0), discounting the stream of residual incomes and discounting the stream of cash flows lead to the same result, i.e.

$$\displaystyle{ \sum _{t=1}^{T}\mathit{RI}_{ t} \cdot \gamma \,^{t} =\sum _{ t=0}^{T}c_{ t} \cdot \gamma \,^{t}\,. }$$

(5)

As the right-hand side of ( 5 ) is the net present value, the latter can also be computed on the basis of residual incomes.

The proof can be found in the Appendix (section “Proof of Theorem 5.2”).

3 One Firm, One Manager

Regarding the manager’s planning horizon τ, we distinguish the cases τ ≧ T and τ < T. In the first case, the (‘patient’) manager’s contract does not expire within the duration T of the investment project under consideration, whereas in the second case, the (‘impatient’) manager plans to leave or retire before all the benefits of the investment are realized. In addition, various scenarios regarding the level of information on the cash flow stream are conceivable. For example, the cash flows or their expected values may be common knowledge. Contrariwise, corporate headquarters may only know the expected net present value or cash flows (or the associated net present value) reported by the manager. Finally, one can distinguish whether manager and/or company are risk neutral or risk averse.

3.1 The Case of the Patient Manager

In the following, we assume τ ≧ T, meaning that the manager’s planning horizon exceeds the duration of the investment project under consideration. If one wishes to achieve goal congruence in the sense that the manager maximizes her discounted remuneration by selecting a project that maximizes the company’s NPV, then the scheme described in Sect. 3.1.1 is the contract of choice. If, however, corporate headquarters are—for the sake of planning certainty—primarily eager to learn the NPV ’s value, extended incentive contracts as described in Sect. 3.1.2 should be preferred.

3.1.1 Remuneration Based on Residual Income

As outlined in Sect. 2.2, the Preinreich/Lücke Theorem 5.2 implies

$$\displaystyle{ \mathit{NPV } =\sum _{ t=0}^{T}c_{ t} \cdot \gamma \,^{t} =\sum _{ t=1}^{T}\mathit{RI}_{ t} \cdot \gamma \,^{t}\,. }$$

(6)

If in period t (with t = 1, …, T) a remuneration proportional to residual income RI _t is provided to the manager, i.e. β ⋅  RI _t with β > 0, goal congruence can be achieved: Provided manager and company apply the same discount factor γ, the right-hand side of (6) is proportional to the manager’s present value of remuneration. Hence, maximizing this present value leads to the maximal NPV, implying goal congruence.

This reasoning tacitly assumes the cash flow stream c ₀, c ₁, …, c _T to be deterministic, regardless of who has what information about it. Only then ‘maximize the NPV ’ or ‘maximize the present value of remuneration’ are sensible directives. If, on the other hand, c ₀, c ₁, …, c _T are (in part) stochastic, (6) turns out to be a correct relationship between random variables. However, maximization then need to be applied to expected utilities or certainty equivalents , cf. Sect. 2.1. Then the certainty equivalent of NPV has to be evaluated by means of the company’s utility function, whereas the certainty equivalent of the remuneration’s present value needs to be evaluated by means of the manager’s utility function. That’s why remuneration based on residual income cannot generally assure goal congruence in the presence of risk aversion. An attempt to tackle this problem by implementing a rather sophisticated risk allocation schedule was recently suggested by Grottke and Schosser (2014) .

In the special case of risk neutrality goal congruence can be obtained, as can be seen from (6) by the formation of expectations, i.e.

$$\displaystyle{ \mathrm{E}(\mathit{NPV }) =\sum _{ t=0}^{T}\mathrm{E}(c_{ t}) \cdot \gamma \,^{t} =\sum _{ t=1}^{T}\mathrm{E}(\mathit{RI}_{ t}) \cdot \gamma \,^{t} =\mathrm{ E}\bigg(\sum _{ t=1}^{T}\mathit{RI}_{ t} \cdot \gamma \,^{t}\bigg)\,. }$$

(7)

Obviously, the expected present value of remuneration is maximal if and only if the expected NPV of the investment project is maximal.

3.1.2 Remuneration Based on Extended Incentive Contracts

A remuneration based on β ⋅  RI _t (or, more general, α + β ⋅  RI _t ) ensures goal congruence provided cash flows are deterministic and company as well as manager are risk neutral. However, such incentive schemes are not capable of extracting the attainable NPV or its expected value ex ante. If such information is desired, e.g. for the sake of planning certainty, extended incentive contracts (Reichelstein and Reichelstein 1987 ; Bamberg 1991 ) are a promising alternative. Then, remuneration is proportional to

$$\displaystyle{ g(\widehat{\mathit{NPV }}) + s(\widehat{\mathit{NPV }}) \cdot [\mathit{NPV } -\widehat{\mathit{NPV }}]\,, }$$

(8)

where $\widehat{\mathit{NPV }}$ denotes the project’s net present value as reported by the manager at date t = 0, whereas NPV is the actual net present value. The latter value is random from an ex ante perspective (i.e., at date t = 0), but certain from an ex post perspective (i.e., at date t = T). Finally, g(⋅ ) and s(⋅ ) are design functions determined by the company. Regarding g(⋅ ) and s(⋅ ) the requirements

$$\displaystyle{ s(\cdot ) = g'(\cdot ),\quad s'(\cdot ) > 0,\quad s(\cdot ) > 0 }$$

(9)

ensure that the manager maximizes her expected remuneration if and only if she reports $\widehat{\mathit{NPV }}_{\text{opt}} =\mathrm{ E}(\mathit{NPV })$ (Bamberg et al. 2013 ). Hence, information on the investment project’s expected net present value can be extracted truthfully if the manager is risk-neutral. Furthermore, s(⋅ ) > 0 also induces the manager to strive for the highest possible realization of NPV when implementing the project, even if $\widehat{\mathit{NPV }}$ was biased.

In the following, we apply the presumably most simple specification of g(⋅ ) and s(⋅ ) satisfying (9), namely g(x) = x ² and hence s(x) = 2x. Then, remuneration is given by

$$\displaystyle{ \beta \cdot \{(\widehat{\mathit{NPV }})^{2} + 2\widehat{\mathit{NPV }} \cdot [\mathit{NPV } -\widehat{\mathit{NPV }}]\} }$$

(10)

with expectation

$$\displaystyle{ \beta \cdot \{(\widehat{\mathit{NPV }})^{2} + 2\widehat{\mathit{NPV }} \cdot [\mathrm{E}(\mathit{NPV }) -\widehat{\mathit{NPV }}]\}\,, }$$

(11)

where β > 0 is a constant of proportionality.

Some remarks regarding formulae (10) and (11) are in order. First, it can easily be verified that reporting the expected net present value is indeed optimal for a risk-neutral manager. As the first derivative of (11) with respect to $\widehat{\mathit{NPV }}$ is $\beta \cdot [-2\widehat{\mathit{NPV }} + 2 \cdot \mathrm{ E}(\mathit{NPV })]$, evaluating the first-order condition immediately yields $\widehat{\mathit{NPV }}_{\text{opt}} =\mathrm{ E}(\mathit{NPV })$. The second-order condition sufficient for a maximum is fulfilled since the second derivative of (11) with respect to $\widehat{\mathit{NPV }}$, − 2β, is clearly negative.

Second, if the manager manages to forecast NPV without any deviation, i.e. $\widehat{\mathit{NPV }} = \mathit{NPV }$, she will earn a remuneration of exactly $\beta \cdot (\widehat{\mathit{NPV }})^{2}$. This scenario is, of course, unrealistic as NPV is ex ante random. If, however, target-actual comparison reveals a rather low discrepancy, i.e. $\widehat{\mathit{NPV }} \approx \mathit{NPV }$, the manager’s remuneration will approximately be $\beta \cdot (\widehat{\mathit{NPV }})^{2}$, providing a hint for the determination of β. If a salary level of for example 200,000 € per year is considered to be realistic in the manager market, and the project duration is T = 5 years, $\beta \cdot (\widehat{\mathit{NPV }})^{2} = 10^{6}$ € seems a reasonable specification. Please note that such a specification does not constitute a fixed remuneration, even if progress payments amounting to for example 200,000 € at dates t = 1, 2, 3, 4 might be agreed. The reason is the final (positive or negative) payment at date t = 5, taking into account possibly accrued earlier payments.

Given the assumption $\beta \cdot (\widehat{\mathit{NPV }})^{2} = 10^{6}$, one can rewrite (10) as follows

$$\displaystyle{ 10^{6} \cdot \bigg [2 \cdot \frac{\mathit{NPV }} {\widehat{\mathit{NPV }}} - 1\bigg]\,, }$$

(12)

yielding the final payment

$$\displaystyle{ 10^{6} \cdot \bigg [2 \cdot \frac{\mathit{NPV }} {\widehat{\mathit{NPV }}} - 1\bigg] - 800,000 }$$

(13)

or

$$\displaystyle{ 10^{6} \cdot \bigg [2 \cdot \frac{\mathit{NPV }} {\widehat{\mathit{NPV }}} - 1\bigg] - 200,000 \cdot (q + q^{2} + q^{3} + q^{4})\,. }$$

(14)

If the actual net present value observed at date T = 5 exceeds the ex ante forecast by 10%, i.e. $\mathit{NPV } = 1,1 \cdot \widehat{\mathit{NPV }}$, the manager earns a final payment of 400,000 € according to (13). If, on the other hand, $\mathit{NPV } = 0,9 \cdot \widehat{\mathit{NPV }}$ turns out to be true, the final payment will be zero.

Third, risk neutrality serves as a decision-theoretical prerequisite for the implementation of extend incentive contracts. In this regard it is worthwhile to note that the company’s risk attitude refers to the net present value evaluated at date t = 0 (whose realization cannot be observed until date t = T). On the other hand, the manager’s risk attitude refers to payments due at date t = T. What is more, the design of the interim payments is, although important for the acceptance in practice, irrelevant from a decision-theoretical perspective. In order to incorporate these payments into the formal analysis, one need to apply multiattributive utility functions (as in Sect. 2.1). This, however, seems hardly be practicable in real-world settings.

Let us finally consider the case of a risk-averse (rather than a risk-neutral) manager. For the sake of convenience, we adopt the well-known LEN setting (Holmström and Milgrom 1987 ; Spremann 1987 ), i.e. we assume NPV to be normally distributed and the manager to be risk-averse with positive constant absolute risk aversion ϱ. The manager then maximizes the certainty equivalent of her remuneration (10) with respect to $\widehat{\mathit{NPV }}$. As can easily be verified, her optimal report is

$$\displaystyle{ \widehat{\mathit{NPV }}_{\text{opt}} = \frac{\mathrm{E}(\mathit{NPV })} {1 + 2\varrho \beta \cdot \mathrm{ Var}(\mathit{NPV })}\,. }$$

(15)

Obviously, the optimal report systematically falls below the true expected net present value. This bias is more pronounced, the greater the manager’s risk aversion ϱ is and the greater the project’s risk Var(NPV ) is. It can be shown that such biases generally occur when the manager is risk-averse (Bamberg 1991) .

3.2 The Case of the Impatient Manager

We now turn to the case of the impatient manager who plans to leave or retire before all the benefits of the investment are realized. Formally, τ < T, where τ is the manager’s planning horizon and T is the duration of the investment project under consideration. The central question is then how to provide incentives for a manager whose contract runs until period τ to only select investment projects with positive net present values, even if τ < T.

Reichelstein (1997) and Rogerson (1997) can be considered the main contributions to this stream of literature. Similar to Sect. 3.1.1, Reichelstein (1997) and Rogerson (1997) suggest the remuneration in period t to be proportional to residual income RI _t , i.e. β ⋅  RI _t . However, the solution outlined in Sect. 3.1.1 does not rely on any specific assumption regarding RI _t aside from NI ₁ + … + NI _T = c ₀ + c ₁ + … + c _T . Since net incomes can be computed according to NI _t = c _t − d _t ⋅  | c ₀ |, the latter premise only imposes the restriction d ₁ + … + d _T = 1. In contrast to that, implementing the Reichelstein/Rogerson solution requires quite specific depreciation factors, namely

$$\displaystyle{ d_{t} = \frac{c_{t}} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma \,^{j}} - r \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\,. }$$

(16)

Although not obvious, these depreciation factors indeed add to one, as stated in the following property.

Property 5.1

The depreciation factors (16) needed for implementing the Reichelstein/Rogerson solution add to one, i.e.

$$\displaystyle{ \sum _{t=1}^{T}d_{ t} =\sum _{ t=1}^{T}\Bigg[ \frac{c_{t}} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma \,^{j}} - r \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\Bigg] = 1\,. }$$

(17)

Hence, the premises of the Preinreich/Lücke Theorem 5.2 are fulfilled.

The proof can be found in the Appendix (section “Proof of Property 5.1”).

In order to implement the Reichelstein/Rogerson solution, special informational requirements regarding the cash flow stream have to be met. Sections 3.2.1 and 3.2.2 discuss these requirements in detail.

3.2.1 Cash Flows Known

The most restrictive conceivable premise regarding the cash flow stream is that it is (up to a common factor, which cancels in (16)) known for each investment project. This should be the case in this section. Furthermore, we must limit ourselves to investment projects that suffice the conditions

$$\displaystyle{ c_{0} < 0,\quad c_{1} > 0,\quad c_{2} > 0,\quad \ldots,\quad c_{T} > 0\,. }$$

(18)

The manager’s present value of remuneration is then proportional to

$$\displaystyle{ \sum _{t=1}^{\tau }\mathit{RI}_{ t} \cdot \gamma \,^{t}\,, }$$

(19)

where residual incomes RI _t are computed according to the depreciation scheme (16). Theorem 5.3 states that this solution ensures goal congruence.

Theorem 5.3

Given an investment project with known cash flows meeting conditions ( 18 ), a remuneration proportional to residual income based on the depreciation scheme ( 16 ) provides goal congruence in the following sense: The manager’s present value of remuneration is positive if and only if the investment project’s NPV is positive.

The proof can be found in the Appendix (section “Proof of Theorem 5.3”).

3.2.2 Risky Cash Flows with Known Expectation

In this section, we assume the cash flows c ₁, …, c _T to be stochastic with known expected values E(c ₁), …, E(c _T ). The same applies to the (deterministic) initial net investment c ₀. Furthermore, we assume manager and company to be risk neutral. Then, the manager strives to maximize the expectation of her remuneration’s present value, E(RI ₁ ⋅ γ ¹ + … + RI _T ⋅ γ ^T), and the company’s goal is to maximize E(NPV ). Similar to (18), the conditions

$$\displaystyle{ \mathrm{E}(c_{1}) > 0,\quad \ldots,\quad \mathrm{E}(c_{T}) > 0 }$$

(20)

shall be met. If this is the case, the analysis of the previous section can easily be translated into the setting considered here. The depreciation factors (16) must of course not be interpreted as random variables, but as known figures

$$\displaystyle{ d_{t} = \frac{\mathrm{E}(c_{t})} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j}) \cdot \gamma \,^{j}} - r \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\,. }$$

(21)

Then, goal congruence can also be achieved, cf. Theorem 5.4.

Theorem 5.4

Given an investment project with risky cash flows meeting conditions ( 20 ) and known c ₀, E(c ₁), …, E(c _T ), a remuneration proportional to residual income based on the depreciation scheme ( 21 ) provides goal congruence in the following sense: The risk neutral manager’s expected present value of remuneration is positive if and only if the investment project’s E(NPV ) is positive.

The proof can be found in the Appendix (section “Proof of Theorem 5.4”).

3.2.3 Cash Flows Reported by the Manager

When the company only knows the initial net investment c ₀, it relies on reports or forecasts $\hat{c}_{1},\ldots,\hat{c}_{T}$ regarding the cash flows c ₁, …, c _T provided by the manager. Then, several residual income based remuneration schemes of the Reichelstein/Rogerson type are conceivable. Amongst others, depreciation factors may solely depend on the manager’s reports, i.e.

$$\displaystyle{ d_{t} = \frac{\hat{c}_{t}} {\sum \limits _{j=1}^{T}\hat{c}_{j} \cdot \gamma \,^{j}} - r \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\,. }$$

(22)

Alternatively, cash flows realized over time may be exploited. At date t, the company knows c ₁, …, c _t and insofar only relies on reports regarding c _t+1, …, c _T . Then depreciation factors

$$\displaystyle{ d_{t} = \frac{c_{t}} {\sum \limits _{j=1}^{t}c_{j} \cdot \gamma \,^{j} +\sum \limits _{ j=t+1}^{T}\hat{c}_{j} \cdot \gamma \,^{j}} - r \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg) }$$

(23)

may be applied. However, such approaches cannot guarantee goal congruence, as the following example illustrates.

Example 5.1

The investment project under consideration involves an initial net investment of c ₀ = −1000 € and spans T = 2 periods. The impatient manager, whose planning horizon is τ = 1, reports the cash flows $\hat{c}_{1} =\hat{ c}_{2} = 600$, whereas the true values are c ₁ = 700 and c ₂ = 300. Using the discount factor γ = 0. 95, one predicts

$$\displaystyle{ \widehat{\mathit{NPV }} = -1000 + 600 \cdot (0.95 + 0.95^{2}) = 111.5 }$$

(24)

based on the manager’s reports, whereas the true value

$$\displaystyle{ \mathit{NPV } = -1000 + 700 \cdot 0.95 + 300 \cdot 0.95^{2} = -64.25 }$$

(25)

is negative. Consequently, the company would prefer to forgo this investment. However, when applying depreciation scheme (23), the manager’s present value of remuneration would be proportional to

$$\displaystyle{ \mathit{RI}_{1}\cdot \gamma =\bigg (700 - \frac{700} {700 \cdot 0.95 + 600 \cdot 0.95^{2}} \cdot 1000\bigg) \cdot 0.95 = 113.82 }$$

(26)

and, hence, positive. Accordingly, there is a considerable disincentive for the manager to propose a project with great c ₁. □

To the best of our knowledge, no incentive-compatible mechanism to cope with the situation of an impatient manager (τ < T) who reports potentially biased cash flows $\hat{c}_{t}$ has been proposed in the literature. This suggests that such a mechanism may indeed not exist. However, literature does also not provide evidence of such an impossibility.

4 Divisionalized Firm, Division Managers

In the preceding sections we assumed investment capital to be available in unlimited quantities. In practice, however, interest rates rise with investment volumes. But even when an uniform interest rate r exists (as assumed in this paper), a hard credit limit may have to be taken into account. We want to focus on this case in the following. Then, divisional managers will compete for the scarce resource investment capital. As less profitable, yet acceptable projects may crowd out perhaps better projects, central management crucially relies on truthful reports regarding potential returns provided by the divisional managers. As has been seen in the last section, truthful reports $\hat{c}_{0},\hat{c}_{1},\ldots,\hat{c}_{T}$ are (too) difficult to achieve. Therefore, we again limit the analysis to reports regarding the net present value.

Let NPV _i (b _i ) denote the net present value attainable by division i (with i = 1, …, n) when equipped with an investment budget of b _i . This function is assumed to be monotonic increasing and concave. Further, let B denote the credit limit, i.e.

$$\displaystyle{ \sum _{i=1}^{n}b_{ i} \leqq B }$$

(27)

must be met. If $\widehat{\mathit{NPV }}_{i}(b_{i})$ is divisional manager i’s report regarding NPV _i (b _i ) (again, not a number, but a function of b _i ), central management will maximize

$$\displaystyle{ \sum _{i=1}^{n}\widehat{\mathit{NPV }}_{ i}(b_{i})\quad \text{subject to}\quad \sum _{i=1}^{n}b_{ i} \leqq B\,. }$$

(28)

As $\widehat{\mathit{NPV }}_{i}(b_{i})$ is also monotonic increasing and concave, the budget constraint will hold in equality in the optimum. We can therefore rewrite (28) as follows: Maximize

$$\displaystyle{ \sum _{i=1}^{n}\widehat{\mathit{NPV }}_{ i}(b_{i})\quad \text{subject to}\quad \sum _{i=1}^{n}b_{ i} = B\,. }$$

(29)

There is an unique solution to this problem, given by (b ₁ ^∗; …; b _n ^∗). This capital allocation is, however, only the real optimum when divisional managers have supplied truthful reports. The latter can be achieved when the remuneration of divisional manager i is a monotonic increasing function of the evaluation measure

$$\displaystyle{ \mathit{EM}_{i} = \mathit{NPV }_{i}(b_{i}^{{\ast}}) +\sum _{ j\neq i}\widehat{\mathit{NPV }}_{j}(b_{j}^{{\ast}})\,. }$$

(30)

Accordingly, the evaluation measure of divisional manager i depends on the actual net present value of her own division as well as on the reports of all other divisions. Then, it is optimal for each divisional manager to provide truthful reports, regardless whether the other managers also convey the truth or distorted messages (Groves 1976 ; Bamberg and Trost 1998 ). Truthful reporting is hence not ‘only’ a Nash equilibrium strategy , but a dominant strategy . The following example inspired by Locarek and Bamberg (1994) serves to illustrate this so-called Groves mechanism.

Example 5.2

A company consisting of n = 2 divisions faces the credit limit B = 10⁸ €. Furthermore, we assume

$$\displaystyle{ \mathit{NPV }_{i}(b_{i}) = 10^{6} \cdot \ln b_{ i}\quad \text{and}\quad \widehat{\mathit{NPV }}_{i}(b_{i}) = e_{i} \cdot \ln b_{i}\,. }$$

(31)

Accordingly, $\widehat{\mathit{NPV }}_{i}(b_{i})$ is distorted if e _i ≠ 10⁶. Central management maximizes $\widehat{\mathit{NPV }}_{1}(b_{1}) +\widehat{ \mathit{NPV }}_{2}(b_{2})$ subject to b ₁ + b ₂ = B. Maximizing the Lagrangian

$$\displaystyle{ \mathcal{L}(b_{i},b_{j},\lambda ) = e_{i} \cdot \ln b_{i} + e_{j} \cdot \ln b_{j} -\lambda \cdot (b_{i} + b_{j} - B) }$$

(32)

with respect to b _i immediately yields

$$\displaystyle{ \frac{e_{i}} {b_{i}} =\lambda \,. }$$

(33)

Taking into account b _i + b _j = B, (33) implies

$$\displaystyle{ \frac{e_{i} + e_{j}} {\lambda } = B\;\Longleftrightarrow\;\lambda = \frac{e_{i} + e_{j}} {B} \Rightarrow b_{i}^{{\ast}} = \frac{B} {e_{i} + e_{j}} \cdot e_{i}\,. }$$

(34)

Divisional manager i maximizes

$$\displaystyle{ \begin{array}{r@{\,\,}c@{\,\,}l} 10^{6} \cdot \ln b_{i}^{{\ast}} + e_{j} \cdot \ln b_{j}^{{\ast}}\,\,& =\,\,&(10^{6} + e_{j}) \cdot \ln \frac{B} {e_{i}+e_{j}} + 10^{6} \cdot \ln e_{i} + e_{j} \cdot \ln e_{j} \\ \,\,& =\,\,&(10^{6} + e_{j}) \cdot [\ln B -\ln (e_{i} + e_{j})] + 10^{6} \cdot \ln e_{i} + e_{j} \cdot \ln e_{j} \end{array} }$$

(35)

with respect to e _i . Evaluating the first-order condition

$$\displaystyle{ -\frac{10^{6} + e_{j}} {e_{i} + e_{j}} + \frac{10^{6}} {e_{i}} = 0 }$$

(36)

immediately yields the prospect solution e _i = 10⁶. A more detailed analysis of the function (35) reveals that it is indeed maximized by e _i = 10⁶ and that this solution is unique. Hence, it is optimal to report the truth regardless of e _j , i.e. no matter what the other manager reports. Truthful reporting is thus a dominant strategy of divisional manager i. Since this applies to both divisional managers, pursuing these strategies establishes a dominant strategy equilibrium in the game played by the divisional managers, providing a substantially more stable solution than an ‘ordinary’ Nash equilibrium. Then, both divisions will be equipped with an investment budget amounting to b _i ^∗ = 0. 5B and the company’s net present value will be 2 ⋅ 10⁶ ⋅ ln(0. 5 ⋅ 10⁸) = 35, 455, 067 ≈ 35. 46 million €. □

Granted all divisional managers possess the mental capacities to grasp this rather sophisticated mechanism, the evaluation measures for all managers’ remunerations will be the same, namely NPV ₁(b ₁ ^∗) + … + NPV _n (b _n ^∗). Its precise value is, however, unknown until date t = T, the planning horizon. As interim payments are needed in practice, implementing such schemes induces great challenges for accounting: The evaluation measures are relevant at the time of reporting. On the other hand, according to the Preinreich/Lücke Theorem 5.2, net present value NPV and the stream of residual incomes RI ₁, …, RI _T are equivalent. Insofar, evaluation measure and residual income RI _t (with respect to all projects) are identical in period t. In the case of rolling application, accounting has to determine RI _t for each new project. This is, of course, a rather involved task. On the other hand, no applicable dynamic version of the Groves mechanism is known until now.

5 Conclusion

We conclude gathering some critical remarks on the approaches presented above. First, as already indicated, mechanisms like the Groves scheme require rather pronounced mental capacities on the side of the managers in order to work properly. If managers fail to comprehend the mechanism, ‘good solutions’ (i.e. goal congruence, truthful reporting etc.) cannot be guaranteed. This is, of course, a problem inherent to all incentive mechanisms.

Another potential obstacle when implementing incentive mechanisms like the ones studied here are their premises. Almost all rely on restrictive assumptions like risk neutrality or even absence of risk, which are hardly fulfilled in practise. As soon as risk-aversion is taken into account, mechanisms based on risk neutrality fail to work properly. In addition to that, the hard to tackle task of measuring the risk attitudes (especially of the managers) arises.

Regarding the discount factor, we have tacitly assumed the same constant and uniform value for company and managers. If the manager uses a different discount factor, the problem of determination arises again. Furthermore, the Preinreich/Lücke Theorem cannot be adopted anymore.

Finally, let us note that the Reichelstein/Rogerson solution relies on rather specific depreciation factors d _t (cf. also the explicit formulae in the Appendix, section “Proof of Property 5.1”). These factors do not resemble common depreciation methods like straight-line or annuity depreciation and, hence, may disturb in practice. From a financial accounting and tax perspective, such modes of depreciation will almost surely violate national commercial or tax law.

Appendix

1.1 Proof of Theorem5.1

Proof

‘ ⇒ ’: Assume (2) holds true. Since this condition covers all possible cash flow streams, it also applies to non-stochastic streams x. Therefore, CE(x + z) needs to be independent of the specific value of z. In particular, it is allowed to determine z so that all components of x + z except the first one, x ₀ − z ₀, are set to zero, i.e. z _t = (−x _t+1 + z _t+1) ⋅ γ for all t = 0, 1, …, T − 1.

Following the recursion

$$\displaystyle{ \begin{array}{l@{\,\,}c@{\,\,}l@{\,\,}c@{\,\,}l} z_{T-1}\,\,& =\,\,& - x_{T}\cdot \gamma \,\, \\ z_{T-2}\,\,& =\,\,& - (-x_{T-1} + z_{T-1})\cdot \gamma \,\,& =\,\,& - x_{T-1} \cdot \gamma -x_{T} \cdot \gamma \,^{2} \\ z_{T-3}\,\,& =\,\,& - (-x_{T-2} + z_{T-2})\cdot \gamma \,\,& =\,\,& - x_{T-2} \cdot \gamma -x_{T-1} \cdot \gamma \,^{2} - x_{T} \cdot \gamma \,^{3}\\ \,\, & \,\, &\ldots \\ z_{0} \,\,& =\,\,& - (-x_{1} + z_{1})\cdot \gamma \,\,& =\,\,& - x_{1} \cdot \gamma -x_{2} \cdot \gamma \,^{2}\cdots - x_{T} \cdot \gamma \,^{T} \end{array} }$$

(37)

one arrives at x ₀ − z ₀ = NPV (x). Therefore, the certainty equivalents CE(x + z) and CE(NPV (x), 0, …, 0) coincide. Assuming (2) holds true, this implies CE(x) = CE(NPV (x), 0, …, 0), stating the indifference x ∼ (NPV (x), 0, …, 0). Since x is non-stochastic, the structure asserted in (3) follows immediately.

‘ ⇐ ’: Assume the structure asserted in (3) applies to the multiattributive utility function . Then, the date 0 certainty equivalent CE(c + z) is implicitly given by

$$\displaystyle{ \begin{array}{l@{\,\,}c@{\,\,}l} u(\mathit{CE}(\mathbf{c} + \mathbf{z}),0,\ldots,0)\,\,& =\,\,&\mathrm{E}u(\mathbf{c} + \mathbf{z}) =\mathrm{ E}u(\mathit{NPV }(\mathbf{c} + \mathbf{z}),0,\ldots,0) \\ \,\,& =\,\,&\mathrm{E}u(\mathit{NPV }(\mathbf{c}) + \mathit{NPV }(\mathbf{z}),0,\ldots,0)\,. \end{array} }$$

(38)

Since

$$\displaystyle\begin{array}{rcl} \mathit{NPV }(\mathbf{z})& =& -z_{0} + \frac{qz_{0} - z_{1}} {q} + \frac{qz_{1} - z_{2}} {q^{2}} +\ldots +\frac{qz_{T-2} - z_{T-1}} {q^{T-1}} + \frac{qz_{T-1}} {q^{T}} \\ & =& -z_{0} + z_{0} -\frac{z_{1}} {q} + \frac{z_{1}} {q} -\frac{z_{2}} {q^{2}} + \cdots + \frac{z_{T-2}} {q^{T-2}} -\frac{z_{T-1}} {q^{T-1}} + \frac{z_{T-1}} {q^{T-1}} = 0\;,\quad \quad {}\end{array}$$

(39)

CE(c + z) does not depend on z and, hence, condition (2) is fulfilled. □

1.2 Proof of Theorem5.2

Proof

Evaluating the shift in equity capital from period t − 1 to period t, EC _t − EC _t−1, one immediately arrives at

$$\displaystyle{ \mathit{EC}_{t} -\mathit{EC}_{t-1} = \mathit{NI}_{t} - c_{t}\;\Longleftrightarrow\;\mathit{NI}_{t} = c_{t} + \mathit{EC}_{t} -\mathit{EC}_{t-1}\,. }$$

(40)

Hence, the sum of discounted residual incomes can be written as

$$\displaystyle{ \begin{array}{@{}r@{\,\,}c@{\,\,}l@{}} \sum _{t=0}^{T}\mathit{RI}_{ t} \cdot \gamma \,^{t}\,\,& =\,\,&\sum _{ t=0}^{T}(c_{ t} + \mathit{EC}_{t} -\mathit{EC}_{t-1} - r \cdot \mathit{EC}_{t-1}) \cdot \gamma \,^{t} \\ \,\,& =\,\,&\sum _{t=0}^{T}c_{ t} \cdot \gamma \,^{t} +\sum _{ t=0}^{T}\mathit{EC}_{ t} \cdot \gamma \,^{t} -\sum _{ t=0}^{T}q\mathit{EC}_{ t-1} \cdot \gamma \,^{t} \\ \,\,& =\,\,&\sum _{t=0}^{T}c_{ t} \cdot \gamma \,^{t} +\sum _{ t=0}^{T}\mathit{EC}_{ t} \cdot \gamma \,^{t} -\sum _{ t=0}^{T}\mathit{EC}_{ t-1} \cdot \gamma \,^{t-1} \\ \,\,& =\,\,&\sum _{t=0}^{T}c_{ t} \cdot \gamma \,^{t} + \mathit{EC}_{ T} \cdot \gamma \,^{T}. \end{array} }$$

(41)

Taking RI ₀ = EC _T = 0 into account, (5) follows immediately. □

1.3 Proof of Property 5.1

Proof

Resolving the recursion, one arrives at

$$\displaystyle{ d_{t} =\zeta ^{-1}\cdot \bigg[c_{ t}+\sum _{j=1}^{t-1}c_{ j}\cdot \sum _{i=1}^{t-j}\Big(\begin{array}{@{}c@{}} t - j - 1 \\ i - 1 \end{array} \Big)\cdot r^{i}\bigg]-\sum _{ i=1}^{t}\Big(\begin{array}{@{}c@{}} t - 1 \\ i - 1 \end{array} \Big)\cdot r^{i}\,, }$$

(42)

where

$$\displaystyle{ \zeta =\sum _{ j=1}^{T}c_{ j} \cdot \gamma \,^{j}\,. }$$

(43)

Please note

$$\displaystyle{ \sum _{i=1}^{t-j}\Big(\begin{array}{@{}c@{}} t - j - 1 \\ i - 1 \end{array} \Big)\cdot r^{i} = r\cdot (1+r)^{t-j-1} = (1-\gamma )\cdot \gamma \,^{j-t} }$$

(44)

and

$$\displaystyle{ \sum _{i=1}^{t}\Big(\begin{array}{@{}c@{}} t - 1 \\ i - 1 \end{array} \Big)\cdot r^{i} = r\cdot (1+r)^{t-1} = (1-\gamma )\cdot \gamma \,^{-t}\,. }$$

(45)

Hence, (42) can be rewritten as follows

$$\displaystyle{ \begin{array}{@{}r@{\,\,}c@{\,\,}l@{}} d_{t}\,\,& =\,\,&\zeta ^{-1}\bigg[c_{ t} - (1-\gamma ) \cdot \gamma \,^{-t} \cdot \zeta +(1-\gamma ) \cdot \sum _{ j=1}^{t-1}c_{ j} \cdot \gamma \,^{j-t}\bigg] \\ \,\,& =\,\,&\zeta ^{-1}\bigg[\gamma \cdot c_{ t} - (1-\gamma ) \cdot \gamma \,^{-t} \cdot \zeta +(1-\gamma ) \cdot \sum _{ j=1}^{t}c_{ j} \cdot \gamma \,^{j-t}\bigg]\,. \end{array} }$$

(46)

We are now able to evaluate the sum

$$\displaystyle\begin{array}{rcl} \sum _{t=1}^{T}d_{ t}& =& \zeta ^{-1} \cdot \bigg [\gamma \cdot \sum _{ t=1}^{T}c_{ t} - (1-\gamma ) \cdot \zeta \cdot \sum _{t=1}^{T}\gamma ^{-t} + (1-\gamma ) \cdot \sum _{ t=1}^{T}\sum _{ j=1}^{t}c_{ j} \cdot \gamma \,^{j-t}\bigg] \\ & =& \zeta ^{-1} \cdot \bigg [\gamma \cdot \sum _{ t=1}^{T}c_{ t} + (1 -\gamma ^{-T}) \cdot \zeta +(1-\gamma ) \cdot \sum _{ t=1}^{T}\sum _{ j=1}^{t}c_{ j} \cdot \gamma \,^{j-t}\bigg] \\ & =& 1 +\zeta ^{-1} \cdot \bigg [\sum _{ t=1}^{T}c_{ t} \cdot (\gamma -\gamma \,^{t-T}) + (1-\gamma ) \cdot \sum _{ t=1}^{T}\sum _{ j=1}^{t}c_{ j} \cdot \gamma \,^{j-t}\bigg]\,. {}\end{array}$$

(47)

In order to prove d ₁ + … + d _T = 1 it is sufficient to verify that the term in square brackets is equal to zero. Since

$$\displaystyle{ \sum _{t=1}^{T}\sum _{ j=1}^{t}c_{ j} \cdot \gamma ^{j-t} =\sum _{ t=1}^{T}c_{ t} \cdot \sum _{j=0}^{T-t}\gamma ^{-j} =\sum _{ t=1}^{T}c_{ t} \cdot \frac{\gamma \,^{t-T}-\gamma } {1-\gamma } }$$

(48)

this is in fact the case. □

1.4 Proof of Theorem5.3

Proof

Since

$$\displaystyle\begin{array}{rcl} \sum _{t=1}^{\tau }\mathit{RI}_{ t} \cdot \gamma \,^{t}& =& \sum _{ t=1}^{\tau }\bigg[c_{ t} + d_{t} \cdot c_{0} + r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\bigg] \cdot \gamma \,^{t} \\ & =& \sum _{t=1}^{\tau }\Bigg[c_{ t} +\mathop{\underbrace{ c_{0} \cdot \frac{c_{t}} {\sum \limits _{j=1}^{T}c_{j}\cdot \gamma ^{j}} - r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{j}\bigg)}}\limits _{=d_{t}\cdot c_{0}} + r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\Bigg] \cdot \gamma \,^{t} \\ & =& \sum _{t=1}^{\tau }\Bigg[c_{ t} + c_{0} \cdot \frac{c_{t}} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma ^{j}}\Bigg] \cdot \gamma \,^{t} =\sum _{ t=1}^{\tau }\Bigg[1 + \frac{c_{0}} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma ^{j}}\Bigg] \cdot c_{t} \cdot \gamma \,^{t} \\ & =& \frac{1} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma ^{j}} \cdot \sum _{t=1}^{\tau }\Bigg[c_{ 0} +\sum _{ j=1}^{T}c_{ j} \cdot \gamma ^{j}\Bigg] \cdot c_{ t} \cdot \gamma \,^{t} = \frac{\sum \limits _{t=1}^{\tau }c_{ t} \cdot \gamma \,^{t}} {\sum \limits _{j=1}^{T}c_{j} \cdot \gamma ^{j}} \cdot \mathit{NPV }\,, {}\end{array}$$

(49)

manager’s present value of remuneration and the investment project’s NPV have the same sign as long as c ₁ > 0, …, c _T > 0. The latter is ensured when condition (18) is met. □

1.5 Proof of Theorem5.4

Proof

Since

$$\displaystyle\begin{array}{rcl} \mathrm{E}\bigg(\sum _{t=1}^{\tau }\mathit{RI}_{ t} \cdot \gamma \,^{t}\bigg)& =& \sum _{ t=1}^{\tau }\mathrm{E}(\mathit{RI}_{ t}) \cdot \gamma \,^{t} =\sum _{ t=1}^{\tau }\mathrm{E}\bigg[c_{ t} + d_{t} \cdot c_{0} + r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\bigg] \cdot \gamma \,^{t} \\ & =& \sum _{t=1}^{\tau }\mathrm{E}\Bigg[c_{ t} +\mathop{\underbrace{ c_{0} \cdot \frac{\mathrm{E}(c_{t})} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j})\cdot \gamma ^{j}} - r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{j}\bigg)}}\limits _{=d_{t}\cdot c_{0}} + r \cdot c_{0} \cdot \bigg (1 -\sum _{j=1}^{t-1}d_{ j}\bigg)\Bigg] \cdot \gamma \,^{t} \\ & =& \sum _{t=1}^{\tau }\mathrm{E}\Bigg[c_{ t} + c_{0} \cdot \frac{\mathrm{E}(c_{t})} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j}) \cdot \gamma ^{j}}\Bigg] \cdot \gamma \,^{t} =\sum _{ t=1}^{\tau }\Bigg[1 + \frac{c_{0}} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j}) \cdot \gamma ^{j}}\Bigg] \cdot \mathrm{ E}(c_{t}) \cdot \gamma \,^{t} \\ & =& \frac{1} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j}) \cdot \gamma ^{j}} \cdot \sum _{t=1}^{\tau }\Bigg[c_{ 0} +\sum _{ j=1}^{T}\mathrm{E}(c_{ j}) \cdot \gamma ^{j}\Bigg] \cdot \mathrm{ E}(c_{ t}) \cdot \gamma \,^{t} \\ & =& \frac{\sum \limits _{t=1}^{\tau }\mathrm{E}(c_{t}) \cdot \gamma \,^{t}} {\sum \limits _{j=1}^{T}\mathrm{E}(c_{j}) \cdot \gamma ^{j}} \cdot \mathrm{ E}(\mathit{NPV })\,, {}\end{array}$$

(50)

manager’s expected present value of remuneration and the investment project’s expected NPV have the same sign as long as E(c ₁) > 0, …, E(c _T ) > 0. The latter is ensured when condition (20) is met. □