Abstract
Polytopic cryptanalysis was introduced at EUROCRYPT 2016 as a cryptanalytic technique for low-data-complexity attacks on block ciphers. In this paper, we give an account of how the technique was developed, quickly go over the basic ideas and techniques of polytopic cryptanalysis, look into how the technique differs from previously existing cryptographic techniques, and discuss whether the attack angle can be useful for developing improved cryptanalytic techniques.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
A few years after differential cryptanalysis [2] had been developed and successfully applied to a range of ciphers, Xuejia Lai realized that differential cryptanalysis can be generalized to higher-order differential cryptanalysis using the concept of higher-order derivatives [7]. He was not able though to give an example that demonstrates that higher-order differential attacks can be stronger than standard differential attacks. Such an example was given shortly thereafter by Knudsen [5] who broke a design proven to be secure against differential cryptanalysis.
Since and including that attack, successful applications of higher-order differential cryptanalysis have been relying on deterministic higher-order differentials, i.e., higher-order differentials of probability one. Those attacks can be put into two main categories. In the first category, upper bounds on the degree of the cipher are derived which can then be used to find higher-order derivatives that evaluate to zero. In the second category, methods of integral cryptanalysis are used to determine that for some combination of input bits, there are no terms in the polynomial representation of the output that contain all of those bits simultaneously. Such property again results in higher-order derivatives that evaluate to zero simply by taking the derivative with respect to those input bits.
The problem of working with probabilistic higher-order differentials seems to be the difficulty to estimate the probability of probabilistic differentials efficiently. While it is usually easy to derive the probability of a higher-order differential over one round, there is no straightforward method to iterate these probabilities to estimate the probability of a multiple-round higher-order differential. In particular the concept of a trail (or characteristic) does not seem to exist for higher-order differentials.
In this paper, we demonstrate how attempting to construct trails for higher-order differentials leads to polytopic trails in a natural progression. We then quickly draw an outline of how the polytopic framework is a direct generalization of the differential cryptanalysis framework that includes higher-order differential cryptanalysis as a special case.
We subsequently show that attempts to apply this framework in the setting that corresponds to standard differential cryptanalysis cannot yield better results than standard differential cryptanalysis due to a large increase in the number of trails that need to be considered. We continue then by demonstrating that the upside to the increase in the number of trails is that impossible polytopic attacks can be successful where standard impossible differential attacks fail. By following this progression, we follow the development process that lead to the low-data attacks detailed in the EUROCRYPT 2016 paper [9].
The paper concludes with a comparison of polytopic cryptanalysis with existing cryptanalytic techniques, a discussion of future research directions and open problems.
2 Difficulties of Higher-Order Differentials
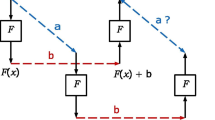
In differential cryptanalysis, the goal is to find a strong correlation between the difference of two input messages to a cipher and the difference of the respective output messages of the cipher. When we let E be the cipher and \(\alpha \) and \(\beta \) be the input and output differences, we are hoping to find many x such that \(E(x+\alpha )+E(x) = \beta \). We denote the difference operation here by a \(+\) sign as we assume we are working with binary values where addition and subtraction correspond to the same operation.Footnote 1 A differential is then defined as a pair of an input difference \(\alpha \) and an output difference \(\beta \) and the associated probability \(\Pr _{\mathbf {X}}\left( E(\mathbf {X} + \alpha ) + E(\mathbf {X}) = \beta \right) \) where \(\mathbf {X}\) is uniformly distributed over the messages.
Lai [7] realized that by writing the output difference as a derivative, we arrive at a formalism that leads to higher-order differentials. First we define the derivative of E at x in the direction \(\alpha \) as:
This discrete derivative shares many of the properties of continuous derivatives over the real numbers: both are additive, commutative, and reduce the degree of the function they are applied to by at least 1. The discrete derivative furthermore features a variant of the product rule (see [7] for details).
Using this derivative, we can now define a higher-order derivative as a concatenation of discrete derivatives as defined above and evaluate it as follows:
where \(\mathcal {L}(\alpha _1, \dots , \alpha _d)\) is the linear space spanned by \(\alpha _1, \dots , \alpha _d\). In this definition it is assumed we have the more interesting case where \(\alpha _1, \dots , \alpha _d\) are linearly independent as the higher-order derivative always evaluates to zero if they are not.
Similarly to the simple derivative used in standard differential cryptanalysis, we can try to find input differences and output differences that show a strong correlation in the higher-order derivative, i.e., we can try to find a set of input differences \(\alpha _1, \dots , \alpha _d\) and an output difference \(\beta \) such that \(\varDelta _{\alpha _1, \dots , \alpha _d} E(x) = \beta \) for as many x as possible. A higher-order differential of order d is then defined as a set of input differences \(\alpha _1, \dots , \alpha _d\) and an output value \(\beta \) with the associated probability \(\Pr _{\mathbf {X}}\left( \varDelta _{\alpha _1, \dots , \alpha _d} E(\mathbf {X}) = \beta \right) \) where \(\mathbf {X}\) is again uniformly distributed over the messages.
There are two problems that we encounter when trying to find such combinations of input differences and output values, and these problems already exist in the case of standard differential cryptanalysis. Firstly, it would be computationally too expensive to evaluate the derivative at all possible values x. Secondly, in applications of differential cryptanalysis the function E is a cipher which is a function parametrized by a key unknown to the attacker, so it will not even be possible to take the exact derivative without knowledge of the key.
In standard differential cryptanalysis, both of these difficulties can be overcome by utilizing the following approach. The cipher is split into a sequence of rounds (luckily most ciphers are round-based anyhow) where each round by itself does not depend on the key and the key is only applied in between rounds. For each round it is then usually easy to determine the probability that an input pair with a given difference is mapped to a given output difference. The trick is now to approximate the probability that an input pair follows a trail of intermediate differences as the product of the probabilities of each round transition. By summing these approximation for all possible trails, we arrive at an approximation for the probability that the input difference is mapped to the output difference irregardless of the differences taken in between rounds, the probability of the differential.
While this approach is an approximation at best and can fail in certain circumstances (see for example [4]), it has proven extremely useful in the practical cryptanalysis of ciphers. It allows us often to efficiently approximate the probability of differentials (i.e., the probability that a given input difference is mapped to a given output difference) by summing only those trails that contribute significantly to its probability. For a discussion of the theoretical framework for this, we refer to [8].
Why does this approach fail when we try to apply it to higher-order differentials? Unlike a standard differential which has exactly one input difference and one output difference, a higher-order differential is taken with respect to a basis of differences (or vectors). But its output is a single value: the sum of the output messages. If we now try to iterate such a higher-order differential, we run into the problem of identifying the output value of one rounds with the set of input differences for the next rounds, or more precisely with the problem of identifying it with the space that is spanned by those basis vectors.
A first guess how to associate the output value with an input space might be to assume it is uniformly randomly chosen from all spaces of the right dimension that sum to the value. But clearly this does not work as all spaces sum to zero, so we cannot associate non-zero output values with a linear (or affine) space.
Ignoring the fact that the messages are summed at the end of a higher-order derivative and trying to work with affine subspaces as a good representation of intermediate states fails similarly: the messages will generally be in arbitrary position to each other after the first round. Thus to adequately represent the intermediate states of a higher-order differential we need to allow the messages to be in arbitrary position to each other.
Before we look into constructing trails where the states are sets of messages in arbitrary position (which is exactly what polytopic trails are), let us mention the two methods which are used to successfully evaluate higher-order differentials despite the lack of trails for them. The first one is using degree arguments. As a higher-order derivative of order d reduces the algebraic degree of function by at least d, we can determine that certain higher-order derivatives have to evaluate to zero by finding sufficient lower bounds for the degree of the cipher. The other method uses structural properties of the cipher to determine that certain terms will not be present in the algebraic representation of the cipher which again determines some higher-order derivatives to evaluate to zero (see for example [6, 10]).
3 Overview over the Polytopic Framework
To be able to accurately describe the set of values in between the rounds of the cipher which we are taking the derivative over we need to describe them as what they are, tuples of points in the state space. We will call such a tuple a polytope.
In this way, we can describe the higher-order derivative as a polytope that consists of the values in the input space which is then transformed to other polytopes while traversing the rounds and finally reduced from a polytope to a single value by summing all values contained in the polytope.
We can reduce the information that we need to describe polytopes in this usage scenario by disregarding the absolute position of the messages in the state space and only caring about their relative positions. Thus we will regard two tuples of messages that can be translated to each other by shifting in the state space as equivalent. The relative positions of the messages to each other are entirely determined by picking one message as an anchor and specifying the position of all other messages in the polytope with respect to this anchor message. We can thus reduce the number of values needed to describe the polytope by one.
Such a description of a polytope is called a d-difference where d specifies the number of differences needed to specify all relative positions, i.e., d is one lower than the number of values in the polytope. Thus for example for a pair of values, we only need one difference to describe the pair when disregarding the absolute position in state space as we know well from standard differential cryptanalysis. For a set of four messages we would then need a tuple of 3 differences, the differences of message 2, 3 and 4 with regard to the first message.
When we want to know the probability that a polytope with a given input d-difference is mapped to a polytope with a given output d-difference, we encounter the same two problems that we had in standard differential cryptanalysis. Luckily now, we can apply the same methodology to counter this. The probability of a trail of d-differences is determined as the product of the round transition probabilities, the probability of a transition over the whole cipher with fixed input and output d-differences is determined as the sum of all trails that have exactly those input and output d-differences. The analogy to a differential in standard differential cryptanalysis is a polytopic transition where we fix only the input and output d-differences but not the intermediate ones. For a rigorous description of this framework, we refer to the EUROCRYPT paper.
Let us go back to the problem of finding trails for higher-order differentials. The input to a higher-order differential uniquely corresponds to a d-difference. The output does not correspond to a single d-difference but to the set of all d-differences that sum to this output value. We can thus now describe the probability of the higher-order differential as the sum of all polytopic transitions where the input d-difference corresponds to the input to the higher-order differential and where the output d-difference sums to the output value of the higher-order differential. We can thus principally determine the probability of a higher-order differential using the same methodology that we use for standard differentials: we sum the probability of all trails that correspond to the transitions.
Can this approach be used to successfully determine the probability of higher-order differentials in practice? Unfortunately, as it turns out, this does generally not seem to be the case. The underlying problem is that the probability of polytopic trails is usually much lower than the probability of trails in differential cryptanalysis. The probabilities are so low that it is not possible to determine a good lower bound for the probability of a polytopic transition by simply summing the probabilities of trails. And thus it is not possible to practically determine a lower bound for the probability of higher-order differentials in typical cryptanalytic cases.
The fact that the probabilities of polytopic trails are so low not only makes determination of the probabilities of higher-order differentials impractical, it also make polytopic transitions uninteresting as a substitute for standard differential attacks: for any polytopic transition there exists a differential of at least the same probability. While this restricts usage of polytopic cryptanalysis in the standard setting, we will see in the next section that the framework nonetheless has practical applications.
4 Impossible Polytopic Transitions
The setting where polytopic transitions turn out to be useful is the setting where we consider transitions of probability zero: impossible transitions. The central property that determines the quality of an impossible transition attack is the ratio of impossible transitions to possible transitions, i.e., to transitions of probability strictly greater than one. While using polytopic transitions in the standard attack setting is not particularly useful due to the increased diffusion of the d-differences, in the impossible setting the diffusion is countered by an exponential increase in the total number of transitions causing the ratio of impossible to possible transitions to shift in the favor of the impossible transitions.
When we describe a polytope consisting of \(d+1\) messages as a d-difference, we increase the state size, i.e., the number of possible d-differences by an exponent of d in comparison to the possible number of single differences. At the same time, the diffusion will increase by at most a constant factor. This allow us to choose the number d sufficiently large to ensure a favorable ratio of impossible to possible transitions: by increasing d we can make the ratio of possible to impossible transitions arbitrarily small.
While this principally would allow for excellent attacks, the problem now lies elsewhere: how can we efficiently tell possible from impossible transitions? The most obvious and straightforward way is to exhaustively compute a set of all reachable d-differences and use this set to distinguish possible from impossible transitions. To reduce both the memory and computational cost needed for this, a meet-in-the-middle approach can be employed. In this approach, two sets of reachable d-differences in the middle of the cipher are determined while coming from both ends of the cipher. When depending on whether or not a collision in these two sets is found, the transition is determined to be possible or impossible. This is the approach that has been used in the EUROCRYPT paper.
A more efficient way of determining the possibility of transitions is to use structural properties of the cipher to find large enough sets of impossible transitions. For standard impossible differential attacks a very successful method is the so-called miss-in-the-middle approach [1] which directly constructs a sufficiently large set of impossible differentials. An alternative approach could be to use structural properties of the cipher to determine a sufficiently small, efficiently testable super-set of all possible transitions, again indirectly giving us a large set of impossible transitions. As we demonstrated, higher-order differentials correspond to a particular collection of polytopic transitions. And indeed, those methods that use structural properties of the cipher to determine deterministic higher-order differentials can be equivalently seen as methods that efficiently determine properties of reachable output d-differences, thus specifying a super-set of all possible polytopic transitions. The standard implementation of higher-order differential attacks using structural properties of the cipher to determine non-probabilistic higher-order differentials can thus be seen as particular versions of impossible polytopic transition attacks. Apart from these attack types, it remains an open question though how structural properties of a cipher can determine such a superset when the polytopic transition does not correspond to a higher-order differential.
5 Comparison to Other Attack Vectors
There already exists a larger repertoire of attack vectors that can be wielded against ciphers. How does polyptopic cryptanalysis differ from those attack vectors? Is it just an existing attack vector in disguise?
A property that sets polytopic cryptanalysis apart from differential and linear cryptanalysis is an increased use of the correlation between different input messages and output messages. In linear cryptanalysis, correlation is only measured on the input message and the corresponding output message. In differential cryptanalysis, we measure only the correlation between two input messages and there corresponding outputs. In polytopic cryptanalysis though by considering the correlations between inputs and outputs of larger tuples, we make better use of the data that we use. This is what essentially allows the impossible polytopic attacks of [9] to have such a low data-complexity.
We already saw that polytopic cryptanalysis can be seen as an extension to the differential cryptanalysis framework sufficiently general to include higher-order differentials. To demonstrate how impossible polytopic attacks differ from differential attacks and other attack vectors, let us consider the following constructed toy cipher. Our cipher has an 8-bit block size and a round that consists of an application of the Rijndael S-box (see [3]) to the state, followed by the XOR-addition of a round key. All round keys are independent and before the first round, a whitening key is added to the input message.
Let us assume that the cipher has sixteen rounds and that our goal is a key recovery attack. Since the Rijndael S-box achieves excellent diffusion, differential and linear attack are easily be thwarted. This includes impossible differential attack as only two rounds are needed to achieve full diffusion and thus impossible differentials seize so exist after only the first few rounds. This is not true though for impossible polytopic transitions if we choose d sufficiently large.
For any d, after r rounds there are at most \(2^{8\cdot r}\) reachable d-differences out of a total of \(2^{d\cdot 8}\) d-differences. Thus if we set d for example to 9, we can guarantee that after eight rounds, only a fraction of 1 over 256 d-differences is reachable. If we thus guess the last eight round keys and decrypt the last eight rounds, we can filter out 255 out of 256 key guesses using only a set of 10 texts. As we can precompute the list of reachable d-differences at a time cost of \(2^{8\cdot 8}\) and an equivalent memory cost, the total time complexity also corresponds to this value.
From the description of this attack, it is clear that the closest related attack is a meet-in-the-middle attack. And indeed impossible polytopic attacks can be seen as a meet-in-the-middle attack where the collision is not found on the state itself, but rather on the d-difference.
6 Discussion
We started out by finding a way to construct trails for higher-order differentials in the hope to be able to determine the probability of probabilistic higher-order differentials efficiently. While we succeeded with the former by constructing polytopic trails and transitions, we failed with the latter. Interestingly though the construction of the polytopic framework did not turn out to be a theoretical dead-end but proved useful when applied to probability zero transitions, impossible transitions.
The attacks that were enabled by this framework (as published in [9] were nonetheless of a somewhat restricted nature: low-data attack on few rounds. Whether or not polytopic cryptanalysis can be applied in a broader collection of attack scenarios depends on an number of open issues:
-
Is it possible to use structural properties of ciphers to efficiently determine the possibility of a given polytopic transition? This excludes of course simple relabeling of the existing techniques of deterministic higher-order differentials. If such techniques exist they could be used to circumvent the restrictions of polytopic attacks to few rounds currently imposed by the strong diffusion and growth of the number of reachable d-differences.
-
Are there attack scenarios where determining the probability of higher-order differentials using the representation as a collection of polytopic trails proves sufficiently efficient to be useful in an attack? Are there more effective methods of determining this probability that avoid iterating through the list of polytopic trails (potentially using structural properties)?
-
Are there other efficient attack vectors that make use of the correlation between larger tuples of texts than pairs? Or are there alternatively strong theoretical arguments why efficient attacks are restricted to using single texts or pairs (such as in linear and differential cryptanalysis)?
We hope that this brief article might serve as an example of how sometimes formalizations that do not directly lead in the direction that one initially hopes for can still prove valuable when we switch the setting. Potentially some ideas may serve someone as an inspiration to derive improved, prospective attack vectors on symmetric ciphers.
Notes
- 1.
To be precise, we assume here that \(\alpha , x\in {{\mathrm{\mathbb {F}}}}_2^n\), \(\beta \in {{\mathrm{\mathbb {F}}}}_2^m\), and \(E:{{\mathrm{\mathbb {F}}}}_2^n\rightarrow {{\mathrm{\mathbb {F}}}}_2^m\).
References
Biham, E., Biryukov, A., Shamir, A.: Cryptanalysis of Skipjack reduced to 31 rounds using impossible differentials. J. Cryptol. 18(4), 291–311 (2005)
Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 4(1), 3–72 (1991)
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography. Springer, Heidelberg (2002)
Daemen, J., Rijmen, V.: Plateau characteristics. IET Inf. Secur. 1(1), 11–17 (2007)
Knudsen, L.R.: Truncated and higher order differentials. In: Preneel, B. (ed.) FSE 1994. LNCS, vol. 1008, pp. 196–211. Springer, Heidelberg (1995). doi:10.1007/3-540-60590-8_16
Knudsen, L., Wagner, D.: Integral cryptanalysis. In: Daemen, J., Rijmen, V. (eds.) FSE 2002. LNCS, vol. 2365, pp. 112–127. Springer, Heidelberg (2002). doi:10.1007/3-540-45661-9_9
Lai, X.: Higher order derivatives and differential cryptanalysis. In: Blahut, R.E., Costello, D.J., Maurer, U., Mittelholzer, T. (eds.) Communications and Cryptography, Two Sides of One Tapestry, pp. 227–233. Kluwer Academic Publishers, Berlin (1994). doi:10.1007/978-1-4615-2694-0_23
Lai, X., Massey, J.L., Murphy, S.: Markov ciphers and differential cryptanalysis. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 17–38. Springer, Heidelberg (1991). doi:10.1007/3-540-46416-6_2
Tiessen, T.: Polytopic cryptanalysis. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 214–239. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_9
Todo, Y.: Structural evaluation by generalized integral property. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 287–314. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_12
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Tiessen, T. (2017). From Higher-Order Differentials to Polytopic Cryptyanalysis. In: Phan, RW., Yung, M. (eds) Paradigms in Cryptology – Mycrypt 2016. Malicious and Exploratory Cryptology. Mycrypt 2016. Lecture Notes in Computer Science(), vol 10311. Springer, Cham. https://doi.org/10.1007/978-3-319-61273-7_29
Download citation
DOI: https://doi.org/10.1007/978-3-319-61273-7_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-61272-0
Online ISBN: 978-3-319-61273-7
eBook Packages: Computer ScienceComputer Science (R0)