Verifying Controllability of Time-Aware Business Processes

Abstract

We present an operational semantics for time-aware business processes, that is, processes modeling the execution of business activities, whose durations are subject to linear constraints over the integers. We assume that some of the durations are controllable, that is, they can be determined by the organization that enacts the process, while others are uncontrollable, that is, they are determined by the external world.

Then, we consider controllability properties, which guarantee the completion of the enactment of the process, satisfying the given duration constraints, independently of the values of the uncontrollable durations. Controllability properties are encoded by quantified reachability formulas, where the reachability predicate is recursively defined by a set of Constrained Horn Clauses (CHCs). These clauses are automatically derived from the operational semantics of the process.

Finally, we present two algorithms for solving the so called weak and strong controllability problems. Our algorithms reduce these problems to the verification of a set of quantified integer constraints, which are simpler than the original quantified reachability formulas, and can effectively be handled by state-of-the-art CHC solvers.

This work has been partially funded by INdAM-GNCS (Italy). E. De Angelis, F. Fioravanti, and A. Pettorossi are research associates at IASI-CNR, Rome, Italy.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A business process model is a procedural, semi-formal specification of the order of execution of the activities in a business process (or BP, for short) and of the way these activities must coordinate to achieve a goal [18, 35]. Many notations for BP modeling, and in particular the popular BPMN [26], allow the modeler to express time constraints, such as deadlines and activity durations. However, time related aspects are neglected when the semantics of a BP model is given through the standard Petri Net formalization [18], which focuses on the control flow only. Thus, formal reasoning about time related properties, which may be very important in many analysis tasks, is not possible in that context.

In order to overcome this difficulty, various approaches to BP modeling with time constraints have been proposed in the literature (see [5] for a recent survey). Some of these approaches define the semantics of time-aware BP models by means of formalisms such as time Petri nets [24], timed automata [33], and process algebras [36]. Properties of these models can then be verified by using very effective reasoning tools available for those formalisms [3, 17, 23].

In this paper we address the problem of verifying the controllability of time-aware business processes. This notion has been introduced in the context of scheduling and planning problems over Temporal Networks [32], but it has not received much attention in the more complex case of time-aware BP models. We assume that some of the durations are controllable, that is, they can be determined by the organization that enacts the process, while others are uncontrollable, that is, they are determined by the external world. Properties like strong controllability and weak controllability guarantee, in different senses, that the process can be completed, satisfying the given duration constraints, for all possible values of the uncontrollable durations. Controllability properties are particularly relevant in scenarios (e.g., healthcare applications [9]) where the completion of a process within a certain deadline must be guaranteed even if the durations of some activities cannot be fully determined in advance.

We propose a method for solving controllability problems by extending a logic-based approach that has been recently proposed for modeling and verifying time-aware business processes [11]. This approach represents both the BP structure and the BP behavior in terms of Constrained Horn Clauses (CHCs) [4], also known as Constraint Logic Programs [19], over Linear Integer Arithmetics. (Here we will use the ‘Constrained Horn Clauses’ term, which is more common in the area of verification.) In our setting, controllability properties can be defined by quantified reachability formulas.

An advantage of the logic-based approach over other approaches is that it allows a seamless integration of the various reasoning tasks needed to analyze business processes from different perspectives. For instance, logic-based techniques can easily perform ontology-related reasoning about the business domain where processes are enacted [29, 34] and reasoning on the manipulation of data objects of an infinite type, such as databases or integers [2, 10, 28]. Moreover, for the various logic-based reasoning tasks, we can make use of very effective tools such as CHC solvers [15] and Constraint Logic Programming systems.

For reasons of simplicity, in this paper we consider business process models where the only time-related elements are constraints over task durations. However, other notions can be modeled by following a similar approach.

The main contributions of this paper are the following. (1) We define an operational semantics of time-aware BP models, which modifies the semantics presented in [11] by formalizing the synchronization of activities at parallel merge gateways and we prove some properties of this new semantics (see Sect. 3). Our semantics is defined under the assumption that the process is safe, that is, during its enactment there are no multiple, concurrent executions of the same task [1]. (2) We provide formal definitions of strong and weak controllability properties as quantified reachability formulas (see Sect. 4). (3) We present a transformation technique for automatically deriving the CHC representation of the reachability relation starting from the CHC encoding of the semantics of time-aware processes, and of the process and property under consideration (see Sect. 4). (4) Finally, we propose two algorithms that solve strong and weak controllability problems for time-aware BPs. These algorithms avoid the direct verification of quantified reachability formulas, which often cannot be handled by state-of-the-art CHC solvers, and they verify, instead, a set of simpler Linear Integer Arithmetic formulas, whose satisfiability can effectively be worked out by the Z3 constraint solver [15] (see Sect. 5). Detailed proofs of the results presented here can be found in a technical report [12].

2 Preliminaries

In this section we recall some basic notions about the constrained Horn clauses (CHCs) and the Business Process Model and Notation (BPMN).

Let $\textit{RelOp}$ be the set $\{=,\ne ,\le ,\ge ,<,>\}$ of predicate symbols denoting the familiar relational operators over the integers. If $p_1$ and $p_2$ are linear polynomials with integer variables and integer coefficients, then $p_1 R\,p_2$, with $R\!\in \!\textit{RelOp}$, is an atomic constraint. A constraint c is either true or false or an atomic constraint or a conjunction or a disjunction of constraints. Thus, constraints are formulas of Linear Integer Arithmetics (LIA). An atom is a formula of the form $p(t_{1},\ldots ,t_{m})$, where p is a predicate symbol not in $\textit{RelOp}$ and $t_{1},\ldots ,t_{m}$ are terms constructed as usual from variables, constants, and function symbols. A constrained Horn clause (or simply, a clause, or a CHC) is an implication of the form $A\leftarrow c, G$ (comma denotes conjunction), where the conclusion (or head) A is either an atom or false, the premise (or body) is the conjunction of a constraint c and a (possibly empty) conjunction G of atoms. The empty conjunction is identified with true. A constrained fact is a clause of the form $A\leftarrow c$, and a fact is a clause whose premise is true. We will write $A\leftarrow \textit{true}$ also as $A\leftarrow$. A clause is ground if no variable occurs in it. A clause $A\leftarrow c, G$ is said to be function-free if no function symbol occurs in (A, G), while arithmetic function symbols may occur in c. For clauses we will use a Prolog-like syntax (in particular, ‘$\_$’ stands for an anonymous variable).

A set S of CHCs is said to be satisfiable if $S\cup \textit{LIA}$ has a model, or equivalently, $S\cup \textit{LIA}\,\not \models \,\textit{false}$. Given two constraints c and d, we write $c \sqsubseteq d$ if $\textit{LIA}\,\models \, \forall (c\rightarrow d)$, where $\forall (F)$ denotes the universal closure of formula F. The projection of a constraint c onto a set X of variables is a new constraint $c'$, with variables in X, which is equivalent, in the domain of rational numbers, to $\exists \textit{Y}. \textit{c}$, where Y is the set of variables occurring in c and not in X. Clearly, $c \sqsubseteq c'$.

A BPMN model of a business process consists of a diagram drawn by using graphical notations representing: (i) flow objects and (ii) sequence flows (also called flows, for short).

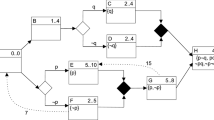
A flow object is: either (i.1) a task, depicted as a rounded rectangle, or (i.2) an event, depicted as a circle, or (i.3) a gateway, depicted as a diamond. A sequence flow is depicted as an arrow connecting a source flow object to a target flow object (see Fig. 1).

Tasks are atomic units of work performed during the enactment (or execution) of the business process. An events is either a start event or an end event, which denote the beginning and the completion, respectively, of the activities of the process. Gateways denote the branching or the merging of activities. In this paper we consider the following four kinds of gateways: (a) the parallel branch, that simultaneously activates all the outgoing flows, if its single incoming flow is activated (see g1 in Fig. 1), (b) the exclusive branch, that (non-deterministically) activates exactly one out of its outgoing flows, if its single incoming flow is activated (see g3 in Fig. 1), (c) the parallel merge, that activates the single outgoing flow, if all the incoming flows are simultaneously activated (see g4 in Fig. 1), and (d) the exclusive merge, that activates the single outgoing flow, if any one of the incoming flows is activated (see g2 in Fig. 1). The diamonds representing parallel gateways and exclusive gateways are labeled by ‘$\varvec{\pmb {+}}$’ and ‘$\varvec{\pmb {\times }}$’, respectively. Branch and merge gateways are also called split and join gateways, respectively.

A sequence flow denotes that the execution of the process can pass from the source object to the target object. If there is a sequence flow from $a_{1}$ to $a_{2}$, then $a_{1}$ is a predecessor of $a_{2}$, and symmetrically, $a_{2}$ is a successor of $a_{1}$. A path is a sequence of flow objects such that every pair of consecutive objects in the sequence is connected by a sequence flow.

We will consider models of business processes that are well-formed, in the sense that they satisfy the following properties: (1) every business process contains a single start event and a single end event, (2) the start event has exactly one successor and no predecessors, and the end event has exactly one predecessor and no successors, (3) every flow object occurs on a path from the start event to the end event, (4) (parallel or exclusive) branch gateways have exactly one predecessor and at least one successor, while (parallel or exclusive) merge gateways have at least one predecessor and exactly one successor, (5) tasks have exactly one predecessor and one successor, and (6) no cycles through gateways only are allowed. Note that we do not require BP models to be block-structured.

Fig. 1.

A business process Proc.

In Fig. 1 we show the BPMN model of a business process, called Proc. After the start event, the parallel branch g1 simultaneously activates the two flow objects g2 and b. The exclusive merge g2 activates the sequential execution of the task a1 which in turn activates the execution of the task a2 which is followed by the exclusive branch g3. After g3, the execution can either return to g2 or proceed to g4. If g3 and b both complete their executions simultaneously, then the parallel merge g4 is executed, the end event occurs, and the process Proc terminates.

3 Specification and Semantics of Business Processes

In this section we introduce the notion of a Business Process Specification (BPS), which formally represents a business process by means of CHCs. Then we define the operational semantics of a BPS.

Business Process Specification via CHCs. A BPS contains: (i) a set of ground facts that specify the flow objects and the sequence flows between them, and (ii) a set of clauses that specify the duration of each flow object and the controllability (or uncontrollability) of that duration.

For the flow objects we will use of the following predicates: $task (X)$, $\textit{event}(X)$, $\textit{gateway}(X)$, , , , with the expected meaning. For the sequence flows we will use the predicate $seq (X,Y)$ meaning that there is a sequence flow from X to Y. For every task X we specify its duration by the constrained fact $\textit{duration}(X,D)\!\leftarrow \!d_{min}\!\le \!D\!\le \!d_{max}$, where $d_{min}$ and $d_{max}$ are positive integer constants representing the minimal and the maximal duration of X, respectively. Events and gateways, being instantaneous, have duration 0. For every task X and its duration, we also specify that they are controllable, or uncontrollable, by the fact $controllable (X) \leftarrow$, or $uncontrollable (X) \leftarrow$, respectively.

In Fig. 2 we show the BPS of process Proc of Fig. 1. For reasons of space, in that specification we did not list all the facts for the tasks, events, gateways, and sequence flows of the diagram of Proc.

Fig. 2.

The CHCs of the Business Process Specification of process Proc of Fig. 1.

Operational Semantics. We define the operational semantics of a business process under the assumption that the process is safe, that is, during its enactment there are no multiple, concurrent executions of the same flow object [1]. By using this assumption, we represent the state of a process enactment as a set of properties, called fluents holding at a time instant. We borrow the notion of fluent from action languages such as the Situation Calculus [25], the Event Calculus [20], or the Fluent Calculus [30], but we will present our semantics by following the structural operational approach often adopted in the field of programming languages.

Formally, a state $s\!\in \! States$ is a pair $\langle F, t \rangle$, where F is a set of fluents and t is a time instant, that is, a non-negative integer. A fluent is a term of the form: (i) $\textit{begins}(x)$, which represents the beginning of the enactment of the flow object x, (ii) $\textit{completes}(x)$, which represents the completion of the enactment of x, (iii) $\textit{enables}(x,y)$, which represents that the flow object x has completed its enactment and it enables the enactment of its successor y, and (iv) $enacting (x,r)$, which represents that the enactment of x requires r units of time to complete (for this reason r is called the residual time of x). We have that $\textit{begins}(x)$ is equivalent to $enacting (x,r)$, where r is the duration of x, and $\textit{completes}(x)$ is equivalent to $enacting (x,0)$. (This redundant representation allows us to write simpler rules for the operational semantics below.)

The operational semantics is defined by a rewriting relation $\longrightarrow$ which is a subset of $States \!\times \! States$. This relation is specified by rules $S_{1}$–$S_{7}$ below, where we use the following predicates, besides the ones introduced in Sect. 3 for defining the BPS: (i) , which holds if x is not a parallel branch, and (ii) , which holds if x is not a parallel merge.

We assume that, for every flow object x, there exists a unique value d of its duration, satisfying the given constraint, which is used for every application of rule $S_{1}$. Note that $S_7$ is the only rule that formalizes the passing of time, as it infers rewritings of the form $\langle F, t \rangle \!\longrightarrow \! \langle F', t\!+\!m \rangle$, with $m\!>\!0$. In contrast, rules $S_1$–$S_6$ infer state rewritings of the form $\langle F, t \rangle \longrightarrow \langle F', t \rangle$, where time does not pass. Here is the explanation of rules $S_1$–$S_7$.

• ($S_1$) If the execution of a flow object x begins at time t, then, at the same time t, x is enacting and its residual time is its duration d;

• ($S_2$) If the execution of the parallel branch x completes at time t, then x enables all its successors at time t;

• ($S_3$) If the execution of x completes at time t and x is not a parallel branch, then x enables precisely one of its successors at time t (in particular, this case occurs when x is a task);

• ($S_4$) If all the predecessors of x enable the parallel merge x at time t, then the execution of x begins at time t;

• ($S_5$) If at least one predecessor p of x enables x at time t and x is not a parallel merge, then the execution of x begins at time t (in particular, this case occurs when x is a task);

• ($S_6$) If a flow object x is enacting at time t with residual time 0, then the execution of x completes at the same time t;

• ($S_7$) Suppose that: (i) none of rules $S_1$–$S_6$ can be applied for computing a state rewriting $\langle F,t\rangle \longrightarrow \langle F',t'\rangle$, (ii) at time t at least one task is enacting with positive residual time (note that flow objects different from tasks cannot have positive residual time), and (iii) m is the least value among the residual times of all the tasks enacting at time t. Then, (i) every task x that is enacting at time t with residual time r, is enacting at time $t\!+\!m$ with residual time $r\!-\!m$ and (ii) all $\textit{enables}(p,s)$ fluents are removed.

Due to rules $S_4$ and $S_5$, if a fluent of the form $\textit{enables}(p,s)$ is removed by applying rule $S_7$, then s necessarily refers to a parallel merge that is not enabled at time t by some of its predecessors. Thus, a parallel merge is executed if and only if it gets simultaneously enabled by all its predecessors. For lack of space we omit to model the asynchronous version of the parallel merge [11], which does not require the simultaneity condition. Note also that, if desired, tasks can be added for modeling delays in an explicit way.

We say that state $\langle F',t'\rangle$ is reachable from state $\langle F,t\rangle$, if $\langle F,t\rangle \longrightarrow ^* \langle F',t'\rangle$, where $\longrightarrow ^*$ denotes the reflexive, transitive closure of the rewriting relation $\longrightarrow$.

The initial state is the state $\langle \{\textit{begins}({ {start}})\},0\rangle$. The final state is the state of the form $\langle \{\textit{completes}({ {end}})\},t\rangle$, for some time instant t.

Properties of the Operational Semantics. Now we first introduce the notions of: (i) a derivation, which is a sequence of states, and (ii) a selection function, which is a rule providing the order in which fluents are rewritten according to the relation $\longrightarrow$. In Theorem 1 below we will prove that the relation $\longrightarrow$ is independent of that order.

Definition 1

(Derivation). A derivation from a state $s_{0}$ in a BPS is a (possibly infinite) sequence of states $s_0, s_1, s_2, \ldots$ such that for all $i\!\ge \!0$, $s_{i}\! \longrightarrow \! s_{i+1}$.

Let $States _{ sat }$ be the subset of ${ States }$ where .

Definition 2

(Selection function). Let $\delta$ be a finite derivation whose last state is $\langle F, t \rangle$, with $F\! \ne \! \emptyset$. A selection function $\mathcal R$ is a function that takes the derivation $\delta$ and returns  :  either (i) a subset of F whose elements satisfy the conditions in the premise of exactly one rule among $S_{1}$–$S_{6}$, or (ii) the union of the set of the ‘$enacting \!$’ fluents in F and the set of the ‘${ enables }\!$’ fluents in F, if $\langle F, t \rangle \!\in \! States _{ sat }$ and at least one ‘$enacting \!$’ fluent belongs to F.

The selection function is well-defined, because each fluent can be rewritten by at the most one rule and the rules $S_{1}$–$S_{6}$ are not overlapping, that is, the sets of fluents which can fire two distinct rules in $S_{1}$–$S_{6}$ (or two different instances of the same rule) are disjoint.

Definition 3

(Derivation via $\mathcal R$ ). Given a selection function $\mathcal R$, we say that a derivation $\delta$ is via $\mathcal R$ iff for each proper prefix $\delta '\!$ of $\delta$ ending with a state s, if $s\longrightarrow s'$ and $(\delta '\, s')$ is a prefix of $\delta$, then $\mathcal R(\delta ')$ are the fluents of s that are rewritten when deriving $s'$.

Theorem 1

For every derivation $\delta$ from a state $s_{0}$, and selection function $\mathcal R$, there exists a derivation $\delta '\!$ from $s_{0}\!$ via $\mathcal R$ such that if $\langle F,\! t\rangle$ is a state in $\delta$ and $f\!$ is a fluent in $F\!$, then there exists a state $\langle F'\!,\! t\rangle$ in $\delta '\!$ such that $f\!$ is a fluent in $F'\!$.

4 Encoding Controllability Properties into CHCs

In this section we show how weak and strong controllability properties are formalized by defining a CHC interpreter, that is, a set of CHCs that encodes the operational semantics of business processes. Then, the interpreter is specialized with respect to the business process and property to be verified.

A CHC Interpreter for Time-Aware Business Processes. A state of the operational semantics is encoded by a term of the form s(F, T), where F is a set of fluents and T is the time instant at which the fluents in F hold. The rewriting relation $\longrightarrow$ between states and its reflexive, transitive closure $\longrightarrow ^{*}$ are encoded by the predicates ${\textit{tr}}$ and $\textit{reach}$, respectively. The clauses defining these predicates are shown in Table 1. In the body of the clauses, the atoms that encode the premises of the rules of the operational semantics have been underlined.

The predicate ${\textit{select}(L,F)}$ encodes a selection function (see Definition 2). We assume that ${\textit{select}(L,F)}$ holds iff L is a subset of the set F of fluents such that: (i) there exists a clause in $\{C1,\ldots , C6\}$ that updates F by replacing the subset L of F by a new set of fluents, and (ii) among all such subsets of F, L is the one that contains the first fluent, in textual order (in this sense ${\textit{select}(L,F)}$ is deterministic). The predicate holds iff $\textit{duration}(X,D)$ holds and D belongs to either the list U of durations of the uncontrollable tasks or the list C of durations of the controllable tasks. The predicate ${\textit{update}(F,R,A,FU)}$ holds iff FU is the set obtained from the set F by removing all the elements of R and adding all the elements of A. The predicate holds iff the premise of every rule in $\{C1,\ldots , C6\}$ is unsatisfiable. The predicate $\textit{mintime}(\textit{Enacts},M)$ holds iff Enacts is a set of fluents of the form ${\textit{enacting}(X,R)}$ and M is the minimum value of R for the elements of Enacts. The predicate holds iff EnactsU is the set of fluents obtained by replacing every element of Enacts, of the form $\textit{enacting}(X,R)$, with the fluent $\textit{enacting}(X,RU)$, where $\textit{RU}\!=\!R\!-\!M$. The predicates $\textit{member}(\textit{El},\textit{Set})$ and are self-explanatory. The predicate $\textit{findall}(X,G,L)$ holds iff X is a term whose variables occur in the conjunction G of atoms, and L is the set of instances of X such that $\exists Y.\, G$ holds, where Y is the tuple of variables occurring in G different from those in X.

We denote by $\textit{Sem}$ the set consisting of clauses $C1,\ldots ,C7, R1,R2$, together with the clauses encoding the business process specification.

Theorem 2

(Correctness of Encoding). Let $\textit{init}$ be the term that encodes the initial state $\langle \{\textit{begins}(\textit{start})\},0\rangle$, and $\textit{fin}(\textit{t})$ be the term that encodes the final state $\langle \{\textit{completes}(\textit{end})\},t\rangle$. Then, $\langle \{\textit{begins}(\textit{start})\},0\rangle \! \longrightarrow ^*\! \langle \{\textit{completes}(\textit{end})\},t\rangle$ iff there exist tuples of integers x and y such that $\textit{Sem}\,\cup LIA \,\models \,\textit{reach}(\textit{init},\!\textit{fin}(\textit{t}),\!x,\!y)$.

Table 1. The CHC interpreter for time-aware business processes.

A reachability property is defined by a clause of the form:

RP. $\textit{reachProp}(U,C)\, \leftarrow \, c(\textit{T},U,C),\, \textit{reach}(\textit{init},\,\textit{fin}(\textit{T}),\,U,\,C)$

where: (i) U and C denote tuples of uncontrollable and controllable durations, respectively, and (ii) $c(\textit{T},U,C)$ is a constraint.

We say that the duration D of task X is admissible iff $\textit{duration}(X,D)$ holds. The strong controllability problem for a BPS consists in checking whether or not there exist durations C such that, for all admissible durations U, the property $\textit{reachProp}(U,C)$ holds. The weak controllability problem for a BPS consists in checking whether or not, for all admissible durations U, there exist durations C such that $\textit{reachProp}(U,C)$ holds. Note that, if $\textit{reachProp}(U,C)$ holds, then all durations used to reach the final state are admissible, and hence in the definition of controllability there is no need to require that the existentially quantified durations C are admissible. We denote by I the set $\textit{Sem} \cup \{{ RP}\}$.

Definition 4

(Strong and weak controllability). Given a BPS $\mathcal B$,

• $\mathcal B$ is strongly controllable iff $I \cup LIA \,\models \,\exists \,C\, \forall \,U.\, \textit{adm}(U) \rightarrow \textit{reachProp}(U,C)$

• $\mathcal B$ is weakly controllable iff $I \cup LIA \,\models \, \forall \,U. \textit{adm}(U)\, \rightarrow \exists \,C\,\textit{reachProp}(U,C)$

  where $\textit{adm}(U)$ holds iff U is a tuple of admissible durations.

If a business process is weakly controllable, in order to determine the durations of the controllable tasks, we need to know in advance the actual durations of all the uncontrollable tasks. This might not be realistic in practice, as uncontrollable tasks may occur after controllable ones. Strong controllability implies weak controllability and guarantees that suitable durations of the controllable tasks can be computed, before the enactment of the process, by using the constraints on the uncontrollable durations, which are provided by the process specification.

Specializing the CHC Interpreter. The clauses in I make use of complex terms, and in particular lists of variable length, to represent states (see clauses C1–C7). However, I can be specialized to the particular BPS under consideration and transformed into an equivalent set $I_{\textit{sp}}$ of function-free CHCs, on which CHC solvers are much more effective. The specialization transformation is a variant of the ones for the so called Removal of the Interpreter proposed in the area of verification of imperative programs [14], and makes use of the following transformation rules: unfolding, definition introduction, and folding [16].

The specialization transformation (see [12] for details) starts off by unfolding clause RP, thereby performing a symbolic exploration of the space of the reachable states. The unfolding rule is defined as follows.

Unfolding Rule. Let C be a clause of the form ${H\leftarrow c,L,A,R}$, where A is an atom. Let $\{{K}_i \leftarrow {c}_i,B_i \mid i=1, \ldots , m\}$ be the set of the (renamed apart) clauses in I such that, for $i=1,\ldots ,m,$ A is unifiable with ${ K}_i$ via the most general unifier $\vartheta _i$ and ${(c,c_i)}\,\vartheta _i$ is satisfiable. Then, from C we derive the following set of clauses: $\{\,({H\leftarrow c,c_i,L,B_i,R})\,\vartheta _i \mid i=1,\ldots , m\,\}$.

After unfolding, by applying the definition rule, for every reach atom occurring in the body of a clause, a new predicate is introduced by a clause of the form:

$\textit{newr}(\textit{Rs},T,\textit{Tf},U,C)\leftarrow f(\textit{Rs}),\ \textit{reach}(s(\textit{fl}(\textit{Rs}),T),\textit{fin}(\textit{Tf}),U,C)$

where ${f(\textit{Rs})}$ is a constraint obtained by projecting the constraint occurring in the body of the clause where the reach atom occurs, onto the tuple $\textit{Rs}$ of variables representing the residual times, and ${{ fl }(\textit{Rs})}$ denotes the set of fluents that hold at time T. Then, by applying the folding rule, reach atoms with complex arguments representing states (i.e., $\textit{reach}(s(\textit{fl}(\textit{Rs}),T),\textit{fin}(\textit{Tf}),U,C)$), are replaced by function-free calls to the newly introduced predicates (i.e., $\textit{newr}(\textit{Rs},T,\textit{Tf},U,C)$). The unfolding-definition-folding transformations are repeated until we derive a set $\textit{I}_{\textit{sp}}$ of function-free CHCs. Since the unfolding, definition introduction, and folding rules preserve satisfiability [16], we have the following result.

Theorem 3

(Correctness of Specialization). Every set I of CHCs encoding a reachability property of a BPS can be transformed into a set $\textit{I}_{\textit{sp}}$ of CHCs such that: (i) $\textit{I}_{\textit{sp}}$ is a set of function-free CHCs, and (ii) for all (tuples of) integer values x and y, $I \cup LIA \,\models \,\textit{reachProp}(x,y)$ iff $I_{\textit{sp}} \cup LIA \,\models \,\textit{reachProp}(x,y)$.

Example 1

Let I be the set of clauses defining the reachability property for the process Proc of Fig. 1, and let clause RP be:

$$\textit{reachProp}(A1,\!A2,\!B)\, \leftarrow \, \textit{reach}(\textit{init}, \textit{fin}(\textit{T}), A1, (A2,\!B))$$

where A1 denotes the duration of the uncontrollable task a1 and (A2, B) denotes the durations of the controllable tasks a2 and b. By applying the specialization transformation to I, we derive the following function-free clauses:

$\textit{reachProp}(A1,\!A2,\!B) \leftarrow A\!=\!A1, B\!=\!B1, A1\!\ge \!2, A1\!\le \!4, B\!\ge \!5, B\!\le \!6,$

                   $\textit{new}2(A,B1,F,G,A1,A2,B)$

$\textit{new}2(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!A\!+\!C, I\!=\!B1\!-\!A, J\!=\!0, A\!\ge \!1, I\!\ge \!0, A\!+\!I\!\ge \!1,$

                   $\textit{new}2(J,I,H,D,A1,A2,B)$

$\textit{new}2(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!B1\!+\!C, I\!=\!A\!-\!B1, J\!=\!0, A\!\ge \!1, I\!\ge \!0, A\!-\!I\!\ge \!1,$

                   $\textit{new}2(I,\!J,\!H,\!D,\!A1,\!A2,\!B)$

$\textit{new}2(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!A2, A\!=\!0, H\!\ge \!1, H\!\le \!2,$ $\textit{new}5(H,\!B1,\!C,\!D,\!A1,\!A2,\!B)$

$\textit{new}5(A,\!B1,\!C,\!C,\!A1,\!A2,\!B) \leftarrow A\!=\!0, B1\!=\!0$

$\textit{new}5(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!A\!+\!C, I\!=\!B1\!-\!A, J\!=\!0, A\!\ge \!1, I\!\ge \!0, A\!+\!I\!\ge \!1,$

                   $\textit{new}5(J,\!I,\!H,\!D,\!A1,\!A2,\!B)$

$\textit{new}5(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!B1\!+\!C, I\!=\!A\!-\!B1, J\!=\!0, A\!\ge \!1, I\!\ge \!0, A\!-\!I\!\ge \!1,$

                   $\textit{new}5(I,\!J,\!H,\!D,\!A1,\!A2,\!B)$

$\textit{new}5(A,\!B1,\!C,\!D,\!A1,\!A2,\!B) \leftarrow H\!=\!A1, A\!=\!0, H\!\ge \!2, H\!\le \!4,$ $\textit{new}2(H,\!B1,\!C,\!D,\!A1,\!A2,\!B)$

5 Solving Controllability Problems

State-of-the-art CHC solvers are often not effective in solving controllability problems defined by a direct encoding of the formulas in Definition 4, where nested universal and existential quantifiers occur. The main problem is that performing quantifier elimination on formulas defined by, possibly recursive, Constrained Horn Clauses is very expensive, and often unsuccessful. Thus, we propose an alternative method that is based on verifying a series of simpler properties, where quantification is restricted to LIA constraints.

We assume the existence of a solver that is sound and complete for Horn clauses with LIA constraints. The solver interface is a procedure $\textit{solve}(P,Q)$ such that, for any set P of CHCs and for any query Q, which is a conjunction of atoms and LIA constraints, returns an answer A, that is, a satisfiable constraint A such that $P\,\models \,\forall (A\rightarrow Q)$, if such an answer exists, and false otherwise.

The method we propose solves controllability problems by looking for a satisfiable constraint a(U, C), where U and C are tuples of variables denoting the durations of the uncontrollable and controllable tasks, respectively, such that $I \cup LIA \, \models \, \forall U\, \forall C.\,a(U,C) \rightarrow \textit{reachProp}(U,C)$ and either

$(\dagger )~ LIA \,\models \,\exists C\, \forall U.\, \textit{adm}(U) \rightarrow a(U,C)$ (for strong controllability), or

$(\ddagger )~ LIA \,\models \,\forall U.\, \textit{adm}(U) \rightarrow \exists C.\,a(U,C)$ (for weak controllability).

In particular, we introduce the Strong and Weak Controllability algorithms (SC and WC for short, respectively) that, given a set of function-free CHCs defining $\textit{reachProp}(U,C)$ (that is, a set of clauses generated by the specialization transformation of Sect. 4), produce a solution for the controllability problem by constructing a(U, C) as a disjunction of the answer constraints provided by the solver until either condition $(\dagger )$ holds (respectively, condition $(\ddagger )$ holds) or there are no more answers (see Fig. 3). In order to avoid repeated answers, at each iteration of the do-while loop, the solver is invoked on a query containing the negation of the (disjunction of the) answers obtained so far.¹

Since the durations of the tasks belong to finite integer intervals, the set of answers that can be returned by the solve procedure is finite. Hence the SC and WC algorithms always terminate. The following theorem states that SC and WC are sound and complete methods for solving strong and weak controllability problems, respectively.

Theorem 4

(Soundness and Completeness of SC and WC). Let I be a set of CHCs defining a reachability property for a BPS $\mathcal B$. Then,

(i)  SC returns a satisfiable constraint if and only if $\mathcal B$ is strongly controllable

(ii) WC returns a satisfiable constraint if and only if $\mathcal B$ is weakly controllable.

Fig. 3.

The SC and WC algorithms for verifying strong and weak controllability.

We now illustrate how the WC algorithm works by applying it to the clauses obtained by specialization in Example 1. During the first iteration of the do-while loop the CHC solver is invoked by executing $\textit{solve}(I,\textit{reachProp}(A1,A2,B) \wedge \forall A2,B. \lnot \textit{false})$, which returns the answer constraint a1(A1, A2, B): $A1\!\ge \!B\!-\!2,$ $A1\!\le \!4, A2\!=\!B\!-\!A1, B\!\ge \!5, {B\!\le \! 6}$. In our example, the constraint $\textit{adm}(A1)$ is $A1\!\ge \! 2, A1\!\le \! 4$. Now we have that $\textit{LIA}\,\not \models \,\forall A1.\, \textit{adm}(A1) \rightarrow \exists A2,B.\, a1(A1,A2,B)$, and hence the algorithm executes the second iteration of the do-while loop. Next, the CHC solver is invoked by executing $\textit{solve}(I,\textit{reachProp}(A1,A2,B) \wedge \forall A2,B.\, \lnot a1(A1,A2,B))$, which returns the answer constraint a2(A1, A2, B): $A1\!=\!2,A2\!=\!1,B\!=\!6$. Now the condition of the do-while loop is false, because $\textit{LIA}\,\models \,\forall A1.\, \textit{adm}(A1) \rightarrow \exists A2,B.\, (a1(A1,A2,B) \vee a2(A1,A2,B))$. Thus, the WC algorithm terminates and we can conclude that the considered weak controllability property holds.

We have used the VeriMAP transformation and verification system for CHCs [13] to implement the specialization transformation of Sect. 4, and SICStus Prolog and the Z3 solver to implement the SC and WC algorithms. We have applied our method to verify the weak controllability of the process Proc. The timings are as follows²: the execution of the specialization transformation requires 0.04 s and the execution of the WC algorithm requires 0.03 s.

We have also solved controllability problems for other small-sized processes, not shown here for reasons of space, whose reachability relation, like the one for process Proc, contains cycles that may generate an unbounded proof search, and hence may cause nontermination if not handled in an appropriate way. In particular, in all the examples we have considered, we noticed that Z3 is not able to provide a proof within a time limit of one hour for a direct encoding of the controllability properties as they are formulated in Definition 4.

6 Related Work and Conclusions

Controllability problems arise in all contexts where the duration of some tasks in a business process cannot be determined in advance by the process designer. We have presented a method for checking strong and weak controllability properties of business processes. The method is based upon well-established techniques and tools in the field of computational logic.

Modeling and reasoning about time in the field of business process management has been largely investigated in the recent years [5]. The notion of controllability, extensively studied in the context of scheduling and planning problems over temporal networks [6,7,8, 27, 31, 32], has been considered as a useful concept for supporting decisions in business process management and design [9, 21, 22].

Algorithms for checking strong and weak controllability properties were first introduced for Simple Temporal Networks with Uncertainty [32]. Later, sound and complete algorithms were developed for both strong [27] and weak [31] controllability of Disjunctive Temporal Problems with Uncertainty (DTPU). More recently, a general and effective method for checking strong [7] and weak [8] controllability of DTPU’s via SMT has been developed.

The task of verifying controllability of BP models we have addressed in this paper is similar to the task of checking controllability of temporal workflows addressed by Combi and Posenato [9]. These authors present a workflow conceptual framework that allows the designer to use temporal constructs to express duration, delays, relative, absolute, and periodic constraints. The durations of tasks are uncontrollable, while the delays between tasks are controllable. The controllability problem, which arises from relative constraints that limit the duration of two non-consecutive tasks, consists in checking whether or not the delays between tasks enforce the relative constraints for all possible durations of tasks. The special purpose algorithms for checking controllability presented in [9] enumerate all possible choices, and therefore are computationally expensive.

Our approach to controllability of BP models exhibits several differences with respect to the one considered by Combi and Posenato in [9]. In our approach the designer has the possibility of explicitly specifying controllable and uncontrollable durations. We also consider workflows with minimal restrictions on the control flow, and unlike the framework in [9], we admit loops. We automatically generate the clauses to be verified from the formal semantics of the BP model, thus making our framework easily extensible to other classes of processes and properties. Finally, we propose concrete algorithms for checking both strong and weak controllability, based on off-the-shelf CHC specializers and solvers.

As future work we plan to perform an extensive experimental evaluation of our method and to apply our approach to extensions of time-aware BP models, whose properties also depend on the manipulation of data objects.