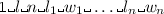A Tutorial on Hybrid Answer Set Solving with clingo

Abstract

Answer Set Programming (ASP) has become an established paradigm for Knowledge Representation and Reasoning, in particular, when it comes to solving knowledge-intense combinatorial (optimization) problems. ASP’s unique pairing of a simple yet rich modeling language with highly performant solving technology has led to an increasing interest in ASP in academia as well as industry. To further boost this development and make ASP fit for real world applications it is indispensable to equip it with means for an easy integration into software environments and for adding complementary forms of reasoning.

In this tutorial, we describe how both issues are addressed in the ASP system clingo. At first, we outline features of clingo’s application programming interface (API) that are essential for multi-shot ASP solving, a technique for dealing with continuously changing logic programs. This is illustrated by realizing two exemplary reasoning modes, namely branch-and-bound-based optimization and incremental ASP solving. We then switch to the design of the API for integrating complementary forms of reasoning and detail this in an extensive case study dealing with the integration of difference constraints. We show how the syntax of these constraints is added to the modeling language and seamlessly merged into the grounding process. We then develop in detail a corresponding theory propagator for difference constraints and present how it is integrated into clingo’s solving process.

T. Schaub—Affiliated with the School of Computing Science at Simon Fraser University, Burnaby, Canada, and the Institute for Integrated and Intelligent Systems at Griffith University, Brisbane, Australia.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Answer Set Programming (ASP [4]) has established itself among the popular paradigms for Knowledge Representation and Reasoning (KRR), in particular, when it comes to solving knowledge-intense combinatorial (optimization) problems. ASP’s unique combination of a simple yet rich modeling language with highly performant solving technology has led to an increasing interest in ASP in academia as well as industry. Another primary asset of ASP is its versatility, arguably elicited by its roots in KRR. On the one hand, ASP’s first-order modeling language offers, for instance, cardinality and weight constraints as well as means to express multi-objective optimization functions. This allows ASP to readily express problems in neighboring fields such as Satisfiability Testing (SAT [7]) and Pseudo-Boolean Solving (PB [37]), as well as Maximum Satisfiability Testing (MaxSAT [28]) and even more general constraint satisfaction problems possibly involving optimization. On the other hand, these constructs must be supported by the corresponding solvers, leading to dedicated treatments of cardinality and weight constraints along with sophisticated optimization algorithms. Moreover, mere satisfiability testing is often insufficient for addressing KRR problems. That is why ASP solvers offer additional reasoning modes involving enumerating, intersecting, or unioning solutions, as well as combinations thereof, e.g., intersecting all optimal solutions.

In a sense, the discussed versatility of modern ASP can be regarded as the result of hybridizing the original approach [24] in several ways. So far, however, most hybridization was accomplished within the solvers and is thus inaccessible to the user. For instance, the dedicated treatment of aggregates like cardinality and weight constraints is fully opaque. The same applies to the control of successive solver calls happening during optimization. Although a highly optimized implementation of such prominent concepts makes perfect sense, the increasing range and resulting diversification of applications of ASP calls for easy and generic means to enrich ASP with dedicated forms of reasoning. This involves the extension of ASP’s solving capacities with means for handling constraints foreign to ASP as well as means for customizing solving processes to define complex forms of reasoning. The former extension is usually called theory reasoning (or theory solving) and the resulting conglomerate of ASP extensions is subsumed under the umbrella term ASP modulo theories. The other extension addresses the customization of ASP solving processes by multi-shot ASP solving, providing operative solving processes that deal with continuously changing logic programs.

Let us motivate both techniques by means of two exemplary ASP extensions, aggregate constraints and optimization. With this end in view, keep in mind that ASP is a model, ground, and solve paradigm. Hence such extensions are rarely limited to a single component but often spread throughout the whole workflow. This begins with the addition of new language constructs to the input language, requiring in turn amendments to the grounder as well as syntactic means for passing the ground constructs to a downstream system. In case they are to be dealt with by an ASP solver, it must be enabled to treat the specific input and incorporate corresponding solving capacities. Finally, each such extension is theory-specific and requires different means at all ends.

So first of all, consider what is needed to extend an ASP system like clingo with a new type of aggregate constraint? The first step consists in defining the syntax of the aggregate type. Afterwards, the ASP grounder has to be extended to be able to parse and instantiate the corresponding constructs. Then, there are two options, either the ground aggregates are translated into existing ASP language constructs (and we are done),¹ or they are passed along to a downstream ASP solver. The first alternative is also referred to as eager, the latter as lazy theory solving. The next step in the lazy approach is to define an intermediate format (or data structure) to pass instances of the aggregate constraints from the grounder to the solver, not to forget respective extensions to the back- and front-ends of the two ASP components. Now, that the solver can internalize the new constructs, it must be equipped with corresponding processing capacities. They are usually referred to as theory propagators and inserted into the solver’s infrastructure for propagation. When solving, the idea is to leave the Boolean solving machinery intact by associating with each theory constraint an auxiliary Boolean variable. During propagation, the truth values of the auxiliary variables are passed to the corresponding theory propagators that then try to satisfy or falsify the respective theory constraints, respectively. Finally, when an overall solution is found, the theory propagators are in charge of outputting their part (if applicable). One can imagine that each such extension involves a quite intricate engineering effort since it requires working with the ASP system’s low level API. clingo allows us to overcome this problem by providing easy and generic means for adding theory solving capacities. On the one side, it offers theory grammars for expressing theory languages whose expressions are seamlessly integrated in its grounding process. On the other side, a simple interface consisting of four methods offers an easy integration of theory propagators into the solver, either in C, C++, Lua, or Python.

Let us now turn to (branch-and-bound-based) optimization and see what infrastructure is needed to extend a basic ASP solver. In fact, for the setup, we face a similar situation as above and all steps from syntax definition to internalization are analogous for capturing objective functions. The first step in optimization is to find an initial solution. If none exists, we are done. Otherwise the system enters a simple loop. The objective value of the previous solution is determined and a constraint is added to the problem specification requiring that a solution must have a strictly better objective value than the one just obtained. Then, the solver is launched again to compute a better solution. If none is found, the last solution is optimal. Otherwise, the system re-enters the loop in order to find an even better solution. This solving process faces a succession of solver invocations dealing with slightly changing problem specifications. The direct way to implement this is to use a script that repeatedly calls an ASP solver after each problem expansion. However, such an approach bears great redundancies due to repeated grounding and solving efforts from scratch. Unlike this, clingo offers evolving grounding and solving processes. Such processes lead to operative ASP systems that possess an internal state that can be manipulated by certain operations. Such operations allow for adding, grounding, and solving logic programs as well as setting truth values of (external) atoms. The latter does not only provide a simple means for incorporating external input but also for enabling or disabling parts of the current logic program. These functionalities allow for dealing with changing logic programs in a seamless way. As above, corresponding application programming interfaces (APIs) are available in C, C++, Lua, or Python.

The remainder of this tutorial is structured as follows. Section 2 provides some formal underpinnings for the following sections without any claim to completeness. Rather we refer the reader to the literature for comprehensive introductions to ASP and its computing machinery, among others [4, 14, 19, 23, 30]. As a result, this tutorial is not self-contained and rather aims at a hands-on introduction to using clingo’s API for multi-shot and theory solving. Both approaches are described in Sects. 3 and 4 by drawing on material from [20, 21] and [18], respectively. Section 5 is dedicated to a case-study detailing how clingo can be extended with difference constraints over integers, or more precisely Quantifier-free Integer Difference Logic (QF-IDL).

2 Answer Set Programming

As usual, a logic program consists of rules of the form

where each ${\texttt {a}}_i$ is an atom of form ${\texttt {p(t}}_{\texttt {1}}{\texttt {,}}\ldots {\texttt {,t}}_k{\texttt {)}}$ and all ${\texttt {t}}_i$ are terms, composed of function symbols and variables. Atoms ${\texttt {a}}_1$ to ${\texttt {a}}_m$ are often called head atoms, while ${\texttt {a}}_{m+1}$ to ${\texttt {a}}_n$ and ${\texttt {not a}}_{n+1}$ to ${\texttt {not a}}_{o}$ are also referred to as positive and negative body literals, respectively. An expression is said to be ground, if it contains no variables. As usual, not denotes (default) negation. A rule is called a fact if $m=o=1$, normal if $m=1$, and an integrity constraint if $m=0$. Semantically, a logic program induces a set of stable models, being distinguished models of the program determined by the stable models semantics; see [25] for details.

To ease the use of ASP in practice, several extensions have been developed. First of all, rules with variables are viewed as shorthands for the set of their ground instances. Further language constructs include conditional literals and cardinality constraints [38]. The former are of the form ${\texttt {a:b}}_{1}{\texttt {,}}\ldots {\texttt {,}}{\texttt {b}}_{m}$, the latter can be written as² ${\texttt {s}}\{{\texttt {d}}{_1}{\texttt {;}}\ldots {\texttt {;}}{\texttt {d}}_{n}\}{} \mathtt{t}$, where a and ${\texttt {b}}_i$ are possibly default-negated (regular) literals and each ${\texttt {d}}_j$ is a conditional literal; s and t provide optional lower and upper bounds on the number of satisfied literals in the cardinality constraint. We refer to ${\texttt {b}}_{1}{\texttt {,}}\ldots {\texttt {,}}{\texttt {b}}_{m}$ as a condition. The practical value of both constructs becomes apparent when used with variables. For instance, a conditional literal like a(X):b(X) in a rule’s antecedent expands to the conjunction of all instances of a(X) for which the corresponding instance of b(X) holds. Similarly, 2{a(X):b(X)}4 is true whenever at least two and at most four instances of a(X) (subject to b(X)) are true. Finally, objective functions minimizing the sum of a set of weighted tuples $(w_i,\varvec{t}_i)$ subject to condition $c_i$ are expressed as ${\texttt {\#minimize\{}}w{_1}{\texttt {@}}l{_1}{\texttt {,}}{\varvec{t}}{_1}{\texttt {:}}c{_1}{\texttt {;}}\ldots {\texttt {;}}w{_n}{\texttt {@}}l{_n}{\texttt {,}}{\varvec{t}}{_n}{\texttt {:}}c{_n} \}$ Lexicographically ordered objective functions are (optionally) distinguished via levels indicated by $l_i$. An omitted level defaults to 0.

As an example, consider the rule in Line 9 of Listing 1.1:

This rule has a single head atom consisting of a cardinality constraint; it comprises all instances of move(D,P,T) where T is fixed by the two body literals and D and P vary over all instantiations of predicates disk and peg, respectively. Given 3 pegs and 4 disks as in Listing 1.2, this results in 12 instances of move(D,P,T) for each valid replacement of T, among which exactly one must be chosen according to the above rule.

Full details on the input language of clingo along with various examples can be found in [16].

3 Multi-shot ASP Solving

Let us begin with an informal overview of the central features and language constructs of clingo’s multi-shot solving capacities. We illustrate them in the two following sections by implementing two exemplary reasoning modes, namely branch-and-bound-based optimization and incremental ASP solving. The material in Sects. 3.1 and 3.3 is borrowed from [20, 21], respectively, where more detailed accounts can be found.

3.1 A Gentle Introduction

A key feature, distinguishing clingo from its predecessors, is the possibility to structure (non-ground) input rules into subprograms. To this end, a program can be partitioned into several subprograms by means of the directive #program; it comes with a name and an optional list of parameters. Once given in the input, the directive gathers all rules up to the next such directive (or the end of file) within a subprogram identified by the supplied name and parameter list. As an example, two subprograms base and acid(k) can be specified as follows:

Note that base is a dedicated subprogram (with an empty parameter list): in addition to the rules in its scope, it gathers all rules not preceded by any #program directive. Hence, in the above example, the base subprogram includes the facts a(1) and a(2), although, only the latter is in the actual scope of the directive in line 5. Without further control instructions (see below), clingo grounds and solves the base subprogram only, essentially, yielding the standard behavior of ASP systems. The processing of other subprograms such as acid(k) is subject to scripting control.

For customized control over grounding and solving, a main routine (taking a control object representing the state of clingo as argument) can be supplied. For illustration, let us consider two Python main routines:³

While the above control program matches the default behavior of clingo, the one below ignores all rules in the base program but rather contains a ground instruction for acid(k) in line 8, where the parameter k is to be instantiated with the term 42.

Accordingly, the schematic fact b(k) is turned into b(42), no ground rule is obtained from ‘c(X,k) :- a(X)’ due to lacking instances of a(X), and the solve command in line 10 yields a stable model consisting of b(42) only. Note that ground instructions apply to the subprograms given as arguments, while solve triggers reasoning w.r.t. all accumulated ground rules.

In order to accomplish more elaborate reasoning processes, like those of iclingo [17] and oclingo [15] or other customized ones, it is indispensable to activate or deactivate ground rules on demand. For instance, former initial or goal state conditions need to be relaxed or completely replaced when modifying a planning problem, e.g., by extending its horizon.⁴ While the two mentioned predecessors of clingo relied on the #volatile directive to provide a rigid mechanism for the expiration of transient rules, clingo captures the respective functionalities and customizations thereof in terms of the #external directive. This directive goes back to lparse [39] and was also supported by clingo’s predecessors to exempt (input) atoms from simplifications (and fixing them to false). As detailed in the following, the #external directive of clingo provides a generalization that, in particular, allows for a flexible handling of yet undefined atoms.

For continuously assembling ground rules evolving at different stages of a reasoning process, #external directives declare atoms that may still be defined by rules added later on. In terms of module theory [35], such atoms correspond to inputs, which (unlike undefined output atoms) must not be simplified. For declaring input atoms, clingo supports schematic #external directives that are instantiated along with the rules of their respective subprograms. To this end, a directive like

is treated similar to a rule ‘p(X,Y) :- q(X,Z), r(Z,Y)’ during grounding. However, the head atoms of the resulting ground instances are merely collected as inputs, whereas the ground rules as such are discarded.

Once grounded, the truth value of external atoms can be changed via the clingo API (until the atoms become defined by corresponding rules). By default, the initial truth value of external atoms is set to false. Then, for example, with clingo’s Python API, assign_external(self,p(a,b),True) ⁵ can be used to set the truth value of the external atom p(a,b) to true. Among others, this can be used to activate and deactivate rules in logic programs. For instance, the integrity constraint ‘:- q(a,c), r(c,b), p(a,b)’ is ineffective whenever p(a,b) is false.

A full specification of clingo’s Python API can be found at https://potassco.org/clingo/python-api/current/clingo.html.

3.2 Branch-and-Bound-Based Optimization

We illustrate clingo’s multi-shot solving machinery in this as well as the next section via a simple Towers of Hanoi puzzle. The complete source code of this example is available at https://github.com/potassco/clingo/tree/master/examples/clingo/opt. Our example consists of three pegs and four disks of different size; it is shown in Fig. 1. The goal is to move all disks from the left peg to the right one. Only the topmost disk of a peg can be moved at a time. Furthermore, a disk cannot be moved to a peg already containing a disk of smaller size. Although there is an efficient algorithm to solve our simple puzzle, we do not exploit it and below merely specify conditions for sequences of moves being solutions. More generally, the Towers of Hanoi puzzle is a typical planning problem, in which the aim is to find a plan, that is, a sequence of actions, that leads from an initial state to a state satisfying a goal.

Fig. 1.

Towers of Hanoi: initial and goal situation

To illustrate how multi-shot solving can be used for realizing branch-and-bound-based optimization, we consider the problem of finding the shortest plan solving our puzzle within a given horizon. To this end, we adapt the Towers of Hanoi encoding from [19] in Listing 1.1. Here, the length of the horizon is given by parameter n. The problem instance in Listing 1.2 together with line 2 in Listing 1.1 gives the initial configuration of disks in Fig. 1. Similarly, the goal is checked in lines 5–6 of Listing 1.1 (by drawing on the problem instance in Listing 1.2). Because the overall objective is to solve the problem in the minimum number of steps within a given bound, it is successively tested in line 5. Once the goal is established, it persists in the following steps. This allows us to read off whether the goal was reached at the planning horizon (in line 6). The state transition function along with state constraints are described in lines 9–19. Since the encoding of the Towers of Hanoi problem is fairly standard, we refer the interested reader to [19] and devote ourselves in the sequel to implementing branch-and-bound-based minimization. In view of this, note that line 9 ensures that moves are only permitted if the goal is not yet achieved in the previous state. This ensures that the following states do not change anymore and allows for expressing the optimization function in line 23 as: minimize the number of states where the goal is not reached.

Listing 1.3 contains a logic program for bounding the next solution and the actual optimization algorithm. The logic program expects a bound b as parameter and adds an integrity constraint in line 3 ensuring that the next stable model yields a better bound than the given one. The minimization algorithm starts by grounding the base program in line 10 before it enters the loop in lines 11–26. This loop implements the branch-and-bound-based search for the minimum by searching for stable models while updating the bound until the problem is unsatisfiable. Note the use of the $\texttt {with}$ clause in line 13 that is used to acquire and release a solve handle. With it, the nested loop in lines 14–21 iterates over the found stable models. If there is a stable model, lines 15–20 iterate over the atoms of the stable model while summing up the current bound by extracting the weight of atoms over predicates ${\texttt {\_minimize/}}n$ with $n>0$.⁶ We check that the first argument of the atom is an integer and ignore atoms where this is not the case; just as is the case of the #sum aggregate in line 3. The loop over the stable models is exited in line 21. Note that this bypasses the $\texttt {else}$ clause in line 22 and the algorithm continues in line 25 with printing the bound and adding an integrity constraint in line 26 making sure that the next stable model is strictly better than the current one. Furthermore, note that grounding happens after the $\texttt {with}$ clause because it must not interfere with an active search for stable models. Finally, if the program becomes unsatisfiable, the branch and bound loop in lines 11–26 is exhausted. Hence, control continues in the $\texttt {else}$ clause in lines 22–24 printing that the previously found stable model (if any) is the optimal solution and exiting the outermost while loop in line 24 terminating the algorithm.

When running the augmented logic program in Listings 1.1, 1.2 and 1.3 with a horizon of 17, the solver finds plans of length 17, 16, and 15 and shows that no plan of length 14 exists. This is reflected by clingo’s output indicating 4 solver calls and 3 found stable models:

Last but not least, note that the implemented above functionality is equivalent to using clingo’s inbuilt optimization mode by replacing line 23 in Listing 1.1 with

3.3 Incremental ASP Solving

As mentioned, clingo fully supersedes its special-purpose predecessor iclingo aiming at incremental ASP solving. To illustrate this, we give below in Listing 1.5 a Python implementation of iclingo’s control loop, corresponding to the one shipped with clingo.^{7 8} Roughly speaking, iclingo offers a step-oriented, incremental approach to ASP that avoids redundancies by gradually processing the extensions to a problem rather than repeatedly re-processing the entire extended problem (as in iterative deepening search). To this end, a program is partitioned into a base part, describing static knowledge independent of the step parameter t, a cumulative part, capturing knowledge accumulating with increasing t, and a volatile part specific for each value of t. In clingo, all three parts are captured by #program declarations along with #external atoms for handling volatile rules. More precisely, the implementation in Listing 1.5 relies upon subprograms named base, step, and check along with external atoms of form query(t).⁹

We illustrate this approach by adapting the Towers of Hanoi encoding from Listing 1.1 in Sect. 3.2 to an incremental version in Listing 1.4. To this end, we arrange the original encoding in program parts base, check(t), and step(t), use t instead of T as time parameter, and simplify checking the goal. Checking the goal is easier here because the iterative deepening approach guarantees a shortest plan and, hence, does not require additional minimization.

At first, we observe that the problem instance in Listing 1.2 as well as line 2 in Listing 1.4 constitute static knowledge and thus belong to the base program. More interestingly, the query is expressed in line 5 of Listing 1.4. Its volatility is realized by making it subject to the truth assignment to the external atom query(t). For convenience, this atom is predefined in line 33 in Listing 1.5 as part of the check program (cf. line 32). Hence, subprogram check consists of a user- and predefined part. Finally, the transition function along with state constraints are described in the subprogram step in lines 8–19.

The idea is now to control the successive grounding and solving of the program parts in Listings 1.3 and 1.4 by the Python script in Listing 1.5. Lines 5–11 fix the values of the constants imin, imax, and istop. In fact, the setting in line 9 and 11 relieves us from adding ‘-c imin=0 -c istop="SAT"’ when calling clingo. All three constants mimic command line options in iclingo. imin and imax prescribe a least and largest number of iterations, respectively; istop gives a termination criterion. The initial values of variables step and ret are set in line 13. The value of step is used to instantiate the parametrized subprograms and ret comprises the solving result. Together, the previous five variables control the loop in lines 14–29.

The subprograms grounded at each iteration are accumulated in the list parts. Each of its entries is a pair consisting of a subprogram name along with its list of actual parameters. In the very first iteration, the subprograms base and check(0) are grounded. Note that this involves the declaration of the external atom query(0) and the assignment of its default value false. The latter is changed in line 28 to true in order to activate the actual query. The solve call in line 29 then amounts to checking whether the goal situation is already satisfied in the initial state. As well, the value of step is incremented to 1.

As long as the termination condition remains unfulfilled, each following iteration takes the respective value of variable step to replace the parameter in subprograms step and check during grounding. In addition, the current external atom query(t) is set to true, while the previous one is permanently set to false. This disables the corresponding instance of the integrity constraint in line 5 of Listing 1.4 before it is replaced in the next iteration. In this way, the query condition only applies to the current horizon.

An interesting feature is given in line 24. As its name suggests, this function cleans up domains used during grounding. That is, whenever the truth value of an atom is ultimately determined by the solver, it is communicated to the grounder where it can be used for simplifications.

The result of each call to solve is printed by clingo. In our example, the solver is called 16 times before a plan of length 15 is found:

4 Theory-Enhanced ASP Solving

This section provides the fundamental concepts for extending clingo with theory-specific reasoning. We begin by showing how its input language can be customized with theory-specific constructs. We then sketch clingo’s algorithmic approach to ASP solving with theory propagation in order to put the following description of clingo’s theory reasoning interface on firm grounds. The below material is an abridged version of [18].

4.1 Input Language

This section introduces the theory-related features of clingo’s input language. All of them are situated in the underlying grounder gringo and can thus also be used independently of clingo. We start with a detailed description of gringo’s generic means for defining theories and complement this in Appendix A with an overview of the corresponding intermediate language.

Our generic approach to theory specification rests upon two languages: the one defining theory languages and the theory language itself. Both borrow elements from the underlying ASP language, foremost an aggregate-like syntax for formulating variable length expressions. To illustrate this, consider Listing 1.6, where a logic program is extended by constructs for handling difference and linear constraints. While the former are binary constraints of the form¹⁰ $x_1-x_2\le k$, the latter have a variable size and are of form $a_1x_1+\dots +a_nx_n\circ k$, where $x_i$ are integer variables, $a_i$ and k are integers, and $\circ \in \{\le ,\ge ,<,>,=\}$ for $1\le i\le n$. Note that solving difference constraints is polynomial, while solving linear equations (over integers) is NP-complete. The theory language for expressing both types of constraints is defined in lines 1–15 and preceded by the directive #theory. The elements of the resulting theory language are preceded by & and used as regular atoms in the logic program in lines 17–27.

To be more precise, a theory definition has the form

where T is the theory name and each $D_i$ is a definition for a theory term or a theory atom for $1\le i\le n$. The language induced by a theory definition is the set of all theory atoms constructible from its theory atom definitions.

A theory atom definition has form

where p is a predicate name and k its arity, $t,t'$ are names of theory term definitions, each $\diamond _i$ is a theory operator for $m\ge 1$, and $o\in \{\texttt {head},\texttt {body},\texttt {any}, \texttt {directive}\}$ determines where theory atoms may occur in a rule. Examples of theory atom definitions are given in lines 11–14 of Listing 1.6. The language of a theory atom definition as above contains all theory atoms of form

where a is an atom over predicate p of arity k, each ${C}_i$ is a tuple of theory terms in the language for t, c is a theory term in the language for $t'$, $\diamond$ is a theory operator among $\{ \diamond _1, \dots , \diamond _m \}$, and each ${L}_i$ is a regular condition (i.e., a tuple of regular literals) for $1\le i\le n$. Whether the last part ‘${}\diamond c$’ is included depends on the form of a theory atom definition. Further, observe that theory atoms with occurrence type any can be used both in the head and body of a rule; with occurrence types head and body, their usage can be restricted to rule heads and bodies only. Occurrence type directive is similar to type head but additionally requires that the rule body must be completely evaluated during grounding. Five occurrences of theory atoms can be found in lines 22–27 of Listing 1.6.

A theory term definition has form

where t is a name for the defined terms and each $D_i$ is a theory operator definition for $1\le i\le n$. A respective definition specifies the language of all theory terms that can be constructed via its operators. Examples of theory term definitions are given in lines 3–9 of Listing 1.6. Each resulting theory term is one of the following:

where each $t_i$ is a theory term, $\diamond$ is a theory operator defined by some $D_i$, c and f are symbolic constants, v is a first-order variable, $k\ge 1$, and $l\ge 0$. (The trailing comma in tuple theory terms is optional if $l \ne 1$.) Parentheses can be used to specify operator precedence.

A theory operator definition has form

where $\diamond$ is a unary or binary theory operator with precedence $p\ge 0$ (determining implicit parentheses). Binary theory operators are additionally characterized by an associativity $a\in \{\texttt {right},\texttt {left}\}$. As an example, consider lines 5–6 of Listing 1.6, where the left associative binary operators + and * are defined with precedence 2 and 1. Hence, parentheses in terms like ‘(X+(2*Y))+Z’ can be omitted. In total, lines 3–9 of Listing 1.6 include nine theory operator definitions. Specific theory operators can be assembled (written consecutively without spaces) from the symbols ‘!’, ‘$\texttt {<}$’, ‘=’, ‘$\texttt {>}$’, ‘+’, ‘-’, ‘*’, ‘

’, ‘

’, ‘?’, ‘&’, ‘|’, ‘.’, ‘:’, ‘;’, ‘

’, and ‘

’. For instance, in line 8 of Listing 1.6, the operator ‘..’ is defined as the concatenation of two periods. The tokens ‘.’, ‘:’, ‘;’, and ‘:-’ must be combined with other symbols due to their dedicated usage. Instead, one may write ‘..’, ‘

’, ‘;;’, ‘::-’, etc.

While theory terms are formed similar to regular ones, theory atoms rely upon an aggregate-like construction for forming variable-length theory expressions. In this way, standard grounding techniques can be used for gathering theory terms. (However, the actual atom &a within a theory atom comprises regular terms only.) The treatment of theory terms still differs from their regular counterparts in that the grounder skips simplifications like, e.g., arithmetic evaluation. This can be nicely seen on the different results in Listing 1.7 of grounding terms formed with the regular and theory-specific variants of operator ‘..’. Observe that the fact task(1..n) in line 19 of Listing 1.6 results in n ground facts, viz. task(1) and task(2) because of n=2. Unlike this, the theory expression 1..m stays structurally intact and is only transformed into 1..1000 in view of m=1000. That is, the grounder does not evaluate the theory term 1..1000 and leaves its interpretation to a downstream theory solver. A similar situation is encountered when comparing the treatment of the regular term ‘200*T’ in line 20 of Listing 1.6 to the theory term ‘end(T)-start(T)’ in line 24. While each instance of ‘200*T’ is evaluated during grounding, instances of the theory term ‘end(T)-start(T)’ are left intact in lines 11 and 12 of Listing 1.7. In fact, if ‘200*T’ had been a theory term as well, it would have resulted in the unevaluated instances ‘200*1’ and ‘200*2’.

4.2 Semantic Underpinnings

Given the hands-on nature of this tutorial, we only give an informal idea of the semantic principles underlying theory solving in ASP.

As mentioned in Sect. 2, a logic program induces a set of stable models. To extend this concept to logic programs with theory expressions, we follow the approach of lazy theory solving [5]. We abstract from the specific semantics of a theory by considering the theory atoms representing the underlying theory constraints. The idea is that a regular stable model of a program over regular and theory atoms is only valid with respect to a theory, if the constraints induced by the truth assignment to the theory atoms are satisfiable in the theory.

In the above example, this amounts to finding a numeric assignment to all theory variables satisfying all difference and linear constraints associated with theory atoms. The ground program in 1.7 has a single stable model consisting of all regular and theory atoms in lines 1–16. Here, we easily find assignments satisfying the induced constraints, e.g. $\texttt {start(1)}\mapsto 1$, $\texttt {end(1)}\mapsto 2$, $\texttt {start(2)}\mapsto 2$, and $\texttt {end(1)}\mapsto 3$.

In fact, there are alternative semantic options for capturing theory atoms, as detailed in [18]. First of all, we may distinguish whether imposed constraints are only determined outside or additionally inside a logic program. This leads to the distinction between defined and external theory atoms.¹¹ While external theory atoms must only be satisfied by the respective theory, defined ones must additionally be derivable through rules in the program. The second distinction concerns the interplay of ASP with theories. More precisely, it is about the logical correspondence between theory atoms and theory constraints. This leads us to the distinction between strict and non-strict theory atoms. The strict correspondence requires a constraint to be satisfied iff the associated theory atom is true. A weaker since only implicative condition is imposed in the non-strict case. Here, a constraint must hold only if the associated theory atom is true. In other words, only non-strict theory atoms assigned true impose requirements, while constraints associated with falsified non-strict theory atoms are free to hold or not. However, by contraposition, a violated constraint leads to a false non-strict theory atom.

4.3 Algorithmic Aspects

The algorithmic approach to ASP solving modulo theories of clingo, or more precisely that of its underlying ASP solver clasp, follows the lazy approach to solving in Satisfiability Modulo Theories (SMT [5]). We give below an abstract overview that serves as light algorithmic underpinning for the description of clingo’s implementation given in the next section.

As detailed in [22], a ground program P induces completion and loop nogoods, called $\varDelta _P$ or $\varLambda _P$, respectively, that can be used for computing stable models of P. Nogoods represent invalid partial assignments and can be thought of as negative Boolean constraints. We represent (partial) assignments as consistent sets of literals. An assignment is total if it contains either the positive or negative literal of each atom. We say that a nogood is violated by an assignment if the former is contained in the latter; a nogood is unit if all but one of its literals are in the assignment. Each total assignment not violating any nogood in $\varDelta _P\cup \varLambda _P$ yields a regular stable model of P, and such an assignment is called a solution (for $\varDelta _P\cup \varLambda _P$). To accommodate theories, we identify a theory T with a set $\varDelta _T$ of theory nogoods,¹² and extend the concept of a solution in the straightforward way.

The nogoods in $\varDelta _P\cup \varLambda _P\cup \varDelta _T$ provide the logical fundament for the Conflict-Driven Constraint Learning (CDCL) procedure (cf. [22, 32]) outlined in Fig. 2. While the completion nogoods in $\varDelta _P$ are usually made explicit and subject to unit propagation,¹³ the loop nogoods in $\varLambda _P$ as well as theory nogoods in $\varDelta _T$ are typically handled by dedicated propagators and particular members are selectively recorded.

Fig. 2.

Basic algorithm for Conflict-Driven Constraint Learning (CDCL) modulo theories

While a dedicated propagator for loop nogoods is built-in in systems like clingo, those for theories are provided via the interface Propagator in Fig. 3. To utilize custom propagators, the algorithm in Fig. 2 includes an initialization step in line (I). In addition to the “registration” of a propagator for a theory as an extension of the basic CDCL procedure, common tasks performed in this step include setting up internal data structures and so-called watches for (a subset of) the theory atoms, so that the propagator will be invoked (only) when some watched literal gets assigned.

As usual, the main CDCL loop starts with unit propagation on completion and loop nogoods, the latter handled by the respective built-in propagator, as well as any nogoods already recorded. If this results in a non-total assignment without conflict, theory propagators for which some of their watched literals have been assigned are invoked in line (P). A propagator for a theory T can then inspect the current assignment, update its data structures accordingly, and most importantly, perform theory propagation determining theory nogoods $\delta \in \varDelta _T$ to record. Usually, any such nogood $\delta$ is unit in order to trigger a conflict or unit propagation, although this is not a necessary condition. The interplay of unit and theory propagation continues until a conflict or total assignment arises, or no (further) watched literals of theory propagators get assigned by unit propagation. In the latter case, some non-deterministic decision is made to extend the partial assignment at hand and then to proceed with unit and theory propagation.

If no conflict arises and an assignment is total, in line (C), theory propagators are called, one by one, for a final check. The idea is that, e.g., a “lazy” propagator for a theory T that does not exhaustively test violations of its theory nogoods by partial assignments can make sure that the assignment is indeed a solution for $\varDelta _T$, or record some violated nogood(s) from $\varDelta _T$ otherwise. Even in case theory propagation on partial assignments is exhaustive and a final check is not needed to detect conflicts, the information that search led to a total assignment can be useful in practice, e.g., to store values for integer variables like start(1), start(2), end(1), and end(2) in Listing 1.7 that witness the existence of a solution for T.

Finally, in case of a conflict, i.e., some completion or recorded nogood is violated by the current assignment, provided that some non-deterministic decision is involved in the conflict, a new conflict constraint is recorded and utilized to guide backjumping in line (U), as usual with CDCL. In a similar fashion as the assignment of watched literals serves as trigger for theory propagation, theory propagators are informed when they become unassigned upon backjumping. This allows the propagators to undo earlier operations, e.g., internal data structures can be reset to return to a state taken prior to the assignment of watches.

In summary, the basic CDCL procedure is extended in four places to account for custom propagators: initialization, propagation of (partial) assignments, final check of total assignments, and undo steps upon backjumping.

4.4 Propagator Interface

We now turn to the implementation of theory propagation in clingo 5 and detail the structure of its interface depicted in Fig. 3. The interface Propagator has to be implemented by each custom propagator. After registering such a propagator with clingo, its functions are called during initialization and search as indicated in Fig. 2. Function Propagator.init ¹⁴ is called once before solving (line (I) in Fig. 2) to allow for initializing data structures used during theory propagation. It is invoked with a PropagateInit object providing access to symbolic (SymbolicAtom) as well as theory (TheoryAtom) atoms. Both kinds of atoms are associated with program literals,¹⁵ which are in turn associated with solver literals.¹⁶ Program as well as solver literals are identified by non-zero integers, where positive and negative numbers represent positive or negative literals, respectively. In order to get notified about assignment changes, a propagator can set up watches on solver literals during initialization.

Fig. 3.

Class diagram of clingo’s (theory) propagator interface

During search, function propagate is called with a PropagateControl object and a (non-empty) list of watched literals that got assigned in the recent round of unit propagation (line (P) in Fig. 2). The PropagateControl object can be used to inspect the current assignment, record nogoods, and trigger unit propagation. Furthermore, to support multi-threaded solving, its thread_id property identifies the currently active thread, each of which can be viewed as an independent instance of the CDCL algorithm in Fig. 2.¹⁷ Function undo is the counterpart of propagate and called whenever the solver retracts assignments to watched literals (line (U) in Fig. 2). In addition to the list of watched literals that have been retracted (in chronological order), it receives the identifier and the assignment of the active thread. Finally, function check is similar to propagate, yet invoked without a list of changes. Instead, it is (only) called on total assignments (line (C) in Fig. 2), independently of watches. Overriding the empty default implementations of propagator methods is optional. For brevity, we below focus on implementations of the methods in Python, while C, C++, or Lua could be used as well.

5 A Case-Study on ASP Modulo Difference Logic

In this section, we develop a propagator to extend ASP with quantifier free integer difference logic (IDL). The complete source code of this propagator is available in the github repository at https://github.com/potassco/clingo/tree/master/examples/clingo/dl.

In addition to the rules introduced in Sect. 2, we now also support rules of form

where u and v are (regular) terms, d is an integer constant, each $a_i$ is an atom, and $0 \le n \le o$. For simplicity, we restrict the occurrence of theory atoms to rule heads.¹⁸ Hence, stable models may now also include theory atoms of form ‘${\texttt { \& diff}}\{u-v\} <= d$’. More precisely, for a stable model X, let $C_X$ be the set of difference constraints such as $u-v \le d$ associated with theory atoms ‘${\texttt { \& diff}}\{u-v\} <= d$’ in X and $V_X$ be the set of all (integer) variables occurring in the difference constraints in $C_X$. In our case, a stable model X is then IDL-stable, if there is a mapping from $V_X$ to the set of integers satisfying all constraints in $C_X$.

To allow for writing difference constraints in rule heads, we define theory dl in lines 1–5 in Listing 1.8, a subset of the theory lc presented in Listing 1.6 in Sect. 4.1. The following lines 16–20 implement a customized main function. The difference to clingo’s regular main function is that a propagator for difference constraints is registered at the beginning; grounding and solving then follow as usual. Note that the solve function in line 20 takes a model callback as argument. Whenever an IDL-stable model X is found, this callback prints the mapping satisfying the corresponding difference constraints $C_X$. The model X (excluding theory atoms) is printed as part of clingo’s default output.

Fig. 4.

Class diagram for the graph class

Our exemplary propagator implements the algorithm presented in [10]. The idea is that deciding whether a set of difference constraints is satisfiable can be mapped to a graph problem. Given a set of difference constraints, let (V, E) be the weighted directed graph where V is the set of variables occurring in the constraints, and E the set of edges (u, v, d) for each constraint $u-v\le d$. The set of difference constraints is satisfiable if the corresponding graph does not contain a negative cycle. The Graph class whose interface is given in Fig. 4 is in charge of cycle detection. We refrain from giving the code of the Graph class and rather concentrate on describing its interface:

• Function add_edge adds an edge of form (u,v,d) to the graph. If after adding the edge to the graph there is a negative cycle, the function returns the cycle in form of a list of edges; otherwise, it returns None. Furthermore, each edge added to the graph is associated with a decision level¹⁹. This additional information is used to backtrack to a previous state of the graph, whenever the solver has to backtrack to recover from a conflict.

• Function backtrack takes a decision level as argument. It removes all edges added on that level from the graph. For this to work, decision levels have to be backtracked in chronological order. Note that the CDCL algorithm in Fig. 2 calling our propagator also backtracks decision levels in chronological order.

• As a side effect, the Graph class internally maintains an assignment of integers to nodes. This assignment can be turned into an assignment to the variables such that the difference constraints corresponding to the edges of the graph are satisfied. Function get_assignment returns this assignment in form of a list of pairs of variables and integers.

We give our exemplary propagator for difference constraints in Listing 1.9. It implements the Propagator interface (except for check) in Fig. 3 in lines 105–133, while featuring aspects like incremental propagation and backtracking, solving with multiple threads, and multi-shot solving. Whenever the set of edges associated with the current partial assignment of a solver induces a negative cycle and, hence, the corresponding difference constraints are unsatisfiable, it adds a nogood forbidding the negative cycle. To this end, it maintains data structures for, given newly added edges, detecting whether there is a conflict. More precisely, the propagator has three data members:

• 1. The self.__l2e dictionary in line 101 maps solver literals for difference constraint theory atoms to their corresponding edges²⁰,

• 2. the self.__e2l dictionary in line 102 maps edges back to solver literals,²¹

• 3. and the self.__state list in line 103 stores for each solver thread its current graph with the edges assigned so far.

Function init in lines 105–119 sets up watches as well as the dictionaries in self.__l2e and self.__e2l. To this end, it traverses the theory atoms over diff/0 in lines 106–119. Note that the loop simply ignores all other theory atoms making it possible to also add propagators for other theories. In lines 109–115 we extract the edge from the theory atom.²² Each such atom is associated with a solver literal, obtained in line 116. The mappings between solver literals and corresponding edges are then stored in the self.__l2e and self.__e2l dictionaries in lines 117 and 118.²³ In the last line of the loop, a watch is added for each solver literal at hand, so that the solver calls propagate whenever the edge has to be added to the graph.

Function propagate, given in lines 121–130, accesses control.thread_id in line 122 to obtain the graph associated with the active thread. The loops in lines 124–130 then iterate over the list of changes and associated edges. In line 126 each such edge is added to the graph. If adding the edge produced a negative cycle, a nogood is added in line 129. Because an edge can be associated with multiple solver literals, we use function ___literal__literal retrieving the first solver literal associated with an edge that is true, to construct the nogood forbidding the cycle. Given that the solver has to resolve the conflict and backjump, the call to add_nogood always yields false, so that propagation is stopped without processing the remaining changes any further.²⁴

Given that each edge added to the graph in line 126 is associated with the current decision level, the implementation of function undo is quite simple. It calls function backtrack on the solver’s graph to remove all edges added on the current decision level.

Fig. 5.

Flow shop: instance with three tasks and two machines

Fig. 6.

Flow shop: solutions for all possible permutations with the total execution length in the top right corner and optimal solutions with a blue background (Color figure online)

To see our propagator in action, we consider the flow shop problem, dealing with a set of tasks T that have to be consecutively executed on m machines. Each task has to be processed on each machine from 1 to m. Different parts of one task are completed on each machine resulting in the completion of the task after execution on all machines is finished. Before a task can be processed on machine i, it has to be finished on machine $i-1$. The duration of different tasks on the same machine may vary. A task can only be executed on one machine at a time and a machine must not be occupied by more than one task at a time. An (optimal) solution to the problem is a permutation of tasks so that all tasks are finished as early as possible.

Figure 5 depicts a possible instance for the flow shop problem. The three tasks a, b, and c have to be scheduled on two machines. The colored boxes indicate how long a task has to run on a machine. Lighter shades of the same color are for the first and darker ones for the second machine. For example, task a needs to be processed for 3 time units on the first and 4 time units on the second machine.

Next we encode this problem using difference constraints. We give in Listing 1.10a straightforward encoding of the instance in Fig. 5. Listing 1.11 depicts the encoding of the flow shop problem. Following the generate, define, and test methodology of ASP, we first generate in lines 1–14 all possible permutations of tasks, where atoms of form permutation(T,U) encode that task T has to be executed before task U. Then, in the following lines 16–21, we use difference constraints to calculate the duration of the generated permutation. The difference constraint in line 20 guarantees that the tasks are executed in the right order. For example, $\texttt {(a,1)} - \texttt {(a,2)} \le -d$ ensures that task a can only be executed on machine 2 if it has finished on machine 1. Hence, variable (a,2) has to be assigned so that it is greater or equal to $\texttt {(a,2)}-d$ where d is the duration of task a on machine 1. Similarly, $\texttt {(a,1)} - \texttt {(b,1)} \le -d$ makes sure that task b can only be executed on machine 1 if task a has finished on machine 1. While the first constraint is a fact (see line 17), the latter is subject to the generated permutation of tasks (see line 18). The difference constraint in line 21 ensures that all time points at which a task is started are greater than zero. Note that this constraint is in principle redundant but since sets of difference constraints always have infinitely many solutions it is good practice to encode relative to a starting point. Furthermore, note that 0 is actually a variable. In fact, the Graph class takes care of subtracting the value of variable 0 from all other variables when returning an assignment to get easier interpretable solutions.

Running encoding and instance with the dl propagator results in the following 6 solutions corresponding to the solutions in Fig. 6.²⁵ One for each possible permutation of tasks:

Finally, to find optimal solutions, we combine the algorithms in Listings 1.3 and 1.8 to minimize the total execution time of the tasks. The adapted algorithm is given in Listing 1.12. As with algorithm in 1.8, a propagator is registered before solving. And the control flow is similar to the branch-and-bound-based optimization algorithm in Listing 1.3 except that we now minimize the variable bound; or better the difference between variable 0 and bound by adding the difference constraint $\texttt {0} - \texttt {bound} \le b$ to the program in line 9 where b is the best known execution time of the tasks as obtained from the assignment in line 23 minus 1. To bound maximum execution time of the task, we have to add one more line to the encoding in Listing 1.11:

This makes sure that each task ends within the given bound. Running encoding and instance with the dl propagator results in the optimum bound 16 where the obtained solution corresponds to the left of the two optimal solutions indicated by a light blue background in Fig. 6:

6 Discussion

We described two essential techniques, viz. multi-shot and theory solving, for enhancing ASP solving by different forms of hybridization. While multi-shot solving allows for fine-grained control of ASP reasoning processes, theory solving allows for refining basic ASP solving by incorporating foreign types of constraints. Since ASP follows a model, ground, and solve methodology both techniques pervade the whole work-flow of ASP, starting with extensions to the input language, over means for incremental and theory-enhanced grounding, to stateful and theory-enhanced solving. Multi-shot solving even adds a fourth dimension to control ASP reasoning processes.

Our focus on clingo should not conceal other approaches to hybrid ASP solving. Foremost, dlvhex [36] builds upon clingo’s infrastructure to provide a higher level of hybridization via higher-order logic programs. As well, clingcon [3] and lc2casp [8] rely on clingo for extending ASP with linear constraints over integers. Similar yet customized approaches include adsolver [33], inca [13], and ezcsp [1]. Another category of ASP systems, such us ezsmt [29], dingo [27], and aspmt [6] translate ASP with constraints to SAT Modulo Theories (SMT [34]) and use appropriate back-ends. Similarly, mingo [31] translates to Mixed Integer Linear Programming (MILP) and aspartame [2] back to ASP using the order encoding [11, 40].

Theory propagators have recently also been added to the ASP solver wasp [12]; these can be made accessible via the theory language of Sect. 4.1 along with the intermediate format described in Appendix A.

A Intermediate Language

To accommodate the richer input language, a more general grounder-solver interface is needed. Although this could be left internal to clingo 5, it is good practice to explicate such interfaces via an intermediate language. This also allows for using alternative downstream solvers or transformations.

Unlike the block-oriented smodels format, the aspif ²⁶ format is line-based. Notably, it abolishes the need of using symbol tables in smodels’ format²⁷ for passing along meta-expressions and rather allows gringo5 to output information as soon as it is grounded. An aspif file starts with a header, beginning with the keyword asp along with version information and optional tags:

where $v_m,v_n,v_r$ are non-negative integers representing the version in terms of major, minor, and revision numbers, and each $t_i$ is a tag for $k\ge 0$. Currently, the only tag is incremental, meant to set up the underlying solver for multi-shot solving. An example header is given in line 1 of Listings 1.13a and 1.14. The rest of the file is comprised of one or more logic programs. Each logic program is a sequence of lines of aspif statements followed by a 0, one statement or 0 per line, respectively. Positive and negative integers are used to represent positive or negative literals, respectively. Hence, 0 is not a valid literal.

Let us now briefly describe the format of aspif statements and illustrate them with a simple logic program in Listing 1.13 as well as the result of grounding a subset of Listing 1.6 in Listing 1.14.

Rule statements have form

in which head H has form

where $h \in \{\texttt {0},\texttt {1}\}$ determines whether the head is a disjunction or choice, $m \ge 0$ is the number of head elements, and each $a_i$ is a positive literal.

Body B has one of two forms:

• Normal bodies have form

  

  where $n \ge 0$ is the length of the rule body, and each $l_i$ is a literal.

• Weight bodies have form

  

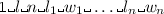
  where l is a positive integer to denote the lower bound, $n \ge 0$ is the number of literals in the rule body, and each $l_i$ and $w_i$ are a literal and a positive integer.

All types of ASP rules are included in the above rule format. Heads are disjunctions or choices, including the special case of singular disjunctions for representing normal rules. As in the smodels format, aggregates are restricted to a singular body, just that in aspif cardinality constraints are taken as special weight constraints. Otherwise, a body is simply a conjunction of literals.

The three rules in Listing 1.13a are represented by the statements in lines 2–4 of Listing 1.13b. For instance, the four occurrences of 1 in line 2 capture a rule with a choice in the head, having one element, identified by 1. The two remaining zeros capture a normal body with no element. For another example, lines 2–7 of Listing 1.14 represent the four facts in lines 1 and 2 of Listing 1.7 along with the ones (comprising theory atoms) in line 6 of Listing 1.7.

Minimize statements have form

where p is an integer priority, $n \ge 0$ is the number of weighted literals, each $l_i$ is a literal, and each $w_i$ is an integer weight. Each of the above expressions gathers weighted literals sharing the same priority p from all #minimize directives and weak constraints in a logic program. As before, maximize statements are translated into minimize statements.

Projection statements result from #project directives and have form

where $n \ge 0$ is the number of atoms, and each $a_i$ is a positive literal.

Output statements result from #show directives and have form

where $n \ge 0$ is the length of the condition, each $l_i$ is a literal, and $m\ge 0$ is an integer indicating the length in bytes of string s (where s excludes byte ‘\0’ and newline). The output statements in lines 5–7 of Listing 1.13b print the symbolic representation of atom a, b, or c, whenever the corresponding atom is true. For instance, the string ‘a’ is printed if atom ‘1’ holds. Unlike this, the statements in lines 8–11 of Listing 1.14 unconditionally print the symbolic representation of the atoms stemming from the four facts in lines 1 and 2 of Listing 1.7.

External statements result from #external directives and have form

where a is a positive literal, and $v \in \{0,1,2,3\}$ indicates free, true, false, and release.

Assumption statements have form

where $n\ge 0$ is the number of literals, and each $l_i$ is a literal. Assumptions instruct a solver to compute stable models such that $l_1,\dots ,l_n$ hold. They are only valid for a single solver call.

Heuristic statements result from #heuristic directives and have form

where $m\in \{0,\dots ,5\}$ stands for the (m+1)th heuristic modifier among level, sign, factor, init, true, and false, a is a positive literal, k is an integer, p is a non-negative integer priority, $n \ge 0$ is the number of literals in the condition, and the literals $l_i$ are the condition under which the heuristic modification should be applied.

Edge statements result from #edge directives and have form

where u and v are integers representing an edge from node u to node v, $n \ge 0$ is the length of the condition, and the literals $l_i$ are the condition for the edge to be present.

Let us now turn to the theory-specific part of aspif. Once a theory expression is grounded, gringo 5 outputs a serial representation of its syntax tree. To illustrate this, we give in Listing 1.14 the (sorted) result of grounding all lines of Listing 1.6 related to difference constraints, viz. lines 2/3, 11, 15/16, and 19, as well as lines 1 and 13.

Theory terms are represented using the following statements:

(1)

(2)

(3)

where $n \ge 0$ is a length, index u is a non-negative integer, integer w represents a numeric term, string s of length n represents a symbolic term (including functions) or an operator, integer t is either -1, -2, or -3 for tuple terms in parentheses, braces, or brackets, respectively, or an index of a symbolic term or operator, and each $u_i$ is an integer for a theory term. Statements (1), (2), and (3) capture numeric terms, symbolic terms, as well as compound terms (tuples, sets, lists, and terms over theory operators).

Fifteen theory terms are given in lines 12–26 of Listing 1.14. Each of them is identified by a unique index in the third spot of each statement. While lines 12–20 stand for primitive entities of type (1) or (2), the ones beginning with represent compound terms. For instance, line 21 and 22 represent end(1) or start(1), respectively, and line 23 corresponds to end(1)-start(1).

Theory atoms are represented using the following

(4)

(5)

(6)

where $n \ge 0$ and $m \ge 0$ are lengths, index v is a non-negative integer, a is a positive literal or 0 for directives, each $u_i$ is an integer for a theory term, each $l_i$ is an integer for a literal, integer p refers to a symbolic term, each $v_i$ is an integer for a theory atom element, and integer g refers to a theory operator. Statement (4) captures elements of theory atoms and directives, and statements (5) and (6) refer to the latter.

For instance, line 27 captures the (single) theory element in ‘{ end(1)-start(1) }’, and line 29 represents the theory atom ‘&diff { end(1)-start(1) }<=200’.

Comments have form

where s is a string not containing a newline.

The aspif format constitutes the default output of gringo 5. With clasp 3.2, ground logic programs can be read in both smodels and aspif format.