Keywords

1 Introduction

Parallel mechanisms in robotic legs are seldom used, since they usually have a smaller workspace than serial mechanisms of the same size. However, parallel architectures perform better in accuracy and payloads [1, 2] and therefore they can substitute serial mechanisms when they fulfil workspace requirements. Some examples of parallel mechanisms used as robot legs can be found in [3,4,5,6]. The novel tripod architecture that is analysed in this paper is proposed in [7,8,9] while its kinematics is briefly described in Sect. 2. In order to find an optimal design for the mechanism, a multi-objective optimization is proposed in this work. The objective functions for the optimization of parallel mechanisms are discussed in many research works, such as [10,11,12,13,14,15,16]. In these studies, several indices have been proposed in order to characterize the workspace of the manipulator, its kinematic and dynamic performance and its stiffness. Among them, the workspace volume and the efficiency in force transmission are the most relevant ones for a robotic leg mechanism. Therefore, these two functions are evaluated in their closed-form expressions in Sect. 3 for the proposed structure, while Sect. 4 shows the multi-objective optimization solution by mapping the objective functions in the parameter space and discussing the results in order to find an optimal design.

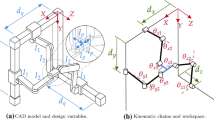
2 Mechanism Description

The subject of the paper is the 3 degrees-of-freedom mechanism shown in Fig. 1 and introduced in [7,8,9]. It is composed by a fixed frame and by an end-effector body that are connected by three U P R chains. Referring to Fig. 1a, each chain consists of a linear actuator with length l i that is connected to the fixed frame by a universal joint in Ai and to the end-effector by a revolute joint, in H. The structure is characterized by the fact that the three revolute joints are located at the end-effector point H thanks to the mechanism shown in Fig. 1b: link 1 rotates around the x-axis of the end-effector mechanism, while link 2 and link 3 can only rotate around the Y-axis. The position of point H can be found as the intersection of three spheres centred in Ai with radius equal to l i , for i = {1, 2, 3}. Thus, this particular configuration of the end-effector notably simplifies the kinematics of the structure. According to this, if the frame is an equilateral triangle with side length a and characterized by Eq. (1),

Fig. 1.
figure 1

Kinematic diagrams of the proposed mechanism: a. tripod structure; b. end-effector mechanism

Full size image
$$ {}_{{}}^{0} \varvec{A}_{1} = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right);\varvec{ }\;\varvec{ }{}_{{}}^{0} \varvec{A}_{2} = \left( {\begin{array}{*{20}c} a \\ 0 \\ 0 \\ \end{array} } \right);\varvec{ }\;\varvec{ }{}_{{}}^{0} \varvec{A}_{3} = \left( {\begin{array}{*{20}c} {a/2} \\ {\surd 3\,a/2} \\ 0 \\ \end{array} } \right), $$
(1)

the direct kinematic problem of the structure is solved as Eq. (2),

$$ x = \frac{1}{2a}\left( {l_{1}^{2} - l_{2}^{2} + a^{2} } \right) $$
(2)
$$ y = \frac{1}{2\sqrt 3 a}\left( {l_{1}^{2} + l_{2}^{2} - 2l_{3}^{2} + a^{2} } \right) $$
$$ z = - \sqrt {\frac{{ - l_{1}^{4} - l_{2}^{4} - l_{3}^{4} - a^{4} + l_{1}^{2} l_{2}^{2} + l_{1}^{2} l_{3}^{2} + l_{2}^{2} l_{3}^{2} + a^{2} \left( {l_{1}^{2} + l_{2}^{2} + l_{3}^{2} } \right)}}{{3a^{2} }}} . $$

where x, y, z are the coordinates of the end point H.

This paper analyses and gives the optimization for a configuration with an equilateral triangle as base frame. Non-equilateral configuration for the base frame have also been investigated but held worse results. The kinematic problem of the structure is written in position only and not in orientation because the end-effector is analytically described as a punctiform body. Since the end-effector is the mechanism in Fig. 1b, it is possible to evaluate its orientation with Euler angles as Eq. (3),

$$ \begin{array}{*{20}c} {\alpha = \tan^{ - 1} \frac{{\left( {l_{1}^{2} + l_{2}^{2} - 2l_{3}^{2} + a^{2} } \right)}}{{2\sqrt { - l_{1}^{4} - l_{2}^{4} - l_{3}^{4} - a^{4} + l_{1}^{2} l_{2}^{2} + l_{1}^{2} l_{3}^{2} + l_{2}^{2} l_{3}^{2} + a^{2} \left( {l_{1}^{2} + l_{2}^{2} + l_{3}^{2} } \right)} }}} \\ {\beta = \arctan \frac{{l_{1}^{2} - l_{2}^{2} }}{{\sqrt {4a^{2} l_{3}^{2} - l_{2}^{4} - l_{1}^{4} + 2l_{1}^{2} l_{2}^{2} } }}} \\ {\gamma = 0} \\ \end{array} $$
(3)

where α is the rotation angle of the end effector around the X-axis, β is the intrinsic rotation around the Y-axis and γ is the one around the Z-axis.

Nevertheless, its Jacobian can be written as a 3 × 3 matrix as Eq. (4).

$$ \varvec{J}_{\varvec{p}} = \left[ {\begin{array}{*{20}c} {\frac{{l_{1} }}{a}} & { - \frac{{l_{2} }}{a}} & 0 \\ {\frac{{l_{1} }}{\sqrt 3 a}} & {\frac{{l_{2} }}{\sqrt 3 a}} & { - \frac{{2l_{3} }}{\sqrt 3 a}} \\ {\frac{{l_{1} \left( { - 2l_{1}^{2} + l_{2}^{2} + l_{3}^{2} + a^{2} } \right)}}{{3a^{2} z}}} & {\frac{{l_{2} \left( {l_{1}^{2} - 2l_{2}^{2} + l_{3}^{2} + a^{2} } \right)}}{{3a^{2} z}}} & {\frac{{l_{3} \left( {l_{1}^{2} + l_{2}^{2} - 2l_{3}^{2} + a^{2} } \right)}}{{3a^{2} z}}} \\ \end{array} } \right] $$
(4)

The inverse Jacobian can be computed from Eq. (4) as Eq. (5).

$$ \varvec{J}_{\varvec{p}}^{ - 1} = \left[ {\begin{array}{*{20}c} {\frac{x}{{l_{1} }}} & {\frac{y}{{l_{1} }}} & {\frac{z}{{l_{1} }}} \\ {\frac{x - a}{{l_{2} }}} & {\frac{y}{{l_{2} }}} & {\frac{z}{{l_{2} }}} \\ {\frac{{x - \frac{a}{2}}}{{l_{3} }}} & {\frac{{y - \frac{\sqrt 3 a}{2}}}{{l_{3} }}} & {\frac{z}{{l_{3} }}} \\ \end{array} } \right] $$
(5)

The singularities of the mechanism are evaluated by using Eq. (4). The Jacobian matrix is singular only in the plane z = 0 that the end-effector cannot physically reach because of the angular limitations of the universal joints on the base frame. Therefore, the reachable workspace of the mechanism can be obtained by computing Eq. (6),

$$ \varvec{H} = \left( {x, y,z} \right)^{T} \;\;for\; l_{1} , \,l_{2} , \,l_{3} \in \left[ {l_{0} ,l_{0} + s} \right] $$
(6)

and it is coincident with its singularity-free workspace.

3 Kinematic and Dynamic Performance

In order to optimise the mechanism design, kinematic and dynamic performances have to be evaluated. Several functions have been proposed as numerical indices to compute both kinematic and dynamic performances of parallel mechanisms [1, 10,11,12,13,14,15,16]. Basic performance for the optimal design of the proposed mechanism can be evaluated in terms of workspace and force transmission, since these two parameters are the most important ones for the application of the manipulator as a robotic leg.

3.1 Workspace Volume

The workspace volume is the first parameter that can be used as objective function for optimization [1]. For the proposed 3-DoF manipulator the workspace can be evaluated as maximal or reachable workspace, which includes all the points that can be reached by the end-effector with at least one orientation. An example of reachable workspace for the proposed mechanism can be computed by discretising the actuation variables [2] and it is shown in Fig. 2.

Fig. 2.
figure 2

Reachable workspace of the mechanism for a = 1, l min  = 2a, l max  = 3a; a. upper view; b. lateral view.

Full size image

The shape of the reachable workspace of the mechanism, however, is irregular and its implementation in control algorithm for particular trajectories can be difficult. Therefore, a workspace formed of simple geometrical shapes is preferred. Since the proposed mechanism has axial symmetry, it is possible to obtain the operational workspace as part of a circular trajectory on the XY plane that is contained in the workspace itself. Figure 3 illustrates an example of operational workspace for the particular geometry that was already used for Fig. 2.

Fig. 3.
figure 3

Workspace as maximum circular trajectories of the mechanism for a = 1, l min  = 2a, l max  = 3a; a. upper view; b. lateral view

Full size image

3.2 Force Transmission

In order to evaluate the static performance of the manipulator, it is necessary to write the actuation forces and the reaction forces on the foot respectively as Eq. (7).

$$ \varvec{\tau}= \left( {\tau_{1} \;\tau_{2} \; \tau_{3} } \right)^{T} ,\;\;\;\varvec{w} = \left( {f_{1} \;f_{2} \;f_{3} } \right)^{T} $$
(7)

It is possible to define an index to evaluate the efficiency of the leg as Eq. (8).

$$ \eta = \frac{\varvec{w}}{{\mathop \sum \nolimits_{i = 1}^{3} \tau_{i} }} $$
(8)

This efficiency index is position dependent and it allows to evaluate the ratio between a force applied on the end-effector and the actuation needed to balance it. In a static condition, the reaction force vector can be defined as Eq. (9),

$$ \varvec{w}_{\varvec{s}} = \left( {0 \;0\; R} \right)^{T} $$
(9)

where the only non-zero component is the reaction force between end-effector and ground, which is along the z-axis. Thus, it is possible to compute Eq. (8) for the proposed leg mechanism as Eq. (10).

$$ \begin{array}{*{20}c} {\eta = \frac{{\left| {a^{2} z} \right|}}{{\mathop \sum \nolimits_{i = 1}^{3} \left| {l_{i} k_{i} } \right|}}} \\ {with\; k_{1} = - 2l_{1}^{2} + l_{2}^{2} + l_{3}^{2} + a^{2} ; \;k_{2} = l_{1}^{2} - 2l_{2}^{2} + l_{3}^{2} + a^{2} ;} \\ {k_{3} = l_{1}^{2} + l_{2}^{2} - 2l_{3}^{2} + a^{2} .} \\ \end{array} $$
(10)

4 A Multi-objective Optimization Design Procedure

A multi-objective optimization is the search of an optimal set of parameters, which are subject to constraint functions, with regards to two or more objective functions. The problem can be defined as Eq. (11),

$$ \begin{array}{*{20}c} {\hbox{min} \varvec{F}\left( \varvec{r} \right) = \hbox{min} \left[ {f_{1} \left( \varvec{r} \right) f_{2} \left( \varvec{r} \right) \cdots f_{n} \left( \varvec{r} \right)} \right]^{T} , \;\;\;\;\varvec{r} = \left[ {r_{1} r_{2} \cdots r_{m} } \right]^{T} } \\ { with\; \;\varvec{F}:{\mathbb{R}}^{m} \to {\mathbb{R}}^{n} , \;\varvec{F}\left( \varvec{r} \right) = \left[ {f_{1} \left( \varvec{r} \right) f_{2} \left( \varvec{r} \right) \cdots f_{n} \left( \varvec{r} \right)} \right]^{T} } \\ \end{array} $$
(11)

subject to Eq. (12),

$$ \begin{array}{*{20}c} {\varvec{g}\left( \varvec{r} \right) \le 0, \;\;\varvec{h}\left( \varvec{r} \right) = 0} \\ {\varvec{g}\left( \varvec{r} \right) = \left[ {g_{1} \left( \varvec{r} \right) g_{2} \left( \varvec{r} \right) \cdots g_{p} \left( \varvec{r} \right)} \right]^{T} } \\ { \varvec{h}\left( \varvec{r} \right) = \left[ {h_{1} \left( \varvec{r} \right) h_{2} \left( \varvec{r} \right) \cdots h_{t} \left( \varvec{r} \right)} \right]^{T} } \\ \end{array} $$
(12)

where F is the vector that contains the objective functions f i , r is the vector of the design parameters of the entire system, g is the disequality constraint function vector and h the equality constraint function vector. The numbers n, m, p and t describe respectively the number of objective functions, design parameters, disequality constraints and equality constraints. The problem is solved by finding the optimal solutions to the problem, which are called Pareto-optimal or non-dominated and are those solutions which cannot be improved in any of the objectives without degrading at least another one. The objective functions that are chosen for the analysis are operational workspace volume and force efficiency as in Eq. (10).

The multi-optimization problem only has two parameters: the ratio of the stroke of the actuator s over the base dimension a and the ratio of the minimum length of each leg l 0 over the base dimension a. Thus, it is possible to employ an exhaustive method that directly generates all the solutions by computing all the objective functions for each possible combination of the design parameters.

The constraint functions for the attached problem can be written as Eq. (13),

$$ \frac{{l_{0,min} }}{a} \le \frac{{l_{0} }}{a} \le \frac{{l_{0,max} }}{a}; \;\;\;\; \frac{{s_{min} }}{a} \le \frac{s}{a} < \frac{{l_{0} }}{a} $$
(13)

where the maximum length of the stroke is limited by the minimum length of the actuator for feasibility reasons. Given the numerical constraints

$$ 0.9 \le \frac{{l_{0} }}{a} \le 2;\;\;\;\;\; 0.9 \le \frac{s}{a} < \frac{{l_{0} }}{a} $$
(14)

it is possible to map the values of each objective function in the whole parameter space. Figure 4 illustrates how the objective functions vary with regards to different configurations by mapping their displacement from the mean value, computed as Eq. (15).

Fig. 4.
figure 4

Objective functions in the parameter space: a. Operational workspace volume; b. Force efficiency from Eq. (10)

Full size image
$$ \Delta f_{i} \left( {\frac{{l_{0} }}{a}, \frac{s}{a}} \right) = \frac{{f_{i} \left( {\frac{{l_{0} }}{a}, \frac{s}{a}} \right)}}{{f_{i,mean} }} $$
(15)

As shown in Fig. 4, objective functions are influenced in different ways by the two optimization parameters.

In particular, the efficiency function presented in Eq. (10) is characterized by a maximum variation of 20% from its average value (Fig. 4c), workspace volume varies over 100% of its average value in the parameter space, as shown in Fig. 4a and b. Furthermore, the optimum of each objective function is located in a different region of the parameter space. A good efficiency can be found for small values of the stroke but it does not show a strong dependency on the minimum length of the link. The workspace volume is optimized in a different region, characterized by high values of both the optimization parameters. Therefore, optimal solutions should be studied in order to find a compromise between the different objectives.

The influence of the design parameters on the operational workspace volume is too different to the one on the force efficiency index to detect a proper set of solutions on the Pareto front, which is characterized by points scattered in the whole parameter space. Therefore, another kind of solution has been chosen. The diagram in Fig. 5 maps the number of objective functions above their average value in each region of the parameter space. In particular, a black region is characterized by 0 objective functions above average, a grey region has one objective function above average and a white region is characterized by both objective functions above their average. Therefore, two optimal solutions for the mechanism design can be found in the two white regions around points (1.46; 1.30) and (1.96; 1.24).

Fig. 5.
figure 5

Map of the parameter space with number of objective functions above average – black region: 0; grey region: 1; white region: 2

Full size image

5 Conclusions

This paper describes the procedure for the optimization procedure of a parallel leg mechanism. First of all, the mechanism is introduced and its kinematics and dynamics are described. Then, its performance is evaluated in terms of workspace volume and force transmission. Finally, the main variables of the design are chosen as parameters and an optimization procedure is presented in order to select a set of solutions with the optimal performance indices. Furthermore, the performance of the mechanism is evaluated and mapped in the whole parameter space.