1 Introduction

Studies of network structures have lead to fundamental insights into the organization and function of social, biological and technological systems [13]. On top of these network structures, different dynamical processes unfold [4, 8], leading to applications ranging from ranking web pages to maximizing social influence and controlling epidemics [9, 14]. Traditionally, most research has focused on the simple graph representation where all verticies and edges are of a single type. More recently, there has been a great interest in network models that are capable of capturing multiple types of connections [1, 15]. In this paper, we adopt the general notion of multi-layer networks, with multiplex network being a special case when inter-layer structures are absent [10].

Structure and dynamics of multi-layer networks have been explored in both theoretical graphs and real world data [2, 5, 12]. However, it remains an open question as how to build a multi-layer network in the first place. They are often constructed simply by stacking or projecting layers into a single network. When inter-layer edges are explicitly modeled, they are usually captured by a simple parameter called the coupling strength. One challenge for modeling inter-layer structures is that they are empirically difficult to measure in most cases [7].

In this paper, we propose a two-stage framework for multi-layer network composition based on a unified dynamical process. In Sect. 2, we will first briefly discuss how to transform the layers into homogeneous Markov processes, followed by the main theorem which infer inter-layer edge weights based on inter-layer dynamics. A real world example will be investigated in Sect. 3.

2 The Multi-layer Composition Framework

We first introduce some basic notations.

Single-layer data: A standard network is represented by weighted directed graph \(G = (V,E,{\varvec{A}})\), where \(V = \{1,...,n\}\) and for \(u,v\in V\), \(a_{uv}\ge 0\) assigns a weight to edge \((u,v)\in E\). We follow the convention that \(a_{uv} = 0\) if and only if \((u,v)\not \in E\). G may have self-loops. For \(u \in V\), let \(d^{out}_u = \sum _{v=1}^n a_{u,v}\) denote the out-degree of vertex u. In this paper, we use \({\varvec{D}}_{{\varvec{A}}}\) (or \({\varvec{D}}\) when the context is clear) to denote the diagonal matrix whose entries are out-degrees.

Multi-layer data: We consider vertex-aligned multi-layer networks [10]. We use l to denote number of layers, and use \(G^i= (V,E^i,{\varvec{A}}^i)\) to denote the network at \(i^{th}\) layer. For clarity, we will use superscripts i, j, r for the layers and subscripts u, v, w for vertices. Note that the vertex set V is the same across the layers.

The simplest dynamical process on graphs G is the discrete time unbiased random walk (URW), represented by the transition matrix \({\varvec{M}}\).

Lemma 1

For every directed network \(G = (V,E,{\varvec{A}})\), there is a unique transition matrix, \({\varvec{M}}_{{\varvec{A}}} = {\varvec{A}}{\varvec{D}}_{{\varvec{A}}}^{-1} \), that captures the URW Markov process on G. Conversely, given a transition matrix \({\varvec{M}}\), there is in fact multi-layer an infinite family of adjacency matrices whose random walk Markov process is consistent with \({\varvec{M}}\): \( \varvec{\mathcal {A}}_{{\varvec{M}}} = \{{\varvec{M}}\varvec{\varGamma }: \varvec{\varGamma } \text{ is } \text{ a } \text{ positive } \text{ diagonal } \text{ matrix }.\} \)

In other words, every directed network uniquely defines a random walk process. However, given a transition matrix \({\varvec{M}}\), there remains n degrees of freedom to specify the underlying network. They are vertex scaling factors. For undirected graphs, there is only one global scaling factor.

In [8], we argued that perceived network structure is a result of the interplay between the network topology and the dynamical process on top of it. We believe this interplay is even more pronounced in multi-layer networks, with each layer represents a different type of connection. It is thus essential to account for the different intra-layer dynamics before we put them together.

For this purpose, we reintroduce the parametrized Laplacian [8], \( \varvec{\mathcal {L}}=({\varvec{D}}'-{\varvec{B}}{\varvec{A}})({\varvec{D}}'{\varvec{T}})^{-1}, \) where \({\varvec{A}}\) is the adjacency and \({\varvec{D}}'\) is the reweighed degree matrix now defined as: \(d'_u= \sum _v [{\varvec{B}}{\varvec{A}}] _{uv}\). The diagonal matrix \({\varvec{T}}\) controls the time delay factors at each vertex. The bias factors form the other diagonal matrix \({\varvec{B}}\). Under the framework, we can transform each input layer to equivalent graphs underlying continuous time URWs as the unifying dynamical process (Please refer to for the details and proofs).

Theorem 1

For a directed network \(G = (V,E,{\varvec{A}})\), the dynamics \(\varvec{\mathcal {L}}=({\varvec{D}}'-{\varvec{B}}{\varvec{A}})({\varvec{D}}'{\varvec{T}})^{-1}\) is equivalent to a continuous time URW with uniform delay factors on another transformed graph.

Corollary 1

For an undirected network \(G = (V,E,{\varvec{A}})\), and the dynamical parameters \(B, {\varvec{T}}\), the interaction matrix \({\varvec{W}}=\alpha (B{\varvec{A}}B + ({\varvec{T}}- {\varvec{I}}){\varvec{D}}')\; \) is unique up to a global scaling factor.

We are now ready to discuss the second stage of the framework. For multiplex composition, simple matrix addition does the trick. However, we need a more general framework when inter-layer structures matter. Consider the following:

Formulation 1

Given l transformed layers \(G^1= (V, E^1,{\varvec{W}}^1), ..., G^l= (V, E^l, {\varvec{W}}^l)\), and egocentric inter-layer dynamics \(({\varvec{M}}_v : v\in V)\), compose a \((ln\times ln)\) weighted super-adjacency matrix, \(\mathbb {W} = \begin{bmatrix} {\varvec{W}}^1&{\varvec{W}}^{12}&...&{\varvec{W}}^{1l}\\ ...\\ {\varvec{W}}^{l1}&{\varvec{W}}^{l2}&...&{\varvec{W}}^{l}\\ \end{bmatrix} \) to integrate the multi-layer network data. In addition, \(\mathbb {W}\) represent a diagonal multi-layer networks, as defined in [10], which means that all inter-layer edges are between the same vertex at different layers. Here, in \(\mathbb {W}\), the l diagonal (\(n\times n\))-blocks are directly fed from the first stage \({\varvec{W}}^1, {\varvec{W}}^2, ..., {\varvec{W}}^l\).

We have used the model of egocentric inter-layer dynamics for each vertex \(({\varvec{M}}_v : v\in V)\), with \({\varvec{M}}_v\) being the stochastic transition matrix for the inter-layer instances of the same vertex v. Such egocentric models are considered to be fundamental in the formation of social structures [6].

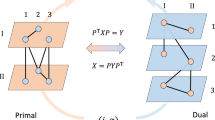
Figure 1a, b is a toy example with three horizontal layers, consisting of (hypothetical) phone contacts, email exchanges and Facebook friendships. At the same time, egocentric inter-layer dynamics form a vertical perspective of the same system. Figure 1c represents the Markov transitions of this joint system when Alice receives a phone call. She might pass on the message directly by calling others with probability \(0.6 = 0.4+0.2\), or relay the message through emails with probability 0.3, or post it on a Facebook wall with probability 0.1.

Fig. 1.
figure 1

A hypothetical toy example

Full size image

By Lemma 1 each layer \({\varvec{W}}^i\) uniquely defines a Markov model, \({\varvec{M}}_{{\varvec{W}}^i}\). Our task is to combine them with the n egocentric Markov models \(({\varvec{M}}_v: v\in V)\). Therefore, we aim to identify a weighted \((ln\times ln)\)-adjacency matrix \(\mathbb {W}\), whose random-walk Markov model, \({\varvec{M}}_{\mathbb {W}}\), satisfies the following two basic conditions:

  1. 1.

    Layer Consistency: The random-walk Markov model of each layer, \({\varvec{M}}_{{\varvec{A}}^i}\), \(i\in [1,2,..,l]\), is the projection of \({\varvec{M}}_{\mathbb {W}}\) to that layer, and

  2. 2.

    Ego Consistency: The egocentric inter-layer dynamics, \({\varvec{M}}_v\), of vertex \(v\in V\), is the layer marginals of \({\varvec{M}}_{\mathbb {W}}\) at vertex v.

The projection of \({\varvec{M}}\) onto a subset is simply the stochastic normalization of corresponding principal submatrix of \({\varvec{M}}\). Thus, Condition 1 is automatically achieved by setting diagonal blocks of \(\mathbb {W}\) as \({\varvec{W}}^1,...,{\varvec{W}}^l\) in Formulation 1.

For Condition 2, notice that \(\mathbb {W}\) also defines an \(l\times l\) interlayer adjacency matrix \({\varvec{W}}_v\) at each \(v\in V\). The corresponding random-walk process, \({\varvec{M}}_{{\varvec{W}}_{v}}\), is the projection of \({\varvec{M}}_{\mathbb {W}}\) to these vertical slices. Let \(q_{v,i}\) denote the transition probability of going from vertex v in the \(i^{th}\) layer to some u in the same layer, according to \({\varvec{M}}_{\mathbb {W}}\). Let \({\varvec{Q}}_v\) be the \(l\times l\) diagonal matrix of \([q_{v,i}: i\in [l]]\). Then, \({\varvec{Q}}_v + {\varvec{M}}_{{\varvec{W}}_{v}} \cdot ({\varvec{I}}- {\varvec{Q}}_v)\) denote the layer marginals of the joint Markov model \({\varvec{M}}_{\mathbb {W}}\) at vertex v. Consequently, Ego Consistency requires that \({\varvec{M}}_v = {\varvec{Q}}_v + {\varvec{M}}_{{\varvec{W}}_{v}} \cdot ({\varvec{I}}- {\varvec{Q}}_v)\). Intuitively, \({\varvec{M}}_v\) bridges between the orthogonal projections by including both \({\varvec{Q}}_v\) and \({\varvec{M}}_{{\varvec{W}}_{v}}\). Now we present the main theorem of this paper:

Theorem 2

For any multi-layer data \(({\varvec{A}}_i: i\in [l], {\varvec{M}}_{v}: v \in V)\), there exists a unique and feasible super-adjacency \(\mathbb {W}\) that satisfies both Layer Consistency and Ego Consistency.

Proof

Because Formulation 1 requires that all off-diagonal blocks of \(\mathbb {W}\) are diagonal matrices, we have \((l^2-l)n\) degrees of freedom after meeting Layer Consistency. Notice that \(({\varvec{M}}_v: v\in V)\) are n stochastic \(l\times l\) matrices. Thus, Ego Consistency represents \((l^2-l)n\) dimensional constraints, which matches perfectly with the remaining degrees of freedom. Uniqueness proven.

To prove the feasibility of the unique solution, we introduce Algorithm 1,

figure a

We need a subroutine Algorithm 2 to satisfy the Ego Consistency. Rearrange \(\mathbb {W}\) so that the counterparts of the same vertex are grouped together. \(\bar{\mathbb {W}} = \begin{bmatrix} {\varvec{W}}_1&{\varvec{W}}_{12}&...&{\varvec{W}}_{1n}\\ ...\\ {\varvec{W}}_{n1}&{\varvec{W}}_{n2}&...&{\varvec{W}}_n, \end{bmatrix} \) where \({\varvec{W}}_{u,v}\) are \(l\times l\) matrices that have already been fixed by Layer Consistency. The diagonal blocks \({\varvec{W}}_v: v\in V\) contains all entries set by Ego Consistency. The diagonal entries of \({\varvec{W}}_v\), \(v\in V\), are also set by Layer Consistency, because they are unaffected by the rearrangement of \(\mathbb {W}\). The rest \(n(l^2-l)\) entries lead to the same degrees of freedom we discussed earlier.

The reordered \({\varvec{W}}_{u}\) blocks are closely related to the egocentric adjacencies \({\varvec{X}}_u\) underlying the egocentric inter-layer dynamics \({\varvec{M}}_u\). The vertical slice in Fig. 1c demonstrates such a \({\varvec{X}}_a\), where intra-layer transitions are captured using self-loops. Subroutine Algorithm 2 can now be specified as

figure b

Using Lemma 1, we can rewrite the steps in Algorithm 2 as \({\varvec{X}}_u = {\varvec{M}}_u \varvec{\varGamma }\), by setting the \(i^{th}\) entry of \(\varvec{\varGamma }\) uniquely as \(d^{i}_u(out)/{\varvec{M}}_u^{ii}\), where \(d^{i}_u(out)\) is the total out edge weights of vertex u in layer i. Intuitively, we are simply using the intra-layer dynamics to determine the vertex scaling factor.

From Fig. 1c, it is clear that the off-diagonal parts of \({\varvec{X}}_u\) is exactly what we are looking for in \({\varvec{W}}_u\) blocks. Or \({\varvec{W}}_u = {\varvec{X}}_u - D_u(out)\), where the diagonal matrix \(D_u(out)\) is composed of \(d^{i}_u(out)\) entries. With the uniquely solvable \({\varvec{X}}_u\) blocks, we can now complete the output \(\mathbb {W}\) by filling its off diagonal blocks \({\varvec{W}}^{ij}\) with reordered \({\varvec{W}}_u\) blocks. On top of that, Algorithm 2 will always lead to feasible solutions with the constrains \({\varvec{X}}_u^{ij}\ge 0\), provided that \({\varvec{M}}_u\) entries are well defined. Uniqueness and feasibility proven.

3 A Real World Example

Figure 2 presents collaboration networks (undirected) centered around four authors: Shang-hua Teng, Daniel Spielman, Gary Miller and Kristina Lerman, as well as their coauthors on papers appearing in the ACM Digital Library. Each layer represents a separate time period: from bottom to top, 1985–1994, 1995–2004, and 2005–2014. The weight of an intra-layer edge represents the number of times two authors collaborated during that decade. The traditional approach, as shown by Fig. 2(a), simply connect the same author between neighboring decades with a constant coupling strength of 2. To use our framework, we assume that an author has a \(10\%/20\%\) transition probability to connect with former self in the previous decade. Specifying inter-layer edges using Algorithms 1 and 2, first between the top tow layers then the bottom two, we have Fig. 2(b), (c).

Fig. 2.
figure 2

Community structures of coauthor networks using different compositions (Color figure online)

Full size image

For comparison, we have visualized the community structures with different multi-layer compositions in Fig. 2, using the Louvain algorithm [3], with the resolution parameter set to 5 [11]. The traditional approach produced some counter-intuitive cross-layer communities, because the constant coupling strength is too strong for peripheral vertices. Our framework, on the other hand, leads to much more sensible results with different inter-layer strength for vertices with different degrees. With a \(10\%\) transition probability, we can see that authors surrounding Teng and Spielman later separated from the red community (which became yellow) of theoretical computer scientists like Miller. As Teng started to collaborate with the social network community surrounding Lerman (green), the newly formed blue community now represents the filed of graph theory.