Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1.1 Introduction

The fundamental goals of network science are: to describe the structure of interactions between the components, and to assess the emergent behavior of many-body systems coupled to the underlying structure. Advances on the theory of complex networks will improve our understanding and modeling capabilities so that we may control or predict the dynamics and function of complex networked systems. In addition, this approach does not rely on a detailed knowledge of the systems components and therefore allows universal results to be obtained that can be generalized with relative ease (e.g., the study of epidemic spreading processes is equivalent to the spread of computer viruses). For example, biological networks like protein interaction networks share many structural (scale-freeness) and dynamical (functional modules) features with other seemingly different systems such as the Internet and interaction patterns in social systems. Thus, systems as diverse as peer-to-peer networks, neural systems, socio-technical phenomena or complex biological networks can be studied within a general unified theoretical and computational framework.

However, almost all of the work to date is based on an ordinary 1-layer or simplex view of the networks in question, where every edge (link) is of the same type and consequently considered at the same temporal and topological scale. Generally speaking, the description of networks so far has been developed using a snapshot of the connectivity, this connectivity being a reflection of instantaneous interactions or accumulated interactions in a certain time window. This description is limiting when trying to understand the intricate variability of real complex systems, which contain many different time scales and coexisting structural patterns forming the real network of interactions. These more realistic multi-layer structures have received a lot of attention from the physicist community [17, 38] with no common terminology yet.

Interacting, interdependent or multiplex networks are different ways of naming the same class of complex systems where networks are not considered as isolated entities but interact with each other. In multiplex, the nodes at each network are instances of the same entity, thus the networks are representing simply different categorical relationships between entities, and usually categories are represented by layers. Interdependent networks is a more general framework where nodes can be different at each network.

Many, if not all, real networks are “coupled” with other real networks. Examples can be found in several domains: social networks (e.g., Facebook, Twitter, etc.) are coupled because they share the same actors [60]; multimodal transportation networks are composed of different layers (e.g., bus, subway, etc.) that share the same locations [4, 18]; the functioning of communication and power grid systems depend one on the other [10]. So far, all phenomena that have been studied on interdependent networks, including percolation [10, 58], epidemics [31, 32, 55], and linear dynamical systems [30], have provided results that differ much from those valid in the case of isolated complex networks. Sometimes the difference is radical: for example, while isolated scale-free networks are robust against failures of their nodes or edges [2], scale-free interdependent networks are instead very fragile [10, 58].

The standard approach towards the characterization of topological and dynamical properties of multiplex networks is similar to the one used for isolated networks. This approach relies on a fundamental approximation about the local structure of the network, generally indicated as tree-like approximation [1, 20, 21, 46]. The tree ansatz assumes the absence of finite loops in a network in the thermodynamic limit and the presence of only infinite loops. Such an approximation is very convenient because it allows one to use techniques typical of the theory of random branching processes [34]. These mainly include degree-based mean field calculations, and the application of the generating function formalism for the statistical characterization of structural and dynamical properties of ensembles of networks [48, 63]. Under this ansatz, the solutions of many problems, that are unsolvable in their exact form, can be instead provided with very good accuracy [20]: percolation [15], epidemiological [51] and opinion dynamical models [59, 61], controllability [42] are just among the most celebrated examples. The same type of approach has been applied to predict the behavior of special types of critical phenomena in multilayered networks. Examples include the analysis of the nature of the percolation transition in multiplex networks [5, 10, 28, 57, 58] and interconnected networks [27, 36, 50], and the study of the features of several dynamical processes defined on these particular type of network topologies [9, 19, 55].

Another theoretical approach used in the characterization of networks is the one based on the analysis of the spectrum of special operators associated with the graphs. This approach often relies on analytic results obtained in the branch of mathematics research known as “Spectral Graph Theory” [13], and it has been proved to be effective in the study of topological and dynamical properties of networks. Fundamental features of networks can be understood by looking at the eigenvalues and eigenvectors not only of the adjacency matrix, but also of other matrices associated with the graph such as the normalized [13] and combinatorial [45] laplacians, the non-backtracking matrix [35, 41], the modularity matrix [47], just to mention a few of them.

The fundamental reason behind the effectiveness of spectral methods is that the spectrum of a graph encodes fundamental physical features of the system: eigenvalues correspond to energy levels, and the corresponding eigenvectors represent configurations of the system associated with them. Spectral graph theory has a wide range of applicability. For example, many useful measures, such as graph energy [12], graph conductance and resistance [22], and the Randić index [39], are quantifiable in terms of the eigenvalues of the normalized laplacian of a graph. Finding the minimal eigenpair of matrices associated with graphs is typically equivalent to identifying the ground state of wide class of energy functions [40] and fitness landscapes [54]. Examples include, among others, Ising spin models [44] and combinatorial optimization problems such as the traveling salesman problem [33]. In the study of isolated networks, the spectrum of the matrices associated with graphs has been successfully applied to several contexts: examples include percolation transition [8], synchronization [3] and epidemiological models [11, 29].

Spectral approaches have recently been proved successful also for the understanding of structural [53] and dynamical [30, 52, 56] properties of networks of networks. In the study of coupled networks, the great advantage of spectral methods, with respect to those based on the tree-like approximation and the use of the generating function formalism, is in their ability to predict the behavior of multiplexes on the basis of features of the individual layers that composed them. In the remaining part of the chapter, we will illustrate a concrete example of a successful application of spectral techniques to the characterization of structural transitions in arbitrary multiplex networks.

1.2 Mathematical Modeling

Multiplex Networks Composed of Two Layers

For simplicity, we first consider the case of two interconnected networks. We will later generalize the method to an arbitrary number of interconnected networks. We assume that the two interconnected networks A and B are undirected and weighted, and that they have the same number of nodes N. The weighted adjacency matrices of the two graphs are indicated as A and B, respectively, and they have both dimensions N × N. With this notation, the element A ij  = A ji is equal to the weight of the connection between the nodes i and j in network A. The definition of B is analogous.

We consider the case of one-to-one symmetric interconnectivity [10] between nodes in the networks A and B (see Fig. 1.1a). The connections between interconnected nodes of the two networks are weighted by a factor p (see Fig. 1.1b), any other weighted factor for the networks A and B is implicitly absorbed in their weights. The supra-adjacency matrix G of the whole network is therefore given by

$$\displaystyle{ G = \left (\begin{array}{cc} A &p1\!\!1\\ p1\!\!1 & B \end{array} \right )\,, }$$
(1.1)

where \(\mathbb1\) is the identity matrix with dimensions N × N. Using this notation we can define the supra-laplacian of the interconnected network as

$$\displaystyle{ \mathcal{L} = \left (\begin{array}{cc} \mathcal{L}_{A} + p1\!\!1& - p1\!\!1 \\ - p1\!\!1 &\mathcal{L}_{B} + p1\!\!1 \end{array} \right )\,. }$$
(1.2)

The blocks present in \(\mathcal{L}\) are square symmetric matrices of dimensions N × N, In particular, \(\mathcal{L}_{A}\) and \(\mathcal{L}_{B}\) are the laplacians of the networks A and B, respectively.

Fig. 1.1
figure 1

(a) Schematic example of two interconnected networks A and B. In this representation, nodes of the same color are one-to-one interconnected. (b) In our model, inter-layer edges have weights equal to p (From Ref. [53])

Full size image

Our investigation focuses on the analysis of the spectrum of the supra-Laplacian to ascertain the origin of the structural changes of the merging of networks in an interconnected system. The spectrum of the laplacian of a graph is a fundamental mathematical object for the study of the structural properties of the graph itself. There are many applications and results on graph Laplacian eigenpairs and their relations to numerous graph invariants (including connectivity, expanding properties, genus, diameter, mean distance, and chromatic number) as well as to partition problems (graph bisection, connectivity and separation, isoperimetric numbers, maximum cut, clustering, graph partition), and approximations for optimization problems on graphs (cutwidth, bandwidth, min-p-sum problems, ranking, scaling, quadratic assignment problem) [6, 13, 14, 43].

Note that, for any graph, all eigenvalues of its laplacian are non negative numbers. The smallest eigenvalue is always equal to zero and the eigenvector associated to it is trivially a vector whose entries are all identical. The second smallest eigenvalue \(\lambda _{2}\) also called the algebraic connectivity [23] is one of the most significant eigenvalues of the Laplacian. It is strictly larger than zero only if the graph is connected. More importantly, the eigenvector associated to \(\lambda _{2}\), which is called the characteristic valuation or Fiedler vector of a graph, provides even deeper information about its structure [24, 25, 45]. For example, the components of this vector associated to the various nodes of the network are used in spectral clustering algorithms for the bisection of graphs [49].

Our approach consists in the study of the behavior of the second smallest eigenvalue of the supra-laplacian matrix \(\mathcal{L}\) and its characteristic valuation as a function of p, given the single-layer network laplacians \(\mathcal{L}_{A}\) and \(\mathcal{L}_{B}\). In the following, we will make use of the standard bra-ket notation for vectors. In this notation, \(\left \vert x\right>\) indicates a column vector, \(\left <x\right \vert\) indicates the transposed (i.e., row vector) of \(\left \vert x\right>\), \(\left <x\vert y\right> = \left <y\vert x\right>\) indicates the inner product between the vectors \(\left \vert x\right>\) and \(\left \vert y\right>\), \(A\left \vert x\right>\) indicates the action of matrix A on the column vector \(\left \vert x\right>\), and \(\left <x\right \vert A\) indicates the action of matrix A on the row vector \(\left <x\right \vert\). According to the theorem by Courant and Fisher (i.e., the so-called min-max principle) [16, 26], the second smallest eigenvalue of \(\mathcal{L}\) is given by

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) =\min _{\left \vert v\right>\in \mathcal{V}}\,\left <v\right \vert \mathcal{L}\left \vert v\right>\;, }$$
(1.3)

where \(\left \vert v\right> \in \mathcal{V}\,\text{ is such that }\,\left <v\vert 1\right> = 0,\left <v\vert v\right> = 1\). The vector \(\left \vert 1\right>\) has 2N entries all equal to 1. Eq. (1.3) means that \(\lambda _{2}\left (\mathcal{L}\right )\) is equal to the minimum of the function \(\left <v\right \vert \mathcal{L}\left \vert v\right>\), over all possible vectors \(\left \vert v\right>\) that are orthogonal to vector \(\left \vert 1\right>\) and that have norm equal to one. The vector for which such minimum is reached is thus the characteristic valuation of the supra-laplacian (i.e., \(\mathcal{L}\left \vert v\right> =\lambda _{2}\left \vert v\right>\)). We distinguish two blocks of size N in the vector \(\left \vert v\right>\) by writing it as \(\left \vert v\right> = \left \vert v_{A},v_{B}\right>\). In this notation, \(\left \vert v_{A}\right>\) is the part of the eigenvector whose components correspond to the nodes of network A, while \(\left \vert v_{B}\right>\) is the part of the eigenvector whose components correspond to the nodes of network B. We can now write

$$\displaystyle{\begin{array}{ll} \left <v\right \vert \mathcal{L}\left \vert v\right> =&\left <v_{A},v_{B}\right \vert \mathcal{L}\left \vert v_{A},v_{B}\right> = \\ &\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right> + \left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right>+ \\ &p\left (\left <v_{A}\vert v_{A}\right> + \left <v_{B}\vert v_{B}\right> - 2\left <v_{A}\vert v_{B}\right>\right )\end{array} }$$

and the previous set of constraints as \(\left <v_{A}\vert 1\right> + \left <v_{B}\vert 1\right> = 0\) and \(\left <v_{A}\vert v_{A}\right> + \left <v_{B}\vert v_{B}\right> = 1\), where now all vectors have dimension N. Accounting for such constraints, we can finally rewrite the minimization problem as

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) = p +\min _{\left \vert v\right>\in \mathcal{V}}\,\left \{\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right>\right.\left.+\left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right> - 2p\left <v_{A}\vert v_{B}\right>\right \}\;. }$$
(1.4)

First of all, we can simply state that the algebraic connectivity of Eq. (1.4) satisfies the inequality

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) \leq \frac{1} {2}\lambda _{2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right )\;, }$$
(1.5)

where this upper bound comes out directly from the definition of the minimum of a function. For every \(\mathcal{Q}\subseteq \mathcal{V}\), we have in fact that

$$\displaystyle{\min _{\left \vert v\right>\in \mathcal{V}}\left <v\right \vert \mathcal{L}\left \vert v\right> \leq \min _{\left \vert v\right>\in \mathcal{Q}}\left <v\right \vert \mathcal{L}\left \vert v\right>}$$

simply because we are restricting the domain where looking for the minimum of the function \(\left <v\right \vert \mathcal{L}\left \vert v\right>\). The particular value of the upper bound of Eq. (1.5) is then given by setting \(\mathcal{Q}\) as

$$\displaystyle{\begin{array}{l} \left \vert v\right> = \left \vert v_{A},v_{B}\right> \in \mathcal{Q}\,\text{ is such that }\,\left \vert v_{A}\right> = \left \vert v_{B}\right> = \left \vert q\right>, \\ \text{ with }\left <q\vert 1\right> = 0,\left <q\vert q\right> = 1/2.\end{array} \;}$$

Note that the upper bound of Eq. (1.5) does not depend on p, and thus represents the asymptotic value of \(\lambda _{2}\left (\mathcal{L}\right )\) in the limit \(p \rightarrow \infty\). This analytically proves the result established by Gómez et al. [30] through approximation methods.

The minimization problem of Eq. (1.4) can be solved using Lagrange multipliers. This means finding the minimum of the function

$$\displaystyle{\begin{array}{ll} M =&\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right> + \left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right> - 2p\left <v_{A}\vert v_{B}\right> \\ & - r\left (\left <v_{A}\vert 1\right> + \left <v_{B}\vert 1\right>\right ) - s\left (\left <v_{A}\vert v_{A}\right> + \left <v_{B}\vert v_{B}\right> - 1\right ),\end{array} \;}$$

where the constraints of the minimization problem have been explicitly inserted in the function to minimize through the Lagrange multipliers r and s. In the following calculations, we will make use of the identities

$$\displaystyle{\begin{array}{l} \frac{\partial \,} {\partial \,\left \vert x\right>}\left <t\vert x\right> = \frac{\partial \,} {\partial \,\left \vert x\right>}\left <x\vert t\right> = \left <t\right \vert \\ \frac{\partial \,} {\partial \,\left \vert x\right>}\left <x\vert x\right> = 2\left <x\right \vert \\ \frac{\partial \,} {\partial \,\left \vert x\right>}\left <x\right \vert A\left \vert x\right> = 2\left <x\right \vert A\text{, if }A = A^{T} \end{array} \;,}$$

where \(\frac{\partial \,} {\partial \,\left \vert x\right>}\) indicates the derivative with respect to all the coordinates of the vector \(\left \vert x\right>\). Equating to zero the derivatives of M with respect to r and s, we obtain the constraints that we imposed. By equating to zero the derivative of M with respect to \(\left \vert v_{A}\right>\), we obtain instead

$$\displaystyle{ \frac{\partial \,M} {\partial \,\left \vert v_{A}\right>} = 2\left <v_{A}\right \vert \mathcal{L}_{A} - 2p\left <v_{B}\right \vert - r\left <1\right \vert - 2s\left <v_{A}\right \vert = \left <0\right \vert \;, }$$
(1.6)

and, similarly for the derivative of M with respect to \(\left \vert v_{B}\right>\),we obtain

$$\displaystyle{ \frac{\partial \,M} {\partial \,\left \vert v_{B}\right>} = 2\left <v_{B}\right \vert \mathcal{L}_{B} - 2p\left <v_{A}\right \vert - r\left <1\right \vert - 2s\left <v_{B}\right \vert = \left <0\right \vert \;. }$$
(1.7)

Multiplying both equations with \(\left \vert 1\right>\), we have \(2\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert 1\right> - 2p\left <v_{B}\vert 1\right> - r\left <1\vert 1\right> - 2s\left <v_{A}\vert 1\right> = 0\) and \(2\left <v_{B}\right \vert \mathcal{L}_{B}\left \vert 1\right> - 2p\left <v_{A}\vert 1\right> - r\left <1\vert 1\right> - 2s\left <v_{B}\vert 1\right> = 0\), that can be simplified in \(2(p - s)\left <v_{A}\vert 1\right> - rN = 0\) and \(2(p - s)\left <v_{B}\vert 1\right> - rN = 0\) because \(\mathcal{L}_{A}\left \vert 1\right> = \mathcal{L}_{B}\left \vert 1\right> = \left \vert 0\right>\) and \(\left <v_{A}\vert 1\right> = -\left <v_{B}\vert 1\right>\). Summing them, we obtain r = 0. Finally, we can write

$$\displaystyle{ \begin{array}{l} (p - s)\left <v_{A}\vert 1\right> = 0 \\ (p - s)\left <v_{B}\vert 1\right> = 0 \end{array} \;. }$$
(1.8)

These equations can be true in two cases: (i) \(\left <v_{A}\vert 1\right>\neq 0\) or \(\left <v_{B}\vert 1\right>\neq 0\) and s = p; (ii) \(\left <v_{A}\vert 1\right> = \left <v_{B}\vert 1\right> = 0\). In the following, we analyze these two cases separately.

First, let us suppose that s = p, and that at least one of the two equations \(\left <v_{A}\vert 1\right>\neq \ 0\) and \(\left <v_{B}\vert 1\right>\neq 0\) is true. If we set s = p in Eqs. (1.6) and (1.7), they become

$$\displaystyle{ \left <v_{A}\right \vert \mathcal{L}_{A} - p\left <v_{B}\right \vert - p\left <v_{A}\right \vert = \left <0\right \vert }$$
(1.9)

and

$$\displaystyle{ \left <v_{B}\right \vert \mathcal{L}_{B} - p\left <v_{A}\right \vert - p\left <v_{B}\right \vert = \left <0\right \vert \;. }$$
(1.10)

If we multiply the first equation with \(\left \vert v_{A}\right>\) and the second equation with \(\left \vert v_{B}\right>\), the sum of these two new equations is

$$\displaystyle{ \left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right> + \left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right> - 2p\left <v_{A}\vert v_{B}\right> = p\;. }$$
(1.11)

If we finally insert this expression in Eq. (1.4), we find that the second smallest eigenvalue of the supra-laplacian is

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) = 2p\;. }$$
(1.12)

We can further determine the components of Fiedler vector in this regime. If we take the difference between Eqs. (1.9) and (1.10), we have \(\left <v_{A}\right \vert \mathcal{L}_{A} = \left <v_{B}\right \vert \mathcal{L}_{B}\). On the other hand, Eq. (1.12) is telling us that \(\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right> = -\left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right>\) because the only term surviving in Eq. (1.11) is the one that depends on p. Since \(\left <v_{A}\right \vert \mathcal{L}_{A}\left \vert v_{A}\right>\) (\(\left <v_{B}\right \vert \mathcal{L}_{B}\left \vert v_{B}\right>\)) is always larger than zero, unless \(\left \vert v_{A}\right> = c\left \vert 1\right>\) (\(\left \vert v_{B}\right> = c\left \vert 1\right>\)), with c arbitrary constant value, we obtain

$$\displaystyle{ \left \vert v_{A}\right> = -\left \vert v_{B}\right>\qquad \text{ where }\left \vert v_{A}\right> = \pm \frac{1} {\sqrt{2N}}\left \vert 1\right>\;. }$$
(1.13)

Thus in this regime, both the relations \(\left <v_{A}\vert 1\right>\neq 0\) and \(\left <v_{B}\vert 1\right>\neq 0\) must be simultaneously true. Eq. (1.13) also means that \(\left <v_{A}\vert v_{B}\right> = -\frac{1} {2}\).

The other possibility is that Eqs. (1.8) are satisfied because \(\left <v_{A}\vert 1\right> = 0\) and \(\left <v_{B}\vert 1\right> = 0\) are simultaneously true. In this case, the average value of the components of the vectors \(\left \vert v_{A}\right>\) and \(\left \vert v_{B}\right>\) is zero, i.e.,

$$\displaystyle{ \left <v_{A}\vert 1\right> = \left <v_{B}\vert 1\right> = 0\;, }$$
(1.14)

and thus the coordinates of the Fiedler vector corresponding to the nodes of the same layer have alternatively negative and positive signs.

To summarize, the second smallest eigenvalue of the supra-laplacian matrix \(\mathcal{L}\) is given by

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) = \left \{\begin{array}{ll} 2p &\text{, if }p \leq p^{{\ast}} \\ \leq \frac{1} {2}\lambda _{2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right )&\text{, if }p \geq p^{{\ast}} \end{array} \right.\;. }$$
(1.15)

Thus indicating that the algebraic connectivity of the interconnected system follows two distinct regimes, one in which its value is independent of the structure of the two layers, and the other in which its upper bound is limited by the algebraic connectivity of the weighted superposition of the two layers whose laplacian is given by \(\frac{1} {2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right )\). More importantly, the discontinuity in the first derivative of \(\lambda _{2}\) is reflected in a radical change of the structural properties of the system happening at p ∗, the tipping point. Such dramatic change is visible in the coordinates of characteristic valuation of the nodes of the two network layers. In the regime p ≤ p ∗, the components of the eigenvector are given by Eq. (1.13). This means that the two network layers are structurally disconnected and independent. For p ≥ p ∗, they instead obey Eq. (1.14), which means that the components of the vector corresponding to interconnected nodes of network A and B have the same sign, while nodes in the same layer have alternating signs. Thus in this second regime, the system connectivity is dominated by inter-layer connections, and the two network layers are structurally indistinguishable.

The tipping point p ∗ at which the transition occurs is the point at which we observe the crossing between the two different behaviors of \(\lambda _{2}\), which means

$$\displaystyle{ p^{{\ast}}\leq \frac{1} {4}\,\lambda _{2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right )\;. }$$
(1.16)

Since inter-layer connections have weights that grows with p, the transition happens at the point at which the weight of the inter-layer connections exceeds the half part of the inverse of the algebraic connectivity of the weighted super-position of both network layers (see Fig. 1.2).

Fig. 1.2
figure 2

Algebraic connectivity and Fiedler vector for two interconnected Erdős-Renyí networks of N = 50 nodes and average degree \(\bar{k} = 5\). We consider a single realization of this model in which the critical point is p ∗ = 0. 602(1). (a) Characteristic valuation of the nodes in the two network layers for p = 0. 602. (b) Algebraic connectivity of the system (black line). The discontinuity of the first derivative of \(\lambda _{2}\) is very clear. The two different regimes 2p and \(\frac{\lambda _{2}\left (\mathcal{L}_{A}+\mathcal{L}_{B}\right )} {2}\) are shown as red dot-dashed and blue dashed lines, respectively. (c) Inner product \(\left <v_{A}\vert v_{B}\right>\) between the part of the Fiedler eigenvector (\(\left \vert v_{A}\right>\)) corresponding to nodes in the network A and the one (\(\left \vert v_{B}\right>\)) corresponding to vertices in network B as a function of p. (d) Inner products \(\left <v_{A}\vert 1\right>\) and \(\left <v_{B}\vert 1\right>\) as functions of p. \(\left <v_{A}\vert 1\right>\) and \(\left <v_{B}\vert 1\right>\) indicate the sum of all components of the Fiedler vectors \(\left \vert v_{A}\right>\) and \(\left \vert v_{B}\right>\), respectively. (e) Characteristic valuation of the nodes in the two network layers for p = 0. 603 (From Ref. [53])

Full size image

Multiplex Networks Composed of More Than Two Layers

The results presented in the previous section can be extended, with analogous calculations, to multiplexes composed of ℓ network layers, with ℓ > 2. The main result of Eq. (1.15) becomes

$$\displaystyle{ \lambda _{2}\left (\mathcal{L}\right ) = \left \{\begin{array}{ll} \ell p &\text{, if }p \leq p^{{\ast}} \\ \leq \frac{1} {\ell} \;\lambda _{2}\left (\sum _{i=1}^{\ell}\mathcal{L}_{ i}\right )&\text{, if }p \geq p^{{\ast}} \end{array} \right.\;, }$$
(1.17)

showing a discontinuity in the derivative of the algebraic connectivity at a certain value p ∗ estimated as

$$\displaystyle{ p^{{\ast}}\leq \frac{1} {\ell^{2}} \,\lambda _{2}\left (\sum _{i=1}^{\ell}\mathcal{L}_{ i}\right )\;. }$$
(1.18)

The algebraic connectivity of the multiplex can be thus written in terms of the algebraic connectivity of the superposition of all network layers that compose the multiplex. Unfortunately in the case of a multiplex network with ℓ > 2, the Fiedler eigenvector cannot be fully characterized, and it is no longer possible to generalize Eqs. (1.13) and (1.14) to an arbitrary number of network layers.

Perturbed Multiplex Networks

The discontinuity in the first derivative of the algebraic connectivity \(\lambda _{2}\) is due to the crossing between different eigenvalues in the spectrum of the supra-laplacian matrix \(\mathcal{L}\). In the case of a multiplex composed of two layers, the presence of this crossing can be viewed as a simple consequence of the fact that the vector \(\left \vert 1,-1\right>\) is always an eigenvector of the matrix in Eq. (1.2) for any value of p. By invoking the non crossing rule by von Neumann and Wigner [62], it is possible to show that the eigenvalue corresponding to this eigenvector, i.e., \(\lambda = 2p\), must intersect all other eigenvalues of \(\mathcal{L}\). Although in multiplex networks with an arbitrary number of coupled networks there is not a trivial eigenvector that can explain the crossing between eigenvalues, it is, however, worth asking if our results are still valid in presence of disorder. To this end, we consider a perturbed version of the matrix in Eq. (1.2). Essentially, instead of using the same p for every entry (i, j) of the off-diagonal blocks of Eq. (1.1), we use a weight of the type p ij  = f(p, ε ij ) with ε ij random variables such that the average \(\langle f(p,\epsilon _{ij})\rangle = p\). By applying this transformation, the vector \(\left \vert 1,-1\right>\) is not longer an eigenvector \(\mathcal{L}\) for every value of p. In presence of disorder, the non crossing rule by von Neumann and Wigner [62] tells us that no eigenvalues can cross as p varies. It is very interesting to note that the structural transition observed for the unperturbed case still holds, even for very small networks and not so small perturbations (see Fig. 1.3).

Fig. 1.3
figure 3

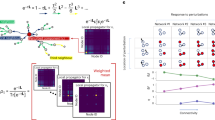
Spectral properties of unperturbed and perturbed supra-laplacian matrices. The multiplex networks analyzed are composed of two Erdős-Rényi network models with N = 50 nodes and average degree \(\bar{k} = 5\) as in the case of Fig. 1.2. (a) Second smallest \(\lambda _{2}\) and third smallest \(\lambda _{3}\) eigenvalues for the unperturbed network (black lines) as functions of the coupling strength p between different layers. We perturbed the coupling matrix by setting p ij  = p + 10−1(1∕2 −ε ij ), with ε ij uniform random variate in the interval [0, 1]. Red lines stand for average values of the second smallest and third smallest eigenvalues obtained over 100 perturbed realizations of the same starting network topology. (b) Sum of the eigenvector components corresponding to nodes in the same network layer, \(\langle v_{A}\vert 1\rangle\), for the unperturbed and the perturbed network of panel a. \(\langle v_{A}\vert 1\rangle\) is rescaled by the factor \(\sqrt{N}\) to obtain values in the interval [0, 1]. (c) Same as in panel (a), but in this case the perturbation applied is p ij  = p∕2 + p ε ij . (d) Same as in panel b, but for the perturbation scheme described in panel c

Full size image

1.3 Conclusions

A physical interpretation of the algebraic structural transition that we are able to analytically predict can be given by viewing the function \(\left <v\right \vert \mathcal{L}\left \vert v\right>\) as an energy-like function. From this point of view, Eq. (1.3) becomes equivalent to a search for the ground state energy, and the characteristic valuation can be viewed as the ground state configuration. Such analogy is straightforward if one realizes that Eq. (1.3) is equivalent to the minimization of the weighted cut of the entire networked system [whose adjacency matrix G is defined in Eq. (1.1)], and that the minimum of this function corresponds to the ground state of a wide class of energy functions [40] and fitness landscapes [54]. These include, among others, the energy associated to the Ising spin models [44] and cost functions of combinatorial optimization problems, such as the traveling salesman problem [33]. In summary, the structural transition of interconnected networks involves a discontinuity in the first derivative of an energy-like function, and thus, according to the Ehrenfest classification of phase transitions, can be understood as a discontinuous transition [7].

Since the transition at the algebraic level has the same nature as the connectivity transition that has been studied by Buldyrev et al. in the same class of networked systems [10], it is worth to discuss about the relations between the two transitions. We can reduce our model to the annealed version of the model considered by Buldyrev et al. by setting A = t 2 A, B = t 2 B and p = t, being 1 − t the probability that one node in one of the networks fails. All the results stated so far hold, with only two different interpretations. First, the upper bound of Eq. (1.16) becomes a lower bound for the critical threshold of the algebraic transition that reads in terms of occupation probability as

$$\displaystyle{ t_{c} \geq \frac{4} {\lambda _{2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right )}\;. }$$
(1.19)

Second, the way to look at the transition must be reversed: network layers are structurally independent (i.e., the analogous of the non percolating phase) for values of t ≤ t c , while become algebraically connected (i.e., analogous of the percolating phase) when t ≥ t c .

As it is well known, the algebraic connectivity represents a lower bound for both the edge connectivity and node connectivity of graph (i.e., respectively the minimal number of edges or nodes that should be removed to disconnect the graph) [24]. Indeed, the algebraic connectivity of a graph is often used as a control parameter to make the graph more resilient to random failures of its nodes or edges [37]. Thus, the lower bound of Eq. (1.19) represents also a lower bound for the critical percolation threshold measured by Buldyrev et al. Interestingly, our prediction turns out to be a sharp estimate of the lower bound. For the Erdős-Rényi model, we have in fact \(t_{c} \geq 2/\bar{k}\), if the two networks have the same average degree \(\bar{k}\), and this value must be compared with \(2.455/\bar{k}\) as predicted by Buldyrev et al. [10, 58]. Similarly, we are able to predict that t c grows as the degree distribution of the network becomes more broad [14], in the same way as it has been numerically observed by Buldyrev et al. [10].

Although we are not able to directly map the algebraic transition to the percolation one, we believe that the existence of a first-order transition at the algebraic level represents an indirect support of the discontinuity of the percolation transition. We further emphasize that the transition is effectively present only if t c  ≤ 1, and thus accordingly to Eq. (1.19) only if \(\lambda _{2}\left (\mathcal{L}_{A} + \mathcal{L}_{B}\right ) \geq 4\). Such condition is verified for network layers that have a sufficiently large connectivity, and this qualitatively confirms the observation by Parshani et al. regarding a change in the nature of the percolation phase transition in interdependent networks with variable number of interdependent nodes [50].

In conclusion, we would like to briefly discuss the deep practical implications of our results. The abrupt nature of the structural transition is, in fact, not only visible in the limit of infinitely large systems, but for networks of any size, even if in presence of disorder. Thus, even real networked systems composed of few elements may be subjected to abrupt structural changes, including failures. Our theory provides, however, fundamental aids for the prevention of such collapses. It allows, in fact, not only the prediction of the critical point of the transition, but, more importantly, to accurately design the structure of such systems to make them more robust. For example, the percolation threshold of interconnected systems can be simply decreased by increasing the algebraic connectivity of the superposition of the network layers. This means that an effective strategy to make an interconnected system more robust is to avoid the repetition of edges among layers, and thus bring the superposition of the layers as close as possible to an all-to-all topology.