Computational Completeness of Path-Structured Graph-Controlled Insertion-Deletion Systems

Abstract

A graph-controlled insertion-deletion (GCID) system is a regulated extension of an insertion-deletion system. It has several components and each component contains some insertion-deletion rules. These components are the vertices of a directed control graph. A rule is applied to a string in a component and the resultant string is moved to the target component specified in the rule, describing the arcs of the control graph. We investigate which combinations of size parameters (the maximum number of components, the maximal length of the insertion string, the maximal length of the left context for insertion, the maximal length of the right context for insertion; a similar three restrictions with respect to deletion) are sufficient to maintain the computational completeness of such restricted systems with the additional restriction that the control graph is a path, thus, these results also hold for ins-del P systems.

1 Introduction

The motivation for insertion-deletion system comes from both linguistics [11] and also from biology, more specifically from DNA processing [14] and RNA editing [1]. Insertion and deletion operations together were introduced into formal language theory in [9]. The corresponding grammatical mechanism is called insertion-deletion system (abbreviated as ins-del system). Informally, the insertion operation means inserting a string $\eta$ in between the strings $w_1$ and $w_2$, whereas the deletion operation means deleting a substring $\delta$ from the string $w_1\delta w_2$. Several variants of ins-del systems have been considered in the literature. We refer to the survey article [16] for details.

One of the important variants of ins-del systems is graph-controlled ins-del systems (abbreviated as GCID systems), introduced in [6] and further studied in [8]. In such a system, the concept of components is introduced, which are associated with insertion or deletion rules. The transition is performed by choosing any applicable rule from the set of rules of the current component and by moving the resultant string to the target component specified in the rule.

If the underlying graph of a GCID system establishes a path structure (loops, multiple edges and directions are ignored), then such a GCID system can be seen as a special form of a P system, namely, an ins-del P system. As P systems (a model for membrane computing) draw their origins from modeling computations of biological systems, considering insertions and deletions in this context is particularly meaningful. There is one small technical issue, namely, in a P system, usually there is no specific initial membrane where the computation begins, since the membranes evolve in a so-called maximally parallel way. But if the collection of axioms in each membrane (except of one) is empty, then this exceptional membrane can be viewed as an initial membrane to begin with, so that such a system works in the same way as a GCID system where the membranes of a P system correspond to the components of a GCID system; see [13].

The mentioned connections motivate to study GCID systems. Much research has then be devoted to restricting the computational resources as far as possible while still maintaining computational completeness. To be more concrete, typical questions are: To what extent can we limit the context of the insertion or of the deletion rules? How many components are needed? Are there kind of trade-offs between these questions? All this is formalized in the following.

The descriptional complexity of a GCID system is measured by its size $(k;n,i',i'';m,j',j'')$ where the parameters from left to right denote (i) number of components (ii) the maximal length of the insertion string (iii) the maximal length of the left context used in insertion rules (iv) the maximal length of the right context used in insertion rules and the last three parameters follow a similar representation with respect to deletion. The generative power of GCID systems for insertion/deletion lengths satisfying $n+m\in \{2,3\}$ has also been studied in [4, 5, 8]. However, the control graph is not a path for many cases.

The main objective of this paper is to characterize recursively enumerable languages (denoted as $\mathrm {RE})$ by GCID systems with bounded sizes, whose underlying (undirected) control graph is a path, as this special case also relates to ins-del P systems [13]. Also, this objective can be seen as a sort of syntactic restriction on GCID systems, on top of the usually considered numerical values limiting the descriptional complexity. We are interested in the question which type of resources of path-structured GCID systems are still powerful enough to characterize $\mathrm {RE}$. We prove that GCID system of sizes $(k;n,i',i'';1,j',j'')$ with $i',i'',j',j''\in \{0,1\}$, $i'+i''=1$ and (i) $k=3, n=1,~j'+j''=2,$ (ii) $k=4, n=1,~j'+j''=1,$ (iii) $k=3, n=2,~j'+j''=1,$ all characterize $\mathrm {RE}$ with a path as a control graph. Previously, such results were only known for GCID systems with arbitrary control graphs [5]. Our results may also revive interest in the conjecture of Ivanov and Verlan [8] which states that $\mathrm {RE} \ne \mathrm {GCID}(s)$ if $k=2$ in $s=(k;1,i',i'';1,j',j'')$, with $i',i'',j',j''\in \{0,1\}$ and $i'+i''+j'+j''\le 3$. In the same situation, this statement is known to be true if $k=1$. If the conjecture were true, then our results for $k=3$ would be optimal.

2 Preliminaries

We assume that the readers are familiar with the standard notations used in formal language theory. We recall a few notations here. Let $\mathbb {N}$ denote the set of positive integers, and $[1\ldots k]=\{i\in \mathbb {N}:1\le i\le k\}$. Given an alphabet (finite set) $\varSigma$, $\varSigma ^*$ denotes the free monoid generated by $\varSigma$. The elements of $\varSigma ^*$ are called strings or words; $\lambda$ denotes the empty string. For a string $w \in \varSigma ^*$, |w| is the length of w and $w^R$ denotes the reversal (mirror image) of w. $L^R$ and $\mathcal {L}^R$ are understood for languages L and language families $\mathcal {L}$. For the computational completeness results, we are using as our main tool the fact that type-0 grammars in Special Geffert Normal Form (SGNF) that characterize $\mathrm {RE}$.

Definition 1

A type-0 grammar $G=(N,T,P,S)$ is said to be in SGNF if

• N decomposes as $N=N'\cup N''$, where $N''=\{A_1,B_1,A_2,B_2\}$ and $N'$ contains at least the two nonterminals S and $S'$;

• the only non-context-free rules in P are $AB \rightarrow \lambda$, where $AB\in \{A_1B_1,A_2B_2\}$;

• the context-free rules are of the form (i) $S'\rightarrow \lambda$, or (ii) $X \rightarrow Y_1Y_2$, where $X\in N'$ and $Y_1Y_2\in ((N'\setminus \{X\})(T \cup N'')) \cup ((T\cup N'')(N'\setminus \{X\}))$.

The way the normal form is constructed is described in [6], based on [7]. We assume in this paper that the context-free rules $r:X\rightarrow Y_1Y_2$ either satisfy $Y_1\in \{A_1,A_2\}$ and $Y_2\in N'$, or $Y_1\in N'$ and $Y_2\in \{B_1,B_2\}\cup T$. This also means that the derivation in G undergoes two phases: in phase I, only context-free rules are applied. This phase ends with applying the context-free deletion rule $S' \rightarrow \lambda$. Then, only non-context-free deletion rules are applied in phase II. Notice that the symbol from $N'$, as long as present, separates $A_1$ and $A_2$ from $B_1$ and $B_2$; this prevents a premature start of phase II. We write $\Rightarrow _r$ to denote a single derivation step using rule r, and $\Rightarrow _G$ (or $\Rightarrow$ if no confusion arises) denotes a single derivation step using any rule of G. Then, $L(G)=\{w\in T^*\mid S\Rightarrow ^* w\}$, where $\Rightarrow ^*$ is the reflexive transitive closure of $\Rightarrow$.

Definition 2

A graph-controlled insertion-deletion system (GCID for short) with k components is a construct $\varPi = (k,V,T,A,H,i_0,i_f,R)$, where (i) k is the number of components, (ii) V is an alphabet, (iii) $T \subseteq V$ is the terminal alphabet, (iv) $A \subset V^*$ is a finite set of strings, called axiom, (v) H is a set of labels associated (in a one-to-one manner) to the rules in R, (vi) $i_0 \in [1 \ldots k]$ is the initial component, (vii) $i_f \in [1 \ldots k]$ is the final component and (viii) R is a finite set of rules of the form l: (i, r, j), where l is the label of the rule, r is an insertion rule of the form $(u, \eta , v)_I$ or deletion rule of the form $(u, \delta , v)_D$, where $u,v \in V^*, ~\eta ,\delta \in V^+$ and $i, j \in [1 \ldots k]$.

If the initial component itself is the final component, then we call the system returning. The pair (u, v) is called the context, $\eta$ is called the insertion string, $\delta$ is called the deletion string and $x \in A$ is called an axiom. We write rules in R in the form l: (i, r, j), where $l \in H$ is the label associated to the rule. Often, the component is part of the label name. This will also (implicitly) define H. We shall omit the label l of the rule wherever it is not necessary for the discussion.

We now describe how GCID systems work. Applying an insertion rule of the form $(u,\eta ,v)_I$ means that the string $\eta$ is inserted between u and v; this corresponds to the rewriting rule $uv \rightarrow u \eta v$. Similarly, applying a deletion rule of the form $(u, \delta ,v)_D$ means that the string $\delta$ is deleted between u and v; this corresponds to the rewriting rule $u \delta v \rightarrow uv$. A configuration of $\varPi$ is represented by $(w)_i$, where $i\in [1\ldots k]$ is the number of the current component and $w\in V^*$ is the current string. We also say that w has entered component Ci. We write $(w)_i \Rightarrow _{l} (w')_j$ or $(w')_j \Leftarrow _{l} (w)_i$ if there is a rule l: (i, r, j) in R, and $w'$ is obtained by applying the insertion or deletion rule r to w. By ${(w)_i}_{\Leftarrow _{l'}} ^{\Rightarrow _{l}} (w')_j$, we mean that $(w')_j$ is derivable from $(w)_i$ using rule l and $(w)_i$ is derivable from $(w')_j$ using rule $l'$. For brevity, we write $(w)_i\Rightarrow (w')_j$ if there is some rule l in R such that $(w)_i\Rightarrow _l (w')_j$. To avoid confusion with traditional grammars, we write $\Rightarrow _*$ for the transitive reflexive closure of $\Rightarrow$ between configurations. The language $L(\varPi )$ generated by $\varPi$ is defined as $\{w\in T^*\mid (x)_{i_0}\Rightarrow _* (w)_{i_f} ~\text {for some}~ x \in A\}$. For returning GCID systems $\varPi$ with initial component C1, we also write $(w)_1\Rightarrow '(w')_1$, meaning that there is a sequence of derivation steps $(w)_1\Rightarrow (w_1)_{c_1}\Rightarrow \cdots \Rightarrow (w_k)_{c_k}\Rightarrow (w')_1$ such that, for all $i=1,\dots ,k$, $c_i\ne 1$.

The underlying control graph of a GCID system $\varPi$ with k components is defined to be a graph with k nodes labelled C1 through Ck and there exists a directed edge from Ci to Cj if there exists a rule of the form (i, r, j) in R of $\varPi$. We also associate a simple undirected graph on k nodes to a GCID system of k components as follows: there is an undirected edge from a node Ci to Cj ($i \ne j$) if there exists a rule of the form $(i,r_1,j)$ or $(j,r_2,i)$ in R of $\varPi$ (hence, loops and multi-edges are excluded). We call a returning GCID system with k components path-structured if its underlying undirected control graph has the edge set $\left\{ \{Ci,C(i+1)\} \mid i\in [1\dots k-1] \right\}$.

The descriptional complexity of a GCID system is measured by its size $s=(k;n,i',i'';m,j',j'')$, where the parameters represent resource bounds as given below. Slightly abusing notation, the language class that can be generated by GCID systems of size s is denoted by $\mathrm {GCID}(s)$ and the class of languages describable by path-structured GCID systems of size s is denoted by $\mathrm {GCID}_P(s)$.

$$\begin{aligned}\begin{array}{|lcl|lcl|} \hline k &{}=&{} \mathrm{{the~number~of~components}} &{}&{}&{} \\ n &{}=&{} \max \{|\eta | :(i,(u, \eta , v)_I,j) \in R\} &{} m&{}=&{} \max \{|\delta | :(i,(u, \delta , v)_D,j) \in R\}\\ i'&{}=&{} \max \{|u| :(i,(u, \eta , v)_I,j) \in R \} &{} j'&{}=&{} \max \{|u| :(i,(u, \delta , v)_D,j) \in R \} \\ i''&{}=&{}\max \{|v| :(i,(u, \eta , v)_I ,j) \in R \} &{} j''&{}=&{}max \{|v| :(i,(u, \delta , v)_D,j) \in R \} \\ \hline \end{array}\end{aligned}$$

3 Computational Completeness

In this section, to prove the computational completeness of GCID system of certain sizes, we start with a type-0 grammar $G=(N,T,P,S)$ in SGNF as defined in Definition 1. The rules of P are labelled injectively with labels from $[1 \ldots |P|]$. We will use these labels and primed variants thereof as nonterminals in the simulating GCID system. Their purpose is to mark positions in the string and also to enforce a certain sequence of rule applications. As per the definition of SGNF, there are, apart from the easy-to-handle context-free deletion rule, context-free rules $r:X\rightarrow Y_1Y_2$ and non-context-free deletion rules $f:AB\rightarrow \lambda$. For these types of rules, we present the simulations in the form of a table, for instance, as in Table 1. A detailed discussion of the working of this simulation will follow in the proof of the next theorem.

To simplify our further results, the following observations from [5] are used.

Proposition 1

[5]. Let $k,n,i',i'',m,j,j''$ be non-negative integers.

• 1. $\mathrm {GCID}_P(k;n,i',i'';m,j',j'') = [\mathrm {GCID}_P(k;n,i'',i';m,j'',j')]^R$

• 2. $\mathrm {RE}=\mathrm {GCID}_P(k;n,i',i'';m,j',j'')$ iff $\mathrm {RE}=\mathrm {GCID}_P(k;n,i'',i';m,j'',j')$

3.1 GCID Systems with Insertion and Deletion Length One

In [15], it has been proved that ins-del systems with size (1,1,1;1,1,1) characterize $\mathrm {RE}$. Notice that it is proved in [10, 12] that ins-del systems of size (1, 1, 1; 1, 1, 0) or (1, 1, 0; 1, 1, 1) cannot characterize $\mathrm {RE}$. It is therefore obvious that we need at least 2 components in a graph-controlled ins-del system of sizes (1, 1, 1; 1, 1, 0) and (1, 1, 0; 1, 1, 1) to characterize $\mathrm {RE}$. In [5], we characterized $\mathrm {RE}$ by path-structured GCID systems of size (3; 1, 1, 1; 1, 1, 0). Also, in [8], it was shown that $\mathrm {GCID}_P(3;1,2,0;1,1,0)=\mathrm {RE}$ and $\mathrm {GCID}_P(3;1,1,0;1,2,0)=\mathrm {RE}$. We now complement these results.

Table 1. Path-structured GCID systems of size (3; 1, 1, 0; 1, 1, 1) simulating type-0 grammars G in SGNF. In the table, $c'\in \{A_1,A_2,\kappa '\}$ and $c\in \{ B_1,B_2,\kappa \} \cup T$, f, r are rule markers, while $\varDelta$ is a dummy symbol that was not part of the alphabet of G.

Theorem 1

$\mathrm {RE} = \mathrm {GCID}_P(3;1,1,0;1,1,1) = \mathrm {GCID}_P(3;1,0,1;1,1,1)$.

At a first glance, the reader might wonder that the simulation would be straightforward (as initially thought by the authors themselves, as there are many resources available). However, this is not the case. The problem is that any rule of a component could be applied whenever a string enters that component. Since insertion is only left-context-sensitive, the insertion string can be adjoined any number of times on the right of this context, similar to context-free insertion. This issue is handled by inserting some markers and then inserting $Y_1$ and $Y_2$ (from rule $X\rightarrow Y_1Y_2$) after the markers. We have to be careful, since a back-and-forth transition may insert many $Y_1$’s and/or $Y_2$’s after the marker.

Proof

Consider a type-0 grammar $G=(N,T,P,S)$ in SGNF as in Definition 1. We construct a $\text {GCID}_P$ system $\varPi$ such that $L(\varPi ) = L(G)$: $\varPi = (3,V,T,\{\kappa 'S\kappa \},H,1,1,R)$. The alphabet of $\varPi$ is $V \subset N \cup T \cup \{r,r' :r \in [1 \ldots |P|]\}\cup \{\kappa ',\kappa \}$. The simulation is explained in Table 1, which completes the description of R and V. Clearly, $\varPi$ has size (3; 1, 1, 0; 1, 1, 1).

With the rules of Table 1, we prove $L(G)\subseteq L(\varPi )$ by showing how the different types of rules are simulated. Let us look into the context-free rules first. The simulation of the deletion rule h is obvious and hence omitted. Applying some rule $r:X\rightarrow Y_1Y_2$, with $X\in N'$, to $w=\alpha X\beta$, where $\alpha ,\beta \in (N''\cup T)^*$, yields $w'=\alpha Y_1Y_2\beta$ in G. In $\varPi$, we can find the following simulation, with $\alpha 'c'=\kappa '\alpha$ and $c\beta '=\beta \kappa$ where $\alpha '\kappa ,\kappa 'c\kappa ,\kappa 'c'\kappa ,\kappa '\beta ' \in \{\kappa '\}(N''\cup T)^*\{\kappa \}$:

$$\begin{aligned} (\kappa ' w\kappa )_1&\Rightarrow _{r1.1} (\alpha 'c' Xrc\beta ' )_2\Rightarrow _{r2.1} (\alpha 'c'rc\beta ')_1 \Rightarrow _{r1.2} (\alpha 'c' rr'c\beta ')_2\Rightarrow _{r2.2} (\alpha 'c' r'c\beta ')_1 \\&\Rightarrow _{r1.3} (\alpha 'c' r'\varDelta c\beta ')_1\Rightarrow _{r1.4} (\alpha 'c' r'Y_2\varDelta c\beta ')_2 \Rightarrow _{r2.3.c} (\alpha 'c' r'Y_2 c\beta ')_3 \Rightarrow _{r3.1}\\&(\alpha 'c' r'Y_1Y_2 c\beta ')_2\Rightarrow _{r2.4.c'} (\alpha 'c' Y_1Y_2 c\beta ')_1 =(\kappa ' \alpha Y_1Y_2\beta \kappa )_1=(\kappa ' w'\kappa )_1\,. \end{aligned}$$

For the non-context-free case, the simulation of $f:AB\rightarrow \lambda$ is straightforward; hence, details are omitted. By induction, this proves that whenever $S\Rightarrow ^*w$ in G, then there is a derivation $(\kappa ' S\kappa )_1\Rightarrow '_*(\kappa ' w\kappa )_1$ in $\varPi$, and finally $(\kappa ' w\kappa )_1\Rightarrow ' (w)_1$ is possible.

In the following we show the converse $L(\varPi ) \subseteq L(G)$ and this is important since it also proves that $\varPi$ not only produces intended strings as above but also does not produce any unintended strings as well.

Conversely, consider a configuration $(w)_1$, with $(\kappa ' S\kappa )_1\Rightarrow '_*(w)_1$. We assume now that w starts with $\kappa '$ and ends with $\kappa$, and that these are the only occurrences of these special letters in w, as no malicious derivations are possible when prematurely deleting $\kappa$ or $\kappa '$. We now discuss five situations for w and prove in each case that, whenever $(w)\Rightarrow '(w')$, then $w'$ satisfies one of these five situations, or from $(w')_1$ no final configuration can be reached. As $S\in N'$, the base case $\kappa 'S\kappa$ is covered in case (iii) which is presented below. Hence, by induction, the case distinction presented in the following considers all possibilities.

(i) Assume that w contains one occurrence of $r'$ (the primed marker of some context-free rule r), but no occurrence of unprimed markers of context-free rules, and no occurrence of any nonterminal from $N'$, neither an occurrence of $\varDelta$. Hence, $w=\kappa '\alpha r'\beta \kappa$ for appropriate strings $\alpha ,\beta \in (N''\cup T)^*$. Then, the rules (i.a) r1.3, (i.b) r1.4, as well as the simulation initiation rules like (i.c) f1.1 are applicable. Let us discuss these possibilities now. Subcase (i.c): If f1.1 is applied, then, say, f is introduced to the right of some occurrence of A. In C2, one can then try to apply (i.c.1) f2.1, (i.c.2) f2, 2, or (i.c.3) $r2.4.c'$ for an appropriate $c'$. However, as we are still simulating phase I of G, B cannot be to the right of A, so that Subcase (i.c.1) cannot occur. Subcase (i.c.2) simply undoes the effect of previously applying f1.1, so that we can ignore its discussion. In Subcase (i.c.3), we are back in C1 with a string that contains no symbols from $N'$, nor any variants of context-free rule markers, nor any $\varDelta$, but one non-context-free rule marker. We will discuss this in Case (v) below and show that such a derivation cannot terminate. Subcase (i.b): If we apply r1.4 to w immediately, we are stuck in C2. Hence, consider finally Subcase (i.a): we apply r1.3 first once. Now, we are in a very similar situation as before, but one $\varDelta$ is added to the right of $r'$. This means that continuing with f1.1 will get stuck again in C2. In order to make progress, we should finally apply r1.4. Now, we are in the configuration $(\kappa '\alpha r'Y_2\varDelta ^n\beta \kappa )_2$ for some $n\ge 1$. As $Y_1\ne Y_2$, $r2.4.c'$ is not applicable for any $c'$, so the derivation is stuck in C2. If we apply r.2.3.c, then we can only proceed if $n=1$, which means that we applied r1.3 exactly once before. Hence, $(\kappa '\alpha r'Y_2\varDelta \beta \kappa )_2\Rightarrow (\kappa '\alpha r'Y_2\beta \kappa )_3\Rightarrow (\kappa '\alpha r'Y_1Y_2\beta \kappa )_2\Rightarrow (\kappa '\alpha Y_1Y_2\beta \kappa )_1$ is enforced. This corresponds to the intended derivation; the assumed occurrence of $r'$ in the string was replaced by $Y_1Y_2$; this corresponds to the situation of Case (iii).

(ii) Assume that w contains one occurrence of r (the unprimed marker of some context-free rule r), but no occurrence of primed markers of context-free rules, and no occurrence of any nonterminal from $N'$, neither an occurrence of $\varDelta$. Hence, $w=\kappa '\alpha r\beta \kappa$ for appropriate strings $\alpha ,\beta \in (N''\cup T)^*$. Similarly as discussed in Case (i), trying to start a simulation of some non-context-free rule gets stuck in C2, in particular, as we are simulating phase I of G and there is no nonterminal from $N'$ in the current string. Hence, we are now forced to apply r1.2. This means that in C2, we have to apply r2.2, leading us to $(w')_1$ with $w'=\alpha r'\beta$, a situation previously discussed in Case (i).

(iii) Assume that w contains one occurrence $X\in N'$, but no occurrence of unprimed or primed markers of context-free rules, and no occurrence of $\varDelta$. Hence, $w=\kappa '\alpha X\beta \kappa$ for appropriate strings $\alpha ,\beta \in (N''\cup T)^*$. As we are still simulating phase I of G, we are now forced to apply r1.1 or simulate the context-free deletion rule (which gives a trivial discussion that is omitted; the important point is that this switches to phase II of the simulation of G). This means that in C2, we have to apply r2.1, leading us to $(w')_1$ with $w'=\kappa '\alpha r\beta \kappa$ for some context-free rule $r:X\rightarrow Y_1Y_2$, a situation already discussed in Case (ii).

(iv) Assume that $w\in \{\kappa '\} (N''\cup T)^*\{\kappa \}$. Now, it is straightforward to analyze that we have to follow the simulation of one of the non-context-free deletion rules, or finally apply the rule deleting the special symbols $\kappa , \kappa '$.

(v) Assume that w contains no primed or unprimed markers of context-free rules, nor a symbol from $N'$, nor any $\varDelta$ but contains a non-context-free rule marker. This means we have to apply some rule f1.1, but although this might successfully simulate a non-context-free deletion rule, it will bring us back to C1 with a non-context-free rule marker in the string. Hence, we are back in Case (v), so that this type of derivation can never terminate.

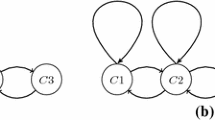
The second claim follows by Proposition 1. The underlying graph of the simulation is shown in Fig. 1(a). The corresponding undirected graph is a path and hence the presented GCID system is path-structured.    $\square$

Fig. 1.

Control graphs underlying the GCID systems (characterizing RE) in this paper

In [6], it was shown that GCID systems of sizes (4; 1, 1, 0; 1, 1, 0) and (4; 1, 1, 0; 1, 0, 1) describe $\mathrm {RE}$, with the underlying control graph not being a path. In [5], the number of components was reduced from 4 to 3, however, with the underlying graph still not being a path. In the next two theorems we characterize $\mathrm {RE}$ by path-structured GCID systems of sizes (4; 1, 1, 0; 1, 1, 0) and (4; 1, 1, 0; 1, 0, 1). The former result also complements an earlier result of [8], which stated that $\mathrm {GCID}_P(3;1,2,0;1,1,0)$ = $\mathrm {GCID}_P(3;1,1,0;1,2,0)$ = $\mathrm {RE}$. We trade-off the number of components against the length of the left context of the insertion/deletion.

Theorem 2

$\mathrm {RE} = \mathrm {GCID}_P(4;1,1,0;1,1,0) = \mathrm {GCID}_P(4;1,0,1;1,0,1)$.

Table 2. GCID rules of size (4; 1, 1, 0; 1, 1, 0) with axiom $\kappa S$ and $c\in N''\cup T\cup \{\kappa \}$.

Proof

Consider a type-0 grammar $G=(N,T,P,S)$ in SGNF as in Definition 1. We construct a $\text {GCID}_P$ system $\varPi = (4,V,T,\{\kappa S\},H,1,1,R)$ such that $L(\varPi ) = L(G)$. The four columns of the table correspond to the four components of $\varPi$. The rows correspond to the simulation of $r:X\rightarrow Y_1Y_2$, $f:AB\rightarrow \lambda$ and of the context-free deletion rule $h: S' \rightarrow \lambda$. The last row deletes the left-end marker $\kappa$ introduced in the axiom. The alphabet of $\varPi$ is $V \subset N \cup T \cup \{p,p',p'',p''' :p \in [1 \ldots |P|]\}\cup \{\kappa \}$. R is defined as shown in Table 2, depending on G. Clearly, $\varPi$ has size (4; 1, 1, 0; 1, 1, 0). We now prove that $L(G) \subseteq L(\varPi )$. To this end, we show that if $w\Rightarrow w'$ in G, with $w,w'\in (N\cup T)^*$, then $(\kappa w)_1\Rightarrow ' (\kappa w')_1$ according to $\varPi$. From this fact, the claim follows by a simple induction argument. As the claim is evident for rule h, we only need to discuss $w\Rightarrow w'$ due to using a context-free rule (Case CF) or due to using a non-context-free rule (Case $\overline{\mathrm {CF}}$).

$\underline{\text {Case CF}}$: The intended simulation works as follows:

$$\begin{aligned}\begin{array}{c} (\kappa \alpha X\beta )_1\Rightarrow _{r1.1} (\kappa \alpha rX\beta )_2 \Rightarrow _{r2.1} (\kappa \alpha rXr'\beta )_3 \Rightarrow _{r3.1} (\kappa \alpha rr'\beta )_4 \Rightarrow _{r4.1} \\ (\kappa \alpha rr'r''\beta )_3 \Rightarrow _{r3.2} (\kappa \alpha rr'r''r'''\beta )_2 \Rightarrow _{r2.2} (\kappa \alpha rr''r'''\beta )_2 \Rightarrow _{r2.3} (\kappa \alpha rr'''\beta )_3 \Rightarrow _{r3.3} \\ (\kappa \alpha rr'''Y_2\beta )_4 \Rightarrow _{r4.2} (\kappa \alpha r'''Y_2\beta )_3 \Rightarrow _{r3.4} (\kappa \alpha r'''Y_1Y_2\beta )_2 \Rightarrow _{r2.4.c} (\kappa \alpha Y_1Y_2\beta )_1. \end{array}\end{aligned}$$

Here, c is the last symbol of $\kappa \alpha$, possibly $\kappa$.

$\underline{{\text {Case }} \overline{\text {CF}}}$: Let us consider $f:AB\rightarrow \lambda$. This means that $w=\alpha AB\beta$ and $w'=\alpha \beta$ for some $\alpha ,\beta \in (N\cup T)^*$. Within $\varPi$, this can be simulated as follows.

$$\begin{aligned}\begin{array}{c} (\kappa w)_1=(\kappa \alpha AB\beta )_1\Rightarrow _{f1.1} (\kappa \alpha fAB\beta )_2 \Rightarrow _{f2.1} (\kappa \alpha fAf'B\beta )_3 \\ \Rightarrow _{f3.1} (\kappa \alpha fAf'\beta )_4 \Rightarrow _{f4.1} (\kappa \alpha ff'\beta )_3 \Rightarrow _{f3.2} (\kappa \alpha f \beta )_2 \Rightarrow _{f2.2} (\kappa w')_1. \end{array}\end{aligned}$$

The converse inclusion $L(\varPi )\subseteq L(G)$ is following an inductive argument as in the previous theorem and hence is omitted here. The second claim follows by Proposition 1. The underlying graph of the simulation is shown in Fig. 1(b).    $\square$

Theorem 3

$\mathrm {RE} = \mathrm {GCID}_P(4;1,1,0;1,0,1) = \mathrm {GCID}_P(4;1,0,1;1,1,0)$.

Table 3. GCID rules of size (4; 1, 1, 0; 1, 0, 1) simulating a type-0 grammar in SGNF

Proof

Consider a type-0 grammar $G=(N,T,P,S)$ in SGNF. The rules of P are labelled injectively with labels from $[1 \ldots |P|]$. We construct a $\text {GCID}_P$ system $\varPi$ such that $L(\varPi ) = L(G)$, with $\varPi = (4,V,T,\{S\},H,1,1,R)$. The alphabet of $\varPi$ is $V \subset N \cup T \cup \{p,p',p'',p''' :p \in [1 \ldots |P|]\}$. R is defined as shown in Table 3. $\varPi$ has the claimed size. The intended simulation of a context-free rule is as follows.

$$\begin{aligned}\begin{array}{c} (\alpha X\beta )_1\Rightarrow _{r1.1} (\alpha Xr\beta )_2 \Rightarrow _{r2.1} (\alpha r\beta )_1 \Rightarrow _{r1.2} (\alpha rr'\beta )_2 \Rightarrow _{r2.2} \\ (\alpha r'\beta )_1 \Rightarrow _{r1.3} (\alpha r'r''\beta )_2 \Rightarrow _{r2.3} (\alpha r' r''Y_2\beta )_3 \Rightarrow _{r3.1} (\alpha r' Y_2 \beta )_4 \Rightarrow _{r4.1} \\ (\alpha r'r'''Y_2\beta )_3 \Rightarrow _{r3.2} (\alpha r'r'''Y_1Y_2\beta )_2 \Rightarrow _{r2.4} (\alpha r'Y_1Y_2\beta )_2 \Rightarrow _{r2.5} (\alpha Y_1Y_2\beta )_1. \end{array}\end{aligned}$$

The intended simulation of a non-context-free rule is as follows.

$$\begin{aligned}\begin{array}{c} (\alpha AB\beta )_1\Rightarrow _{f1.1} (\alpha ABf\beta )_2 \Rightarrow _{f2.1} (\alpha Af'Bf\beta )_3 \Rightarrow _{f3.1} \\ (\alpha f'Bf\beta )_4 \Rightarrow _{r4.1} (\alpha f'f\beta )_3 \Rightarrow _{r3.2} (\alpha f\beta )_2 \Rightarrow _{r2.2} (\alpha \beta )_1. \end{array}\end{aligned}$$

This shows that $L(G) \subseteq L(\varPi )$. The main complication for the correctness proof is the fact that we may return to C1 with strings containing rule markers. This brings along a detailed discussion of four different situations for w when considering $(S)_1\Rightarrow '_*(w)_1\Rightarrow '(w')_1$ according to $\varPi$. A detailed explanation of these different situations follows a similar argument as in Theorem 1 and is omitted here in view of page constraint.    $\square$

3.2 GCID Systems with Insertion Length Two

In [6], it is shown that $\mathrm {GCID}_P(4;2,0,0;1,1,0)=\mathrm {RE}$. Here, we show that, if we allow a context (either left or right) for insertion, then we can still describe $\mathrm {RE}$ while decreasing the number of components from 4 to 3, yet obtaining path-structured GCID systems.

Theorem 4

$\mathrm {RE} = \mathrm {GCID}_P(3;2,1,0;1,0,1)= \mathrm {GCID}_P(3;2,0,1;1,1,0)$.

Table 4. GCID rules of size (3; 2, 1, 0; 1, 0, 1) simulating a type-0 grammar in SGNF.

Proof

Consider a type-0 grammar $G=(N,T,P,S)$ in SGNF as in Definition 1. We construct a $\text {GCID}_P$ system $\varPi = (3,V,T,\{S\},H,1,1,R)$ of size (3; 2, 1, 0; 1, 0, 1) such that $L(\varPi ) = L(G)$. Here, let $V\subset N\cup T\cup [1 \ldots |P|]$ contain in particular those rule labels used in the rules listed in Table 4. $\varPi$ is of size (3; 2, 1, 0; 1, 0, 1). We now prove that $L(G) \subseteq L(\varPi )$. As the claim is evident for $h:S'\rightarrow \lambda$, we show that if $w\Rightarrow w'$ in G, then $(w)_1\Rightarrow ' (w')_1$ according to $\varPi$ in two more cases.

$\underline{\text {Case CF}}$: Here, $w=\alpha X\beta$ and $w'=\alpha Y_1Y_2\beta$ for some $\alpha ,\beta \in (N''\cup T)^*$. The simulation of $r:X\rightarrow Y_1Y_2$ performs as follows:

$$\begin{aligned}\begin{array}{c} (\alpha X\beta )_1 ~_{\Rightarrow _{r1.1}}^{\Leftarrow _{r2.2}} (\alpha Xr\beta )_2 \Rightarrow _{r2.1} (\alpha r\beta )_3 \Rightarrow _{r3.1} (\alpha rY_1Y_2\beta )_2 \Rightarrow _{r2.2} (\alpha Y_1Y_2\beta )_1\,. \end{array} \end{aligned}$$

Note the role of the right context r in r2.1. If the marker r is not present for the deletion, then after applying r3.1, when we come back to C2, we can apply r2.1 again and could end-up with a malicious derivation.

$\underline{{\text {Case }} \overline{\text {CF}}}$: Here $w=\alpha AB\beta$ and $w'=\alpha \beta$ for some $\alpha ,\beta \in (N\cup T)^*$. The rules $f:AB\rightarrow \lambda$ can be simulated as follows.

$$\begin{aligned}\begin{array}{c} (\alpha AB\beta )_1 ~_{\Rightarrow _{f1.1}}^ {\Leftarrow _{f2.2}} (\alpha ABf\beta )_2 \Rightarrow _{f2.1} (\alpha Af\beta )_3 \Rightarrow _{f3.1} (\alpha f\beta )_2 \Rightarrow _{f2.2} (\alpha \beta )_1\,. \end{array}\end{aligned}$$

We leave it to the reader to verify that no malicious derivations are possible. Proposition 1 shows that also GCID systems of size (3; 2, 0, 1; 1, 1, 0) are computationally complete. Figure 1(a) shows the control graph of the simulation.    $\square$

Theorem 5

$\mathrm {RE} = \mathrm {GCID}_P(3;2,1,0;1,1,0) = \mathrm {GCID}_P(3;2,0,1;1,0,1)$.

The simulation is very similar to Theorem 4 and hence we provide only the simulating rules in Table 5.    $\square$

Table 5. GCID rules of size (3; 2, 1, 0; 1, 1, 0) simulating a type-0 grammar in SGNF.

3.3 Consequences for ins-del P Systems

Representing the family of languages generated by ins-del P system with k membranes and size $(n,i',i'',m,j',j'')$, where the size parameters have the same meaning as in GCID system by $\mathrm {ELSP}_k(\mathrm {INS}_n^{i',i''}\mathrm {DEL}_m^{j',j''})$ (this notation was used in [8], based on [13]), we know that $\mathrm {ELSP}_4(\mathrm {INS}_1^{1,0}\mathrm {DEL}_2^{0,0})$, $\mathrm {ELSP}_4(\mathrm {INS}_2^{0,0}\mathrm {DEL}_1^{1,0})$ ([6]) and $\mathrm {ELSP}_3(\mathrm {INS}_1^{2,0}\mathrm {DEL}_1^{1,0})$, $\mathrm {ELSP}_3(\mathrm {INS}_1^{1,0}\mathrm {DEL}_1^{2,0})$ ([8]) are computationally complete. Since the underlying control graph of all the GCID systems (characterizing $\mathrm {RE}$) in this paper has a path structure, the results that we obtained correspond to ins-del P systems in the following way, complementing [6, 8].

Corollary 1

For $i', i'', j',j'' \in \{0,1\}$ with $i'+i'' = j'+j''=1$, the following ins-del P systems are computationally complete.

• 1. $\mathrm {RE}= \mathrm {ELSP}_3(\mathrm {INS}_2^{i',i''}\mathrm {DEL}_1^{j',j''})$ = $\mathrm {ELSP}_4(\mathrm {INS}_1^{i',i''}\mathrm {DEL}_1^{j',j''})$.

• 2. $\mathrm {RE}= \mathrm {ELSP}_3(\mathrm {INS}_1^{1,0}\mathrm {DEL}_1^{1,1}) = \mathrm {ELSP}_3(\mathrm {INS}_1^{0,1}\mathrm {DEL}_1^{1,1})$.    $\square$

4 Summary and Open Problems

In this paper, we focused on examining the computational power of graph-controlled ins-del systems with paths as control graphs, which naturally correspond to variants of P systems. We lowered the resource needs to describe RE. However, we still do not know if these resource bounds are optimal.

Here we considered the underlying graph of $\mathrm {GCID}$ systems to be path-structured only. One may also consider also tree structure, which may give additional power, especially to ins-del P systems. The resources used in the results of ins-del P systems need not be optimal since in ins-del P systems, each membrane can have initial strings and they all evolve in parallel which may reduce the size.

The reader may have noticed that we discussed in detail the case of insertion strings of length two, but a similar discussion for the case of deletion strings of length two is missing. More precisely, to state one concrete question, it is open whether $\mathrm {RE} = \mathrm {GCID}_P(3;1,1,0;2,1,0) = \mathrm {GCID}_P(3;1,1,0;2,0,1)$.

In view of the connections with P systems, it would be also interesting to study Parikh images of (restricted) graph-controlled ins-del systems, as started out for matrix-controlled ins-del systems in [3]. This also relates to the macroset GCID systems considered in [2].