1 Introduction

Reversible circuits represent an emerging technology based on a computation paradigm which significantly differs from conventional circuits. In fact, they allow bijective operations only, i.e., n-input n-output functions that map each possible input vector to a unique output vector. Reversible computation enables several promising applications and, indeed, surpasses conventional computation paradigms in many domains including but not limited to quantum computation (see, e.g., [1]), certain aspects of low-power design (as experimentally observed, e.g., in [2]), encoding and decoding devices (see, e.g., [3, 4]), or verification (see, e.g., [5]).

Accordingly, also the consideration of the design of reversible circuits received significant interest. In comparison to conventional circuit design, new concepts and paradigms have to be considered here. For example, fanout and feedback are not directly allowed. This affects the design of reversible circuits and requires alternative solutions. To this end, several design approaches have been introduced. An overview of that is, e.g., provided in [6, 7].

In parallel, how to physically build reversible and quantum circuits is being investigated and led to first promising results (see, e.g., [8, 9]). With this, also the question of how to prevent and detect faults in the physical realization became relevant. In particular for quantum computation, this is a crucial issue: Quantum systems are much more fault-prone than conventional circuits, since the phenomenon of quantum de-coherence forces the qubit states to decay – resulting in a loss of quantum information which, eventually, causes faults. Faults also do originate from the fact that quantum computations are conducted by a stepwise application of gates on qubits.

As a result, researchers studied different fault models and the respective methods for Automatic Test Pattern Generation (ATPG). In that regard, one of the earliest works on different fault models for quantum circuits is [10], which proposed these models based on the implementation principles of quantum circuits using trapped ion technology [1]. The types of fault model included, for example, the single missing gate fault (SMGF), the partial missing gate fault (PMGF), and the multiple missing gate fault (MMGF). However, mainly ATPG methods for single faults have been proposed thus far (see e.g. [11,12,13]).

2 Background

To keep the remainder of this work self-contained, this section briefly reviews the basics of reversible circuits as well as ATPG and the fault models considered for this kind of circuits.

2.1 Reversible Circuits

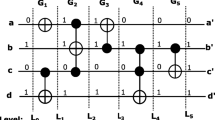
Reversible circuits are digital circuits with the same number of input signals and output signals. Furthermore, reversible circuits realize bijections, i.e. each input assignment maps to a unique output assignment. Accordingly, computations can not only be performed from the inputs to the outputs but also in the other direction. Reversible circuits are composed as cascades of reversible gates. The Toffoli gate [14] is widely used in the literature and also considered in this paper.

Definition 1

Given a set of variables or signals \(X=\{x_1,x_2,\dots ,x_n\}\), a Toffoli gate G(C, t) is a tuple of a possibly empty set \(C\subset X\) of control lines and a single target line \(t\in X\setminus C\). The Toffoli gate inverts the value on the target line if all values on the control lines are set to 1 or if \(C=\emptyset \). All remaining values are passed through unaltered. In the following, Toffoli gates are also denoted as Multiple Controlled Toffoli (MCT) gates.

2.2 Test of Reversible Circuits

As in conventional circuits, Automatic Test Pattern Generation (ATPG) methods for reversible circuits aim at determining a set of stimulus patterns (denoted as testset) in order to detect faults in a circuit with respect to an underlying fault model. A single missing gate fault is defined as follows.

Definition 2

Let G(C, t) be a gate of a reversible circuit. Then, a Single Missing Gate Fault (SMGF) appears if instead of G no gate is executed (i.e. G completely disappears). The method to detect SMGF is widely studied and can be referred in previous works.

Definition 3

Let \(\mathcal {G}\) be a set of k gates from a reversible circuit. Then, a Multiple Missing Gate Fault (MMGF) appears if instead of \(\mathcal {G}\) no gates are executed (i.e. all gates \(\mathcal {G}\) completely disappear in G).

In the following, we consider MMGFs with two missing gates. However, the methods described below can easily be extended for an arbitrary number of faulty gates. From here on forward, MMGF is referred to as missing of two gates. In order to detect MMGFs, the respective gates have to be activated so that the faulty behaviour can be observed at the outputs of the circuit. However, in case of multiple faults, the absence of one gate within the circuit may cause the deactivation of another gate in the circuit – leading to masking effects. Besides that, the absence of two gates may lead to no change in the outputs – leading to an undetectable fault. Because of that, the dependencies of two gates considered as one MMGF have to be analyzed in order to generate a test pattern.

Definition 4

Two gates \(G_x\) and \(G_y\) \((x < y)\) are said to be dependent if the target line of \(G_x\) is involved in the activation of the SMGF of \(G_y\). More precisely, a Toffoli gate \(G_y\) is dependent from gate \(G_x\), if the target line of \(G_y\) is the control line of \(G_x\) or if \(G_y\) is dependent on another gate \(G_z\) which is dependent from \(G_x\).

3 ATPG for MMGF Detection

This section describes the proposed approach for ATPG of MMGFs. The goal is to obtain a test set that covers all possible faults with a minimum number of test patterns. The proposed solution has four phases. First, test patterns for SMGFs, i.e. for the single faults, are obtained and compactly stored in a BDD. Based on that, the dependencies already discussed in the previous section are analyzed. The results from these two steps (i.e. the patterns for all SMGFs as well as the information about the dependencies of the gates in the currently considered circuit) are then utilized in order to obtain MMGF test sets. Finally, a covering algorithm is applied to minimize the obtained test set – yielding a minimal result covering all MMGFs.

3.1 Test Generation for SMGFs

In order to obtain all desired test patterns, it is assumed that only one gate is faulty at a time in this step. Also, the faults are detected at the primary outputs of the circuits and no distinction is made between different types of lines like output, garbage etc. Constant inputs of the circuit are assumed to be variable for the purpose of testing. For a circuit with n lines and N gates, there are N SMGFs, and the test patterns are obtained by activating the considered gate. Overall, this yields \(2^{n-k}\) possible test patterns that can be obtained for testing a SMGF. In order to compactly store them, Binary Decision Diagrams (BDDs, [15]) are applied.

3.2 Dependency Analysis

The next step is to analyse the dependencies between all combinations of two faulty gates as discussed in Sect. 2.2. The following pseudo-code describes how the dependencies between the gates are obtained.

figure a

3.3 MMGF Test Generation

Using the test patterns for SMGFs as well as information about the dependencies of all combinations of two faulty gates, now the respective test patterns for MMGFs with two faulty gates can be obtained. More precisely, without loss of generality, consider two gates \(G_x\) and \(G_y\) as well as their test patterns for corresponding SMGFs (denoted as \(S(G_x)\) and \(S(G_y)\)). If these two gates are independent to each other, we determine two test patterns (denoted as \(M(G_y,G_x)_1\) and \(M(G_y,G_x)_2\)): one test pattern to activate the gate \(G_x\) and not \(G_y\) and another to activate \(G_y\). More precisely:

$$\begin{aligned} M(G_y,G_x)_1 = S(G_y) \quad \quad \quad M(G_y,G_x)_2 = ( S(G_x) \cap \overline{S(G_y)}) \end{aligned}$$

If the two gates are dependent on each other, we determine two other tests patterns: one test pattern to activate the gate \(G_x\) and not \(G_y\) and vice versa. More precisely:

$$\begin{aligned} M(G_y,G_x)_1 = (S(G_y) \cap \overline{S(G_x)}) \quad \quad \quad M(G_y,G_x)_2 = ( S(G_x) \cap \overline{S(G_y)}) \end{aligned}$$

Besides that, masking may occur leading to untestable faults (as discussed in Sect. 2.2). A fault is untestable using this method if

$$\begin{aligned} M(G_y,G_x)_i = \{\emptyset \} \,\,{\text {where}} \,\, i=\{1,2\} \end{aligned}$$

Using this as basis, the respective determinations can efficiently be conducted on the BDD. More precisely, the BDD containing the SMGF test patterns are manipulated for all the MMGF yielding a BDD with n inputs and 2 \(*\) \(^NC_2\) outputs.

3.4 Minimal Test Set Determination

Once all the test patterns for the individual MMGFs are obtained, it is tried to derive the minimal testset covering all the faults. To that effect, two different techniques are proposed.

First, row and column reduction of a covering table [16] is implemented following a greedy scheme. Second, a covering algorithm is implemented using the BDDs to determine a minimum cover of the stored patterns. For a circuit with n lines, the covering BDD has \(2^n\) inputs and 1 output. Having that, the minimum test set is equivalently represented by the minimum-weighted path from the output of the BDD to the 1-terminal of the BDD, where the then arc has a weight of 1 and the else arc has a weight of 0.

Table 1. Experimental results
Full size table

4 Experimental Results

The ideas proposed above have prototypically been implemented on a Ubuntu Linux system running on a Intel(R) Core(TM) \(i7-3630QM\) CPU 64bit@2.4Ghz and 6GB of RAM. For the first two steps, i.e. determining the SMGF testset and the dependency analysis, Revkit [17] has been applied. For the remaining steps, the BDD package CUDD [18] was employed. All experiments were conducted on benchmark circuits obtained from Revlib [19]. Table 1 presents the obtained experimental results. The results show that the algorithm performed well for larger circuits covering a large number of faults. We obtained \(100\%\) fault coverage for circuits like \(rd73\_140\) and \(rd84\_142\), whereas the worst performance was for the circuit \(ex3\_229\) with a coverage of 28.6. This was due to a large number of NOT gates, and hence the performance could be improved by DFT techniques. For the circuits \(rd32-v0\_66\) and \(root\_255\), the SMGF and MMGF test patterns are identical. This is because all the dependent faults of these circuits are untestable. Considering the two covering methods, i.e. the greedy heuristic vs. the BDD-based approach, clearly shows the difference in runtime – especially for large circuits, where the BDD-based covering could not be completed after a long time. This was expected as the BDD-based approach obtains an exact, i.e. minimal cover, while the heuristic solution only approximates that. Besides that, it can be observed that the test set size determined by the greedy heuristic is, for most cases, the same as the minimal size obtained by the BDD-based approach. That is, the quality of the heuristic is rather good and often yields test sets which are close to the optimum. It should also be noted that the untestable faults are due to the function of the algorithm, and other methods can be used to detect these faults, which will be considered in the future work where we try to increase the coverage to 100%.