Learning Decision Trees with Flexible Constraints and Objectives Using Integer Optimization

Abstract

We encode the problem of learning the optimal decision tree of a given depth as an integer optimization problem. We show experimentally that our method (DTIP) can be used to learn good trees up to depth 5 from data sets of size up to 1000. In addition to being efficient, our new formulation allows for a lot of flexibility. Experiments show that we can use the trees learned from any existing decision tree algorithms as starting solutions and improve the trees using DTIP. Moreover, the proposed formulation allows us to easily create decision trees with different optimization objectives instead of accuracy and error, and constraints can be added explicitly during the tree construction phase. We show how this flexibility can be used to learn discrimination-aware classification trees, to improve learning from imbalanced data, and to learn trees that minimise false positive/negative errors.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Decision trees [3] have gained increasing popularity these years due to their effectiveness in solving classification and regression problems. As the problem of learning optimal decision trees is a NP-complete problem [11], greedy based heuristics such as CART [3] and ID3 [15] are widely used to construct sub-optimal trees. Greedy decision tree algorithm builds a tree recursively starting from a single node. At each decision node, an optimization problem is solved to determine the locally best split decision based on a subset of the training data such that the training data is further split into two subsets. Decisions are determined in turn for each of these subsets on children nodes of the starting node. The advantage of such a greedy approach is its computational efficiency. The limitation is that the constructed trees may be far from optimal.

In this paper, we aim to build optimal decision trees by optimizing all decisions concurrently. We formulate the problem of constructing the optimal decision tree of a given depth as an integer linear program. We call our method DTIP. One benefit of this formulation is that we can take advantage of the powerful mixed-integer linear programming (i.e., MIP) solver to find good trees. Researcher have previously investigated using solvers for learning different kinds of models and rules, see e.g., [4, 6, 8, 10]. We are not the first who try such an approach for decision tree learning. Bennett and Blue [1] proposed a formulation to solve the problem of constructing binary classification trees with fixed structure and labels, where paths of the tree are encoded as disjunctive linear inequalities, and non-linear objective functions are introduced to minimize errors. Norouzi et al. [14] linked the decision tree optimization problem with the problem of structured prediction with latent variables. To the best of our knowledge, our method is the first that encodes decision tree learning entirely in an integer program. A similar approach for more general models is given in [2]. This method, however, is quadratic instead of linear in the data set size and therefore requires a lot of preprocessing in order to reduce the number of generated constraints. [4] discusses modeling the problem of finding the smallest size decision tree that perfectly separates the training data as a constraint program.

Section 2 shows the proposed encoding of learning optimal decision trees as an integer optimization problem only requires O(2dn) constraints for regression and $O(nu+nv)$ constraints for classification, where n is the size of the dataset, v is the number of leafs, and u is the number of tree nodes. In addition, it requires $O(mu+nk+vy)$ variables, where k is the tree depth and y is the unique target values in the dataset. This makes the encoding linear in the dataset size for fixed size trees. Moreover, the number of binary variables depends on the dataset size up to a small constant factor (the tree depth). The formulated problem can be directly solved by any MIP solver such as CPLEX. In Sect. 3, we show experimentally that our method can be used to learn good trees up to depth 5 from datasets of size up to 1000. In addition to being efficient, our new formulation allows for a lot of flexibility. Our formulation enables that the trees obtained from existing greedy algorithms from Scikit-learn can be used as starting solutions for the CPLEX optimizer. Experiments with several real datasets show that our method improves the starting solutions. Moreover, the proposed formulation allows us to create decision trees with different optimization objectives other than standard objectives such as accuracy and error, and constraints can be added explicitly when learning trees. We show how this flexibility can be used to learn discrimination-aware trees and to improve learning from imbalanced data. Starting from a solution given by Scikit-learn, our method can find trees of good performance that are discrimination-free, and trees that return zero false-positives on training data.

2 Learning Decision Trees as Integer Programs (DTIP)

We assume the reader to be familiar with decision trees. We refer to [9] for more information. The optimization problem that we aim to solve is to find an optimal classification/regression tree of depth exactly k for a given dataset of n rows (samples) and m features. The Boolean decisions and predictions are variables and need to be set such that accuracy, absolute error, or any other linear measures, is optimized. We solve this problem by translating/encoding it entirely into linear constraints and providing this to an off-the-shelf MIP solver.

It has been shown in our previous work (e.g., [16]) that it is beneficial to keep encoding from machine learning models to linear constraints as small as possible, thereby increasing the data size it can handle. In contrast to earlier decision tree encodings (e.g. [1, 4, 16]), we therefore encode the leaf every data row ends up in using a binary instead of a unary encoding, i.e., using k variables instead of $2^k$. We start our encoding with a transformation of the input data.

Table 1. Feature values from first few rows from the Iris data before (left) and after (right) our data transform. The feature values are first sorted, and then identical values are mapped to integers in increasing order. Several feature values (such as SepLen {4.9, 4.7, 4.6}, PetLen, PetWid) are combined into a single integer because these only occur for Iris-setosa flowers. A SepWid value of 3.0 occurs most frequently in the data and is mapped to 0. The target values are not transformed.

2.1 Data Transformation

Earlier encodings of decision trees [1] or similar classification/regression models [2] linearly scale the input data to the interval [0.0, 1.0]. There are good reasons for doing so. For instance, this avoids large values in so-called big-M formulations (a way to encode binary decisions in integer programming), which can lead to numerical issues and long run-times. In spite of the benefits of a linear scaling, we advocate the use of a non-linear transform that assigns every unique value of every feature to a unique integer, only maintaining the ordering of these values. Using this transform:

• The thresholds in decision nodes can be represented by integer values instead of continuous ones. This allows MIP solvers to branch on these values instead of whether a certain row takes a left or right branch, reducing and balancing the search tree used by these algorithms.

• When all rows having successive integers as feature values also have the same class label, these values can be merged into a single integer.

• The most frequently occurring feature value can be mapped to the value 0, reducing the number of non-zero coefficients in the linear constraints.

• The ranges of feature values can all be centered around 0, see Table 1 for an example. This reduces the size of M values used in the big-M formulations.

These benefits all affect the MIP solvers capacity to solve problems efficiently, and therefore they are important considerations when encoding decision tree learning problems. Although a simple linear scaling can provide better results for some problem instances, we have experienced significant improvements in the obtained solutions using the non-linear transform. In our experiments, we demonstrate that our encoding is capable of producing good results when there are 1000 rows in the input data, which is significantly greater than previous works on integer programming encodings for decision trees and would not have been possible without this data transform.

Table 2. Summary of notation, constants, and variables used in the encoding.

2.2 Encoding Classification Trees

Our encoding for classification and regression trees is partly based on earlier work where we translated already learned models into linear constraints in order to deal with optimization under uncertainty [16]. Two key differences between this work and our new encoding are: (1) the coefficients denoting which constant threshold and feature to use in a node’s binary decision are free variables, and (2) the leaf that a data row ends up in is represented in binary instead of unary. Table 2 summarizes the notation and variables that we use to encode trees. The objective function minimizes the total prediction error for all data rows:

$$\begin{aligned} \min \sum _{1 \le r \le n} e_r, ~~\text { for all } r \in [1, n] \end{aligned}$$

(1)

where n is the number of input rows and $e_r \in \mathbb {R}$ is the error for data row r, defined in Eq. 5. Every node j, excluding leaf nodes, in the tree needs a binary decision variable $f_{i,j} \in \{0,1\}$ to specify whether feature $i \in [1,m]$ is used in the decision rule on node j:

$$\begin{aligned} \sum _{1 \le i \le m} f_{i, j} = 1~~\text{ for } \text{ all } j \in [1, u] \end{aligned}$$

(2)

Every node j requires an integer decision variable $c_j \in [LF,UF]$ that represents the threshold, where $LF = \min \{v(r, i)| i \in [1,m], r \in [1,n] \},$ $UF = \max \{v(r,i)| i \in [1,m], r \in [1, n]\},$  and v(r, i) denoting feature value for row r and feature i. For each row r, we encode whether it takes the left or right branch of a node using a variable $d_{h, r} \in \{0, 1\}$ for every depth h, $\text {for all } j \in [1, u], r \in [1, n]:$

$$\begin{aligned} \sum _{1 \le h \le d(j)} M_{r}{} \texttt {dlr}(h, j, r) + M_{r}d_{d(j), r} + \sum _{1 \le i \le m} v(r, i) f_{i, j} \le M_{r}d(j) + c_j \nonumber \\ \sum _{1 \le h \le d(j)} M_{r}'{} \texttt {dlr}(h, j, r) - M_{r}'d_{d(j), r} - \sum _{1 \le i \le m} v(r,i) f_{i, j} \le M_{r}'(d(j) - 1)-c_j \end{aligned}$$

(3)

where $M_r = \max \{ (v(r,i)-LF) | i \in [1, m] \}$  and $M'_r = \max \{ (UF - v(r,i)) | i \in [1,m] \}$  are tight big-M values, d(j) is the depth of node j, and $\texttt {dlr}(h, j,r)$ returns the path directions from the root node required to reach node j:

$$\begin{aligned} \texttt {dlr}(h,j,r) = {\left\{ \begin{array}{ll} d_{h,r} \qquad \,\,\, \text { if the path to node } j \text { goes } \mathbf {left} \text { at depth } h \\ 1 - d_{h,r} \quad \text { if the path to node } j \text { goes } \mathbf {right} \text { at depth } h \end{array}\right. } \end{aligned}$$

(4)

The formulation is essentially a big-M formulation for the constraint that if row r takes the left (right) branch at depth d(j) of node j, denoted by $d_{d(j),r}$, and row r takes the path to node j (i.e., $\sum _{1 \le h < d(j)} (\texttt {dlr}(h, j, r)) = d(j) - 1),$ then the feature value v(r, i) for which $f_{i,j}$ is true has to be smaller (greater) than threshold $c_j$. This encodes all possible paths through the tree for all rows using only O(nu) constraints and O(nk) binary variables, where k is the depth of the tree. What remains is the computation of the classification error:

$$\begin{aligned} \sum _{1 \le t \le y} p_{l,t} = 1 ~~\text { for all } l \in [1,v] \nonumber \\ \sum _{1 \le h \le k } \texttt {dlr'}(h, l,r) + \sum _{t \not = t(r)} p_{l,t} \le e_r + k ~~\text { for all } l \in [1,v], r \in [1,n] \end{aligned}$$

(5)

where $p_{l,t} \in \{0,1\}$ is the prediction on leaf l, y is the number of unique target values (2 for binary classification), v is the number of leafs in the tree, $\texttt {dlr'}(h,l,r)$  is the same as $\texttt {dlr}(h,j,r)$  but for leafs l instead of internal nodes j, and t(r) is the target value for row r. These constraints force that if a row ends in a leaf l (setting $\texttt {dlr'}(h, l,r)$  to 1 along the path to l), then the error $e_r$ for row r is 1 if the leaf prediction type (for which $p_{l,t}$ is 1) is different from the rows target t(r). This adds O(vn) constraints and O(vy) to the encoding. This fully encodes classification tree learning in $O(n(u+v))$  constraints, $O(mu + nk + vy)$  binary variables, and u integers. A nice property is that the number of variables grows with a very small constant factor (the depth of the tree k) in the dataset size n.

Fig. 1.

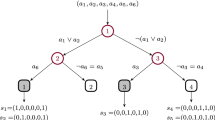
The encoding of an example row r, with features values (5, 8, 10) and target value 2 out of three possible targets $\{1,2,3\}$. We show the path taken by an assignment of $(d_{1,r}, d_{2,r}, d_{3,r}) = (0,1,1),$ i.e., the row first takes the right branch to node 3, and then two left branches to node 6 and leaf 5. Observe that the big-M formulation forces many of the path constraints to be satisfied, e.g., $5 f_{1,1} + 8 f_{2,1} + 10 f_{3,1} + d_{1, r}M_r \le c_1 + M_r$  reduces to $5 f_{1,1} + 8 f_{2,1} + 10 f_{3,1} \le c_1 + M_r,$ which is always true. The same holds for all constraints in subtrees rooted under a $\top$ symbol. The constraint $-5 f_{1,1} - 8 f_{2,1} - 10 f_{3,1} - d_{1, r}M_r' \le - c_1$ reduces to $-5 f_{1,1} - 8 f_{2,1} - 10 f_{3,1} \le - c_1,$ which is true only if the feature value of the feature type of node 1 ($f_{i,1}$) is greater than the constraint value for node 1 ($c_1$). The same reasoning holds for the constraints on other depths. This thus encodes the node constraints of a decision tree. The depth values $(d_{1,r}, d_{2,r}, d_{3,r})$ have a similar effect on the leaf constraints. Only leaf 5 reached by r forces the error $e_r$ of row r to be 1 when the prediction type ($p_{t,5}$) of leaf 5 is unequal to 2 (the target type of r). All other leaf constraints are true for any error $\ge 0$.

We strengthen the above encoding by bounding the node thresholds between the minimum and maximum values of the features used in the binary decisions:

$$\begin{aligned} \sum _{1 \le i \le m} LF \cdot f_{i,j} \le c_j \le \sum _{1 \le i \le m} UF \cdot f_{i,j} ~~\text { for all } j \in [1,u] \end{aligned}$$

In addition, it does not make sense for the two leaf nodes l and $l'$ of the same parent node to have the same values. The following breaks this symmetry:

$$\begin{aligned} p_{l,t} + p_{l',t} = 1~~\text { for all } t \in [1,y] \text { and all such pairs } (l,l'). \end{aligned}$$

Figure 1 shows the encoding for an example row.

2.3 Encoding Regression Trees

Our regression tree formulation is identical to the classification tree formulation. We only replace the error computation in Eq. 5 with the following constraints, for all $l \in [1,v], r \in [1,n]:$

$$\begin{aligned} \sum _{1 \le h \le k} M_t\texttt {dlr'}(h, l,r) + p_l - t(r) \le e_r + M_tk \nonumber \\ \sum _{1 \le h \le k} M_t'{} \texttt {dlr'}(h, l,r) + t(r) - p_l \le e_r + M_t'k \end{aligned}$$

(6)

where $p_l \in [LT, UT]$ is the prediction value of leaf l, $LT = \min \{ t(r) | r \in [1,n] \},$ $UT = \max \{ t(r) | r \in [1,n] \},$ $M_t = \max \{ UT - t(r) | r \in [1,n] \}$  and $M'_t = \max \{ t(r) - LT | r \in [1,n] \}.$  This computes the absolute error for each row r from the prediction value $p_l$ of the leaf it ends up in, depending on the path variables from $\texttt {dlr'}$, using O(2vn) constraints.

3 Experiments

We conducted experiments on several benchmark datasets for both classification and regression tasks from the UCI machine learning repository [12]. We compared the performance of the following three methods: (1) the classification and regression method from sciki-learn (i.e., optimized version of CART), (2) the proposed decision tree as linear programs (DTIP) method that is solved by CPLEX, and (3) DTIP solved by CPLEX with starting trees learned from CART (DTIPs). The time limit for solving each problem is set to 30 min. We learn decision trees of various depths, ranging from 1 to 5.

Classification. We tested our method on three real datasets. The “Iris” data have 4 attributes and 150 data points with 3 classes. The “Diabetes” data are from the Pima Indian Diabetes database, which have 8 attributes and 768 data points to two classes. The “Bank” data are from direct marketing campaigns of a Portuguese banking institution [13]. The “Bank” dataset is considerable larger than Iris and Diabetes, with 51 attributes and 4521 instances. As the purpose of this paper is to demonstrate the performance of DTIP, we use all data points for constructing the trees and use the classification accuracy of the method on all data points as the performance measurement. Table 3 reports the results.

With Iris data, CART is able to find the optimal trees for depths 1, 2 and 5. Our proposed methods (DTIP and DTIPs) can always find the optimal trees with depths 1 to 5, no matter whether it starts with initial trees returned from CART or not. For Diabetes, DTIP and DTIPs can construct the optimal trees with depth 1. When the trees are larger, the encoded MIP models become more and more difficult to solve. This can be seen for depths 4 and 5, the performances of DTIP are worse than CART when CPLEX tries to solve from scratch within the limited running time (i.e., 30 min). This difficulty of CPLEX in solving large instances becomes very obvious when DTIP builds the classification trees of depth 4 for the Bank data. The accuracy drops below 0.2, it is essentially still preprocessing the data. However, when CPLEX starts with initial solutions, DTIPs always improves the initial trees that are found by CART, resulting higher or equal accuracies on all datasets and all different sized trees.

Table 3. Classification accuracy (top) and absolute error (bottom) of three regression methods with trees of depths 1–5. The values with * indicate the optimal solutions.

Regression. We used two real datasets. The first one “RedWine” is from the wine quality dataset [7]. It contains 1599 data points, each with 11 input variables, and 1 output variable indicating the wine quality with scores between 0 and 10. The “Boston” data have 13 input attributes and 1 output attribute containing median value of owned houses in suburbs of Boston. There are 506 instances. The bottom of Table 3 shows the performances, measured with absolute error. The conclusions of this set of experiments are similar to those from the classification trees. The best performed one is DTIPs, where the regression trees learned from CART are used as initial solutions to DTIP.

Discrimination-aware DTIP. In order to model the discrimination level of a learned tree, we include a simple constraint that computes the difference in positive class probability for different sets of rows (by summing and comparing errors $e_r$). This difference is added to the objective function with a large multiplier (the data size), in this way the solver will try find the most accurate tree with zero discrimination. For this experiment, we assume that $\texttt {married}$ is a sensitive attribute in the bank data set. Since bank is too large to solve efficiently using DTIP, we only use the top 1000 rows. After running DTIP for 15 min from a Scikit-learn starting solution with accuracy 0.86 and 0.05 discrimination, we obtain 0 discrimination for a depth 3 tree, with 0.85 accuracy. For comparison, we also ran DTIP without discrimination constraints, which gives an accuracy of 0.81 after 15 min. This result demonstrates the flexibility of DTIP: adding a single constraint gives solutions satisfying a different objective.

Imbalanced DTIP. For imbalanced data problems, such as the first 1000 rows from the bank set, depending on the problem context it can be important to find solutions with very few false positives or very few false negatives. In order to demonstrate the flexibility of DTIP, we again add a single constraint for counting false positives or negatives (by summing $e_r$ values) and add it to the objective function with a large multiplier. We ran DTIP for 15 min, starting from the Scikit-learn solution, and obtain a depth 3 tree with 0 false positives and 101 false negatives, or one with 672 false positives and 0 false negatives.

4 Conclusion

We give an efficient encoding of decision tree learning in integer programming. Experimental results demonstrate the strengths and limitations of our approach. Decision trees of depth up to 5 can be learned from data sets of size up to 1000. Larger data sets create to many constraints to be solved effectively using a MIP solver. We show how to use our approach to improve existing solutions provided by a standard greedy approach. Moreover, we demonstrate the flexibility of our approach by modelling different objective functions. In the future, we will investigate other objectives, integration with existing MIP models, and speeding up the search by fixing variables and using lazy constraints.