Introduction

Brain tumors represent a rare but serious medical condition. With an incidence of six cases per 100,000, gliomas are the most frequent primary brain tumors in adults, accounting for 70% (Ricard et al. 2012) of cases. Gliomas are classified into four grades by increasing aggressiveness, based on their microscopic structure and cellular activity. Glioblastoma multiforme (GBM) is the most frequent and most malignant subtype of glioma (grade IV), accounting for about 50% of diffuse gliomas. These tumors infiltrate surrounding healthy tissue, grow rapidly, and form a necrotic core of high cell density which is often accompanied by compression and displacement of surrounding tissue. This so-called ‘mass effect’ leads to an increase in intracranial pressure (ICP) and the progressive onset of a multitude of pressure-related symptoms, from headache and nausea to coma or death due to herniation which is the leading cause of death for GBM patients (Sizoo et al. 2010). The standard treatment therefore involves surgical resection of the bulk tumor to reduce the symptoms of mass effect, followed by a combination of chemo- and/or radiation therapy. Long-term prognosis for GBM remains poor, with median overall survival between 1 and 2 years (Ricard et al. 2012).

Different types of mathematical models (discrete, continuous, hybrid) on different spatial and spatiotemporal scales have been employed to improve the understanding of GBM and to optimize treatment approaches (Hatzikirou et al. 2005). Continuous representations are particularly well suited for clinical applications as they allow modeling the temporal evolution of macroscopic processes on the tissue level and at low computational cost. Emphasis has been placed on simulating the invasion dynamics of glioma due to the direct clinical importance of this growth characteristic. A framework for simulating GBM invasion was introduced by Tracqui et al. (1995), Woodward et al. (1996), Burgess et al. (1997) based on a reaction–diffusion equation that describes tumor cell migration as a random walk process modeled by Fickian diffusion. These initial models were soon extended to account for more realistic brain geometries and differences between cell motility in gray and white matter (Swanson et al. 2000). Patient-specific parameters have been estimated from routine clinical imaging to compute the invisible portion of the tumor and to predict tumor recurrence after surgical resection (Swanson et al. 2003). Further extensions aim to incorporate heterogeneity and anisotropy of the brain anatomy informed by routine clinical MRIs (Jbabdi et al. 2005) and consider the effects of different treatments (Swanson et al. 2002, 2008a; Rockne et al. 2009).

Despite the recognized importance of the biomechanical environment for tumor evolution (Jain et al. 2014), the mass effect caused by the growing tumor received less attention from the modeling community and has been investigated mainly in the context of improving image registration methods (Mohamed and Davatzikos 2005; Hogea et al. 2007; Gooya et al. 2012; Bauer et al. 2012) for atlas-based segmentation. Few models, such as (Clatz et al. 2005; Hogea et al. 2008), consider both tumor invasion and mass effect in a realistic 3D model of the human brain using solid mechanics approaches. Accurate morphological representation is crucial also for the validation of macroscopic tumor models, which often relies on multimodality imaging data. Indeed, the lack of anatomical correspondence has been identified as one of the limitations of advanced reaction–diffusion based GBM models (Gu et al. 2012).

We report first results of a comparative study that evaluates the ability of a simple computational model of mechanically coupled diffusive tumor growth to reproduce characteristics of pathologies found in patients. GBM invasion into brain tissue and the mechanical interaction between tumor and healthy tissue components are simulated using the finite element method (FEM).

Materials and Methods

The mathematical model employed in this study is designed to capture three interrelated aspects of macroscopic glioma growth: (a) tumor cell proliferation, (b) the diffuse invasion of the growing tumor into surrounding healthy tissue, and (c) the resulting mass effect. The model operates on a domain that represents the human brain. For the present study, each component of the domain was considered homogeneous, with distinct isotropic material properties in each subdomain: white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF).

The invasive growth pattern of glioma was modeled as a reaction–diffusion process (Tracqui et al. 1995; Woodward et al. 1996; Burgess et al. 1997):

$$ \frac{\partial c}{\partial t} = \nabla \cdot \left( {D\nabla c} \right) + \rho c\left( {1 - c} \right), $$

where c represents the normalized concentration of tumor cells in function of time and space. The isotropic and locally constant diffusion D represents the migration rate of GBM cells in brain tissue, with higher values in WM than in GM (Swanson et al. 2000). Logistic growth with growth rate ρ was assumed as reaction term. This formulation is known as Fisher’s equation (Fisher 1937) and leads to the creation of a non-proliferating zone in regions of high tumor cell concentration, in agreement with clinical observation of the formation of a necrotic core.

The creation of new tumor cells during growth results in volumetric increase of the tumor and introduces growth-related strain ε g in the tissue. The present model assumes a linear relation between local cell concentration and tumor-induced strain with a coupling constant λ:

$$ \hat{\varvec{\epsilon}}^{g} = {\lambda }\,c $$

Simulations were carried out over the SRI24 human brain atlas (Rohlfing et al. 2010). This atlas represents the normal brain anatomy and provides separate labels for WM, GM, and CSF. The CSF domain was subdivided into two compartments, separating the fluid-filled brain ventricles from the remaining CSF. Brain tissues were modeled as linear elastic materials in this study with Poisson ratio ν and Young’s modulus E as the mechanical properties. The CSF of the brain ventricles was modeled as a compressible elastic solid to account for physiological mechanisms that compensate elevated ICP. Mechanical parameters for the model constituents are chosen similar to Wittek et al. (2010) and are summarized in Table 1.

Table 1 Mechanical parameters for model constituents
Full size table

Parameter choices for diffusivity and proliferation were derived from literature data based on clinical observations in glioblastoma patients (Swanson et al. 2008b; Wang et al. 2009; Szeto et al. 2009; Rockne et al. 2010). Under the assumption of fivefold higher diffusion in WM compared to GM (Swanson et al. 2000), three sets of parameters (D GM/WM, ρ) were obtained, corresponding to low, medium, and high levels of invasiveness, Table 2.

Table 2 Reaction–diffusion parameters in GM and WM for different levels of invasiveness
Full size table

A volumetric expansion coefficient λ = 0.15 was chosen for all simulations, corresponding to a maximum tumor-related increase in local volume of 15% (Bauer et al. 2012).

The healthy brain atlas was seeded at multiple locations, and simulated until the tumor had reached a maximum volume corresponding to 3.5 cm equivalent radius. Seed positions were obtained from a publicly accessible dataset of preoperative GBM images (NCI–MICCAI 2013), which were registered to the healthy atlas and segmented using an automatic GBM segmentation software (Porz et al 2014). Center-of-mass positions of the tumors visible in T1-weighted MRI were extracted and used as patient-specific seed position for all patients of the dataset, Fig. 1.

Fig. 1
figure 1

Cross-section of the anatomical atlas for an exemplary seeding scenario (a), and overview of all seed positions within the healthy brain atlas (b)

Full size image

A tetrahedral mesh was generated from each seeded atlas using CGAL (http://www.cgal.org). Spatial confinement of the brain within the skull was modeled by imposing zero-displacement and zero-flux boundary conditions on the surface nodes of the mesh. The model was implemented as thermal expansion analysis in Abaqus (Simulia) by identifying relative cell concentration c with ‘temperature’ as simulation variable.

For each seed position, three tumor growth simulations were carried out, corresponding to the different levels of invasiveness defined in Table 2. Simulated tumors were compared to actual tumors in terms of shape and invasiveness when volumetric agreement was reached. Additionally, the mechanical impact of the simulated tumor was computed.

Results

Simulation of this mechanically coupled reaction–diffusion model yields as outputs the temporal evolution of tumor cell concentration over the brain anatomy as well as the mechanical impact of the tumor in terms of displacement and tissue stresses.

Parameter choices for different levels of invasiveness were correctly reflected in simulation results with larger D/ρ consistently resulting in a higher portion of invisible (c < 0.8) compared to visible (c > 0.8) tumor.

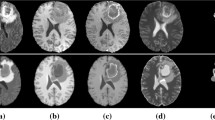
While the shape of near-spherical tumors was well reproduced in simulations, more complex shapes were not. Figure 2 compares simulation and actual tumor for two representative tumor shapes. Statistical evaluation showed the simulated tumors to be more symmetric, as measured by their aspect ratio, compared to their real counterparts.

Fig. 2
figure 2

Comparison of simulated (red) to observed tumor shapes (yellow) for selected cases. Concentration field values c ≥ 0.8 were chosen to represent the solid tumor. Good agreement is observed for regularly structured shapes (a), whereas highly irregular shapes are not reproduced in simulations (b)

Full size image

The mechanical impact of the growing tumor was estimated for each simulated case by computing the tumor-induced pressure acting on the skull. For a fatal tumor burden, assumed at 3.5 cm equivalent radius (Swanson et al. 2008a), simulations yield excess pressures between 1.0 and 1.4 kPa in addition to the normal intracranial pressure of about 0.7–2.0 kPa (Rangel-Castillo et al. 2008).

Discussion

The tumor model in this implementation assumed isotropic and locally constant material properties and did not take into account biological processes other than cell proliferation. Growth and mechanical properties were not personalized and simulations were carried out over a standardized atlas of healthy brain anatomy. These limitations explain the observed discrepancy in the shapes of simulated compared to real tumors from the dataset, particularly the overall underestimation of tumor asymmetry in simulations. Inclusion of anisotropic diffusion properties, with increased diffusion along the fiber structure of the brain, has been shown to improve spatial agreement between simulated and actual tumor (Jbabdi et al. 2005) in a pure reaction–diffusion model. Anisotropic diffusion, as well as anisotropic mechanical material properties, can be integrated in this model.

Despite its simplicity, the model yielded realistic order-of-magnitude estimates of the mechanical impact of a growing tumor. According to simulations and under the assumption of linear elasticity, the excess pressure caused by a tumor of 3.5 cm equivalent radius would increase total ICP to up to 3.4 kPa representing a state of mild intracranial hypertension that requires treatment in most circumstances (Rangel-Castillo et al. 2008). Replacement of the currently linear elastic by a more accurate material model for brain tissue is expected to increase these estimates further into the range of life-threatening intracranial hypertension (>5.3 kPa; Rangel-Castillo et al. 2008).

Tumor seed positions were derived from center-of-mass positions of preoperative MR images. This approach is expected to provide realistic estimates under (mostly) isotropic growth conditions. However, simulation results indicate that the assumption of isotropic growth does not hold for irregularly shaped tumors, suggesting that center-of-mass position is not a suitable indicator for tumor seed location in those cases.

Conclusion

A FEM-based approach for simulating diffusive growth and mass effect of GBM was presented. Tumor evolution was simulated over a healthy brain atlas for a range of seed positions and three sets of reaction–diffusion parameters. We showed qualitative agreement of resulting tumor invasiveness with simulation parameters and found tumor-induced pressures of realistic magnitude. Comparison to real tumor shapes confirmed previous observations from a pure reaction–diffusion model (Jbabdi et al. 2005) that tumor shape depends on seed position and that asymmetric shapes cannot be reproduced by isotropic growth assumptions. We therefore plan to carry out a sensitivity study to investigate the role of seed position on shape and to extend the present model to account for anisotropic material properties.