Long-Lived Tasks

Abstract

The predominant notion for specifying problems to study distributed computability are tasks. Notable examples of tasks are consensus, set agreement, renaming and commit-adopt. The theory of task solvability is well-developed using topology techniques and distributed simulations. However, concurrent computing problems are usually specified by objects. Tasks and objects differ in at least two ways. While a task is a one-shot problem, an object, such as a queue or a stack, typically can be invoked multiple times by each process. Also, a task, defined in terms of sets, specifies its responses when invoked by each set of processes concurrently, while an object, defined in terms of sequences, specifies the outputs the object may produce when it is accessed sequentially.

In a previous paper we showed how tasks can be used to specify one-shot objects (where each process can invoke only one operation, only once). In this paper we show how the notion of tasks can be extended to model any object. A potential benefit of this result is the use of topology, and other distributed computability techniques to study long-lived objects.

1 Introduction

A predominant formalism for specifying one-shot distributed problems, especially in distributed computability, is through the notion of a task [12]. Tasks are one-shot because each process invokes exactly one operation, and receives exactly one response. We think of the operation invoked by the process as its proposal, or its input value, and of the response, as its output value. Informally, a task is specified by an input/output relation, defining for each set of processes that may run concurrently, and each assignment of inputs to the processes in the set, the valid outputs of the processes. A central task is consensus, where processes agree on one of the proposed input values. In k-set agreement, processes agree on at most k different input values. Thus, 1-set agreement is the same as consensus. Tasks have been intensively studied in distributed computability, leading to an understanding of their relative power [8], to the design of simulations between models [2], and to the development of a deep connection between distributed computing and topology [7].

In concurrent computing, problems are typically specified sequentially, instead of as tasks, because it is harder to reason about concurrent specifications. Tasks and objects model in a different way the concurrency that naturally arises in distributed systems: while tasks explicitly state what might happen when a set of processes run concurrently, objects only specify what happens when processes access the object sequentially.

An object is specified in terms of a sequential specification, i.e., an automaton describing the outputs the object produces when it is accessed sequentially. There are various ways of defining how the object behaves when it is accessed concurrently by several processes. The linearizability [11] consistency condition is a way of producing a sequential execution out of a concurrent execution, which then can be used against the object specification. Linearizability is very popular because it is local, namely, one can consider linearizable object implementations in isolation, and their composition is guaranteed to be linearizable. Also, linearizability is a non-blocking property, which means that a pending invocation (of a total operation) is never required to wait for another pending invocation to complete.

Contributions. In a previous paper [4] we showed how tasks can be used to specify one-shot objects (where each process can invoke only one operation, only once). In this paper we show how the notion of tasks can be extended to model any object. More precisely, for any object X, we describe how to construct a task $T_X$, the long-lived task derived from X, with the property that an execution E is linearizable with respect to X if and only if E satisfies $T_X$. Then we explore the opposite direction, namely, transforming long-lived tasks to sequential objects. As shown in [4, 13], there are tasks (in the usual sense) that cannot be expressed as objects. Notable examples are the set agreement and immediate snapshot tasks. Interval-sequential objects, introduced in [4], are a generalization of sequential objects, which can describe any pattern of concurrent invocations. We show that from any long-lived task T can be obtained an interval-sequential object $X_T$ such that an execution E satisfies T if and only if E is interval-linearizable with respect to $X_T$. Thus, interval-sequential objects and long-lived tasks have the same expressive power.

Related work. Tasks and objects have largely been independently studied. The first to study the relation between tasks and objects was Neiger [13] in a brief announcement in 1994, where he noticed that there are tasks, like immediate snapshot [1], with no specification as sequential objects. An object modeling the immediate snapshot task is necessarily stronger than the immediate snapshot task, because such an object implements test-and-set. In contrast there are read/write algorithms solving the immediate snapshot task and it is well-known that there are no read/write linearizable implementations of test-and-set. Therefore, Neiger proposed the notion of a set-sequential object, that specifies the values returned when sets of processes access it simultaneously. Then, one can define an immediate snapshot set-sequential object, and there are set-linearizable implementations. Much more recently, it was again observed that for some concurrent objects it is impossible to provide a sequential specification, and concurrency-aware linearizability was defined [9], and studied further in [10]. In [4] we initiated an in-depth study of the relation between tasks and objects. We introduced the notion of interval-sequential object, and showed that it can model any task. Also, we showed that a natural extension of the notion of a task is expressive enough to specify any one-shot object.

Set linearizability and concurrency-aware linearizability are closely related and both are strictly less powerful than interval-linearizability to model tasks.

Transforming the question of wait-free read/write solvability of a one-shot sequential object, into the question of solvability of a task was suggested in [6]. That transformation takes a sequential object X and produces a task $T_X$ such that X is solvable in the read/write wait-free crash-failure model of computation if and only if $T_X$ is solvable in that model. In $T_X$, processes produce outputs for X and an additional snapshot. Our construction here and in [4] is reminiscent to the construction in [6].

2 Tasks and Objects

2.1 Tasks

A simplicial complex, or complex for short, is a generalization of a graph. A complex is a collection of sets closed under containment. The sets of a complex are called simplices. A graph consists of two types of simplices: sets of dimension 1, namely edges (which are sets of vertices), and sets of dimension 0, namely vertices. A 2-dimensional complex consists of simplices of 3 vertices, simplices of 2 vertices, and simplices of 1 vertex. It is always required that if a simplex is in the complex, all its subsets also belong to the complex.

Formally, a task is a triple $\langle \mathcal {I}, \mathcal {O}, \varDelta \rangle$, where $\mathcal {I}$ and $\mathcal {O}$ are complexes, with $\mathcal {I}$ containing valid input configuration to the processes and $\mathcal {O}$ containing valid output configurations. Each simplex of $\mathcal {I}$ has the form $\{(\text {id}_1,x_1),\dots ,(\text {id}_k,x_k)\}$, where the $id_i's$ are distinct ID’s of processes and the $x_i's$ are inputs. The vertices of $\mathcal {I}$ are its singleton sets. The meaning of an input simplex $\sigma$ is that the processes in $\sigma$ might start with those inputs in the simplex. The output complex $\mathcal {O}$ is defined similar.

In Fig. 1 part of the input complex $\mathcal {I}$ for 2-set agreement, for 3 processes, is illustrated. It is the part where each process proposes as input its own id. The simplex $\sigma$ represents the initial configuration where each processes proposes as input its own id. Inside a vertex is the id of the process, and outside is its input value. The edges of $\sigma$ are input simplexes, where only two processes participate, and the third process never wakes up. The vertices of $\sigma$ represent initial configurations where only one process participate.

Each simplex of the output complex represents the decisions of the processes in some execution solving the task. Vertices are labeled, on the inside with ids, and on the outside with decision values. For instance, in $\sigma _1$ the decisions are p, r and p, respectively for p, q, r. Notice that there is no simplex in the center, there is a hole, because the processes are not allowed to decide 3 different values in 2-set agreement. An example of a 1-dimensional simplex is $\sigma _3$, where p decides p and q decides q.

The relation $\varDelta$ states that if a process sees only itself in an execution, it should decide its own input value. For instance, $\varDelta$ of input vertex for p contains only the output vertex of p labeled p at the top corner of $\mathcal {O}$. Similarly, if p and q see each other in an execution, where r does not participate, $\varDelta$ of the input edge for p and q contains only $\sigma _3$. Finally, $\varDelta (\sigma )$ contains all triangles of $\mathcal {O}$, because it specifies output values when all three processes see all input values.

Fig. 1.

An input simplex $\sigma$ and the corresponding output complex $\varDelta (\sigma )$, for 2-set agreement task.

The function $\varDelta$ is the artefact that relates valid inputs and outputs. Formally, $\varDelta$ is a function mapping each input simplex $\sigma \in \mathcal {I}$ to a subcomplex $\varDelta (\sigma ) \subseteq \mathcal {O}$ such that each output simplex $\tau \in \varDelta (\sigma )$ has the same cardinality as $\sigma$ and both simplexes, $\sigma$ and $\tau$, contain the same ID’s of processes. In words, $\varDelta (\sigma )$ describes all possible output configurations in executions in which only the processes in $\sigma$ participate in the computation and all of them run to completion.

Tasks have their own notion of solvability, that is, a mechanism to distinguish between valid from invalid executions, with respect to a given task. Let E be an execution in which every participating process decides an output value (to its unique invocation). Namely, there are no pending invocations in E. Let $\sigma _E$ be the set with all pairs $(\text {id}_i,x_i)$, where $x_i$ is the input of process $\text {id}_ i$, and, similarly, let $\tau _E$ be the set with all pairs $(\text {id}_i,y_i)$, where $y_i$ is the output of process $\text {id}_ i$. Then, we say that E satisfies a task T if $\tau _E \in \varDelta (\sigma _E)$, i.e., the processes decide an output assignment that agrees with the specification of the task.

2.2 Objects

A long-lived sequential object, or object for short, allows each process to invoke any number of times any of the operations provided by the object. For example, in a stack, each process can invoke push and pop operation as many times as it wants, in any order. Typically, a long-lived object is formally specified in terms of a sequential specification, i.e., an automaton describing the outputs the object produces when it is accessed sequentially. Thus, an execution with concurrent operations needs to emulate somehow an allowed sequential behavior of the automaton.

There are various ways of defining what it means for an execution to be valid with respecto a sequential specification (or the meaning of emulating a sequential behavior of the automaton). One of the most popular consistency conditions is linearizability [11].

Given a sequential specification of an object, an execution is linearizable if it can be transformed into a sequential one such that (1) it respects the real-time order of invocation and responses and (2) the sequential execution is recognized by the automaton specifying the object. Thus, an execution is linearizable if, for each operation call, it is possible to find a unique point in the interval of real-time defined by the invocation and response of the operation, and these linearization points induce a valid sequential execution.

Linearizability is very popular to design components of large systems because it is local, namely, one can consider linearizable object implementations in isolation and compose them without sacrificing linearizability of the whole system [5]. Also, linearizability is a non-blocking property, which means that a pending invocation (of a total operation, i.e., an operation that always can be invoked regardless of the state of the automaton) is never required to wait for another pending invocation to complete.

2.3 Limitations of the Standard Semantics of Task

It has been observed [4] that tasks are too weak to represent some objects, under the usual semantics of a task described above. We briefly recall the following example from [4].

Consider a restricted queue O for three processes, p, q and r, in which, in every execution, p and q invoke enq(1) and enq(2), respectively, and r invokes deq(). If the queue is empty, r’s dequeue operation gets $\bot$.

Suppose, for contradiction, that there is a corresponding task $T_O=(\mathcal {I},\mathcal {O},\varDelta )$, that corresponds to O. The input complex $\mathcal {I}$ consists of one vertex for each possible operation by a process, namely, the set of vertices is $\{(p,enq(1)),(q,enq(2)),(r,deq())\}$, and $\mathcal {I}$ consists of all subsets of this set. Similarly, the output complex $\mathcal {O}$ contains one vertex for every possible response to a process, therefore it consists of the set of vertices $\{(p,ok),(q,ok),(r,1),(r,2),(r,\bot )\}$. It should contain a simplex $\sigma _x=\{(p,ok),(q,ok),(r,x)\}$ for each value of $x\in \{1,2,\bot \}$, because there are executions where p, q, r get such values, respectively. See Fig. 2.

Fig. 2.

Counterexample for a simple queue object

Now, consider the three sequential executions of the figure, $\alpha _1,\alpha _2$ and $\alpha _\bot$. In $\alpha _1$ the process execute their operations in the order p, q, r, while in $\alpha _2$ the order is q, p, r. In $\alpha _1$ the response to r is 1, and if $\alpha _2$ it is 2. Given that these executions are linearizable for O, they should be valid for $T_O$. This means that every prefix of $\alpha _1$ should be valid:

$$\begin{aligned} \{ (p,ok)\}&= \varDelta ((p,enq(1)) \\ \{ (p,ok),(q,ok)\}&\in \varDelta (\{ (p,enq(1),(q,enq(2)\}) \\ \sigma _1=\{ (p,ok),(q,ok),(r,1)\}&\in \varDelta (\{ (p,enq(1),(q,enq(2),(r,deq())\})=\varDelta (\sigma ) \end{aligned}$$

Similarly from $\alpha _2$ we get that

$$\begin{aligned} \sigma _2=\{ (p,ok),(q,ok),(r,2)\} \in \varDelta (\sigma ) \end{aligned}$$

But now consider $\alpha _3$, with the same sequential order p, q, r of operations, but now r gets back value 2. This execution is not linearizable for O, but is accepted by $T_O$ because each of the prefixes of $\alpha _3$ is valid. More precisely, the set of inputs and the set of outputs of $\alpha _2$ are identical to the sets of inputs and set of outputs of $\alpha _3$.

3 Long-Lived Tasks

Tasks provide a compact and static formalism for specifying one-shot distributed problems. Could it be that long-lived objects can be specified as a task? Is it possible to have a static representation of a queue or list? As explained above, tasks are not expressive enough to model even restricted queues or stacks in which each process can execute at most one operation. However, the task formalism can be extended to handle long-lived objects.

In order to model long-lived objects, the task formalism has to be extended to deal with two issues: (1) each process might invoke several operations (in any order) and (2) model valid executions, i.e., executions that are linearizable with respect to the object (which in the end involves modeling the interleaving pattern in a given execution).

A long-lived task is a triple $\langle \mathcal {I}, \mathcal {O}, \varDelta \rangle$, where $\mathcal {I}$ and $\mathcal {O}$ are input and output complexes and $\varDelta$ is a function from simplexes of $\mathcal {I}$ to subcomplexes of $\mathcal {O}$. A main difference with regular tasks is the meaning of input and output vertices and the solvability condition, which will be slightly modified. Roughly speaking, for a long-lived task, a vertex of $\mathcal {I}$ represents the invocation of an operation by a particular process. Then, an input simplex $\sigma \in \mathcal {I}$ represents a collection of invocations (maybe all of them by the same process) that are to be performed on the object, and $\varDelta (\sigma )$ is the subcomplex containing all allowed responses the invocations in $\sigma$ might obtain, in all sequential interleavings. We will use Fig. 3 as a running example.

Fig. 3.

An input simplex of the long-lived task modeling the stack in which p executes a push and a pop and q a push. Two ways of drawing the output complex are shown. The one on the bottom emphasizes the role of the map $\varDelta$: input vertices are sent to corner output vertices, edges are sent to edges on the boundary of $\mathcal {O}$, and $\sigma$ is sent to all of $\mathcal {O}$.

3.1 Modeling Multiple Invocations

Let X be any sequential object. To make things simple, we will treat each invocation as unique by tagging each of them with an invocation ID made of a pair composed of the ID of the invoking process and an additional integer which makes invocations of the same process to the same operation type unique.

Let Inv be the infinite set with all invocations to X. Each element in Inv has the form $Inv(\text {id}_i, op\_type, input_i)$. Then, $\mathcal {I}$ is the complex containing every finite subset of Inv as simplex. Thus, $\mathcal {I}$ is a simplex of infinite dimension whose faces are of finite dimension. Note that simplices in $\mathcal {I}$ might contain invocations by the same process.

The output complex $\mathcal {O}$ has the responses to the invocations in $\mathcal {I}$. Let Res be the infinite set with all response values X might produce to the invocation in Inv. The output complex $\mathcal {O}$ is the complex containing every finite set in $Inv \times Res \times 2^{Inv}$, where $2^{Inv}$ is the power set of Inv. Thus, each vertex in $\mathcal {O}$ is a triple with an invocation, a response to the invocation and set of invocations. This set is called set-view and is the mechanism to model valid sequential executions, as explained below.

3.2 Modeling Valid Executions

Let E be sequential execution accepted by X in which every invocation has a matching response. We would like to represent that execution and its interleaving pattern as an output simplex in $\mathcal {O}$, that is, we identify that sequential interleaving and the output values as correct and encode it somehow in $\mathcal {O}$. It turns out that this can be easily done by adding to each response in E, the set of invocations preceding the response in E. These are the set-views mentioned before. Intuitively, the set-view of a response is the set of all invocation a process sees when computing the output for its invocation. Thus, the set-view of a response is a subset of the set of all invocations in E.

Let $\sigma _E$ be the set with all invocation in E and $\tau _E$ be set of all pairs invocation, response in E, each of them with its corresponding set-view. The importance of the set-views is that they together fully capture the interleaving pattern in E. More precisely, two executions E and $E'$ (not necessarily sequential) induce the same set of set-views (namely, $\tau _E = \tau _{E'}$) if and only if they have the same interleaving pattern, i.e., they are the same execution. Therefore, using set-views, we can model valid executions.

We can now define the mapping $\varDelta$: for every input simplex $\sigma \in \mathcal {I}$, $\varDelta (\sigma )$ is the subcomplex of $\mathcal {O}$ containing $\tau _E$, as defined above, for every sequential execution E accepted by X with only invocations in $\sigma$ and every invocation has a matching response.

3.3 Solvability Condition

Se far we have encoded all valid sequential executions with the help of the set-views. Now we need a way to identify any execution as valid, namely, as one which is linearizable with respect to X.

For a given sequential object X, let $T_X = \langle \mathcal {I}, \mathcal {O}, \varDelta \rangle$ be the long-lived task constructed from X as described above. Consider any execution E without pending operations let $\sigma _E$ and $\tau _E$ be the simplexes defined above from E. Then, we say that E satisfies $T_X$ if there is a simplex $\lambda \in \varDelta (\sigma _E)$ such that for every $(inv, resp, view) \in \tau _E$ there is a $(inv', resp', view') \in \lambda$ such that $inv' = inv$, $resp' = resp$ and $view' \subseteq view$. Intuitively, E satisfies the task if its set-views can be sequentially arranged so that the sequence induce an execution in $\varDelta (\sigma _E)$, hence, by construction, accepted by X.

Theorem 1

Let X be any sequential object and let $T_X$ be the long-lived task derived from X. Consider any execution E without pending operations. Then, E is linearizable with respect to X if and only if E satisfies $T_X$.

Proof

We first show that if E is linearizable then E satisfies $T_X$. By linearizability, E can be transformed into a sequential execution S accepted by X such that S respects the real-time order of E. Consider the simplexes $\sigma _E, \sigma _S, \tau _E$ and $\tau _S$ obtained from E and S. We have that $\sigma _E = \sigma _S$ because E and S have the same invocations. Also, $\tau _S \in \varDelta (\sigma _E)$, by the definition of $T_X$ and because S is accepted by X. Pick any $(inv, resp, view) \in \tau _E$ and let $(inv', resp', view') \in \tau _S$ with $inv' = inv$. Since S is a linearization of E, it must be that $resp' = resp$. Observe that if we prove that $view' \subseteq view$, then it follows that E satisfies $T_X$. For the sake of contradiction, assume that $view' \supset view$. Then, in the sequential execution S, the invocation inv appears after the response of an invocation $inv^*$ in $view' \setminus view$. However, since $inv^* \notin view$, hence, the response of inv occurs before $inv^*$ in E, from which follows that S does not respect the real-time order in E. A contradiction.

We now show that if E satisfies $T_X$ then E is linearizable. Let $\sigma _E$ and $\tau _E$ be the simplexes induced by E. Since E satisfies $T_X$, there is a $\lambda \in \varDelta (\sigma _E)$ such that for every $(inv, resp, view) \in \tau _E$ there is a $(inv', resp', view') \in \lambda$ such that $inv' = inv$, $resp' = resp$ and $view' \subseteq view$. By definition, $\lambda$ is induced by a sequential execution S accepted by X. Let $\sigma _S$ and $\tau _S$ be the simplexes induced by S. Note that E and S contain the same invocations and responses. If we prove that S respects the real-time order in E, then S is a linearization of E. By contradiction, suppose the opposite. Then, there are invocations inv and $inv'$ such that the response of inv appears before $inv'$ in E but the response of $inv'$ appears before inv in S. Let $view_E$ and $view_S$ be the set-views of inv in E and S. Thus, $inv' \notin view_E$ and $inv' \in view_S$, and hence $view_S \nsubseteq view_E$. A contradiction. Then, S is a linearization of E.    $\square$

We stress that set-views are not output values produced by processes, they are a mechanism to identify executions as correct. An alternative way to think of set-views is that they model the memory of a long-lived object in a static manner. It is also worth to stress that the set-views of any execution (possibly non sequential) are essentially snapshots: each set-view contains its corresponding invocation and every pair of set-views are comparable under containment.

Remark 1

If a long-lived task is restricted so that each process executes at most one operation and every set-view is the empty set, then we obtain a regular task and the solvability condition is equivalent to the usual solvability condition for tasks.

4 Interval-Sequential Objects

A natural question is if we can do the opposite direction of the construction described in the previous section. Namely, if for every long-lived task there is an object such that any execution satisfies the task if and only if it is linearizable with respect to the object. As shown in [4, 13], there are tasks (in the usual sense) that cannot be expressed as objects, e.g., the set agreement and immediate snapshot tasks. Generally speaking, the reason is that tasks (and hence also long-lived tasks) have the ability to describe executions in which there are concurrent invocations, which cannot be naturally described with sequential objects (this can be done at the cost of getting counterintuitive objects, like objects that can predict future invocations).

Interval-sequential objects, introduced in [4], are a generalization of sequential objects. Intuitively, they allow concurrent invocations by more than a single process in some states. As we shall see later, these objects can model long-lived tasks.

4.1 The Notion of an Interval-Sequential Object

To generalize the usual notion of a sequential object e.g. [3, 11], instead of considering sequences of invocations and responses, we consider sequences of sets of invocations and responses. An invoking concurrency class $C\subseteq 2^{Inv}$, is a non-empty subset of the set of invocations Inv such that C contains at most one invocation by the same process. A responding concurrency class C, $C\subseteq 2^{Res}$, is defined similarly, where Rev is the set of possible responses.

Interval-sequential execution. An interval-sequential execution h is an alternating sequence of invoking and responding concurrency classes, starting in an invoking class, $h=I_0,R_0,I_1,R_1,\ldots ,I_m,R_m$, where the following conditions are satisfied.

• 1. For each $I_i\in h$, any two invocations $in_1,in_2\in I_i$ are by different processes. Similarly, for $R_i\in h$ if $r_1,r_2\in R_i$ then both responses are from distinct processes.

• 2. Let $r\in R_i$ for some $R_i\in h$. Then there is $in\in I_j$ for some $j\le i$, such that res is matching response for in and furthermore, there is no other $in'$ such that in and $in'$ are from the same processes and $in'\in I_{j'}$, $j<j'\le i$.

In words, an interval-sequential execution h consists of matching invocations and responses, perhaps with some pending invocations with no response.

Interval-sequential object. An interval-sequential object X is a (not necessarily finite) Mealy state machine $(Q,2^{Inv},2^{Res},\delta )$ whose output values R are responding concurrency classes R of X, $R\subseteq 2^{Res}$, are determined both by its current state $s\in Q$ and the current input $I\in 2^{Inv}$, where I is an invoking concurrency class of X. There is a set of initial states $Q_0$ of X, $Q_0\subseteq Q$. The transition relation $\delta \subseteq Q\times 2^{inv}\times 2^{Res}\times Q$ specifies both, the output of the automaton and its next state. If X is in state q and it receives as input a set of invocations I, then, if $(R,q') \in \delta (q,I)$, the meaning is that X may return the non-empty set of responses R and move to state $q'$. We stress that always both I and R are non-empty sets.

Interval-sequential execution of an object. Consider an initial state $q_0\in Q_0$ of X and a sequence of inputs $I_0,I_1,\ldots I_m$. Then a sequence of outputs that X may produce is $R_0,R_1,\ldots R_m$, where $(R_i,q_{i+1})\in \delta (q_i,I_i)$. Then the interval-sequential execution of X starting in $q_0$ is $q_0,I_0,R_0,q_1,I_1,R_1,\ldots ,q_m,I_m,R_m$. However, we require that the object’s response at a state uniquely determines the new state, i.e. we assume if $\delta (q,I_i)$ contains $(R_i,q_{i+1})$ and $(R_i,q'_{i+1})$ then $q_{i+1}=q'_{i+1}$. Then we may denote the interval-sequential execution of X, starting in $q_0$ by $h=I_0,R_0,I_1,R_1,\ldots ,I_m,R_m$, because the sequence of states $q_0,q_1,\ldots ,q_m$ is uniquely determined by $q_0$, and by the sequences of inputs and responses.

Notice that X may be non-deterministic, in a given state $q_i$ with input $I_i$ it may move to more than one state and return more than one response. Also, sometimes it is convenient to require that the object is total, meaning that, for every singleton set $I \in 2^{Inv}$ and every state q in which the invocation inv in I is not pending, there is an $(R,q') \in \delta (q,I)$ in which there is a response to inv in R. In what follows we consider only objects whose operations are total.

Our definition of interval-sequential execution is motivated by the fact that we are interested in well-formed executions $h=I_0,R_0,I_1,R_1,\ldots ,I_m,R_m$. Informally, the processes should behave well, in the sense that a process does not invoke a new operation before its last invocation received a response. Also, the object should behave well, in the sense that it should not return a response to an operation that is not pending.

Representation of interval-sequential executions. An interval sequential execution $h=I_0,R_0,I_1,R_1,\ldots ,I_m,R_m$ can be represented by a table, with a column for each element in the sequence h, and a row for each process. A member $in\in I_j$ invoked by $p_k$ (resp. a response $r\in R_j$ to $p_k$) is placed in the kth row, at the 2jth column (resp. $(2j+1)$th column). Thus, a transition of the automaton will correspond to two consecutive columns, $I_j,R_j$. See Fig. 4.

Interval-sequential objects include as particular cases sequential objects and the set-sequential objects and its corresponding set linearizability consistency condition suggested in [13].

Remark 2

(Sequential and Set-sequential objects). Let X be an interval-sequential object, $(Q,2^{Inv},2^{Res},\delta )$. Suppose for all states q and all I, if $\delta (q,I)=(R,q')$, then $|R|=|I|$, and additionally each $r\in R$ is a response to one $in\in I$. Then X is a set-sequential object. If in addition, $|I|=|R|=1$, then X is a sequential object in the usual sense.

4.2 An Example: The Validity Problem

Consider an object X with a single operation $\mathsf{validity}(x)$, that can be invoked by each process, with a proposed input parameter x, and a very simple specification: an operation returns a value that has been proposed. This problem is easily specified as a task. Indeed, many tasks include this apparently simple property, such as consensus, set-agreement, etc. It turns out that the validity task cannot be expressed as a sequential object. As an interval-sequential object, it is formally specified by an automaton, where each state q is labeled with two values, q.vals is the set of values that have been proposed so far, and q.pend is the set of processes with pending invocations. The initial state $q_0$ has $q_0.vals=\emptyset$ and $q_0.pend=\emptyset$. If in is an invocation to the object, let val(in) be the proposed value, and if r is a response from the object, let val(r) be the responded value. For a set of invocations I (resp. responses R) vals(I) denotes the proposed values in I (resp. vals(R)). The transition relation $\delta (q,I)$ contains all pairs $(R,q')$ such that:

• If $r\in R$ then $id(r)\in q.pend$ or there is an $in\in I$ with $id(in)=id(r)$,

• If $r\in R$ then $val(r)\in q.vals$ or there is an $in\in I$ with $val(in)=val(r)$, and

• $q'.vals= q.val\cup vals(I)$ and $q'.pend= (q.pend \cup ids(I))\setminus ids(R)$.

Fig. 4.

An execution of a validity object, and the corresponding part of an interval-sequential automata

On the right of Fig. 4 there is part of a validity object automaton. On the left of Fig. 4 is illustrated an interval-sequential execution with the vertical red double-dot lines: $I_0,R_0,I_1,R_1$, where $I_0=\{p.\mathsf{validity}(1),q.\mathsf{validity}(2)\}$, $R_0=\{p.\mathsf{resp}(2)\}$, $I_1=\{r.\mathsf{validity}(3)\}$, $R_1=\{q.{sf resp}(3),r.\mathsf{resp}(1)\}$.

The interval-linearizability consistency notion described in subsection 4.3 will formally define how a general execution (blue double-arrows in the figure) can be represented by an interval-sequential execution (red double-dot lines), and hence tell if it satisfies the validity object specification. The execution in Fig. 4 roughly shows that the validity object has no specification as a natural sequential object: if one tries to transform the execution into a sequential one respecting real-time order, then always an invocation outputs a value that has not been proposed, namely, the invocation “predicts” the future.

4.3 Interval Linearizability

Interval-sequential come with its own consistency condition, called interval linearizability, that generalizes the linearizability condition of sequential objects.

Given an interval-sequential specification of an object, an execution is interval linearizable if it can be transformed into an interval-sequential execution such that (1) it respects the real-time order of invocation and responses and (2) the interval-sequential execution is recognized by the automaton specifying the object.

In other words, an execution is interval-linearizable if, for each operation call, it is possible to find two points, defining an interval, in the interval of real-time defined by the invocation and response of the operation, and these linearization intervals induce a valid interval-sequential execution. Although being more general, and hence expressive, interval linearizability retains the good properties of linearizability of being local and non-blocking.

We can now complete the example of the validity object. In Fig. 5 there is an interval linearization of the execution in Fig. 4.

Fig. 5.

An execution of a validity object

Remark 3

(Linearizability and set-linearizability). When restricted to interval-sequential executions in which for every invocation there is a response to it in the very next concurrency class, then interval-linearizability boils down to set-linearizability. If in addition we demand that every concurrency class contains only one element, then we have linearizability.

5 Interval-Sequential Objects = Long-Lived Tasks

In this section, we finally show that long-lived tasks and interval-sequential objects have the same expressiveness power, i.e., they are able to describe the same set of distributed problems.

5.1 From Interval-Sequential Objects to Long-Lived Tasks

Let X be an interval-sequential object. Using the construction in Sect. 3, one can obtain a long-lived task $T_X$ modeling X. The only difference is that, when defining $\varDelta (\sigma )$, we consider all valid executions of X in which only the invocations in $\sigma$ appear. Some of these executions might be non-sequential, i.e., they might be strictly interval-sequential executions but that is not a problem, the interleaving pattern in those executions can be succinctly modeled by the set-views. The solvability conditions remains the same.

The proof of the following theorem is almost the same as the proof of Theorem 1, we just need to replace the word linearizability by interval linearizability.

Theorem 2

Let X be any interval sequential object and let $T_X$ be the long-lived task derived from X. Consider any execution E without pending operations. Then, E is interval-linearizable with respect to X if and only if E satisfies $T_X$.

5.2 From Long-Lived Tasks to Interval-Sequential Objects

Let $T = \langle \mathcal {I}, \mathcal {O}, \varDelta \rangle$ be a long-lived task. We require the task is well-defined in the following sense. We say that T is well-defined if its set-views have the snapshot property: for every $\sigma \in \mathcal {I}$, for every $\tau \in \varDelta (\sigma )$, the set-views in $\tau$ satisfy the following: (1) for every $v \in \tau$, its set-view contains the invocation in v and (2) for every $u, v \in \tau$, the set-views of u and v are comparable under containment.

In what follows we consider only well-formed long-lived tasks. It can be checked that the tasks constructed from interval-sequential objects above are well-formed.

We define an interval-sequential object $X_T$ from T as follows. The set of invocations, Inv, is the infinite set with all invocations in $\mathcal {I}$ and the set of responses, rev, is the infinite set with all responses in $\mathcal {O}$. The set of states Q contains every pair (I, R) where I and R are finite sets of Inv and Res, respectively. The interval-sequential object $X_T$ has one initial state: $(\emptyset , \emptyset )$.

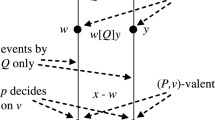
The transition function $\delta$ is defined as follows. Let E be an execution without pending operations that satisfies T. Let $\sigma _E$ and $\tau _E$ be the simplexes induced by E. Since E satisfy T, there is a simplex $\lambda \in \varDelta (\sigma _E)$ such that for every $(inv, resp, view) \in \tau _E$ there is a $(inv', resp', view') \in \lambda$ such that $inv' = inv$, $resp' = resp$ and $view' \subseteq view$. Since T is well-defined, the set-views in $\lambda$ can be ordered $V_1 \subset V_2 \subset \ldots \subset V_m$ (with $V_m = \sigma _E$). Set $W_0, V_0 = \emptyset$. For $i = 1, \ldots , m$, let $I_i = V_i \setminus V_{i-1}$, $R_i = \{ resp : \exists inv \in V_i, (inv, resp, V_i) \in \lambda \}$ and $W_i = \cup _{j = 1, \ldots , i} R_i$. One can check that the sequence $S = I_1, R_1, I_2, R_2, \ldots , I_m, R_m$ has the form a interval sequential execution. The reason is that $R_i$ contains every matching response, resp, to an invocation, $inv \in V_i$, whose set-view is precisely $V_i$. Then, inv can be completed with resp right after $I_i$ because, at that point, the set-view of inv is the needed one, i.e., $V_i$ (see Fig. 6). Then, for every $i = 1, \ldots , m$, $\delta ((V_{i-1}, W_{i-1}), I_i)$ contains $((V_i, W_i), R_i)$. In other words, $X_T$ accepts the interval-sequential execution S obtained from $\lambda$. We repeat the previous construction for every such execution E.

Fig. 6.

From output simplexes to interval-sequential. The two simplexes have set-views with the snapshot property. Each invocation in a set-view is represented by its subindex. The corresponding interval-sequential executions are shown at the right.

Theorem 3

Let T be any long-lived task and let $X_T$ be the interval-sequential object derived from T. Consider any execution E without pending operations. Then, E satisfies T if and only if E is interval-linearizable with respect to $X_T$.

Proof

We first show that if E satisfies T then E is interval linearizable with respect to $X_T$. Let $\sigma _E$ and $\tau _E$ be the simplexes induced by E. Since E satisfies T, there is a $\lambda \in \varDelta (\sigma _E)$ such that for every $(inv, resp, view) \in \tau _E$ there is a $(inv', resp', view') \in \lambda$ such that $inv' = inv$, $resp' = resp$ and $view' \subseteq view$. By construction, $\lambda$ induces an interval sequential execution S accepted by $X_T$. Note that E and S contain the same invocations and responses. If we prove that S respects the real-time order in E, then S is an interval linearization of E. By contradiction, suppose the opposite. Then, there are invocations inv and $inv'$ such that the response of inv appears before $inv'$ in E but the response of $inv'$ appears before inv in S. Let $view_E$ and $view_S$ be the set-views of inv in E and S. Thus, $inv' \notin view_E$ and $inv' \in view_S$, and hence $view_S \nsubseteq view_E$. A contradiction. Then, S is an interval linearization of E.

We now show that if E is interval linearizable with respect to $O_T$ then E satisfies T. By interval linearizability, E can be transformed into an interval sequential execution S accepted by $X_T$ such that S respects the real-time order of E. Consider the simplexes $\sigma _E, \tau _E$ obtained from E. We have that E and S have the same invocations. By construction, there is a $\lambda \in \varDelta (\sigma _E)$ that induces S in $X_T$. Since S is an interval linearization of E and the execution S is induced by $\lambda$, for any $(inv, resp, view) \in \tau _E$, there is a $(inv', resp', view') \in \lambda$ with $inv' = inv$ and $resp' = resp$. Observe that if we prove that $view' \subseteq view$, then it follows that E satisfies $T_O$. For the sake of contradiction, assume that $view' \supset view$. Then, in the interval sequential execution S, the invocation inv appears after the response of an invocation $inv^* \in view' \setminus view$. However, since $inv^* \notin view$, the response of inv occurs before $inv^*$ in E, from which follows that S does not respect the real-time order in E. A contradiction.    $\square$