Keywords

1 Introduction

Two of the most crucial aspects of any such construction project are time and project cost, both of which have received considerable research attention [9, 12]. One particularly important element of effective project scheduling theory and applications is the discrete time-cost trade-off problem (DTCTP) introduced by Harvey and Patterson [6]. Of more recent concern, however, are accusations that the construction industry is causing environmental problems that range from excessive consumption of global resources-both in terms of construction and operation-to pollution of the surrounding environment. Hydroelectric projects, particularly, contribute significantly to changes in river environments [2, 17]. Yet previous studies have paid more attention to evaluating the environmental impact at later stages of reservoirs and hydraulic electricity rather than considering it from the construction stage. Recently, however, a tightening of environmental protection regulations, especially for hydroelectric projects, has increased pressure on project managers to reduce the environmental impact through the selection of optimal construction modes. There is an imminent need, therefore, to study management decisions on selection methods to ensure more environmentally friendly means of construction during the project planning stage when the environmental impact can best be incorporated into other project objectives. For hydroelectric projects such as the JHS-I, this planning stage should include the optimization of construction and subsequent operations for environmental impact as well as time and cost.

The expanding scale of such construction projects worldwide, however, makes effective project management extremely complex. To deal with this complexity while still achieving management objectives, construction managers must employ a project management decision system that effectively controls total project duration, penalty costs, and environmental impact. One effective method for such control is the discrete time-cost-environment trade-off problem with multiple projects (DTCETP-mP), which is an extension of the original DTCTP. This analysis thus applies DTCETP-mP to solve the three main objectives of the JHS-I problem: (1) minimization of the total project duration, (2) minimization of the total project penalty cost, and (3) minimization of the environmental impact.

In non-routine projects such as the new construction at JHS-I [10], the duration of each activity and completion time may be uncertain, so the project manager must handle multiple conflicting goals in an uncertain environment in which information may be incomplete or unavailable. In this context, activity duration uncertainty can be modeled using either probability-based methods [12] or fuzzy set-based methods [18, 19] depending on the situation and the project manager’s preference. When a project manager has difficulty characterizing the random variables, as in the current scenario of a new construction project with unique activities and a lack of historical data, the fuzzy method is the most effective approach.

Because the DTCETP-mP is an extension of the DTCTP, it is an NP-hard problem that is difficult to solve [15]. Yet even the most exact of currently available methods can only solve small projects with under 60 activities, a far cry from the numerous activities and modes per activity involved in the large-scale, complex JHS-I project, whose optimal solutions are beyond the capabilities of traditional production scheduling methods like PERT (Program Evaluation and Review Technique) and CPM (Critical Path Method) [3]. More suitable heuristic solution procedures for solving the DTCETP-mP are thus needed, several of which have been suggested in the literature. For example, Franck et al. [4] demonstrated that a genetic algorithm (GA) performed slightly better than a tabu search (TS) procedure but required more computing. In earlier work, Wang et al. [16] addressed larger, more complex problems by introducing an improved hybrid genetic algorithm (hGA) that uses a fuzzy logic controller (flc) to adaptively regulate the GA parameters (including generation number, population size, crossover ratio, mutation ratio) and automate mutation ratio fine tuning. The effectiveness and efficiency of the proposed flc-hGA is evaluated through comparison with other methods.

This present application of the DTCETP-mP to identify optimal solutions for the JHS-I large-scale deeply buried tunnel group project amends the GA first introduced by Holland [7] to an flc-hGA. The analytic results indicate that this optimization method is both practical and highly efficient in solving the JHS-II problem and achieving minimization of the project’s total duration, penalty costs, and environmental impact.

2 Problem Description and Mathematical Model

2.1 Problem Description

Because the JHS-I project is unique, lacking in historical data, technically difficult to construct, structurally complex, and subject to strict requirements and many construction uncertainties, it is difficult to estimate the exact duration of each activity or assign each a strict function [8, 11]. Duration is thus characterized by fuzziness and subjective uncertainty [18, 19]. In such a situation, not only the duration but also the cost and environmental impact of each activity depends on construction mode selection, which is in turn related to the assignment of construction materials and machines, crew formation, and overtime policies. In this case, therefore, a DTCETP-mP discrete mode selection for these variables is more practical than a continuous mode selection.

In the DTCETP-mP analysis, each subproject activity is assigned certain discrete well-defined construction methods so that the analysis can determine the best combination(s) of duration, cost, and environmental impact for all activities. The start time for each subproject activity is optimized by the flc-hGA, and all activities are executed in a certain order to achieve completion under budgetary, environmental, and cash flow constraints in any time period. The project completion date is as estimated by project experts and lies between the earliest start time for the first activity and the latest finish time for the last activity. The total project penalty costs, also assessed by these experts, comprise penalty costs for delays in all subprojects and for the environmental impact. Project planning involves the selection of proper methods, crew sizes, equipment, and technologies to ensure efficient activity completion.

Despite such careful planning, however, project completion inherently involves a trade-off between time, cost, and environmental impact. For example, using more productive resources or technologies (e.g., more efficient equipment, more workers, increased overtime) may save time but raise costs. Conversely, a reduction in time may lower environmental impact, while a reduction in cost may increase both time and environmental impact. These three important considerations of time, cost, and environmental impact are thus the criteria used to determine the best scheduling and combination for the DTCETP-mP, thereby pinpointing the optimal construction mode combination for all activities.

2.2 Assumptions

The DTCETP-mP model for the JHS-I makes the following assumptions:

  1. (1)

    The DTCETP-mP comprises multiple projects, each containing several activities;

  2. (2)

    The start time of each activity is dependent upon the completion of its predecessor;

  3. (3)

    The capital used by all activities does not exceed the limited quantities in any time period, and the total project budget is within a predetermined limit;

  4. (4)

    The environmental impact caused by the activities does not exceed the limited quantities in any time period, and the total project environmental impact is within a predetermined limit;

  5. (5)

    When an activity begins, it cannot be interrupted;

  6. (6)

    The managerial objective is to minimize the total project time, total tardiness penalty, and total environmental impact for all subprojects.

2.3 Model Formulation

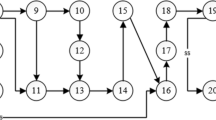
The problem is represented on an activity-on-node (AON) network with a single starting and a single ending node, each of which corresponds to dummy activities. The analysis uses the following notation:

Index:

figure a

Parameters:

figure b

Decision variables:

figure c

Functions:

figure d

2.4 Multiobjective Model

The solution proposed by the multiobjective optimization model is based on managerial objectives and project constraints, which for clarity are discussed separately in the subsections below.

(1) Objective Functions

The first objective is to minimize total project time; that is, the sum of the completion times for all subprojects, which can be expressed as follows:

$$\begin{aligned} \min {z_1} = \sum \limits _{i = 1}^I {E(\tilde{t}_{iJ}^F)}. \end{aligned}$$
(1)

The second objective is to measure and minimize the total cost by minimizing the total penalty costs of multiple projects:

$$\begin{aligned} \min {z_2} = \sum \limits _{i = 1}^I {c_i^p(E(\tilde{t}_{iJ}^F) - E(\tilde{t}_i^D))}. \end{aligned}$$
(2)

The third and final objective is to minimize total environmental impact:

$$\begin{aligned} \min {z_3} = \sum \limits _{i = 1}^I {\frac{{\sum _{j = 1}^J {{V_{ij}} \times {w_{ij}}(E(\tilde{t}_{iJ}^F) - E(\tilde{t}_i^D))} }}{{E(\tilde{t}_{iJ}^F)}}}. \end{aligned}$$
(3)

(2) Constraints

Because a specific subproject must be completed before another subproject can be initiated (the precedence constraint of multiple projects), the model includes the following constraint:

$$\begin{aligned} E(\tilde{t}_{eJ}^S) \le E(\tilde{t}_{i,1}^S) - E({\tilde{d}_{eJ}}),~~ e \in \Pr e(i). \end{aligned}$$
(4)

Likewise, because the start time of each activity is dependent upon the completion of some other activities (the precedence constraint of activities), the next activity must be started after a specific activity is completed:

$$\begin{aligned} E(\tilde{t}_{il}^S) \le E(\tilde{t}_{ij}^S) - E({\tilde{d}_{il}}),~~l \in \Pr e(j). \end{aligned}$$
(5)

The project is also subject to a limitation on the total capital and capital per time period,

$$\begin{aligned} \sum \limits _{j \in {S_p}} {{l_{ijc}} \le {b_c}} i = 1,2, \cdots , I, \end{aligned}$$
(6)

as well as on the total environmental impact and the environmental impact per time period:

$$\begin{aligned}&\sum \limits _{i \in {S_p}} {\sum \limits _{j \in {S_p}} {{l_{ijc}} \le {B_c}} }, \end{aligned}$$
(7)
$$\begin{aligned}&\sum \limits _{j \in {S_p}} {{l_{ije}} \times {w_{ij}} \le {b_e}},~~ i = 1,2, \cdots , I, \end{aligned}$$
(8)
$$\begin{aligned}&\sum \limits _{i \in {S_p}} {\sum \limits _{j \in {S_p}} {{l_{ije}} \times {w_{ij}} \le {B_e}} }, ~~{l_{ije}} = \frac{{{V_{ij}}}}{{{d_{ij}}}}. \end{aligned}$$
(9)

The nonnegative variables are described in the model by the following equation:

$$\begin{aligned} E(\tilde{t}_{ij}^S), E(\tilde{t}_{ij}^F), E({\tilde{d}_{ij}}) \ge 0,~~ \forall i \in I,~~\forall j \in J. \end{aligned}$$
(10)

3 Hybrid Genetic Algorithm with Fuzzy Controller

Although mathematically, several Pareto optimal solutions are possible for the multiobjective model formulated above, in real-world construction, only one optimized solution is needed in each time-constrained decision-making situation. Hence, the multiobjective model is transformed into a single-objective model using a weighting method. Additionally, because accurately determining the GA parameters is especially important in solving large-scale problems like the JHS-I project, GA effectiveness is improved by adaptively regulating the crossover and mutation rate during the genetic search process using the fuzzy logic controller (flc) [16]. This regulation reduces CPU time and enhances optimization quality and stability by regulating the increasing and decreasing crossover and mutation rate ranges [1, 5, 13, 14, 20].

3.1 Overall Procedure for the Proposed Method

Solving the problem with the flc-hGA involves the following steps:

  1. Step 1.

    Concentration of multiple objectives using the weight-sum procedure.

  2. Step 2.

    Setting of the genetic algorithm parameters: population size, crossover rate, mutation rate, and maximum generation.

  3. Step 3.

    Generation of an initial set of individuals.

  4. Step 4.

    Choosing of the selection and hybrid genetic operators: crossover and mutation.

  5. Step 5.

    Evaluation of the fitness value of the chromosome.

  6. Step 6.

    Selection of the best total penalty for the minimized total project time and minimized environmental impact and storage of an alternative schedule for the minimized total project time.

  7. Step 7.

    Check of the termination: If one individual has achieved the predefined fitness value, the process stops: otherwise, it goes on to step 8.

  8. Step 8.

    Regulation of the mutation rate through adaptive use of the fuzzy logic controller; otherwise, the process returns to step 4.

The model uses two hybrid genetic operators, a position-based crossover and a swap mutation (SM) operator. The crossover operator randomly takes some genes from one parent and fills any vacuum with genes from the other parent by scanning from left to right, while the SM operator selects two projects at random and swaps their contents.

3.2 Hybrid Genetic Operators

The model uses two hybrid genetic operators, a position-based crossover and a swap mutation (SM) operator. The crossover operator randomly takes some genes from one parent and fills any vacuum with genes from the other parent by scanning from left to right, while the SM operator selects two projects at random and swaps their contents.

3.3 Fuzzy Logic Controller

The fuzzy logic controller (flc) is used to automatically tune the GA parameters whose determination is so important in large-scale problems. Here, only a mutation flc is used because in the proposed hGA, the effects of the crossover and crossover flc are almost the same. The main difference between the hGA and the flc-hGA is that a mutation flc based on the flc is implemented independently to adaptively regulate the mutation ratio during the genetic search process by considering the changes in average fitness in each parent and offspring population over two continuous generations. Mathematically, this procedure can be expressed as follows: letting f(t) be the difference in the average fitness function between the \(t^{th}\) and \((t-1)^{th}\) generation, \(\varepsilon \) is a small positive number near to zero (in this paper, \(\varepsilon = 0.1\)), allowing the mutation ratio for the next generation to be derived using an if-then procedure:

  1. (1)

    If \(\left| {f(t) - f(t - 1)} \right| < \varepsilon \), then the mutation ratio \({p_m}\) for the next generation should be rapidly increased;

  2. (2)

    If \(f(t) - f(t - 1) < \varepsilon \), then the mutation ratio \({p_m}\) for the next generation should be decreased;

  3. (3)

    If \(f(t) - f(t - 1) > \varepsilon \), then the mutation ratio \({p_m}\) is selected for the next generation.

When f(t) and \(f(t - 1)\) are the flc’s inputs and the change in mutation ratio m(t) is its outputs. m(t) Once the input values are assigned, the scaling value Z(a, b) can be determined by setting \(\lambda \in [ - 1.0,1.0]\) as the given values for regulating an increasing and decreasing range for the mutation ratio. The changes in the mutation ratios are then determined by \({\varDelta {m}}(t) = \lambda Z(a,b)\) and the mutation ratio values for the next generation by \({p_m}(t + 1) = {p_m}(t) + \varDelta m(t)\), where \({p_m}(t)\) is the mutation ratio at generation t.

4 Case Study: The Jinping-I Hydropower Station

The Jinping-I (JHS-I) and Jinping-II Hydropower Stations, which epitomize the large-scale constructions of China’s West-East Electric Transmission Project, have a combined capacity of 8,400 MW and were planned for Jingping River Bend, a major artery 150 Km in length whose downstream river section is separated from the opposite bank by only 16 km. Along that length, the elevation drops 310 m, creating an excellent site for hydroelectric production. Whereas JHS-I will rely on its high dam and reservoir to supply water, JHS-II, located 7.5 Km downstream (at coordinates \({28^ \circ }07'42''N{101^ \circ }14'27''E\)) is diverted by a much smaller dam and will rely on the world’s four largest and longest (16.7 km) diversion tunnels. This latter has a total installed capacity of 4,800 MW (\(8 \times 600\) MW), for a multiyear average annual generation of 24.23 TWh.

Because such scale and complexity presents computational challenges, our model includes only the elements typical of constructions, making it generalizable to similar projects. As previously emphasized, the study goal is to identify the most effective strategies and thus the most effective and viable project management methods for JHS-I, so that these may be implemented in future large-scale projects (Table 1).

Table 1. Subprojects and activities
Full size table

4.1 Data Collection

The data for the JHS-I project, obtained primarily from the Ertan Hydropower Development Company, includes observations of managerial practice and interviews with designers, consultants, contractors, subcontractors, and a city government officer at the station. This data set is supplemented by information from prior research. The construction manager’s project experience, in particular, was invaluable for researcher comprehension of the projects’ specific nature and configuration. In addition to two dummy (start and end) projects, JHS-I has five subprojects: a transport and power system, river diversion during construction, dam construction, a stream power capacity project, and a spillway project (see Table 2).

Table 2. Detailed information for each activity
Full size table

Each activity must be performed in one of \({m_i}\) possible modes, each with a corresponding duration, cost, environmental impact, and budget and cash flow limit (see Tables 3 and 4). Hence, each activity has a certain maximal cost and environmental impact unit requirement. Other relevant data for the analysis are as follows: The maximum capital (units: million RMB) and environmental impact for each time period are 14 and 10 units, \(({B_c},{B_e}) = (12,10)\), respectively, while the maximum capital (units: million RMB) and environmental impact for each subproject time period are 6 and 6 units, \(({b_c},{b_e}) = (8,6)\). The penalty cost for each subproject in each time period is \(c_i^p = 12\) (units: million RMB). The evolutionary parameters are a population size of 20, maximal generation of 200, an optimistic-pessimistic index of \(\lambda = 0.5\), and a weight for each objective of \({\eta _1} = 0.5,{\eta _2} = 0.2,{\eta _3} = 0.3\). The remaining variables are activity duration, cost, activity predecessors, project duration, and project predecessors.

Table 3. Optimal solution for the JHS-I case study
Full size table
Table 4. Contrast between the optimal solution and actual data
Full size table

4.2 Case Study Results

To achieve managerial objectives, all project aspects must be optimized through the best possible arrangement of start times and construction modes for each subproject activity. According to the proposed model, for optimal scheduling, the JHS-I activities should be arranged in the order below and corresponding construction modes chosen to fulfil the decision maker’s requirements:

$$\begin{aligned} S = \{ {P_2}(1,2,3,5,4) \rightarrow {P_3}(1,2,3,4) \rightarrow {P_1}(1,3,2,4) \rightarrow {P_4}(2,1,3,5,4) \rightarrow {P_5}(2,1,3,4)\}. \end{aligned}$$

It should also be noted, however, that, because of cost and environmental impact constraints, certain noncritical activities in subproject 1 (2), executable between the \(4^{th}\) and \(9^{th}\) month, are flexible but other noncritical activities in subproject 3 (2), executable between the \(3^{rd}\) and \(8^{th}\) month, are not. The model thus defines the critical path meaningfully enough to be used in practical (rather than simply theoretical) scheduling. In particular, it enables the project manager to schedule activities according to the situation, which can be affected by such factors as available manpower, equipment, holidays and the need to harmonize with other parallel projects or activities. Moreover, even though a comparison of the actual project data with the optimal result generated by the flc-hGA reveals differences, these differences move in a positive direction. For example, the net decrease from plus to minus in each objective, when considered specifically for the changes in penalty costs and environmental impact, signals a shift from penalty to reward. Overall, the rate of this decrease for each objective, which ranges from 9.56% to 200%, signals an improvement in construction efficiency that could bring considerable economic benefit to any construction project, but especially to one that is large scale.

Admittedly, because the assumptions on which the mathematical model is based may generate certain modeling errors, the results do not represent a 100% optimal DTCETP-mP solution. Nevertheless, they can still serve as a useful optimal scheduling guideline for decision makers in current construction projects.

5 Conclusions and Implications for Future Research

The multiple objective optimization model developed in this paper extends a traditional single project model to an advanced multiple project trade-off model able to determine optimal scheduling and construction mode selection for the project at Jinping-I Hydropower Station. The model is designed to not only minimize duration and penalty costs but also reduce the DTCETP-mP’s environmental impact. It thus controls for the project constraints of duration, cost, and environmental impact.

Because the DTCETP-mP is an NP-hard problem, the optimization method employs an flc-hGA to solve it. The analytical results for the JHS-I case study indicate that the trade-off between competing incommensurate objectives is actually dominated by the project manager’s determination of the weight for each objective. Hence, decision makers can use the importance of project objectives to determine the optimum trends for time, cost, and environmental impact. One major advantage of the proposed method is that it enables decision makers to systematically and feasibly control the schedule according to an optimistic-pessimistic index. In addition, the flc-hGA developed for the study can be used to enhance optimization quality and stability.

The findings reported here suggest three important areas for future research, all of which warrant equal concern. Firstly, a more holistic measurement should be developed for environmental impact to ensure a more reasonable and effective model. Secondly, future studies should address more complex practical problems, such as those involving resource constraints, and uncertainties. Lastly, more efficient heuristic methods need to be developed to solve NP-hard problems with a greater number of constraints. The method and model proposed here offer a useful foundation for all such investigations.