The Saleman’s Improved Tours for Fundamental Classes

Abstract

Finding the exact integrality gap $\alpha$ for the LP relaxation of the metric Travelling Salesman Problem (TSP) has been an open problem for over thirty years, with little progress made. It is known that $4/3 \le \alpha \le 3/2$, and a famous conjecture states $\alpha = 4/3$. For this problem, essentially two “fundamental” classes of instances have been proposed. This fundamental property means that in order to show that the integrality gap is at most $\rho$ for all instances of metric TSP, it is sufficient to show it only for the instances in the fundamental class.

However, despite the importance and the simplicity of such classes, no apparent effort has been deployed for improving the integrality gap bounds for them. In this paper we take a natural first step in this endeavour, and consider the 1/2-integer points of one such class. We successfully improve the upper bound for the integrality gap from 3/2 to 10/7 for a superclass of these points, as well as prove a lower bound of 4/3 for the superclass.

Our methods involve innovative applications of tools from combinatorial optimization which have the potential to be more broadly applied.

S. Boyd—Partially supported by the National Sciences and Engineering Research Council of Canada. This work was done during visits in Laboratoire G-SCOP, Grenoble; support from the CNRS and Grenoble-INP is gratefully acknowledged.

A. Sebő—Supported by LabEx PERSYVAL-Lab (ANR 11-LABX-0025), équipe-action GALOIS.

1 Introduction

Given the complete graph $K_n = (V_n, E_n)$ on n nodes with non-negative edge costs $c \in {\mathbb R}^{E_n}$, the Traveling Salesman Problem (henceforth TSP) is to find a Hamiltonian cycle of minimum cost in $K_n$. When the costs satisfy the triangle inequality, i.e. $c_{ij} + c_{jk} \ge c_{ik}$ for all $i,j,k \in V_n$, the problem is called the metric TSP. If the metric is defined by the shortest (cardinality) paths of a graph, then it is called a graph-metric; the TSP specialized to graph-metrics is the graph-TSP.

For $G=(V,E)$, $x \in {\mathbb R}^E$ and $F \subseteq E$, $x(F):=\sum _{e \in F} x_e$; for $U \subseteq V$, $\delta (U):=\delta _G(U):=\{uv \in E : u \in U, v \in V{\setminus }U\}$; $E[U]:=\{uv \in E : u \in U, v \in U\}$.

A natural linear programming relaxation for the TSP is the following subtour LP:

$$\begin{aligned} \hbox {minimize } cx \end{aligned}$$

(1)

$$\begin{aligned} \hbox {subject to:}\, x(\delta (v)) = 2&\quad \hbox {for all}~v \in V_n,\end{aligned}$$

(2)

$$\begin{aligned} x(\delta (S)) \ge 2&\quad \hbox {for all}~\emptyset \ne S\subsetneq V_n, \end{aligned}$$

(3)

$$\begin{aligned} 0 \le x_e \le 1&\quad \hbox {for all}~e \in E_n. \end{aligned}$$

(4)

For a given cost function $c\in \mathbb {R}^{E_n}$, we use LP(c) to denote the optimal solution value for the subtour LP and OPT(c) to denote the optimal solution value for the TSP. The polytope associated with the subtour LP, called the subtour elimination polytope and denoted by $S^n$, is the set of all vectors x satisfying the constraints of the subtour LP, i.e. $S^n = \{ x \in \mathbb {R}^{E_n} : x \, \hbox {satisfies} \, (2), (3), (4) \}$.

The metric TSP is known to be NP-hard. One approach taken for finding reasonably good solutions is to look for a $\rho$ -approximation algorithm for the problem, i.e. a polynomial-time algorithm that always computes a solution of value at most $\rho$ times the optimum. Currently the best such algorithm known for the metric TSP is the algorithm due to Christofides [7] for which $\rho = \frac{3}{2}$. Although it is widely believed that a better approximation algorithm is possible, no one has been able to improve upon Christofides algorithm in four decades. For arbitrary nonnegative costs not constrained by the triangle inequality there does not exist a $\rho$-approximation algorithm for any $\rho \in \mathbb {R}$, unless $P=NP$, since such an algorithm would be able to decide if a given graph is Hamiltonian.

For an approximation guarantee of a minimization problem one needs lower bounds for the optimum, often provided by linear programming. For the TSP a commonly used lower bound is LP(c). Then finding a solution of objective value at most $\rho \,LP(c)$ in polynomial time implies a $\rho$-approximation algorithm. The theoretically best possible bound for $\rho$ is the integrality gap $\alpha$ for the subtour LP, which is the worst-case ratio between OPT(c) and LP(c) over all metric cost functions c.

It is known that $\alpha \le \frac{3}{2}$ [19, 20], however no example for which the ratio is greater than $\frac{4}{3}$ is known. In fact, a famous conjecture, often referred to as the $\frac{4}{3}$ Conjecture, states the following:

Conjecture 1

The integrality gap for the subtour LP is at most $\frac{4}{3}$.

Well-known examples show that $\alpha$ is at least $\frac{4}{3}$. In almost thirty years, there have been no improvements made for the upper bound of $\frac{3}{2}$ or lower bound of $\frac{4}{3}$ for the integrality gap for the subtour LP.

The definition of the integrality gap can be reformulated in terms of a containment relation between two polyhedra that do not depend on the objective function and involve only a sparse subset of (less than 2n) edges, which is well-known, but not always exploited. We will not only use it here, but it is the very tool that we need.

Define a tour to be the edge-set of a spanning Eulerian (connected with all degrees even) multi-subgraph of $K_n$. If none of the multiplicities can be decreased, then all multiplicities are at most two; however, there are some technical advantages to allowing higher multiplicities. Given a metric cost function, a tour can always be shortcut to a Hamiltonian cycle of the same cost or less.

For any multi-set $J\subseteq E_n$, the incidence vector of J, denoted by $\chi ^J$, is the vector in $\mathbb {R}^{E_n}$ for which $\chi ^{J}_e$ is equal to the number of copies of edge e in J for all $e \in E_n$.

Showing for some constant $\rho \in \mathbb {N}$ that $\rho \,x$ is a convex combination of incidence vectors of tours for each $x\in S^n$ gives an upper bound of $\rho$ on the integrality gap for the subtour LP: it implies that for any cost function $c\in \mathbb {R}^{E_n}$ for which $cx = LP(c)$, at least one of the tours in the convex combination has cost at most $\rho \,(cx) = \rho \,LP(c)$. If the costs are metric, this tour can be shortcut to a TSP solution of cost at most $\rho \,LP(c)$, giving a ratio of $OPT(c)/LP(c) \le \rho$. The essential part “(ii) implies (i)” of the following theorem asserts that the converse is also true: if $\rho$ is at least the integrality gap then $\rho \,S^n := \{y \in \mathbb {R}^{E_n}: y= \rho x, x\in S^n\}$ is a subset of the convex hull of incidence vectors of tours:

Theorem 1

[6]. Let $K_n = (V_n, E_n)$ be the complete graph on n nodes and let $\rho \in \mathbb {R}, \rho \ge 1$. The following statements are equivalent:

• (i) For any weight function $c:E_n\rightarrow \mathbb {R}_+: OPT(c)\le \rho LP(c)$.

• (ii) For any $x\in S^n$, $\rho x$ is in the convex hull of incidence vectors of tours.

• (iii) For any vertex x of $S^n$, $\rho x$ is in the convex hull of incidence vectors of tours.

So Conjecture 1 can also be reformulated as follows:

Conjecture 2

The polytope $\frac{4}{3}\,S^n$ is a subset of the convex hull of the incidence vectors of tours.

Given a vector $x \in S^n$, the support graph $G_x=(V_n, E_x)$ of x is defined with $E_x = \{e\in E_n: x_e >0 \}$. We call a point $x \in S_n$ $\frac{1}{2}$ -integer if $x_e \in \{0, \frac{1}{2}, 1\}$ for all $e \in E_n$. For such a vector we call the edges $e \in E_n$ $\frac{1}{2}$ -edges if $x_e = \frac{1}{2}$ and 1-edges if $x_e = 1$. Note that the 1-edges form a set of disjoint paths that we call 1-paths of x, and the $\frac{1}{2}$-edges form a set of edge-disjoint cycles we call the $\frac{1}{2}$ -cycles of x. Cycles and paths are simple (without repetition of nodes) in this article.

For Conjecture 2, it seems that $\frac{1}{2}$-integer vertices play an important role (see [1, 5, 14]). In fact it has been conjectured by Schalekamp et al. [14] that a subclass of these $\frac{1}{2}$-integer vertices are the ones that give the biggest gap. Here we state their conjecture more broadly:

Conjecture 3

The integrality gap for the subtour LP is reached on $\frac{1}{2}$-integer vertices.

Very little progress has been made on the above conjectures, even though they have been around for a long time and have been well-studied. For the special case of graph-TSP an upper bound of $\frac{7}{5}$ is known for the integrality gap [17]. Conjecture 2 has been verified for the so-called triangle vertices $x\in S^n$ for which the values are $\frac{1}{2}$-integer, and the $\frac{1}{2}$-edges form triangles in the support graph [3]. The lower bound of $\frac{4}{3}$ for the integrality gap is provided by triangle vertices with just two triangles.

A concept first introduced by Carr and Ravi [5] (for the 2-edge-connected subgraph problem) is that of a fundamental class, which is a class of points F in the subtour elimination polytope with the following property: showing that $\rho \,x$ is in the convex hull of incidence vectors of tours for all vertices $x \in F$ implies the same holds for all vertices of the polytope, and thus implies that the integrality gap for the subtour LP is at most $\rho$.

Two main classes of such vertices have been introduced, one by Carr and Vempala [6], the other by Boyd and Carr [3]. In this paper we will focus on the latter one, i.e. we define a Boyd-Carr point to be a point $x \in S^n$ that satisfies the following conditions:

• (i) The support graph $G_x$ of x is cubic and 3-edge connected.

• (ii) In $G_x$, there is exactly one 1-edge incident to each node.

• (iii) The fractional edges of $G_x$ form disjoint 4-cycles.

A Carr-Vempala point is one that satisfies (i), (ii) and instead of (iii) the fractional edges form a Hamiltonian cycle.

Despite their significance and simplicity, no effort has been deployed to exploring new integrality gap bounds for these classes, and no improvement on the general $\frac{3}{2}$ upper bound on the integrality gap has been made for them, not even for special cases. A natural first step in this endeavour is to try to improve the general bounds for the special case of $\frac{1}{2}$-integer Boyd-Carr or Carr-Vempala points.

In this paper we improve the upper bound for the integrality gap from $\frac{3}{2}$ to $\frac{10}{7}$ for $\frac{1}{2}$-integer Boyd-Carr points. In fact we prove this for a superclass of these points. Replacing the 1-edges by paths of arbitrary length between their two endpoints, we get all the $\frac{1}{2}$-integer vectors of $S^n$ for which the $\frac{1}{2}$-edges form disjoint 4-cycles, or squares in the support graph. We call these square points. We also show that square points contain a subclass for which the integrality gap is at least $\frac{4}{3}$. Note that this subclass is not in the class of $\frac{1}{2}$-integer vertices conjectured by Schalekamp et al. [14] to give the biggest integrality ratio, which makes the class of square points interesting with respect to this conjecture.

In the endeavour to find improved upper bounds on the integrality gap we examine the structure of the support graphs of Boyd-Carr points, which we call Boyd-Carr graphs. We show that they are all Hamiltonian, an important ingredient of our bounding of their integrality gap. The proof uses a simple and nice theorem by Kotzig [12] on Eulerian trails with forbidden transitions. An Eulerian trail in a graph is a closed walk containing each of its edges exactly once. Note that contrary to tours, it is more than just an edge-set.

Similarly, Carr-Vempala graphs are the support graphs of Carr-Vempala points. These are by definition Hamiltonian.

In Sect. 2.1 we show a first, basic application of these ideas, where some parts of the difficulties do not occur. We prove that all edges can be uniformly covered 6/7 times by tours in the support graphs of both fundamental classes. This is better than the conjectured general bound 8/9 that would follow for arbitrary cubic graphs from Conjecture 2.

Another new way of using classical combinatorial optimization for the TSP occurs in Sect. 2.2, where we use an application of Edmonds’ matroid intersection theorem to write the optimum x of the subtour elimination polytope as the convex hull of incidence vectors of “rainbow” spanning trees in edge-coloured graphs. The idea of using spanning trees with special structures to get improved results has recently been used successfully in [10] for graph-TSP, and in [11, 18] for a related problem, namely the metric $s-t$ path TSP. However, note that we obtain and use our trees in a completely different way.

Our main results concerning the integrality ratio of $\frac{1}{2}$-integer Boyd-Carr points are proved in Sect. 3. We conclude that section by outlining a potential strategy for using the Carr-Vempala points of [6] for proving the $\frac{4}{3}$ Conjecture.

2 Polyhedral Preliminaries and Other Useful Tools

In this section we will discuss some useful and powerful tools that we will need in the proof of our main result in Sect. 3. We begin with some preliminaries.

Given a graph $G=(V,E)$ with a node in V labelled 1, a 1-tree is a subset F of E such that $|F\cap \delta (1)| = 2$ and $F\backslash \delta (1)$ forms a spanning tree on $V\backslash \{1\}$. The convex hull of the incidence vectors of 1-trees of G, which we will refer to as the 1-tree polytope of the graph G, is given by the following [13]:

$$\begin{aligned} \{x\in \mathbb {R}^E: x(\delta (1)) = 2, x((E[U])) \le |U| - 1 \text{ for } \text{ all } \emptyset \ne U \subseteq V\backslash \{1\},\nonumber \\ 0 \le x_e \le 1 \text{ for } \text{ all } e \in E \text{, } x(E)=|V|\}\qquad \qquad \qquad . \end{aligned}$$

(5)

It is well-known that the 1-trees of a connected graph satisfy the basis axioms of a matroid (see [13]).

Given $G=(V,E)$ and $T\subseteq V$, |T| even, a T-join of G is a set $J\subseteq E$ such that T is the set of odd degree nodes of the graph (V, J). A cut $C=\delta (S)$ for some $S\subset V$ is called a T-cut if $|S\cap T|$ is odd. We say that a vector majorates another if it is coordinatewise greater than or equal to it. The set of all vectors x that majorate some vector y in the convex hull of incidence vectors of T-joins of G is given by the following [9]:

$$\begin{aligned} \{x\in \mathbb {R}^E: x(C) \ge 1 \hbox {for each} \, T\hbox {-cut C,} \, x_e \ge 0 \, \hbox {for al }\, e \in E\}. \end{aligned}$$

(6)

This is the T -join polyhedron of the graph G.

The following two results are well-known (see [19, 20]), but we include the proofs as they illustrate the methods we will use:

Lemma 1

[19, 20]. If $x\in S^n$, then (i) it is a convex combination of incidence vectors of 1-trees of $K_n$, and (ii) x/2 majorates a convex combination of incidence vectors of T-joins of $K_n$ for every $T\subseteq V_n$, |T| even.

Proof

By using the Eq. (2) of the subtour LP, we see that $x(E_n) = |V_n|$ and that the inequalities (3) can be replaced by $x(E_n[S])\le |S|-1$, for all $\emptyset \ne S\subsetneq V_n$. Thus $x\in S^n$ satisfies all of the constraints of the 1-tree polytope for $K_n$ and (i) of the lemma follows. To check (ii), note that x/2 satisfies the constraints of the T-join polyhedron of $K_n$ for all $T\subseteq V_n$, |T| even (in fact $x(C)/2\ge 1$ on every cut C), that is, it majorates a convex combination of incidence vectors of T-joins.    $\square$

Theorem 2

[19, 20]. If $x\in S^n$, $\frac{3}{2} x$ is in the convex hull of incidence vectors of tours.

Proof

By (i) of Lemma 1, x is a convex combination of incidence vectors of 1-trees of $K_n$. Let F be any 1-tree of such a convex combination, and $T_F$ be the set of odd degree nodes in the graph $(V_n,F)$. Then by (ii) of Lemma 1, x/2 majorates a convex combination of incidence vectors of $T_F$-joins. So $\chi ^F + x/2$ majorates a convex combination of incidence vectors of tours, and taking the average with the coefficients of the convex combination of 1-trees, we get that $x+x/2$ majorates a convex combination of incidence vectors of tours. Since adding 2 to the multiplicity of any edge in a tour results in another tour, it follows that $\frac{3}{2} x$ is a convex combination of incidence vectors of tours.   $\square$

The tools of the following two subsections are new for the TSP and appear to be very useful.

2.1 Eulerian Trails with Forbidden Bitransitions

Let $G=(V,E)$ be a connected 4-regular multigraph. For any node $v\in V$, a bitransition (at v) means a partition of $\delta (v)$ into two pairs of edges. Clearly every Eulerian trail of G uses exactly one bitransition at every node, meaning the two disjoint pairs of consecutive edges of the trail at the node. There are 3 bitransitions at every node and the simple theorem below, which follows from a nice result due to Kotzig [12], states that we can forbid one of these and still have an allowed Eulerian trail. As we will show, this provides Hamiltonian cycles containing all the 1-edges of square points.

Theorem 3

[12]. Let $G=(V,E)$ be a 4-regular connected multigraph with a forbidden bitransition for every $v\in V$. Then G has an Eulerian trail not using the forbidden bitransition of any node.

Lemma 2

Let x be any square point, and let $G_x=(V_n,E_x)$ be its support graph. Then $G_x$ has a Hamiltonian cycle H that contains all the 1-edges of $G_x$.

Proof

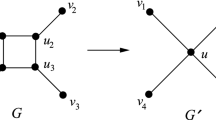
Shrinking all the 1/2-squares of $G_x$ and replacing each path of 1-edges by a single edge, we obtain a 4-regular connected multigraph $G^\prime =(V^\prime ,E^\prime )$ whose edges are precisely the 1-paths of $G_x$ and whose nodes are precisely the squares of $G_x$. To each contracted square we associate the forbidden bitransition consisting of the pairs of 1-edges incident with the square in $G_x$ which are diagonally opposite to each other, as shown in Fig. 1. By Theorem 3, there is an Eulerian trail K of $G^\prime$ that does not use these forbidden bitransitions. Consecutive edges in K at each node in $G^\prime$ are thus joined by a set of parallel edges in the corresponding square in $G_x$, and by adding these edges to K and replacing the edges in K with their corresponding 1-paths in $G_x$, we obtain the desired Hamiltonian cycle for $G_x$.   $\square$

Fig. 1.

Shrinking a square in $G_x$ to node u; forbidden: $\{(uv_1,uv_3),(uv_2,uv_4)\}$.

The exhibited connection of Eulerian graphs with forbidden bitransitions sends us to a link on delta-matroids [2] with well-known optimization properties that we wish to explore in a forthcoming work. We content ourselves in this section by providing a simple first application of Lemma 2 which shows a basic idea we will use in the proof of our main result in Sect. 3, without the additional difficulty of the more refined application.

Given a graph $G=(V,E)$ and a value k, we call $y \in \mathbb {R}^{E_{|V|}}$ the everywhere k vector for G if $y_e=k$ for all edges $e\in E$ and $y_e=0$ for all the other edges in the complete graph $K_{|V|}$.

Theorem 4

If $G=(V,E)$ is cubic, 3-edge-connected and Hamiltonian, so in particular if it is a Boyd-Carr or Carr-Vempala graph, then the everywhere 6/7 vector for G is a convex combination of incidence vectors of tours.

Proof

Let H be a Hamiltonian cycle of G, and let $M:=E{\setminus }H$ be the perfect matching complementary to H. It can be easily seen that the point $x \in \mathbb {R}^{E_{|V|}}$ defined by $x_e=1$ if $e\in M$, $x_e=1/2$ if $e\in H$ and $x_e=0$ otherwise is in the subtour elimination polytope $S^{|V|}$. By Theorem 2, $\frac{3}{2} x$ is then a convex combination of incidence vectors of tours.

Now take the convex combination $t:=\frac{3}{7}\chi ^H + \frac{4}{7} \frac{3}{2} x$. Then for edges $e\in M$ we have $t_e = 0 + \frac{4}{7}\frac{3}{2}=\frac{6}{7}$. For edges $e\in H$ we have $t_e =\frac{3}{7} + \frac{4}{7}\frac{3}{2}\frac{1}{2}=\frac{6}{7}$, and $x_e = 0$ for all edges e not in G, finishing the proof. The additional statement follows from the Hamiltonicity of the graphs (by Lemma 2 for Boyd-Carr, and by definition for Carr-Vempala).    $\square$

Note that $\frac{6}{7} < \frac{8}{9}$, where $\frac{8}{9}$ is the value one gets from Conjecture 2 applied to the everywhere $\frac{2}{3}$ vector for G, which is feasible for $S^{|V|}$. However, the problem of whether the everywhere $\frac{8}{9}$ vector is a convex combination of incidence vectors of tours remains open for general cubic 3-edge-connected graphs [16], while the corresponding problem for the $s-t$ path TSP has been solved [18].

2.2 Rainbow 1-trees

We now use matroid intersection to prove that not only is x is in the convex hull of incidence vectors of 1-trees, but we can also require that these 1-trees satisfy some additional useful properties.

Given a graph $G=(V,E)$, let every edge of G be given a colour. We call a 1-tree F of G a rainbow 1-tree if every edge of F has a different colour. Rainbow trees are discussed by Broersma and Li in [4], where they note they are the common independent sets of two matroids. Similarly, rainbow 1-trees are common bases of two matroids, namely 1-trees, that we saw to be bases of a matroid (see after (5)), and subsets of E containing exactly one edge of each colour, which are bases of a partition matroid [15]. Luckily, $\frac{1}{2}$-integer points of $x\in S^n$ will be readily checked to be in the intersection of the convex hulls of each of these two sets of matroid bases. A Corollary of Edmonds’ matroid intersection theorem [8] then presents x as a convex combination of rainbow 1-trees:

Theorem 5

Let $x\in S^n$ be $\frac{1}{2}$-integer, and let $\mathcal {P}$ be any partition of the $\frac{1}{2}$-edges into pairs. Then x is in the convex hull of incidence vectors of 1-trees that each contain exactly one edge from each pair in $\mathcal {P}$.

Proof

Let $G_x = (V_n, E_x)$ be the support graph of x. Consider the partition matroid defined on $E_x$ by the partition $\mathcal {P}\cup \{\{e\} : e\in E_x, \hbox { e{ isa}1-edge} \}$. By Lemma 1, x is in the convex hull of incidence vectors of 1-trees in $E_x$; since $x(Q)=1$ for every class Q of the defined partition matroid, it is also in the convex hull of its bases. Thus by [15, Corollary 41.12d], x is in the convex hull of incidence vectors of the common bases of the two matroids.    $\square$

3 Improved Bounds for 1/2-Integer Points

In this section we show that $\frac{10}{7} x$ is a convex combination of incidence vectors of tours for all square points $x\in S^n$, and thus for all $\frac{1}{2}$-integer Boyd-Carr points x as well. We also analyze the possibility of a similar proof for Carr-Vempala points. We begin by stating two properties which we will later prove to be sufficient to guarantee this for any $\frac{1}{2}$-integer vector x in $S^n$:

• (A) The support graph $G_x$ of x has a Hamiltonian cycle H.

• (B) Vector x is a convex combination of incidence vectors of 1-trees of $K_n$, each containing exactly two edges in every cut of $G_x$ consisting of four $\frac{1}{2}$-edges in H.

We will use $\chi ^H$ of (A) as part of the convex combination for $\frac{10}{7} x$, which is globally good, since H has only n edges, but the $\frac{1}{2}$-edges of H have too high a value (equal to 1), contributing too much in the convex combination. To compensate for this, property (B) ensures that x is not only a convex combination of 1-trees, but these 1-trees are even for certain edge cuts $\delta (S)$, allowing us to use a value essentially less than the $\frac{x}{2}=\frac{1}{4}$ for $\frac{1}{2}$ edges in H for the corresponding T-join. The details of how to ensure we still remain feasible for the T-join polyhedron overall will be given in the proof of Theorem 6.

While condition (A) may look at first sight impossibly difficult to meet, Lemma 2 shows that one can count on the bonus of the naturally arising properties: any square point x satisfies property (A), and the additional property stated in this lemma together with the “rainbow 1-tree decomposition” of Theorem 5 will also imply (B) for square points. The reason we care about the somewhat technical property (B) instead of its more natural consequences is future research: in a new situation we may have to use the most general condition.

Lemma 3

Let x be any square point. Then x satisfies both (A) and (B).

Proof

Point x satisfies Property (A) by Lemma 2. Moreover, by the additional statement in this lemma, H contains all the 1-edges in $G_x$: it follows that H contains a perfect matching from each square of $G_x$.

Define $\mathcal {P}$ to be the partition of the set of $\frac{1}{2}$-edges of $G_x$ into pairs whose classes are the perfect matchings of squares. Then by Theorem 5, x is in the convex hull of incidence vectors of 1-trees that contain exactly one edge from each pair $P\in \mathcal {P}$. Property (B) follows, since every cut that contains four $\frac{1}{2}$-edges of H is partitioned by two classes $P_1,P_2\in \mathcal {P}$ by the preceding first paragraph of this proof, and both $P_1$ and $P_2$ are met by exactly one edge of each tree of the just constructed convex combination.    $\square$

Next we prove that properties (A) and (B) are sufficient to guarantee that $\frac{10}{7} x$ is a convex combination of incidence vectors of tours for any $\frac{1}{2}$-integer point of $S^n$. Recall that properties (A) and (B) are more general than what we need for square points; the condition of the theorem we prove does not require that the Hamiltonian cycle for property (A) contains the 1-edges of $G_x$, as Lemma 2 asserts for square points. However, we keep the generality of (A) and (B) to remain open to eventual posterior demands of future research:

Theorem 6

Let $x\in S^n$ be a $\frac{1}{2}$-integer point satisfying properties (A) and (B). Then $\frac{10}{7} x$ is in the convex hull of incidence vectors of tours.

Proof

Let H be the Hamiltonian cycle of (A) and let $G_x=(V_n,E_x)$ be the support graph of x. Let the 1-trees in the convex combination for property (B) be $F_i$, $i = 1, 2,...,k$, and for each tree $F_i$ let $T_{F_i}$ be the set of odd degree nodes in the graph $(V_n,F_i)$. Consider the vector $y\in \mathbb {R}^{E_n}$ defined as follows:

$$\begin{aligned} y_e = {\left\{ \begin{array}{ll} \frac{1}{6} &{} \text {if } x_e=\frac{1}{2} \text { and } e\in H,\\ \frac{1}{3} &{} \text {if } x_e=\frac{1}{2} \text { and } e\notin H,\\ \frac{1}{2} &{} \text {if } x_e=1 \text { and } e\in H,\\ \frac{2}{3} &{} \text {if } x_e=1 \text { and } e\notin H,\\ 0 &{} \text {if } x_e=0. \end{array}\right. } \end{aligned}$$

Claim: Vector y is in the $T_{F_i}$-join polyhedron for $K_n$ for $i=1,\ldots ,k$.

Let C be a $T_{F_i}$-cut in $K_n$ for some $i \in \{1,\ldots ,k\}$.

Case 1: Cut C contains a 1-edge of $G_x$. If C contains another 1-edge then $y(C)\ge 1$, as required. Otherwise it contains exactly one 1-edge. Since $x(C)\ge 2$, and the $\frac{1}{2}$-edges in $G_x$ form edge-disjoint cycles, C contains an even (non-zero) number of $\frac{1}{2}$-edges, thus $|C\cap E_x|$ is odd. Since $|H\,\cap \,C|$ is even and non-zero, at least one edge e of $C\cap E_x$ is not in H. If e is the single 1-edge in C, then $y(C)\ge \frac{2}{3} + \frac{1}{6} + \frac{1}{6} = 1$. If e is a $\frac{1}{2}$-edge, then $y(C)\ge \frac{1}{2} +\frac{1}{3} + \frac{1}{6} = 1$.

Case 2: Cut C does not contain a 1-edge of $G_x$. Again using the facts that $x(C)\ge 2$ and the $\frac{1}{2}$-edges in $G_x$ form edge-disjoint cycles, we have that C contains an even number of $\frac{1}{2}$-edges, and $|C \cap E_x| \ge 4$. If $|C\cap E_x| \ge 6$, then $y(C) \ge 6(\frac{1}{6})=1$. Otherwise we have $|C\cap E_x|=4$ and $|C\cap H| = 2$ or 4. If $|C\cap H|=2$, then $y(C)=2(\frac{1}{6}) + 2(\frac{1}{3})=1$. If $|C\cap H| =4$, then by property (B), tree $F_i$ has exactly two edges in $C \cap E_x$ (and thus in C as well), which means that $|C\cap F_i|$ is even. Thus C is not a $T_{F_i}$-cut, so $y(C) \ge 1$ is not required. This completes the proof of the claim.

Using the claim, it follows that $\chi ^{F_i} + y$ is in the convex hull of incidence vectors of tours for all $i=1,\ldots ,k$, and therefore $x +y$ is in the convex hull of incidence vectors of tours. Now $z:= \frac{1}{7}\chi ^H + \frac{6}{7}(x + y)$ is also in the convex hull of incidence vectors of tours, and $z=\frac{10}{7} x$ is easy to check: indeed, the value of $\chi ^H_e + 6x_e+6y_e$ $(e\in E_x)$ is apparent from the definition of $y_e$ (above the claim): this value is 5 if $x_e=\frac{1}{2}$, and 10 if $x_e=1$.   $\square$

Our main result is an immediate corollary of this theorem:

Theorem 7

Let x be a square point. Then $\frac{10}{7}x$ is in the convex hull of incidence vectors of tours. In particular, this holds if x is a $\frac{1}{2}$-integer Boyd-Carr point.

Proof

By Theorem 6 it is enough to make sure that x satisfies properties (A) and (B), which is exactly the assertion of Lemma 3.    $\square$

We can also show that square points are worst-case with respect to Conjecture 2, in that they have an integrality gap of at least $\frac{4}{3}$. Consider the subclass of square points we call k-donuts, $k\in \mathbb {Z}$, $k\ge 2$, defined as follows: the support graph $G_x=(V_n,E_x)$ consists of k $\frac{1}{2}$-squares arranged in a circular donut fashion, where the squares are joined by 1-paths, each of length k. In other words, $G_x$ consists of an outer cycle $C_\mathrm{out}$ and inner cycle $C_\mathrm{in}$, both consisting of k paths of $k+1$ edges, the last of which is a $\frac{1}{2}$-edge, and the others are 1-edges. There are 2k $\frac{1}{2}$-edges between the two cycles so that the $\frac{1}{2}$-edges form squares. In Fig. 2 the support graph of a 4-donut is shown. In the figure, dashed edges represent $\frac{1}{2}$-edges and solid edges represent 1-edges.

We define the cost of each edge in $E_x$ to be 1, except for the $\frac{1}{2}$-edges in each of $C_\mathrm{out}$ and $C_\mathrm{in}$ which are defined to have cost k (see the figure, where only edges of cost k are labelled). The costs of other edges of $K_n$ are defined by the metric closure (cost of shortest paths in $G_x$). For these defined costs $c^{(k)}$, we have $OPT(c^{(k)})= 4k^2 - 2k + 2$ and $LP(c^{(k)})=3k^2 + k$, thus $\lim _{k\rightarrow \infty }\frac{OPT(c^{(k)})}{LP(c^{(k)})}=\frac{4}{3}$. Along with Theorem 7, this gives the following:

Corollary 1

The integrality gap for square points lies between $\frac{4}{3}$ and $\frac{10}{7}$.

Fig. 2.

Graph $G_x$ for a k-donut x, k=4.

We finally discuss the structure of Carr-Vempala points.

Note that for the Boyd-Carr points that have been our focus, the transformation used from general vertices $x\in S^n$ to these Boyd-Carr points does not completely preserve the denominators. In particular, $\frac{1}{2}$-integer vertices of $S^n$ get transformed into Boyd-Carr points $x^*$ with $x^*_e$ values in $\{1, \frac{1}{2}, \frac{3}{4}, \frac{1}{4}, 0\}$. However, for the Carr-Vempala points, general $\frac{1}{2}$-integer vertices of $S^n$ lead to $\frac{1}{2}$-integer Carr-Vempala vertices. In fact we have the following theorem which, if Conjecture 3 is true, would provide a nice approach for proving Conjecture 2, since it is given for free that Carr-Vempala vertices satisfy property (A):

Theorem 8

If $\rho x$ is in the convex hull of incidence vetors of tours for each $\frac{1}{2}$-integer Carr-Vempala point $x\in S^n$, then $\rho x$ is in the convex hull of incidence vectors of tours for every $\frac{1}{2}$-integer point $x \in S^n$.

In light of these results and conjectures it seems worthwhile to study further “fundamental classes” and the role of $\frac{1}{2}$-integer points.