Keywords

1 Introduction

Compared with traditional single rotor UAV, the most significant advantage of the quadrotor unmanned aerial vehicles (QUAV) is that the latter has better stability, more compact structure and larger load, etc.. So the QUAV pertains to a wide area of possible applications including patrolling for forest fires, traffic monitoring, surveillance rescue, etc., and as a remarkable platform for the UAV, the QUAV has been attracting numerous research [1,2,3,4,5,6].

The QUAV is a complex nonlinear strongly coupled system with more than one input and output, and thereby leading to great challenges in controller design and synthesis. In [7], PID control scheme is used to achieve the trajectory tracking control. However, this control method is classical linear control scheme, which only work better when the QUAV is near hovering state. Backstepping control scheme has an extensive application in controlling the QUAV in recent years. In [8], the QUAV dynamic system has been divided into two subsystems, i.e., translational subsystem and rotational subsystem and two subcontrollers have been designed. However, general backstepping control schemes need accurate model parameters and is not robust to model uncertainties and external disturbances, for this reason, adaptive integral backstepping control scheme [9] has been applied in the QUAV, which Only suitable for the model uncertainty and external disturbances are slow-varying or constant. Sliding mode control is a powerful control method with characteristics of simple and robust [10]. Combining with adaptive control strategy or observer [11], this kind control methods have widespread used various systems, however, chattering phenomenon is inevitable for the continuous switching logic. Adaptive fuzzy backstepping control has been used to the trajectory tracking control for the QUAV in [12], in which the fuzzy system is employed to approximate directly a model using backstepping techniques. For the reason of underactuation, the virtual controller is designed in most control schemes for the QUAV, while, the derivative of the virtual controller will be complex. In this context, we focus on a QUAV with the lumped unknown nonlinearity including system uncertainties and external disturbances, and a filtered sliding mode trajectory tracking control scheme based on fuzzy uncertainty observer (FUO) for the QUAV is proposed.

2 QUAV Dynamics and Problem Formulation

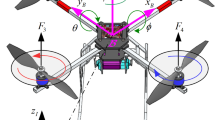
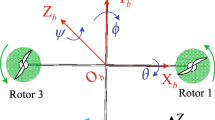
As shown in Fig. 1, defining the earth-fixed coordinate \(OX_0Y_0Z_0\) and the body-fixed coordinate \(O'XYZ\) which are respectively considered with the origin coinciding to the starting point and the gravity center of the QUAV. Vectors (x, y, z) and \((\phi , \theta , \psi )\) are respectively denote the positions of the QUAV in earth-fixed coordinate \(OX_0Y_0Z_0\) and the Euler angles in body-fixed coordinate \(O'XYZ\), in which \(\phi \) refers as to roll angle, \(\theta \) refers as to pitch angle and \(\psi \) refers as to yaw angle.

Fig. 1.
figure 1

The configuration of a QUAV.

Full size image
Fig. 2.
figure 2

The overall control diagram.

Full size image

The position dynamics can be described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\pmb {\eta }}_{11} = \pmb {\eta }_{12} \\ \dot{\pmb {\eta }}_{12} = \pmb {f}_1\left( \pmb {\eta }_{12}\right) + \pmb {u}_1\left( \pmb {\eta }_2,\tau \right) + \pmb {d}_1\left( \pmb {\eta }_{11},\pmb {\eta }_{12},t\right) \end{array}\right. } \end{aligned}$$
(1)

with the lumped model uncertainties and/or external disturbances \(\pmb {d}_1=[d_{11},d_{12},d_{13}]^T\), \(\pmb {f}_1 = [D_x {\dot{x}}^2, D_y {\dot{y}}^2, D_z {\dot{z}}^2-g]^T\) and

$$\begin{aligned} \pmb {u}_1\left( \pmb {\eta }_2,\tau \right)&= \frac{\tau }{m} \left[ {\begin{array}{ccc} C_{\phi } S_{\theta } C_{\psi } + S_{\phi } S_{\psi } \\ C_{\phi } S_{\theta } S_{\psi } - S_{\phi } C_{\psi } \\ C_{\phi } C_{\theta } \end{array}} \right] \end{aligned}$$
(2)

where \(\pmb {\eta }_{11}=[x,y,z]^T\) and \(\pmb {\eta }_{12}=[{\dot{x}},{\dot{y}},{\dot{z}}]^T\) are vectors of the positions and linear velocities in the earth-fixed frame, respectively, m is the mass of the QUAV, g is the acceleration of the gravity, \(C_*\) and \(S_*\) are the functions \(\mathrm {cos}(*)\) and \(\mathrm {sin}(*)\), respectively, \(\tau \) is the total thrust.

The vector of Euler angles \(\pmb {\eta }_2=[\phi ,\theta ,\psi ]^T\) is governed by

$$\begin{aligned} \dot{\pmb {\eta }}_2 = \pmb {g}_2(\pmb {\eta }_2)\pmb {u}_2(\pmb {\eta }_3) + \pmb {d}_2(\pmb {\eta }_2,t) \end{aligned}$$
(3)

with the lumped model uncertainties and/or external disturbances \(\pmb {d}_2=[d_{21},d_{22},d_{23}]^T\), and

$$\begin{aligned} \pmb {g}_2(\pmb {\eta }_2)&= \left[ \begin{array}{ccc} 1 &{} S_{\phi } T_{\theta } &{} C_{\phi } T_{\theta }\\ 0 &{} C_{\phi } &{} - S_{\phi }\\ 0 &{} \frac{S_{\phi }}{C_{\theta }} &{} \frac{C_{\phi }}{C_{\theta }} \end{array} \right] \end{aligned}$$
(4)
$$\begin{aligned} \pmb {u}_2(\pmb {\eta }_3)&= \pmb {\eta }_3 \end{aligned}$$
(5)

where \(T_*\) denotes the function \(\mathrm {tan}(*)\), \(\pmb {\eta }_3=[p,q,r]^T\) is the angular velocity vector in body-fixed coordinate given by the following dynamics:

$$\begin{aligned} \dot{\pmb {\eta }}_3 = \pmb {f}_3(\pmb {\eta }_3) + \pmb {g}_3 \pmb {u}_3 + \pmb {d}_3(\pmb {\eta }_3,t) \end{aligned}$$
(6)

with the diagonal matrix \(\pmb {g}_3=\mathrm {diag} \left( 1/J_x,1/J_y,1/J_z\right) \) where \(J_i (i=x,y,z)\) is the moment of inertia with respect to each axis, \(\pmb {d}_3=[d_{31},d_{32},d_{33}]^T\) include unmodeled dynamics and/or external disturbances, and \(\pmb {f}_3({\pmb {\eta }_3}) = [\frac{J_y - J_z}{J_x} qr, \frac{J_z - J_x}{J_y} pr, \frac{J_x - J_y}{J_z} pq]^T\), where \(\pmb {u}_3 = [u_{31},u_{32},u_{33}]^T\) is the control input and the final control input vector of the QUAV system is \(\pmb {u} = [\tau ,\pmb {u}_3^T]^T\).

The control objective in this study is to design filtered sliding mode controller of the QUAV with FUO and achieve the trajectory tracking control \((x \rightarrow x_d, y \rightarrow y_d, z \rightarrow z_d, \psi \rightarrow \psi _d)\) in presence of the external disturbances and system uncertainties. Before ending this section, the following assumption is introduced:

Assumption 1

The desired trajectory and its time derivatives are bounded.

3 Filtered Sliding Mode Controller Design

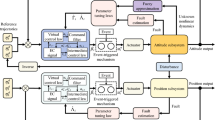
In this section, three subcontrollers will be designed. The overall control diagram is as shown in Fig. 2.

3.1 Position Controller

Given a reference trajectory \(\pmb {\eta }_{11d}:=[x_d,y_d,z_d]^T\), combining with position dynamics (1), we design sliding surfaces as follows:

$$\begin{aligned} \pmb {s}_{11}(t)&= \pmb {e}_{11}(t) + \pmb {k}_{11} \int _0^t \pmb {e}_{11}(\tau ) d \tau \end{aligned}$$
(7)
$$\begin{aligned} \pmb {s}_{12}(t)&= \pmb {e}_{12}(t) + \pmb {k}_{12} \int _0^t \pmb {e}_{12}(\tau ) d \tau \end{aligned}$$
(8)

where \(\pmb {k}_{11}=\mathrm {diag}(k_{111},k_{112},k_{113})>0\), \(\pmb {k}_{12}=\mathrm {diag}(k_{121},k_{122},k_{123})>0\), \(\pmb {e}_{11} = \pmb {\eta }_{11} - \pmb {\eta }_{11d}\), \( \pmb {e}_{12} = \pmb {\eta }_{12} - \bar{\pmb {\eta }}_{12d}\), and \(\bar{\pmb {\eta }}_{12d}\) is the filtered output of the virtual control signal \(\pmb {\eta }_{12d}\) given by

$$\begin{aligned} \epsilon _{1} \dot{\bar{\pmb {\eta }}}_{12d} + \bar{\pmb {\eta }}_{12d} = \pmb {\eta }_{12d} \end{aligned}$$
(9)

here, \(\epsilon _1 > 0 \) is an user-defined filtering time constant and let \(\pmb {y}_{1} = \bar{\pmb {\eta }}_{12d} - \pmb {\eta }_{12d}\).

In this context, the virtual control signal \(\pmb {\eta }_{12d}\) can be selected as follows:

$$\begin{aligned} \pmb {\eta }_{12d} = - \pmb {p}_{11}\pmb {s}_{11} + \dot{\pmb {\eta }}_{11d} - \pmb {k}_{11}\pmb {e}_{11} - \pmb {e}_{12} \end{aligned}$$
(10)

where \(\pmb {p}_{11} = \mathrm {diag}(p_{111},p_{112},p_{113})>0\) and a desired position control law for sub-system (1) can be designed as follows:

$$\begin{aligned} \pmb {u}_1 =&- \pmb {p}_{12} \pmb {s}_{12} - \pmb {f}_1(\pmb {\eta } _{12}) + \dot{\bar{\pmb {\eta }}} _{12d} - \pmb {k}_{12}\pmb {e}_{12} - \hat{\pmb {d}}_1 \end{aligned}$$
(11)

with the FUO given by

$$\begin{aligned} \hat{\pmb {d}}_1(\pmb {\omega }_1\mid \hat{\pmb {\vartheta }}_1) = \hat{\pmb {\vartheta }}_1^T \pmb {\xi }_1(\pmb {\omega }_1) \end{aligned}$$
(12)

Choosing the parameter matrix update rule as

$$\begin{aligned} \dot{\hat{\pmb {\vartheta }}}_1 = -r_{11}\hat{\pmb {\vartheta }}_1 + r_{12}\pmb {\xi }_1(\pmb {\omega }_1)(\pmb {s}_{12} + \pmb {\varepsilon }_1)^T \end{aligned}$$
(13)

where \(r_{11} > 0\) and \(r_{12} > 0\) are user-defined positive definite parameters, \(\pmb {\omega }_1 = [\pmb {\eta }_{11}^T,\pmb {\eta }_{12}^T]^T\) is the input vector of the fuzzy system, \(\pmb {\varepsilon }_1 = \pmb {\eta }_{12} - \pmb {\upsilon }_1\) is the observation error vector with

$$\begin{aligned} \dot{\pmb {\upsilon }}_1 =&-r_{13}\pmb {\upsilon }_1 + \pmb {f}_1(\pmb {\eta }_{12}) + \pmb {u}_1 + \hat{\pmb {d}}_1(\pmb {\omega }_1|\hat{\pmb {\vartheta }}_1) + r_{13}\pmb {\eta }_{12} \end{aligned}$$
(14)

where \(r_{13} > 0\) is user-defined positive definite parameter.

3.2 Euler Angle Controller

Substituting the control law (11) into the input nonlinearity (2), we can obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \tau = m \Vert \pmb {u}_1\Vert \\ \phi _d = \arcsin \left( \frac{m}{\tau } (S_{\psi _d} u_{11} - C_{\psi _d} u_{12})\right) \\ \theta _d = \arcsin \Big ( \frac{ \frac{m}{\tau } u_{11} - S_{\psi _d} S_{\phi _d} }{ C_{\psi _d} C_{\phi _d}}\Big ) \end{array}\right. } \end{aligned}$$
(15)

Let \(\pmb {\eta }_{2d}:=[\phi _d,\theta _d,\psi _d]^T\) and \(\bar{\pmb {\eta }}_{2d}:=[{\bar{\phi }}_d,{\bar{\theta }}_d,{\bar{\psi }}_d]^T\) where \(\bar{\pmb {\eta }}_{2d}\) is the filtered output of \(\pmb {\eta }_{2d}\) given by

$$\begin{aligned} \epsilon _2\dot{\bar{\pmb {\eta }}}_{2d} + \bar{\pmb {\eta }}_{2d} = \pmb {\eta }_{2d} \end{aligned}$$
(16)

here, \(\epsilon _2 > 0 \) is an user-defined filtering time constant and let \(\pmb {y}_{2} = \bar{\pmb {\eta }}_{2d} - \pmb {\eta }_{2d}\).

Combining with Euler angles dynamics (3), we design a sliding surface as follows:

$$\begin{aligned} \pmb {s}_2 (t) = \pmb {e}_2 (t) + \pmb {k}_2 \int _0^t \pmb {e}_2 (\tau ) d\tau \end{aligned}$$
(17)

where \(\pmb {e}_{2} = \pmb {\eta }_{2} - \bar{\pmb {\eta }}_{2d}\), \(\pmb {k}_2 = \mathrm {diag}(k_{21},k_{22},k_{23})>0\).

In this context, a desired Euler angles control law for sub-system (3) can be designed as follows:

$$\begin{aligned} \pmb {u}_2 = \pmb {g}_2^{-1}(\pmb {\eta }_2 ) [&\dot{\bar{\pmb {\eta }}}_{2d} - \pmb {k}_2 \pmb {e}_2 - \pmb {p}_2 \pmb {s}_2 + \pmb {y}_2 - \hat{\pmb {d}}_2 ] \end{aligned}$$
(18)

with the FUO given by

$$\begin{aligned} \hat{\pmb {d}}_2(\pmb {\omega }_2\mid \hat{\pmb {\vartheta }}_2) = \hat{\pmb {\vartheta }}_2^T \pmb {\xi }_2(\pmb {\omega }_2) \end{aligned}$$
(19)

Choosing the parameter matrix update rule as

$$\begin{aligned} \dot{\hat{\pmb {\vartheta }}}_2 = -r_{21}\hat{\pmb {\vartheta }}_2 + r_{22}\pmb {\xi }_2(\pmb {\omega }_2)(\pmb {s}_{2} + \pmb {\varepsilon }_2)^T \end{aligned}$$
(20)

where \(\pmb {p}_2 = \mathrm {diag}(p_{21},p_{22},p_{23})>0\), \(r_{21} > 0\) and \(r_{22} > 0\) are user-defined positive definite parameters, \(\pmb {\omega }_2 = [\pmb {\eta }_{2}^T, \dot{\pmb {\eta }}_2^T]^T\) is the input vector of the fuzzy system, \(\pmb {\varepsilon }_2 = \pmb {\eta }_{2} - \pmb {\upsilon }_2\) is the observation error vector with

$$\begin{aligned} \dot{\pmb {\upsilon }}_2 =&-r_{23}\pmb {\upsilon }_2 + \pmb {g}_2(\pmb {\eta }_{2})\pmb {u}_2 + \hat{\pmb {d}}_2(\pmb {\omega }_2|\hat{\pmb {\vartheta }}_2) + r_{23}\pmb {\eta }_{2} \end{aligned}$$
(21)

where \(r_{23} > 0\) is user-defined positive definite parameter.

3.3 Angular Velocity Controller

Let \(\pmb {\eta }_{3d}: =[p_d,q_d,r_d]^T= \pmb {u}_2\), together with angular velocity dynamics (6), we design a sliding surface as follows:

$$\begin{aligned} \pmb {s}_3 (t) = \pmb {e}_3 (t) + \pmb {k}_3 \int _0^t \pmb {e}_3 (\tau ) d\tau \end{aligned}$$
(22)

where \(\pmb {e}_3 = \pmb {\eta }_3 - \bar{\pmb {\eta }}_{3d}\), \(\pmb {k}_3 = \mathrm {diag}(k_{31},k_{32},k_{33})>0\) and \(\bar{\pmb {\eta }}_{3d}:=[{\bar{p}}_d,{\bar{q}}_d,{\bar{r}}_d]^T\) is the filtered output of \(\pmb {\eta }_{3d}\) given by

$$\begin{aligned} \epsilon _3\dot{\bar{\pmb {\eta }}}_{3d} + \bar{\pmb {\eta }}_{3d} = \pmb {\eta }_{3d} \end{aligned}$$
(23)

here, \(\epsilon _3 > 0 \) is an user-defined filtering time constant and let \(\pmb {y}_{3} = \bar{\pmb {\eta }}_{3d} - \pmb {\eta }_{3d}\).

Accordingly, an nominal angular velocity control law for sub-system (6) can be governed as follows:

$$\begin{aligned} \pmb {u}_3 = \pmb {g}_3^{-1}[\dot{\bar{\pmb {\eta }}}_{3d} - \pmb {f}_3 (\pmb {\eta }_3) - \pmb {k}_3 \pmb {e}_3 - \pmb {p}_3 \pmb {s}_3 + \pmb {y}_3 - \hat{\pmb {d}}_3] \end{aligned}$$
(24)

with the FUO given by

$$\begin{aligned} \hat{\pmb {d}}_3(\pmb {\omega }_3\mid \hat{\pmb {\vartheta }}_3) = \hat{\pmb {\vartheta }}_3^T \pmb {\xi }_3(\pmb {\omega }_3) \end{aligned}$$
(25)

Choosing the parameter matrix update rule as

$$\begin{aligned} \dot{\hat{\pmb {\vartheta }}}_3 = -r_{31}\hat{\pmb {\vartheta }}_3 + r_{32}\pmb {\xi }_3(\pmb {\omega }_3)(\pmb {s}_{3} + \pmb {\varepsilon }_3)^T \end{aligned}$$
(26)

where \(\pmb {p}_3 = \mathrm {diag}(p_{31},p_{32},p_{33})>0\), \(r_{31} > 0\) and \(r_{32} > 0\) are user-defined positive definite parameters, \(\pmb {\omega }_3 = [\pmb {\eta }_{3}^T, \dot{\pmb {\eta }}_3^T]^T\) is the input vector of the fuzzy system, \(\pmb {\varepsilon }_3 = \pmb {\eta }_{3} - \pmb {\upsilon }_3\) is the observation error vector with

$$\begin{aligned} \dot{\pmb {\upsilon }}_3 =&-r_{33}\pmb {\upsilon }_3 + \pmb {f}_3(\pmb {\eta }_3) + \pmb {g}_3\pmb {u}_3 + \hat{\pmb {d}}_3(\pmb {\omega }_3|\hat{\pmb {\vartheta }}_3) + r_{33}\pmb {\eta }_3 \end{aligned}$$
(27)

where \(r_{33} > 0\) is user-defined positive definite parameter.

Then, the final control law is

$$\begin{aligned} \pmb {u}: = \left[ \begin{array}{c} \tau \\ \pmb {u}_3 \end{array}\right] = \left[ \begin{array}{c} m \Vert \pmb {u}_1 \Vert \\ \pmb {u}_3 \end{array}\right] \end{aligned}$$
(28)

4 Stability Analysis

Theorem 1

Consider an uncertain QUAV system (1)–(3)–(6), together with control scheme (11), (18), (24) with FUO given by (12), (19), (25), all system states and signals and all tracking errors are globally uniformly ultimately bounded.

Proof

Together with system (14), (21) and (27), we have

$$\begin{aligned} \dot{\pmb {\varepsilon }}_i + r_{i3}\pmb {\varepsilon }_i = \pmb {d}_i - \hat{\pmb {d}}_i(\pmb {\omega }_i|\hat{\pmb {\vartheta }}_i) \end{aligned}$$
(29)

where \(i=1,2,3\).

Define the optimal parameter as

$$\begin{aligned} \pmb {\vartheta } _{i}^* = \arg \mathop {\min }\limits _{{{\hat{\pmb {\vartheta }}}_{i}} \in {M_{{\pmb {\vartheta } _{i}}}}} (\mathop {\sup }\limits _{{\pmb {\omega } _{i}} \in {M_{{\pmb {\omega } _{i}}}}} \Vert {{\pmb {d}_{i}} - {{\hat{\pmb {d}}}_{i}}} \Vert ) \end{aligned}$$
(30)

where \(M_{{\pmb {\vartheta } _{i}}}\) and \(M_{{\pmb {\omega } _{i}}}\) are bounded sets.

Then we have

$$\begin{aligned} \pmb {d}_{i}=\hat{\pmb {d}}_{i}(\pmb {\omega }_{i}|{\pmb {\vartheta }}^*_{i}) +\pmb {\zeta }_{i}(\pmb {\omega }_{i}) \end{aligned}$$
(31)

where \(\pmb {\zeta }_i(\pmb {\omega }_i)\) is reconstruction error vector and \(\Vert \pmb {\zeta }_i(\pmb {\omega }_i)\Vert <{\bar{\zeta }}_i\), \({\bar{\zeta }}_i > 0\). Let \(\tilde{\pmb {\vartheta }}_{i}=\pmb {\vartheta }^*_{i}- \hat{\pmb {\vartheta }}_{i}\), together with system (29), we can obtain

$$\begin{aligned} \dot{\pmb {\varepsilon }}_{i}+r_{i3}\pmb {\varepsilon }_{i}= \tilde{\pmb {\vartheta }}_{i}^T\pmb {\xi }_{i}(\pmb {\omega }_{i})+ \pmb {\zeta }_{i}(\pmb {\omega }_{i}) \end{aligned}$$
(32)

Combining with system (12), (19), (25), (31), the following equation holds

$$\begin{aligned} \pmb {d}_i - \hat{\pmb {d}}_i = \tilde{\pmb {\vartheta }}_i^T\pmb {\xi }_i(\pmb {\omega }_i) + \pmb {\zeta }_i(\pmb {\omega }_i) \quad i=1,\ldots ,3 \end{aligned}$$
(33)

then together with system (8), (17), (22) and (33), we can obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\pmb {s}}_{12} = - \pmb {p}_{12}\pmb {s}_{12} + \tilde{\pmb {\vartheta }}_1^T\pmb {\xi }_1(\pmb {\omega }_1) + \pmb {\zeta }_1(\pmb {\omega }_1) \\ \dot{\pmb {s}}_i = -\pmb {p}_i\pmb {s}_i + \pmb {y}_i + \tilde{\pmb {\vartheta }}_i^T\pmb {\xi }_i(\pmb {\omega }_i) + \pmb {\zeta }_i(\pmb {\omega }_i) &{}i = 2,3 \end{array}\right. } \end{aligned}$$
(34)

Choosing the following Lyapunov function

$$\begin{aligned} V = \frac{1}{2}\bigg [&\sum \limits _{i=1}^3\bigg ( \pmb {y}_i^T\pmb {y}_i + \pmb {\varepsilon }_i^T \pmb {\varepsilon }_i +\frac{\mathrm {tr}(\tilde{\pmb {\vartheta }}_i^T \tilde{\pmb {\vartheta }}_i)}{r_{i2}}\bigg ) + \pmb {s}_{11}^T\pmb {s}_{11} + \pmb {s}_{12}^T\pmb {s}_{12} + \pmb {s}_{2}^T\pmb {s}_{2} + \pmb {s}_{3}^T\pmb {s}_{3} \bigg ] \end{aligned}$$
(35)

Together with system (32) and (34), the time derivative of (35) can be given as

$$\begin{aligned} {\dot{V}} =&\sum \limits _{i=2}^3 \bigg ( -\pmb {s}_i^T\pmb {p}_i\pmb {s}_i + \pmb {s}_i^T\pmb {y}_i - r_{i3}\pmb {\varepsilon }_i^T\pmb {\varepsilon }_i + (\pmb {s}_i^T + \pmb {\varepsilon }_i^T)\pmb {\zeta }_i(\pmb {\omega }_i) + \pmb {y}_i^T\dot{\pmb {y}}_i\bigg ) - \pmb {s}_{11}^T\pmb {p}_{11}\pmb {s}_{11} \nonumber \\&+ \pmb {s}_{11}^T\pmb {y}_1 - \pmb {s}_{12}^T\pmb {p}_{12}\pmb {s}_{12} - r_{13}\pmb {\varepsilon }_1^T\pmb {\varepsilon }_1 + (\pmb {s}_{12}^T + \pmb {\varepsilon }_1^T)\pmb {\zeta }_1(\pmb {\omega }_1) + \pmb {y}_{1}^T\dot{\pmb {y}}_{1} \nonumber \\&+ \underbrace{ \sum \limits _{i=2}^3 \bigg ( (\pmb {s}_i^T + \pmb {\varepsilon }_i^T)\tilde{\pmb {\vartheta }}_i^T\pmb {\xi }_i(\pmb {\omega }_i) - \frac{\mathrm {tr}(\tilde{\pmb {\vartheta }}_i^T\dot{\hat{\pmb {\vartheta }}}_i)}{r_{i2}} \bigg ) + (\pmb {s}_{12}^T + \pmb {\varepsilon }_1^T)\tilde{\pmb {\vartheta }}_1^T\pmb {\xi }_1(\pmb {\omega }_1) - \frac{\mathrm {tr}(\tilde{\pmb {\vartheta }}_1^T\dot{\hat{\pmb {\vartheta }}}_1)}{r_{12}}}_{M} \end{aligned}$$
(36)

together with systems (13), (20) and (26), we can obtain

$$\begin{aligned} M =&\sum \limits _{i=2}^3 \bigg (\sum \limits _{j=1}^3(\tilde{\pmb {\vartheta }}_{ij}^T((s_{ij} + \varepsilon _{ij})\pmb {\xi }_i(\pmb {\omega }_i) - \frac{\dot{\hat{\pmb {\vartheta }}}_{ij}}{r_{i2}}))\bigg ) + \sum \limits _{j=1}^3(\tilde{\pmb {\vartheta }}_{1j}^T((s_{12j} + \varepsilon _{1j})\pmb {\xi }_1(\pmb {\omega }_1) - \frac{\dot{\hat{\pmb {\vartheta }}}_{1j}}{r_{12}})) \nonumber \\ =&\sum \limits _{i=1}^3\frac{r_{i1}}{r_{i2}}\mathrm {tr}(\tilde{\pmb {\vartheta }}_{i}^T \hat{\pmb {\vartheta }}_{i}) \end{aligned}$$
(37)

where \(\pmb {s}_{12} = [s_{121}, s_{122}, s_{123}]^T\), \(\pmb {s}_{i} = [s_{i1}, s_{i2}, s_{i3}]^T\), \(\pmb {\varepsilon }_i = [\varepsilon _{i1}, \varepsilon _{i2}, \varepsilon _{i3}]^T\), \(\tilde{\pmb {\vartheta }}_i = [\tilde{\pmb {\vartheta }}_{i1}, \tilde{\pmb {\vartheta }}_{i2}, \tilde{\pmb {\vartheta }}_{i3}]\) and \(\dot{\hat{\pmb {\vartheta }}}_i = [\dot{\hat{\pmb {\vartheta }}}_{i1}, \dot{\hat{\pmb {\vartheta }}}_{i2}, \dot{\hat{\pmb {\vartheta }}}_{i3}]\) with \(i=1,2,3\).

Together with systems (9)–(10) and Assumption 1, we can obtain

$$\begin{aligned} \bigg \Vert \dot{\pmb {y}}_1 + \frac{\pmb {y}_1}{\epsilon _{1}} \bigg \Vert \le z_1(\dot{\pmb {s}}_{11},\ddot{\bar{\pmb {\chi }}}_{11d}, \dot{\pmb {e}}_{11},\dot{\pmb {e}}_{12}) \end{aligned}$$
(38)

where \(z_1\) is continuous bounded function. Then, we have

$$\begin{aligned} \pmb {y}_1^T\dot{\pmb {y}}_1 \le -\frac{\pmb {y}_1^T\pmb {y}_1}{\epsilon _{1}} + \frac{1}{2}\pmb {y}_1^T\pmb {y}_1 + \frac{1}{2}z_1^2 \end{aligned}$$
(39)

Similarly, there exists continuous bounded function \(z_2(\cdot )\) and \(z_3(\cdot )\), such that

$$\begin{aligned} \pmb {y}_i^T\dot{\pmb {y}}_i \le -\frac{\pmb {y}_i^T\pmb {y}_i}{\epsilon _{i}} + \frac{1}{2}\pmb {y}_i^T\pmb {y}_i + \frac{1}{2}z_i^2, \;i=2,3 \end{aligned}$$
(40)

In addition, using the Young’s inequality, we have

$$\begin{aligned} \sum \limits _{i=1}^3\bigg (\frac{r_{i1}}{r_{i2}}\mathrm {tr}(\tilde{\pmb {\vartheta }}_i^T \hat{\pmb {\vartheta }}_i)\bigg ) \le \sum \limits _{i=1}^3\bigg (&\frac{r_{i1}}{2r_{i2}}\mathrm {tr}(\pmb {\vartheta }_i^{*T}\pmb {\vartheta }_i^*) - \frac{r_{i1}}{2r_{i2}}\mathrm {tr}(\tilde{\pmb {\vartheta }}_i^T\tilde{\pmb {\vartheta }}_i)\bigg ) \end{aligned}$$
(41)

Substituting system (37), (39), (40) and (41) into system (36), it is easy to obtain

$$\begin{aligned} {\dot{V}} \le&\sum \limits _{i=2}^3 \bigg (-\pmb {s}_i^T(\pmb {p}_i - \pmb {I})\pmb {s}_i - \bigg (\frac{1}{\epsilon _i} - 1\bigg )\pmb {y}_i^T\pmb {y}_i - \bigg (r_{i3} - \frac{1}{2} \bigg )\pmb {\varepsilon }_i^T\pmb {\varepsilon }_i - \frac{r_{i1}}{2r_{i2}}\mathrm {tr}(\tilde{\pmb {\vartheta }}_i^T\tilde{\pmb {\vartheta }}_i) \bigg ) \nonumber \\&- \pmb {s}_{11}^T\bigg (\pmb {p}_{11} - \frac{\pmb {I}}{2}\bigg )\pmb {s}_{11} - \pmb {s}_{12}^T\bigg (\pmb {p}_{12} - \frac{\pmb {I}}{2}\bigg )\pmb {s}_{12} - \bigg (r_{13} - \frac{1}{2}\bigg )\pmb {\varepsilon }_1^T\pmb {\varepsilon }_1 - \bigg (\frac{1}{\epsilon _1} - 1\bigg )\pmb {y}_1^T\pmb {y}_1 \nonumber \\&- \frac{r_{11}}{2r_{12}}\mathrm {tr}(\tilde{\pmb {\vartheta }}_1^T\tilde{\pmb {\vartheta }}_1) +\sum \limits _{i=1}^3\bigg ( {\bar{\zeta }}_i^2 + \frac{r_{i1}}{2r_{i2}}\mathrm {tr}(\pmb {\vartheta }_i^{*T}\pmb {\vartheta }_i^*) + \frac{{\bar{z}}_i^2}{2}\bigg ) \end{aligned}$$
(42)

where \({\bar{z}}_i(t)\) is the upper bound value of \(z_i(t)\).

Selecting the following design parameters

$$\begin{aligned} \pmb {p}_j&\ge \frac{2 + \alpha }{2}\pmb {I}, \frac{1}{\epsilon _i}\ge 1+\frac{\alpha }{2},\ \pmb {p}_{11}\ge \frac{1 + \alpha }{2}\pmb {I},\ \pmb {p}_{12}\ge \frac{ 1 + \alpha }{2}\pmb {I},\ r_{i3} \ge \frac{1 + \alpha }{2}, \frac{r_{i1}}{r_{i2}} \ge \alpha \end{aligned}$$

with \(j=2,3\) and \(i=1,\ldots ,3\), we have

$$\begin{aligned} {\dot{V}}\le&- \alpha V + C \end{aligned}$$
(43)

with

$$\begin{aligned} C = \sum \limits _{i=1}^3\bigg ( {\bar{\zeta }}_i^2 + \frac{r_{i1}}{2r_{i2}}\mathrm {tr}(\pmb {\vartheta }_i^{*T}\pmb {\vartheta }_i^*) + \frac{{\bar{z}}_i^2}{2}\bigg ) \end{aligned}$$
(44)

Together with the system (35) and (42), the following inequality holds

$$\begin{aligned} 0\le V(t) \le V(0)e^{-\alpha t} + (1- e^{-\alpha t}) \frac{C}{\alpha } < \infty \end{aligned}$$
(45)

It is obvious that the function V(t) is bounded and together with system (35), we can find that the trajectory error \(\pmb {e}_{11}\) and the other error signals are uniformly ultimately bounded.

5 Simulation Studies

In this section, the effectiveness of the proposed control scheme for the QUAV is evaluated. The lumped uncertainties and/or external disturbances are given by \(\pmb {d}_i(t) = 3[\sin t, \cos t, \sin t]^T + 0.1\pmb {\eta }_i\), where \(\pmb {\eta }_1 = \pmb {\eta }_{11} + \pmb {\eta }_{12}\), \(i=1, 2, 3\).

Fig. 3.
figure 3

States of x, y, z and \(\psi \).

Full size image
Fig. 4.
figure 4

Unknown nonlinearities.

Full size image

The reference tracking trajectory is given as \([x_d, y_d, z_d, \psi _d] = [-2\sin t/2, 2\cos t/2, 2 \sin t + 3, \sin t]\) and the initial conditions of the QUAV are set as follows: \(x(0) = 2\), \(y(0) = -0.5\), \(z(0) = 2\), \(\phi (0) = 1\).

Figure 3 shows the tracking of three positions and the yaw, where FSMC denotes the proposed filtered sliding mode control scheme and SMC denotes the traditional sliding mode control scheme. From Fig. 3 we can find that both the proposed control scheme and the SMC scheme are able to robustly stabilize the QUAV and make it track the desired trajectory, while it is obvious that the proposed control scheme has faster response and higher accuracy. Figure 4 shows the estimate state of the FUO for the lumped unknown nonlinearities including system uncertainties and external disturbances on the trajectory, i.e., x, y, z and the yaw \(\psi \), from which we can see, although the unknown lumped nonlinearities continuous change along with the time, FUO can estimate the unknown nonlinearities well. In summary, we can conclude that the proposed tracking control approach can achieve remarkable performance in terms of tracking accuracy and disturbance rejection.

6 Conclusion

In this paper, a filtered sliding mode control scheme based on FUO for trajectory tracking of a QUAV has been proposed. To be specific, three cascaded sub-controllers are designed by incorporating underactuation constraints. First-order filters are employed to reconstruct sliding mode control signals together with their first derivatives, and thereby decoupling the iterative design within the QUAV tracking control scheme. Furthermore, FUOs have been designed to estimate the lumped unknown nonlinearities. By the Lyapunov approach, we have proven that all system states and signals and tracking errors are globally uniformly ultimately bounded. Simulation studies have demonstrated the effectiveness and superiority of the proposed tracking control scheme.