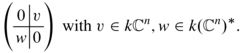Abstract
Let \(\mathfrak{g}\) be a complex reductive Lie algebra and V the underlying vector space of a finite-dimensional representation of \(\mathfrak{g}\). Then one can consider a new Lie algebra \(\mathfrak{q} = \mathfrak{g}\ltimes V\), which is a semi-direct product of \(\mathfrak{g}\) and an Abelian ideal V. We outline several results on the algebra \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) of symmetric invariants of \(\mathfrak{q}\) and describe all semi-direct products related to the defining representation of \(\mathfrak{s}\mathfrak{l}_{n}\) with \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) being a free algebra.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Let Q be a connected complex algebraic group. Set \(\mathfrak{q} =\mathop{ \mathrm{Lie}}\nolimits Q\). Then  and
and  . We will call the latter object the algebra of symmetric invariants of \(\mathfrak{q}\). An important property of
. We will call the latter object the algebra of symmetric invariants of \(\mathfrak{q}\). An important property of  is that it is isomorphic to \(Z\mathbf{U}(\mathfrak{q})\) as an algebra by a classical result of M. Duflo (here \(Z\mathbf{U}(\mathfrak{q})\) is the centre of the universal enveloping algebra of \(\mathfrak{q}\)).
is that it is isomorphic to \(Z\mathbf{U}(\mathfrak{q})\) as an algebra by a classical result of M. Duflo (here \(Z\mathbf{U}(\mathfrak{q})\) is the centre of the universal enveloping algebra of \(\mathfrak{q}\)).
Let \(\mathfrak{g}\) be a reductive Lie algebra. Then by the Chevalley restriction theorem  is a polynomial ring (in \(\mathrm{rk\,}\mathfrak{g}\) variables). A quest for non-reductive Lie algebras with a similar property has recently become a trend in invariant theory. Here we consider finite-dimensional representations \(\rho: \mathfrak{g} \rightarrow \mathfrak{g}\mathfrak{l}(V )\) of \(\mathfrak{g}\) and the corresponding semi-direct products \(\mathfrak{q} = \mathfrak{g}\ltimes V\). The Lie bracket on \(\mathfrak{q}\) is defined by
is a polynomial ring (in \(\mathrm{rk\,}\mathfrak{g}\) variables). A quest for non-reductive Lie algebras with a similar property has recently become a trend in invariant theory. Here we consider finite-dimensional representations \(\rho: \mathfrak{g} \rightarrow \mathfrak{g}\mathfrak{l}(V )\) of \(\mathfrak{g}\) and the corresponding semi-direct products \(\mathfrak{q} = \mathfrak{g}\ltimes V\). The Lie bracket on \(\mathfrak{q}\) is defined by
for all \(\xi,\eta \in \mathfrak{g}\), v, u ∈ V. Let G be a connected simply connected Lie group with \(\mathop{\mathrm{Lie}}\nolimits G = \mathfrak{g}\). Then \(\mathfrak{q} =\mathop{ \mathrm{Lie}}\nolimits Q\) with \(Q = G\ltimes \exp (V )\).
It is easy to see that \(\mathbb{C}[V ^{{\ast}}]^{G} \subset \mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) and therefore \(\mathbb{C}[V ^{{\ast}}]^{G}\) must be a polynomial ring if \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is, see [10, Section 3]. Classification of the representations of complex simple algebraic groups with free algebras of invariants was carried out by Schwarz [7] and independently by Adamovich and Golovina [1]. One such representation is the spin-representation of \(\mathop{\mathrm{Spin}}\nolimits _{7}\), which leads to \(Q =\mathop{ \mathrm{Spin}}\nolimits _{7}\ltimes \mathbb{C}^{8}\). Here \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is a polynomial ring in three variables generated by invariants of bi-degrees (0, 2), (2, 2), (6, 4) with respect to the decomposition \(\mathfrak{q} = \mathfrak{s}\mathfrak{o}_{7}\oplus \mathbb{C}^{8}\), see [10, Proposition 3.10].
In this paper, we treat another example, G = SL n , \(V = m(\mathbb{C}^{n})^{{\ast}}\oplus k\mathbb{C}^{n}\) with \(n\geqslant 2\), \(m\geqslant 1\), \(m\geqslant k\). Here \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is a polynomial ring in exactly the following three cases:
-
k = 0, \(m\leqslant n + 1\), and \(n \equiv t\pmod m\) with t ∈ {−1, 0, 1};
-
m = k, k ∈ {n − 2, n − 1};
-
\(n\geqslant m> k> 0\) and m − k divides n − m.
We also briefly discuss semi-direct products arising as \(\mathbb{Z}_{2}\)-contractions of reductive Lie algebras.
2 Symmetric Invariants and Generic Stabilisers
Let \(\mathfrak{q} =\mathop{ \mathrm{Lie}}\nolimits Q\) be an algebraic Lie algebra, Q a connected algebraic group. The index of \(\mathfrak{q}\) is defined as
where \(\mathfrak{q}_{\gamma }\) is the stabiliser of γ in \(\mathfrak{q}\). In view of Rosenlicht’s theorem, \(\mathrm{ind}\mathfrak{q} =\mathrm{ tr.deg}\,\mathbb{C}(\mathfrak{q}^{{\ast}})^{Q}\). In case \(\mathrm{ind}\mathfrak{q} = 0\), we have \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}} = \mathbb{C}\). For a reductive \(\mathfrak{g}\), \(\mathrm{ind}\mathfrak{g} =\mathrm{ rk\,}\mathfrak{g}\). Recall that \((\mathrm{dim}\mathfrak{g} +\mathrm{ rk\,}\mathfrak{g})/2\) is the dimension of a Borel subalgebra of \(\mathfrak{g}\). For \(\mathfrak{q}\), set \(\mathbf{b}(\mathfrak{q}):= (\mathrm{ind}\mathfrak{q} + \mathrm{dim}\mathfrak{q})/2\).
Let {ξ
i
} be a basis of \(\mathfrak{q}\) and  the structural matrix with entries in \(\mathfrak{q}\). This is a skew-symmetric matrix of rank \(\mathrm{dim}\mathfrak{q} -\mathrm{ ind}\mathfrak{q}\). Let us take Pfaffians of the principal minors of
the structural matrix with entries in \(\mathfrak{q}\). This is a skew-symmetric matrix of rank \(\mathrm{dim}\mathfrak{q} -\mathrm{ ind}\mathfrak{q}\). Let us take Pfaffians of the principal minors of  of size
of size  and let \(\mathbf{p} = \mathbf{p}_{\mathfrak{q}}\) be their greatest common divisor. Then p is called the fundamental semi-invariant of \(\mathfrak{q}\). The zero set of p is the maximal divisor in the so called singular set
and let \(\mathbf{p} = \mathbf{p}_{\mathfrak{q}}\) be their greatest common divisor. Then p is called the fundamental semi-invariant of \(\mathfrak{q}\). The zero set of p is the maximal divisor in the so called singular set
of \(\mathfrak{q}\). Since \(\mathfrak{q}_{\mathrm{sing}}^{{\ast}}\) is clearly a Q-stable subset, p is indeed a semi-invariant, \(Q\cdot \mathbf{p} \subset \mathbb{C}\mathbf{p}\). One says that \(\mathfrak{q}\) has the “codim-2” property (satisfies the “codim-2” condition), if \(\mathrm{dim}\mathfrak{q}_{\mathrm{sing}}^{{\ast}}\leqslant \mathrm{dim}\mathfrak{q} - 2\) or equivalently if p = 1.
Suppose that  are homogenous algebraically independent polynomials. The Jacobian locus
are homogenous algebraically independent polynomials. The Jacobian locus
 of these polynomials consists of all \(\gamma \in \mathfrak{q}^{{\ast}}\) such that the differentials d
γ
F
1, …, d
γ
F
r
are linearly dependent. In other words,
of these polynomials consists of all \(\gamma \in \mathfrak{q}^{{\ast}}\) such that the differentials d
γ
F
1, …, d
γ
F
r
are linearly dependent. In other words,  if and only if (dF
1 ∧ … ∧ dF
r
)
γ
= 0. The set
if and only if (dF
1 ∧ … ∧ dF
r
)
γ
= 0. The set  is a proper Zariski closed subset of \(\mathfrak{q}^{{\ast}}\).
is a proper Zariski closed subset of \(\mathfrak{q}^{{\ast}}\).
Suppose that  does not contain divisors. Then by the characteristic zero version of a result of Skryabin, see [5, Theorem 1.1], \(\mathbb{C}[F_{1},\ldots,F_{r}]\) is an algebraically closed subalgebra of
does not contain divisors. Then by the characteristic zero version of a result of Skryabin, see [5, Theorem 1.1], \(\mathbb{C}[F_{1},\ldots,F_{r}]\) is an algebraically closed subalgebra of  , each
, each  that is algebraic over \(\mathbb{C}(F_{1},\ldots,F_{r})\) is contained in \(\mathbb{C}[F_{1},\ldots,F_{r}]\).
that is algebraic over \(\mathbb{C}(F_{1},\ldots,F_{r})\) is contained in \(\mathbb{C}[F_{1},\ldots,F_{r}]\).
Theorem 1 (cf. [3, Section 5.8])
Suppose that
\(\mathbf{p}_{\mathfrak{q}} = 1\)
and suppose that
 are homogeneous algebraically independent polynomials such that
\(r =\mathrm{ ind}\mathfrak{q}\)
and
\(\sum _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{q})\)
. Then
are homogeneous algebraically independent polynomials such that
\(r =\mathrm{ ind}\mathfrak{q}\)
and
\(\sum _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{q})\)
. Then
 is a polynomial ring in r generators.
is a polynomial ring in r generators.
Proof
Under our assumptions  , see [5, Theorem 1.2] and [9, Section 2]. Therefore \(\mathbb{C}[H_{1},\ldots,H_{r}]\) is an algebraically closed subalgebra of
, see [5, Theorem 1.2] and [9, Section 2]. Therefore \(\mathbb{C}[H_{1},\ldots,H_{r}]\) is an algebraically closed subalgebra of  by [5, Theorem 1.1]. Since
by [5, Theorem 1.1]. Since  , each symmetric \(\mathfrak{q}\)-invariant is algebraic over \(\mathbb{C}[H_{1},\ldots,H_{r}]\) and hence is contained in it. □
, each symmetric \(\mathfrak{q}\)-invariant is algebraic over \(\mathbb{C}[H_{1},\ldots,H_{r}]\) and hence is contained in it. □
For semi-direct products, we have some specific approaches to the symmetric invariants. Suppose now that \(\mathfrak{g} =\mathop{ \mathrm{Lie}}\nolimits G\) is a reductive Lie algebra, no non-zero ideal of \(\mathfrak{g}\) acts on V trivially, G is connected, and \(\mathfrak{q} = \mathfrak{g}\ltimes V\), where V is a finite-dimensional G-module.
The vector space decomposition \(\mathfrak{q} = \mathfrak{g}\oplus V\) leads to \(\mathfrak{q}^{{\ast}} = \mathfrak{g}\oplus V ^{{\ast}}\), where we identify \(\mathfrak{g}\) with \(\mathfrak{g}^{{\ast}}\). Each element x ∈ V ∗ is considered as a point of \(\mathfrak{q}^{{\ast}}\) that is zero on \(\mathfrak{g}\). We have exp(V )⋅ x = ad∗(V )⋅ x + x, where each element of ad∗(V )⋅ x is zero on V. Note that \(\mathrm{ad}^{{\ast}}(V )\cdot x \subset \mathrm{ Ann}(\mathfrak{g}_{x}) \subset \mathfrak{g}\) and dim(ad∗(V )⋅ x) is equal to \(\mathrm{dim}(\mathrm{ad}^{{\ast}}(\mathfrak{g})\cdot x) = \mathrm{dim}\mathfrak{g} -\mathrm{dim}\mathfrak{g}_{x}\). Therefore \(\mathrm{ad}^{{\ast}}(V )\cdot x =\mathrm{ Ann}(\mathfrak{g}_{x})\).
The decomposition \(\mathfrak{q} = \mathfrak{g}\oplus V\) defines also a bi-grading on  and clearly
and clearly  is a bi-homogeneous subalgebra, cf. [10, Lemma 2.12].
is a bi-homogeneous subalgebra, cf. [10, Lemma 2.12].
A statement is true for a “generic x” if and only if this statement is true for all points of a non-empty open subset.
Lemma 1
A function \(F \in \mathbb{C}[\mathfrak{q}^{{\ast}}]\) is a V -invariant if and only if F(ξ + ad∗(V )⋅ x, x) = F(ξ, x) for generic x ∈ V ∗ and any \(\xi \in \mathfrak{g}\) .
Proof
Condition of the lemma guaranties that for each v ∈ V, exp(v)⋅ F = F on a non-empty open subset of \(\mathfrak{q}^{{\ast}}\). Hence F is a V -invariant. □
For x ∈ V
∗, let \(\varphi _{x}\!: \mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} \rightarrow \mathbb{C}[\mathfrak{g} + x]^{G_{x}\ltimes \exp (V )}\) be the restriction map. By [10, Lemma 2.5]  . Moreover, if we identify \(\mathfrak{g} + x\) with \(\mathfrak{g}\) choosing x as the origin, then
. Moreover, if we identify \(\mathfrak{g} + x\) with \(\mathfrak{g}\) choosing x as the origin, then  for any \(\mathfrak{q}\)-invariant F [10, Section 2]. Under certain assumptions on G and V the restriction map φ
x
is surjective, more details will be given shortly.
for any \(\mathfrak{q}\)-invariant F [10, Section 2]. Under certain assumptions on G and V the restriction map φ
x
is surjective, more details will be given shortly.
There is a non-empty open subset U ⊂ V ∗ such that the stabilisers G x and G y are conjugate in G for any pair of points x, y ∈ U see e.g. [8, Theorem 7.2]. Any representative of the conjugacy class {hG x h −1∣h ∈ G, x ∈ U} is said to be a a generic stabiliser of the G-action on V ∗.
There is one easy to handle case, \(\mathfrak{g}_{x} = 0\) for a generic x ∈ V ∗. Here \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} = \mathbb{C}[V ^{{\ast}}]^{G}\), see e.g. [10, Example 3.1], and \(\xi +y \in \mathfrak{q}_{\mathrm{sing}}^{{\ast}}\) only if \(\mathfrak{g}_{y}\neq 0\), where \(\xi \in \mathfrak{g}\), y ∈ V ∗. The case \(\mathrm{ind}\mathfrak{g}_{x} = 1\) is more involved.
Lemma 2
Assume that G has no proper semi-invariants in
\(\mathbb{C}[V ^{{\ast}}]\)
. Suppose that
\(\mathrm{ind}\mathfrak{g}_{x} = 1\),  , and the map φ
x
is surjective for generic x ∈ V
∗
. Then
\(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}} = \mathbb{C}[V ^{{\ast}}]^{G}[F]\)
, where F is a bi-homogeneous preimage of a generator of
, and the map φ
x
is surjective for generic x ∈ V
∗
. Then
\(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}} = \mathbb{C}[V ^{{\ast}}]^{G}[F]\)
, where F is a bi-homogeneous preimage of a generator of
 that is not divisible by any non-constant G-invariant in
\(\mathbb{C}[V ^{{\ast}}]\)
.
that is not divisible by any non-constant G-invariant in
\(\mathbb{C}[V ^{{\ast}}]\)
.
Proof
If we have a Lie algebra of index 1, in our case \(\mathfrak{g}_{x}\), then the algebra of its symmetric invariants is a polynomial ring. There are many possible explanations of this fact. One of them is the following. Suppose that two non-zero homogeneous polynomials f 1, f 2 are algebraically dependent. Then f 1 a = cf 2 b for some coprime integers a, b > 0 and some \(c \in \mathbb{C}^{^{\times } }\). If f 1 is an invariant, then so is a polynomial function \(\root{b}\of{f_{1}} = \root{ab}\of{c}\root{a}\of{f_{2}}\).
Since  , it is generated by some homogeneous f. The group G
x
has finitely many connected components, hence
, it is generated by some homogeneous f. The group G
x
has finitely many connected components, hence  is generated by a suitable power of f, say f = f
d.
is generated by a suitable power of f, say f = f
d.
Let \(F \in \mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) be a preimage of f. Each its bi-homogeneous component is again a \(\mathfrak{q}\)-invariant. Without loss of generality we may assume that F is bi-homogenous. Also if F is divisible by some non-scalar \(H \in \mathbb{C}[V ^{{\ast}}]^{G}\), then we replace F with F∕H and repeat the process as long as possible.
Whenever G
y
(with y ∈ V
∗) is conjugate to G
x
and φ
y
(F) ≠ 0, φ
y
(F) is a G
y
-invariant of the same degree as f and therefore is a generator of  . Clearly
. Clearly  and
and  . If
. If  contains a homogeneous in \(\mathfrak{g}\) polynomial T that is not proportional (over \(\mathbb{C}(V ^{{\ast}})^{G}\)) to a power of F, then φ
u
(T) is not proportional to a power of φ
u
(F) for generic u ∈ V
∗. But
contains a homogeneous in \(\mathfrak{g}\) polynomial T that is not proportional (over \(\mathbb{C}(V ^{{\ast}})^{G}\)) to a power of F, then φ
u
(T) is not proportional to a power of φ
u
(F) for generic u ∈ V
∗. But  . This implies that
. This implies that  . It remains to notice that \(\mathbb{C}(V ^{{\ast}})^{G} =\mathrm{ Quot}\,\mathbb{C}[V ^{{\ast}}]^{G}\), since G has no proper semi-invariants in \(\mathbb{C}[V ^{{\ast}}]\), and by the same reason \(\mathbb{C}(V ^{{\ast}})^{G}[F] \cap \mathbb{C}[\mathfrak{q}] = \mathbb{C}[V ^{{\ast}}]^{G}[F]\) in case F is not divisible by any non-constant G-invariant in \(\mathbb{C}[V ^{{\ast}}]\). □
. It remains to notice that \(\mathbb{C}(V ^{{\ast}})^{G} =\mathrm{ Quot}\,\mathbb{C}[V ^{{\ast}}]^{G}\), since G has no proper semi-invariants in \(\mathbb{C}[V ^{{\ast}}]\), and by the same reason \(\mathbb{C}(V ^{{\ast}})^{G}[F] \cap \mathbb{C}[\mathfrak{q}] = \mathbb{C}[V ^{{\ast}}]^{G}[F]\) in case F is not divisible by any non-constant G-invariant in \(\mathbb{C}[V ^{{\ast}}]\). □
It is time to recall the Raïs’ formula [6] for the index of a semi-direct product:
Lemma 3
Suppose that
 are homogenous polynomials such that φ
x
(H
i
) with
\(i\leqslant \mathrm{ind}\mathfrak{g}_{x}\)
freely generate
are homogenous polynomials such that φ
x
(H
i
) with
\(i\leqslant \mathrm{ind}\mathfrak{g}_{x}\)
freely generate
 for generic x ∈ V
∗
and
\(H_{j} \in \mathbb{C}[V ^{{\ast}}]^{G}\)
for
\(j>\mathrm{ ind}\mathfrak{g}_{x}\)
; and suppose that
\(\sum \limits _{i=1}^{\mathrm{ind}\mathfrak{g}_{x}}\mathrm{deg}_{\mathfrak{g}}H_{i} = \mathbf{b}(\mathfrak{g}_{x})\)
. Then
\(\sum \limits _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{q})\)
if and only if
\(\sum \limits _{i=1}^{r}\mathrm{deg}_{V }H_{i} = \mathrm{dim}V\)
.
for generic x ∈ V
∗
and
\(H_{j} \in \mathbb{C}[V ^{{\ast}}]^{G}\)
for
\(j>\mathrm{ ind}\mathfrak{g}_{x}\)
; and suppose that
\(\sum \limits _{i=1}^{\mathrm{ind}\mathfrak{g}_{x}}\mathrm{deg}_{\mathfrak{g}}H_{i} = \mathbf{b}(\mathfrak{g}_{x})\)
. Then
\(\sum \limits _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{q})\)
if and only if
\(\sum \limits _{i=1}^{r}\mathrm{deg}_{V }H_{i} = \mathrm{dim}V\)
.
Proof
In view of the assumptions, we have \(\sum \limits _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{g}_{x}) +\sum \limits _{ i=1}^{r}\mathrm{deg}_{V }H_{i}\). Further, by Eq. (2)
The result follows. □
From now on suppose that G is semisimple. Then both G and Q have only trivial characters and hence cannot have proper semi-invariants. In particular, the fundamental semi-invariant is an invariant. We also have  . Set \(r =\mathrm{ ind}\mathfrak{q}\) and let x ∈ V
∗ be generic. If \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring, then there are bi-homogenous generators H
1, …, H
r
such that H
i
with \(i>\mathrm{ ind}\mathfrak{g}_{x}\) freely generate \(\mathbb{C}[V ^{{\ast}}]^{G}\) and the invariants H
i
with \(i\leqslant \mathrm{ind}\mathfrak{g}_{x}\) are mixed, they have positive degrees in \(\mathfrak{g}\) and V.
. Set \(r =\mathrm{ ind}\mathfrak{q}\) and let x ∈ V
∗ be generic. If \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring, then there are bi-homogenous generators H
1, …, H
r
such that H
i
with \(i>\mathrm{ ind}\mathfrak{g}_{x}\) freely generate \(\mathbb{C}[V ^{{\ast}}]^{G}\) and the invariants H
i
with \(i\leqslant \mathrm{ind}\mathfrak{g}_{x}\) are mixed, they have positive degrees in \(\mathfrak{g}\) and V.
Theorem 2 ([3, Theorem 5.7] and [10, Proposition 3.11])
Suppose that G is semisimple and \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is a polynomial ring with homogeneous generators H 1, …, H r . Then
-
(i)
\(\sum _{i=1}^{r}\mathrm{deg}H_{i} = \mathbf{b}(\mathfrak{q}) + \mathrm{deg}\mathbf{p}_{\mathfrak{q}}\) ;
-
(ii)
for generic x ∈ V ∗ , the restriction map
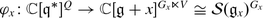 is surjective,
is surjective,
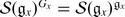 , and
, and
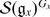 is a polynomial ring in
\(\mathrm{ind}\mathfrak{g}_{x}\)
variables.
is a polynomial ring in
\(\mathrm{ind}\mathfrak{g}_{x}\)
variables.
It is worth mentioning that φ x is also surjective for stable actions. An action of G on V is called stable if generic G-orbits in V are closed, for more details see [8, Sections 2.4 and 7.5]. By [10, Theorem 2.8] φ x is surjective for generic x ∈ V ∗ if the G-action on V ∗ is stable.
3 \(\mathbb{Z}/2\mathbb{Z}\)-contractions
The initial motivation for studying symmetric invariants of semi-direct products was related to a conjecture of D. Panyushev on \(\mathbb{Z}_{2}\)-contractions of reductive Lie algebras. The results of [10], briefly outlined in Sect. 2, have settled the problem.
Let \(\mathfrak{g} = \mathfrak{g}_{0}\oplus \mathfrak{g}_{1}\) be a symmetric decomposition, i.e., a \(\mathbb{Z}/2\mathbb{Z}\)-grading of \(\mathfrak{g}\). A semi-direct product, \(\tilde{\mathfrak{g}} = \mathfrak{g}_{0}\ltimes \mathfrak{g}_{1}\), where \(\mathfrak{g}_{1}\) is an Abelian ideal, can be seen as a contraction, in this case a \(\mathbb{Z}_{2}\)
-contraction, of \(\mathfrak{g}\). For example, starting with a symmetric pair \((\mathfrak{s}\mathfrak{o}_{n+1},\mathfrak{s}\mathfrak{o}_{n})\), one arrives at \(\tilde{\mathfrak{g}} = \mathfrak{s}\mathfrak{o}_{n}\ltimes \mathbb{C}^{n}\). In [4], it was conjectured that  is a polynomial ring (in \(\mathrm{rk\,}\mathfrak{g}\) variables).
is a polynomial ring (in \(\mathrm{rk\,}\mathfrak{g}\) variables).
Theorem 3 ([4, 9, 10])
Let
\(\tilde{\mathfrak{g}}\)
be a
\(\mathbb{Z}_{2}\)
-contraction of a reductive Lie algebra
\(\mathfrak{g}\)
. Then
 is a polynomial ring (in
\(\mathrm{rk\,}\mathfrak{g}\)
variables) if and only if the restriction homomorphism
\(\mathbb{C}[\mathfrak{g}]^{\mathfrak{g}} \rightarrow \mathbb{C}[\mathfrak{g}_{1}]^{\mathfrak{g}_{0}}\)
is surjective.
is a polynomial ring (in
\(\mathrm{rk\,}\mathfrak{g}\)
variables) if and only if the restriction homomorphism
\(\mathbb{C}[\mathfrak{g}]^{\mathfrak{g}} \rightarrow \mathbb{C}[\mathfrak{g}_{1}]^{\mathfrak{g}_{0}}\)
is surjective.
If we are in one of the “surjective” cases, then one can describe the generators of  . Let H
1, …, H
r
be suitably chosen homogeneous generators of
. Let H
1, …, H
r
be suitably chosen homogeneous generators of  and let H
i
• be the bi-homogeneous (w.r.t. \(\mathfrak{g} = \mathfrak{g}_{0}\oplus \mathfrak{g}_{1}\)) component of H
i
of the highest \(\mathfrak{g}_{1}\)-degree. Then
and let H
i
• be the bi-homogeneous (w.r.t. \(\mathfrak{g} = \mathfrak{g}_{0}\oplus \mathfrak{g}_{1}\)) component of H
i
of the highest \(\mathfrak{g}_{1}\)-degree. Then  is freely generated by the polynomials H
i
• (of course, providing the restriction homomorphism \(\mathbb{C}[\mathfrak{g}]^{\mathfrak{g}} \rightarrow \mathbb{C}[\mathfrak{g}_{1}]^{\mathfrak{g}_{0}}\) is surjective) [4, 9].
is freely generated by the polynomials H
i
• (of course, providing the restriction homomorphism \(\mathbb{C}[\mathfrak{g}]^{\mathfrak{g}} \rightarrow \mathbb{C}[\mathfrak{g}_{1}]^{\mathfrak{g}_{0}}\) is surjective) [4, 9].
Unfortunately, this construction of generators cannot work if the restriction homomorphism is not surjective, see [4, Remark 4.3]. As was found out by Helgason [2], there are four “non-surjective” irreducible symmetric pairs, namely, (E 6, F 4), \((E_{7},E_{6}\oplus \mathbb{C})\), \((E_{8},E_{7}\oplus \mathfrak{s}\mathfrak{l}_{2})\), and \((E_{6},\mathfrak{s}\mathfrak{o}_{10}\oplus \mathfrak{s}\mathfrak{o}_{2})\). The approach to semi-directproducts developed in [10] showed that Panyushev’s conjecture does not hold for them. Next we outline some ideas of the proof.
Let G
0 ⊂ G be a connected subgroup with \(\mathop{\mathrm{Lie}}\nolimits G_{0} = \mathfrak{g}_{0}\). Then G
0 is reductive, it acts on \(\mathfrak{g}_{1}\cong \mathfrak{g}_{1}^{{\ast}}\), and this action is stable. Let \(x \in \mathfrak{g}_{1}\) be a generic element and G
0,x
be its stabiliser in G
0. The groups G
0,x
are reductive and they are known for all symmetric pairs. In particular,  is a polynomial ring. It is also known that \(\mathbb{C}[\mathfrak{g}_{1}]^{G_{0}}\) is a polynomial ring. By [4] \(\tilde{\mathfrak{g}}\) has the “codim-2” property and \(\mathrm{ind}\tilde{\mathfrak{g}} =\mathrm{ rk\,}\mathfrak{g}\).
is a polynomial ring. It is also known that \(\mathbb{C}[\mathfrak{g}_{1}]^{G_{0}}\) is a polynomial ring. By [4] \(\tilde{\mathfrak{g}}\) has the “codim-2” property and \(\mathrm{ind}\tilde{\mathfrak{g}} =\mathrm{ rk\,}\mathfrak{g}\).
Making use of the surjectivity of φ x one can show that if \(\mathbb{C}[\tilde{\mathfrak{g}}^{{\ast}}]^{\tilde{\mathfrak{g}}}\) is freely generated by some H 1, …, H r , then necessary \(\sum \limits _{i=1}^{r}\mathrm{deg}H_{i}> \mathbf{b}(\tilde{\mathfrak{g}})\) for \(\tilde{\mathfrak{g}}\) coming from one of the “non-surjective” pairs [10]. In view of some results from [3] this leads to a contradiction.
Note that in case of \((\mathfrak{g},\mathfrak{g}_{0}) = (E_{6},F_{4})\), \(\mathfrak{g}_{0} = F_{4}\) is simple and \(\tilde{\mathfrak{g}}\) is a semi-direct product of F 4 and \(\mathbb{C}^{26}\), which, of course, comes from one of the representations in Schwarz’s list [7].
4 Examples Related to the Defining Representation of \(\mathfrak{s}\mathfrak{l}_{n}\)
Form now assume that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{n}\) and \(V = m(\mathbb{C}^{n})^{{\ast}}\oplus k\mathbb{C}^{n}\) with \(n\geqslant 2\), \(m\geqslant 1\), \(m\geqslant k\). According to [7] \(\mathbb{C}[V ]^{G}\) is a polynomial ring if either k = 0 and \(m\leqslant n + 1\) or \(m\leqslant n\), \(k\leqslant n - 1\). One finds also the description of the generators of \(\mathbb{C}[V ^{{\ast}}]^{G}\) and their degrees in [7]. In this section, we classify all cases, where \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is a polynomial ring and for each of them give the fundamental semi-invariant.
Example 1
Suppose that either \(m\geqslant n\) or m = k = n − 1. Then \(\mathfrak{g}_{x} = 0\) for generic x ∈ V ∗ and therefore \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} = \mathbb{C}[V ^{{\ast}}]^{G}\), i.e., \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring if and only if \(\mathbb{C}[V ^{{\ast}}]^{G}\) is. The latter takes place for (m, k) = (n + 1, 0), for m = n and any k < n, as well as for m = k = n − 1. Non-scalar fundamental semi-invariants appear here only for
-
m = n, where p is given by det(v)n−1−k with \(v \in n\mathbb{C}^{n}\);
-
m = k = n − 1, where p is the sum of the principal 2k×2k-minors of
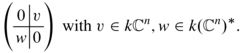
In the rest of the section, we assume that \(\mathfrak{g}_{x}\neq 0\) for generic x ∈ V ∗.
4.1 The Case k = 0
Here the ring of G-invariants on V ∗ is generated by
where each Δ I (v) is the determinant of the corresponding submatrix of v ∈ V ∗. The generators are algebraically independent if and only if \(m\leqslant n + 1\), see also [7].
We are interested only in m that are smaller than n. Let n = qm + r, where \(0 <r\leqslant m\), and let I ⊂ {1, …, m} be a subset of cardinality r. By choosing the corresponding r columns of v we get a matrix w = v I . Set
Clearly each F I is an SL n -invariant. Below we will see that they are also V -invariants. If r = m, then there is just one invariant, F = F {1,…, m}. If r is either 1 or m − 1, we get m invariants.
Lemma 4
Each F I defined by Eq. (3) is a V -invariant.
Proof
According to Lemma 1 we have to show that F I (ξ + ad∗(V )⋅ x, x) = F(ξ, x) for generic x ∈ V ∗ and any \(\xi \in \mathfrak{s}\mathfrak{l}_{n}\). Since m < n, there is an open SL n -orbit in V ∗ and we can take x as E m . Let \(\mathfrak{p} \subset \mathfrak{g}\mathfrak{l}_{n}\) be the standard parabolic subalgebra corresponding to the composition (m, n − m) and let \(\mathfrak{n}_{-}\) be the nilpotent radical of the opposite parabolic. Each element (matrix) \(\xi \in \mathfrak{g}\mathfrak{l}_{n}\) is a sum ξ = ξ − + ξ p with \(\xi _{-}\in \mathfrak{n}_{-}\), \(\xi _{p} \in \mathfrak{p}\). In this notation \(F_{I}(A,E_{m}) = \mathrm{det}\left (A_{-}\vert (A^{2})_{-}\vert \ldots \vert (A^{q-1})_{-}\vert (A^{q})_{-,I}\right )\).
Let α = α A and β = β A be m×m and (n − m)×(n − m)-submatrices of A standing in the upper left and lower right corner, respectively. Then (A s+1)− = ∑ t = 0 s β t A − α s−t. Each column of A − α is a linear combination of columns of A − and each column of β t A − α j+1 is a linear combination of columns of β t A − α j. Therefore
Notice that \(\mathfrak{g}_{x} \subset \mathfrak{p}\) and the nilpotent radical of \(\mathfrak{p}\) is contained in \(\mathfrak{g}_{x}\) (with x = E m ). Since \(\mathrm{ad}^{{\ast}}(V )\cdot x =\mathrm{ Ann}(\mathfrak{g}_{x}) = \mathfrak{g}_{x}^{\perp }\subset \mathfrak{g}\) (after the identification \(\mathfrak{g}\cong \mathfrak{g}^{{\ast}}\)), A − = 0 for any \(A \in \mathfrak{g}_{x}^{\perp }\); and we have β A = cE n−m with \(c \in \mathbb{C}\) for this A. An easy observation is that
Hence F I (ξ + A, E m ) = F I (ξ, E m ) for all A ∈ ad∗(V )⋅ E m and all \(\xi \in \mathfrak{s}\mathfrak{l}_{n}\). □
Theorem 4
Suppose that \(\mathfrak{q} = \mathfrak{s}\mathfrak{l}_{n}\ltimes m(\mathbb{C}^{n})^{{\ast}}\) . Then \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring if and only if \(m\leqslant n + 1\) and m divides either n − 1, n or n + 1. Under these assumptions on m, \(\mathbf{p}_{\mathfrak{q}} = 1\) exactly then, when m divides either n − 1 or n + 1.
Proof
Note that the statement is true for \(m\geqslant n\) by Example 1. Assume that \(m\leqslant n - 1\). Suppose that n = mq + r as above. A generic stabiliser in \(\mathfrak{g}\) is \(\mathfrak{g}_{x} = \mathfrak{s}\mathfrak{l}_{n-m}\ltimes m\mathbb{C}^{n-m}\). On the group level it is connected. Notice that  , since G
x
has no non-trivial characters. Note also that \(\mathbb{C}[V ^{{\ast}}]^{G} = \mathbb{C}\), since m < n. If \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring, then so is \(\mathbb{C}[\mathfrak{g}_{x}^{{\ast}}]^{G_{x}}\) by Theorem 2(ii) and either n − m = 1 or, arguing by induction, \(n - m \equiv t\pmod m\) with t ∈ {−1, 0, 1}.
, since G
x
has no non-trivial characters. Note also that \(\mathbb{C}[V ^{{\ast}}]^{G} = \mathbb{C}\), since m < n. If \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is a polynomial ring, then so is \(\mathbb{C}[\mathfrak{g}_{x}^{{\ast}}]^{G_{x}}\) by Theorem 2(ii) and either n − m = 1 or, arguing by induction, \(n - m \equiv t\pmod m\) with t ∈ {−1, 0, 1}.
Next we show that the ring of symmetric invariants is freely generated by the polynomials F
I
for the indicated m. Each element \(\gamma \in \mathfrak{g}_{x}^{{\ast}}\) can be presented as γ = β
0 + A
−, where \(\beta _{0} \in \mathfrak{s}\mathfrak{l}_{n-m}\). Each restriction φ
x
(F
I
) can be regarded as an element of  . Equation (4) combined with Lemma 4 and the observation that \(\mathfrak{g}_{x}^{{\ast}}\cong \mathfrak{g}/\mathrm{Ann}(\mathfrak{g}_{x})\) shows that φ
x
(F
I
) is either Δ
I
of \(\mathfrak{g}_{x}\) (in case q = 1, where F
I
(A, E
m
) = detA
−,I
) or F
I
of \(\mathfrak{g}_{x}\). Arguing by induction on n, we prove that the restrictions φ
x
(F
I
) freely generate
. Equation (4) combined with Lemma 4 and the observation that \(\mathfrak{g}_{x}^{{\ast}}\cong \mathfrak{g}/\mathrm{Ann}(\mathfrak{g}_{x})\) shows that φ
x
(F
I
) is either Δ
I
of \(\mathfrak{g}_{x}\) (in case q = 1, where F
I
(A, E
m
) = detA
−,I
) or F
I
of \(\mathfrak{g}_{x}\). Arguing by induction on n, we prove that the restrictions φ
x
(F
I
) freely generate  for x = E
m
(i.e., for a generic point in V
∗). Notice that n − m = (q − 1)m + r.
for x = E
m
(i.e., for a generic point in V
∗). Notice that n − m = (q − 1)m + r.
The group SL n acts on V ∗ with an open orbit SL n ⋅ E m . Therefore the restriction map φ x is injective. By the inductive hypothesis it is also surjective and therefore is an isomorphism. This proves that the polynomials F I freely generate \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\).
If m divides n, then \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} = \mathbb{C}[F]\) and the fundamental semi-invariant is a power of F. As follows from the equality in Theorem 2(i), p = F m−1.
Suppose that m divides either n − 1 or n + 1. Then we have m different invariants F I . By induction on n, \(\mathfrak{g}_{x}\) has the “codim-2” property, therefore the sum of degφ x (F I ) is equal to \(\mathbf{b}(\mathfrak{g}_{x})\) by Theorem 2(i). The sum of V -degrees is m×n = dimV and hence by Lemma 3 \(\sum \mathrm{deg}F_{I} = \mathbf{b}(\mathfrak{q})\). Thus, \(\mathfrak{q}\) has the “codim-2” property. □
Remark 1
Using induction on n one can show that the restriction map φ x is an isomorphism for all m < n. Therefore the polynomials F I generate \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) for all m < n.
4.2 The Case m = k
Here \(\mathbb{C}[V ^{{\ast}}]^{G}\) is a polynomial ring if and only if \(k\leqslant n - 1\); a generic stabiliser is \(\mathfrak{s}\mathfrak{l}_{n-k}\), and the G-action on \(V \cong V ^{{\ast}}\) is stable. We assume that \(\mathfrak{g}_{x}\neq 0\) for generic x ∈ V ∗ and therefore \(k\leqslant n - 2\).
For an N×N-matrix C, let Δ i (C) with \(1\leqslant i\leqslant N\) be coefficients of its characteristic polynomial, each Δ i being a homogeneous polynomial of degree i. Let \(\gamma = A + v + w \in \mathfrak{q}^{{\ast}}\) with \(A \in \mathfrak{g}\), \(v \in k\mathbb{C}^{n}\), \(w \in k(\mathbb{C}^{n})^{{\ast}}\). Having these objects we form an (n + k)×(n + k)-matrix

and set F i (γ) = Δ i (Y γ ) for each i ∈ {2k + 1, 2k + 2, 2k + 3, …, n + k}. Each F i is an \(\mathrm{SL}_{n}\times \mathop{\mathrm{GL}}\nolimits _{k}\)-invariant. Unfortunately, these polynomials are not V -invariants.
Remark 2
If we repeat the same construction for \(\tilde{\mathfrak{q}} = \mathfrak{g}\mathfrak{l}_{n}\ltimes V\) with \(k\leqslant n - 1\), then \(\mathbb{C}[\tilde{\mathfrak{q}}^{{\ast}}]^{\tilde{Q}} = \mathbb{C}[V ^{{\ast}}]^{\mathop{\mathrm{GL}}\nolimits _{n}}[\{F_{i}\mid 2k + 1\leqslant i\leqslant n + k\}]\) and it is a polynomial ring in \(\mathrm{ind}\tilde{\mathfrak{q}} = n - k + k^{2}\) generators.
Theorem 5
Suppose that \(m = k\leqslant n - 1\) . Then \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) is a polynomial ring if and only if k ∈ {n − 2, n − 1}. In case k = n − 2, \(\mathfrak{q}\) has the “codim-2” property.
Proof
Suppose that k = n − 2. Then a generic stabiliser \(\mathfrak{g}_{x} = \mathfrak{s}\mathfrak{l}_{2}\) is of index 1 and since the G-action on V is stable, \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}}\) has to be a polynomial ring by [10, Example 3.6]. One can show that the unique mixed generator is of the form F 2k+2 H 2k − F 2k+1 2, where H 2k is a certain \(\mathrm{SL}_{n}\times \mathop{\mathrm{GL}}\nolimits _{k}\)-invariant on V of degree 2k and then see that the sum of degrees is \(\mathbf{b}(\mathfrak{q})\).
More generally, \(\mathfrak{q}\) has the “codim-2” property for all \(k\leqslant n - 2\). Here each G-invariant divisor in V ∗ contains a G-orbit of maximal dimension, say Gy. Set u = n − k − 1. If G y is not SL n−k , then \(\mathfrak{g}_{y} = \mathfrak{s}\mathfrak{l}_{u} \ltimes (\mathbb{C}^{u}\oplus (\mathbb{C}^{u})^{{\ast}}\oplus \mathbb{C})\) is a semi-direct product with a Heisenberg Lie algebra. Following the proof of [4, Theorem 3.3], one has to show that \(\mathrm{ind}\mathfrak{g}_{y} = u\) in order to prove that \(\mathfrak{q}\) has the “codim-2” property. This is indeed the case, \(\mathrm{ind}\mathfrak{g}_{y} = 1 +\mathrm{ ind}\mathfrak{s}\mathfrak{l}_{u}\).
Suppose that 0 < k < n − 2 and assume that  is a polynomial ring. Then there are bi-homogeneous generators h
2, …, h
n−k
of \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) over \(\mathbb{C}[V ^{{\ast}}]^{G}\) such that their restrictions to \(\mathfrak{g} + x\) form a generating set of
is a polynomial ring. Then there are bi-homogeneous generators h
2, …, h
n−k
of \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) over \(\mathbb{C}[V ^{{\ast}}]^{G}\) such that their restrictions to \(\mathfrak{g} + x\) form a generating set of  for a generic x (with \(\mathfrak{g}_{x}\cong \mathfrak{s}\mathfrak{l}_{n-k}\)), see Theorem 2(ii). In particular, \(\mathrm{deg}_{\mathfrak{g}}\mathbf{h}_{t} = t\).
for a generic x (with \(\mathfrak{g}_{x}\cong \mathfrak{s}\mathfrak{l}_{n-k}\)), see Theorem 2(ii). In particular, \(\mathrm{deg}_{\mathfrak{g}}\mathbf{h}_{t} = t\).
Take \(\tilde{\mathfrak{g}} = (\mathfrak{s}\mathfrak{l}_{n}\oplus \mathfrak{g}\mathfrak{l}_{k}) \ltimes V\), which is a \(\mathbb{Z}_{2}\)-contraction of \(\mathfrak{s}\mathfrak{l}_{n+k}\). Then \(\mathfrak{q}\) is a Lie subalgebra of \(\tilde{\mathfrak{g}}\). Note that \(\mathop{\mathrm{GL}}\nolimits _{k}\) acts on \(\mathfrak{q}\) via automorphisms and therefore we may assume that the \(\mathbb{C}\)-linear span of {h t } is \(\mathop{\mathrm{GL}}\nolimits _{k}\)-stable. By degree considerations, each h t is an SL k -invariant as well. The Weyl involution of SL n acts on V and has to preserve each line \(\mathbb{C}\mathbf{h}_{t}\). Since this involution interchanges \(\mathbb{C}^{n}\) and \((\mathbb{C}^{n})^{{\ast}}\), each h t is also a \(\mathop{\mathrm{GL}}\nolimits _{k}\)-invariant. Thus,

Since \(\tilde{\mathfrak{g}}\) is a “surjective” \(\mathbb{Z}_{2}\)-contraction, its symmetric invariants are known [4, Theorem 4.5]. The generators of  are Δ
j
• with \(2\leqslant j\leqslant n + k\). Here degΔ
j
• = j and the generators of (\(\mathfrak{s}\mathfrak{l}_{n}\oplus \mathfrak{g}\mathfrak{l}_{k}\))-degrees 2, 3, …, n − k are Δ
2k+2
•, Δ
2k+3
•, …, Δ
n+k
•. As the restriction to \(\mathfrak{s}\mathfrak{l}_{n}\oplus \mathfrak{g}\mathfrak{l}_{k} + x\) shows, none of the generators Δ
j
• with \(j\geqslant 2k + 2\) lies in
are Δ
j
• with \(2\leqslant j\leqslant n + k\). Here degΔ
j
• = j and the generators of (\(\mathfrak{s}\mathfrak{l}_{n}\oplus \mathfrak{g}\mathfrak{l}_{k}\))-degrees 2, 3, …, n − k are Δ
2k+2
•, Δ
2k+3
•, …, Δ
n+k
•. As the restriction to \(\mathfrak{s}\mathfrak{l}_{n}\oplus \mathfrak{g}\mathfrak{l}_{k} + x\) shows, none of the generators Δ
j
• with \(j\geqslant 2k + 2\) lies in  . This means that h
t
cannot be equal or even proportional over \(\mathbb{C}[V ^{{\ast}}]^{G}\) to Δ
2k+t
• and hence has a more complicated expression. More precisely, a product Δ
2k+1
•
Δ
2k+t−1
• necessary appears in h
t
with a non-zero coefficient from \(\mathbb{C}[V ^{{\ast}}]^{G}\) for \(t\geqslant 2\). Since deg
V
Δ
2k+1
• = 2k, we have \(\mathrm{deg}_{V }\mathbf{h}_{t}\geqslant 4k\) for every \(t\geqslant 2\). The ring \(\mathbb{C}[V ^{{\ast}}]^{G}\) is freely generated by k
2 polynomials of degree two. Therefore, the total sum of degrees over all generators of
. This means that h
t
cannot be equal or even proportional over \(\mathbb{C}[V ^{{\ast}}]^{G}\) to Δ
2k+t
• and hence has a more complicated expression. More precisely, a product Δ
2k+1
•
Δ
2k+t−1
• necessary appears in h
t
with a non-zero coefficient from \(\mathbb{C}[V ^{{\ast}}]^{G}\) for \(t\geqslant 2\). Since deg
V
Δ
2k+1
• = 2k, we have \(\mathrm{deg}_{V }\mathbf{h}_{t}\geqslant 4k\) for every \(t\geqslant 2\). The ring \(\mathbb{C}[V ^{{\ast}}]^{G}\) is freely generated by k
2 polynomials of degree two. Therefore, the total sum of degrees over all generators of  is greater than or equal to
is greater than or equal to
This contradicts Theorem 2(i) in view of the fact that \(\mathbf{p}_{\mathfrak{q}} = 1\). □
4.3 The Case 0 < k < m
Here \(\mathbb{C}[V ^{{\ast}}]^{G}\) is a polynomial ring if and only if \(m\leqslant n\), [7]. If n = m, then \(\mathfrak{g}_{x} = 0\) for generic x ∈ V ∗. For m < n, our construction of invariants is rather intricate.
Let π
1, …, π
n−1 be the fundamental weights of \(\mathfrak{s}\mathfrak{l}_{n}\). We use the standard convention, π
i
= ɛ
1 + … + ɛ
i
, \(\varepsilon _{n} = -\sum \limits _{i=1}^{n-1}\varepsilon _{i}\). Recall that for any t, \(1\leqslant t <n\), \(\varLambda ^{t}\mathbb{C}^{n}\) is irreducible with the highest weight π
t
. Let {e
1, …, e
n
} be a basis of \(\mathbb{C}^{n}\) such that each e
i
is a weight vector and ℓ
t
: = e
1 ∧ … ∧ e
t
is a highest weight vector of \(\varLambda ^{t}\mathbb{C}^{n}\). Clearly  . Write n − k = d(m − k) + r with \(0 <r\leqslant (m - k)\). Let \(\varphi \!: m\mathbb{C}^{n} \rightarrow \varLambda ^{m}\mathbb{C}^{n}\) be a non-zero m-linear G-equivariant map. Such a map is unique up to a scalar and one can take φ with φ(v
1 + … + v
m
) = v
1 ∧ … ∧ v
m
. In case r ≠ m − k, for any subset I ⊂ {1, …, m} with | I | = k + r, let \(\varphi _{I}\!: m\mathbb{C}^{n} \rightarrow (k + r)\mathbb{C}^{n} \rightarrow \varLambda ^{k+r}\mathbb{C}^{n}\) be the corresponding (almost) canonical map. By the same principle we construct \(\tilde{\varphi }\!: k(\mathbb{C}^{n})^{{\ast}}\rightarrow \varLambda ^{k}(\mathbb{C}^{n})^{{\ast}}\).
. Write n − k = d(m − k) + r with \(0 <r\leqslant (m - k)\). Let \(\varphi \!: m\mathbb{C}^{n} \rightarrow \varLambda ^{m}\mathbb{C}^{n}\) be a non-zero m-linear G-equivariant map. Such a map is unique up to a scalar and one can take φ with φ(v
1 + … + v
m
) = v
1 ∧ … ∧ v
m
. In case r ≠ m − k, for any subset I ⊂ {1, …, m} with | I | = k + r, let \(\varphi _{I}\!: m\mathbb{C}^{n} \rightarrow (k + r)\mathbb{C}^{n} \rightarrow \varLambda ^{k+r}\mathbb{C}^{n}\) be the corresponding (almost) canonical map. By the same principle we construct \(\tilde{\varphi }\!: k(\mathbb{C}^{n})^{{\ast}}\rightarrow \varLambda ^{k}(\mathbb{C}^{n})^{{\ast}}\).
Let us consider the tensor product \(\mathbb{W}:= (\varLambda ^{m}\mathbb{C}^{n})^{\otimes d}\otimes \varLambda ^{k+r}\mathbb{C}^{n}\) and its weight subspace \(\mathbb{W}_{d\pi _{k}}\). One can easily see that \(\mathbb{W}_{d\pi _{k}}\) contains a unique up to a scalar non-zero highest weight vector, namely
This means that \(\mathbb{W}\) contains a unique copy of \(V _{d\pi _{k}}\), where \(V _{d\pi _{k}}\) is an irreducible \(\mathfrak{s}\mathfrak{l}_{n}\)-module with the highest weight dπ
k
. We let ρ denote the representation of \(\mathfrak{g}\mathfrak{l}_{n}\) on \(\varLambda ^{m}\mathbb{C}^{n}\) and ρ
r
the representation of \(\mathfrak{g}\mathfrak{l}_{n}\) on \(\varLambda ^{k+r}\mathbb{C}^{n}\). Let ξ = A + v + w be a point in \(\mathfrak{q}^{{\ast}}\). (It is assumed that \(A \in \mathfrak{s}\mathfrak{l}_{n}\).) Finally let ( , ) denote a non-zero \(\mathfrak{s}\mathfrak{l}_{n}\)-invariant scalar product between \(\mathbb{W}\) and  that is zero on the \(\mathfrak{s}\mathfrak{l}_{n}\)-invariant complement of \(V _{d\pi _{k}}\) in \(\mathbb{W}\). Depending on r, set
that is zero on the \(\mathfrak{s}\mathfrak{l}_{n}\)-invariant complement of \(V _{d\pi _{k}}\) in \(\mathbb{W}\). Depending on r, set
for each I as above in case r < m − k. By the constructions the polynomials F and F I are SL n -invariants.
Lemma 5
The polynomials F and F I are V -invariants.
Proof
We restrict F and F I to \(\mathfrak{g}^{{\ast}} + x\) with x ∈ V ∗ generic. Changing a basis in V if necessary, we may assume that x = E m + E k . If r < m − k, some of the invariants F I may become linear combinations of such polynomials under the change of basis, but this does not interfere with V -invariance. Now φ(v) is a vector of weight π m and \(\tilde{\varphi }(w)^{d}\) of weight − dπ k . Notice that dm + (k + r) = n + kd. If \(\sum \limits _{i=1}^{n+kd}\lambda _{i} = d\sum \limits _{i=1}^{k}\varepsilon _{i}\) and each λ i is one of the ɛ j , \(1\leqslant j\leqslant n\), then in the sequence (λ 1, …, λ n+kd ) we must have exactly one ɛ j for each \(k <j\leqslant n\) and d + 1 copies of each ɛ i with \(1\leqslant i\leqslant k\). Hence the only summand of ρ(A s)m−k φ(E m ) that plays any rôle in F or F I is ℓ k ∧A s e k+1∧…∧A s e m . Moreover, in A s e k+1∧…∧A s e m we are interested only in vectors lying in Λ m−kspan(e k+1, …, e n ).
Let us choose blocks α, U, β of A as shown in Fig. 1.Then up to a non-zero scalar F(A, E m + E k ) is the determinant of
Each column of Uα is a linear combination of the columns of U, a similar relation exists between β t Uα s+1 and β t Uα s. Therefore
We have to check that F(ξ + A, x) = F(ξ, x) for any A ∈ ad∗(V )⋅ x and any \(\xi \in \mathfrak{g}\), see Lemma 1. Recall that \(\mathrm{ad}^{{\ast}}(V )\cdot x =\mathrm{ Ann}(\mathfrak{g}_{x}) = \mathfrak{g}_{x}^{\perp }\subset \mathfrak{g}\). In case x = E m + E k , U is zero in each \(A \in \mathfrak{g}_{x}^{\perp }\) and β corresponding to such A is a scalar matrix. Therefore F(ξ + ad∗(V )⋅ x, x) = F(ξ, x).
The case r < m − k is more complicated. If {1, …, k} ⊂ I, then \(I = \tilde{I}\sqcup \{ 1,\ldots,k\}\). Let \(U_{\tilde{I} }\) be the corresponding submatrix of U and \(\alpha _{\tilde{I} \times \tilde{I}}\) of α. One just has to replace U by \(U_{\tilde{I} }\) and α by \(\alpha _{\tilde{I}\times \tilde{I}}\) in the last polynomial P d−1(α, U, β) obtaining
These are \(\binom{m - k}{r}\) linearly independent invariants in  .
.
Suppose that {1, …, k} ⊄ I. Then ρ I (A d)r has to move more than r vectors e i with \(k + 1\leqslant i\leqslant m\), which is impossible. Thus, F I (A, x) = 0 for such I. □
Theorem 6
Suppose that 0 < k < m < n and m − k divides n − m, then \(\mathrm{ind}\mathfrak{g}_{x} = 1\) for generic x ∈ V ∗ and \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} = \mathbb{C}[V ^{{\ast}}]^{G}[\mathbf{F}]\) is a polynomial ring, the fundamental semi-invariant is equal to F m−k−1 .
Proof
A generic stabiliser \(\mathfrak{g}_{x}\) is \(\mathfrak{s}\mathfrak{l}_{n-m}\ltimes (m - k)\mathbb{C}^{n-m}\). Its ring of symmetric invariants is generated by F = φ x (F), see Theorem 4 and Eq. (5). We also have \(\mathrm{ind}\mathfrak{g}_{x} = 1\). It remains to see that F is not divisible by a non-constant G-invariant polynomial on V ∗. By the construction, F is also invariant with respect to the action of SL m ×SL k . The group L = SL n ×SL m ×SL k act on V ∗ with an open orbit. As long as rk w = k, rk v = m, the L-orbit of y = v + w contains a point v′ + E k , where also rk v′ = m. If in addition the upper k×m-part of v has rank k, then L⋅ y contains x = E m + E k . Here F is non-zero on \(\mathfrak{g} + y\). Since the group L is semisimple, the complement of L⋅ (E m + E k ) contains no divisors and F is not divisible by any non-constant G-invariant in \(\mathbb{C}[V ^{{\ast}}]\). This is enough to conclude that \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q} = \mathbb{C}[V ^{{\ast}}]^{G}[\mathbf{F}]\), see Theorem 2.
The singular set \(\mathfrak{q}_{\mathrm{sing}}^{{\ast}}\) is L-stable. And therefore \(\mathbf{p}_{\mathfrak{q}}\) is also an SL m ×SL k -invariant. Hence p is a power of F. In view of Theorem 2(i), p = F m−k−1. □
Theorem 7
Suppose that 0 < k < m < n and m − k does not divide n − m, then \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is not a polynomial ring.
Proof
The reason for this misfortune is that \(\binom{m}{k + r}> \binom{m - k}{r}\) for r < m − k. One could prove that each F I must be in the set of generators and thereby show that \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{Q}\) is not a polynomial ring. But we present a different argument.
Assume that the ring of symmetric invariants is polynomial. It is bi-graded and SL
m
acts on it preserving the bi-grading. Since SL
m
is reductive, we can assume that there is a set {H
1, …, H
s
} of bi-homogeneous mixed generators such that  and the \(\mathbb{C}\)-linear span
and the \(\mathbb{C}\)-linear span  is SL
m
-stable. The polynomiality implies that a generic stabiliser \(\mathfrak{g}_{x} = \mathfrak{s}\mathfrak{l}_{n-m}\ltimes (m - k)\mathbb{C}^{n-m}\) has a free algebra of symmetric invariants, see Theorem 2(ii), and by the same statement φ
x
is surjective. This means that r is either 1 or m − k − 1, see Theorem 4, s = m − k, and φ
x
is injective on
is SL
m
-stable. The polynomiality implies that a generic stabiliser \(\mathfrak{g}_{x} = \mathfrak{s}\mathfrak{l}_{n-m}\ltimes (m - k)\mathbb{C}^{n-m}\) has a free algebra of symmetric invariants, see Theorem 2(ii), and by the same statement φ
x
is surjective. This means that r is either 1 or m − k − 1, see Theorem 4, s = m − k, and φ
x
is injective on  . Taking our favourite (generic) x = E
m
+ E
k
, we see that there is SL
m−k
embedded diagonally into G×SL
m
, which acts on
. Taking our favourite (generic) x = E
m
+ E
k
, we see that there is SL
m−k
embedded diagonally into G×SL
m
, which acts on  as on \(\varLambda ^{r}\mathbb{C}^{m-k}\). The group SL
m−k
acts on
as on \(\varLambda ^{r}\mathbb{C}^{m-k}\). The group SL
m−k
acts on  in the same way. Since m − k does not divide n − m, we have \(m - k\geqslant 2\). The group SL
m
cannot act on an irreducible module \(\varLambda ^{r}\mathbb{C}^{m-k}\) of its non-trivial subgroup SL
m−k
, this is especially obvious in our two cases of interest, r = 1 and r = m − k − 1. A contradiction. □
in the same way. Since m − k does not divide n − m, we have \(m - k\geqslant 2\). The group SL
m
cannot act on an irreducible module \(\varLambda ^{r}\mathbb{C}^{m-k}\) of its non-trivial subgroup SL
m−k
, this is especially obvious in our two cases of interest, r = 1 and r = m − k − 1. A contradiction. □
Conjecture 1
It is very probable that \(\mathbb{C}[\mathfrak{q}^{{\ast}}]^{\mathfrak{q}} = \mathbb{C}[V ^{{\ast}}]^{G}[\{\mathbf{F}_{I}\}]\) for all \(n> m> k\geqslant \ 1\).
References
O.M. Adamovich, E.O. Golovina, Simple linear Lie groups having a free algebra of invariants. Sel. Math. Sov. 3, 183–220 (1984); originally published in Voprosy teorii grupp i gomologicheskoi algebry, Yaroslavl, 1979, 3–41 (in Russian)
S. Helgason, Some results on invariant differential operators on symmetric spaces. Amer. J. Math. 114(4), 789–811 (1992)
A. Joseph, D. Shafrir, Polynomiality of invariants, unimodularity and adapted pairs. Transformation Groups 15(4), 851–882 (2010)
D. Panyushev, On the coadjoint representation of \(\mathbb{Z}_{2}\)-contractions of reductive Lie algebras. Adv. Math. 213(1), 380–404 (2007)
D. Panyushev, A. Premet, O. Yakimova, On symmetric invariants of centralisers in reductive Lie algebras. J. Algebra 313, 343–391 (2007)
M. Raïs, L’indice des produits semi-directs \(E \times _{\rho }\mathfrak{g}\), C. R. Acad. Sci. Paris Ser. A, 287, 195–197 (1978)
G.W. Schwarz, Representations of simple Lie groups with regular rings of invariants. Invent. Math. 49, 167–191 (1978)
E.B. Vinberg, V.L. Popov, Invariant theory, in Algebraic Geometry IV, (Itogi Nauki i Tekhniki, Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1989), pp. 137–314; English translation: Encyclopaedia Math. Sci., vol. 55, Springer, Berlin, 1994
O. Yakimova, One-parameter contractions of Lie-Poisson brackets. J. Eur. Math. Soc. 16, 387–407 (2014)
O. Yakimova, Symmetric invariants of \(\mathbb{Z}_{2}\)-contractions and other semi-direct products. Int. Math. Res. Not. 2017(6), 1674–1716 (2017).
Acknowledgements
I would like to thank the organisers of the intensive period on “Perspectives in Lie theory”, especially Giovanna Carnovale and Martina Lanini, for the invitation to Pisa and a very warm welcome.
This work is partially supported by the DFG priority programme SPP 1388 “Darstellungstheorie” and by the Graduiertenkolleg GRK 1523 “Quanten- und Gravitationsfelder”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Yakimova, O. (2017). Some Semi-Direct Products with Free Algebras of Symmetric Invariants. In: Callegaro, F., Carnovale, G., Caselli, F., De Concini, C., De Sole, A. (eds) Perspectives in Lie Theory. Springer INdAM Series, vol 19. Springer, Cham. https://doi.org/10.1007/978-3-319-58971-8_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-58971-8_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58970-1
Online ISBN: 978-3-319-58971-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





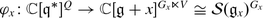 is surjective,
is surjective,
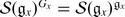 , and
, and
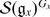 is a polynomial ring in
is a polynomial ring in