Abstract
Abstract In these notes we give an introduction to representation theory of simple finite-dimensional Lie superalgebras. We concentrate on so called basic superalgebras. Those are superalgebras which have even reductive part and admit an invariant form. We start with structure theory of basic superalgebras emphasizing abstract properties of roots and then proceed to representations, trying to demonstrate the variety of methods: Harish-Chandra homomorphism, support variety, translation functors, Borel-Weil-Bott theory and localization.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
- Atypicality
- Blocks
- BorelWeilBott theorem
- Harish-Chandra homomorphism
- Lie superalgebras
- Supermanifold
- Translation functors
1 Introduction
In these notes we give an introduction to representation theory of simple finite-dimensional Lie superalgebras. We concentrate on so called basic superalgebras. Those are superalgebras which have even reductive part and admit an invariant form. Representation theory of these superalgebras was initiated in 1978 by V. Kac, see [23]. It turned out that finite-dimensional representations of basic superalgebras are not easy to describe completely and questions which arise in this theory are analogous to similar questions in positive characteristic.
We start with structure theory of basic superalgebras emphasizing abstract properties of roots and then proceed to representations, trying to demonstrate the variety of methods: Harish-Chandra homomorphism, support variety, translation functors, Borel-Weil-Bott theory and localization.
We assume from the reader the thorough knowledge of representation theory of reductive Lie algebras (in characteristic zero) and rudimentary knowledge of algebraic geometry.
Let me mention several monographs related to the topic of these lectures: [32] and [4] on Lie superalgebras and [3] on supermanifolds. The reader can find some details in these books.
2 Preliminaries
2.1 Superalgebras in General
In supermathematics we study Z 2-graded objects. The word super means simply “Z 2-graded”, whenever it is used (superalgebra, superspace etc.).
We denote by k the ground field and assume that char(k) ≠ 2.
Definition 1
An associative superalgebra is a Z 2 graded algebra A = A 0 ⊕ A 1. If a ∈ A i is a homogeneous element, then \(\bar{a}\) will denote the parity of a, that is \(\bar{a} = 0\) if a ∈ A 0 or \(\bar{a} = 1\) if a ∈ A 1.
All modules over an associative superalgebra A are also supposed to be Z 2-graded. Thus, an A-module M has a grading M = M 0 ⊕ M 1 such that A i M j ⊂ M i+j .
In particular, a vector superspace is a Z 2-graded vector space. The associative algebra \(\mathop{\mathrm{End}}\nolimits _{k}(V )\) of all k-linear transformation of a vector superspace V has a natural structure of a superalgebra with the Z 2-grading given by:
If e 1, …, e m is a basis of V 0 and e m+1, …, e m+n is a basis of V 1, then we can identify \(\mathop{\mathrm{End}}\nolimits _{k}(V )\) with block matrices \(\left (\begin{array}{*{10}c} A&B\\ C &D \end{array} \right )\) and
All formulas are written for homogeneous elements only and then extended to all objects by linearity. Every term has a sign coefficient, which is determined by following the sign rule:
If one term is obtained from another by swapping adjacent symbols x and y we put the coefficient \((-1)^{\bar{x}\bar{y}}\).
Example 1
Consider the commutator [x, y]. In the classical world it is defined by [x, y] = xy − yx. In superworld we write instead:
The sign rule has its roots in the tensor category theory. More precisely, the category SV ect of supervector spaces is an abelian rigid symmetric tensor category with brading s: V ⊗ W → W ⊗ V given by the sign rule
All objects, which can be defined in context of tensor category: affine schemes, algebraic groups etc. can be generalized to superschemes, supergroups etc. if we work in the category SV ect instead of the category V ect of vector spaces. We refer the reader to [9] for details in this approach. We will follow the sign rule naively and see that it always gives the correct answer.
Definition 2
We say that a superalgebra A is supercommutative if
for all homogeneous x, y ∈ A.
Exercise
Show that a free supercommutative algebra with odd generators ξ 1, …, ξ n is the exterior (Grassmann) algebra Λ(ξ 1, …ξ n ).
All the morphisms between superalgebras, modules etc. have to preserve parity. In this way if A is a superalgebra then the category of A-modules is an abelian category. This category is equipped with the parity change functor Π. If M = M 0 ⊕ M 1 is an A-module we set ΠM: = M with new grading (ΠM)0 = M 1, (ΠM)1 = M 0 and the obviuos A-action. It is clear that Π is an autoequivalence of the abelian category of A-modules.
Exercise
Let V be a finite dimensional vector superspace and V ∗ be the dual vector space with Z 2-grading defined in the obvious way. Consider a linear operator X: V ⟶ V. We would like to define the adjoint operator X ∗: V ∗ ⟶ V ∗ following the sign rule. For ϕ ∈ V ∗ and v ∈ V we set
where < ⋅ , ⋅ >: V ∗⊗ V → k is the natural pairing. Let {e i }, i = 1, …, m + n be a homogeneous basis of V as above and { f i } be the dual basis of V ∗ in the sense that < f j , e i > = δ i, j . Show that if the matrix of X in the basis {e i } is \(\left (\begin{array}{*{10}c} A&B\\ C &D \end{array} \right )\), then the matrix of X ∗ in the basis { f i } equals \(X^{st} = \left (\begin{array}{*{10}c} A^{t} &-C^{t} \\ B^{t}& D^{t} \end{array} \right )\). The operation X ↦ X st is called the supertransposition and it satisfies the identity
Our next example is the supertrace. To define it we use the canonical identification \(V \otimes V ^{{\ast}}\cong \mathop{\mathrm{End}}\nolimits _{k}(V )\) given by
The supertrace \(\mathop{\mathrm{str}}\nolimits:\mathop{ \mathrm{End}}\nolimits _{k}(V ) \rightarrow k\) is the composition
Exercise
Prove that if \(X = \left (\begin{array}{*{10}c} A&B\\ C &D \end{array} \right )\) then
-
(a)
\(\mathop{\mathrm{str}}\nolimits (X) =\mathrm{ tr}(A) -\mathrm{ tr}D\),
-
(b)
\(\mathop{\mathrm{str}}\nolimits ([X,Y ]) = 0\).
The superdimension \(\mathop{\mathrm{sdim}}\nolimits V\) of a superspace V is by definition the supertrace of the identity operator in V. It follows from the above exercise that \(\mathop{\mathrm{sdim}}\nolimits V =\mathrm{ dim}V _{0} -\mathrm{ dim}V _{1}\). It is important sometimes to remember both even and odd dimension of V. So we set dimV = (dimV 0 | dimV 1) = (m | n) be an element m + nɛ in the ring Z(ɛ)∕(ɛ 2 − 1).
Exercise
Show that
-
(a)
\(\mathop{\mathrm{sdim}}\nolimits (V \oplus W) =\mathop{ \mathrm{sdim}}\nolimits V +\mathop{ \mathrm{sdim}}\nolimits W\) and dim(V ⊕ W) = dimV + dimW,
-
(b)
\(\mathop{\mathrm{sdim}}\nolimits (V \otimes W) =\mathop{ \mathrm{sdim}}\nolimits V \mathop{\mathrm{sdim}}\nolimits W\) and dim(V ⊗ W) = dimV dimW,
-
(c)
\(\mathop{\mathrm{sdim}}\nolimits (\varPi V ) = -\mathop{\mathrm{sdim}}\nolimits V\) and dim(ΠV ) = ɛdimV.
2.2 Lie Superalgebras
Definition 3
A Lie superalgebra
 is a vector superspace with a bilinear even map
is a vector superspace with a bilinear even map  such that:
such that:
-
1.
\([x,y] = -(-1)^{\bar{x}\bar{y}}[y,x]\),
-
2.
\([x,[y,z]] = [[x,y],z] + (-1)^{\bar{x}\bar{y}}[y,[x,z]]\).
Example 2
If A is an associative superalgebra, one can make it into a Lie superalgebra \(\mathop{\mathrm{Lie}}\nolimits (A)\) by defining the bracket:
For example if \(A =\mathop{ \mathrm{End}}\nolimits (V )\), dim(V ) = (m | n), then Lie(A) is the Lie superalgebra which we denote by  .
.
Definition 4
If A is an associative superalgebra, d: A ⟶ A is a derivation of A if:
Exercise
-
(a)
Check that the space Der(A) of all derivations of A with bracket given by the supercommutator is a Lie superalgebra.
-
(b)
Consider A = Λ(ξ 1, …ξ n ). Then Der(A) is a finite-dimensional superalgebra denoted by W(0 | n). Show that its dimension is (2n−1 n | 2n−1 n).
Exercise
Show that  with bracket [⋅ , ⋅ ] is a Lie superalgebra if and only if
with bracket [⋅ , ⋅ ] is a Lie superalgebra if and only if
-
1.
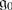 is a Lie algebra;
is a Lie algebra; -
2.
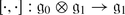 equips
equips 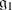 with the structure of a
with the structure of a 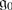 -module;
-module; -
3.
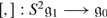 is a homomorphism of
is a homomorphism of 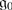 -modules;
-modules; -
4.
for all
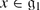 , [x, [x, x]] = 0.
, [x, [x, x]] = 0.
Example 3
Let us introduce the “smallest” simple Lie superalgebra  of dimension (3 | 2). Take
of dimension (3 | 2). Take  and
and  , where V is the two dimensional irreducible representation of
, where V is the two dimensional irreducible representation of  . The isomorphims
. The isomorphims  of
of  -modules defines the bracket
-modules defines the bracket  . One can easily check that [x, [x, x]] = 0 for all
. One can easily check that [x, [x, x]] = 0 for all  and hence by the previous exercise these data define a Lie superalgebra structure.
and hence by the previous exercise these data define a Lie superalgebra structure.
Example 4 (Bernstein)
Consider a symplectic manifold M, with symplectic form ω ∈ Ω 2 M. Consider the following operators acting on the de Rham complex Ω(M):
-
ω: Ω i(M) ⟶ Ω i+2(M), given by ∧ω,
-
i ω : Ω i(M) ⟶ Ω i−2(M), given by contraction with bivector ω ∗,
-
grading operator h: Ω i(M) ⟶ Ω i(M).
It is a well known fact that ω, h, i ω form an sl(2)-triple.
Assume now that  is a line bundle on M with a connection ∇. Assume further that the curvature of ∇ equals tω for some non-zero t. Recall that ∇ is an operator of degree 1 on the sheaf
is a line bundle on M with a connection ∇. Assume further that the curvature of ∇ equals tω for some non-zero t. Recall that ∇ is an operator of degree 1 on the sheaf  of differential forms with coefficients in
of differential forms with coefficients in 

On the other hand, ω, h, i
ω
act on  in the same manner as before. Set ∇∗: = [∇, i
ω
]. One can check that ∇, ∇∗, together with ω, h, i
ω
span the superalgebra isomorphic to
in the same manner as before. Set ∇∗: = [∇, i
ω
]. One can check that ∇, ∇∗, together with ω, h, i
ω
span the superalgebra isomorphic to  .
.
The universal enveloping algebra
 is the associative superalgebra which satisfies the natural universality property in the category of superalgebras. It can be defined as the quotient of the tensor superalgebra
is the associative superalgebra which satisfies the natural universality property in the category of superalgebras. It can be defined as the quotient of the tensor superalgebra  by the ideal generated by \(XY - (-1)^{\bar{X}\bar{Y }}Y X - [X,Y ]\) for all homogeneous
by the ideal generated by \(XY - (-1)^{\bar{X}\bar{Y }}Y X - [X,Y ]\) for all homogeneous  . The PBW theorem holds in the supercase, i.e.
. The PBW theorem holds in the supercase, i.e.  . However,
. However,  is a free commutative superalgebra. From the point of view of the usual tensor algebra we have an isomorphism
is a free commutative superalgebra. From the point of view of the usual tensor algebra we have an isomorphism  .
.
3 Basic Lie Superalgebras
3.1 Simple Lie Superalgebras
A Lie superalgebra is simple if it does not have proper non-trivial ideals (ideals are of course Z 2-graded).
Exercise
Prove that if a Lie superalgebra  is simple, then
is simple, then  and
and  .
.
In 1977 Kac classified simple Lie superalgebras over an algebraically closed field k of characteristic zero, [22]. He divided simple Lie superalgebras into three groups:
-
basic: classical and exceptional,
-
strange: P(n), Q(n),
-
Cartan type: W(0 | n) = DerΛ(ξ 1, …ξ n ) and some subalgebras of it.
Basic and strange Lie superalgebras have a reductive even part. Cartan type superalgebras have a non-reductive  .
.
Definition 5
A simple Lie superalgebra  is basic if
is basic if  is reductive and if
is reductive and if  admits a non-zero invariant even symmetric form (⋅ , ⋅ ), i. e. the form satisfying the condition
admits a non-zero invariant even symmetric form (⋅ , ⋅ ), i. e. the form satisfying the condition

or, equivalently,
and (x, y) ≠ 0 implies \(\bar{x} =\bar{ y}\).
Exercise 1
Let V be a finite-dimensional  -module. Then the form
-module. Then the form
is an invariant even symmetric form.
In this section we describe the basic Lie superalgebras. We start with classical Lie superalgebras. The invariant symmetric form is given by the supertrace in the natural module V.
Special linear Lie Superalgebra
 is the subalgebra of
is the subalgebra of  of matrices with supertrace zero. It is not hard to verify that
of matrices with supertrace zero. It is not hard to verify that  is simple if m ≠ n and \(m + n\geqslant 2\). What happens when m = n? In this case the supertrace of the identity matrix is zero and therefore
is simple if m ≠ n and \(m + n\geqslant 2\). What happens when m = n? In this case the supertrace of the identity matrix is zero and therefore  has a one-dimensional center
has a one-dimensional center  consisting of all scalar matrices. We define
consisting of all scalar matrices. We define  .
.
Exercise
Check that  is simple if \(n\geqslant 2\).
is simple if \(n\geqslant 2\).
Look at the case n = 1. Then  , where
, where
Then the commutators are:
and we see that  is a nilpotent (1 | 2)-dimensional Lie superalgebra, which is the superanalogue of the Heisenberg algebra. Furthermore,
is a nilpotent (1 | 2)-dimensional Lie superalgebra, which is the superanalogue of the Heisenberg algebra. Furthermore,  is an abelian (0 | 2)-dimensional superalgebra.
is an abelian (0 | 2)-dimensional superalgebra.
We have  . Hence
. Hence

Note also that  has a compatible Z-gradingFootnote 1:
has a compatible Z-gradingFootnote 1:

with  and
and

The Orthosymplectic Lie Superalgebra
 is also a subalgebra of
is also a subalgebra of  . Let V be a vector superspace of dimension (m | n) equipped with an even non-degenerate bilinear symmetric form (⋅ , ⋅ ), i.e. for all homogeneous v, w ∈ V we have
. Let V be a vector superspace of dimension (m | n) equipped with an even non-degenerate bilinear symmetric form (⋅ , ⋅ ), i.e. for all homogeneous v, w ∈ V we have
Note that (⋅ , ⋅ ) is symmetric on V 0 and symplectic on V 1. Hence the dimension of V 1 must be even, n = 2l. We define:

It is easy to see that  . So the two classical series, orthogonal and symplectic, come together in the superalgebra theory. One can see also that
. So the two classical series, orthogonal and symplectic, come together in the superalgebra theory. One can see also that  is isomorphic to V
0 ⊗ V
1 as a
is isomorphic to V
0 ⊗ V
1 as a  -module. Furthermore it is easy to check that
-module. Furthermore it is easy to check that  is simple for all m, l > 0.
is simple for all m, l > 0.
Lemma 1
Let
 be a simple finite-dimensional Lie superalgebra over an algebraically closed field k. Then the center of
be a simple finite-dimensional Lie superalgebra over an algebraically closed field k. Then the center of
 is at most one dimensional.
is at most one dimensional.
Proof
Assume the opposite. Let z
1, z
2 be two linearly independent elements in the center of  . For all a, b ∈ k set
. For all a, b ∈ k set

Then we have
-
1.
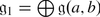 ;
; -
2.
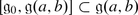 ;
; -
3.
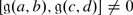 implies a = −c, b = −d.
implies a = −c, b = −d.
These conditions imply that  is an ideal in
is an ideal in  . Therefore by simplicity of
. Therefore by simplicity of  we obtain that for some a, b ∈ k,
we obtain that for some a, b ∈ k,  . Set z = bz
1 − az
2 if a ≠ 0 and z = z
1 if a = 0. Then ad
z
acts nilpotently on
. Set z = bz
1 − az
2 if a ≠ 0 and z = z
1 if a = 0. Then ad
z
acts nilpotently on  . But
. But  is an ideal in
is an ideal in  . Hence z = 0 and we obtain a contradiction.
. Hence z = 0 and we obtain a contradiction.
Lemma 2
Let
 be a basic Lie superalgebra and
be a basic Lie superalgebra and
 . Then one of the following holds.
. Then one of the following holds.
-
1.
There is a Z -grading
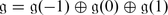 , such that
, such that
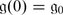 and
and
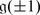 are irreducible
are irreducible
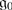 -modules.
-modules.
-
2.
The even part
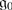 is semisimple and
is semisimple and
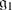 is an irreducible
is an irreducible
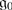 -module.
-module.
Proof
Consider the restriction of the invariant form (⋅ , ⋅ ) on  . Let
. Let  be two
be two  submodules such that (M, N) = 0. Then by invariance of the form we have
submodules such that (M, N) = 0. Then by invariance of the form we have  . Hence [M, N] = 0. In particular, let
. Hence [M, N] = 0. In particular, let  be an irreducible
be an irreducible  submodule. Then the restriction of (⋅ , ⋅ ) on M is either non-degenerate or zero.
submodule. Then the restriction of (⋅ , ⋅ ) on M is either non-degenerate or zero.
In the first case, let N = M
⊥ and I = M ⊕ [M, M]. Then [N, I] = 0 and  . Hence I is an ideal of
. Hence I is an ideal of  , which implies N = 0,
, which implies N = 0,  and
and  satisfies 2. It follows from the proof of Lemma 1 that
satisfies 2. It follows from the proof of Lemma 1 that  has trivial center.
has trivial center.
In the second case there exists an irreducible isotropic submodule  such that (⋅ , ⋅ ) defines a
such that (⋅ , ⋅ ) defines a  -invariant non-degenerate pairing M × M
′ → k. By the same argument as in the previous case we have
-invariant non-degenerate pairing M × M
′ → k. By the same argument as in the previous case we have  , [M, M] = [M
′, M
′] = 0. Thus, we can set
, [M, M] = [M
′, M
′] = 0. Thus, we can set

Hence  satisfies 1.
satisfies 1.
We say that a basic  is of type 1 (resp. of type 2) if it satisfies 1 (resp. 2). Note that if
is of type 1 (resp. of type 2) if it satisfies 1 (resp. 2). Note that if  is of type 1, then
is of type 1, then  and
and  are dual
are dual  -modules.
-modules.
Exercise
Check that  ,
,  and
and  are of type 1, and
are of type 1, and  is of type 2 if m ≠ 2.
is of type 2 if m ≠ 2.
In contrast with simple Lie algebras, simple Lie superalgebras can have non-trivial central extensions, derivations and deformations. Besides, finite-dimensional representations of simple Lie superalgebras are not completely reducible.
Example 5
Consider the short exact sequence of Lie superalgebras:

One can see that this sequence does not split. In other words, a simple Lie superalgebra  has a non-trivial central extension. The dual of this example implies that a finite-dimensional representation of a simple Lie algebra may be not completely reducible, just look at the representation of
has a non-trivial central extension. The dual of this example implies that a finite-dimensional representation of a simple Lie algebra may be not completely reducible, just look at the representation of  in
in  and the exact sequence
and the exact sequence

The next example will show that sometimes simple Lie superalgebras have non-trivial deformations.
Example 6
Let  . We have
. We have

In fact, this is the only example of a classical Lie superalgebra whose even part has more then two simple ideals. If V denotes the irreducible 2-dimensional representation of  , then
, then  is isomorphic to V ⊠ V ⊠ V as a
is isomorphic to V ⊠ V ⊠ V as a  -module.
-module.
We will construct a one parameter deformation of this superalgebra by deforming the bracket  . Let
. Let  and
and  be non-trivial
be non-trivial  -equivariant maps. Define the bracket between two odd elements by the formula
-equivariant maps. Define the bracket between two odd elements by the formula
for some t 1, t 2, t 3 ∈ k.
Exercise
The Jacobi identity holds if and only if t 1 + t 2 + t 3 = 0.
When t
1 + t
2 + t
3 = 0 we obtain a new Lie superalgebra structure on  : we denote the corresponding Lie superalgebra by D(2, 1 | t
1, t
2, t
3). We see immediately that
: we denote the corresponding Lie superalgebra by D(2, 1 | t
1, t
2, t
3). We see immediately that
for all c ∈ k
∗ and s ∈ S
3. One can check that  and that D(2, 1 | t
1, t
2, t
3) is simple whenever t
1
t
2
t
3 ≠ 0. By setting \(a = \frac{t_{2}} {t_{1}}\) one obtains a one-parameter family D(2, 1, a) of Lie superalgebras. One can consider a as a local coordinate in P
1
∖{0, −1, ∞}.
and that D(2, 1 | t
1, t
2, t
3) is simple whenever t
1
t
2
t
3 ≠ 0. By setting \(a = \frac{t_{2}} {t_{1}}\) one obtains a one-parameter family D(2, 1, a) of Lie superalgebras. One can consider a as a local coordinate in P
1
∖{0, −1, ∞}.
Exercise
Prove that, if a = 0, then D(2, 1, a) has the ideal J isomorphic to  with the quotient D(2, 1, a)∕J isomorphic to
with the quotient D(2, 1, a)∕J isomorphic to  . Use this to prove that the superalgebra of derivations of
. Use this to prove that the superalgebra of derivations of  is isomorphic to D(2, 1, 0).
is isomorphic to D(2, 1, 0).
Consider now the following general construction of a basic Lie superalgebra of type 2. Let

where  and
and  are simple Lie algebras, M is a simple
are simple Lie algebras, M is a simple  -module and N a simple
-module and N a simple  -module. Assume in addition that M has an
-module. Assume in addition that M has an  -invariant skewsymmetric form ω, while N has an
-invariant skewsymmetric form ω, while N has an  -invariant symmetric form γ. Then we have isomorphisms
-invariant symmetric form γ. Then we have isomorphisms  and
and  . Hence
. Hence  is a submodule in S
2
M and
is a submodule in S
2
M and  is a submodule in Λ
2
N. Let
is a submodule in Λ
2
N. Let  ,
,  denote the projections on the corresponding submodules. For some t ∈ k and all x, x
′ ∈ M, y, y
′ ∈ N we set
denote the projections on the corresponding submodules. For some t ∈ k and all x, x
′ ∈ M, y, y
′ ∈ N we set
If for a suitable t ∈ k we have [X, [X, X]] = 0 for all  , then
, then  is a Lie superalgebra. For instance, this construction works for
is a Lie superalgebra. For instance, this construction works for  with
with  and M, N being the standard modules.
and M, N being the standard modules.
This construction also works for exceptional Lie superalgebras: G 3 and F 4 (in Kac’s notation). We prefer to use the notation AG 2 and AB 3 to avoid confusion with Lie algebras.
-
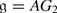 with
with 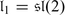 ,
, 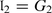 , M is the 2-dimensional irreducible
, M is the 2-dimensional irreducible 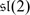 -module and N is the smallest irreducible G
2-module of dimension 7. One can easily see that dimAG
2 = (17 | 14).
-module and N is the smallest irreducible G
2-module of dimension 7. One can easily see that dimAG
2 = (17 | 14). -
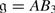 with
with 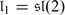 ,
, 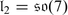 , M is again the 2-dimensional irreducible
, M is again the 2-dimensional irreducible 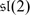 -module, N is the spinor representation of
-module, N is the spinor representation of  . Clearly, dimAB
3 = (24 | 16).
. Clearly, dimAB
3 = (24 | 16).
Theorem 1 (Kac, [22])
Let k be an algebraically closed field of characteristic zero and
 be a basic Lie superalgebra over k with nontrivial
be a basic Lie superalgebra over k with nontrivial
 . Then
. Then
 is isomorphic to one of the following superalgebras:
is isomorphic to one of the following superalgebras:
-
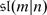 ,
\(1\leqslant m <n\)
;
,
\(1\leqslant m <n\)
;
-
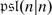 ,
\(n\geqslant 2\)
;
,
\(n\geqslant 2\)
;
-
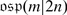 ,
\(m,n\geqslant 1\)
, (m, n) ≠ (2, 1), (4, 1);
,
\(m,n\geqslant 1\)
, (m, n) ≠ (2, 1), (4, 1);
-
D(2, 1, a), a ∈ (P 1 ∖{0, −1, ∞})∕S 3 ;
-
AB 3 ;
-
AG 2.
For the proof of Theorem 1 we refer the reader to the original paper of Kac. Some hints can be also found in the next Section.
Exercise
Show that  and
and  are isomorphic Lie superalgebras. Check that the list in Theorem 1 does not contain isomorphic superalgebras.
are isomorphic Lie superalgebras. Check that the list in Theorem 1 does not contain isomorphic superalgebras.
3.2 Roots Decompositions of Basic Lie Superalgebras
From now on we will always assume that k is algebraically closed of characteristic zero.
Let  be a basic Lie superalgebra,
be a basic Lie superalgebra,  be a Cartan subalgebra of
be a Cartan subalgebra of  and W denote the Weyl group of
and W denote the Weyl group of  . If
. If  is of type 1 but
is of type 1 but  is semisimple it will be convenient to consider a bigger superalgebra
is semisimple it will be convenient to consider a bigger superalgebra  by adding to
by adding to  the grading element z (if
the grading element z (if  , then
, then  ). In this case we set
). In this case we set  , otherwise
, otherwise  . Let
. Let  be the centralizer of
be the centralizer of  in
in  .
.
Lemma 3
We have
 and
and
 .
.
Proof
If  is of type 1, the statement is trivial. If
is of type 1, the statement is trivial. If  is of type 2, then
is of type 2, then  is an irreducible
is an irreducible  -module which admits invariant symplectic form. Then such representation does not have zero weight, see [34, Chap. 4.3, Exercise 13].
-module which admits invariant symplectic form. Then such representation does not have zero weight, see [34, Chap. 4.3, Exercise 13].
Lemma 3 implies that  acts semisimply on
acts semisimply on  . Hence we have a root decomposition
. Hence we have a root decomposition

Here Δ is a finite subset of non-zero vectors in  , whose elements are called roots. The subalgebra
, whose elements are called roots. The subalgebra  is called a Cartan subalgebra of
is called a Cartan subalgebra of  .
.
The following conditions are straightforward
-
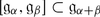 if α + β ≠ 0 and
if α + β ≠ 0 and 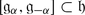 .
. -
The invariant form (⋅ , ⋅ ) defines a non-degenerate pairings
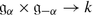 for all α ∈ Δ and
for all α ∈ Δ and 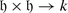 .
. -
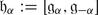 is a one-dimensional subspace in
is a one-dimensional subspace in 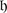 . That follows from the first two properties and the identity ([x, y], h) = α(h)(x, y) for
. That follows from the first two properties and the identity ([x, y], h) = α(h)(x, y) for 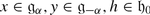 .
.
We can define the non-degenerate symmetric form on (⋅ | ⋅ ) on  as the pull back of (⋅ , ⋅ ) with respect to
as the pull back of (⋅ , ⋅ ) with respect to  , where p is the canonical projection and
, where p is the canonical projection and  is an isomorphism induced by (⋅ , ⋅ ). For any two roots α, β ∈ Δ
is an isomorphism induced by (⋅ , ⋅ ). For any two roots α, β ∈ Δ

Lemma 4
Let α ∈ Δ be a root.
-
1.
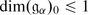 ;
;
-
2.
If
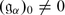 , then
, then
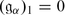 .
.
Proof
Since  is reductive 1 is trivial. To prove 2 consider the root
is reductive 1 is trivial. To prove 2 consider the root  -subalgebra
-subalgebra  . Let
. Let  and x ≠ 0. Then from representation theory of
and x ≠ 0. Then from representation theory of  we know that [y
α
, x] ≠ 0. But
we know that [y
α
, x] ≠ 0. But  . Contradiction.
. Contradiction.
We call α ∈ Δ even (resp. odd) if  , (resp.
, (resp.  ). We denote by Δ
0 (resp. Δ
1) the set of even (resp. odd roots). The preceding lemma implies that Δ is the disjoint union of Δ
0 and Δ
1.
). We denote by Δ
0 (resp. Δ
1) the set of even (resp. odd roots). The preceding lemma implies that Δ is the disjoint union of Δ
0 and Δ
1.
Lemma 5
-
1.
If α ∈ Δ 0 , then (α | α) ≠ 0.
-
2.
If α ∈ Δ 1 and (α | α) ≠ 0, then for any non-zero
 , [x, x] ≠ 0. Hence 2α ∈ Δ
0.
, [x, x] ≠ 0. Hence 2α ∈ Δ
0. -
3.
If α ∈ Δ 1 and (α | α) ≠ 0, then \(\frac{2(\alpha \vert \beta )} {(\beta \vert \beta )} \in \{-1,0,1\}\) for any β ∈ Δ 0.
-
4.
If α ∈ Δ 1 and (α | α) = 0, then \(\frac{2(\alpha \vert \beta )} {(\beta \vert \beta )} \in \{-2,-1,0,1,2\}\) for any β ∈ Δ 0.
Proof
1 is the property of root decomposition of reductive Lie algebras. To show 2 let  be such that (x, y) ≠ 0. Then h = [y, x] ≠ 0 and by (1) we obtain
be such that (x, y) ≠ 0. Then h = [y, x] ≠ 0 and by (1) we obtain
To prove the last two statements we consider the root  -triple {x
β
, h
β
, y
β
}. Then from the representation theory of
-triple {x
β
, h
β
, y
β
}. Then from the representation theory of  we obtain that \(\frac{2(\alpha \vert \beta )} {(\beta \vert \beta )} =\alpha (h_{\beta })\) must be an integer.
we obtain that \(\frac{2(\alpha \vert \beta )} {(\beta \vert \beta )} =\alpha (h_{\beta })\) must be an integer.
To show 3 we use the fact that 2α is an even root. We know from the structure theory of reductive Lie algebras that
Taking into account that \(\frac{2(\alpha \vert \beta )} {(\beta \vert \beta )} \in \mathbf{Z}\), we obtain the assertion.
Finally, let us prove 4. Without loss of generality we may assume that k = α(h
β
) > 1. Then we claim that  , hence α −β is a root. Moreover
, hence α −β is a root. Moreover
Therefore γ: = 2(α −β) is an even root and we have
which implies k = 2.
Exercise
An odd root α is called isotropic if (α | α) = 0. Show that if  is of type 1, then all odd roots are isotropic.
is of type 1, then all odd roots are isotropic.
It is clear that W acts on Δ and preserves the parity and the scalar products between roots.
Lemma 6
-
(a)
If
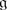 is of type 1 then W has two orbits in Δ
1
, the roots of
is of type 1 then W has two orbits in Δ
1
, the roots of
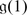 and the roots of
and the roots of
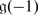 .
. -
(b)
If
 is of type 2, then W acts transitively on the set of isotropic and the set of non-isotropic odd roots.
is of type 2, then W acts transitively on the set of isotropic and the set of non-isotropic odd roots.
Proof
If all roots of  are isotropic, then it follows from the proof of Lemma 5 (4) that α(h
β
) = ±1 or 0 for any odd root α and even root β. In particular, if we fix positive roots in Δ
0 and consider a highest weight α in
are isotropic, then it follows from the proof of Lemma 5 (4) that α(h
β
) = ±1 or 0 for any odd root α and even root β. In particular, if we fix positive roots in Δ
0 and consider a highest weight α in  (or
(or  in type 1 case), the above condition implies that
in type 1 case), the above condition implies that  (resp.
(resp.  ) is a minuscule representation of
) is a minuscule representation of  .
.
If  is of type 2 and the highest weight α is isotropic, then we have α(h
β
) = ±1, ±2 or 0 for any positive β. That implies the existence of two orbits. Finally if α is not isotropic, then
is of type 2 and the highest weight α is isotropic, then we have α(h
β
) = ±1, ±2 or 0 for any positive β. That implies the existence of two orbits. Finally if α is not isotropic, then  is minuscule, hence there is one W-orbit consisting of non-isotropic roots.
is minuscule, hence there is one W-orbit consisting of non-isotropic roots.
Corollary 1
For any root α ∈ Δ the root space
 has dimension (1 | 0) or (0 | 1).
has dimension (1 | 0) or (0 | 1).
Proof
We need to prove the statement only for odd α. If  is of type 1 or of type 2 with only isotropic or only non-isotropic odd roots, then the statement follows from Lemma 6 since the multiplicity of the highest weight is 1. If
is of type 1 or of type 2 with only isotropic or only non-isotropic odd roots, then the statement follows from Lemma 6 since the multiplicity of the highest weight is 1. If  contains both isotropic and non-isotropic roots, we have to show only that
contains both isotropic and non-isotropic roots, we have to show only that  for a non-isotropic odd root α, which easily follows from Lemma 5 (2).
for a non-isotropic odd root α, which easily follows from Lemma 5 (2).
Remark 1
Note that if we do not extend  to
to  , then Corollary 1 does not hold since the dimension of
, then Corollary 1 does not hold since the dimension of  equals (0 | 2) for any odd α.
equals (0 | 2) for any odd α.
Example 7
Let  . We take as our Cartan subalgebra
. We take as our Cartan subalgebra  the subalgebra of diagonal matrices. Let us denote by ε
1, …ε
m
, δ
1, …δ
n
the roots in
the subalgebra of diagonal matrices. Let us denote by ε
1, …ε
m
, δ
1, …δ
n
the roots in  (\(\epsilon _{i}(\mathop{\mathrm{diag}}\nolimits (a_{1},\ldots a_{m})) = a_{i}\) and similarly for δ
j
). We have:
(\(\epsilon _{i}(\mathop{\mathrm{diag}}\nolimits (a_{1},\ldots a_{m})) = a_{i}\) and similarly for δ
j
). We have:
The invariant form is:
All odd roots are isotropic.
Example 8
Let  .
.  .
.
This is the only example of a basic superalgebra such that all odd roots are non-isotropic.
The above implies that we have in general three types of roots:
-
1.
α ∈ Δ 0. In this case the root spaces
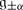 generate a
generate a 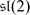 subalgebra (white node in a Dynkin diagram).
subalgebra (white node in a Dynkin diagram). -
2.
α ∈ Δ 1, (α, α) ≠ 0. Then the root spaces
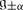 generate a subalgebra isomorphic to
generate a subalgebra isomorphic to 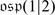 (black node in a Dynkin diagram).
(black node in a Dynkin diagram). -
3.
α ∈ Δ 1, (α, α) = 0. The roots spaces
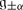 generate a subalgebra isomorphic to
generate a subalgebra isomorphic to 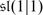 (grey node in a Dynkin diagram).
(grey node in a Dynkin diagram).
Definition 6
Let E be a vector space (over k) equipped with non-degenerate scalar product (⋅ | ⋅ ). A finite subset Δ ⊂ E∖{0} is called a generalized root system if the following conditions hold:
-
if α ∈ Δ, then −α ∈ Δ;
-
if α, β ∈ Δ and (α | α) ≠ 0, then \(k_{\alpha,\beta } = \frac{2(\alpha \vert \beta )} {(\alpha \vert \alpha )}\) is an integer and β − k α, β α ∈ Δ;
-
if α ∈ Δ and (α | α) = 0, then there exists an invertible map r α : Δ → Δ such that
$$\displaystyle{r_{\alpha }(\beta ) = \left \{\begin{array}{@{}l@{\quad }l@{}} \beta \,\text{if}\,(\alpha \vert \beta ) = 0\quad \\ \beta \pm \alpha \,\text{if} \,(\alpha \vert \beta )\neq 0\quad \end{array} \right..}$$
Exercise
Check that if  is a basic Lie superalgebra, then the set of roots Δ is a generalized root system.
is a basic Lie superalgebra, then the set of roots Δ is a generalized root system.
Indecomposable generalized root systems are classified in [39]. In fact, they coincide with root systems of basic Lie superalgebras. That gives an approach to the proof of Theorem 1.
Exercise
Let Q 0 be the lattice generated by Δ 0 and Q be the lattice generated by Q. Check that
-
If
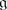 is of type 1, then Q
0 is a sublattice of corank 1 in Q.
is of type 1, then Q
0 is a sublattice of corank 1 in Q. -
If
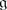 is of type 2, then Q
0 is a finite index subgroup in Q.
is of type 2, then Q
0 is a finite index subgroup in Q.
3.3 Bases and Odd Reflections
As in the case of simple Lie algebras we can represent Δ as a disjoint union Δ
+
∐Δ
− of positive and negative roots (by dividing  in two half-spaces).
in two half-spaces).
We are going to use the triangular decomposition:

The subalgebra  is called a Borel subalgebra of
is called a Borel subalgebra of  .
.
We call α ∈ Δ + indecomposable if it is not a sum of two positive roots. We call the set of indecomposable roots α 1, …α n ∈ Δ + simple roots or a base as in the Lie algebra case. Clearly, W action on Δ permutes bases. However, not all bases can be obtained from one by the action of W.
Example 9
The Weyl group of  is isomorphic to S
2 × S
2. One can see that the following two bases are not conjugate by the action of W: Π = { ε
1 −ε
2, ε
2 −δ
1, δ
1 −δ
2}, Π
′ = { ε
1 −δ
1, δ
1 −ε
2, ε
2 −δ
2}.
is isomorphic to S
2 × S
2. One can see that the following two bases are not conjugate by the action of W: Π = { ε
1 −ε
2, ε
2 −δ
1, δ
1 −δ
2}, Π
′ = { ε
1 −δ
1, δ
1 −ε
2, ε
2 −δ
2}.
Since W does not act transitively on the set of bases, more than one Dynkin diagram may be associated to the same Lie superalgebra. The existence of several Dynkin diagrams implies existence of several non conjugate Borel subalgebras, which in turn implies that there are several non isomorphic flag supervarieties.
To every base Π we associate the Cartan matrix in the following way. Take  ,
,  , and set H
i
: = [X
i
, Y
i
] and a
ij
: = α
j
(H
i
). In the classical theory of Kac-Moody algebras Cartan matrices are normalized so that the diagonal entries are equal to 2. In the supercase we can do the same for non-isotropic simple roots. It is not difficult to see that H
i
, X
i
, Y
i
for i = 1, …, n generate
, and set H
i
: = [X
i
, Y
i
] and a
ij
: = α
j
(H
i
). In the classical theory of Kac-Moody algebras Cartan matrices are normalized so that the diagonal entries are equal to 2. In the supercase we can do the same for non-isotropic simple roots. It is not difficult to see that H
i
, X
i
, Y
i
for i = 1, …, n generate  and satisfy the relations
and satisfy the relations
Let  be the free Lie superalgebra with above generators and relations. We define the Kac-Moody superalgebra
be the free Lie superalgebra with above generators and relations. We define the Kac-Moody superalgebra  as the quotient of
as the quotient of  by the maximal ideal which intersects trivially the Cartan subalgebra. In this way we recover basic finite dimensional Lie superalgebras. In contrast with Lie algebra case we may get a finite-dimensional Kac-Moody superalgebra even if det(A) = 0, for example,
by the maximal ideal which intersects trivially the Cartan subalgebra. In this way we recover basic finite dimensional Lie superalgebras. In contrast with Lie algebra case we may get a finite-dimensional Kac-Moody superalgebra even if det(A) = 0, for example,  . Note that in this case
. Note that in this case  is not simple but a non-trivial central extension of the corresponding simple superalgebra. In many applications, it is better to consider
is not simple but a non-trivial central extension of the corresponding simple superalgebra. In many applications, it is better to consider  instead of the corresponding quotient, which essentially means that in what follows we rather discuss representations and structure theory of
instead of the corresponding quotient, which essentially means that in what follows we rather discuss representations and structure theory of  instead of
instead of  .
.
Definition 7
Let Π be a base (set of simple roots) and let α ∈ Π be an isotropic odd root. We define an odd reflection r α : Π → Π ′ by
Exercise
Check that Π ′ = r α (Π) is a base.
Notice that if (α | α) ≠ 0 we can define the usual reflection \(r_{\alpha }(x):= x -\frac{2(x\vert \alpha )} {(\alpha \vert \alpha )} \alpha\), which is an orthogonal linear transformation of  . In fact, since r
α
= r
2α
, one can see that these reflections generate W. Though the odd reflections are defined on simple roots only, one can show that they may be extended (uniquely) to permutations of all roots. However, in most cases such extension can not be further extended to a linear map of the root lattice.
. In fact, since r
α
= r
2α
, one can see that these reflections generate W. Though the odd reflections are defined on simple roots only, one can show that they may be extended (uniquely) to permutations of all roots. However, in most cases such extension can not be further extended to a linear map of the root lattice.
Proposition 1
Let
 be a basic Lie superalgebra.
be a basic Lie superalgebra.
-
1.
If Π and Π ′ are two bases, then Π ′ can be obtained from Π by application of odd and even reflections.
-
2.
If Π and Π ′ are bases such that Δ + ∩Δ 0 = (Δ ′)+ ∩Δ 0 , then Π ′ can be obtained from Π by application of odd reflections.
Go back to the example of  . The Cartan matrix associated with Π is
. The Cartan matrix associated with Π is
The odd reflection r α associated with the root α = ε 2 −δ 1 ∈ Π maps Π to Π ′. Indeed, we have:
The Cartan matrix associated with Π ′ is
Exercise
Use odd reflections to get all bases of AG 2.
Remark 2
Let  be of type 1 and let us fix a Borel subalgebra
be of type 1 and let us fix a Borel subalgebra  . We have two especially convenient Borel subalgebras:
. We have two especially convenient Borel subalgebras:

We call them distinguished and antidistinguished, respectively.
4 Representations of Basic Superalgebras
4.1 Highest Weight Theory
We assume in this section that  is a basic superalgebra or its Kac Moody extension (in the case of
is a basic superalgebra or its Kac Moody extension (in the case of  ). Let us fix a triangular decomposition:
). Let us fix a triangular decomposition:  and the Borel subalgebra
and the Borel subalgebra  . Define the Verma module:
. Define the Verma module:

where C
λ
is the one-dimensional  -module with trivial action of
-module with trivial action of  and weight λ. One can prove exactly as in the Lie algebra case that
and weight λ. One can prove exactly as in the Lie algebra case that  has a unique simple quotient which we denote by
has a unique simple quotient which we denote by  .
.
We say that λ is integral dominant if  is finite dimensional.
is finite dimensional.
Exercise
Prove that if λ is integral dominant, then  has the unique maximal finite dimensional quotient
has the unique maximal finite dimensional quotient  . If
. If  is of type 1 and
is of type 1 and  is distinguished, then
is distinguished, then  is isomorphic to the induced module
is isomorphic to the induced module  , where
, where  is the simple
is the simple  -module with trivial action of
-module with trivial action of  . In this case it is called a Kac module.
. In this case it is called a Kac module.
Proposition 2
Any finite-dimensional simple
 -module is isomorphic to
-module is isomorphic to
 for some integral dominant λ.
for some integral dominant λ.
Proof
Any finite dimensional simple module M is semisimple over  and hence has a finite number of weights. Let λ be a weight such that λ + α is not a weight for all positive roots α. Then, by Frobenius reciprocity, M is a quotient of
and hence has a finite number of weights. Let λ be a weight such that λ + α is not a weight for all positive roots α. Then, by Frobenius reciprocity, M is a quotient of  .
.
Remark 3
Let  be the category of finitely generated
be the category of finitely generated  -semisimple
-semisimple  -modules with locally nilpotent action of
-modules with locally nilpotent action of  . Note that this definition depends on the choice of a Borel subalgebra
. Note that this definition depends on the choice of a Borel subalgebra  . In fact, it depends only on the choice of
. In fact, it depends only on the choice of  , since the local nilpotency of
, since the local nilpotency of  implies the local nilpotency of
implies the local nilpotency of  .
.
How do we check whether λ is dominant integral with respect to a particular Borel subalgebra  ? If
? If  is of type 1 and
is of type 1 and  is distinguished or antidistinguished, it is sufficient to check that λ is integral dominant with respect to
is distinguished or antidistinguished, it is sufficient to check that λ is integral dominant with respect to  , i.e. \(\lambda (h_{\alpha }) \in \mathbb{N}\) for all simple even roots α. In general, the condition of dominance is more complicated.
, i.e. \(\lambda (h_{\alpha }) \in \mathbb{N}\) for all simple even roots α. In general, the condition of dominance is more complicated.
Exercise
-
(a)
If
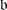 and
and 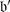 are two Borel subalgebras of
are two Borel subalgebras of 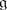 with the same even part, then we must have an isomorphism
with the same even part, then we must have an isomorphism 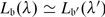 for some weights λ and λ
′. Let
for some weights λ and λ
′. Let 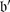 be obtained from
be obtained from 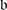 by an odd reflection r
α
. Check that $$\displaystyle{ \lambda ^{{\prime}} = \left \{\begin{array}{@{}l@{\quad }l@{}} \lambda -\alpha \,\mbox{ if}\,(\lambda,\alpha )\neq 0 \quad \\ \lambda \,\mbox{ if}\,(\lambda,\alpha ) = 0.\quad \end{array} \right. }$$(2)
by an odd reflection r
α
. Check that $$\displaystyle{ \lambda ^{{\prime}} = \left \{\begin{array}{@{}l@{\quad }l@{}} \lambda -\alpha \,\mbox{ if}\,(\lambda,\alpha )\neq 0 \quad \\ \lambda \,\mbox{ if}\,(\lambda,\alpha ) = 0.\quad \end{array} \right. }$$(2) -
(b)
Fix a base Π and the corresponding Borel subalgebra
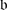 . Let Π
0 denote the base of Δ
0
+. Prove that
. Let Π
0 denote the base of Δ
0
+. Prove that 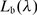 is finite-dimensional if and only if for any β ∈ Π
0 and a base Π
′ obtained from Π by odd reflections such that β ∈ Π
′ or \(\frac{\beta }{2} \in \varPi ^{{\prime}}\) we have \(\frac{2(\lambda \vert \beta )} {(\beta \vert \beta )} \in \mathbb{N}\). (Hint: you just have to check that
is finite-dimensional if and only if for any β ∈ Π
0 and a base Π
′ obtained from Π by odd reflections such that β ∈ Π
′ or \(\frac{\beta }{2} \in \varPi ^{{\prime}}\) we have \(\frac{2(\lambda \vert \beta )} {(\beta \vert \beta )} \in \mathbb{N}\). (Hint: you just have to check that 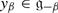 acts locally nilpotently on
acts locally nilpotently on 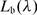 .)
.)
4.2 Typicality
We define the Weyl vector  by:
by:

If  is fixed and clear we simplify notation by setting
is fixed and clear we simplify notation by setting  .
.
Exercise
Let Π be the base corresponding to  . Show that
. Show that
Definition 8
A weight λ is called typical if (λ + ρ, α) ≠ 0 for all isotropic roots α ∈ Δ.
Exercise
Check that the definition of typicality does not depend on the choice of  . To show this assume that
. To show this assume that  is obtained from
is obtained from  by an odd reflection r
α
and λ is typical. Then
by an odd reflection r
α
and λ is typical. Then  and
and  , where
, where  .
.
4.3 Characters of Simple Finite-Dimensional Modules
If M is in the category  , then, by definition, M is
, then, by definition, M is  -semisimple, and therefore has weight decomposition
-semisimple, and therefore has weight decomposition  . The character \(\mathop{\mathrm{ch}}\nolimits M\) is the generating function
. The character \(\mathop{\mathrm{ch}}\nolimits M\) is the generating function
Exercise
Show, using Corollary 1, that if M is generated by one weight vector, in particular, if M is simple then every weight space M μ is either purely even or purely odd.
Theorem 2 ([23])
If λ is a typical integral dominant weight then

where W is the Weyl group of the even part
 and
and
Exercise
Using the isomorphism of  -modules
-modules  show that
show that

and

Remark 4
-
If
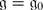 then we get the usual Weyl character formula.
then we get the usual Weyl character formula. -
The formula (3) is invariant with respect to the change of Borel subalgebra.
-
The formula (3) can be rewritten in the form
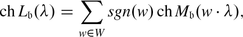
where w ⋅ λ: = w(λ + ρ) −ρ is the shifted action.
Proof of Theorem 2
We will give the proof for type 1 superalgebras, i.e. assuming a compatible grading  . By Remark 4 it suffices to prove the formula for the distinguished
. By Remark 4 it suffices to prove the formula for the distinguished  .
.
Note that the Kac module  is isomorphic to
is isomorphic to  as a
as a  -module. Therefore
-module. Therefore

Furthermore, if \(\rho _{i} = \frac{1} {2}\sum _{\alpha \in \varDelta _{i}}\alpha\), for i = 0, 1, then

Note also that w(ρ
1) = ρ
1 for all w ∈ W. Therefore  is given by (3). Thus, it remains to show that
is given by (3). Thus, it remains to show that  .
.
One can see easily that any submodule of  contains a simple
contains a simple  -submodule
-submodule
 Hence
Hence  has a unique simple submodule isomorphic to
has a unique simple submodule isomorphic to  for some μ.
for some μ.
Next we observe that
is the highest weight of  with respect to the anti-distinguished Borel
with respect to the anti-distinguished Borel  , since λ
′ is the
, since λ
′ is the  -highest weight in
-highest weight in  and
and 
Therefore we have

Applying (2) several times to move from  to
to  and using the typicality of λ we obtain λ = μ. Hence
and using the typicality of λ we obtain λ = μ. Hence  .
.
4.4 The Center of
Let  denote the center of the universal enveloping algebra
denote the center of the universal enveloping algebra  . In the supersetting the Duflo theorem states that there exists an isomorphism of supercommutative rings
. In the supersetting the Duflo theorem states that there exists an isomorphism of supercommutative rings

For the proof in the supercase see [26].
Recall that if  is a reductive Lie algebra then
is a reductive Lie algebra then  is a polynomial ring, see, for example, [10]. This fact follows from so called Harish-Chandra homomorphism. One can generalize the Harish-Chandra homomorphism for basic superalgebras, however, as we will see,
is a polynomial ring, see, for example, [10]. This fact follows from so called Harish-Chandra homomorphism. One can generalize the Harish-Chandra homomorphism for basic superalgebras, however, as we will see,  is not Noetherian.
is not Noetherian.
Choose a triangular decomposition  , then by PBW theorem we have the decomposition
, then by PBW theorem we have the decomposition

The Harish-Chandra map

is the projection with kernel  . The restriction
. The restriction

is a homomorphism of rings.
For any w ∈ W and  we set w ⋅ λ: = w(λ + ρ) −ρ.
we set w ⋅ λ: = w(λ + ρ) −ρ.
Theorem 3
The homomorphism
 is injective and
is injective and
 belongs to
belongs to
 if and only if
if and only if
-
f(w ⋅ λ) = f(λ), for any
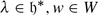 ;
;
-
if (λ + ρ | α) = 0 for some isotropic root α then f(λ + tα) = f(λ) for all t ∈ k.
The proof of this Theorem can be found in [24, 45] or [16]. One of the consequences of the above theorem is that the supercommutative ring  has trivial odd part and hence is in fact a usual commutative ring.
has trivial odd part and hence is in fact a usual commutative ring.
The proof in [45] makes use of the superanalogue of the Chevalley restriction theorem. Since  is basic, then the adjoint representation is self-dual. Thus, we can identify the invariant polynomials on
is basic, then the adjoint representation is self-dual. Thus, we can identify the invariant polynomials on  and
and  :
:

If  denotes the restriction map induced by the embedding
denotes the restriction map induced by the embedding  , then the image of F consists of W-invariant polynomials on
, then the image of F consists of W-invariant polynomials on  satisfying the additional condition:
satisfying the additional condition:
if (λ | α) = 0 for some isotropic root α then f(λ + tα) = f(λ) for all t ∈ k.
Example 10
Let  . The ring
. The ring  is generated by str(X
s) s = 1, 2, 3…. After restriction to the diagonal subalgebra they become polynomials in P
1, P
2, … ∈ k[x
1, …, x
m
, y
1, …, y
n
] given by the formula Set
is generated by str(X
s) s = 1, 2, 3…. After restriction to the diagonal subalgebra they become polynomials in P
1, P
2, … ∈ k[x
1, …, x
m
, y
1, …, y
n
] given by the formula Set
One can see that the subring in k[x 1, …, x m , y 1, …, y n ] generated by P s is not a Noetherian ring.
If Specm stands for the spectrum of maximal ideals, then HC induces the map  . In other words we associate with every weight
. In other words we associate with every weight  the central character
the central character  by setting χ
λ
(z): = HC(z)(λ). We would like to describe the fibers of θ. The following corollary implies that every fiber is a union of finitely many affine subspaces of the same dimension.
by setting χ
λ
(z): = HC(z)(λ). We would like to describe the fibers of θ. The following corollary implies that every fiber is a union of finitely many affine subspaces of the same dimension.
Corollary 2
Let
 and let {α
1, …, α
k
} be a maximal set of mutually orthogonal linearly independent isotropic roots such that (λ + ρ | α
i
) = 0. If χ = χ
λ
, then
and let {α
1, …, α
k
} be a maximal set of mutually orthogonal linearly independent isotropic roots such that (λ + ρ | α
i
) = 0. If χ = χ
λ
, then
Example 11
If  , then
, then  and the image of the Harish Chandra homomorphism in k[x, y] consists of polynomials k[x, y
2] which are constant on the cross y = ±x.
and the image of the Harish Chandra homomorphism in k[x, y] consists of polynomials k[x, y
2] which are constant on the cross y = ±x.
Corollary 3
If λ is typical then (θ)−1(χ λ ) = W ⋅ λ.
Corollary 4
If λ is dominant integral and typical, then
 for any integral dominant μ ≠ λ. Hence
for any integral dominant μ ≠ λ. Hence
 is projective in the category
is projective in the category
 of finite-dimensional
of finite-dimensional
 -modules semisimple over
-modules semisimple over
 .
.
Proof
If λ is dominant integral and typical, then W ⋅ λ does not contain any other integral dominant weight. Therefore  and
and  admit different central characters. Hence
admit different central characters. Hence  . Semisimplicity over
. Semisimplicity over  ensures that
ensures that  .
.
Remark 5
If  is of type 2, then any finite-dimensional
is of type 2, then any finite-dimensional  -module is semisimple over
-module is semisimple over  . In type 1 case,
. In type 1 case,  is not projective in the category of all finite-dimensional
is not projective in the category of all finite-dimensional  -modules since it has non-trivial self-extension.
-modules since it has non-trivial self-extension.
Definition 9 (Kac–Wakimoto)
The dimension of θ −1(χ) is called the atypicality degree of χ. We will denote it by at(χ). It follows from Corollary 2 that if χ λ = χ, then at(χ) is the maximal number of mutually orthogonal linearly independent isotropic roots α such that (λ + ρ | α) = 0. We also use the notation at(λ) = at(χ λ ). The central character χ is typical (resp. atypical) if at(χ) = 0 (resp. f(χ) > 0).
The defect
 of
of  is the maximal number of mutually orthogonal linearly independent isotropic roots, i.e. the maximal dimension of the fiber of θ.
is the maximal number of mutually orthogonal linearly independent isotropic roots, i.e. the maximal dimension of the fiber of θ.
Exercise
Show that

Check that the defect of the exceptional superalgebras AG 2, AB 3 and D(1, 2; a) is 1.
Note that  is the only basic superalgebra with defect zero. Hence we have the following proposition.
is the only basic superalgebra with defect zero. Hence we have the following proposition.
Proposition 3
All finite-dimensional representations of
 are completely reducible and the character of any irreducible finite-dimensional representation of
are completely reducible and the character of any irreducible finite-dimensional representation of
 is given by (
3
).
is given by (
3
).
Finally, let us formulate without proof the following general result which allows to reduce many questions about typical representations (finite or infinite-dimensional) to the same questions for the even part  .
.
Theorem 4 ([15, 36])
Suppose that χ = χ
λ
is a typical central character such that (λ + ρ | β) ≠ 0 for any non-isotropic root β. Let
 . Then there exists a central character χ
0
of
. Then there exists a central character χ
0
of
 such that
such that
 is Morita equivalent to
is Morita equivalent to
 .
.
Remark 6
If  is of type 1, then
is of type 1, then  is isomorphic to the matrix algebra over
is isomorphic to the matrix algebra over  .
.
5 Associated Variety
5.1 Self-Commuting Cone
Let  be a finite-dimensional Lie superalgebra. The self-commuting cone X is the subvariety of
be a finite-dimensional Lie superalgebra. The self-commuting cone X is the subvariety of  defined by
defined by

This cone was studied first in [17] for applications to Lie superalgebras cohomology.
Example 12
Let  . Then
. Then
We discuss geometry of X for basic classical  . Let G
0 be a connected, reductive algebraic group such that
. Let G
0 be a connected, reductive algebraic group such that  and let B
0 be a Borel subgroup of G
0. It is clear that X is G
0-stable with respect to the adjoint action of G
0 on
and let B
0 be a Borel subgroup of G
0. It is clear that X is G
0-stable with respect to the adjoint action of G
0 on  . Denote by X∕B
0 (resp. X∕G
0) the set of B
0 (resp. G
0)-orbits in X. We will see that both sets are finite.
. Denote by X∕B
0 (resp. X∕G
0) the set of B
0 (resp. G
0)-orbits in X. We will see that both sets are finite.
Denote by S p the set of all p-tuples of linearly independent and mutually orthogonal isotropic roots and set

Let u = { α
1, …, α
p
} ∈ S
p
, choose non-zero  and set
and set
Then x
u
∈ X and it is not hard to see that a different choice of the x
i
-s produces an element in the same H-orbit, where H is the maximal torus in G
0 with Lie algebra  . Therefore we have a well-defined map
. Therefore we have a well-defined map
Furthermore, the Weyl group W acts on S and clearly x w(u) and x u belong to the same G 0-orbit. Therefore we also have a map
Theorem 5
Both maps Φ and Ψ are bijections.
The proof that Ψ is a bijection can be found in [11] and it is done by case by case inspection. It would be interesting to find a conceptual proof, using for example only properties of the root decomposition. For the proof that Φ is a bijection we refer the reader to [7]. It uses the result about Ψ and the Bruhat decomposition of G 0. It is possible that a conceptual proof of Theorem 5 is related to the following analogue of the Jacobson–Morozov theorem.
Theorem 6
Let
 be a basic classical Lie superalgebra and
be a basic classical Lie superalgebra and
 be an odd element such that [x, x] is nilpotent. Then
be an odd element such that [x, x] is nilpotent. Then
-
1.
If [x, x] = 0, then x can be embedded into an
 -subalgebra of
-subalgebra of
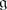 .
. -
2.
If [x, x] ≠ 0 then x can be embedded into an
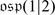 -subalgebra of
-subalgebra of
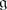 .
.
As a consequence of Theorem 5 we know that every x ∈ X is G
0-conjugate to x
u
for u ∈ S
p
. We call the number p the rank of x. If  , then the rank coincides with the usual rank of the matrix. We denote by X
p
the set of all elements in X of rank p. In this way we define the stratification
, then the rank coincides with the usual rank of the matrix. We denote by X
p
the set of all elements in X of rank p. In this way we define the stratification

where X 0 = {0}. Clearly, the Zariski closure of X p is the disjoint union of X q for all \(q\leqslant p\).
Proposition 4
The closure of every stratum X p is an equidimensional variety or, equivalently, if x, y ∈ X have the same rank, then dimG 0 x = dimG 0 y. Furthermore, if u = { α 1, …, α p } ∈ S p and
then
Proof
We start with proving the second assertion. For any  consider the odd analogue of the Kostant-Kirillov form:
consider the odd analogue of the Kostant-Kirillov form:
This is an odd skew-symmetric form. It is easy to see that ker (ω) = ker (ad
x
). Using the isomorphism  we can push forward ω to
we can push forward ω to  , where it becomes non-degenerate. Since ω is odd, we obtain
, where it becomes non-degenerate. Since ω is odd, we obtain

We compute  . Let x = x
u
= x
1 + … + x
p
. Fix some
. Let x = x
u
= x
1 + … + x
p
. Fix some  and let
and let  . Consider a generic linear combination y = c
1
y
1 + … + c
p
y
p
and set h = [x, y]. Then x, h, y span an
. Consider a generic linear combination y = c
1
y
1 + … + c
p
y
p
and set h = [x, y]. Then x, h, y span an  -subalgebra
-subalgebra  . Let
. Let  be the direct sum of all eigenspaces of ad
h
with non-zero eigenvalue and
be the direct sum of all eigenspaces of ad
h
with non-zero eigenvalue and  denote the centralizer of h. Clearly,
denote the centralizer of h. Clearly,  and
and  are
are  -stable. Furthermore, it is easy to see that
-stable. Furthermore, it is easy to see that

For generic c 1, …, c p we have

Therefore we obtain

On the other hand, a simple calculation shows that

Therefore  .
.

The first assertion follows from the fact that for any two u, u ′ ∈ S p there exists w ∈ W such that wu ′ ⊂ u ∪−u. This fact is established by case by case inspection.
Corollary 5
X is an equidimensional variety.
5.2 Functor F x
Let  be an arbitrary superalgebra and
be an arbitrary superalgebra and  satisfy [x, x] = 2x
2 = 0. For any
satisfy [x, x] = 2x
2 = 0. For any  -module M we have x
2
M = 0 and therefore can define the cohomology
-module M we have x
2
M = 0 and therefore can define the cohomology
Lemma 7
-
1.
(M ⊕ N) x = M x ⊕ N x .
-
2.
\(\mathop{\mathrm{sdim}}\nolimits (M_{x}) =\mathop{ \mathrm{sdim}}\nolimits (M)\) (superdimension).
-
3.
M x ∗ ≃ (M x )∗.
-
4.
We have a canonical isomorphism (M ⊗ N) x ≃ M x ⊗ N x .
Proof
1, 2 and 3 are straightforward. To prove 4 consider M as a k[x]∕(x 2)-module. We have the obvious map M x ⊗ N x → (M ⊗ N) x . On the other hand, we have decompositions M = M x ⊕ F and N = N x ⊕ F ′, where F and F ′ are free k[x]∕(x 2)-modules.
Since a tensor product of any k[x]∕(x 2)-module with a free k[x]∕(x 2)-module is free we obtain the isomorphism (M ⊗ N) x ≃ M x ⊗ N x .
Applying the above construction to the adjoint representations we get

Exercise
Check that  is an ideal in
is an ideal in  . Hence
. Hence  is a Lie superalgebra.
is a Lie superalgebra.
Let M be a  -module. Then we have a canonical
-module. Then we have a canonical  -module structure on M
x
. Indeed, it is easy to check that both ker x and xM are
-module structure on M
x
. Indeed, it is easy to check that both ker x and xM are  -stable, For any
-stable, For any  we have
we have  . Therefore
. Therefore  and the induced action of
and the induced action of  on M
x
is trivial. Thus, we obtain the following proposition.
on M
x
is trivial. Thus, we obtain the following proposition.
Proposition 5
Let
 be a superalgebra and x be an odd self-commuting element. The assignment M → M
x
induces a tensor functor F
x
from the category of
be a superalgebra and x be an odd self-commuting element. The assignment M → M
x
induces a tensor functor F
x
from the category of
 -modules to the category of
-modules to the category of
 -modules.
-modules.
Remark 7
F x is neither left nor right exact.
Note that if x, y lie in the same orbit of G
0 then  and
and  are isomorphic Lie superalgebras. Moreover, if
are isomorphic Lie superalgebras. Moreover, if  is basic, then
is basic, then  is constant on each stratum X
p
⊂ X.
is constant on each stratum X
p
⊂ X.
Lemma 8
Let
 be a basic Lie superalgebra, then
be a basic Lie superalgebra, then
 if x, y ∈ X
p
.
if x, y ∈ X
p
.
Proof
Let x = x
u
= x
1 + … + x
p
, y
i
and h
i
be as in the proof of Proposition 4. Let  be the subalgebra generated by x
i
, y
i
, h
i
for all \(i\leqslant p\). Then it follows from the proof of Proposition 4 that
be the subalgebra generated by x
i
, y
i
, h
i
for all \(i\leqslant p\). Then it follows from the proof of Proposition 4 that  is the quotient of the centralizer of
is the quotient of the centralizer of  by the center of
by the center of  . Note that by the last remark in the same proof we know that y is G
0-conjugate to x
v
for some v ∈ u ∪−u. It follows that
. Note that by the last remark in the same proof we know that y is G
0-conjugate to x
v
for some v ∈ u ∪−u. It follows that  . Hence the statement.
. Hence the statement.
Exercise
Let  be one of the basic superalgebras and x ∈ X
p
, check that
be one of the basic superalgebras and x ∈ X
p
, check that  is the following:
is the following:
-
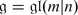 ,
, 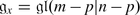 ;
; -
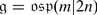 ,
, 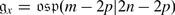 ;
; -
 , p = 1,
, p = 1, 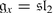 ;
; -
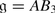 , p = 1,
, p = 1, 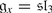 ;
; -
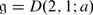 , p = 1,
, p = 1, 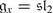 .
.
Consider  as the adjoint
as the adjoint  -module. Then it is not difficult to see that
-module. Then it is not difficult to see that  , hence we have a projection
, hence we have a projection  . Note that
. Note that  and the restriction of f
x
to
and the restriction of f
x
to  defines a homomorphism
defines a homomorphism  .
.
We are interested in the dual map.

Theorem 7
Let
 , x ∈ X
p
, then
, x ∈ X
p
, then
-
1.
\(\mathrm{at}(\check{\phi }_{x}(\psi )) = p +\mathrm{ at}(\psi )\).
-
2.
The image of \(\check{\phi }_{x}\) consists of all central characters of atypicality degree greater or equal than p.
-
3.
If \(\mathrm{at}(\chi )\geqslant p\) , then the fiber \(\check{\phi }_{x}^{-1}(\chi )\) consists of one or two points.
Proof
Let x = x
u
where u = { α
1, …, α
p
}. It is always possible to find a triangular decomposition such that α
1, …, α
p
are simple roots. We consider the Harish-Chandra map  related to this particular triangular decomposition and the analogous map
related to this particular triangular decomposition and the analogous map  with dual map denoted by θ
x
. Let
with dual map denoted by θ
x
. Let

from the proof of Lemma 8 we have

Let  be the map dual to the natural projection. We claim the existence of the following commutative diagram
be the map dual to the natural projection. We claim the existence of the following commutative diagram

Indeed, for any  let λ = i
x
(μ) and
let λ = i
x
(μ) and  be the irreducible module with highest weight λ (may be infinite-dimensional). The highest weight vector of this module belongs to M
x
and therefore M
x
contains a
be the irreducible module with highest weight λ (may be infinite-dimensional). The highest weight vector of this module belongs to M
x
and therefore M
x
contains a  -submodule which admits central character χ
μ
while M admit central character χ
λ
. That implies \(\check{\phi }_{x}(\chi _{\mu }) =\chi _{\lambda }\).
-submodule which admits central character χ
μ
while M admit central character χ
λ
. That implies \(\check{\phi }_{x}(\chi _{\mu }) =\chi _{\lambda }\).
2 is a direct consequence of 1 and 3 is obtained by case by case inspection using Corollary 2.
Exercise
If a  -module M admits central character χ, then M
x
is a sum of modules which admit central characters in \(\check{\phi }_{x}^{-1}(\chi )\).
-module M admits central character χ, then M
x
is a sum of modules which admit central characters in \(\check{\phi }_{x}^{-1}(\chi )\).
Corollary 6
Assume that M admits central character χ with atypicality degree p.
-
(a)
F x (M) = 0 for any x ∈ X q such that q > p. In particular, if χ is typical, then F x (M) = 0 for any x ≠ 0.
-
(b)
If x ∈ X p , then F x (M) is a direct sum of
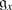 -modules with typical central character.
-modules with typical central character.
Conjecture 1
Let  be a basic Lie superalgebra. If M is a finite dimensional simple
be a basic Lie superalgebra. If M is a finite dimensional simple  -module, then M
x
is a semisimple
-module, then M
x
is a semisimple  -module.
-module.
By Corollary 6 Conjecture 1 is true when the rank of x equals the atypicality degree of M. In particular, it holds if the rank of x equals the defect of  . In this case
. In this case  is either a Lie algebra or
is either a Lie algebra or  . For general x the conjecture is proven for
. For general x the conjecture is proven for  in [21].
in [21].
5.3 Associated Variety
Definition 10
Let  be a Lie superalgebra, X self-commuting cone and M a
be a Lie superalgebra, X self-commuting cone and M a  -module. The associated variety of M is
-module. The associated variety of M is
Exercise
In general X
M
may be not closed, see [7]. Prove that if M is finite dimensional then X
M
is a closed G
0 invariant subvariety of X. If M is an object of the category  , then X
M
is B
0-invariant.
, then X
M
is B
0-invariant.
The following properties of X M follow immediately from the corresponding properties of F x
-
1.
X M⊕N = X M ∪ X N .
-
2.
X M⊗N = X M ∩ X N .
-
3.
\(X_{M^{{\ast}}} = X_{M}\).
Note also that Corollary 6 implies the following:
Proposition 6
Let
 be a basic superalgebra. If M admits a central character χ of atypicality degree p, then X
M
belongs to the Zariski closure of X
p
.
be a basic superalgebra. If M admits a central character χ of atypicality degree p, then X
M
belongs to the Zariski closure of X
p
.
The following result has a rather complicated proof which can be found in [42] for classical superalgebras and in [14, 29] for exceptional.
Theorem 8
Let
 be a classical Lie superalgebra and L be a finite dimensional simple
be a classical Lie superalgebra and L be a finite dimensional simple
 -module of atypicality degree p. Then the associated variety X
L
coincides with the Zariski closure of X
p
.
-module of atypicality degree p. Then the associated variety X
L
coincides with the Zariski closure of X
p
.
Finally, let us mention that to every  -module M integrable over G
0 we can associate a G
0-equivariant coherent sheaf
-module M integrable over G
0 we can associate a G
0-equivariant coherent sheaf  on X in the following way. Let k[X] denote the ring of regular functions on X and k[X] ⊗ M be a free k[X]-module. Define ∂: k[X] ⊗ M → k[X] ⊗ M by setting
on X in the following way. Let k[X] denote the ring of regular functions on X and k[X] ⊗ M be a free k[X]-module. Define ∂: k[X] ⊗ M → k[X] ⊗ M by setting
Then ∂
2 = 0 and the cohomology of ∂ is a k[X]-module  . It is clear that supp
. It is clear that supp  and it is proven in [11] that supp
and it is proven in [11] that supp  if X
M
= X.
if X
M
= X.
Conjecture 2
supp  .
.
5.4 Some Applications
Conjecture 3 (Kac–Wakimoto,[25])
Let  be a basic Lie superalgebra and L be a simple finite-dimensional
be a basic Lie superalgebra and L be a simple finite-dimensional  -module. Then \(\mathop{\mathrm{sdim}}\nolimits L\neq 0\) if and only the degree of atypicality of L equals the defect of
-module. Then \(\mathop{\mathrm{sdim}}\nolimits L\neq 0\) if and only the degree of atypicality of L equals the defect of  .
.
Kac-Wakimoto conjecture was verified for classical superalgebras in [42] and for exceptional in [29]. Here we can give a simple proof in one direction. Since F x preserves superdimension, Corollary 6 (a) implies the following statement.
Corollary 7
Let M be a finite-dimensional
 -module which admits central character χ. If
-module which admits central character χ. If
 then
\(\mathop{\mathrm{sdim}}\nolimits M = 0\).
then
\(\mathop{\mathrm{sdim}}\nolimits M = 0\).
Let k = C, M be a finite dimensional  -module,
-module,  a Cartan subalgebra. Define a function p
M
on
a Cartan subalgebra. Define a function p
M
on  by setting
by setting
It is clear that p M is analytic. Consider the Taylor series for p M at h = 0
where p i is a homogeneous polynomial of degree i. The order of zero is the minimal i such that p i ≠ 0.
The following result can be considered as a generalization of the Kac-Wakimoto conjecture.
Theorem 9 ([11])
Assume that
 does not have non-isotropic odd roots and let M be simple. Then the order of p
M
(h) equals the codimension of X
M
in X.
does not have non-isotropic odd roots and let M be simple. Then the order of p
M
(h) equals the codimension of X
M
in X.
6 Classification of Blocks
6.1 General Results
Let  be a finite-dimensional Lie superalgebra. Recall that we denote by
be a finite-dimensional Lie superalgebra. Recall that we denote by  the category of finite-dimensional
the category of finite-dimensional  -modules semisimple over
-modules semisimple over  .
.
Lemma 9
Let
 be reductive and
be reductive and
 be a semisimple
be a semisimple
 -module. Then the category
-module. Then the category
 has enough projective and injective objects. Moreover,
has enough projective and injective objects. Moreover,
 is a Frobenius category, i.e. every projective module is injective and vice versa.
is a Frobenius category, i.e. every projective module is injective and vice versa.
Proof
To prove the first assertion note that if M is a simple  -module, then by Frobenius reciprocity the induced module
-module, then by Frobenius reciprocity the induced module  is projective in
is projective in  and the coinduced module
and the coinduced module  is injective. For the second assertion use the following.
is injective. For the second assertion use the following.
Exercise
Show the isomorphism of  -modules
-modules

From now on we assume that  is basic. For a central character
is basic. For a central character  let
let  be the subcategory of
be the subcategory of  consisting of modules which admit generalized central character χ.
consisting of modules which admit generalized central character χ.
Lemma 10
-
(a)
We have a decomposition of
 into a direct sum of subcategories
into a direct sum of subcategories
-
(b)
For every χ with non-empty
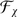 we have a decomposition
we have a decomposition
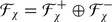 such that
such that
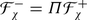 . (Recall that Π is the change of parity functor.)
. (Recall that Π is the change of parity functor.)
Proof
-
(a)
If M is finite-dimensional, then
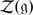 acts locally finitely on M, so M decomposes into the direct sum of generalized weight spaces of
acts locally finitely on M, so M decomposes into the direct sum of generalized weight spaces of 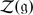 .
. -
(b)
Every module
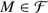 is
is 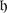 -semisimple. Thus, M has a weight decomposition M = ⊕M
μ
. One can define a function
-semisimple. Thus, M has a weight decomposition M = ⊕M
μ
. One can define a function 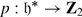 such that p(λ + α) = p(λ) for any even root α and p(λ + α) = p(λ) + 1 for any odd root α. Set $$\displaystyle{M_{\mu }^{+}:= \left \{\begin{array}{@{}l@{\quad }l@{}} (M_{\mu })_{0}\,\text{if}\,p(\mu ) = 0\quad \\ (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 1\quad \end{array} \right.,\quad M_{\mu }^{-}:= \left \{\begin{array}{@{}l@{\quad }l@{}} (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 1\quad \\ (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 0\quad \end{array} \right.,}$$
such that p(λ + α) = p(λ) for any even root α and p(λ + α) = p(λ) + 1 for any odd root α. Set $$\displaystyle{M_{\mu }^{+}:= \left \{\begin{array}{@{}l@{\quad }l@{}} (M_{\mu })_{0}\,\text{if}\,p(\mu ) = 0\quad \\ (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 1\quad \end{array} \right.,\quad M_{\mu }^{-}:= \left \{\begin{array}{@{}l@{\quad }l@{}} (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 1\quad \\ (M_{\mu })_{1}\,\text{if}\,p(\mu ) = 0\quad \end{array} \right.,}$$and let M ±: = ⊕M μ ±. Then M ± are submodules of M and M is the direct sum M + ⊕ M −. Therefore we can define
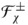 as the full subcategory of
as the full subcategory of 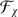 consisting of modules M such that \(M^{\mp } = 0\).
consisting of modules M such that \(M^{\mp } = 0\).
We call principal block the subcategory  which contains the trivial module.
which contains the trivial module.
Theorem 10
-
1.
The subcategories
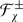 are indecomposable.
are indecomposable.
-
2.
If
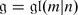 (resp.
(resp.
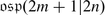 ), and p = atχ, then
), and p = atχ, then
 is equivalent to the principal block of
is equivalent to the principal block of
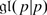 (resp.
(resp.
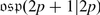 ).
).
-
3.
If
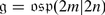 then
then
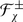 is equivalent to the principal block of
is equivalent to the principal block of
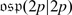 or
or
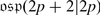 .
. -
4.
For exceptional superalgebras D(2, 1, a) AG 2 or AB 3
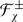 with atypical χ is equivalent to the principal block of
with atypical χ is equivalent to the principal block of
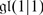 or
or
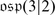 .
.
In these notes we give the proof for  . One can find the proof for all classical superalgebras in [19] and for exceptional in [14] and [29].
. One can find the proof for all classical superalgebras in [19] and for exceptional in [14] and [29].
Remark 8
If χ is typical, then  is semisimple and has one up to isomorphism simple object.
is semisimple and has one up to isomorphism simple object.
Remark 9
The problem of classifying blocks in the category  is still open. In contrast with
is still open. In contrast with  , there are infinitely many non-equivalent blocks of given atypicality degree, [7].
, there are infinitely many non-equivalent blocks of given atypicality degree, [7].
6.2 Tame Blocks
Using general approach, see [12], every block is equivalent to the category of finite-dimensional representations of a certain quiver with relations. This approach for Lie superalgebras was initiated by J. Germoni, [13]. In this method an important role is played by the dichotomy: wild vs tame categories. Roughly speaking, in tame categories, we can describe indecomposable modules by a finite number of parameters, while in wild categories it is impossible.
The following statement was originally conjectured by Germoni and now follows from Theorem 10 and results in [14, 18, 29] and [33].
Proposition 7
A block
 is tame if and only if
\(\mathrm{at}(\chi )\leqslant 1\)
. An atypical tame block is equivalent to the category of finite-dimensional representations of one of the following two quivers:
is tame if and only if
\(\mathrm{at}(\chi )\leqslant 1\)
. An atypical tame block is equivalent to the category of finite-dimensional representations of one of the following two quivers:

with relations ba = cd, ac = 0 = db for any subquiver isomorphic to:

Remark 10
It follows from Corollary 6 that for any x ∈ X the functor F
x
maps a block  to
to

There is some evidence that a more subtle relation is true, namely

In the case of the most atypical block it is possible to show that the superdimension is constant on a Zariski open subset of simple modules in the block.
6.3 Proof of Theorem 10 for
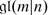
In this subsection  ,
,  is the distinguished Borel, and we skip the low index in the notation for simple, Kac and projective modules. For instance
is the distinguished Borel, and we skip the low index in the notation for simple, Kac and projective modules. For instance  . The weight
. The weight
is integral dominant if and only if c i − c i+1 ∈ Z +, d j − d j+1 ∈ Z + for all \(i\leqslant m - 1\), \(j\leqslant n - 1\). We assume in addition that c i , d j ∈ Z.Footnote 2
For the Weyl vector we use
In [2] Brundan and Stroppel introduced an extremely useful way to represent weights by the so called weight diagrams.
Let λ be a dominant integral weight, and
The weight diagram f λ is the map Z → {∘, >, <, ×} defined as follows
We represent f λ by a picture on the number line with position t ∈ {0, ±1, ±2, ±3, …} filled with f λ (t). We consider ∘ as a placeholder for an empty position. The core diagram \(\bar{f}_{\lambda }\) is obtained from f λ by removing all ×. We call > and < core symbols.
Example 13
Take the adjoint representation of  . Then
. Then
and f
λ
can be represented by the picture 
where all negative positions and all positions t > 3 are empty. The core diagram is

Exercise
Check that
-
The degree of atypicality of λ equals the number of ×-s in the weight diagram f λ .
-
Core diagrams parametrize blocks, namely, χ λ = χ μ if and only if \(\bar{f}_{\lambda } =\bar{ f}_{\mu }\).
The above exercise implies that blocks  can be parametrized by weight diagrams without ×-s. We use the notation \(f_{\chi }:=\bar{ f}_{\lambda }\) for any λ such that χ = χ
λ
.
can be parametrized by weight diagrams without ×-s. We use the notation \(f_{\chi }:=\bar{ f}_{\lambda }\) for any λ such that χ = χ
λ
.
Definition 11
We define the following operations on a weight diagram:
-
Left simple move: Move > one position to the right or move < one position to the left.
-
Right simple move: Move > one position to the left or move < one position to the right.
In this definition we assume that × is the union > <, and we can split it or join > < into ×.
Example 14
Let f be as in the previous example: 
Then the following are possible right simple moves
-
1.
Moving the rightmost < one position right:
-
2.
Moving the leftmost < one position right (new × in position 2 appears):
-
3.
Moving > one position left (new × in position 1 appears):
-
4.
Splitting ×. Here we can not move < to the right since it does not produce a valid diagram. But we can move > to the left.
Let V and V ∗ denote the natural and conatural representations respectively.
Lemma 11
If K(λ) is the Kac module with highest weight λ, then K(λ) ⊗ V (resp. K(λ) ⊗ V ∗ ) has a filtration by Kac modules K(μ) for all f μ obtained from f λ by a left (resp. right) simple move.
Proof
Recall that  . Hence
. Hence

Since the weights of V are {ε 1, …, ε m , δ 1, …, δ n }, then K(λ) ⊗ V has a filtration by K(μ) for all dominant μ in {λ + ε 1, …, λ + ε m , λ + δ 1, …, λ + δ n }. The corresponding weight diagrams are exactly those obtained from f λ by a right simple move. The case of K(λ) ⊗ V ∗ is similar.
Next step is to define translation functors inspired by translation functors in classical category  . For every M in
. For every M in  we denote by (M)
τ
the projection on the block
we denote by (M)
τ
the projection on the block  . Then the translation functors between
. Then the translation functors between  and
and  are defined by
are defined by

Exercise
Show that:
-
1.
The functors T χ, τ , T τ, χ ∗ are exact.
-
2.
T τ, χ ∗ is left and right adjoint to T χ, τ .
-
3.
T χ, τ , T τ, χ ∗ map projective modules to projective modules.
-
4.
Assume that T χ, τ and T τ, χ ∗ establish a bijection between simple modules in both blocks, then they establish an equivalence
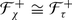 of abelian categories.
of abelian categories. -
5.
If T χ, τ and T τ, χ ∗ establish a bijection between Kac modules in both blocks, they also establish a bijection between simple modules.
Proposition 8
Assume that at(χ) = at(τ) and f
τ
is obtained from f
χ
by a left (resp. right) simple move, then
 (resp.
(resp.
 ) is an equivalence of abelian categories.
) is an equivalence of abelian categories.
Proof
Without loss of generality we do the proof in the case of a left move. Using Lemma 11 one can easily check that T χ, τ and T τ, χ ∗ provide a bijection between Kac modules in both blocks. Hence the statement follows from the preceding exercise.
Definition 12
A weight λ is stable if all ×-s in the weight diagram f λ stay to the left of < and >.
Introduce an order on the set of weights in the same block by setting \(\nu \leqslant \mu\) if μ −ν is a sum of positive roots. One can easily see that ν < μ if ν is obtained from μ by moving some × to the left. Therefore if μ is stable and ν < μ, then ν is also stable. We denote by  the full subcategory of
the full subcategory of  whose simple constituents L(λ) satisfy \(\lambda \leqslant \mu\). We call
whose simple constituents L(λ) satisfy \(\lambda \leqslant \mu\). We call  a truncated block.
a truncated block.
Proposition 9
Let μ be a stable weight of atypicality degree p, χ = χ
μ
. Let s ∈ Z
be minimal such that f
χ
(s) ≠ ∘. Let ν be the weight of the principal block of
 with weight diagram
with weight diagram
Then
 is equivalent to the truncation
is equivalent to the truncation
 of the principal block of
of the principal block of
 .
.
Proof (Sketch)
We just explain how to define the functors establishing the equivalence. Let μ = (c 1, …, c m | d 1, …, d n ). Start with defining the parabolic subalgebra

where
in other words  consists of block matrices of the form
consists of block matrices of the form
where the middle square block has size p | p. Set

Clearly,  is a semi-direct product of the subalgebra
is a semi-direct product of the subalgebra  and the nilpotent ideal
and the nilpotent ideal  . Consider the functor
. Consider the functor  defined by
defined by  . Then its left adjoint
. Then its left adjoint  maps a
maps a  -module N to the maximal finite-dimensional quotient of the parabolically induced module
-module N to the maximal finite-dimensional quotient of the parabolically induced module

where C μ is the one-dimensional representation of k m+n−2p with weight
It suffices to show that R and I are exact and establish the bijection between simple modules. Indeed, the exactness of R can be proven by noticing that R picks up the eigenspace of k
m+n−2p with weight μ. Furthermore, if L(λ) is a simple module in  , then
, then
for some t 1, …, t p . It is easy to see that R(L(λ)) = L(λ ′), where λ ′ = (t 1, …, t p | − t p , …, −t 1) and that I(L(λ ′)) = L(λ). The exactness of I can be now proven by induction on the length of a module.
The following combinatorial lemma is straightforward.
Lemma 12
For any weight diagram f μ there exists a stable weight diagram \(f_{\mu ^{{\prime}}}\) obtained from f μ by a sequence of simple moves which do not change the degree of atypicality.
Now we are ready to prove Theorem 10. Indeed, let  be a block with atypicality degree p. Lemma 12 and Proposition 8 imply that any truncated block
be a block with atypicality degree p. Lemma 12 and Proposition 8 imply that any truncated block  is equivalent to a stable truncated block of the same atypicality. Hence by Proposition 9
is equivalent to a stable truncated block of the same atypicality. Hence by Proposition 9
 is equivalent to some truncation of a principal block of
is equivalent to some truncation of a principal block of  . Taking the direct limit of
. Taking the direct limit of  we obtain equivalence between
we obtain equivalence between  and the principal block of
and the principal block of  .
.
It remains to prove the indecomposability of the principal block of  . Note that \(f_{\nu ^{{\prime}}}\) is obtained from f
ν
by moving a × one position left, then [K(ν): L(ν
′)] = 1. Since K(ν) is indecomposable, L(ν) lies in the indecomposable block containing L(ν
′). Since any diagram in the principal block can be obtained from the fixed one by repeatedly moving ×-s one position left or right, the statement follows.
. Note that \(f_{\nu ^{{\prime}}}\) is obtained from f
ν
by moving a × one position left, then [K(ν): L(ν
′)] = 1. Since K(ν) is indecomposable, L(ν) lies in the indecomposable block containing L(ν
′). Since any diagram in the principal block can be obtained from the fixed one by repeatedly moving ×-s one position left or right, the statement follows.
6.4 Calculating the Kazhdan-Lusztig Multiplicities
We would like to mention without proof other applications of weight diagrams and translation functors. We still assume that  . Then the category
. Then the category  is a highest weight category, [47], where standard objects are Kac modules. In particular, we have BGG reciprocity for the multiplicities:
is a highest weight category, [47], where standard objects are Kac modules. In particular, we have BGG reciprocity for the multiplicities:
where P(μ) denotes the projective cover of L(μ). It is useful to compute these multiplicities. It was done in [40] and in [1] by different methods. The answer is very easy to formulate in terms of weight diagrams.
Let f be some weight diagram. We decorate it with caps by the following rule:
-
Every cap has left end at × and right end at ∘.
-
Every × is engaged in some cap, so the number of caps equals the number of crosses.
-
There are no ∘ under a cap.
-
Caps do not cross.
We say that f ′ is adjacent to f if f ′ is obtained from f by moving one × from the left end of its cap to the right end. We say that f ′ is adjoint to f if f ′ is obtained from f by moving several × from the left end of its cap to the right end. We assume that f is adjoint to itself. If f has p ×-s, then it has exactly p adjacent diagrams and 2p adjoint diagrams
Theorem 11 ([1, 33])

Theorem 12 ([1])
7 Supergeometry and Borel–Weil–Bott Theorem
7.1 Supermanifolds
The notion of supermanifold exists in three flavors: smooth, analytic and algebraic. We concentrate here on the algebraic version. The main idea is the same: we define first superdomains and then glue them together.
By a superdomain we understand a pair  , where U
0 is an affine manifold and
, where U
0 is an affine manifold and  is the sheaf of superalgebras isomorphic to
is the sheaf of superalgebras isomorphic to

 denotes the structure sheaf on U
0. The dimension of U is (m | n) where m = dimU
0.
denotes the structure sheaf on U
0. The dimension of U is (m | n) where m = dimU
0.
For example, the affine superspace \(\mathbb{A}^{m\vert n}\) is a pair  . The ring of global sections of
. The ring of global sections of  is a free supercommutative ring k[x
1
…x
m
, ξ
1, …ξ
n
]. If we work in local coordinates, then we use roman letters for even variables, greek letters for odd ones.
is a free supercommutative ring k[x
1
…x
m
, ξ
1, …ξ
n
]. If we work in local coordinates, then we use roman letters for even variables, greek letters for odd ones.
Definition 13
A supermanifold is a pair  where X
0 is a manifold and
where X
0 is a manifold and  is a sheaf locally isomorphic to
is a sheaf locally isomorphic to  for a superdomain U. The manifold X
0 is called the underlying manifold of X and
for a superdomain U. The manifold X
0 is called the underlying manifold of X and  is called the structure sheaf.
is called the structure sheaf.
One way to define a supermanifold is by introducing local charts U i and then gluing them together.
Example 15
Consider two copies of \(\mathbb{A}^{1\vert 2}\) with coordinates (x, ξ 1, ξ 2) and (y, η 1, η 2). We give the gluing by setting:
Example 16
Let X
0 be a manifold,  be a vector bundle on X
0 and
be a vector bundle on X
0 and  is the sheaf of sections of the exterior algebra bundle
is the sheaf of sections of the exterior algebra bundle  . In particular, X
0 with the sheaf of forms \(\varOmega _{X_{0}}\) is a supermanifold.
. In particular, X
0 with the sheaf of forms \(\varOmega _{X_{0}}\) is a supermanifold.
Given the supermanifold X, we have the canonical embedding X
0 → X and the corresponding morphism of structure sheaves  . Denote by \(I_{X_{0}}\) the kernel of this map. It is not difficult to see that \(I_{X_{0}}\) is the nilpotent ideal generated by all odd sections of
. Denote by \(I_{X_{0}}\) the kernel of this map. It is not difficult to see that \(I_{X_{0}}\) is the nilpotent ideal generated by all odd sections of  . Consider the filtration
. Consider the filtration

Then  is again a supermanifold. One can identify Gr(X) with \((X_{0},\varGamma (\varLambda (N_{X_{0}}^{{\ast}}X))\), where \(N_{X_{0}}^{{\ast}}X\) denotes the conormal bundle for X
0 ⊂ X.
is again a supermanifold. One can identify Gr(X) with \((X_{0},\varGamma (\varLambda (N_{X_{0}}^{{\ast}}X))\), where \(N_{X_{0}}^{{\ast}}X\) denotes the conormal bundle for X
0 ⊂ X.
A supermanifold X is called split if it is isomorphic to Gr(X). In the category of smooth supermanifolds all supermanifolds are split but this is not true for algebraic supermanifolds.
Exercise
Show that any supermanifold of dimension (m | 1) is split. Is the supermanifold defined in Example 15 split?
Another way to define a supermanifold is to use the functor of points, which is a functor from the category (Salg) of commutative superalgebras to the category (Sets). For general definitions see [3]. Let us illustrate this approach with the following example.
Example 17
We define the projective superspace X = P
1 | 1 as follows. For a commutative superalgebra  the set of
the set of  -points is the set of all submodules
-points is the set of all submodules  . This is the set of all triples (z
1, z
2, ζ) with
. This is the set of all triples (z
1, z
2, ζ) with  and
and  , such that at least one of z
1, z
2 is invertible, modulo rescaling by an invertible element of
, such that at least one of z
1, z
2 is invertible, modulo rescaling by an invertible element of  . This supermanifold has two affine charts {(1, x, ξ)} and {(y, 1, η)} with gluing functions ξ = x
−1
η, y = x
−1.
. This supermanifold has two affine charts {(1, x, ξ)} and {(y, 1, η)} with gluing functions ξ = x
−1
η, y = x
−1.
Exercise
Check that in Example 17
X
0 = P
1 and  .
.
8 Algebraic Supergroups
An affine supermanifold G equipped with morphisms m: G × G → G, i: D → G and e: { point} → G satisfying usual group axioms is called an affine algebraic supergroup. We skip the word “affine” in what follows.
The ring  of global sections of
of global sections of  has a structure of Hopf superalgebra. In fact, one can start with a Hopf superalgebra
has a structure of Hopf superalgebra. In fact, one can start with a Hopf superalgebra  and define a supergroup as a functor:
and define a supergroup as a functor:

Properties of Hopf algebras allow one to define the group structure on  .
.
The ideal I generated by the odd elements in  is an Hopf ideal. The quotient Hopf algebra
is an Hopf ideal. The quotient Hopf algebra  is the Hopf algebra of regular functions on the underlying algebraic group G
0.
is the Hopf algebra of regular functions on the underlying algebraic group G
0.
Exercise
\(\mathop{\mathrm{GL}}\nolimits (m\vert n)\).

satisfying the following conditions
-
the entries on A and D are even elements in
 , while the the entries of B and C are odd;
, while the the entries of B and C are odd; -
Y is invertible.
Show that \(\mathop{\mathrm{GL}}\nolimits (m\vert n)\) is representable and construct the corresponding Hopf superalgebra.
Example 18 (Exercise)
Consider the functor
Check that \(\mathop{\mathrm{Ber}}\nolimits\) is a homomorphism. Hint: Write
We define \(\mathop{\mathrm{SL}}\nolimits (m\vert n)\) by imposing the condition \(\mathop{\mathrm{Ber}}\nolimits = 1\).
Show that \(\mathop{\mathrm{GL}}\nolimits (m\vert n)_{0} =\mathop{ \mathrm{GL}}\nolimits (m) \times \mathop{\mathrm{GL}}\nolimits (n)\) and
Definition 14
\(\mathop{\mathrm{Lie}}\nolimits (G)\) is the Lie superalgebra of left invariant derivations of  and can be identified with T
e
(G).
and can be identified with T
e
(G).
Exercise
 ,
,  .
.
A useful approach to algebraic supergroups is via the so called Harish-Chandra pairs. In the case of Lie groups it is due to Koszul and Kostant, [27, 28], for complex analytic category it is done in [46], for algebraic groups see [31].
We call an HC pair the following data
-
a finite-dimensional Lie superalgebra
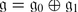 ;
; -
an algebraic group G 0 such that
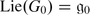 ;
; -
a G 0-module structure on
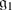 with differential equal to the superbracket
with differential equal to the superbracket 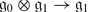 .
.
Theorem 13
The category of HC pairs is equivalent to the category of algebraic supergroups.
Let us comment on the proof. It is clear that every supergroup G defines uniquely a HC pair  . The difficult part is to go back: given an HC pair
. The difficult part is to go back: given an HC pair  , define a Hopf superalgebra
, define a Hopf superalgebra  . One way to approach this problem is to set
. One way to approach this problem is to set

Define a multiplication map m: R ⊗ R → R by
where m
0 is the multiplication in  and Δ
U
is the comultiplication in
and Δ
U
is the comultiplication in  :
:

It is easy to see that R is a commutative superalgebra isomorphic to  , [28]. In particular, this implies that an algebraic group is a split supermanifold.
, [28]. In particular, this implies that an algebraic group is a split supermanifold.
Next define the comultiplication Δ: R → R ⊗ R. For g, h ∈ G
0 and  we set
we set
The counit map ε: R → k is defined by
where ε
0 is the counit in  . Finally, define the antipode s: R → R by setting for all g ∈ G
0,
. Finally, define the antipode s: R → R by setting for all g ∈ G
0, 
where s
U
is the antipode in  .
.
Theorem 14 ([31])
The category of representations of G is equivalent to the category of
 -modules.
-modules.
We now concentrate on the case of reductive G
0. By the above Theorem the category Rep(G) of finite-dimensional representations of G is a full subcategory of  . Therefore we immediately obtain the following.
. Therefore we immediately obtain the following.
Corollary 8
Let G 0 be reductive.
-
Then Rep(G) has enough projective and injective objects.
-
Every injective G-module is projective.
Exercise
Assume that G 0 is reductive. Check that

is an isomorphism of  -modules and use it prove that
-modules and use it prove that

where L runs the set of irreducible representations of G and P(L) is the projective cover of L. Hint: Use Frobenius reciprocity and the structure of  as a G
0-module.
as a G
0-module.
9 Geometric Induction
9.1 General Construction
Let H ⊂ G be a subsupergroup. It is possible to show that G∕H is a supermanifold, see [30]. The space of global sections of the structure sheaf is given by

where H-invariants are defined with respect to the right action of H on G. Furthermore, if M is a representation of H, then G × H M is a G-equivariant vector bundle on G∕H. We define:

Thus, we associated in functorial way to every representation of H a representation of G, namely, the space of global sections of G × H M. The corresponding functor Γ: Rep(H) ⟶ Rep(G) is left exact. The right derived functor is given by the cohomology
It is a little bit more convenient to us to work with dual functors Γ i (G∕H, ⋅ ) defined by
The following statement is the Frobenius reciprocity for geometric induction and the proof is the same as for algebraic groups.
Proposition 10
For any H-module M and G-module N we have a canonical isomorphism
Exercise
If G = G
0, then Γ
i
(M) = 0 for i > 0 and  .
.
9.2 The Borel-Weil-Bott Theorem
Let G be an algebraic supergroup with basic Lie superalgebra  . Fix a Cartan subalgebra
. Fix a Cartan subalgebra  and a Borel subalgebra
and a Borel subalgebra  and denote by B ⊂ G and H ⊂ B the corresponding subgroups. The supermanifold G∕B is called a flag supermanifold. Its underlying manifold G
0∕B
0 is a classical flag manifold.
and denote by B ⊂ G and H ⊂ B the corresponding subgroups. The supermanifold G∕B is called a flag supermanifold. Its underlying manifold G
0∕B
0 is a classical flag manifold.
Recall that in the Lie algebra case flag manifolds play a crucial role in the representation theory of  . In particular, all the irreducible representations of a reductive algebraic group can be realized as global sections of line bundles on the flag variety by the Borel–Weil–Bott theorem. Let us see what happens in the supercase.
. In particular, all the irreducible representations of a reductive algebraic group can be realized as global sections of line bundles on the flag variety by the Borel–Weil–Bott theorem. Let us see what happens in the supercase.
Consider the H-weight lattice Λ in  . Every λ ∈ Λ defines a unique one-dimensional representation of B which we denote by c
λ
. We are interested in computing Γ
i
(G∕B, c
λ
) = 0. The Frobenius reciprocity (Proposition 10) implies the following
. Every λ ∈ Λ defines a unique one-dimensional representation of B which we denote by c
λ
. We are interested in computing Γ
i
(G∕B, c
λ
) = 0. The Frobenius reciprocity (Proposition 10) implies the following
Corollary 9
Γ
i
(G∕B, c
λ
) is isomorphic to the maximal finite-dimensional quotient
 of the Verma module
of the Verma module
 .
.
Lemma 13
Assume that the defect of
 is positive. Then the flag supervariety G∕B is split if and only if
is positive. Then the flag supervariety G∕B is split if and only if
 is type 1 and
is type 1 and
 is distinguished or antidistinguished.
is distinguished or antidistinguished.
Proof
First, let us assume that G∕B is split. Then we have a projection π: G∕B → G 0∕B 0 and the pull back map
which induces the embedding
After dualizing we obtain a surjection
If λ is a G
0-dominant weight, then  . By Corollary 9
. By Corollary 9
 . Hence λ is G-dominant. Thus, every dominant G
0-weight is G dominant and this is possible only for distinguished Borel or for
. Hence λ is G-dominant. Thus, every dominant G
0-weight is G dominant and this is possible only for distinguished Borel or for  .
.
Now let  be a distinguished or antidistinguished Borel subalgebra. Then it is easy to see that
be a distinguished or antidistinguished Borel subalgebra. Then it is easy to see that

The following result is a generalization of Borel–Weil–Bott theorem in the case of typical λ. We call a weight μ regular (resp. singular) if it has trivial (resp. non-trivial) stabilizer in W. We denote by Λ + ⊂ Λ the set of all μ ∈ Λ such that \(\frac{2(\mu \vert \alpha )} {(\alpha \vert \alpha )} \in \mathbf{Z}_{+}\) for all even positive roots α. It follows from Sect. 4.1 that a typical λ is dominant if and only if λ + ρ ∈ Λ +.
Theorem 15 ([35])
Let λ ∈ Λ be typical.
-
1.
If λ + ρ is singular then Γ i (G∕B, c λ ) = 0 for all i.
-
2.
If λ + ρ is regular there exists a unique w ∈ W such that w(λ + ρ) ∈ Λ + . Let l be the length of w. Then
$$\displaystyle{\varGamma _{i}(G/B,c_{\lambda }) = \left \{\begin{array}{@{}l@{\quad }l@{}} 0\quad \mathit{\mbox{ if }}\,i\neq l, \quad \\ L(w\cdot \lambda ), \quad \mathit{\mbox{ if }} i = l.\quad \end{array} \right.}$$
Proof
We give here just the outline, see details in [35]. First, if λ is dominant then by Corollary 9
 and by typicality of λ we have
and by typicality of λ we have  .
.
If α or \(\frac{1} {2}\alpha\) is a simple root of B, then one can show using the original Demazure argument, that
if \(\frac{2(\mu \vert \alpha )} {(\alpha \vert \alpha )}> 0\). Furthermore, if \(\frac{2(\mu \vert \alpha )} {(\alpha \vert \alpha )} = 0\), then
for all i.
However, not every simple root of  is a simple root of
is a simple root of  and therefore we need to involve odd reflections and change of Borel subalgebras.
and therefore we need to involve odd reflections and change of Borel subalgebras.
Let α be an isotropic simple root and  be obtained from
be obtained from  by the odd reflection r
α
. Then we claim that
by the odd reflection r
α
. Then we claim that
where λ + ρ = λ
′ + ρ
′. To show this we consider the parabolic subalgebra  . Then we have two projections
. Then we have two projections
the fiber of both projections is a (0 | 1)-dimensional affine space and we have
where V λ is the two-dimensional simple P-module with weights −λ and −λ ′. Note that here we use that (λ + ρ, α) ≠ 0 by the typicality of λ. This implies
After dualization we obtain (6).
Let us assume again that λ is dominant and consider the Borel subalgebra  opposite to
opposite to  . Combining (4) and (6) we obtain
. Combining (4) and (6) we obtain
where w 0 is the longest element of W and its length d equals dimG 0∕B 0. That implies the second statement of the theorem for dominant λ. Using (4) and (6) we can reduce the case of arbitrary regular λ + ρ to the dominant case.
If λ + ρ is singular, then there is a simple root α of  such that (λ + ρ, α) = 0. Using odd reflections and (6) we can change the Borel subgroup B to B
′ and λ so that α or \(\frac{1} {2}\alpha\) is a simple root of B
′. Then the vanishing of cohomology follows from (5).
such that (λ + ρ, α) = 0. Using odd reflections and (6) we can change the Borel subgroup B to B
′ and λ so that α or \(\frac{1} {2}\alpha\) is a simple root of B
′. Then the vanishing of cohomology follows from (5).
Computing Γ i (G∕B, c λ ) for atypical λ is an open question. The main reason why the proof in this case does not work is the absence of (6). It is known from examples that Γ i (G∕B, c λ ) may not vanish for several i.
Finally let us formulate the following analogue of Bott’s reciprocity relating Γ i with Lie superalgebra cohomology. The proof is straightforward using the definition of the derived functor (see [20]).
Proposition 11
For any finite-dimensional B-module M and any dominant weight λ, we have

where
 denotes the projective cover of
denotes the projective cover of
 .
.
After dualizing and setting M = c −ν we obtain the following
Corollary 10

9.3 Application to Characters
Although we do not know Γ i (G∕B, c λ ) for atypical λ, we can calculate the character of the Euler characteristic.
Theorem 16
The character of the Euler characteristic is given by the typical character formula, i.e.
Proof
Consider the associated split manifold Gr(G∕B) and the associated graded  of the sheaf Γ of sections of G ×
B
c
−λ
. Since Euler characteristic is preserved after going to the associated graded sheaf we have
of the sheaf Γ of sections of G ×
B
c
−λ
. Since Euler characteristic is preserved after going to the associated graded sheaf we have

Note that  is a G
0-equivariant vector bundle on G
0∕B
0, and the classical Borel–Weil–Bott theorem allows us to calculate the right hand side of the above equality. Indeed, if
is a G
0-equivariant vector bundle on G
0∕B
0, and the classical Borel–Weil–Bott theorem allows us to calculate the right hand side of the above equality. Indeed, if  denotes the conormal bundle to G
0∕B
0, then
denotes the conormal bundle to G
0∕B
0, then

and

which is equivalent to the typical character formula.
Note that Theorems 16 and 15 imply Theorem 2.
Definition 15
Let λ be a weight of atypicality degree p. It is called tame with respect to the Borel subalgebra  if there exists isotropic mutually orthogonal simple roots α
1, …, α
p
such that
if there exists isotropic mutually orthogonal simple roots α
1, …, α
p
such that
Conjecture 4 (Kac–Wakimoto, [25])
If λ is dominant and tame with respect to  , then
, then

The right hand side of formula (7) is the character of the Euler characteristic
where Q is the parabolic subgroup with Lie superalgebra

Hence one way to prove Conjecture 4 is to prove the following
Conjecture 5
If λ is tame with respect to  , then Γ
i
(G∕Q, c
λ
) = 0 if i > 0 and
, then Γ
i
(G∕Q, c
λ
) = 0 if i > 0 and  .
.
For classical Lie superalgebras Conjecture 5 is proven in [5].
9.4 Weak BGG Reciprocity
Let  denote the Grothendieck group of the category Rep(G) and [M] denote the class of a G-module M. Clearly
denote the Grothendieck group of the category Rep(G) and [M] denote the class of a G-module M. Clearly  , for all dominant λ ∈ Λ, is a basis of
, for all dominant λ ∈ Λ, is a basis of  . Set
. Set

As we already mentioned in Sect. 6.4, if  is of type 1 then Rep(G) is a highest weight category. For type 2 superalgebras this is not true. Nevertheless one can use virtual modules
is of type 1 then Rep(G) is a highest weight category. For type 2 superalgebras this is not true. Nevertheless one can use virtual modules  instead of
instead of  and obtain the following weak BGG reciprocity.
and obtain the following weak BGG reciprocity.
Theorem 17 ([20])
Let λ ∈ Λ be dominant and μ ∈ Λ be such that μ + ρ ∈ Λ + . There exists unique a λ, μ ∈ Z such that

and

9.5
 -Modules
-Modules
In this subsection we discuss briefly possible generalizations of the Beilinson-Bernstein localization theorem for basic classical Lie superalgebras. The basics on  -modules on supermanifold can be found in [36]. The main result there is that if X is a supermanifold with underlying manifold X
0 then Kashiwara extension functor provides the equivalence between categories of
-modules on supermanifold can be found in [36]. The main result there is that if X is a supermanifold with underlying manifold X
0 then Kashiwara extension functor provides the equivalence between categories of  -modules and
-modules and  -modules.
-modules.
This fact is easy to explain in the case when X is a superdomain. Indeed, in this case

and this implies an isomorphism

where D(Λ(ξ
1, …, ξ
n
) is the superalgebra of the differential operators on (0 | n)-dimensional supermanifold \(\mathbb{A}^{(0\vert n)}\). Since Λ(ξ
1, …, ξ
n
) is finite-dimensional, the superalgebra D(Λ(ξ
1, …, ξ
n
)) coincides with the superalgebra \(\mathop{\mathrm{End}}\nolimits _{k}(\varLambda (\xi _{1},\ldots,\xi _{n}))\). This immediately implies the Morita equivalence of  and
and  .
.
Let λ be a weight of  and X = G∕B be a flag supermanifold. As in the usual case one can define the sheaf of twisted differential operators D
X
λ. Let
and X = G∕B be a flag supermanifold. As in the usual case one can define the sheaf of twisted differential operators D
X
λ. Let  denote the quotient of
denote the quotient of  by the ideal generated by the kernel of the central character
by the ideal generated by the kernel of the central character  . The embedding of the Lie superalgebra
. The embedding of the Lie superalgebra  to the Lie superalgebra of vector fields on X induces the homomorphism of superalgebras
to the Lie superalgebra of vector fields on X induces the homomorphism of superalgebras

Recall that it is an isomorphism if  is a reductive Lie algebra. Moreover, for dominant λ the localization functor provides equivalence of categories of
is a reductive Lie algebra. Moreover, for dominant λ the localization functor provides equivalence of categories of  -modules and
-modules and  -modules. In the supercase, the similar result is true for generic typical λ, see [36].
-modules. In the supercase, the similar result is true for generic typical λ, see [36].
Theorem 18
Let λ be a generic typical weight such that
\(\frac{2(\lambda \vert \alpha )} {(\alpha \vert \alpha )} \notin \mathbf{Z}_{<0}\)
for all even positive roots α. Then the functors of localization and global sections establish equivalence of categories of
 -modules and
-modules and
 -modules.
-modules.
Note that essentially this theorem is equivalent to Theorem 4. In fact Theorem 18 was used by Penkov for the proof of Theorem 4. If λ is not typical, then the homomorphism p
λ
is neither surjective nor injective. On the other hand, it is not difficult to see that for atypical λ the superalgebra  has a non-trivial Jacobson radical, see [41]. There is an evidence that the following conjecture may hold.
has a non-trivial Jacobson radical, see [41]. There is an evidence that the following conjecture may hold.
Conjecture 6
Let λ be a regular weight, tame with respect to  , and let
, and let  denote the quotient of
denote the quotient of  by the Jacobson radical. Let
by the Jacobson radical. Let  denote the center of
denote the center of  . Let Q ⊃ B be the maximal parabolic subgroup of G such that its Lie superalgebra
. Let Q ⊃ B be the maximal parabolic subgroup of G such that its Lie superalgebra  admits one-dimensional representation c
λ
. Finally let Y: = G∕Q.
admits one-dimensional representation c
λ
. Finally let Y: = G∕Q.
If  is a generic central character and
is a generic central character and  is the quotient of
is the quotient of  by the ideal (ker τ), then the categories of
by the ideal (ker τ), then the categories of  -modules and
-modules and  -modules are equivalent.
-modules are equivalent.
10 Direct Limits of Lie Algebras and Superalgebras
The goal of this section is to say few words about representations of direct limits of classical Lie superalgebras. We will discuss here only the case of  and refer to [43] for the case of
and refer to [43] for the case of  . Surprisingly, for some class of representations the difference between the Lie superalgebra
. Surprisingly, for some class of representations the difference between the Lie superalgebra  and the Lie algebra
and the Lie algebra  disappears.
disappears.
10.1 Category of Tensor Modules
Let V, W be countable-dimensional vector spaces (resp. superspaces) with non-degenerate even pairing 〈⋅ , ⋅ 〉: W × V → k. It is known that one can choose a pair of dual bases in V and W. The tensor product V ⊗ W is a Lie algebra (resp. superalgebra)  with the following bracket:
with the following bracket:
We denote this (super)algebra  in the even case and
in the even case and  in the supercase. Note that both V and W are
in the supercase. Note that both V and W are  -modules and
-modules and  acts on V and W by linear operators of finite rank. It is not difficult to see that
acts on V and W by linear operators of finite rank. It is not difficult to see that  can be identified with infinite matrices with finitely many non-zero entries and hence
can be identified with infinite matrices with finitely many non-zero entries and hence

Let T
p, q = V
⊗p ⊗ W
⊗q. We would like to understand the structure of  -module on T
p, q. It is clear that the product of symmetric groups S
p
× S
q
acts on T
p, q and this action commutes with the action of
-module on T
p, q. It is clear that the product of symmetric groups S
p
× S
q
acts on T
p, q and this action commutes with the action of  . Irreducible representations of S
p
× S
q
are parametrized by bipartitions (λ, μ) such that | λ | = p, | μ | = q. The following result is a classical Schur–Weyl duality. In the supercase its proof is due to Sergeev, [44].
. Irreducible representations of S
p
× S
q
are parametrized by bipartitions (λ, μ) such that | λ | = p, | μ | = q. The following result is a classical Schur–Weyl duality. In the supercase its proof is due to Sergeev, [44].
Theorem 19
Let
 or
or
 . Then we have the following decomposition
. Then we have the following decomposition
where S
λ
(V ) and S
μ
(W) are simple
 -modules and Y
λ, μ
is the irreducible representation of S
p
× S
q
associated with a bipartition (λ, μ).
-modules and Y
λ, μ
is the irreducible representation of S
p
× S
q
associated with a bipartition (λ, μ).
Let  . It is proven in [37] that S
λ
(V ) ⊗ S
μ
(W) is an indecomposable
. It is proven in [37] that S
λ
(V ) ⊗ S
μ
(W) is an indecomposable  -module of finite length with simple socle V (λ, μ). Denote by
-module of finite length with simple socle V (λ, μ). Denote by  the abelian category of
the abelian category of  -modules generated by finite direct sums of T
p, q and all their subquotients. This is a symmetric monoidal category which in the case of
-modules generated by finite direct sums of T
p, q and all their subquotients. This is a symmetric monoidal category which in the case of  was studied in [8] and [38].
was studied in [8] and [38].
Theorem 20 ([8])
Let
 . Any simple object of
. Any simple object of
 is isomorphic to V (λ, μ) for some bipartition (λ, μ) and S
λ
(V ) ⊗ S
μ
(W) is the injective hull of V (λ, μ). In particular, the category
is isomorphic to V (λ, μ) for some bipartition (λ, μ) and S
λ
(V ) ⊗ S
μ
(W) is the injective hull of V (λ, μ). In particular, the category
 has enough injective objects. Moreover, any object in
has enough injective objects. Moreover, any object in
 has a finite injective resolution.
has a finite injective resolution.
It is also proven in [8] that  is a Koszul self-dual category.
is a Koszul self-dual category.
Let us consider the case  . We start by constructing two functors F
l
and F
r
from the category
. We start by constructing two functors F
l
and F
r
from the category  to the category
to the category  . Observe that the even part
. Observe that the even part  is a direct sum
is a direct sum  with both
with both  and
and  isomorphic to
isomorphic to  . For any
. For any  we set
we set

Theorem 21 ([43])
Let
 .
.
-
(a)
F l and F r are exact tensor functors, i.e. F l (M ⊗ N) = F l (M) ⊗ F l (N) and the same for F r .
-
(b)
F l and F r have left adjoint functors which we denote by R l and R r respectively.
-
(c)
F l and R l (resp. F r and R r ) are mutually inverse equivalences of tensor categories
 and
and
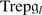 (resp.
(resp.
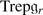 ).
).
Remark 11
The compositions F
r
∘ R
l
and F
l
∘ R
r
provide an autoequivalence of  which sends a simple module V (λ, μ) to the simple module V (λ
′, μ
′), where ν
′ stands for the partition conjugate to ν.
which sends a simple module V (λ, μ) to the simple module V (λ
′, μ
′), where ν
′ stands for the partition conjugate to ν.
Remark 12
The corresponding construction works as well for the Lie superalgebra  . Here
. Here  and
and  . In particular, we establish equivalence of tensor categories
. In particular, we establish equivalence of tensor categories  and
and  .
.
Remark 13
The category  contains a semisimple subcategory
contains a semisimple subcategory  consisting of modules appearing in T
p, 0, \(p \in \mathbb{N}\).
consisting of modules appearing in T
p, 0, \(p \in \mathbb{N}\).
10.2 Equivalences for Parabolic Category
In this subsection we will show how functors F
r
and F
l
help to prove equivalence of certain parabolic category  for
for  and
and  . This result is originally proven in [6] by using infinite chain of odd reflections.
. This result is originally proven in [6] by using infinite chain of odd reflections.
Let  ,
,  and
and  . We fix the embeddings
. We fix the embeddings  and
and  into
into  in the following way. Realize
in the following way. Realize  as matrices with finitely many non-zero entries written in the block form
as matrices with finitely many non-zero entries written in the block form
where A
1,1 has size m × m, A
1,2 and A
1,3 have size m ×∞, A
2,1 and A
3,1 have size ∞× m and A
2,2 and A
3,3 have size ∞×∞. The even part  consists of matrices of the form
consists of matrices of the form
and the odd part  of matrices of the form
of matrices of the form
Then  consists of matrices
consists of matrices
and  of matrices
of matrices
Let  and
and  be subalgebras of matrices of the form
be subalgebras of matrices of the form
respectively. Then it is not hard to see that  is the centralizer of
is the centralizer of  and
and  is the centralizer of
is the centralizer of  .
.
Next we consider the parabolic subalgebra  consisting of matrices
consisting of matrices
with abelian ideal 
and the Levi subalgebra 
isomorphic to  .
.
Finally we set  and
and  . Note that
. Note that  and
and  are parabolic subalgebras. Now we consider the category
are parabolic subalgebras. Now we consider the category  consisting of all
consisting of all  -modules M satisfying the following conditions
-modules M satisfying the following conditions
-
M is finitely generated;
-
M is semisimple over the diagonal subalgebra of
 with integral weights;
with integral weights; -
M is an integrable
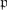 -module and the restriction to the subalgebra
-module and the restriction to the subalgebra 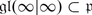 belongs to the inductive completion of
belongs to the inductive completion of 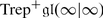 .
.
In a similar way we define the categories  and
and  for algebras
for algebras  and
and  respectively. As in the previous subsection we define the functors
respectively. As in the previous subsection we define the functors

by setting

Then we have the following analogue of Theorem 21.
Theorem 22
-
(a)
F ′ and F ″ have left adjoint functors which we denote by R ′ and R ″ respectively.
-
(b)
F ′ and R ′ (resp. F ″ and R ″ ) are mutually inverse equivalences of abelian categories
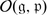 and
and
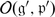 (resp.
(resp.
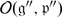 ).
).
-
(c)
The composite functors F ″∘ R ′ and F ′∘ R ″ are mutually inverse equivalences of abelian categories
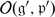 and
and
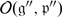 .
.
Notes
- 1.
A grading
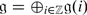 is compatible if
is compatible if 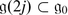 and
and 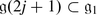 .
. - 2.
This assumption is not essential and can be dropped. It is here only for convenience of notations.
References
J. Brundan, Kazhdan-Lusztig polynomials and character formulae for the Lie superalgebra gl(m | n). J. Am. Math. Soc. 16(1), 185–231 (2003)
J. Brundan, C. Stroppel, Highest weight categories arising from Khovanov’s diagram algebra IV: the general linear supergroup. J. Eur. Math. Soc. 14(2), 373–419 (2012)
C. Carmeli, L. Caston, R. Fioresi, Mathematical Foundations of Supersymmetry. EMS Series of Lectures in Mathematics (EMS, Zurich, 2011)
S.J. Cheng, W. Wang, Dualities and Representations of Lie Superalgebras. Graduate Studies in Mathematics, vol. 144 (American Mathematical Society, Providence, RI, 2012)
S.J. Cheng, J.H. Kwon, Kac-Wakimoto character formula for ortho-symplectic Lie superalgebras (2017). arxiv:1406.6739
S.J. Cheng, N. Lam, W. Wang, Super duality for general linear Lie superalgebras and applications. Proc. Symposia Pure Math. Am. Math. Soc. 86, 113–136 (2012)
K. Coulembier, V. Serganova, Homological invariants in category O for the general linear superalgebra. Trans. Am. Math. Soc. (2017)
E. Dan-Cohen, I. Penkov, V. Serganova, A Koszul category of representations of finitary Lie algebras. Adv. Math. 289, 250–278 (2016)
P. Deligne, Catégories tannakiennes. The Grothendieck Festschrift (Birkhauser, Boston, 1990), pp. 111–195
J. Dixmier, Enveloping Algebras (Akademie-Verlag, Berlin, 1977)
M. Duflo, V. Serganova, On associated variety for Lie superalgebras (2005). arXiv: math/0507198
P. Gabriel, Indecomposable Representations II. Symposia Mathematica, vol. XI (Academic, London, 1973), pp. 81–104
J. Germoni, Representations indecomposables des algebres de Lie speciales lineaires. These de l’universite de Strasbourg (1997)
J. Germoni, Indecomposable representations of osp(3, 2), D(2, 1, a) and G 2, in Colloquium in Homology and Representation Theory, vol. 65, Bol. Acad. Nac. Cienc, Cordoba (2000), pp. 147–163
M. Gorelik, Strongly typical representations of the basic classical Lie superalgebras. J. Am. Math. Soc. 15(1), 167–184 (2002)
M. Gorelik, The Kac construction of the centre of
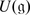 for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)
for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)C. Gruson, Sur l’ideal du cone autocommutant des super algebres de Lie basiques classiques et etranges. Ann. Inst. Fourier (Grenoble) 50(3), 807–831 (2000)
C. Gruson, Cohomologie des modules de dimension finie sur la super algebre
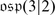 . J. Algebra 259, 581–598 (2003)
. J. Algebra 259, 581–598 (2003)C. Gruson, V. Serganova, Cohomology of generalized supergrassmannians and character formulae for basic classical Lie superalgebras. Proc. Lond. Math. Soc. (3) 101(3), 852–892 (2010)
C. Gruson, V. Serganova, Bernstein-Gelfand-Gelfand reciprocity and indecomposable projective modules for classical algebraic supergroups. Mosc. Math. J. 13(2), 281–313 (2013)
T. Heidersdorf, R. Wassauer, Cohomological tensor functors on representations of the general linear supergroup (2014). arXiv:1406.0321
V.G. Kac, Lie superalgebras. Adv. Math. 26, 8–96 (1977)
V.G. Kac, Representations of classical Lie superalgebras. Differential Geometrical Methods in Mathematical Physics, II. Proceedings of the Conference, University of Bonn, Bonn, 1977. Lecture Notes in Mathematics, vol. 676 (Springer, Berlin, 1978), pp. 597–626
V.G. Kac, Laplace operators of infinite-dimensional Lie algebras and theta functions. Proc. Nat. Acad. Sci. U. S. A. 81(2), 645–647 (1984). Phys. Sci.
V.G. Kac, M. Wakimoto, Integrable highest weight modules over affine superalgebras and number theory, in Lie Theory and Geometry. Progress in Mathematics, vol. 123 (Birkhäuser Boston, Boston, MA, 1994), pp. 415–456
M. Kontsevich, Defomation quantization of Poisson manifold. Lett. Math. Phys. 66(3), 157–216 (2003)
B. Kostant, Graded Manifolds, Graded Lie Theory, and Prequantization. Lecture Notes in Mathematics, vol. 570 (Springer, Berlin, 1977), pp. 177–306
J.L. Koszul, Graded manifolds and graded Lie algebras. International Meeting on Geometry and Physics (Bologna), Pitagora (1982), pp. 71–84
L. Martirosyan, The representation theory of the exceptional Lie superalgebras F(4) and G(3). J. Algebra 419, 167–222 (2014)
A. Masuoka, A. Zubkov, Quotient sheaves of algebraic supergroups are superschemes. J. Algebra 348, 135–170 (2011)
A. Masuoka, Harish-Chandra pairs for algebraic affine supergroup schemes over an arbitrary field. Transform. Groups 17(4), 1085–1121 (2012)
I. Musson, Lie Superalgebras and Enveloping Algebras. Graduate Studies in Mathematics, vol. 131 (American Mathematical Society, Providence, RI, 2012)
I. Musson, V. Serganova, Combinatorics of character formulas for the Lie superalgebra gl(m, n). Transform. Groups 16(2), 555–578 (2011)
A.L. Onishchik, E.B. Vinberg, Lie Groups and Algebraic Groups (Springer, Berlin, 1980)
I. Penkov, Borel-Weil-Bott theory for classical Lie supergroups. Translated in J. Soviet Math. 51(1), 2108–2140 (1990) [Russian]
I. Penkov, Characters of strongly generic irreducible Lie superalgebra representations. Internat. J. Math. 9(3), 331–366 (1998)
I. Penkov, K. Styrkas, Tensor representations of infinite-dimensional root-reductive Lie algebras, in Developments and Trends in Infinite-Dimensional Lie Theory, Progress in Mathematics, vol. 288 (Birkhäuser, Basel, 2011), pp. 127–150
S. Sam, A. Snowden, Stability patterns in representation theory. arXiv:1302.5859
V. Serganova, On generalized root systems. Commun. Algebra 24 (13), 4281–4299 (1996)
V. Serganova, Kazhdan-Lusztig polynomials and character formula for the Lie superalgebra gl(m | n). Selecta Math. (N.S.) 2(4), 607–651 (1996)
V. Serganova, A reduction method for atypical representations of classical Lie superalgebras. Adv. Math. 180, 248–274 (2003)
V. Serganova, On the superdimension of an irreducible representation of a basic classical Lie superalgebra, in Supersymmetry in Mathematics and Physics. Lecture Notes in Mathematics, vol. 2027 (Springer, Heidelberg, 2011), pp. 253–273
V. Serganova, Classical Lie superalgebras at infinity, in Advances in Lie Superalgebras. Springer INdAM Series, vol. 7 (Springer, Berlin, 2014), pp. 181–201
A. Sergeev, The tensor algebra of the tautological representation as a module over the Lie super-algebras gl(n, m) and Q(n). Mat. Sb. 123, 422–430 (1984) [in Russian]
A. Sergeev, The invariant polynomials on simple Lie superalgebras. Represent. Theory 3, 250–280 (1999)
E. Vishnyakova, On complex Lie supergroups and split homogeneous supermanifolds. Transform. Groups 16(1), 265–285 (2011)
Y.M. Zou, Categories of finite-dimensional weight modules over type I classical Lie superalgebras. J. Algebra 180, 459–482 (1996)
Acknowledgements
I thank the organizers of the workshop in Pisa for giving me the opportunity to give this minicourse and Rita Fioresi for writing the lecture notes. I thank the referee for pointing out numerous missprints in the first version of the paper. I also acknowledge partial support of NSF grant DMS-1303301.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Serganova, V. (2017). Representations of Lie Superalgebras. In: Callegaro, F., Carnovale, G., Caselli, F., De Concini, C., De Sole, A. (eds) Perspectives in Lie Theory. Springer INdAM Series, vol 19. Springer, Cham. https://doi.org/10.1007/978-3-319-58971-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-58971-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58970-1
Online ISBN: 978-3-319-58971-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 is a Lie algebra;
is a Lie algebra; equips
equips  with the structure of a
with the structure of a 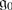 -module;
-module;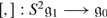 is a homomorphism of
is a homomorphism of 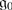 -modules;
-modules;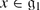 , [x, [x, x]] = 0.
, [x, [x, x]] = 0.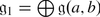 ;
;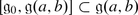 ;
;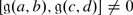 implies a = −c, b = −d.
implies a = −c, b = −d.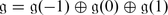 , such that
, such that
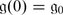 and
and
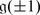 are irreducible
are irreducible
 -modules.
-modules.
 is semisimple and
is semisimple and
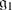 is an irreducible
is an irreducible
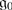 -module.
-module.
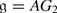 with
with 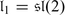 ,
, 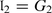 , M is the 2-dimensional irreducible
, M is the 2-dimensional irreducible 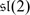 -module and N is the smallest irreducible G
2-module of dimension 7. One can easily see that dimAG
2 = (17 | 14).
-module and N is the smallest irreducible G
2-module of dimension 7. One can easily see that dimAG
2 = (17 | 14).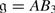 with
with 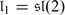 ,
, 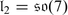 , M is again the 2-dimensional irreducible
, M is again the 2-dimensional irreducible 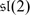 -module, N is the spinor representation of
-module, N is the spinor representation of  . Clearly, dimAB
3 = (24 | 16).
. Clearly, dimAB
3 = (24 | 16).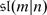 ,
,
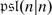 ,
,
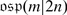 ,
,
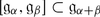 if α + β ≠ 0 and
if α + β ≠ 0 and 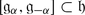 .
.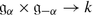 for all α ∈ Δ and
for all α ∈ Δ and 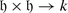 .
.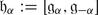 is a one-dimensional subspace in
is a one-dimensional subspace in 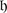 . That follows from the first two properties and the identity ([x, y], h) = α(h)(x, y) for
. That follows from the first two properties and the identity ([x, y], h) = α(h)(x, y) for 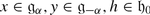 .
.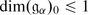 ;
;
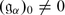 , then
, then
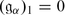 .
. , [x, x] ≠ 0. Hence 2α ∈ Δ
0.
, [x, x] ≠ 0. Hence 2α ∈ Δ
0.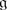 is of type 1 then W has two orbits in Δ
1
, the roots of
is of type 1 then W has two orbits in Δ
1
, the roots of
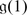 and the roots of
and the roots of
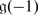 .
. is of type 2, then W acts transitively on the set of isotropic and the set of non-isotropic odd roots.
is of type 2, then W acts transitively on the set of isotropic and the set of non-isotropic odd roots.
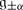 generate a
generate a 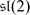 subalgebra (white node in a Dynkin diagram).
subalgebra (white node in a Dynkin diagram).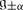 generate a subalgebra isomorphic to
generate a subalgebra isomorphic to 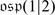 (black node in a Dynkin diagram).
(black node in a Dynkin diagram).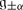 generate a subalgebra isomorphic to
generate a subalgebra isomorphic to 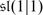 (grey node in a Dynkin diagram).
(grey node in a Dynkin diagram). is of type 1, then Q
0 is a sublattice of corank 1 in Q.
is of type 1, then Q
0 is a sublattice of corank 1 in Q. is of type 2, then Q
0 is a finite index subgroup in Q.
is of type 2, then Q
0 is a finite index subgroup in Q. and
and  are two Borel subalgebras of
are two Borel subalgebras of 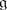 with the same even part, then we must have an isomorphism
with the same even part, then we must have an isomorphism 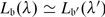 for some weights λ and λ
′. Let
for some weights λ and λ
′. Let 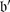 be obtained from
be obtained from 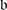 by an odd reflection r
α
. Check that
by an odd reflection r
α
. Check that 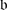 . Let Π
0 denote the base of Δ
0
+. Prove that
. Let Π
0 denote the base of Δ
0
+. Prove that 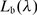 is finite-dimensional if and only if for any β ∈ Π
0 and a base Π
′ obtained from Π by odd reflections such that β ∈ Π
′ or
is finite-dimensional if and only if for any β ∈ Π
0 and a base Π
′ obtained from Π by odd reflections such that β ∈ Π
′ or 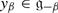 acts locally nilpotently on
acts locally nilpotently on 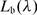 .)
.)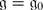 then we get the usual Weyl character formula.
then we get the usual Weyl character formula.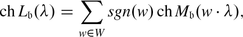
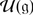
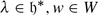 ;
;
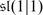 -subalgebra of
-subalgebra of
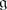 .
. -subalgebra of
-subalgebra of
 .
.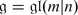 ,
, 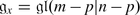 ;
;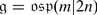 ,
, 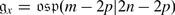 ;
;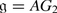 , p = 1,
, p = 1, 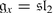 ;
;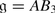 , p = 1,
, p = 1, 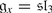 ;
;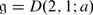 , p = 1,
, p = 1,  .
. -modules with typical central character.
-modules with typical central character.
 into a direct sum of subcategories
into a direct sum of subcategories
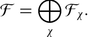
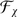 we have a decomposition
we have a decomposition
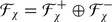 such that
such that
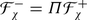 . (Recall that Π is the change of parity functor.)
. (Recall that Π is the change of parity functor.)
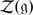 acts locally finitely on M, so M decomposes into the direct sum of generalized weight spaces of
acts locally finitely on M, so M decomposes into the direct sum of generalized weight spaces of 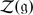 .
.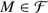 is
is 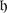 -semisimple. Thus, M has a weight decomposition M = ⊕M
μ
. One can define a function
-semisimple. Thus, M has a weight decomposition M = ⊕M
μ
. One can define a function 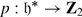 such that p(λ + α) = p(λ) for any even root α and p(λ + α) = p(λ) + 1 for any odd root α. Set
such that p(λ + α) = p(λ) for any even root α and p(λ + α) = p(λ) + 1 for any odd root α. Set  as the full subcategory of
as the full subcategory of  consisting of modules M such that
consisting of modules M such that  are indecomposable.
are indecomposable.
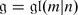 (resp.
(resp.
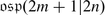 ), and p = atχ, then
), and p = atχ, then
 is equivalent to the principal block of
is equivalent to the principal block of
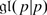 (resp.
(resp.
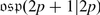 ).
).
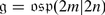 then
then
 is equivalent to the principal block of
is equivalent to the principal block of
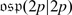 or
or
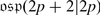 .
. with atypical χ is equivalent to the principal block of
with atypical χ is equivalent to the principal block of
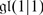 or
or
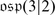 .
.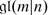
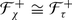 of abelian categories.
of abelian categories.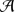 , while the the entries of B and C are odd;
, while the the entries of B and C are odd;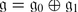 ;
;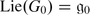 ;
; with differential equal to the superbracket
with differential equal to the superbracket  .
. -Modules
-Modules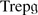 and
and
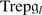 (resp.
(resp.
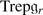 ).
).
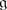 with integral weights;
with integral weights;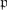 -module and the restriction to the subalgebra
-module and the restriction to the subalgebra 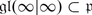 belongs to the inductive completion of
belongs to the inductive completion of 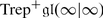 .
.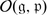 and
and
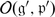 (resp.
(resp.
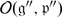 ).
).
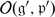 and
and
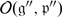 .
.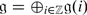 is compatible if
is compatible if 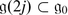 and
and 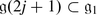 .
.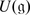 for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)
for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)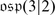 . J. Algebra 259, 581–598 (2003)
. J. Algebra 259, 581–598 (2003)