Keywords

Introduction

Nowadays, due to the rapid advances in technologies, micro- and nano-sized mechanical systems like microbeams, microbars, biosensors, nanowires, atomic force microscope, nanotubes, micro actuators, nano probes, micro- and nano-electromechanical systems (MEMS and NEMS), and ultra-thin films have been widely used in modern applications such as mechanical, biomedical, chemical, and biological applications (Fu et al. 2003; Li et al. 2003; Najar et al. 2005; Faris and Nayfeh 2007; Moser and Gijs 2007; Kahrobaiyan et al. 2011a). The insight of the mechanical behavior characteristics of micro- and nanostructures is very important for the optimum design of such structures. Bending, buckling, and vibration responses of these structures can be investigated by experimental studies and computer simulation techniques at atomistic levels. The effects of size dependency on the deformation behaviors of the aforementioned structures have been experimentally observed (Fleck et al. 1994; Chong and Lam 1999; Senturia 2001; Haque and Saif 2003; Lam et al. 2003; Lou et al. 2006).

Due to the difficulty and computationally expensiveness of experimentation and simulation techniques at atomistic levels (e.g., molecular dynamic simulation), many scientists and researchers tended the continuum mechanics modeling as an alternative. However, the classical continuum mechanics approaches do not the ability for interpretation and explanation of the microstructural dependency of small-sized structures due to the lack of any additional (intrinsic) material length scale parameters. Then, higher-order (nonclassical) continuum theories, which include at least one additional material length scale parameter in addition to classical ones, have been proposed to predict the microstructure-dependent behavior of these small-scale structures.

Higher-order continuum theories include Cosserat elasticity by Cosserat and Cosserat (1909), strain gradient elasticity of Mindlin (1964,1965), micropolar theory (Eringen and Suhubi 1964), nonlocal elasticity (Eringen 1983), couple stress theory by Mindlin and Tiersten (1962), Toupin (1962), and Koiter (1964), strain gradient theory (Fleck and Hutchinson 1993), simple gradient elasticity with surface energy (Vardoulakis and Sulem 1995; Altan et al. 1996; Altan and Aifantis 1997), modified couple stress (Yang et al. 2002), and modified strain gradient theories (Lam et al. 2003). Some earlier studies based on these theories available in the literature have been briefly given here.

Peddieson et al. (2003) formulated a nonlocal Bernoulli-Euler beam model with nonlocal elasticity theory. Also, Reddy (2007a) investigated bending, buckling, and free vibration analysis of nonlocal beams for different beam theories. Wang et al. (2008) studied bending problem of micro- and nano-sized beams based on nonlocal Timoshenko beam theory. Aydogdu (2009) investigated the small-scale effect on longitudinal vibration of a nanorod on the basis of Eringen’s nonlocal elasticity theory.

The classical couple stress theory has been used to investigate the bending analysis of a circular cylinder by Anthoine (2000). Tsepoura et al. (2002) investigated static and dynamic analysis of bars based on simple gradient elasticity theory with surface energy. Papargyri-Beskou et al. (2003a) and Lazopoulos (2012) observed dynamic analysis of gradient elastic beams. Bending and buckling analysis of gradient elastic beams is studied on the basis of Bernoulli-Euler beam model by Papargyri-Beskou et al. (2003b) and Lazopoulos and Lazopoulos (2010).

Modified couple stress theory is a higher-order continuum theory that has been elaborated by Yang et al. (2002) which contains the symmetric rotation gradient tensor and one additional material length scale parameter in addition to the conventional (classical) strain tensor. Park and Gao (2006) and Ma et al. (2008) developed new size-dependent Bernoulli-Euler and Timoshenko beam models, respectively. Kong et al. (2008) investigated free vibration analysis of the Bernoulli-Euler microbeam model based on this theory.

The modified strain gradient elasticity theory is one of the popular higher-order continuum theories, which was proposed by Lam et al. (2003), that includes dilatation and deviatoric stretch gradient tensors besides the symmetric rotation gradient and classical strain tensor and also three additional material length scale parameters for linear elastic isotropic materials. Kong et al. (2009), Akgöz and Civalek (2011), and Wang et al. (2010) used modified strain gradient elasticity for static and dynamic analyses of microbeams on the basis of Bernoulli-Euler and Timoshenko beam models, respectively. Furthermore, static torsion and torsional free vibration analyses of microbars based on this theory were presented by Kahrobaiyan et al. (2011b) and Narendar et al. (2012). Recently, longitudinal vibration responses of microbars were investigated by Akgöz and Civalek (2013, 2014), Kahrobaiyan et al. (2013), and Güven (2014).

In this chapter, size-dependent axial vibration response of micro-sized rods is investigated on the basis of modified strain gradient elasticity theory. The equation of motion together with initial conditions, classical and nonclassical corresponding boundary conditions, for micro-rods is derived with the aid of Hamilton’s principle. The resulting higher-order equation is solved for two different boundary conditions as clamped-free and clamped-clamped. Influences of micro-rod characteristic lengths, slenderness ratio, additional material length scale parameters, and mode number on the vibrational response of the size-dependent micro-rod are investigated.

Formulation for Modified Strain Gradient Theory

The strain energy U in a linear elastic isotropic material occupying volume V based on the modified strain gradient elasticity theory can be written by Lam et al. (2003) and Kong et al. (2009).

$$ U=\frac{1}{2}{\int}_V\left({\sigma}_{ij}{\varepsilon}_{ij}+{p}_i{\gamma}_i+{\tau}_{ij k}^{(1)}{\eta}_{ij k}^{(1)}+{m}_{ij}^s{\chi}_{ij}^s\right) dv $$
(1)
$$ {\varepsilon}_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right) $$
(2)
$$ {\gamma}_i={\varepsilon}_{mm,i} $$
(3)
$$\begin{aligned} {\eta}_{ij k}^{(1)}=&\frac{1}{3}\left({\varepsilon}_{jk,i}+{\varepsilon}_{ki,j}+{\varepsilon}_{ij,k}\right)-\frac{1}{15}\left[{\delta}_{ij}\left({\varepsilon}_{mm,k}+2{\varepsilon}_{mk,m}\right)\right.\\&+\left.{\delta}_{jk}\left({\varepsilon}_{mm,i}+2{\varepsilon}_{mi,m}\right)+{\delta}_{ki}\left({\varepsilon}_{mm,j}+2{\varepsilon}_{mj,m}\right)\right] \end{aligned} $$
(4)
$$ {\chi}_{ij}^s=\frac{1}{2}\left({\theta}_{i,j}+{\theta}_{j,i}\right) $$
(5)
$$ {\theta}_i=\frac{1}{2}{e}_{ijk}{u}_{k,j} $$
(6)

where ui, εij, γi, \( {\eta}_{ijk}^{(1)} \), \( {\chi}_{ij}^s \), and θi are the components of the displacement vector, the strain tensor, the dilatation gradient vector, the deviatoric stretch gradient tensor, the symmetric rotation gradient tensor, and the rotation vector, respectively. Also δij is the Kronecker delta, and eijk is the permutation symbol. The stress measures σij, pi, \( {\tau}_{ijk}^{(1)} \), and \( {m}_{ij}^s \) are the components of classical and higher-order stresses defined as Lam et al. (2003).

$$ {\sigma}_{ij}={\lambda \delta}_{ij}{\varepsilon}_{mm}+2{\mu \varepsilon}_{ij} $$
(7)
$$ {p}_i=2\mu {l}_0^2{\gamma}_i $$
(8)
$$ {\tau}_{ijk}^{(1)}=2\mu {l}_1^2{\eta}_{ijk}^{(1)} $$
(9)
$$ {m}_{ij}^s=2\mu {l}_2^2{\chi}_{ij}^s $$
(10)

where λ and μ are the well-known Lamé constants and l0, l1, l2 are additional material length scale parameters which represent the size dependency and related to dilatation gradients, deviatoric stretch gradients, and rotation gradients, respectively.

Microstructure-Dependent Rod Model

It is considered that the case of axial vibration of a straight thin micro-rod (see Fig. 1). Due to axial vibrations take place in x− direction, the deformation of the cross section in y− and z− directions is assumed to be negligible by a simple theory for axial vibration of thin rods. The components of displacement vector can be expressed as Rao (2007).

$$ {u}_1=u\left(x,t\right),{u}_2=0,{u}_3=0 $$
(11)

where u1, u2, and u3 are the components of displacement vector in x−, y−, and z− directions, respectively.

Fig. 1
figure 1

Geometry and coordinate system of a straight micro-rod

Full size image

In view of Eqs. (2) and (11), the non-zero strain component of the micro-rod is

$$ {\varepsilon}_{xx}=\frac{\partial u}{\partial x} $$
(12)

Use of Eqs. (12) into (3), the non-zero component of dilatation gradient vector is obtained as

$$ {\gamma}_x=\frac{\partial^2u}{\partial {x}^2} $$
(13)

From Eqs. (2) and (4), non-zero components of deviatoric stretch gradient tensor are achieved as

$$ {\eta}_{xxx}^{(1)}=\frac{2}{5}\frac{\partial^2u}{\partial {x}^2},{\eta}_{xyy}^{(1)}={\eta}_{xzz}^{(1)}={\eta}_{yxy}^{(1)}={\eta}_{yyx}^{(1)}={\eta}_{zxz}^{(1)}={\eta}_{zzx}^{(1)}=-\frac{1}{5}\frac{\partial^2u}{\partial {x}^2} $$
(14)

Furthermore, all components of rotation vector and so symmetric rotation gradient tensor are equal to zero as

$$ {\theta}_i=0,\left(i=x,y,z\right) $$
(15)
$$ {\chi}_{ij}^s=0,\left(i,j=x,y,z\right) $$
(16)

The non-zero stress σij can be obtained by neglecting Poisson’s effect in Eq. (7) as

$$ {\sigma}_{xx}=E\frac{\partial u}{\partial x} $$
(17)

where E is the elastic modulus. By inserting Eqs. (13) into (8) and Eqs. (14) into (9), the non-zero components of higher-order stresses pi and \( {\tau}_{ijk}^{(1)} \) can be expressed as

$$ {p}_x=2\mu {l}_0^2\frac{\partial^2u}{\partial {x}^2} $$
(18)
$$ {\tau}_{xxx}^{(1)}=\frac{4}{5}\mu {l}_1^2\frac{\partial^2u}{\partial {x}^2},{\tau}_{xyy}^{(1)}={\tau}_{xzz}^{(1)}={\tau}_{yxy}^{(1)}={\tau}_{yyx}^{(1)}={\tau}_{zxz}^{(1)}={\tau}_{zzx}^{(1)}=-\frac{2}{5}\mu {l}_1^2\frac{\partial^2u}{\partial {x}^2}, $$
(19)

Substituting above equations into Eq. (1), the strain energy U can be rewritten as

$$ U=\frac{1}{2}{\int}_0^L\left\{ EA{\left({u}^{\prime}\right)}^2+\left(2\mu {Al}_0^2+\frac{4}{5}\mu {Al}_1^2\right){\left({u}^{{\prime\prime}}\right)}^2\right\} dx $$
(20)

where A is the cross-sectional area of the micro-rod and

$$ {u}^{\prime }=\frac{\partial u}{\partial x},{u}^{{\prime\prime} }=\frac{\partial^2u}{\partial {x}^2} $$
(21)

The first variation of strain energyU in Eq. (20) on the time interval [t0, t1] can be calculated as following expression

$$\begin{aligned} \delta U&={\int}_{t_0}^{t_1}{\int}_0^L\left\{{Bu}^{(4)}- EA{u}^{{\prime\prime}}\right\}{}\delta udxdt+{\int}_{t_0}^{t_1}\left\{{{}{}\left[\left( EA{u}^{\prime }-B{u}^{{\prime\prime\prime}}\right)\delta u\right]}_0^L\right.\\ &\left.+{\left[B{u}^{{\prime\prime}}\delta {u}^{\prime}\right]}_0^L\right\}{}dt \end{aligned}$$
(22)

where

$$ {u}^{{\prime\prime\prime} }=\frac{\partial^3u}{\partial {x}^3},{u}^{(4)}=\frac{\partial^4u}{\partial {x}^4},B=2\mu A\left({l}_0^2+\frac{2}{5}{l}_1^2\right) $$
(23)

On the other hand, the first variation of the work done by external force q , axial force N, and higher-order axial force Nh on the time interval [t0, t1] takes the following form

$$ \delta W={\int}_{t_0}^{t_1}{\int}_0^L q\delta u dxdt+{\int}_{t_0}^{t_1}\left\{{\left[ N\delta u\right]}_0^L+{\left[{N}^h\delta {u}^{\prime}\right]}_0^L\right\}{}dt $$
(24)

Also, the first variation of kinetic energy K of the micro-rod on the time interval [t0, t1] reads as

$$ \delta K=-{\int}_{t_0}^{t_1}{\int}_0^Lm\ddot{u}\delta u dxdt+{\int}_0^L{\left[m\dot{u}\delta u\right]}_{t_0}^{t_1} dx $$
(25)

where m is the mass per unit length and

$$ \dot{u}=\frac{\partial u}{\partial t},\ddot{u}=\frac{\partial^2u}{\partial {t}^2} $$
(26)

The following relation is written by employing Hamilton’s principle with Eqs. (22, 24, and 25)

$$ \delta \left\{{\int}_{t_0}^{t_1}\left[K-\left(U-W\right)\right] dt\right\}=0 $$
(27)
$$\begin{aligned} &{\int}_{t_0}^{t_1}{\int}_0^L\left[ EA{u}^{{\prime\prime} }-{Bu}^{(4)}-m\ddot{u}+q\right]\delta u dxdt+{\int}_{t_0}^{t_1}{\left[\left\{N-\left( EA{u}^{\prime }-B{u}^{{\prime\prime\prime}}\right)\right\}\delta u\right]}_0^L dt\\&\quad+{\int}_{t_0}^{t_1}{\left[\left\{{N}^h-B{u}^{{\prime\prime}}\right\}\delta {u}^{\prime}\right]}_0^L dt+{\int}_0^L{\left[m\dot{u}\delta u\right]}_{t_0}^{t_1} dx=0 \end{aligned}$$
(28)

According to the fundamental lemma of calculus of variation (Reddy 2007b), the equation of motion for the micro-rod reads as

$$ EA{u}^{{\prime\prime} }-{Bu}^{(4)}+q=m\ddot{u} $$
(29)

Also, initial conditions and boundary conditions satisfy the following equations, respectively, as

$$ \dot{u}\left(x,{t}_1\right)\delta u\left(x,{t}_1\right)-\dot{u}\left(x,{t}_0\right)\delta u\left(x,{t}_0\right)=0 $$
(30)
$$\begin{aligned} &\left[N\left(L,t\right)-\left( EA{u}^{\prime}\left(L,t\right)-B{u}^{{\prime\prime\prime}}\Big(L,t\Big)\right)\right]\delta u\left(L,t\right)\\&\quad-\left[N\left(0,t\right)-\left( EA{u}^{\prime}\left(0,t\right)-B{u}^{{\prime\prime\prime}}\Big(0,t\Big)\right)\right]\delta u\left(0,t\right)=0 \end{aligned}$$
(31)
$$ \left[{N}^h\left(L,t\right)-B{u}^{{\prime\prime}}\Big(L,t\Big)\right]\delta {u}^{\prime}\left(L,t\right)-\left[{N}^h\left(0,t\right)-B{u}^{{\prime\prime}}\Big(0,t\Big)\right]\delta {u}^{\prime}\left(0,t\right)=0 $$
(32)

Solution of Axial Vibration Problem

u can be expressed as the following form by employing separation of variables method

$$ u\left(x,t\right)=U(x){e}^{i\omega t} $$
(33)

By substituting above equation into Eq. (29) in the absence of q yields

$$ B\frac{d^4U}{dx^4}- EA\frac{d^2U}{dx^2}-{\omega}^2 mU=0 $$
(34)

Analytical solution of Eq. (34) can be obtained as follows

$$ U(x)={D}_1\sin \alpha x+{D}_2\cos \alpha x+{D}_3\sinh \beta x+{D}_4\cosh \beta x $$
(35)

where

$$ \alpha ={\left(\frac{- EA+\sqrt{(EA)^2+4 Bm{\omega}^2}}{2B}\right)}^{1/2},\beta ={\left(\frac{EA+\sqrt{(EA)^2+4 Bm{\omega}^2}}{2B}\right)}^{1/2} $$
(36)

and Di (i = 1, 2, 3, 4) are constants which can be determined by corresponding boundary conditions. For a micro-rod that both ends are clamped, classical and nonclassical boundary conditions are

$$ U(0)=0\;\mathrm{and}\;U(L)=0 $$
(37)
$$ B{U}^{{\prime\prime} }(0)=0\;\mathrm{and}\;B{U}^{{\prime\prime} }(L)=0 $$
(38)

By using of above boundary conditions in Eq. (35), solution can be written in a matrix form as

$$ \left[\begin{array}{cccc}0& 1& 0& 1\\ {}\sin \alpha L& \cos \alpha L& \sinh \beta L& \cosh \beta L\\ {}0& -{\alpha}^2& 0& {\beta}^2\\ {}-{\alpha}^2\sin \alpha L& -{\alpha}^2\cos \alpha L& {\beta}^2\sinh \beta L& {\beta}^2\cosh \beta L\end{array}\right]\, \left[\begin{array}{c}{D}_1\\ {}{D}_2\\ {}{D}_3\\ {}{D}_4\end{array}\right]=0 $$
(39)

For a nontrivial solution, the determinant of coefficient matrix of above equation must be vanished. This leads to the following condition as

$$ \sin \alpha L=0\;\mathrm{namely}\;\alpha =\frac{n\pi}{L},\left(n=1,2,\dots \right) $$
(40)

By inserting Eqs. (40) in (36), the natural longitudinal frequencies of a clamped-clamped micro-rod are obtained as

$$ {\omega}_n=\frac{n\pi}{L}\sqrt{\frac{1}{m}\left( EA+B\frac{n^2{\pi}^2}{L^2}\right)} $$
(41)

For a clamped-free micro-rod, classical and nonclassical boundary conditions are

$$ U(0)=0\;\mathrm{and}\; EA{U}^{\prime }(L)-B{U}^{{\prime\prime\prime} }(L)=0 $$
(42)
$$ B{U}^{{\prime\prime} }(0)=0\;\mathrm{and}\;{U}^{\prime }(L)=0 $$
(43)

By using of above boundary conditions in Eq. (35), solution can be given in a matrix form as

$$ {\displaystyle \begin{array}{cc}\left[\begin{array}{cccc}0& 1& 0& 1\\ {}{\alpha \lambda}_1\cos \alpha L& -{\alpha \lambda}_1\sin \alpha L& {\beta \lambda}_2\cosh \beta L& {\beta \lambda}_2\sinh \beta L\\ {}0& -{\alpha}^2& 0& {\beta}^2\\ {}\alpha \cos \alpha L& -\alpha \sin \alpha L& \beta \cosh \beta L& \beta \sinh \beta L\end{array}\right]& \left[\begin{array}{c}{D}_1\\ {}{D}_2\\ {}{D}_3\\ {}{D}_4\end{array}\right]\end{array}}=0 $$
(44)

where

$$ {\lambda}_1=\left( EA+{\alpha}^2B\right),{\lambda}_2=\left( EA-{\beta}^2B\right) $$
(45)

Similarly, the determinant of coefficient matrix of Eq. (44) must be vanished for a nontrivial solution. This leads to the following condition as

$$ \cos \alpha L=0\;\mathrm{namely}\;\alpha =\frac{\left(2n-1\right)\pi }{2L},\left(n=1,2,\dots \right) $$
(46)

By inserting Eqs. (46) in (36), the natural longitudinal frequencies of a clamped-free micro-rod are achieved as

$$ {\omega}_n=\frac{\left(2n-1\right)\pi }{2L}\sqrt{\frac{1}{m}\left( EA+B\frac{{\left(2n-1\right)}^2{\pi}^2}{4{L}^2}\right)} $$
(47)

It is evident that if the additional material length scale parametersl0 and l1 are equal to zero, the natural longitudinal frequencies ωn in Eqs. (41) and (47) will be transformed those in classical theory.

Numerical Results and Discussion

In this section, some illustrative examples for clamped-free and clamped-clamped micro-sized rods are presented. In the figures, the natural longitudinal frequencies obtained by MSGT and CT represented by ωs and ωc, respectively, and unless otherwise stated, L = 20D, l0 = l1 = l are considered, and Poisson’s ratio is chosen as 0.38.

A comparison of nondimensional first three natural frequencies of the micro-rod corresponding to various values of the additional material length scale parameters-to-diameter ratio is tabulated in Tables 1 and 2 for clamped-free and clamped-clamped boundary conditions, respectively. It is seen from the tables that the results of classical and newly developed model are identical for l/D = 0. It can be said that the nondimensional natural frequencies obtained by the new model increase gradually for bigger values of l/D, while those obtained by a classical model are not affected by the variation in l/D. It is also notable that differences between the results of the classical model and the current model are more prominent for larger values of l/D and higher modes.

Table 1 Comparison of dimensionless natural frequencies \( \left(\varpi =\omega L\sqrt{\frac{\rho }{E}}\right) \) of clamped-free micro-rod for the first three modes with various values of l/D
Full size table
Table 2 Comparison of dimensionless natural frequencies \( \left(\varpi =\omega L\sqrt{\frac{\rho }{E}}\right) \) of clamped-clamped micro-rod for the first three modes with various values of l/D
Full size table

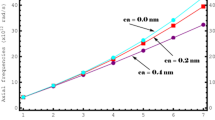
Variations of the frequency ratios (ωc/ωs) with respect to D/l for the first three modes are illustrated in the Fig. 2 for clamped-free and clamped-clamped boundary conditions, respectively. It is evident that an increase in the values of D/l leads to an increment in the frequency ratios, and the frequency ratios are nearly equal to one for D/l ≥ 4. Also, higher values of ωc/ωs are obtained for lower modes. It can be concluded that the divergence between classical and size-dependent frequencies becomes more significant for higher modes.

Fig. 2
figure 2

Variations of the frequency ratio with respect to D/l for the first three modes. (a) Clamped-free (b) clamped-clamped

Full size image

Variations of the first three frequency ratios are plotted versus l/D in Fig. 3 for clamped-free and clamped-clamped micro-rods, respectively. When the values of l/D increases, the frequency ratios for first, second, and third modes decrease. Also, it is noted that the frequency ratios are equal one for l/D = 0.

Fig. 3
figure 3

Variations of the first three frequency ratios versus l/D. (a) Clamped-free (b) clamped-clamped

Full size image

Influences of slenderness ratio on the frequency ratios are depicted for the first three modes in Fig. 4. It can be interpreted that the difference between natural frequencies predicted by the newly developed and classical models becomes more prominent for both lower slenderness ratios and higher modes. In addition, it can be said that the size dependency of the micro-rod diminishes due to an increase in the slenderness ratio.

Fig. 4
figure 4

Effect of slenderness ratio of the micro-rod on the frequency ratios for the first three modes (l = D). (a) Clamped-free (b) clamped-clamped

Full size image

It can be seen clearly from the present results that additional material length scale parameters are more important both clamped-free and clamped-clamped cases for smaller sizes and higher modes. Also, the values of the frequency ratios for clamped-clamped boundary condition are smaller than those of the other case.

Conclusion

A higher-order continuum theory is used for modeling of longitudinal vibration problem of micro-sized rod. Some parametric results have been presented in order to show the effect of additional length scale parameters. The results of modified strain gradient theory (MSGT) compared with those obtained by classical theory (CT). It has been seen that the frequency ratios decrease when l/D increases. It is also shown that the length scale parameters have some notable influences on axial vibration of the micro-sized rod. It is also possible to say that the effect of the length scale parameters is more significant for slender rods. An increase in slenderness ratio of the micro-rod leads to a decrease in the difference between natural frequencies predicting by the newly developed and classical models. It is also observed that additional material length scale parameters play an important role for smaller size of the micro-rod and higher modes. It is also notable that when additional material length scale parameters are zero, the present model directly becomes the classical model.