Peridynamics: Introduction

Abstract

The peridynamic theory is a nonlocal extension of continuum mechanics that is compatible with the physical nature of cracks as discontinuities. It avoids the need to evaluate the partial derivatives of the deformation with respect to the spatial coordinates, instead using an integro-differential equation for the linear momentum balance. This chapter summarizes the peridynamic theory, emphasizing the continuum mechanical and thermodynamic aspects. Formulation of material models is discussed, including details on the statement of models using mathematical objects called peridynamic states that are nonlocal and nonlinear generalizations of second-order tensors. Damage evolution is treated within a nonlocal thermodynamic framework making use of the dependence of free energy on damage. Continuous, stable growth of damage can suddenly become unstable, leading to dynamic fracture. Peridynamics treats fracture and long-range forces on the same mathematical basis as continuous deformation and contact forces, extending the applicability of continuum mechanics to new classes of problems.

Purpose of the Peridynamic Theory

In spite of its many successes, the local theory of continuum mechanics has some limitations that have hindered its applicability to many important problems:

• Its equations cannot be applied directly on a growing discontinuity in the deformation, making it impossible to model fracture using these equations alone.

• It does not include long-range forces such as electrostatic and van der Waals forces that are important in many technologies.

• It cannot be applied to the mechanics of discrete particles, creating a fundamental divide between molecular dynamics and continuum mechanics.

The peridynamic theory addresses these limitations in the local theory. Its field equations are integro-differential equations that do not require a smooth deformation, allowing fracture to be modeled on the same basis as continuous deformation. It treats all internal forces as long range, allowing interactions such as electrostatic forces to be included in a material description in a natural way. Discrete particles can be treated as a type of peridynamic material, allowing continuous media and systems of particles to be included within the same model, following the same basic equations.

The general idea is that the peridynamic theory replaces the local equilibrium equation with a nonlocal expression as follows:

$$ \nabla \cdotp \boldsymbol{\sigma} +\mathbf{b}=0\quad \to \quad \int_{{\mathcal{H}}_{\mathrm{x}}}\mathbf{f}\left(\mathbf{q},\mathbf{x}\right) \mathrm{d}{V}_{\mathbf{q}}+\mathbf{b}=0, $$

(1)

where σ is the stress field, b is the body force density field, and f is a vector field representing the force density (per unit volume squared) that material point q exerts on x. ${\mathcal{H}}_{\mathrm{x}}$ is a neighborhood of x to be described below.

The main purposes of this chapter are as follows:

• To explain the origin of the second of (Eq. 1)

• To show how the deformation determines f through the material model

• To describe material models within the framework of nonlocal thermodynamics

• To demonstrate that damage and fracture fit naturally into this framework

• To describe how some aspects of the local theory can be obtained as a limiting case of the peridynamic equations

Basic Concepts

In a peridynamic body ${\mathcal{B}}$, each material point x interacts directly with its neighbors $\boldsymbol{\mathrm{q}}\, \in \,{ \mathcal{B}}$ located within a cutoff distance δ of x in the reference configuration. Let q denote such a neighbor and define the bondξ = q − x. The family of x, denoted by ${\mathcal{H}}_{\mathrm{x}}$, consists of all the bonds with length no greater than δ:

$$ {\mathcal{H}}_{\mathrm{x}}=\left\{\mathbf{q}-\mathbf{x}:0<|\mathbf{q}-\mathbf{x}|\le \delta, \mathbf{q}\in \mathrm{\mathcal{B}}\right\}. $$

The cutoff distance δ is called the horizon and is assumed for purposes of this discussion to be independent of x (Fig. 1).

Fig. 1

Bond and family

Let y(x) denote the deformation. Suppose there is a strain-energy density field W(x), and that its value at x depends on the collective deformation of ${\mathcal{H}}_{\mathrm{x}}$. This means that W(x) depends not on ∂y/∂x (which may not exist if a crack is present) but on y(q) for all the material points within the horizon of x.

To express the dependence of W on the collective deformation of ${\mathcal{H}}_{\mathrm{x}}$, it is convenient to use mathematical objects called states. A state is simply a mapping from ${\mathcal{H}}_{\mathrm{x}}$ to some other quantity, which can be a scalar, a vector, or a tensor. By convention, the bond that the state operates on is written in angle brackets, $\underline {\mathbf{A}}\left\langle \boldsymbol{\upxi} \right\rangle$. State-valued fields depend on position and possibly time, denoted by

$$ \underline {\mathbf{A}}\left[\mathbf{x},t\right]\left\langle \boldsymbol{\upxi} \right\rangle . $$

The fundamental kinematical quantity for purposes of material modeling is the deformation state Y, defined by:

$$ \underline {\mathbf{Y}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\mathbf{y}\left(\mathbf{q}\right)-\mathbf{y}\left(\mathbf{x}\right)\quad \forall \mathbf{q}\in {\mathcal{H}}_{\mathrm{x}},\quad \forall \mathrm{x}\in \mathrm{\mathcal{B}} $$

Geometrically, the deformation state maps each bond to its image under the deformation.

Returning to our strain-energy density field W(x), we can now represent its dependence on the collective deformation of ${\mathcal{H}}_{\mathrm{x}}$. We write this function in the form:

$$ W\left(\mathbf{x}\right)=\widehat{W}\left(\underline {\mathbf{Y}}\left[x\right]\right)\quad \forall \mathrm{x}\in \mathrm{\mathcal{B}} $$

where Ŵ (Y) is the strain-energy density function for the material. The dependence of Ŵ on Y contains all the material-dependent characteristics of the model. Examples of such a material model are given by:

• Isotropic bond-based material:

  $$ \widehat{W}\left(\underline {\mathbf{Y}}\right)=\frac{1}{2}\int_{{\mathcal{H}}_{\mathbf{x}}}C\left(|\boldsymbol{\xi} |\right){\left(|\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle |-|\boldsymbol{\xi} |\right)}^2\mathrm{d}{V}_{\boldsymbol{\xi}}, $$

where C is a scalar-valued function of bond length.

• A possible model for a fluid (one of many, see section “Effectively Eulerian Material Models”):

  $$ \widehat{W}\left(\underline {\mathbf{Y}}\right)=\frac{1}{2}{\left(\int_{{\mathcal{H}}_{\mathbf{x}}}C\left(|\boldsymbol{\xi} |\right)\left(|\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle |-|\boldsymbol{\xi} |\right)\mathrm{d}{V}_{\boldsymbol{\xi}}\right)}^2. $$

Properties of States

Vector-valued states are similar to second-order tensors in that they both map vectors onto vectors. However, states can be nonlinear and even discontinuous mappings. It is useful to define the dot product of two vector-valued states $\underline {\mathbf{A}}$ and $\underline {\mathbf{B}}$ by:

$$ \underline {\mathbf{A}}\bullet \underline {\mathbf{B}}=\int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\mathrm{A}}\left\langle \boldsymbol{\xi} \right\rangle \cdotp \underline {\mathbf{B}}\left\langle \boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\boldsymbol{\xi}} $$

(2)

and of two scalar-valued states a and b by:

$$ \underline {\mathrm{a}}\bullet \underline{b}=\int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\mathrm{a}}\left\langle \boldsymbol{\xi} \right\rangle \underline{b}\left\langle \boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\boldsymbol{\xi}}. $$

The unit state1 and zero state0 are defined by:

$$ \underline{1}\left\langle \boldsymbol{\xi} \right\rangle =1,\quad \underline{0}\left\langle \boldsymbol{\xi} \right\rangle =0\quad \forall \boldsymbol{\xi} . $$

The identity state leaves bonds unchanged:

$$ \underline {\mathrm{X}}\left\langle \boldsymbol{\xi} \right\rangle =\boldsymbol{\xi} \quad \forall \boldsymbol{\xi} . $$

The norm of a state A is defined by:

$$ \left\Vert \underline {\mathbf{A}}\right\Vert =\sqrt{\underline {\mathbf{A}}\bullet \underline {\mathbf{A}}}\quad \mathrm{or}\quad \left\Vert \underline{a}\right\Vert =\sqrt{\underline{a}\bullet \underline{a}}. $$

The composition of two states $\underline {\mathbf{A}}$ and $\underline {\mathbf{B}}$ is a state defined by:

$$ \left(\underline {\mathbf{A}}\circ \underline {\mathbf{B}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\underline {\mathbf{A}}\left\langle \underline {\mathbf{B}}\left\langle \boldsymbol{\xi} \right\rangle \right\rangle; $$

The “∘” symbol distinguishes this operation from the point product, to be defined below. If R is a second-order tensor, it may similarly be combined with a state $\underline {\mathbf{A}}$; in this case, a special symbol is not necessary:

$$ \left(\underline {\mathbf{A}}\mathbf{R}\right)\left\langle \boldsymbol{\xi} \right\rangle =\underline {\mathbf{A}}\left\langle \mathbf{R}\boldsymbol{\xi } \right\rangle, \quad \left(\mathbf{R}\underline {\mathbf{A}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\mathbf{R}\left(\underline {\mathbf{A}}\left\langle \boldsymbol{\xi} \right\rangle \right). $$

The point product of two states, at least one of which is scalar-valued, is defined by:

$$ {\displaystyle \begin{array}{c}\left(\underline {a\mathbf{A}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\left(\underline {\mathbf{A}a}\right)\left\langle \boldsymbol{\xi} \right\rangle =\underline{a}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathbf{A}}\left\langle \boldsymbol{\xi} \right\rangle, \\ {}(\underline{ab})\left\langle \boldsymbol{\xi} \right\rangle =\left(\underline{ba}\right)\left\langle \boldsymbol{\xi} \right\rangle =\underline{a}\left\langle \boldsymbol{\xi} \right\rangle \underline{b}\left\langle \boldsymbol{\xi} \right\rangle .\end{array}} $$

Double states operate on two bonds rather than just one and are denoted by $\underline {\mathbb{K}}\left\langle \boldsymbol{\xi}, \eta \right\rangle$, where ξ and η are bonds. Double states are usually tensor-valued. An example is the dyadic product double state defined by:

$$ \left(\underline {\mathbf{A}}\star \underline {\mathbf{B}}\right)\left\langle \boldsymbol{\xi}, \eta \right\rangle =\underline {\mathbf{A}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline {\mathbf{B}}\left\langle \boldsymbol{\eta} \right\rangle . $$

The dot product of a tensor-valued double state $\underline {\mathbb{K}}$ with a vector-valued state $\underline {\mathbf{A}}$ is the vector-valued state given by:

$$ \left(\underline {\mathbb{K}}\bullet \underline {\mathbf{A}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\mathbb{K}}\left\langle \boldsymbol{\xi}, \boldsymbol{\eta} \right\rangle \underline {\mathbf{A}}\left\langle \boldsymbol{\eta} \right\rangle\;\mathrm{d}{V}_{\eta },\quad \left(\underline {\mathbf{A}}\bullet \underline {\mathbb{K}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\mathbf{A}}\left\langle \eta \right\rangle \underline {\mathbb{K}}\left\langle \boldsymbol{\eta}, \boldsymbol{\xi} \right\rangle\;\mathrm{d}{V}_{\boldsymbol{\eta}}. $$

It is necessary to define a notion of differentiation of functions of states. Let $\Psi \left(\underline {\mathbf{A}}\right)$ be a scalar-valued function of a vector-valued state. Consider a small increment $\Delta \underline {\mathbf{A}}$. Suppose there is a vector-valued state denoted ${\Psi}_{\underline {\mathbf{A}}}\left(\underline {\mathbf{A}}\right)$ such that for any $\Delta \underline {\mathbf{A}}$,

$$ \Psi \left(\underline {\mathbf{A}}+\Delta \underline {\mathbf{A}}\right)-\Psi \left(\underline {\mathbf{A}}\right)={\Psi}_{\underline {\mathbf{A}}}\left(\underline {\mathbf{A}}\right)\bullet \Delta \underline {\mathbf{A}}+o\left(\left\Vert \Delta \underline {\mathbf{A}}\right\Vert \right). $$

(3)

Then ${\Psi}_{\underline {\mathbf{A}}}\left(\underline {\mathbf{A}}\right)$ is called the Fréchet derivative of Ψ at $\underline {\mathbf{A}}$. The Fréchet derivative of a function whose value is a vector-valued state is a double state.

Fréchet derivatives obey a form of the chain rule. For example, if $\underline {\mathbf{B}}$ is a state-valued function of the state $\underline {\mathbf{A}}$,

$$ {\Psi}_{\underline {\mathbf{A}}}\left(\underline {\mathbf{B}}\left(\underline {\mathbf{A}}\right)\right)={\Psi}_{\underline {\mathbf{B}}}\bullet {\underline {\mathbf{B}}}_{\underline {\mathbf{A}}}, $$

or

$$ {\Psi}_{\underline {\mathbf{A}}}\left\langle \boldsymbol{\xi} \right\rangle =\int_{{\mathcal{H}}_{\mathbf{x}}}{\Psi}_{\underline {\mathbf{B}}}\left\langle \boldsymbol{\eta} \right\rangle \cdotp {\underline {\mathbf{B}}}_{\underline {\mathbf{A}}}\left\langle \boldsymbol{\eta}, \boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\boldsymbol{\eta}}. $$

Note that ${\underline {\mathbf{B}}}_{\underline {\mathbf{A}}}$ is a tensor-valued double state. More details about the use of states can be found in Silling et al. (2007). The symmetries of double states play an interesting role in the linearized peridynamic theory, which is beyond the scope of the present chapter (Silling 2010).

Balance of Momentum

Using the nonlocal concept of strain energy described in section “Basic Concepts,” expressions for balance of linear momentum will now be derived. Assume that ${\mathcal{B}}$ is bounded, and consider a time-independent deformation y(x) under external body force density field b(x). Define the total potential energy of the body by:

$$ {\Phi}_{\mathbf{y}}=\int_{\mathrm{\mathcal{B}}}\left(W\left(\mathbf{x}\right)-\mathbf{b}\left(\mathbf{x}\right)\cdot \mathbf{y}\left(\mathbf{x}\right)\right)\;\mathrm{d}{V}_{\mathbf{x}}. $$

(4)

Let Δy be a small increment in the deformation and assume that the Fréchet derivative ${\widehat{\mathrm{W}}}_{\underline {\mathbf{Y}}}\left(\underline {\mathbf{Y}}\right)$ exists for all $\underline {\mathbf{Y}}$. Define

$$ \underline {\mathbf{T}}\left[\mathbf{x}\right]={\widehat{W}}_{\underline {\mathbf{Y}}}\left(\underline {\mathbf{Y}}\left[\mathbf{x}\right]\right). $$

In the following, it is convenient to adopt the convention that states produce the value 0 for bonds longer than δ. This permits us to replace ${\mathcal{H}}_{\mathrm{x}}$ with ${\mathcal{B}}$ as the region of integration in some of the expressions below. From Eqs. 2, 3, and 4,

$$ {\displaystyle \begin{aligned} \Delta {\Phi}_{\mathbf{y}}&=\int_{\mathcal{B}}\left(\underline {\mathbf{T}}\left[\mathbf{x}\right]\bullet \Delta \underline {\mathbf{Y}}\left[\mathbf{x}\right]-\mathbf{b}\left(\mathbf{x}\right)\cdotp \Delta \mathbf{y}\left(\mathbf{x}\right)\right)\;\mathrm{d}{V}_{\mathbf{x}}\\[3pt] &=\int_{\mathcal{B}}\left(\int_{\mathcal{B}}\left\{\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle \cdot \left(\Delta \mathbf{y}\left(\mathbf{q}\right)-\Delta \mathbf{y}\left(\mathbf{x}\right)\right)\right\}\;\mathrm{d}{V}_{\mathbf{q}}-\mathbf{b}\left(\mathbf{x}\right)\cdot \Delta \mathbf{y}\left(\mathbf{x}\right)\right)\, \mathrm{d}{V}_{\mathbf{x}}\\[3pt] &=\int_{\mathcal{B}}\left(\int_{\mathcal{B}}\left\{\underline {\mathbf{T}}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \cdot \Delta \mathbf{y}\left(\mathbf{x}\right)-\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle \cdot \Delta \mathbf{y}\left(\mathbf{x}\right)\right\}\, \mathrm{d}{V}_{\mathbf{q}}-\mathbf{b}\left(\mathbf{x}\right)\cdot \mathbf{y}\left(\mathbf{x}\right)\right)\, \mathrm{d}{V}_{\mathbf{x}}\\[3pt] &=\int_{\mathcal{B}}\left(\int_{\mathcal{B}}\Big\{\underline {\mathbf{T}}\left[\mathbf{q}\right]\left\langle \mathbf{x}{-}\mathbf{q}\right\rangle -\underline{\mathbf{T}}\left[\mathbf{x}\right]\Big\langle\mathbf{q}{-}\mathbf{x}\Big\rangle \Big\}\mathrm{d}{V}_{\mathbf{q}}-\mathbf{b}\left(\mathbf{x}\right)\right)\cdot \Delta \mathbf{y}\left(\mathbf{x}\right)\mathrm{d}{V}_{\mathbf{x}},\end{aligned}} $$

(5)

where an interchange of dummy variables of integration x ↔ q is used in the third line. Stationary potential energy requires ∆Φy = 0 for all Δy and hence Eq. 5 can be localized to yield:

$$ \int_{{\mathcal{H}}_{\mathbf{x}}}\left\{\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -\underline {\mathbf{T}}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \right\}\mathrm{d}{V}_{\mathrm{q}}+\mathbf{b}\left(\mathbf{x}\right)=0\quad \forall \mathbf{x}\in \mathrm{\mathcal{B}}. $$

(6)

Equation 6 is the equilibrium equation in peridynamics. It is frequently written in the more suggestive form:

$$ \int_{{\mathcal{H}}_{\mathbf{x}}}\mathbf{f}\left(\mathbf{q},\mathbf{x}\right)\, \mathrm{d}{V}_{\mathbf{q}}+\mathbf{b}\left(\mathbf{x}\right)=0\quad \forall \mathbf{x}\in \mathrm{\mathcal{B}} $$

(7)

where f (q, x) is the pairwise bond force density field, given by:

$$ \mathbf{f}\left(\mathbf{q},\mathbf{x}\right)=\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle\mathbf{q}-\mathbf{x}\right\rangle -\underline {\mathbf{T}}\left[\mathbf{q}\right]\left\langle\mathbf{x}-\mathbf{q}\right\rangle \quad \forall \mathbf{x},\mathbf{q}\in \mathrm{\mathcal{B}}. $$

Observe that f(q, x) is comprised of two terms arising from the material models at x and at q.

The pairwise bond force density field obeys the antisymmetry condition:

$$ \mathbf{f}\left(\mathbf{x},\mathbf{q}\right)=-\mathbf{f}\left(\mathbf{q},\mathbf{x}\right)\quad \forall \mathbf{x},\mathbf{q}\in \mathrm{\mathcal{B}}. $$

Mechanically, the vector f(q, x) can be thought of the force density (force per unit volume squared) that q exerts on x. However, it is best not to take this intuitive picture too literally, because there is not necessarily a direct physical interaction between the two points.

By d’Alembert’s rule, the time-dependent equation of motion is found from Eq. 7 to be:

$$ \rho \left(\mathbf{x}\right)\ddot{\mathbf{y}}\left(\mathbf{x},t\right)=\int_{{\mathcal{H}}_{\mathbf{x}}}\mathbf{f}\left(\mathbf{q},\mathbf{x},t\right)\, \mathrm{d}{V}_{\mathbf{q}}+\mathbf{b}\left(\mathbf{x},t\right)\quad \forall \mathbf{x}\in \mathrm{\mathcal{B}},t\ge 0 $$

(8)

where ρ is the mass density field.

A more axiomatic and general derivation of the linear momentum balance in peridynamics, which does not assume the existence of a strain-energy density field, can be found in Silling and Lehoucq (2010). Also, a derivation from statistical mechanics is available in Lehoucq and Sears (2011).

Energy Balance and Thermodynamics

The laws of thermodynamics can be written in a form compatible with the nonlocal nature of the peridynamic theory. The first law of thermodynamics takes the following form:

$$ \dot{\varepsilon}\left(\mathbf{x},t\right)=\underline {\mathbf{T}}\left[\mathbf{x},t\right]\bullet \underline {\dot{\mathrm{Y}}}\left[\mathbf{x},t\right]+h\left(\mathbf{x},t\right)+s\left(\mathbf{x},t\right)\quad \forall \mathbf{x}\in \mathrm{\mathcal{B}},t\ge 0, $$

where ε is the internal energy density (per unit volume), h is the rate of heat transport to x, and s is the energy source rate. More simply,

$$ \dot{\varepsilon}=\underline {\mathbf{T}}\bullet \underline {\dot{\mathbf{Y}}}+h+s. $$

(9)

To provide an intuitive picture of this expression, recall that by Eq. 2,

$$ \underline {\mathbf{T}}\bullet \underline {\overset{.}{\mathbf{Y}}}=\int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle \cdotp \underline {\overset{.}{\mathbf{Y}}}\left\langle \boldsymbol{\xi} \right\rangle\;\mathrm{d}{V}_{\boldsymbol{\xi}}. $$

The energy balance (9) therefore sums up the rate of work done by the bond forces acting against the rate of extension of the individual bonds. The key point is that only the force state at x, that is, $\underline {\mathbf{T}}\left[\mathbf{x},t\right]$, contributes to the energy change at x. The force state $\underline {\mathbf{T}}\left[\mathbf{q},t\right]$ does not, even though it appears in the momentum balance (6). This partitioning of the pairwise bond force into energy contributions at x and q is the unique feature of the peridynamic version of thermodynamics that causes the internal energy density to be additive, provided that h is conserved. This fact apparently resolves a long-standing question about whether it is even possible to define a nonlocal internal energy density that is additive (Gurtin and Williams 1971); see (Silling and Lehoucq 2010) for a more complete discussion.

The energy balance (9) applies regardless of how the heat transport h is specified. This could be supplied by the Fourier heat conduction expression or by a nonlocal diffusion law such as:

$$ h\left(\mathbf{x},t\right)=\int_{{\mathcal{H}}_{\mathbf{x}}}\Big[\underline{H}\left[\mathbf{x},t\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -\underline{H}[\mathbf{q},t]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \Big]\, \mathrm{d}{V}_{\mathrm{q}} $$

where $\underline{H}$ is a scalar-valued state. The most intuitive form of such an $\underline{H}$ models heat diffusion along bonds as though they are conducting wires that are insulated from each other (Bobaru and Duangpanya 2010):

$$ \underline{H}\left[\mathbf{x},t\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\underline{K}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle \left(\theta \left(\mathbf{q},t\right)-\theta \left(\mathbf{x},t\right)\right) $$

(10)

where θ is the temperature field and K is the bond conductivity. The heat flow expression (10) is useful in modeling systems with inherently nonlocal diffusion mechanisms such as radiative heat transport, as well as in treating discontinuities and singularities in the temperature field. A model for heat transport that is more general than (Eq. 10) could have the form:

$$ \underline{H}\left[\mathbf{x},t\right]=\underline {\widehat{H}}\left(\underline{\Theta}\left[\mathbf{x}, t\right]\right),\quad \underline{\Theta}\left[\mathbf{x},t\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\theta \left(\mathbf{q},t\right)-\theta \left(\mathbf{x},t\right). $$

(11)

This representation could model systems in which the heat flow in each bond can depend not only on the temperature difference between its own endpoints but also on the temperature difference in other bonds in the family.

The local form of second law of thermodynamics as implemented in peridynamics has the following form:

$$ \theta \dot{\eta}\ge h+s $$

(12)

where η is the entropy density field (per unit volume) in the reference configuration. A restriction on the admissible forms of $\underline {\widehat{H}}$ arises from the second law, as discussed in section “Restriction on the Heat Transport Model.”

Material Models

A peridynamic material model $\widehat{\underline {\mathbf{T}}}$ determines the force state at every material point x and time t. For most materials, the force state depends on the deformation state $\underline {\mathbf{Y}}\left[\mathbf{x},t\right]$ and possibly other variables as well. If $\underline {\mathbf{Y}}$ is the only quantity that the material model depends on, we write:

$$ \underline {\mathbf{T}}\left[\mathbf{x},t\right]=\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\left[\mathbf{x},t\right]\right). $$

If the body is heterogeneous, that is, if the material model depends explicitly on position, we write:

$$ \underline {\mathbf{T}}\left[\mathbf{x},t\right]=\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\left[\mathbf{x},t\right],\mathbf{x}\right). $$

The material model can also depend on the rate of deformation,$\underline {\overset{.}{\mathbf{Y}}}$, and other physically relevant quantities such as temperature (section “Thermodynamic Form of A Material Model”), damage (section “Damage as a Thermodynamic Variable”), or plastic deformation (section “Plasticity”).

Material models are required to satisfy certain general rules. The requirement of nonpolarity is written as:

$$ \int_{{\mathcal{H}}_{\mathbf{x}}}\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\left\langle \boldsymbol{\xi} \right\rangle \times \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \, \mathrm{d}{V}_{\boldsymbol{\xi}}=0\quad \forall \underline {\mathbf{Y}}. $$

(13)

Nonpolarity guarantees that global balance of angular momentum holds, that is, the material model does not nonphysically create angular momentum. It is similar to the required symmetry of the Cauchy stress tensor in the local theory. Nonpolarity is not a requirement in the micropolar versions of peridynamics that have been proposed (Gerstle et al. 2007) or in a peridynamic shell theory that includes rotational degrees of freedom (Chowdhury et al. 2016).

In the absence of external fields that provide a special physical direction that affects material response, a peridynamic material model is required to satisfy objectivity. This is a requirement that if the family is deformed and then rigidly rotated, then the force state undergoes the same rigid rotation. This condition is written as follows:

$$ \underline {\widehat{\mathbf{T}}}\left(\mathbf{Q}\underline {\mathbf{Y}}\right)=\mathbf{Q}\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\quad \forall \mathbf{Q},\quad \forall \underline {\mathbf{Y}} $$

where Q is any proper orthogonal tensor. Unlike objectivity, isotropy is not a general requirement but is appropriate for modeling materials that have no internal special direction (such as embedded unidirectional reinforcement fibers). Isotropy means that if the body is first rigidly rotated, then deformed, the force state is the same as if there were no rotation:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\mathbf{Q}\right)=\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\quad \forall \mathbf{Q},\quad \forall \underline {\mathbf{Y}} $$

where Q is any proper orthogonal tensor.

If there is a strain-energy function ${\widehat{W}}_{\underline {\mathbf{Y}}}\left(\underline {\mathbf{Y}}\right)$ such that:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)={\widehat{W}}_{\underline {\mathbf{Y}}}\left(\underline {\mathbf{Y}}\right)\quad \forall \underline {\mathbf{Y}}, $$

then the material is elastic. An elastic material is objective if and only if$\widehat{W}\left(\mathbf{Q}\underline {\mathbf{Y}}\right)=\widehat{W}\left(\underline {\mathbf{Y}}\right)\quad \forall \mathbf{Q},\quad \forall \underline {\mathbf{Y}}.$ An elastic material is isotropic if and only if:

$$ \widehat{W}\left(\underline {\mathbf{Y}}\mathbf{Q}\right)=\widehat{W}\left(\underline {\mathbf{Y}}\right)\quad \forall \mathbf{Q},\quad \forall \underline {\mathbf{Y}}. $$

A material that is elastic and objective is necessarily nonpolar (Silling 2010). This property is a convenience to developers of material models, because it is often much easier to prove objectivity of $\widehat{W}$ than to prove nonpolarity directly from Eq. 13.

Peridynamic material models fall into the following categories:

• Bond-based: Each bond has a force response that depends only on its own deformation and damage, independent of all other bonds in the family. For a bond-based material model,

  $$ \underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\widehat{\mathbf{t}}\left(\underline {\mathbf{Y}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle, \mathbf{q},\mathbf{x}\right). $$

Note that the function $\widehat{\mathbf{t}}$ and its arguments are all vectors rather than vector-valued states. For a homogeneous body, the equilibrium equation for a bond-based material is often written as:

$$ \int_{{\mathcal{H}}_{\mathbf{x}}}\mathbf{f}\left(\mathbf{u}\left(\mathbf{q}\right)-\mathbf{u}\left(\mathbf{x}\right),\mathbf{q}-\mathbf{x}\right)\mathrm{d}{V}_{\mathbf{q}}+\mathbf{b}\left(\mathbf{x}\right)=0, $$

with f rather than $\underline {\widehat{\mathbf{T}}}$ as the material model. An example is given by:

$$ \mathbf{f}\left(\boldsymbol{\eta}, \boldsymbol{\xi} \right)=\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \left(|\boldsymbol{\eta} +\boldsymbol{\xi} |-|\boldsymbol{\xi} |\right)\underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle,\quad \underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle =\frac{\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle }{\mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mid } $$

where $\underline{C}$ is a scalar-valued state. In this material model, each bond acts like a linear spring.

• State based: Each bond has a force response that can depend on the deformation and damage in all the bonds in the family. Among state-based material models, there are two classes: ordinary, in which the bond forces are always parallel to the deformed bond direction $\underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle$, and all others, which are called non-ordinary. Ordinary materials have the advantage of automatically being nonpolar.

Thermodynamic Form of a Material Model

This section describes a thermodynamic formulation of peridynamic material models . Material response that can be defined in terms of static variables (without rates, gradients, and loading history) can often be written in terms of a free-energy function. The advantage of this way of characterizing material response is that the resulting values for the force state, temperature, entropy, damage, coefficient of thermal expansion, and heat capacity are always consistent. It also permits us to incorporate restrictions on the material model derived from the second law of thermodynamics. Additional terms such as rate dependence can be added to the force state obtained from the thermodynamic form.

Define the free-energy density at a material point x and time t by:

$$ \psi =\varepsilon -\theta \eta $$

(14)

where, as before, ε, θ, and η are the internal energy density, temperature, and entropy density, respectively. Taking the time derivative of Eq. 14 and applying the second law expression, Eq. 12 leads to:

$$ \dot{\varepsilon}-\dot{\theta}\eta -\dot{\psi}\ge 0. $$

Combining this with the first law expression (9) yields:

$$ \underline {\mathbf{T}}\bullet \underline {\overset{.}{\mathbf{Y}}}+h+s-\dot{\theta}\eta -\dot{\psi}\ge 0. $$

(15)

Suppose the material model is expressed in terms of the dependence of free-energy density on both the deformation state and temperature, thus $\psi \left(\underline {\mathbf{Y}},\theta \right)$. By the chain rule,

$$ \dot{\psi}={\psi}_{\theta}\dot{\theta}+{\psi}_{\underline {\mathbf{Y}}}\bullet \underline {\overset{.}{\mathbf{Y}}}. $$

(16)

In this expression, ψ_θ is a partial derivative and ${\psi}_{\underline {\mathbf{Y}}}$ is a Fréchet derivative, and therefore, its value is a state. Combining Eq. 15 with Eq. 16 and regrouping terms yields:

$$ \left(\underline {\mathbf{T}}-{\psi}_{\underline {\mathbf{Y}}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}+h+\mathbf{s}-\left(\eta +{\psi}_{\theta}\right)\dot{\theta}\ge 0. $$

(17)

Following the reasoning of Coleman and Noll (1963; Gurtin et al. 2010), in principle, we can contrive an experiment in which h = s = 0 and the quantities $\underline {\overset{.}{\mathbf{Y}}}$ and $\dot{\theta}$ are prescribed independently of each other.

Suppose that in such a thought experiment $\dot{\theta}=0$ but $\underline {\overset{.}{\mathbf{Y}}}$ is varied, and vice versa. Enforcing the inequality (17) then leads to the conclusions

$$ \underline {\mathbf{T}}={\psi}_{\underline {\mathbf{Y}}},\quad \eta =-{\psi}_{\theta }. $$

(18)

The first of these provides the force state in the thermodynamic form of a rate-independent material model. Rate dependence can be including by assuming the dependence $\psi \left(\underline {\mathbf{Y}},\underline {\dot{\mathbf{Y}}},\theta, \dot{\theta}\right)$, leading to an additional term in Eq. 17:

$$ \left(\underline {\mathbf{T}}-{\psi}_{\underline {\mathbf{Y}}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}+h+s-\left(\eta +{\psi}_{\theta}\right)\dot{\theta}+{\psi}_{\dot{\theta}}\ddot{\theta}-{\psi}_{\underline {\overset{.}{\mathbf{Y}}}}\bullet \underline {\overset{..}{\mathbf{Y}}}\ge 0. $$

From this, using the same reasoning as before, one concludes that ${\psi}_{\dot{\theta}}={\psi}_{\underline {\overset{.}{\mathbf{Y}}}}=0$, that is, the free energy density cannot depend explicitly on $\dot{\theta}$ or $\underline {\overset{.}{\mathbf{Y}}}$. However, without loss of generality, rate effects can be incorporated by partitioning the force state response into equilibrium and rate-dependent parts:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}},\underline {\overset{.}{\mathbf{Y}}},\theta \right)={\underline {\mathbf{T}}}^e\left(\underline {\mathbf{Y}},\theta \right)+{\underline {\mathbf{T}}}^d\left(\underline {\mathbf{Y}},\underline {\overset{.}{\mathbf{Y}}},\theta \right),\quad {\underline {\mathbf{T}}}^d\left(\underline {\mathbf{Y}},\underline{0},\theta \right)=\underline{0}. $$

From this assumption, it follows by a similar Coleman-Noll type of argument (Fried 2010) that

$$ {\underline {\mathbf{T}}}^e={\psi}_{\underline {\mathbf{Y}}},\, {\underline {\mathbf{T}}}^d\bullet \underline {\overset{.}{\mathbf{Y}}}\ge 0. $$

(19)

The second of Eq. 19 is a dissipation inequality . It implies that

$$ {\underline {\mathbf{T}}}^d\left\langle \boldsymbol{\xi} \right\rangle \cdot \underline {\overset{.}{\mathbf{Y}}}\left\langle \boldsymbol{\xi} \right\rangle \ge 0,\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

Work done by both ${\underline {\mathbf{T}}}^e$ and ${\underline {\mathbf{T}}}^d$ contribute to the internal energy density according to the first law (9), in general changing the temperature. These temperature changes affect ψ indirectly, even though ${\psi}_{\underline {\overset{.}{\mathbf{Y}}}}=\underline{0}$.

Thermal expansion arises from the coupling between $\underline {\mathbf{Y}}$ and θ in the form of ψ. For example, for an elastic material with strain-energy density function $\widehat{W}$, a model with thermal expansion can be defined by:

$$ \psi \left(\underline {\mathbf{Y}},\theta \right)=\frac{\widehat{W}\left(\left(1-\alpha \Delta \theta \right)\underline {\mathrm{Y}}\right)}{1-\alpha \Delta\theta},\quad \Delta \theta := \theta -{\theta}_0 $$

where α is a linear coefficient of thermal expansion. Then by the chain rule,

$$ \underline {\mathbf{T}}={\psi}_{\underline {\mathbf{Y}}}={\widehat{W}}_{\underline {\mathbf{Y}}}\left(\left(1-\alpha \Delta \theta \right)\underline {\mathbf{Y}}\right)\approx {\widehat{W}}_{\underline {\mathbf{Y}}}\left(\underline {\mathbf{Y}}\right)-\alpha \Delta \theta \underline {\mathrm{K}}\bullet \underline {\mathbf{X}} $$

where the approximation holds if $\mid\alpha \Delta \theta\mid \ll 1$ and $\mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle -\boldsymbol{\xi} \mid \ll \mid \boldsymbol{\xi} \mid$ for all ξ. $\underline {\mathbb{K}}$ is the micromodulus double state , defined by:

$$ \underline {\mathbb{K}}={\widehat{W}}_{\underline {\mathbf{YY}}}. $$

(See Silling (2010) for details on the properties of $\underline {\mathbb{K}}$ and its role in the linearized theory.)

Restriction on the Heat Transport Model

Recall the local form of the second law of thermodynamics,

$$ \theta \dot{\eta}\ge h+s. $$

(20)

All of us are familiar with the restriction in the local theory that heat cannot flow from cold to hot, which is a consequence of the second law. It is interesting to investigate the analogous restriction in peridynamics.

To do this, consider a bounded, nondeforming, thermodynamically isolated body. Assume that the material model is as described in the section “Thermodynamic Form of a Material Model,” in which the free-energy density has the dependence $\psi \left(\underline {\mathbf{Y}},\theta \right)$. As a consequence of the second of Eq. 18, since $\underline {\mathbf{\dot{Y}}}=\mathbf{0}$, it follows that η can depend only on θ. This implies that equality holds in Eq. 20, that is,

$$ \theta \dot{\eta}=h. $$

(21)

(This is not a result of reversibility, which is not assumed here.) Now compute the total entropy change in the body. From Eqs. 11 and 21 (dropping t from the notation),

$$ {\displaystyle \begin{aligned}\int_{\mathrm{\mathcal{B}}}\dot{\eta}\left(\mathbf{x}\right)\mathrm{d}{V}_{\mathbf{x}}&=\int_{\mathrm{\mathcal{B}}}\frac{h\left(\mathbf{x}\right)}{\theta \left(\mathbf{x}\right)}\mathrm{d}{V}_{\mathrm{x}}\\ &=\int_{\mathrm{\mathcal{B}}}\int_{\mathrm{\mathcal{B}}}\frac{\underline{H}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -\underline{H}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle }{\theta \left(\mathbf{x}\right)}\mathrm{d}{V}_{\mathbf{q}}\mathrm{d}{V}_{\mathbf{x}}\\ &=\int_{\mathrm{\mathcal{B}}}\int_{\mathrm{\mathcal{B}}}\left(\frac{1}{\theta \left(\mathbf{x}\right)}-\frac{1}{\theta \left(\mathbf{q}\right)}\right)\underline{H}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle \mathrm{d}{V}_{\mathbf{q}}\mathrm{d}{V}_{\mathbf{x}}\\ &=-\int_{\mathrm{\mathcal{B}}}\underline{\beta}\left[\mathbf{x}\right]\bullet \underline{H}\left[\mathbf{x}\right]\mathrm{d}{V}_{\mathbf{x}}\end{aligned}} $$

(22)

where β is the scalar-valued state defined by:

$$ \underline{\beta}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\frac{1}{\theta \left(\mathbf{q}\right)}-\frac{1}{\theta \left(\mathbf{x}\right)}. $$

Suppose that the heat transport model $\underline {\widehat{H}}$ obeys

$$ \underline{\beta}\bullet \underline {\widehat{H}}\left(\underline{\Theta}\right)\le 0\quad\quad \forall \underline{\Theta}, $$

(23)

or equivalently

$$ \int_{{\mathcal{H}}_{\mathbf{x}}}\underline{\beta}\left\langle \boldsymbol{\xi} \right\rangle \underline {\widehat{H}}\left\{\boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\mathbf{x}}\le 0\quad\quad \forall \underline{\Theta}. $$

Working backwards through the steps in Eq. 22, evidently Eq. 23 implies that

$$ \int_{\mathrm{\mathcal{B}}}\dot{\eta}\left(\mathbf{x}\right)\mathrm{d}{V}_{\mathbf{x}}\ge 0, $$

which is the global form of the second law for an isolated body. Note that the stronger restriction

$$ \underline{\beta}\left\langle \boldsymbol{\xi} \right\rangle \underline {\widehat{H}}\left\langle \boldsymbol{\xi} \right\rangle \le 0\quad\quad \forall \boldsymbol{\xi} $$

is sufficient but not necessary for Eq. 23 to hold.

The inequality (23) is a restriction on the constitutive model for heat transport $\underline {\widehat{H}}$; it is the peridynamic form of the rule that “heat cannot flow from cold to hot.” Details on peridynamic modeling of heat transport can be found in Bobaru and Duangpanya (2010), Bobaru and Duangpanya (2012), and Oterkus et al. (2014b). A fully coupled thermomechanical treatment is discussed in Oterkus et al. (2014a). The relation of the restriction (Eq. 23) to the Clausius-Duhem inequality is discussed in section “Convergence of Peridynamics to the Local Theory” below.

Damage as a Thermodynamic Variable

In the previous section, it was assumed that the material model is stated in terms of the free-energy density function given by:

$$ \psi \left(\underline {\mathbf{Y}},\theta \right). $$

An important characteristic of the response of real materials is that they fracture and fail. To help model this aspect of material response, it is assumed that there is a scalar-valued state field called the damage state , denoted by $\underline{\phi}$, that has the distinguishing feature of monotonicity over time:

$$ \underline {\dot{\phi}}\left\langle \boldsymbol{\xi} \right\rangle \ge 0\quad\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

(24)

By convention, it is usually assumed that 0≤ $\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle$ ≤1 for all bonds ξ, with $\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle$ = 0 representing an undamaged bond. By assuming a material model of the form:

$$ \psi \left(\underline {\mathbf{Y}},\theta, \underline{\phi}\right) $$

(25)

and working through the free-energy inequality discussed previously, one concludes (Silling and Lehoucq 2010) that the following dissipation inequality holds:

$$ {\psi}_{\underline{\phi}}\bullet \underline {\dot{\phi}}\le 0, $$

(26)

which also implies:

$$ {\psi}_{\underline{\phi}}\left\langle \boldsymbol{\xi} \right\rangle \le 0\quad\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

(27)

Damage evolves according to a prescribed material-dependent damage growth law,

$$ \underline {\dot{\phi}}=\underline{D}\left(\underline {\mathbf{Y}},\underline {\dot{\mathbf{Y}}},\underline{\phi}\right) $$

where $\underline{D}$ is a scalar state-valued function (section “Damage Evolution”).

Examples of Material Models

The following examples of material models illustrate the connection between free-energy density and mechanical forces. They also demonstrate how to evaluate Fréchet derivatives in practice.

Bond-Based Linear Material with Damage

Consider the free-energy density function defined by:

$$ \psi \left(\underline {\mathbf{Y}},\theta, \underline{\phi}\right)=\frac{1}{2}\left(\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline{e}\right)\bullet \underline{e}+ c\theta \left(1-\log \left(\theta /{\theta}_0\right)\right) $$

(28)

or equivalently

$$ \psi \left(\underline {\mathbf{Y}},\theta, \underline{\phi}\right)=\frac{1}{2}\int_{{\mathcal{H}}_{\mathrm{x}}}\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \left(1-\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle \right){\underline{e}}^2\left\langle \boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\boldsymbol{\xi}}+c\theta \left(1-\log \left(\theta /{\theta}_0\right)\right) $$

(29)

where $\underline{C}$ is the prescribed scalar-valued micromodulus state and c is the heat capacity (at constant $\underline {\mathbf{Y}}$). The scalar-valued state $\underline{e}$ is the extension state, defined by:

$$ \underline{e}\left\langle \boldsymbol{\xi} \right\rangle =\, \mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mid -\mid \boldsymbol{\xi} \mid . $$

(30)

To explain how to evaluate the force state $\underline {\mathbf{T}}$ = $\psi \underline {\mathbf{Y}}$, we go through in detail the process of obtaining the Fréchet derivative. Recalling (Eq. 3), we seek to express a first-order approximation for incremental changes in ψ in response to any small $\Delta \underline {\mathbf{Y}}$ in the form:

$$ \Delta \psi =\int_{{\mathcal{H}}_{\mathbf{x}}}\left[\mathrm{something}\right]\cdot \Delta \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \, \mathrm{d}{V}_{\boldsymbol{\xi}}. $$

The process of finding the Fréchet derivative consists of finding an expression of this form. The [something], which is a function of the dummy variable of integration ξ (and therefore is a state), is the Fréchet derivative. For the example material model (29),

$$ \Delta \psi =\underline {\mathbf{T}}\bullet \Delta \underline {\mathbf{Y}}=\int_{{\mathcal{H}}_{\mathbf{x}}}\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \left(1-\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle \right)\underline{e}\left\langle \boldsymbol{\xi} \right\rangle \Delta \underline{e}\left\langle \boldsymbol{\xi} \right\rangle \, \mathrm{d}{V}_{\boldsymbol{\xi}}. $$

Since

$$ \Delta \underline{e}\left\langle \boldsymbol{\xi} \right\rangle =\underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle \cdot \Delta \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle, \quad\quad \underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle =\frac{\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle }{\mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mid }, $$

it follows that

$$ \underline {\mathbf{T}}\bullet \Delta \underline {\mathbf{Y}}=\int_{{\mathcal{H}}_{\mathbf{x}}}\left[\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \left(1-\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle \right)\underline{e}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle \right]\cdot \Delta \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mathrm{d}{V}_{\boldsymbol{\xi}}. $$

Comparing this with Eq. 3 leads to the conclusion that

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)=\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline {e\mathbf{M}}. $$

(31)

or

$$ \underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle =\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \left(1-\underline{\phi}\left\langle \boldsymbol{\xi} \right\rangle \right)\underline{e}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle \quad\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

Some features of the material model (31) are as follows:

• The bond force density vector in each bond is parallel to the deformed bond.

• Holding damage fixed, the magnitude of the bond force density varies linearly with bond extension.

• The model is bond-based: each bond responds independently of all the others.

• The model is geometrically nonlinear: it allows for large deformation.

• Increasing the damage in each bond decreases the magnitude of each bond force density in that bond.

From Eq. 28 and the second of Eq. 18, one finds that for this material model,

$$ \eta =-{\psi}_{\theta }=c\log \left(\theta /{\theta}_0\right) $$

(32)

From Eq. 14, the second of Eq. 18, and the time derivative of Eq. 32, it follows that if $\underline {\mathbf{Y}}$ and $\underline{\phi}$ are held constant,

$$ {\displaystyle \begin{array}{c}\dot{\varepsilon}={\psi}_{\theta}\dot{\theta}+\dot{\theta}\eta +\theta \dot{\eta}\\ {}=\theta \dot{\eta}\\ {}=c\dot{\theta}.\end{array}} $$

Thus, unlike the free energy, the internal energy varies linearly with temperature under these conditions, with the heat capacity as the constant of proportionality.

Ordinary State-Based Linear Material with Damage

A modification of Eq. 31 that includes a volume change may be written as:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)=\left(\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline{e}+ A\vartheta \underline{1}\right)\underline {\mathbf{M}},\quad\quad \vartheta =\frac{\underline{1}\bullet \underline{e}}{\underline{1}\bullet \underline{1}} $$

where A is a constant and ϑ is the dilatation. (See Eq. 40 below for a more general definition of dilatation.) Note that the dilatation depends on all the bonds in the family.

Non-ordinary State-Based Material

The following material model tends to resist bending:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\left\langle \boldsymbol{\upxi} \right\rangle =\left\{\begin{array}{ll}A\left(\underline{e}\left\langle \boldsymbol{\upxi} \right\rangle +\underline{e}\left\langle -\boldsymbol{\upxi} \right\rangle \right)\left(\underline {\mathbf{Y}}\left\langle \boldsymbol{\upxi} \right\rangle -\underline {\mathbf{Y}}\left\langle -\boldsymbol{\upxi} \right\rangle \right)& \mathrm{if}\;\boldsymbol{\upxi} \in {\mathcal{H}}_{\mathbf{x}}\;\mathrm{and}-\boldsymbol{\upxi} \in {\mathcal{H}}_{\mathbf{x}},\\ {}0& \mathrm{otherwise}.\end{array}\right. $$

where A is a constant. Another way to write this is to define the reversal state by

$$ \underline {\mathbf{R}}\left\langle \boldsymbol{\upxi} \right\rangle =-\boldsymbol{\upxi} \quad \forall \boldsymbol{\upxi} \in {\mathcal{H}}_{\mathbf{x}}, $$

then

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)=A\left(\underline{e}+\underline{e}\circ \underline {\mathbf{R}}\right)\left(\underline {\mathbf{Y}}-\underline {\mathbf{Y}}\circ \underline {\mathbf{R}}\right). $$

This material is nonpolar even though the bond forces are not necessarily parallel to the deformed bonds. It is interesting that a state-based peridynamic material model without changing the equilibrium equation can resist bending; see Diyaroglu et al. (2015) and Grady and Foster (2014). for details and specific material models. This is in contrast to the standard theory of beams and plates, in which a special fourth-order PDE replaces the fundamental second-order PDEs of local continuum mechanics.

Bond-Based Viscoelastic Material

The material model (31) can be modified to include a rate-dependent damping term:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}},\underline {\overset{.}{\mathbf{Y}}}\right)=\left(\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline{e}+A\underline {\dot{e}}\right)\underline {\mathbf{M}} $$

where A is a nonnegative constant. More information on viscoelastic peridynamic models can be found in Mitchell (2011a) and Weckner and Mohamed (2013).

Isotropic Bond-Based Material

In the material model (31), different bonds can have different stiffness, because $\underline{C}$ is a state (that is, its value depends on the bond). (See Hu et al. 2012a; Oterkus and Madenci 2012). for examples of anisotropic material models.) To model isotropic materials , set

$$ \underline{C}\left\langle \boldsymbol{\upxi} \right\rangle ={C}^i\left(|\boldsymbol{\upxi} |\right) $$

where Cⁱ is a function of bond length only, thus

$$ \underline {\mathbf{T}}=\left({C}^i\left(\underline{1}-\underline{\phi}\right)\underline{e}\right)\underline {\mathbf{M}}. $$

The most general form for Cⁱ is discussed in Silling (2000).

Nonconvex Bond-Based Material

If the bond force density is not a monotonic function of extension, and if it is elastic, then its strain-energy density function is called nonconvex . An example is:

$$ \underline {\mathbf{T}}\left\langle \boldsymbol{\upxi} \right\rangle =A\underline{e}\left\langle \boldsymbol{\upxi} \right\rangle \exp \left(-{\underline{e}}^2\left\langle \boldsymbol{\upxi} \right\rangle \right)\underline {\mathbf{M}}\left\langle \boldsymbol{\upxi} \right\rangle\;\mathrm{or}\;\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)=A\underline{e}\exp \left(-{\underline{e}}^2\right)\underline {\mathbf{M}}. $$

The properties of nonconvex bond-based materials, including their stability and relation to brittle fracture, are discussed by Lipton (2014, 2016). More general concepts of convexity that apply to state-based materials are, to the best of the author’s knowledge, a totally unexplored area.

Discrete Particles as Peridynamic Materials

Consider a set of N particles with equal mass m that interact through a multibody potential such that the potential energy of particle i is given by:

$$ {\Phi}_i={U}_i\left({\mathbf{r}}_{1i},{\mathbf{r}}_{2i},\dots, {\mathrm{r}}_{Ni}\right)-{\mathbf{b}}_i\cdot {\mathbf{y}}_i,\quad {\mathbf{r}}_{ji}:= {\mathbf{y}}_j-{\mathbf{y}}_i $$

where y_i and b_i are the position of and external force on particle i. The potential energy of the entire set of particles is found from:

$$ \Phi =\sum \limits_{i=1}^N{\Phi}_i. $$

The acceleration of each particle i is obtained from Newton’s second law in the form:

$$ {\displaystyle \begin{array}{c}{\mathbf{F}}_i=m{\ddot{\mathbf{y}}}_i=-\frac{\mathrm{\partial \Phi }}{\partial {\mathbf{y}}_i}\\ {}=\sum \limits_{j=1}^N\left(\frac{\partial {U}_i}{\partial {\mathbf{r}}_{ji}}-\frac{\partial {U}_j}{\partial {\mathbf{r}}_{ij}}\right)+{\mathbf{b}}_i.\end{array}} $$

(33)

Now consider the peridynamic body with mass-density field and body-force density field defined by:

$$ \rho \left(\mathbf{x}\right)=\sum \limits_{i=1}^Nm\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right),\quad \mathrm{b}\left(\mathbf{x}\right)=\sum \limits_{i=1}^N{\mathbf{b}}_i\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right) $$

(34)

where ∆(·) denotes the 3D Dirac delta function. Here, the reference positions of the particles x_i are arbitrary and merely serve to identify the particles for purposes of the mathematics. For this peridynamic body, let the material model be elastic with strain-energy density function given by:

$$ \widehat{W}\left(\underline {\mathbf{Y}}\left[\mathbf{x}\right],\mathbf{x}\right)=\sum \limits_{i=1}^N{U}_i\left({\mathbf{r}}_{1i},{\mathbf{r}}_{2i},\dots, {\mathbf{r}}_{Ni}\right)\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right),\quad {\mathbf{r}}_{ji}=\underline {\mathbf{Y}}\left[{\mathbf{x}}_i\right]\left\langle {\mathbf{x}}_j-{\mathbf{x}}_i\right\rangle . $$

(35)

After evaluating the Fréchet derivative of this $\widehat{W}$^, the force state field is found to be:

$$ \underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\sum \limits_{i=1}^N\sum \limits_{j=1}^N\frac{\partial {U}_i}{\partial {\mathrm{r}}_{ji}}\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right)\Delta \left(\mathbf{q}-{\mathbf{x}}_j\right). $$

(36)

Evaluating the acceleration field using Eqs. 8, 34, and 36, the terms involving ∆(q − x_j) integrate to 1 and hence

$$ \rho \left(\mathbf{x}\right)\overset{..}{\mathbf{y}}\left(\mathbf{x}\right)=\int_{\mathcal{B}}\left\{\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -\underline {\mathbf{T}}\left[\mathbf{q}\right]\Big\langle\mathbf{x}-\mathbf{q}\Big\rangle \right\}\mathrm{d}{V}_{\mathbf{q}}+\mathbf{b}\left(\mathbf{x}\right) $$

becomes

$$ {\displaystyle \begin{array}{c}\sum \limits_{i=1}^N\left(m\overset{..}{\mathbf{y}}\left(\mathbf{x}\right)-\mathbf{b}\left(\mathbf{x}\right)\right)\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right)=\sum \limits_{i=1}^N\sum \limits_{j=1}^N\frac{\partial {U}_i}{\partial {\mathbf{r}}_{ji}}\left(\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right)-\Delta \left(\mathbf{x}-{\mathbf{x}}_j\right)\right)\\ {}=\sum \limits_{i=1}^N\sum \limits_{j=1}^N\left(\frac{\partial {U}_i}{\partial {\mathbf{r}}_{ji}}-\frac{\partial {U}_j}{\partial {\mathbf{r}}_{ij}}\right)\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right)\end{array}} $$

which implies

$$ m\overset{..}{\mathbf{y}}\left({\mathbf{x}}_i\right)=\sum \limits_{j=1}^N\left(\frac{\partial {U}_i}{\partial {\mathbf{r}}_{ji}}-\frac{\partial {U}_j}{\partial {\mathbf{r}}_{ij}}\right)+{\mathbf{b}}_i,\quad i=1,2,\dots, N. $$

So, the peridynamic equation of motion for the body specified in Eqs. 34 and 35 reduces to Newton’s second law, (Eq. 33).

The applicability of peridynamics to both continuous and discrete systems can be useful in modeling the interaction of particles with continuous bodies. For example, certain aspects of the mechanics of a suspension of particles in a liquid can be treated simply by adding the responses of the two media, one discrete and one continuous:

$$ \widehat{W}\left(\underline {\mathbf{Y}},\mathbf{x}\right)=\sum \limits_{i=1}^N{U}_i\left(\underline {\mathbf{Y}},\mathbf{x}\right)\Delta \left(\mathbf{x}-{\mathbf{x}}_i\right)+{\widehat{W}}_c\left(\underline {\mathbf{Y}}\right) $$

where ${\widehat{W}}_c$ is the strain-energy density function for the continuum. Since the machinery of peridynamics can be applied to this unconventional medium, this model could potentially be used to study interesting phenomena such as wave dispersion, attenuation, scattering in suspensions of interacting particles.

Effectively Eulerian Material Models

The material models described up to now in this chapter have been Lagrangian; they refer explicitly to a reference configuration, and the bond forces arise from movement of the bonds from their reference positions. For modeling fluids under large deformations, the Lagrangian approach becomes impractical because of the gross distortion of the families. In these cases, an Eulerian approach to material modeling may be preferable.

An effectively Eulerian material model for a fluid can be derived by letting the horizon be infinite but limiting the response to bonds that currently have length less than a prescribed distance δ in the deformed configuration. For example, such a model for a fluid could be specified by defining a nonlocal density as follows:

$$ \overline{\rho}\left(\mathbf{x}\right)={\rho}_0\int_{\mathcal{B}}\omega \left(|\underline {\mathbf{Y}}\left[\mathbf{x}\right]\left\langle \mathrm{q}-\mathbf{x}\right\rangle |\right)\mathbf{d}{V}_{\boldsymbol{\upxi}} $$

(37)

where ρ₀ is the reference density and ω is a differentiable weighting function on [0, ∞) such that:

$$ {\displaystyle \begin{array}{l}\int_{\mathcal{B}}\omega \left(|\boldsymbol{\xi} |\right)\mathrm{d}{V}_{\boldsymbol{\xi}}=1,\\ {}\omega =0\, \mathrm{on}\, \left[\delta, \infty \right),\quad {\omega}^{\prime}\le 0\, \mathrm{on}\, \left[0,\delta \right].\end{array}} $$

Even though the region of integration in Eq. 37 is ${\mathcal{B}}$ in the reference configuration, in effect only a neighborhood of radius δ in the deformed configuration needs to be computed. The nonlocal density Eq. 37 can be used in any conventional equation of state. The energy balance (9) continues to apply without change, since its form is independent of the material model. The pressure from the equation of state determines the bond forces through the usual Fréchet derivative:

$$ \begin{aligned}\underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle &=\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\left\langle \boldsymbol{\xi} \right\rangle ={\psi}_{\underline {\mathbf{Y}}}=\frac{\partial \psi }{\partial v}\frac{\partial v}{\partial \overline{\rho}}{\overline{\rho}}_{\underline {\mathbf{Y}}}\\ &=\left(-p\right)\left(\frac{-{\rho}_0}{{\overline{\rho}}^2}\right)\left({\rho}_0{\omega}^{\prime}\left(|\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle |\right)\underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle \right)\\ &={pv}^2{\omega}^{\prime}\left(|\underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle |\right)\underline {\mathbf{M}}\left\langle \boldsymbol{\xi} \right\rangle \quad \forall \boldsymbol{\xi} \in \mathrm{\mathcal{B}}\end{aligned} $$

where p is the pressure and $v={\rho}_0/\overline{\rho}$ is the nonlocal relative volume. This approach to modeling fluids has been successfully applied to very large deformations and strong shock waves (Silling et al. 2017).

Some Lagrangian material models can be converted to effectively Eulerian models. To do this, we must eliminate any explicit dependence of $\underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle$ on ξ except as an identifier for bonds. For example, recall the example bond-based material model (30), (31) with $\underline{\phi}=\underline{0}$:

$$ \underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle =\underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}}\right)\left\langle \boldsymbol{\xi} \right\rangle =\underline{C}\left\langle \boldsymbol{\xi} \right\rangle \underline{e}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathrm{M}}\left\langle \boldsymbol{\xi} \right\rangle, \quad \underline{e}\left\langle \boldsymbol{\xi} \right\rangle =\mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mid -\mid \boldsymbol{\xi} \mid . $$

This model contains ξ explicitly through the ∣ξ∣ term, so it is Lagrangian. But consider this alternative model:

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}},\underline {\overset{.}{\mathbf{Y}}}\right)\left\langle \boldsymbol{\xi} \right\rangle := \underline{C}\left\langle \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \right\rangle \underline{E}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathrm{M}}\left\langle \boldsymbol{\xi} \right\rangle $$

(38)

where $\underline{E}$ is a scalar-valued state, that is a function of time, defined by:

$$ \underline{E}\left[0\right]=\underline{0},\quad \underline {\dot{E}}\left[t\right]=\left\{\begin{array}{ll}\underline {\dot{\mathbf{Y}}}\left\langle \boldsymbol{\xi} \right\rangle \cdotp \underline {\mathrm{M}}\left\langle \boldsymbol{\xi} \right\rangle & \mathrm{if}\ \mid \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \mid \le \delta, \\ {}0& \mathrm{otherwise},\end{array}\right. $$

or, more succinctly,

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}},\underline {\overset{.}{\mathbf{Y}}}\right)=\left(\underline{C}\circ \underline {\mathbf{Y}}\right)\underline {E\mathrm{M}},\quad \underline {\dot{E}}=\underline {\overset{.}{\mathbf{Y}}}\cdot\underline {\mathrm{M}}. $$

(39)

Since ξ does not appear explicitly in Eq. 38 except as an identifier, this alternative model is effectively Eulerian. In Eq. 39, it is assumed that $\underline{C}\left\langle \mathbf{p}\right\rangle =0$ whenever ∣p∣ > δ. Interactions can occur in bonds that start out with length greater than δ but get shorter over time. Similarly, bonds that are initially short will have zero bond force density if they elongate over time to length greater than δ. The material model (39) is effectively Eulerian but is not elastic.

Plasticity

For small deformations, it is conventional to express volume changes in the form of the dilatation, denoted ϑ. By linearization of Eq. 37, this is found to be:

$$ v-1\approx \vartheta \left(\underline {\mathbf{Y}}\right):= \frac{3\left(\underline {\Omega x}\right)\bullet \underline{e}}{\left(\underline {\Omega x}\right)\bullet \underline{x}},\quad \underline{\Omega}\left\langle \boldsymbol{\xi} \right\rangle =-\mid \boldsymbol{\xi} \mid {\omega}^{\prime}\left(|\boldsymbol{\xi} |\right),\quad \underline{x}\left\langle \boldsymbol{\xi} \right\rangle =\mid \boldsymbol{\xi} \mid . $$

(40)

where $\underline{e}$ is the extension state defined in Eq. 30. In terms of rates, since $\underline {\dot{e}}=\underline {\mathrm{M}}\cdotp \underline {\overset{.}{\mathbf{Y}}}$, Eq. 40 can be written as

$$ \dot{\vartheta}\left(\underline {\overset{.}{\mathbf{Y}}}\right):= \frac{3\left(\underline {\Omega \mathbf{X}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}}{\left(\underline {\Omega \mathbf{X}}\right)\bullet \underline {\mathbf{X}}}. $$

(41)

We will not make further use of the connection between $\underline{\Omega}$ and ω given in the second of Eq. 40, so $\underline{\Omega}$ can be regarded as essentially arbitrary, except that it must be nonnegative and depend only on |ξ|. Similarly, for small deformations, the pressure is given by:

$$ p\left(\underline {\mathbf{T}}\right)=-\frac{1}{3}\underline {\mathbf{X}}\bullet \underline {\mathbf{T}}. $$

(42)

Plastic deformation can be incorporated into an elastic material model by introducing a new vector-valued state called the permanent deformation state , denoted $\underline {\mathbf{P}}$. Given a free-energy density function ${\psi}^0\left(\underline {\mathbf{Y}},\theta \right)$, define a new free-energy density function by

$$ \psi \left(\underline {\mathbf{Y}},\underline {\mathbf{P}},\theta \right)={\psi}^0\left(\underline {\mathbf{Y}}-\underline {\mathbf{P}},\theta \right). $$

Since $\underline {\mathbf{T}}={\psi}_{\underline {\mathbf{Y}}}$, it follows that

$$ \underline {\widehat{\mathbf{T}}}\left(\underline {\mathbf{Y}},\underline {\mathbf{P}},\theta \right)={\underline {\widehat{\mathbf{T}}}}^0\left(\underline {\mathbf{Y}}-\underline {\mathbf{P}},\theta \right) $$

and similarly

$$ {\psi}_{\underline {\mathbf{P}}}=-\underline {\mathbf{T}}. $$

(43)

By repeating the steps leading up to Eq. 17, one finds that

$$ \left(\underline {\mathbf{T}}-{\psi}_{\underline {\mathbf{Y}}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}-{\psi}_{\underline {\mathbf{P}}}\bullet \underline {\overset{.}{\mathbf{P}}}+h+s-\left(\eta +{\psi}_{\theta}\right)\dot{\theta}\ge 0. $$

(44)

From Eqs. 43 and 44, it follows that

$$ {\dot{\psi}}^p:= \underline {\mathbf{T}}\bullet \underline {\overset{.}{\mathbf{P}}}\ge 0 $$

(45)

where ${\dot{\psi}}^p$ is the rate of plastic work. Equation 45 is the dissipation inequality for plastic materials.

Plastic flow can occur when the force state is on or outside of a yield surface defined by:

$$ \mathcal{P}\left(\underline {\mathbf{T}}\right)=0 $$

where $\mathcal{P}$ is a scalar-valued function. A possible evolution law for $\underline {\mathbf{P}}$ is given by:

$$ \underline {\overset{.}{\mathbf{P}}}=\lambda {\mathcal{P}}_{\underline {\mathbf{T}}}, $$

(46)

where λ > 0. Equation 46 can be thought of as an associated flow rule. The dissipation inequality (Eq. 45), which is a consequence of the second law of thermodynamics, places a restriction on $\mathcal{P}$:

$$ {\mathcal{P}}_{\underline {\mathbf{T}}}\bullet \underline {\mathbf{T}}\ge 0\quad \forall \underline {\mathbf{T}}, $$

which is a type of convexity condition on the yield surface.

Many materials, especially metals under moderate stress, have yield surfaces that are nearly independent of the pressure. To account for this, the peridynamic yield surface can be defined to be a function of the deviatoric force state , which is obtained by subtracting off the hydrostatic part of the force state:

$$ {\underline {\mathbf{T}}}^d=\underline {\mathbf{T}}-\frac{\underline {\mathbf{X}}\bullet \underline {\mathbf{T}}}{\left(\underline {\Omega \mathbf{X}}\right)\bullet \underline {\mathbf{X}}}\underline {\Omega \mathbf{X}}. $$

(47)

From Eqs. 42 and 47,

$$ p\left({\underline {\mathbf{T}}}^d\right)=0, $$

that is, the deviatoric force state has zero pressure. For a material model in which the yield surface depends only on ${\underline {\mathbf{T}}}^d$, the associated flow rule (Eq. 46) can be evaluated using the chain rule for Fréchet derivatives, with the result:

$$ {\displaystyle \begin{aligned}\underline {\overset{.}{\mathbf{P}}}&=\lambda {\mathcal{P}}_{\underline {\mathbf{T}}}\\ &=\lambda {\mathcal{P}}_{{\underline {\mathbf{T}}}^d}\bullet {\underline {\mathbf{T}}}_{\underline {\mathbf{T}}}^d\\ &=\lambda \left({\mathcal{P}}_{{\underline {\mathbf{T}}}^d}-\frac{\left(\underline {\Omega \mathbf{X}}\right)\bullet {\mathcal{P}}_{{\underline {\mathbf{T}}}^d}}{\left(\underline {\Omega \mathbf{X}}\right)\bullet \underline {\mathbf{X}}}\underline {\mathbf{X}}\right).\end{aligned}} $$

(48)

Comparing the structure of Eqs. 47 and 48, it is subtle but significant that in the latter, the $\underline{\Omega}$ is shifted from outside the fraction to inside the numerator. Using this fact, Eqs. 41 and 48 imply that:

$$ \dot{\vartheta}\left(\underline {\overset{.}{\mathbf{P}}}\right)=0, $$

that is, the associated flow rule applied to a yield surface that depends only on the deviatoric force state results in zero volume change. This echoes the familiar result in the plasticity of metals that plastic strain has zero dilatation. Additional details on modeling plasticity within peridynamics can be found in Foster et al. (2010), Madenci and Oterkus (2016), Mitchell (2011b), Sun and Sundararaghavan (2014), and Warren et al. (2009).

Damage Evolution

The monotonicity condition (24) is the only general requirement on the evolution of damage :

$$ \underline {\dot{\phi}}\left\langle \boldsymbol{\xi} \right\rangle =\underline{D}\left\langle \boldsymbol{\xi} \right\rangle \ge 0\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

Otherwise, we are free to dream up damage growth laws. The second law restriction (Eq. 26) is really a condition on the material model, not the damage growth law.

One approach to specifying how damage grows is to define a failure surface in state space:

$$ \mathcal{S}\left(\underline {\mathbf{T}},\underline {\mathbf{Y}},\underline{\phi}\right)=0 $$

such that damage does not increase if $\mathcal{S}$ is in the interior of the surface, that is, if $\mathcal{S}$ < 0.

An example of a plausible damage growth law is given by:

$$ \underline{D}\left\langle \boldsymbol{\xi} \right\rangle =\left\{\begin{array}{ll}0& \mathrm{if}\ \mathcal{S}<0,\\ {}\uplambda \underline{F}\left\langle \boldsymbol{\xi} \right\rangle & \mathrm{otherwise}.\end{array}\right. $$

(49)

where λ(t) is a nonnegative scalar-valued function and $\underline{F}$ is the thermodynamic force state defined by:

$$ \underline{F}=-{\psi}_{\underline{\phi}}. $$

(50)

The damage growth law (49) satisfies the monotonicity condition (24) because of the result (27), which is a consequence of the dissipation inequality for damage:

$$ \underline {\dot{\phi}}\left\langle \boldsymbol{\xi} \right\rangle =\underline{D}\left\langle \boldsymbol{\xi} \right\rangle =\uplambda \underline{F}\left\langle \boldsymbol{\xi} \right\rangle =-\uplambda {\psi}_{\underline{\phi}}\left\langle \boldsymbol{\xi} \right\rangle \ge 0\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}. $$

The remaining question is how to determine λ.

In dynamics, we can reasonably assume a dependence of the form:

$$ \uplambda =a\mathcal{S} $$

(51)

where a is a nonnegative constant. This relation allows the value of $\mathcal{S}$ to be outside the failure surface, that is, $\mathcal{S}$> 0, while damage is evolving. It is interesting to investigate the stability of the resulting damage growth. Consider a uniformly deformed body and hold the deformation fixed. Allow damage to evolve and analyze whether damage growth speeds up or slows down over time. To study this, take the total time derivative of $\mathcal{S}\left(\underline {\mathbf{T}},\underline {\mathbf{Y}},\underline{\phi}\right)$ holding $\underline {\dot{\mathrm{Y}}}=\underline{0}$:

$$ \dot{\mathcal{S}}=\left({\mathcal{S}}_{\underline {\mathrm{T}}}\bullet {\underline {\mathbf{T}}}_{\underline{\phi}}+{\mathcal{S}}_{\underline{\phi}}\right)\bullet \underline {\dot{\phi}}. $$

Using Eqs. 49 and 50 yields:

$$ \dot{\uplambda}=a\dot{\mathcal{S}}= a\lambda \left({\mathcal{S}}_{\underline {\mathbf{T}}}\bullet {\underline {\mathbf{T}}}_{\underline{\phi}}+{\mathcal{S}}_{\underline{\phi}}\right)\bullet \underline{F}. $$

The solution to this ODE for λ is given by:

$$ \uplambda (t)=\uplambda (0){e}^{art},\quad r=\left({\mathcal{S}}_{\underline {\mathrm{T}}}\bullet {\underline {\mathbf{T}}}_{\underline{\phi}}+{\mathcal{S}}_{\underline{\phi}}\right)\bullet \underline{F}. $$

(52)

Thus, the damage growth is stable if r ≤ 0 and unstable otherwise. Mechanically, this criterion says that if $\mathcal{S}$ is being driven toward the failure surface by the ${\mathcal{S}}_{\underline {\mathbf{T}}}$ term faster than it is being pushed away from it by the ${\mathcal{S}}_{\underline{\phi}}$ term (if this term is positive), then it is unstable.

In the case of quasi-static deformation, it can be assumed that, instead of Eq.~51, the condition that determines the growth of damage is that the system always remains on the failure surface as $\underline {\mathbf{Y}}$ changes, thus:

$$ \dot{\mathcal{S}}=0. $$

Under this assumption, writing out the time derivative of $\mathcal{S}$ using Eq. 49 yields:

$$ {\displaystyle \begin{array}{c}0=\dot{\mathcal{S}}\left(\underline {\mathbf{T}},\underline {\mathbf{Y}},\underline{\phi}\right)\\ {}={\mathcal{S}}_{\underline {\mathrm{T}}}\bullet \left({\underline {\mathbf{T}}}_{\underline {\mathbf{Y}}}\bullet \underline {\overset{.}{\mathbf{Y}}}+{\underline {\mathbf{T}}}_{\underline{\phi}}\bullet \underline {\dot{\phi}}\right)+{\mathcal{S}}_{\underline {\mathrm{Y}}}\bullet \underline {\overset{.}{\mathbf{Y}}}+{\mathcal{S}}_{\underline{\phi}}\bullet \underline {\dot{\phi}}\\ {}={\mathcal{S}}_{\underline {\mathbf{T}}}\bullet \left({\underline {\mathbf{T}}}_{\underline {\mathbf{Y}}}\bullet \underline {\overset{.}{\mathbf{Y}}}+\uplambda {\underline {\mathbf{T}}}_{\underline{\phi}}\bullet \underline{F}\right)+{\mathcal{S}}_{\underline {\mathbf{Y}}}\bullet \underline {\overset{.}{\mathbf{Y}}}+\uplambda {\mathcal{S}}_{\underline{\phi}}\bullet \underline{F}.\end{array}} $$

Solving this for λ and applying the monotonicity requirement for damage leads to:

$$ \uplambda =\max \left\{0,-\frac{\left({\mathcal{S}}_{\underline {\mathbf{T}}}\bullet {\underline {\mathbf{T}}}_{\underline {\mathbf{Y}}}+{\mathcal{S}}_{\underline {\mathrm{Y}}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}}{r}\right\}\, \forall \underline {\overset{.}{\mathbf{Y}}} $$

(53)

where r is given by the second of Eq. 52. Observe that Eq. 53 blows up as r → 0, indicating the onset of unstable damage growth, as discussed previously. The relations (49) and (53) allow us to explicitly determine the rate of damage growth for every bond at every point in the body, provided the deformation is quasi-static and $\mathcal{S}$ = 0:

$$ \underline {\dot{\phi}}=\max \left\{0,-\frac{\left({\mathcal{S}}_{\underline {\mathrm{T}}}\bullet {\underline {\mathbf{T}}}_{\underline {\mathbf{Y}}}+{\mathcal{S}}_{\underline {\mathbf{Y}}}\right)\bullet \underline {\overset{.}{\mathbf{Y}}}}{\left({\mathcal{S}}_{\underline {\mathrm{T}}}\bullet {\underline {\mathbf{T}}}_{\underline{\phi}}+{\mathcal{S}}_{\phi}\right)\bullet \underline{F}}\right\}\underline{F}\quad \forall \underline {\overset{.}{\mathbf{Y}}}. $$

(54)

As an example of a failure surface, consider the material model (28) with a slight modification that introduces a binary variable to indicate intact bonds or broken bonds:

$$ \underline{b}\left\langle \boldsymbol{\xi} \right\rangle =\left\{\begin{array}{ll}1& \mathrm{if}\ \underline {\phi}\left\langle \boldsymbol{\xi} \right\rangle <1,\\ {}0& \mathrm{otherwise}.\end{array}\right. $$

The modified free-energy expression is given by:

$$ \psi \left(\underline {\mathbf{Y}},\theta, \underline{\phi}\right)=\frac{1}{2}\left(\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline{be}\right)\bullet \underline{e}+ c\theta \left(1-\log \left(\theta /{\theta}_0\right)\right). $$

An example of a failure surface is given by:

$$ \mathcal{S}\left(\underline {\mathbf{T}},\underline{\phi}\right)=\left(\underline {k\mathbf{T}}\right)\bullet \underline {\mathbf{M}}+\frac{s_1}{2}{\left\Vert \underline{\phi}\right\Vert}^2-{s}_0 $$

(55)

where s₀ and s₁ are constants, s₀≥ 0, and k is a nonnegative, constant, scalar-valued state. The bond force density is given by:

$$ \underline {\mathbf{T}}={\psi}_{\underline {\mathbf{Y}}}=\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline {be\mathbf{M}}. $$

Evaluating the required Fréchet derivatives in Eq. 54 leads to:

$$ {\displaystyle \begin{array}{c}\underline{F}=-{\psi}_{\underline{\phi}}=\frac{1}{2}{\underline{Cbe}}^2,\quad{\underline {\mathbf{T}}}_{\underline {\mathbf{Y}}}=\underline{C}\left(\underline{1}-\underline{\phi}\right)\underline {b\mathbf{M}}\star \underline {\mathbf{M}},\quad {\underline {\mathbf{T}}}_{\underline{\phi}}=- \underline{Cbe\mathbf{M}},\\ {}{\mathcal{S}}_{\underline {\mathbf{Y}}}=\underline{0},\quad{\mathcal{S}}_{\underline {\mathbf{T}}}=\underline {k\mathbf{M}},\quad{\mathcal{S}}_{\underline{\phi}}={s}_1\left\Vert \underline{\phi}\right\Vert \underline{\phi}.\end{array}} $$

Suppose that a specimen has zero deformation and damage at time 0 and then is deformed homogeneously and quasi-statically. By Eqs. 49 and 55, damage first starts growing when the condition $\mathcal{S}$ = 0 occurs, hence:

$$ \left(\underline {k\mathbf{T}}\right)\bullet \underline {\mathbf{M}}={s}_0. $$

Under continued quasi-static deformation with stable damage growth, Eq. 54 then leads to:

$$ \underline {\dot{\phi}}=\underline{D}=\frac{\left(\underline{kC}\left(\underline{1}-\underline{\phi}\right)\underline{b}\right)\bullet \underline {\dot{e}}}{\left(\underline {kC be}-{s}_1\left\Vert \underline{\phi}\right\Vert \underline{\phi}\right)\bullet \left({\underline{Cbe}}^2\right)}{\underline{Cbe}}^2. $$

(56)

Damage growth is stable until the denominator in Eq. 56 becomes nonpositive; then it becomes unstable. Figure 2 illustrates the behavior of this example material and damage growth model for a 1D body with:

$$ \underline{C}=\underline{k}=\underline{1},\quad \delta =1,\quad {s}_0=0.02. $$

Fig. 2

Stress-strain curves for a bar under tension

The different stress-strain curves are for different values of s₁, indicating the transition from stable to unstable damage growth as s₁ is increased. The stress is computed using Eq. 58, to be discussed below.

In 2D, similar material and damage models (for a material with a bulk modulus of 10MPa) can simulate the stable accumulation of diffuse damage near a stress singularity, as shown in Fig. 3. The specimen contains a semicircular notch and is under combined normal and transverse loading corresponding to strain rates of ${\dot{\upepsilon}}_{22}=2.0{\mathrm{s}}^{-1}$ and ${\dot{\upepsilon}}_{12}=1.0{\mathrm{s}}^{-1}$. Until a strain of about ϵ₂₂ = 0.12, there is a stable growth of damage near the notch. Then there is a sudden transition to dynamic fracture. The crack rapidly propagates to the opposite free edge of the specimen. This transition from stable to unstable can be seen in the stress-strain curve shown in Fig. 4. This curve represents the total normal load in the vertical direction divided by the cross-sectional area of the specimen (on a cross-sectional plane that does not include the notch).

Fig. 3

Transition of stable damage growth at a stress concentration to dynamic fracture

Fig. 4

Remote normal stress as a function of global strain for damage growth and fracture near a semicircular notch

These examples demonstrate the potential usefulness of peridynamic damage mechanics in modeling materials that either fracture immediately or after a period of accumulated continuous damage. The compatibility of the peridynamic field equations with both continuous and discontinuous deformations is helpful in modeling the spontaneous nucleation and growth of fractures within a damaged material.

Bond Breakage

A simpler approach to damage modeling in peridynamics has $\underline{\phi}\left\langle \boldsymbol{\upxi} \right\rangle$ jump discontinuously from 0 to 1 according to some criterion, which can be quite general. This approach, which is called bond breakage, is used in the vast majority of peridynamic codes because of its simplicity and reduced memory requirements. It has the disadvantage compared with continuously varying $\underline{\phi}$ that instantaneous bond breakage can excite unwanted oscillations in a numerical grid. However, these can be suppressed in practice by applying damping forces to nodes after their bonds break.

A bond-breakage criterion can be as simple as a critical value of bond strain (Silling and Askari 2005). In this case, the critical bond strain for bond breakage can be calibrated to match a given critical energy release rate for the material. This bond-breakage strain depends on the horizon as well as the critical energy release rate. Critical bond strain as a failure criterion is a natural way to model brittle fracture, particularly in mode I. For other modes, it becomes trickier to specify the critical strain, which may depend on the conditions in other bonds in the family. Nucleation of cracks is predicted by bond breakage damage growth laws, but with a simple bond-strain criterion, it is difficult to prescribe both the critical energy release rate and the critical conditions for crack nucleation simultaneously. Postfailure response of the bonds depends on the material model; for example, it may or may not be appropriate in a given material to allow bonds to sustain compressive force after they break.

In spite of the many successes of the bond breakage approach to peridynamic damage modeling, the above considerations help motivate the development of the more general approach using the thermodynamic force and failure surfaces as described in section “Damage Evolution.”

Connections with the Local Theory

This section summarizes the mathematical and conceptual connections between the nonlocal peridynamic theory and the local theory. The connections discussed here include the relations between the force state and the stress tensor, between the deformation state and the deformation gradient tensor, between nonlocal heat transport and the Clausius-Duhem inequality, the scaling and convergence of material models, and local damage mechanics. Not discussed below but also important is the peridynamic version of the Eshelby-Rice J -integral (Hu et al. 2012b; Silling and Lehoucq 2010).

Local Kinematics and Kinetics

Suppose a First Piola stress tensor σ is given. Let $\underline{\omega}$ be a positive scalar-valued state called the influence function . Consider the force state defined by:

$$ \underline {\overline{\mathbf{T}}}\left(\boldsymbol{\sigma} \right)=\boldsymbol{\sigma} \underline{\omega}{\mathbf{K}}^{-1}\underline {\mathbf{X}}\quad \mathrm{or}\quad \underline {\overline{\mathbf{T}}}\left(\boldsymbol{\sigma} \right)\left\langle \boldsymbol{\xi} \right\rangle =\boldsymbol{\sigma} \underline{\omega}\left\langle \boldsymbol{\xi} \right\rangle {\mathbf{K}}^{-1}\boldsymbol{\xi} \quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}} $$

(57)

where K is the shape tensor defined by:

$$ \mathbf{K}=\int_{{\mathcal{H}}_{\mathbf{x}}}\underline{\omega}\left\langle \boldsymbol{\xi} \right\rangle \boldsymbol{\xi} \otimes \boldsymbol{\xi} \mathrm{d}{V}_{\boldsymbol{\upxi}}. $$

The force state $\underline {\overline{\mathrm{T}}}\left(\sigma \right)$ defined by Eq. 57 has the property that in a uniform deformation of a homogeneous body, the force per unit area across any plane transferred by all the bonds that cross this plane is equal to:

$$ \boldsymbol{\tau} =\boldsymbol{\sigma} \mathbf{n} $$

where n is a unit normal to the plane. Conversely, for a given force state $\underline {\mathrm{T}}$, the stress tensor defined by:

$$ \overline{\boldsymbol{\sigma}}\left(\underline {\mathbf{T}}\right)=\underset{{\mathcal{H}}_{\mathbf{x}}}\int\underline {\mathbf{T}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \boldsymbol{\xi} \mathrm{d}{V}_{\boldsymbol{\xi}} $$

(58)

has the same property. $\overline{\boldsymbol{\sigma}}$ is called the partial stress tensor. For any σ,

$$ \overline{\boldsymbol{\sigma}}\left(\underline {\overline{\mathbf{T}}}\left(\boldsymbol{\sigma} \right)\right)=\boldsymbol{\sigma} . $$

Analogous expressions can be derived for deformation states and deformation gradient tensors:

$$ \underline {\overline{\mathbf{Y}}}\left(\mathbf{F}\right)\left\langle \boldsymbol{\xi} \right\rangle =\mathbf{F}\boldsymbol{\xi }, \quad\quad \overline{\mathbf{F}}\left(\underline {\mathbf{Y}}\right)=\left(\int_{{\mathcal{H}}_{\mathbf{x}}}\underline{\omega}\left\langle \boldsymbol{\xi} \right\rangle \underline {\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \boldsymbol{\xi}\ \mathrm{d}{V}_{\boldsymbol{\xi}}\right){\mathrm{K}}^{-1}\quad\quad \forall \mathbf{F},\underline {\mathbf{Y}}. $$

(59)

It is easily confirmed that for any tensor F,

$$ \overline{\mathbf{F}}\left(\underline {\overline{\mathbf{Y}}}\left(\mathbf{F}\right)\right)=\mathbf{F}. $$

The relations (57) and (59) provide a way to adapt a local material model σ(F) to peridynamics by setting

$$ \underline {\mathbf{T}}\left(\underline {\mathbf{Y}}\right)=\underline {\overline{\mathbf{T}}}\Big(\boldsymbol{\sigma} \left(\overline{\mathbf{F}}\left(\underline {\mathbf{Y}}\right)\right) $$

(60)

for any $\underline {\mathbf{Y}}$. A peridynamic material model of the form (60) is called a correspondence model . These models have the properties that they are elastic, isotropic, and objective whenever the underlying local material model σ(F) has these properties, in the sense of the local theory. Correspondence models generally exhibit zero-energy modes of deformation (Tupek and Radovitzky 2014) due to the noninvertibility of $\overline{\mathbf{F}}$, that is,

$$\overline{\mathbf{F}}\left({\underline{\mathbf{Y}}}\right) = \overline{\mathbf{F}}\left({{\underline{\mathbf{Y}}}}^{{\prime}}\right))\Longrightarrow {\underline{\mathbf{Y}}} = {{\underline{\mathbf{Y}}}}^{{\prime}}.$$

Several practical ways of reducing this type of instability in numerical models have been proposed. One such method penalizes the departures of the deformation state from a uniform deformation within the family. In this method, the material model is modified by including an additional term as follows:

$$ \underline {\mathbf{T}}\left(\underline {\mathbf{Y}}\right)=\underline {\overline{\mathbf{T}}}\Big(\boldsymbol{\sigma} \left(\overline{\mathbf{F}}\left(\underline {\mathbf{Y}}\right)\right)+A{\left\Vert \underline {\mathbf{Y}}-\overline{\mathbf{F}}\left(\underline {\mathbf{Y}}\right)\underline {\mathbf{X}}\right\Vert}_{\underline {\mathbf{Y}}} $$

where the subscript denotes the Fréchet derivative and A is a constant (Silling 2017).

For any deformation (not necessarily uniform) of any peridynamic body (not necessarily homogeneous), the peridynamic stress tensor is defined by:

$$ \nu\left(\mathbf{x}\right)=\int_{\mathcal{U}}\int_0^{\infty }\int_0^{\infty }{\left(y+z\right)}^2\left(\underline {\mathbf{T}}\left[\mathbf{x}-z\mathbf{m}\right]\left\langle\left(y+z\right)\mathbf{m}\right\rangle \right)\otimes \mathbf{m}\ \mathrm{d}y\ \mathrm{d}z\ \mathrm{d}{\Omega}_{\mathbf{m}} $$

where $\mathcal{U}$ is the unit sphere and dΩ_m is a differential spherical angle in the direction of the unit vector m. ν has the surprising property (Lehoucq and Silling 2008; Lehoucq and von Lilienfeld 2010; Noll 1955) that

$$ \nabla \cdot \nu =\int_{{\mathcal{H}}_{\mathbf{x}}}\left\{\underline {\mathbf{T}}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -\underline {\mathbf{T}}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \right\}\mathrm{d}{V}_{\mathbf{q}}. $$

This means that the peridynamic equilibrium equation can be written as:

$$ \nabla \cdot \nu+\mathbf{b}=0, $$

which is formally the same as in the local theory.

The partial stress tensor $\overline{\boldsymbol{\sigma}}$ is equal to ν in the special case of a uniform deformation of a homogeneous body. Otherwise, the sense in which it approximates v is discussed in Silling et al. (2015).

Convergence of Peridynamics to the Local Theory

It seems reasonable to require that a proper nonlocal theory should converge, in some sense, to the local theory in the limit of “zero nonlocality.” To investigate how this convergence works in the peridynamic equations, we first consider how material models scale as the horizon decreases.

As the horizon is changed, holding the bulk properties of the material fixed, peridynamic material models satisfy certain scaling relations. Let ${\underline {\mathbf{T}}}_{\delta }$ and ${\underline {\mathbf{Y}}}_{\delta }$ denote the force state and the deformation state, respectively, for any δ > 0. Let δ₁ and δ₂ be two values of the horizon and ${\mathcal{H}}_{1}$ and ${\mathcal{H}}_{2}$ the corresponding families. Suppose a material model ${\underline {\widehat{\mathbf{T}}}}_1$ is given for the horizon δ₁. For any ${\underline {\mathbf{Y}}}_2$ on ${\mathcal{H}}_{2}$, define the state ${\underline {\mathbf{Y}}}_1$ by:

$$ {\underline {\mathbf{Y}}}_1\left\langle {\boldsymbol{\xi}}_1\right\rangle =\frac{\delta_1}{\delta_2}{\underline {\mathbf{Y}}}_2\left\langle \frac{\delta_2}{\delta_1}{\boldsymbol{\xi}}_1\right\rangle \quad \forall {\boldsymbol{\xi}}_1\in {\mathcal{H}}_1. $$

Consider the material model defined by:

$$ {\underline {\widehat{\mathbf{T}}}}_2\left({\underline {\mathbf{Y}}}_2\right)\left\langle{\boldsymbol{\xi}}_{\mathbf{2}}\right\rangle ={\left(\frac{\delta_1}{\delta_2}\right)}^4{\underline {\widehat{\mathbf{T}}}}_1\left({\underline {\mathbf{Y}}}_1\right)\left\langle \frac{\delta_1}{\delta_2}{\boldsymbol{\xi}}_2\right\rangle \quad \forall {\boldsymbol{\xi}}_2\in {\mathcal{H}}_2. $$

(61)

It is easily confirmed that for a uniform deformation of a homogeneous body, $\overline{\boldsymbol{\sigma}}$ defined in Eq. 58 is invariant with respect to this change in horizon:

$$ \overline{\boldsymbol{\sigma}}\left({\underline {\widehat{\mathbf{T}}}}_1\left({\underline {\mathbf{Y}}}_1\right)\right)=\overline{\boldsymbol{\sigma}}\left({\underline {\widehat{\mathbf{T}}}}_2\left({\underline {\mathbf{Y}}}_2\right)\right). $$

In general, it can be shown that if a deformation is twice continuously differentiable, and if ${\underline {\widehat{\mathbf{T}}}}_{\delta }$ scales according to Eq. 61, then the limit:

$$ {\boldsymbol{\sigma}}_0:= \underset{\delta \to 0}{\lim}\overline{\boldsymbol{\sigma}}\left({\underline {\widehat{\mathbf{T}}}}_{\delta}\left({\underline {\mathbf{Y}}}_{\delta}\right)\right) $$

exists and that:

$$ \underset{\delta \to 0}{\lim }\int_{{\mathcal{H}}_{\delta }}\Big\{{\underline {\mathbf{T}}}_{\delta}\left[\mathbf{x}\right]\langle\mathbf{q}-\mathbf{x}\rangle -{\underline {\mathbf{T}}}_{\delta}\left[\mathbf{q}\right]\langle\mathbf{x}-\mathbf{q}\rangle \Big\}\mathrm{d}{V}_{\mathbf{q}}=\nabla \cdot {\boldsymbol{\sigma}}_0. $$

(62)

In summary, we now have a stress tensor field σ₀ such that, in the limit of zero horizon, the peridynamic accelerations equal the accelerations in the local theory computed from the divergence of σ₀; see Silling and Lehoucq (2008) for details. More rigorous results concerning convergence of peridynamics to local elasticity have been established (Emmrich et al. 2007).

Remarkably, Lipton has extended these results to discontinuous deformations; the limiting case of a peridynamic body containing a growing crack approaches a smooth solution in the local theory augmented by a Griffith crack that consumes energy at a definite rate as it grows. This result requires a peridynamic material model with a nonconvex strain-energy density function (Lipton 2014, 2016).

For heat transport, the statement analogous to Eq. 62 is as follows:

$$ \underset{\delta \to 0}{\lim }\int_{{\mathcal{H}}_{\delta }}\left\{{\underline{H}}_{\delta}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -{\underline{H}}_{\delta}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \right\}\mathrm{d}{V}_{\mathbf{q}}=\nabla \cdot {\mathbf{Q}}_0 $$

(63)

where Q₀ is the limiting heat flux vector field given by:

$$ {\mathbf{Q}}_0:= \underset{\delta \to 0}{\lim }{\overline{\mathbf{Q}}}_{\delta },\quad {\overline{\mathbf{Q}}}_{\delta}:= \overline{\mathbf{Q}}\left({\underline{H}}_{\delta}\right)=-\int_{{\mathcal{H}}_{\mathbf{x}}}{\underline{H}}_{\delta}\left\langle \boldsymbol{\xi} \right\rangle \boldsymbol{\xi} \mathrm{d}{V}_{\boldsymbol{\xi}}. $$

(64)

The minus sign appears by convention in the second of Eq. 64 so that the heat flux $\overline{\mathbf{Q}}\cdot \mathbf{n}$ through a plane normal to a unit vector n will be positive if energy is flowing parallel to n, rather than opposite to it. Recall the inequality (23) derived from the second law,

$$ \underline{\beta}\bullet {\underline{H}}_{\delta}\le 0,\quad \underline{\beta}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle =\frac{1}{\theta \left(\mathbf{q}\right)}-\frac{1}{\theta \left(\mathbf{x}\right)}. $$

(65)

For a smooth temperature field, as δ → 0, we can use the first term of a Taylor series to write down the first-order approximation:

$$ \underline{\beta}\left\langle \boldsymbol{\xi} \right\rangle \approx \boldsymbol{\xi} \cdot \nabla \beta \left(\mathbf{x}\right)\quad \forall \boldsymbol{\xi} \in {\mathcal{H}}_{\mathbf{x}}, $$

hence Eq. 65 can be approximated by:

$$ 0\ge \underline{\beta}\bullet {\underline{H}}_{\delta}\approx \int_{{\mathcal{H}}_{\mathbf{x}}}\boldsymbol{\xi} \cdot \left(\nabla \beta \right){\underline{H}}_{\delta}\left\langle \boldsymbol{\xi} \right\rangle =-\nabla \beta \cdot {\overline{\mathbf{Q}}}_{\delta }. $$

(66)

Similarly, for small δ, Eq. 63 is approximated by:

$$ {h}_{\delta}:= \int_{{\mathcal{H}}_{\delta }}\left\{{\underline{H}}_{\delta}\left[\mathbf{x}\right]\left\langle \mathbf{q}-\mathbf{x}\right\rangle -{\underline{H}}_{\delta}\left[\mathbf{q}\right]\left\langle \mathbf{x}-\mathbf{q}\right\rangle \right\}\mathrm{d}{V}_{\mathbf{q}}\approx \int_{{\mathcal{H}}_{\mathbf{x}}}\boldsymbol{\xi} \cdot \nabla {\underline{H}}_{\delta}\left\langle \boldsymbol{\xi} \right\rangle =-\nabla \cdot {\overline{\mathbf{Q}}}_{\delta }. $$

(67)

From Eqs. 20, 66, and 67,

$$ {\displaystyle \begin{aligned}\dot{\eta}&\ge \beta {h}_{\delta }+\beta s\\ {}&\approx -\beta \nabla \cdot {\overline{\mathbf{Q}}}_{\delta }+\beta s\\ {}&\ge -\beta \nabla \cdot {\overline{\mathbf{Q}}}_{\delta }-\nabla \beta \cdot {\overline{\mathbf{Q}}}_{\delta }+\beta s\\ {}&=-\nabla \left(\beta {\overline{\mathbf{Q}}}_{\delta}\right)+\beta s.\end{aligned}} $$

Omitting some of the details of taking the limit, the result for δ → 0 is:

$$ \dot{\eta}\ge \frac{s}{\theta }-\nabla \cdot \left(\frac{{\mathbf{Q}}_0}{\theta}\right). $$

This is a form of the Clausius-Duhem inequality of local continuum thermodynamics. It is interesting that this local form of the second law with heat transport can be derived from the peridynamic version of the second law without specifying any particular form of the constitutive model $\underline {\widehat{H}}\left(\underline{\Theta}\right)$ or assuming a particular physical mechanism for heat transport (conduction, convection, radiation, etc.).

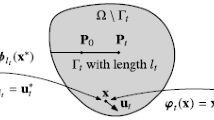
Local Continuum Damage Mechanics

The failure characteristics of engineering materials are frequently expressed in terms of failure surfaces, with or without some specification of postfailure behavior. These expressions can sometimes be converted to peridynamic failure surfaces using the partial stress and approximate deformation gradient defined in Eq. 58 and 59 above. For example, if a failure surface in terms of the stress tensor and deformation gradient tensor is given in the form ${\mathcal{S}}^0\left(\boldsymbol{\sigma}, \mathbf{F},\varphi \right)$, where φ is a scalar damage variable, we can define a peridynamic failure surface by:

$$ \mathcal{S}\left(\underline {\mathbf{T}},\underline {\mathbf{Y}},\underline{\phi}\right)={\mathcal{S}}^0\left(\overline{\boldsymbol{\sigma}}\left(\underline {\mathbf{T}}\right),\overline{\mathbf{F}}\left(\underline {\mathbf{Y}}\right),\overline{\varphi}\left(\underline{\phi}\right)\right),\quad \overline{\varphi}\left(\underline{\phi}\right)=\frac{\underline{\omega}\bullet \underline{\phi}}{\underline{\omega}\bullet \underline{1}}. $$

Evaluating the required Fréchet derivatives in Eq. 54 then leads to:

$$ {\mathcal{S}}_{\underline {\mathbf{T}}}=\frac{\partial {\mathcal{S}}^0}{\partial \boldsymbol{\sigma}}\underline {\mathbf{X}},\quad {\mathcal{S}}_{\underline {\mathbf{Y}}}=\frac{\partial {\mathcal{S}}^0}{\partial \mathbf{F}}\underline{\omega}\left\langle \boldsymbol{\xi} \right\rangle {\mathbf{K}}^{-1}\underline {\mathbf{X}},\quad {\mathcal{S}}_{\underline{\phi}}=\frac{\partial {\mathcal{S}}^0}{\partial \varphi}\frac{\underline{\omega}}{\underline{\omega}\bullet \underline{1}}. $$

The remaining derivatives that appear in Eq. 54 are obtained from the peridynamic material model, as before.

Discussion

Why and how does a crack grow? How does a continuous body become discontinuous? Why does nature seem to favor these discontinuities as energy minimizers, yet equip real materials with energy barriers that resist their formation and growth? How can real materials be designed or optimized to resist cracking? These and other fundamental questions possibly can be studied within the peridynamic theory.

Although peridynamics is often used to model brittle fracture and fragmentation (for example, (Hu et al. 2013)), diverse new applications are continually being discovered. These have recently included, for example:

• Electromigration in integrated circuits (Gerstle et al. 2008; Oterkus et al. 2013)

• Biological cell mechanics and tumor growth (Lejeune and Linder 2017a, b; Taylor et al. 2016)

• Damage in materials due to high voltage breakdown (Wildman and Gazonas 2015)

• Effects of residual thermal stress on fracture in glass (Jeon et al. 2015; Kilic and Madenci 2009)

• Failure of reinforced concrete (Gerstle et al. 2010)

• Mechanics of nanocomposites (Prakash and Seidel 2016)

• Fluid transport and hydraulic fracture in rocks (Katiyar et al. 2014; Nadimi 2015; Ouchi et al. 2015; Van Der Merwe 2014)

• Solitons (Silling 2016)

• Corrosion (Chen and Bobaru 2015) and many others.