Canonical Duality Theory for Solving Non-monotone Variational Inequality Problems

Abstract

This paper presents a canonical dual approach for solving a class of non-monotone variational inequality problems. It shows that by using the canonical dual transformation, these challenging problems can be reformulated as a canonical dual problem, which is equivalent to the primal problems in the sense that they have the same set of KKT points. Existence theorem for global optimal solutions is obtained. Based on the canonical duality theory, this dual problem can be solved via well-developed convex programming methods. Applications are illustrated with several examples.

1 Problems and Motivation

We are interesting in solving the following non-monotone variational inequality problem:

$$\begin{aligned} ({ VI}): \quad&\langle F({\bar{\mathbf{{x}}}}) , \mathbf{{x}}- \bar{\mathbf{{x}}} \rangle \ge 0, \quad \forall \mathbf{{x}}\in {\mathscr {K}}, \end{aligned}$$

(1)

where the notation $\langle * , * \rangle$ denotes for inner product, $F :{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ is a non-monotone operator, defined by

$$\begin{aligned} F (\mathbf{{x}}) = {Q}\mathbf{{x}}- \mathbf{{f}}+ \nabla {W}(\mathbf{{x}}), \end{aligned}$$

(2)

in which ${Q}\in {\mathbb {R}}^{n\times n}$ is a symmetric matrix, $\mathbf{{f}}\in {\mathbb {R}}^n$ is a given vector, and ${W}(\mathbf{{x}}): {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ is a nonconvex differentiable function. The feasible set ${\mathscr {K}}$ in this paper is defined by

$$\begin{aligned} {\mathscr {K}}= \left\{ \mathbf{{x}}\in {\mathbb {R}}^n | \; \phi (\mathbf{{x}}) \le 0 \right\} , \end{aligned}$$

where $\phi (\mathbf{{x}}):\ {\mathbb {R}}^n\rightarrow {\mathbb {R}}^q$ is assumed to be a vector value convex function. In this paper, we assume that $\mathrm {ri}({\mathscr {K}})$ is nonempty, i.e., there exists at least one $\bar{\mathbf{{x}}}$ such that $\phi (\bar{\mathbf{{x}}})<0$.

The first problem involving a variational inequality is the well known Signorini problem, proposed by A. Signorini in 1959 as a frictionless contact problem in linear elastic mechanics and solved by G. Fichera in 1963 (cf. [4]). Mathematical theory of variational inequality was first studied by G. Stampacchia in 1964 [21]. It is known that the Signorini problem is actually equivalent to a variational problem subjected to inequality constraint. By the fact that the total potential energy for linear elasticity is convex, it turns out that extensive mathematical research has been focused mainly on monotone variational inequality problems (see [1, 2, 5, 9, 12, 14, 15, 19]). However, variational problems in large deformation mechanics are usually nonconvex [6, 11, 22]. For example, the total potential energy of the Gao nonlinear beam model [16, 17] is given by

$$\begin{aligned} J(w) = \int \left[ \frac{1}{2}a (w_{,xx})^2 + \frac{1}{2}\left( \frac{1}{2}(w_{,x})^2 - {\lambda }\right) ^2 - w f \right] d x , \end{aligned}$$

(3)

where $a > 0$ is a material constant, f(x) is a given distributive load, and the unknown function w(x) is the deformation of the beam. Clearly, J(w) is nonconvex if the beam is subjected to a compressive load ${\lambda }> 0$. If the beam is supported by an obstacle $\psi (x)$, the associated variational inequality problem was formulated in [7, 8]

$$ \langle \delta J(w) , v - w \rangle \ge 0 \;\; \forall v \in {\mathscr {V}}_a , $$

where ${\mathscr {V}}_a$ is a convex set with the inequality constraint $v(x) \ge \psi (x)$, and $\delta J(w)$ is the Gâteaux derivative of J(w) given by

$$ \delta J(w) = a w_{,xxxx} - \frac{3}{2} (w_{,x})^2 w_{,xx} + {\lambda }w_{,xx} - f $$

which is a non-monotone differential operator. In finite element analysis, if the displacement w(x) is numerically discretized by a finite vector $\mathbf{{x}}\in {\mathbb {R}}^n$, the total potential functional J(w) can be written in a nonconvex function in ${\mathbb {R}}^n$ (see [20])

$$ P(\mathbf{{x}}) = W(\mathbf{{x}}) + \frac{1}{2}\langle \mathbf{{x}}, Q \mathbf{{x}}\rangle - \langle \mathbf{{x}}, \mathbf{{f}}\rangle $$

where ${W}(\mathbf{{x}})$ is the so-called double-well potential

$$\begin{aligned} {W}(\mathbf{{x}}) =\sum _{k=1}^p \frac{1}{2}{\alpha }_k \left( \frac{1}{2}\langle \mathbf{{x}}, {B}_k \mathbf{{x}}\rangle + \langle \mathbf{{x}}, b_k\rangle - d_k \right) ^2, \end{aligned}$$

in which ${\alpha }_k, d_k > 0$ are given constants, $b_k \in {\mathbb {R}}^n$, and ${B}_k \in {\mathbb {R}}^{n\times n}$ is given symmetric matrix for each $k \in \{1, \dots , p\}$. This double-well function appears extensively in computational physics, including Landau-Ginzburg equation in phase transitions [13], von Karmen plate [22], nonlinear Schödinger equation, and much more [10, 11]. Due to the nonconvexity of ${W}(\mathbf{{x}})$, the operator $F (\mathbf{{x}})$ is non-monotone. Traditional direct methods for solving such problems are very difficult.

Duality theory in convex analysis has been well studied in [3]. Application to monotone variational inequality problems was first proposed by Mosco [18]. However, in nonconvex variational problems and non-monotone variational inequalities, these well-developed duality theory and methods usually lead to a so-called duality gap. In order to close this gap, a potentially useful canonical duality theory has been developed in [10].

In this paper, we will demonstrate the application of this method by solving the non-monotone variational inequality problem $({ VI})$. In the next section, the canonical dual of the problem is presented, which is equivalent to the primal problem in the sense that they have the same set of KKT points. The extremality conditions for these KKT points are discussed in Sect. 3. In Sect. 4, we discuss the properties of the dual problem and give a sufficient condition for the existence of solution. Applications are illustrated in Sect. 5. Some conclusions are given in the final section.

2 Optimization Problem and Its Canonical Dual

It is known that the variational inequality problem $({ VI})$ is related to the following optimization problem:

$$\begin{aligned} ({ OP}): \;&\displaystyle \min _{\mathbf{{x}}\in {\mathbb {R}}^n } \,\, \left\{ P(\mathbf{{x}}) = {W}(\mathbf{{x}})+\frac{1}{2} \langle \mathbf{{x}}, {Q}\mathbf{{x}}\rangle - \langle \mathbf{{x}}, \mathbf{{f}}\rangle \right\} \\&s.t. \quad \phi (\mathbf{{x}})\le 0.\nonumber \end{aligned}$$

(4)

By introducing Lagrange multipliers ${\lambda }\in {\mathbb {R}}^q_{+}$ to relax the inequality constraint $\phi (\mathbf{{x}}) \le 0$, the classical Lagrangian associated with this constrained optimization problem is

$$\begin{aligned} {L}(\mathbf{{x}}, {\lambda }) = {P}(\mathbf{{x}}) + {\lambda }^{\top } \phi (\mathbf{{x}}). \end{aligned}$$

Thus, the criticality condition $\nabla _{\mathbf{{x}}} {L}(\mathbf{{x}}, {\lambda }) = 0$ leads to the equilibrium equation

$$\begin{aligned} \nabla {W}(\mathbf{{x}})+Q \mathbf{{x}}- \mathbf{{f}}+ \displaystyle \sum _{s=1}^q\lambda _s \nabla \phi _s(\mathbf{{x}}) =0 . \end{aligned}$$

By the KKT theory, the Lagrange multipliers have to satisfies the following complementarity conditions

$$\begin{aligned} \lambda ^{\top } \phi (\mathbf{{x}})=0, \quad \phi (\mathbf{{x}})\le 0,\quad \lambda \ge 0. \end{aligned}$$

We call the point which satisfies the above two conditions the KKT stationary point of the problem $({ OP})$ and $({ VI})$. Because we have already assumed that $\mathrm {ri}({\mathscr {K}})$ is nonempty, then the basic constraints qualification must hold for the problem $({ VI})$ and $({ OP})$, and the following result is obvious.

Lemma 1.

If $\bar{\mathbf{{x}}}$ solves $({ VI})$, then it is a KKT stationary point of $({ OP})$ or $({ VI})$.

Due to the nonconvexity of the object function ${P}(\mathbf{{x}})$, to solve problem $({ VI})$ is very difficult. For a given ${\lambda }\ge 0$, the Lagrangian dual function can be defined by

$$\begin{aligned} {P}^*({\lambda }) = \inf _{\mathbf{{x}}\in {\mathbb {R}}^n} {L}(\mathbf{{x}}, {\lambda }). \end{aligned}$$

In the case that ${P}(\mathbf{{x}})$ is convex, we have the well-known saddle duality theorem

$$ {P}(\bar{\mathbf{{x}}}) = \inf _\mathbf{{x}}\sup _{{\lambda }\ge 0} {L}(\mathbf{{x}}, {\lambda }) = \sup _{{\lambda }\ge 0} \inf _{\mathbf{{x}}} {L}(\mathbf{{x}}, {\lambda }) = {P}^*(\bar{\lambda }). $$

However, if ${P}(\mathbf{{x}})$ is nonconvex, we have the so-called weak duality

$$ \theta = \inf _\mathbf{{x}}\sup _{{\lambda }\ge 0} {L}(\mathbf{{x}}, {\lambda }) - \sup _{{\lambda }\ge 0} \inf _{\mathbf{{x}}} {L}(\mathbf{{x}}, {\lambda }) \ge 0. $$

Very often, this duality gap $\theta = \infty$.

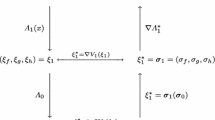
Following the standard procedure of the canonical dual transformation, we assume that there exists a geometrical operator

$$\begin{aligned} {\varvec{\xi }}={\varLambda }(\mathbf{{x}})= \{ {\varvec{\varepsilon }}(\mathbf{{x}}) ,\phi (\mathbf{{x}})\}: {\mathbb {R}}^n \rightarrow {\mathscr {E}}_{a} \subset {\mathbb {R}}^{p} \times {\mathbb {R}}^{q} \end{aligned}$$

and a canonical function $\bar{V} ({\varvec{\xi }}): {\mathscr {E}}_a \rightarrow {\mathbb {R}}\cup \{ \infty \}$ such that the nonconvex optimization problem $({ OP})$ can be written in the canonical form:

$$\begin{aligned} \displaystyle \min _{\mathbf{{x}}} \varPi (\mathbf{{x}})&=\bar{ V }(\varLambda (\mathbf{{x}}))-{U}(\mathbf{{x}}), \end{aligned}$$

(5)

where ${ U}(\mathbf{{x}})=-\frac{1}{2}\langle \mathbf{{x}}, {Q}\mathbf{{x}}\rangle + \langle \mathbf{{x}}, \mathbf{{f}}\rangle$, and $\bar{ { V} } ({\varvec{\xi }})$ is defined by

$$\begin{aligned} \bar{{ V} }({\varvec{\xi }}(\mathbf{{x}}) )={{ V}}({\varvec{\varepsilon }}(\mathbf{{x}}) )+\varPsi (\phi (\mathbf{{x}})), \end{aligned}$$

(6)

in which, ${ V}(\varepsilon (\mathbf{{x}}))={W}(\mathbf{{x}})$ and

$$\begin{aligned} \varPsi (\phi )=\left\{ \begin{array}{ll} 0 &{} \text{ if } \phi \le 0\\ +\infty &{} \text{ otherwise }.\end{array} \right. \end{aligned}$$

We assume that V is convex in this paper, and let $\partial$ denote the sub-gradients set of a convex function such the same as in [3]. Then, we can express the stationary condition for $({ VI})$ or $({ OP})$ as

$$\begin{aligned} 0\in \partial \varPi ( \mathbf{x}). \end{aligned}$$

(7)

For any given ${\varvec{\varsigma }}\in {\mathbb {R}}^{p+q}$, the Fenchel sup-conjugate function $\bar{V}^\sharp$ of the convex function $\bar{V}$ is given as

$$\begin{aligned} \bar{V}^\sharp ({\varvec{\varsigma }})=\displaystyle \sup _{ {\varvec{\xi }}\in {\mathscr {E}}_a}\{ \langle {\varvec{\xi }}, {\varvec{\varsigma }}\rangle - \bar{V}({\varvec{\xi }})\} ={ V}^\sharp ({\varvec{\sigma }}) + \varPsi ^\sharp ({\lambda }) , \end{aligned}$$

where

$$\begin{aligned} \varPsi ^\sharp ({\lambda }) = \sup _{\phi \le 0} \{ \langle \phi , {\lambda }\rangle - \varPsi (\phi ) \} = \left\{ \begin{array}{ll} 0 &{} \text{ if } {\lambda }\ge 0 \\ +\infty &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

We let

$$\begin{aligned} {\mathscr {S}}_a=\mathrm{dom} (\bar{V}^\sharp )=\{{\varvec{\varsigma }}\in {\mathbb {R}}^{p+q} \; | \;\; \bar{V}^\sharp ({\varvec{\varsigma }})<+\infty \}. \end{aligned}$$

By the definition introduced in [10], the pair $({\varvec{\xi }},{\varvec{\varsigma }})$ is called an extended canonical duality pair on ${\mathscr {E}}_a \times {\mathscr {S}}_a$ if the following duality relations hold on ${\mathscr {E}}_a \times {\mathscr {S}}_a$

$$\begin{aligned} {\varvec{\varsigma }}\in \partial \bar{V}({\varvec{\xi }}) \;\; \Leftrightarrow \;\; {\varvec{\xi }}\in \partial \bar{V}^\sharp ({\varvec{\varsigma }})\;\; \Leftrightarrow \;\; \langle {\varvec{\xi }}, {\varvec{\varsigma }}\rangle = \bar{V}({\varvec{\xi }}) + \bar{V}^{\sharp }({\varvec{\varsigma }}) . \end{aligned}$$

(8)

Thus, for this canonical duality pair, ${W}(\mathbf{{x}})+ \varPsi (\phi (\mathbf{{x}}))$ can be replaced by $\bar{V}({\varLambda }(\mathbf{{x}})) = \langle {\varLambda }(\mathbf{{x}}), {\varvec{\varsigma }}\rangle - \bar{V}^\sharp ({\varvec{\varsigma }})$, the so-called total complementary function $\varXi (\mathbf{{x}}, {\varvec{\varsigma }})$ can be defined by

$$\begin{aligned} \varXi (\mathbf{{x}}, {\varvec{\varsigma }}) = \langle {\varLambda }(\mathbf{{x}}), {\varvec{\varsigma }}\rangle - \bar{V}^\sharp ({\varvec{\varsigma }}) - { U}(\mathbf{{x}}). \end{aligned}$$

For a given ${\varvec{\varsigma }}\in {\mathscr {S}}_a$, the canonical dual function can be obtained as

$$\begin{aligned} {P}^d({\varvec{\varsigma }}) = \displaystyle {\mathrm{{sta}}}_{\mathbf{{x}}}\{ \varXi (\mathbf{{x}}, {\varvec{\varsigma }}) : \;\; \mathbf{{x}}\in {\mathbb {R}}^n \} = { U}^{\varLambda }({\varvec{\varsigma }}) - \bar{V}^\sharp ({\varvec{\varsigma }}), \end{aligned}$$

where ${ U}^{\varLambda }({\varvec{\varsigma }})$ is called the ${\varLambda }$-conjugate of U, defined by

$$\begin{aligned} { U}^{\varLambda }({\varvec{\varsigma }}) = \displaystyle {\mathrm{{sta}}}_{\mathbf{{x}}}\{ \langle {\varLambda }(\mathbf{{x}}), {\varvec{\varsigma }}\rangle - { U}(\mathbf{{x}}) \; : \; \mathbf{{x}}\in {\mathbb {R}}^n \}, \end{aligned}$$

and the notation sta$_x \{ ... \}$ stands for solving the stationary point problem given in $\{ ... \}$ with respect to x. Let ${\mathscr {S}}_c$ denotes the feasible space such that ${ U}^{\varLambda }$ is well-defined on ${\mathscr {S}}_c$, then the canonical dual problem $({\mathscr {P}}^d)$ is eventually proposed as the following

$$\begin{aligned} ({\mathscr {P}}^d): \;\; \max \{ {P}^d({\varvec{\varsigma }}) : \;\; {\varvec{\varsigma }}\in {\mathscr {S}}_c \}. \end{aligned}$$

(9)

In many applications, the geometrical operator ${\varLambda }$ is usually a vector-valued quadratic function:

$$ \begin{array}{ll} {\varLambda }(\mathbf{{x}}) &{}= (\varepsilon (\mathbf{{x}}), \phi (\mathbf{{x}}))\\ &{}=\left\{ \frac{1}{2}\langle \mathbf{{x}}, \; \mathbf{{B}}_k \mathbf{{x}}\rangle + \langle \mathbf{{x}}, b_k \rangle -d_k , \ \ \frac{1}{2}\langle \mathbf{{x}},C_s \mathbf{{x}}\rangle + \langle \mathbf{{x}}, c_s \rangle -e_s \right\} , \end{array} $$

where $b_k\in {\mathbb {R}}^n$ and $B_k\in {\mathbb {R}}^{n\times n}$ is a given symmetric matrix for each $k\in \{1,2,\cdots ,p\}$; $c_s\in {\mathbb {R}}^n$ for each $s\in \{1,2,\cdots ,q\}$, $C_s\in {\mathbb {R}}^{n\times n}$ is a given positive definite matrix for each $s\in \{1,2,\cdots ,q\}$; $d\in {\mathbb {R}}^p$ and $e\in {\mathbb {R}}^q$. In this case, the canonical dual function has an explicit form

$$\begin{aligned} {P}^d({\varvec{\varsigma }}) = -\frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }}) , \; {{\varvec{\tau }}}({\varvec{\varsigma }}) \rangle -\langle d,\ {\sigma }\rangle - \langle e,\ {\lambda }\rangle -\bar{V}^\sharp ({\varvec{\varsigma }}), \end{aligned}$$

where ${\varvec{\varsigma }}=({\sigma },{\lambda })$ and

$$\begin{aligned} \mathbf{{G}}({\varvec{\varsigma }}) = {Q}+ \sum _{k=1}^p \mathbf{{B}}_k {\sigma }_k + \sum _{s=1}^q C_s {\lambda }_s , \;\; {{\varvec{\tau }}}({\varvec{\varsigma }}) = \mathbf{{f}}- \sum _{k=1}^p b_k {\sigma }_k - \sum _{s=1}^q c_s {\lambda }_s. \end{aligned}$$

The notation $\mathbf{{G}}^\dagger$ stands for the Moore–Penrose inverse of $\mathbf{{G}}$. We use ${\mathscr {C}}_{ol}\mathbf{{G}}$ to denote the column space of $\mathbf{{G}}$, then the dual feasible space ${\mathscr {S}}_c$ can be defined by

$$\begin{aligned} {\mathscr {S}}_c = \{ {\varvec{\varsigma }}= \{ {\varvec{\sigma }}, {\lambda }) \in {\mathscr {S}}_a | \;\; {{\varvec{\tau }}}({\varvec{\varsigma }}) \in {\mathscr {C}}_{ol} \mathbf{{G}}({\varvec{\varsigma }}) \}. \end{aligned}$$

Now, consider the derivative of ${P}^d$, we first have

$$\begin{aligned} {U}^{\varLambda }({\varvec{\varsigma }}) = -\frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }}) , \; {{\varvec{\tau }}}({\varvec{\varsigma }}) \rangle -\langle d,\ {\sigma }\rangle - \langle e,\ {\lambda }\rangle . \end{aligned}$$

It follows that

$$\begin{aligned} \nabla _{{\sigma }_k} { U}^{\varLambda }= \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }}),{{B}_k} \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})\rangle +\langle b_k,\mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }})\rangle -d_k,\quad k=1,2,\cdots ,p \end{aligned}$$

(10)

and

$$\begin{aligned} \nabla _{{\lambda }_s} { U}^{\varLambda }= \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }}),{C_s} \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})\rangle +\langle c_s,\mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }})\rangle -e_s,\quad s=1,2,\cdots ,q. \end{aligned}$$

(11)

Therefore, the dual problem associated with $({ VI})$ can be given as

$$ (DVI):\ \ \ \ \langle \nabla \bar{{P}}^d({\varvec{\varsigma }}),\ {\varvec{\varsigma }}-\bar{{\varvec{\varsigma }}} \rangle \ge 0,\ \ \forall {\varvec{\varsigma }}\in {\mathbb {R}}^p\times {\mathbb {R}}^q_{+}, $$

where

$$ \bar{{P}}^d({\varvec{\varsigma }}) = \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }}) , \; {{\varvec{\tau }}}({\varvec{\varsigma }}) \rangle +\langle d,\ {\sigma }\rangle + \langle e,\ {\lambda }\rangle +V^\sharp ({\sigma }). $$

The stationary conditions for both $({\mathscr {P}}^d)$ and (DVI) is given as:

$$\begin{aligned} 0\in \partial \bar{{P}}^d({\varvec{\varsigma }}). \end{aligned}$$

(12)

Similar to Lemma 1, we have the following result.

Lemma 2.

If $\bar{{\varvec{\varsigma }}}$ solves (DVI), then it is a stationary point of $({\mathscr {P}}^d)$ or (DVI).

In fact, for any stationary point $\bar{ \mathbf{x}}$ of $({ VI})$, there is a $\bar{{\varvec{\varsigma }}}\in \partial \bar{V}(\bar{{\varvec{\xi }}})$ with $\bar{{\varvec{\xi }}}=\varLambda (\bar{ \mathbf{x}})$ such that

$$\begin{aligned} \mathbf{{G}}({{\varvec{\bar{\varsigma }}}}) \bar{ \mathbf{x}} - {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})=0. \end{aligned}$$

(13)

On the other hand, if we can solve the dual problem (DVI) for $\bar{{\varvec{\varsigma }}}$, then the solution $\bar{ \mathbf{x}}$ to the primal problem $({ VI})$ should be obtained via the above relation (13).

Theorem 1.

If $\bar{{\varvec{\varsigma }}}$ is a solution of (DVI), then $\bar{ \mathbf{x}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})$ is a KKT point of the problem $({ VI})$. Moreover, if $\bar{ \mathbf{x}}$ is a solution of $({ VI})$ with $\mathbf{{G}}(\bar{{\varvec{\varsigma }}})$ is invertible, then $\bar{{\varvec{\varsigma }}}$ is a KKT point of (DVI).

Proof.

First, assume that $\bar{{\varvec{\varsigma }}} \in {\mathbb {R}}^p\times {\mathbb {R}}^q_{+}$ is a solution of (DVI), it is obvious that $\bar{{\varvec{\varsigma }}}\in {\mathscr {S}}_c\cap \text{ dom }(\bar{{ V}}^{\sharp })$ and we have that

$$\begin{aligned} 0\in \partial {{P}}^d(\bar{{\varvec{\varsigma }}})=\nabla { U}^{\varLambda }(\bar{{\varvec{\varsigma }}}) - \partial \bar{V}^\sharp (\bar{{\varvec{\varsigma }}}). \end{aligned}$$

(14)

Let

$$\begin{aligned} {\bar{\mathbf{x}}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}}), \end{aligned}$$

then by (10) and (11), we have

$$\begin{aligned} \nabla { U}^{\varLambda }(\bar{{\varvec{\varsigma }}})=\varLambda (\bar{ \mathbf{x}}). \end{aligned}$$

By (14), we have $\bar{{\varvec{\xi }}}=\varLambda (\bar{ \mathbf{x}})\in \partial \bar{V}^\sharp (\bar{{\varvec{\varsigma }}}).$ which is equivalent to $\bar{{\varvec{\varsigma }}}\in \partial \bar{V}(\bar{{\varvec{\xi }}}).$ It follows that

$$ \begin{array}{ll} \partial \varPi (\bar{\mathbf{{x}}})&{}=\partial _{\xi }\bar{{ V}}(\bar{{\varvec{\xi }}})\nabla \varLambda (\bar{\mathbf{{x}}})+Q\bar{\mathbf{{x}}}- \mathbf{{f}}\\ &{}\ni \bar{{\varvec{\varsigma }}}\nabla \varLambda (\bar{\mathbf{{x}}})+Q\bar{\mathbf{{x}}}- \mathbf{{f}}\\ &{}=\mathbf{{G}}({{\varvec{\bar{\varsigma }}}}) \bar{ \mathbf{x}}-{{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}}) =0. \end{array} $$

This shows that $\bar{ \mathbf{x}}$ is a KKT of $({ VI})$.

Now, we assume that $\bar{ \mathbf{x}}$ is a solution of $({ VI})$ with $\mathbf{{G}}(\bar{{\varvec{\varsigma }}})$ is invertible. By (13), we have ${\bar{\mathbf{x}}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}}).$ Therefore, $\bar{{\varvec{\varsigma }}}$ is a KKT point of (DVI). $\Box$

Remark 1

In fact, for a stationary point $\bar{ \mathbf{x}}$ of $({ VI})$, the associated stationary point $\bar{{\varvec{\varsigma }}}$ may not be unique if the linear independence constraint qualification (LICQ) does not hold at $\bar{ \mathbf{x}}$ for $({ VI})$. This situation is different from the canonical dual for unconstrained optimization problems.

3 Global and Local Extremalities

Because the feasible solution set ${\mathscr {K}}$ is convex and we assume that the basic constraint qualification always holds at any feasible point, then any local minimizer of $({ OP})$ is a solution of $({ VI})$. In fact, we can give some sufficient conditions for a stationary point of $({ OP})$ to be a local minimizer or a global minimizer. In this section, we assume that V is twice differentiable. In order to state the results of this section, we need to give a new notation. For any given $\bar{ \mathbf{x}}\in {{\mathbb {R}}^n}$, let ${\mathscr {B}}(\bar{ \mathbf{x}})$ be a $p\times n$ matrix, whose $k-$th row is given as ${\mathscr {B}}_k(\bar{ \mathbf{x}})=\bar{ \mathbf{x}}^{\top }{B}_k$, $k=1,2,\cdots p$.

Theorem 2.

Suppose that $\bar{{\varvec{\varsigma }}}$ is a solution of (DVI) and $\bar{ \mathbf{x}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})$. If the matrix ${\mathscr {B}}^{\top }(\bar{ \mathbf{x}})\nabla ^2_{{\varepsilon }{\varepsilon }}{ V} ({\bar{{\varepsilon }}}){\mathscr {B}}(\bar{ \mathbf{x}})+\mathbf{{G}}({{\varvec{\bar{\varsigma }}}})$ is positive definite, then $\bar{ \mathbf{x}}$ is a local minimizer of the problem $({ OP})$.

Proof.

Consider the Lagrangian function of the problem $({ OP})$:

$$\begin{aligned} L( \mathbf{x},\lambda )&=W ( \mathbf{x})+\frac{1}{2}{ \mathbf{x}}^{\top } Q \mathbf{x}- \mathbf{{f}}^{\top } \mathbf{x}+{\lambda }^{\top }\phi ( \mathbf{x}), \end{aligned}$$

we know that

$$ \nabla _{ \mathbf{x}}L(\bar{ \mathbf{x}},{\bar{\lambda } }) =\mathbf{{G}}({{\varvec{\bar{\varsigma }}}}) {\bar{\mathbf{x}}} - {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}}) =0. $$

We also have that

$$\begin{aligned} \nabla ^2_{ \mathbf{x} \mathbf{x}}L(\bar{ \mathbf{x}},\bar{{\lambda }})={\mathscr {B}}^{\top }(\bar{ \mathbf{x}})\nabla ^2_{{\varepsilon }{\varepsilon }}{ V} ({\bar{{\varepsilon }}}){\mathscr {B}}(\bar{ \mathbf{x}})+\mathbf{{G}}({{\varvec{\bar{\varsigma }}}}). \end{aligned}$$

By assumption of the theorem, $\nabla ^2_{ \mathbf{x} \mathbf{x}}L(\bar{ \mathbf{x}},\bar{{\lambda }})$ is positive definite. Then, the vector $\bar{\mathbf{{x}}}$ is a local minimizer of the problem $({ OP})$. $\Box$

Corollary 1.

Suppose that $\bar{{\varvec{\varsigma }}}$ is a solution of (DVI) and $\bar{ \mathbf{x}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})$. If $\mathbf{{G}}({{\varvec{\bar{\varsigma }}}})$ is positive definite, then $\bar{\mathbf{{x}}}$ is a local minimizer of the problem $({ OP})$.

Proof.

Because V is convex, we have ${\mathscr {B}}^{\top }(\bar{ \mathbf{x}})\nabla ^2_{{\varepsilon }{\varepsilon }}{ V} ({\bar{{\varepsilon }}}){\mathscr {B}}(\bar{ \mathbf{x}})$ is positive semi-definite for any given $\bar{ \mathbf{x}}$. By the assumption of this proposition, we know that $\mathbf{{G}}({{\varvec{\bar{\varsigma }}}})$ is positive definite, then we must have that $\nabla ^2_{ \mathbf{x} \mathbf{x}}L(\bar{ \mathbf{x}},\bar{{\lambda }})$ is positive definite, hence we can conclude that $\bar{ \mathbf{x}}$ is a local minimizer of $({ OP})$ by Theorem 2. $\Box$

In fact, the above Corollary can be enhanced and we give a sufficient condition for a global minimizer of $({ OP})$.

Theorem 3.

Suppose that $\bar{{\varvec{\varsigma }}}$ is a solution of (DVI) and $\bar{ \mathbf{x}} = \mathbf{{G}}^\dagger ({{\varvec{\bar{\varsigma }}}}) {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})$. If $\mathbf{{G}}({{\varvec{\bar{\varsigma }}}})$ is positive semi-definite, then $\bar{ \mathbf{x}}$ is a global minimizer of the problem $({ OP})$.

Proof.

If $\bar{ \mathbf{x}}$ is a stationary point of $({ OP})$, then we have that

$$\begin{aligned} \mathbf{{G}}({{\varvec{\bar{\varsigma }}}}) {\bar{\mathbf{x}}} - {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})=0. \end{aligned}$$

Now, consider the function $\varLambda ( \mathbf{x})$, we have

$$ {\varepsilon }_k( \mathbf{x})-{\varepsilon }_k(\bar{ \mathbf{x}})= \langle \mathbf{x}-\bar{ \mathbf{x}}, {B}_k\bar{ \mathbf{x}}+b_k+\frac{1}{2}{B}_k( \mathbf{x}-\bar{ \mathbf{x}})\rangle ,\quad k=1,2,\cdots ,p $$

and

$$ \phi _{s}( \mathbf{x})-\phi _{s}(\bar{ \mathbf{x}})= \langle \mathbf{x}-\bar{ \mathbf{x}},\ C_s\bar{ \mathbf{x}}+c_s+\frac{1}{2}C_s( \mathbf{x}-\bar{ \mathbf{x}})\rangle ,\quad s=1,2,\cdots ,q. $$

We also have that

$$ { U}( \mathbf{x})-{ U}(\bar{ \mathbf{x}})= \langle \mathbf{x}-\bar{ \mathbf{x}},\ Q\bar{ \mathbf{x}}- \mathbf{{f}}+\frac{1}{2}Q( \mathbf{x}-\bar{ \mathbf{x}})\rangle . $$

Then, we have

$$\begin{array}{ll} \varPi ( \mathbf{x})-\varPi (\bar{ \mathbf{x}})&{}\ge \quad \displaystyle \langle \bar{{\sigma }},\ {\varepsilon }( \mathbf{x})-{\varepsilon }(\bar{ \mathbf{x}})\rangle + \langle \bar{{\lambda }},\ \phi ( \mathbf{x})-\phi (\bar{ \mathbf{x}})\rangle +{ U}( \mathbf{x})-{ U}(\bar{ \mathbf{x}})\\ &{}= \quad \langle \mathbf{x}-\bar{ \mathbf{x}},\ \mathbf{{G}}({{\varvec{\bar{\varsigma }}}}) {\bar{\mathbf{x}}} - {{\varvec{\tau }}}({{\varvec{\bar{\varsigma }}}})\rangle +\frac{1}{2}\langle \mathbf{x}-\bar{ \mathbf{x}},\ \mathbf{{G}}({{\varvec{\bar{\varsigma }}}})( \mathbf{x}-\bar{ \mathbf{x}})\rangle \\ &{}=\quad \frac{1}{2}\langle \mathbf{x}-\bar{ \mathbf{x}},\ \mathbf{{G}}({{\varvec{\bar{\varsigma }}}})( \mathbf{x}-\bar{ \mathbf{x}})\rangle \\ &{} \ge 0 \end{array}$$

for any $\mathbf{x}\in {\mathbb {R}}^{n}$. Now, we have proved that $\bar{ \mathbf{x}}$ is a global minimizer of $({ OP})$ and the proof of the theorem is finished. $\Box$

4 Existence of the Solution

In order to discuss the existence of solution to the problem, we need the following sets:

$$ {\mathscr {S}}_c^{+}=\{{{\varvec{\bar{\varsigma }}}}\in {\mathbb {R}}^p\times {\mathbb {R}}^q_{+}| \;\; \gamma _{\mathbf{{G}}} ({{\varvec{\bar{\varsigma }}}})>0\}, $$

$$ \bar{\mathscr {S}}_c=\{{{\varvec{\bar{\varsigma }}}}\in {\mathbb {R}}^p\times {\mathbb {R}}^q_{+}| \;\; \gamma _{\mathbf{{G}}} ({{\varvec{\bar{\varsigma }}}})=0\}, $$

where $\gamma _{\mathbf{{G}}} ({{\varvec{\bar{\varsigma }}}})$ is the smallest eigenvalue of the matrix ${\mathbf{{G}}} ({{\varvec{\bar{\varsigma }}}})$ for any given ${{\varvec{\bar{\varsigma }}}}\in {\mathscr {S}}_c$. We also need to define a $n\times (p+q)$ matrix $\bar{\mathscr {E}}(\bar{ \mathbf{x}})$ for any given $\bar{ \mathbf{x}}$ with its $k-$th column is given as $\bar{\mathscr {E}}_k(\bar{ \mathbf{x}})={B}_k \bar{ \mathbf{x}}+b_k$, $k=1,2,\cdots p$ and $(p+s)-$th column as $\bar{\mathscr {E}}_{p+s}(\bar{ \mathbf{x}})=C_s \bar{ \mathbf{x}}+c_s$, $s=1,2,\cdots q$. The notation $\Vert \cdot \Vert$ can be any norm of a vector in this paper. Then we have the following result.

Theorem 4.

The canonical dual function ${P}^d$ is concave in ${\mathscr {S}}_c^{+}$.

Proof.

Because $\bar{{ V}}$ is convex, we need only to prove that ${ U}^{\varLambda }$ is concave in order to show that ${P}^d$ is concave. We have

$$\begin{aligned} \frac{\partial { U} ^{\varLambda }}{\partial {{\sigma }_k}} = \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }}),{{B}_k} \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})\rangle +\langle b_k,\mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }})\rangle -d_k,\quad k=1,2,\cdots ,p \end{aligned}$$

and

$$ \frac{\partial { U} ^{\varLambda }}{\partial {\lambda _s}} = \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }}),{C_s} \mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})\rangle +\langle c_s,\mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }})\rangle -e_s,\quad s=1,2,\cdots ,q. $$

Let $\mathbf{x}=\mathbf{{G}}^\dagger ({\varvec{\varsigma }}) {{\varvec{\tau }}}({\varvec{\varsigma }})$ for any ${\varvec{\varsigma }}\in {\mathscr {S}}_c^{+}$, we have

$$\begin{aligned} \frac{\partial ^2 { U} ^{\varLambda }}{\partial {\varvec{\varsigma }}\partial {\varvec{\varsigma }}} =-\bar{{\mathscr {E}}}^{\top }( \mathbf{x})\mathbf{{G}}^\dagger ({\varvec{\varsigma }})\bar{{\mathscr {E}}}( \mathbf{x}). \end{aligned}$$

Hence, the Hessian matrix ${\partial ^2 { U}^{\varLambda }}/{\partial {\varvec{\varsigma }}\partial {\varvec{\varsigma }}}$ is negative semi-definite and ${ U}^{{\varLambda }}$ is concave, then ${P}^d$ is concave in ${\mathscr {S}}_c^{+}$. $\Box$

We denote ${\mathscr {T}}_{\mathbf{{G}}} ({\varvec{\varsigma }})=\{\xi \in {\mathbb {R}}^n | \;\;\mathbf{{G}}({\varvec{\varsigma }})\xi =\gamma _{\mathbf{{G}}}({\varvec{\varsigma }}) \xi \; \; \forall {\varvec{\varsigma }}\in {\mathscr {S}}_c^{+}\cup \bar{\mathscr {S}}_c^{+}\}$.

Theorem 5.

Assume that $\text{ dom }({V}^{\sharp })$ is closed, $\text{ dom }({V}^{\sharp })\cap {\mathscr {S}}_c^{+}\not =\phi$ and

$$ \lim _{\Vert {\varvec{\varsigma }}\Vert \rightarrow \infty } \frac{{ V}^{\sharp }({\varvec{\varsigma }})}{\Vert {\varvec{\varsigma }}\Vert } =+\infty . $$

If $\langle {{\varvec{\tau }}}({\varvec{\varsigma }}),\xi \rangle \not =0$ for any $\xi \in {\mathscr {T}}_{\mathbf{{G}}} ({\varvec{\varsigma }})$ and any ${\varvec{\varsigma }}\in \bar{\mathscr {S}}_c^{+}$, then there must be a $\bar{{\varvec{\varsigma }}}\in {\mathscr {S}}_c^{+}$ such that $\bar{ \mathbf{x}}=\mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})$ is a global minimizer of the problem $({ OP})$.

Proof.

In order to simply the proof, we assume that $\text{ dom }({V}^{\sharp })={\mathbb {R}}^{p+q}$. For any $\delta >0$, we denote a set

$$ {\varOmega }(\delta )=\left\{ {\varvec{\varsigma }}\in {\mathscr {S}}_c|\quad \Vert {\varvec{\varsigma }}\Vert \le \delta ,\;\;\gamma ({\mathbf{{G}}({\varvec{\varsigma }})})\ge \frac{1}{\delta }\right\} . $$

Let

$$ \varGamma (\delta )=\displaystyle \sup _{{\varvec{\varsigma }}\in {\mathscr {S}}_c^{+}\setminus \varOmega (\delta )}{P}^d ({\varvec{\varsigma }}), $$

for any $\delta >0$. We will show that

$$ \displaystyle \lim _{\delta \rightarrow +\infty }\varGamma (\delta )=-\infty . $$

By contradiction, assume that this conclusion is not true, then there is a sequence $\{{\varvec{\varsigma }}_i\}_{i=1,2,\cdots ,}\subseteq {\mathscr {S}}_c^{+}$ with ${\varvec{\varsigma }}_i\in {\mathscr {S}}_c^{+}\setminus \varOmega (i)$ and ${P}^d({\varvec{\varsigma }}_i)\ge \varGamma (i) -\frac{1}{i}$ for any $i=1,2,\cdots ,$ such that

$$\begin{aligned} \displaystyle \lim _{i \rightarrow +\infty }{P}^d ({\varvec{\varsigma }}_i)=M, \end{aligned}$$

(15)

where $M\in {\mathbb {R}}$. If $\{{\varvec{\varsigma }}_i\}_{i=1,2,\cdots }$ is unbounded, then there is ${\mathscr {K}}_1\subseteq \{1,2,\cdots ,\}$ such that

$$ \lim _{i\rightarrow +\infty ,\ i\in {\mathscr {K}}_1} \Vert {\varvec{\varsigma }}_i\Vert =\infty . $$

Then, we have that

$$ \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}_i) {{\varvec{\tau }}}({\varvec{\varsigma }}_i) , \; {{\varvec{\tau }}}({\varvec{\varsigma }}_i) \rangle \ge 0,\quad \forall i\in {\mathscr {K}}_1 $$

and

$$ \lim _{i\rightarrow +\infty ,\ i\in {\mathscr {K}}_1}\langle d,\ {\sigma }_i\rangle + \langle e,\ {\lambda }_i\rangle +\bar{{ V}}^{\sharp }({\varvec{\varsigma }}_i)=+\infty . $$

It follows that

$$ \displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_1}{P}^d({\varvec{\varsigma }}_i)=-\infty , $$

which contradicts (15).

Now, assume that $\{{\varvec{\varsigma }}_i\}_{i=1,2,\cdots }$ is bounded. Let $\xi _i \in {\mathscr {T}}_{\mathbf{{G}}} ({\varvec{\varsigma }}_i)$ with $\Vert \xi _i\Vert =1$ for $i=1,2,\cdots$. Then there must be a ${\mathscr {K}}_2\subseteq \{1,2,\cdots \}$ such that

$$\begin{array}{ll} &{}\displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_2}\gamma _{\mathbf{{G}}} ({\varvec{\varsigma }}_i)=0\\ &{}\displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_2}{\varvec{\varsigma }}_i=\bar{{\varvec{\varsigma }}}\\ &{}\displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_2}\xi _i =\bar{\xi }. \end{array} $$

Now, we have that

$$ \bar{\xi } \in {\mathscr {T}}_{\mathbf{{G}}} (\bar{{\varvec{\varsigma }}}),\ \bar{{\varvec{\varsigma }}}\in \bar{\mathscr {S}}_c,\ \Vert \bar{\xi }\Vert =1. $$

Let

$$ {{\varvec{\tau }}}_{\xi }({\varvec{\varsigma }}_i)=\langle {{\varvec{\tau }}}({\varvec{\varsigma }}_i),\xi _i\rangle \xi _i, \ {{\varvec{\tau }}}_{\xi }^c({\varvec{\varsigma }}_i)={{\varvec{\tau }}}({\varvec{\varsigma }}_i)-\langle {{\varvec{\tau }}}({\varvec{\varsigma }}_i),\xi _i\rangle \xi _i, $$

for $i=1,2,\cdots .$ Because

$$ \xi _i\in {\mathscr {T}}_{\mathbf{{G}}} ({\varvec{\varsigma }}_i),\quad i=1,2,\cdots , $$

we have

$$ \langle {{\varvec{\tau }}}_{\xi }({\varvec{\varsigma }}_i),\ \mathbf{{G}}({\varvec{\varsigma }}_i) {{\varvec{\tau }}}_{\xi }^c({\varvec{\varsigma }}_i)\rangle =0,\quad i\in {\mathscr {K}}_2. $$

Therefore,

$$ \langle {{\varvec{\tau }}}_{\xi }({\varvec{\varsigma }}_i),\ \mathbf{{G}}^{\dagger }({\varvec{\varsigma }}_i) {{\varvec{\tau }}}_{\xi }^c({\varvec{\varsigma }}_i)\rangle =0,\quad i\in {\mathscr {K}}_2. $$

Now, we have

$$\begin{array}{ll} { U}^{{\varLambda }}({\varvec{\varsigma }}_i) &{}= - \frac{1}{2}\langle \mathbf{{G}}^\dagger ({\varvec{\varsigma }}_i) {{\varvec{\tau }}}({\varvec{\varsigma }}_i) , \; {{\varvec{\tau }}}({\varvec{\varsigma }}_i) \rangle -\langle d,\ {\sigma }_i\rangle - \langle e,\ {\lambda }_i\rangle \\ &{}=-\frac{1}{2} \langle {{\varvec{\tau }}}_{\xi }({\varvec{\varsigma }}_i),\mathbf{{G}}^{\dagger }({\varvec{\varsigma }}_i){{\varvec{\tau }}}_{\xi }({\varvec{\varsigma }}_i)\rangle - \frac{1}{2}\langle {{\varvec{\tau }}}_{\xi }^c({\varvec{\varsigma }}_i),\mathbf{{G}}^{\dagger }({\varvec{\varsigma }}_i){{\varvec{\tau }}}_{\xi }^c({\varvec{\varsigma }}_i)\rangle -\langle d,\ {\sigma }_i\rangle - \langle e,\ {\lambda }_i\rangle \\ &{}\le -\frac{1}{2 \gamma _{\mathbf{{G}}} ( {\varvec{\varsigma }}_i)}\langle {{\varvec{\tau }}}({\varvec{\varsigma }}_i),\xi _i\rangle ^2-\langle d,\ {\sigma }_i\rangle - \langle e,\ {\lambda }_i\rangle , \end{array} $$

for $i\in {\mathscr {K}}_2$. Then, we have

$$ \displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_2}{ U}^{{\varLambda }}({\varvec{\varsigma }}_i)=-\infty . $$

Therefore,

$$ \displaystyle \lim _{i \rightarrow +\infty ,\ i\in {\mathscr {K}}_2}{{P}}^d({\varvec{\varsigma }}_i)=-\infty , $$

which contradicts (15). Now, we have proved that

$$ \displaystyle \lim _{\delta \rightarrow +\infty }\varGamma (\delta )=-\infty . $$

Choose a $\bar{{\varvec{\varsigma }}}\in {\mathscr {S}}_c^{+}$, there must be a $\bar{\delta }>0$ such that

$$ \varGamma (\bar{\delta })\le {P}^d(\bar{{\varvec{\varsigma }}}). $$

Because $\varOmega (\bar{\delta })$ is compact, then there is a $\tilde{{\varvec{\varsigma }}}\in \varOmega (\bar{\delta })$ such that

$$ {P}^d(\tilde{{\varvec{\varsigma }}})=\max _{{\varvec{\varsigma }}\in \varOmega (\bar{\delta })}{P}^d({\varvec{\varsigma }}). $$

It follows that

$$ {P}^d(\tilde{{\varvec{\varsigma }}})=\max _{{\varvec{\varsigma }}\in {\mathscr {S}}_c^{+}}{P}^d({\varvec{\varsigma }}). $$

Then, $\tilde{{\varvec{\varsigma }}}$ is stationary point of (DVI) with $\mathbf{{G}}(\tilde{{\varvec{\varsigma }}})$ is positive definite. By Theorem 3, $\bar{ \mathbf{x}}=\mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})$ is a global minimizer of the problem $({ OP})$. $\Box$

In fact, the condition $\displaystyle \lim _{{\varvec{\varsigma }}\rightarrow \infty }{ V}^{\sharp }({\varvec{\varsigma }})/\Vert {\varvec{\varsigma }}\Vert =+\infty$ can be weaken in some cases.

Theorem 6.

In case $b_k=0$, $k=1,2,\cdots , p$ and $c_s=0$, $s=1,2,\cdots , q$, assume that $\text{ dom }({V}^{\sharp })$ is closed, $\text{ dom }({V}^{\sharp })\cap {\mathscr {S}}_c^{+}\not =\phi$ and $\displaystyle \lim _{\Vert {\varvec{\varsigma }}\Vert \rightarrow \infty }{ V}^{\sharp }({\varvec{\varsigma }})=+\infty$. If $\langle {{\varvec{\tau }}}({\varvec{\varsigma }}),\xi \rangle \not =0$ for any $\xi \in {\mathscr {T}}_{\mathbf{{G}}} ({\varvec{\varsigma }})$ and any ${\varvec{\varsigma }}\in \bar{\mathscr {S}}_c^{+}$, then there must be a vector $\bar{{\varvec{\varsigma }}}\in {\mathscr {S}}_c^{+}$ such that $\bar{ \mathbf{x}}=\mathbf{{G}}^\dagger ({\varvec{\varsigma }}){{\varvec{\tau }}}({\varvec{\varsigma }})$ is a global minimizer of the problem $({ OP})$.

Proof.

It is similar with the Theorem 5. $\Box$

5 Some Examples

We now present some examples to show how to apply the canonical dual theory for solving real problems. Consider the problem $({ VI})$ with

$$ F(\mathbf{{x}})=(\frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)-\mu )\left( \begin{array}{l} \mathbf{{x}}_1\\ \mathbf{{x}}_2\end{array}\right) + \left( \begin{array}{l} 2\mathbf{{x}}_1+\mathbf{{x}}_2\\ \mathbf{{x}}_1+2\mathbf{{x}}_2\end{array}\right) -\left( \begin{array}{l} 2\\ 2\end{array}\right) $$

and

$$ {\mathscr {K}}=\left\{ \mathbf{{x}}|\frac{1}{2} (\mathbf{{x}}_1^2+\mathbf{{x}}^2_2)\le e\right\} . $$

The primal optimization problem $({ OP})$ of $({ VI})$ is given as follows:

$$\begin{array}{ll} \displaystyle \min _\mathbf{{x}}P(\mathbf{{x}})&{}=\frac{1}{2}(\frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)-\mu )^2+ (\mathbf{{x}}_1^2+\mathbf{{x}}_2\mathbf{{x}}_2+\mathbf{{x}}_2^2)-(2\mathbf{{x}}_1+2\mathbf{{x}}_2)\\ s.t. &{} \frac{1}{2} (\mathbf{{x}}_1^2+\mathbf{{x}}^2_2)\le e. \end{array}$$

For the dual problem, we have that

$$\begin{array}{ll} \mathbf{{G}}^\dagger ({\varvec{\varsigma }})&{}=\frac{1}{2}\left( \begin{array}{cc} 1, &{} 1\\ 1, &{} -1\end{array}\right) \left( \begin{array}{cc }\frac{1}{3+({\sigma }+{\lambda })},&{} 0\\ 0,&{}\frac{1}{1+({\sigma }+{\lambda })}\end{array}\right) \left( \begin{array}{cc} 1, &{} 1\\ 1, &{} -1\end{array}\right) . \end{array}$$

It follows that

$$\begin{array}{ll} \nabla { U}^{{\varLambda }}({\varvec{\varsigma }}) &{}=\frac{1}{2}(2,2) \left( \begin{array}{cc}1, &{} 1\\ 1, &{} -1\end{array}\right) \left( \begin{array}{cc}\frac{1}{(3+({\sigma }+{\lambda }))^2},&{} 0\\ 0,&{}\frac{1}{(1+({\sigma }+{\lambda }))^2}\end{array}\right) \left( \begin{array}{cc}1, &{} 1\\ 1, &{} -1\end{array}\right) \left( \begin{array}{l}2\\ 2\end{array}\right) \\ &{}=\frac{8}{(3+({\sigma }+{\lambda }))^2}-\left( \begin{array}{cc}\mu \\ e\end{array}\right) . \end{array}$$

Then the critical condition of the dual problem becomes

$$\begin{array}{ll} \frac{4}{(3+({\sigma }+{\lambda }))^2}-{\sigma }&{}=\mu \\ \frac{4}{(3+({\sigma }+{\lambda }))^2}-e&{}\in \partial \varPsi ^{\sharp } ({\lambda }). \end{array}$$

We consider three cases with various values of $\mu$ and e.

Example 1

First, we let $\mu =2$ and $e=2$, then we can find that $\bar{ \mathbf{x}}=(1,1)$ is a stationary point of the problem. At this point, we have $\bar{\xi }=(-1,-1)$ and $\bar{{\varvec{\varsigma }}}=(-1,0)$. Note that

$$ \mathbf{{G}}(\bar{{\varvec{\varsigma }}})=\left( \begin{array}{l}1,\quad 1\\ 1,\quad 1\end{array}\right) $$

is singular, by Theorem 3.2, we can conclude that (1, 1) is a solution of $({ VI})$ because $\mathbf{{G}}(\bar{{\varvec{\varsigma }}})$ is semi-positive. This result can also be verified graphically in Fig. 1.

Fig. 1

Contours and graph of $P(\mathbf{x})$ in Example 1

Example 2.

We now let $\mu =2$ and $e=1/2$. In this case we have

$$\begin{array}{ll} \nabla P (\mathbf{{x}})&{}=( \frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)-2)\left( \begin{array}{l} \mathbf{{x}}_1\\ \mathbf{{x}}_2\end{array}\right) + \left( \begin{array}{l} 2\mathbf{{x}}_1+\mathbf{{x}}_2\\ \mathbf{{x}}_1+2\mathbf{{x}}_2\end{array}\right) -\left( \begin{array}{l} 2\\ 2\end{array}\right) \\ &{}=\left( \begin{array}{l} \frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)\mathbf{{x}}_1+\mathbf{{x}}_2-2\\ \frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)\mathbf{{x}}_2+\mathbf{{x}}_1-2\end{array}\right) \\ &{}\le \left( \begin{array}{l} |\mathbf{{x}}_1|+|\mathbf{{x}}_2|-2\\ |\mathbf{{x}}_2|+|\mathbf{{x}}_1|-2\end{array}\right) \\ &{}<\left( \begin{array}{l} 0\\ 0\end{array}\right) , \end{array}$$

for any $\mathbf{{x}}$ with $\frac{1}{2}(\mathbf{{x}}_1^2+\mathbf{{x}}_2^2)\le \frac{1}{2}$, and the stationary point of the problem is $\bar{\mathbf{{x}}}=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ with $\bar{{\varvec{\varsigma }}}=(-\frac{3}{2},2\sqrt{2}-\frac{3}{2})$, which satisfies the following critical condition of the dual problem

$$\begin{aligned} \frac{4}{(3+({{\sigma }}+{{\lambda }}))^2}-{{\sigma }}-2=0\\ \frac{4}{(3+({{\sigma }}+{{\lambda }}))^2}-\frac{1}{2}=0. \end{aligned}$$

By the fact that

$$ \mathbf{{G}}(\bar{{\varvec{\varsigma }}})=\left( \begin{array}{cc}2\sqrt{2}-1,&{}1 \\ 1,&{}2\sqrt{2}-1\end{array}\right) $$

is positive definite, we know that $\mathbf{x} = (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ is a solution of $({ VI})$ (Fig. 2).

Fig. 2

Contours and graph for Example 2

Example 3.

Finally, we let $\mu =4/9$ and $e=2$. In this case, the critical condition of the dual problem becomes

$$\begin{aligned} \frac{4}{(3+({\sigma }+{\lambda }))^2}-{\sigma }=\frac{4}{9}\\ \frac{4}{(3+({\sigma }+{\lambda }))^2}-2\in \partial \varPsi ^{\sharp }({\lambda }). \end{aligned}$$

It is easily find that ${{\varvec{\bar{\varsigma }}}}= (0,0)$ is a solution of the dual problem with $\bar{\mathbf{x}} = (\frac{2}{3},\frac{2}{3})$ a stationary point of the primal problem. Since

$$ \mathbf{{G}}(\bar{{\varvec{\varsigma }}})=\left( \begin{array}{cc}2,&{}1 \\ 1,&{}2\end{array}\right) $$

is positive definite, this solution $\bar{\mathbf{x}} =(\frac{2}{3},\frac{2}{3})$ is a solution of the primal problem (Fig. 3).

Fig. 3

Contours and graph of Example 3

6 Conclusions

In this paper, we have proposed the canonical duality theory for solving a class of non-monotone variational inequalities problems. A sufficient condition for a global minimizer of the associated optimization problem $({ OP})$ is presented. By the fact that the canonical dual problem is equivalent to a convex minimization problem on a convex dual feasible set ${\mathscr {S}}^+_c$ with only simple non-negative constraints, which can be solved easily via well-developed methods. Existence of the solution of $({ VI})$ is also discussed. Examples given in the paper show the various cases that the solution may either exist on the boundary of the feasible space, or a point where $\mathbf{{G}}({{\varvec{\bar{\varsigma }}}})$ is singular. These facts can help us to understand the difficulties of the primal problem and to develop some effective methods for solving the canonical dual problem in the future.