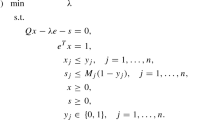1 Introduction

In recent years, nonconvex quadratic minimization problems with quadratic constraints have attracted more and more attentions. The problems are arising from applications in diverse fields such as computational science, machine learning, data mining, pattern recognition, computational mechanics, and so on.

In 2012, Feng, Lin, Sheu, and Xia [7] had studied the (nonconvex) quadratic minimization problem with one quadratic constraint(QP1QC). They showed that under given assumption, the nonconvex (QP1QC) problem could be solved through a dual approach with no duality gap. In 2014, Fabian and Gabriel [6] had considered quadratic minimization problems with finitely many linear equality and a single (nonconvex) quadratic inequality constraints. They characterized the strong duality, necessary and sufficient optimality conditions with or without the Slater assumption geometrically.

In 2013, Tuy and Tuan [28] had studied new strong duality conditions for multiple constrained quadratic optimization based on the topological minimax theorem. Their results showed that many quadratic programs to be solved by solving one or just a few semidefinite programs. In the last work of Tuy and Hoai-Phuong [27], they had proposed novel approach to get more appropriate approximate optimal solutions of the problems. In 2007, Jeyakumar et al. [21] had studied necessary global optimality conditions for special classes of quadratic optimization problems such as weighted least squares with ellipsoidal constraints, quadratic minimization with binary constraints, and so on.

In 2013, Misener and Floudas [23] had introduced the global mixed-integer quadratic optimizer(GloMIQO). The problems can be considered as the special cases of \(\mathscr {P}_{qq}\). They proposed a novel algorithm to solve the problems based on branch-and-bound method. In 2013, Peter et al. [22] had studied the spatial branch-and-bound method [26]. They proposed a novel method to perturb infeasible iterates along Mangasarian–Fromovitz directions to feasible points. Their numerical results showed that their proposed algorithm could perform well even for optimization problems where the standard branch-and-bound method did not converge to the correct optimal value.

In 2012, Yuan, Fang, and Gao [33] had considered a class of quadrinomial minimization problems with one quadratic constraint. In that work, the objective function is fourth order polynomial. Before this work, the canonical duality was employed to solve the altering support vector machine [32] and the corresponding problems with linear inequality constraints had been studied [31].

The nonconvex quadratic minimization problems with quadratic constraints can be formulated as follows (\((\mathscr {P}_{qq})\) in short)

$$\begin{aligned} (\mathscr {P}_{qq}): \;\; \min \left\{ P(x)=\frac{1}{2}{x}^{T}{A x}-{ f}^{T}{ x} \; : \;\; x \in \mathscr {X}_a \right\} , \end{aligned}$$
(1)

where \({ A} ={ A}^{T}\in {\mathbb R}^{n \times n}\) is an indefinite matrix, the feasible space \(\mathscr {X}_a\) is defined by

$$\begin{aligned} \mathscr {X}_a\triangleq \left\{ x\in {\mathbb R}^n | \; \frac{1}{2} x^{T} Q_{i} x+b_{i}^{T}x\leqslant c_{i},i=1,2,\cdots ,m\right\} , \end{aligned}$$
(2)

in which, \({ Q_{i}}^{T} ={ Q_{i}}\in {\mathbb R}^{n \times n}\;\;(i=1,2,\cdots , m)\) are given nonsingular matrices, \(b_{i}\in {\mathbb R}^n,(i=1,2,\cdots , m)\) are given vectors which control the geometric centers. \(c_{i}(i=1,2,\cdots , m)\in {\mathbb R}\) are given input constants.

In order to make sure that the feasible space \(\mathscr {X}_a \) is nonempty, the quadratic constraints must satisfy the Slater regularity condition, i.e., there exists one point \(x_0\) such that \({\frac{1}{2} x_0^{T} Q_{i} x_0}+b_{i}^{T}x_0\leqslant {c_{i}},i=1,2,\cdots ,m\).

In this work, one hard restriction is given that \(f \ne 0 \in {\mathbb R}^n\). The restriction is very important to guarantee the uniqueness of global optimization solution of \((\mathscr {P}_{qq})\). In physics, \(P(x)=\frac{1}{2}{x}^{T}{A x}-{ f}^{T}{ x}\) means energy function. The first part \(\frac{1}{2}{x}^{T}{A x}\) means kinetic energy or elastic energy or other one. The second part \({ f}^{T}{ x}\) means work under an input force f. If force \(f=0\)(object is on the stable state), the problems may have infinite global optimization solutions. For example, we consider the following problem

$$ \begin{array}{cl} {{\min \limits _{(x,y)\in \mathbb R^2}}}&{}\left\{ P(x,y)=-x^2-y^2\right\} \\ {s.t. }&{}{x^2}+y^2\le 4. \end{array} $$

This problem has infinite solutions (x, y) in \(\mathbb R^2\) and \({x^2}+y^2=4\). In another word, the boundary points of feasible space are the global optimization solutions. If force \(f=(2,2)^{T}\), the problem is formulated as follows

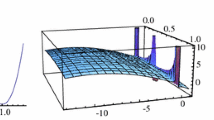
$$ \begin{array}{cl} {{\min \limits _{(x,y)\in \mathbb R^2}}}&{}\left\{ P(x,y)=-x^2-y^2-2x-2y\right\} \\ {s.t. }&{}{x^2}+y^2\le 4. \end{array} $$

This problem has unique global optimization solution \((x^*,y^*)=(\sqrt{2},\sqrt{2})\) (Fig. 1).

Fig. 1
figure 1

Flowchart to show the difference between \(f=0\) and \(f\ne 0\). The color surface is the figure of the objective function on the feasible space (the disk). The left one is \(f=0\) and it shows that the problem has infinite global optimization solutions on the feasible space’s boundary. The right one is \(f=(2,2)^{T}\) and it shows that the problem has unique global optimization solution on the point \((\sqrt{2},\sqrt{2})\)

Full size image

It is known that linear mixed 0–1, fractional, polynomial, bilevel, generalized linear complementarity problems, can be reformulated as special cases of \((\mathscr {P}_{qq})\). Such problems have attracted the attention of many researchers in recent years. The problem of minimizing nonconvex quadratic function with one convex quadratic constraint arises from applying the trust region method in solving unconstrained optimization. It was first proposed by Celis, Dennis, and Tapia (see in [2] and developed by Powell and Yuan in 1990 and 1991(see in [25, 30]. The subproblem of trust region method is described as follows

(3)

In which, \(\delta \) is the objective vector(after solving the model (3), we can construct the next iteration points with (\(x^{(k+1)}\) \(=x^{(k)}+\delta \))), \(g^{(k)}=\nabla f(x^{(k)})\) is the gradient vector, \(B^{(k)}\) is the Hessian matrix or approximate matrix of Hessian and \(\rho _{k}\) is the trust region parameter. If the objective function is nonconvex, this problem is NP-hard [24].

With two (general) convex quadratic constraints, recently, the problem is termed as the extended trust region subproblem(see in [2, 25, 29, 30]. In general, it is proved to be NP-hard (see in [1, 24]. Actually, the extended trust region subproblem is a special case of our presented problem \((\mathscr {P}_{qq})\). It can be formulated as follows [29]

$$\begin{aligned} {({\mathscr {STTR}}):}\begin{array}{cl} {\min \limits _{x\in {\mathbb R}^n}} &{}{\{ P({ x})=\frac{1}{2}{ x}^{T}{ A x}-{ f}^{T}{ x}\}}\\ {s.t.}&{} {\frac{1}{2} x^{T} Q_{1} x}+b_{1}^{T}x\leqslant { c_{1}},\\ {}&{} {{\frac{1}{2} x^{T} Q_{2} x}+b_{2}^{T}x\leqslant { c_{2}}.}\end{array} \end{aligned}$$
(4)

Motivated by the difficulty of solving these problems, we are looking for some good and powerful method to check out the global optimization solution. There is a very powerful method proposed by Gao David (see in [12, 18]) and it is called as canonical duality. The idea is from Legendre duality(presented and explored by Ekeland (readers can refer to [3,4,5]). It is proved that it has some advantages in global optimization and nonlinear mechanics (see in [8,9,10,11,12,13,14,15,16,17,18,19,20]). In this work, we employ it to deal with a special class of \(\mathscr {P}_{qq}\) and use it to convert \(\mathscr {P}_{qq}\) into a concave maximization dual problem over a convex set .

The paper is organized as follows. In Sect. 2, one novel definition is introduced and stated as complementary positive definite matrix group. The basic procedure is presented to convert \(\mathscr {P}_{qq}\) into a concave maximization dual problem. Two theorems are presented to support us to find out the global optimization solution. Main result in Theorem 1 is the equation between optimization solution of \(\mathscr {P}_{qq}\) and canonical duality problem. Main result in Theorem 2 is to give conditions to make sure that the canonical duality problem has a unique optimization solution. In Sect. 3, we present the basic framework of the proposed algorithm. In Sect. 4, several examples are illustrated to show the correctness of given conditions and effectiveness of presented theorems. Finally, we make a conclusion.

2 Canonical Duality Problem

2.1 Complementary Positive Definite Matrix

In order to study the existence of the problem \(\mathscr {P}_{qq}\), we introduce a definition.

Definition 1 For a given matrix \(A\in \mathbb R^{n\times n}\), \(\mathscr {G}_{+}(A)\subset \mathbb R^{n\times n}\) is called as complementary positive definite matrix group of A, if for any \( B \in \mathscr {G}_{+}(A)\), \(A+B\) is positive definite. Mathematically,

$$\begin{aligned} \mathscr {G}_{+}(A)\triangleq \left\{ B\in \mathbb R^{n\times n}|A+B\succ 0\right\} . \end{aligned}$$
(5)

Especially, if \(A+B=I\), B is called identity complementary matrix of A, where I is the identity matrix of order n by n.

With the same idea, a new definition on complementary negative definite matrix group can be given.

2.2 Canonical Duality Problem of \(\mathscr {P}_{qq}\)

Following the standard procedure and ideas proposed by David Gao [15,16,17,18], we construct the geometrical mapping as follows

$$\begin{aligned} \varvec{\varepsilon }(x) =\{ \varepsilon _{i}(x) \} = \left\{ \frac{1}{2} {x^{T}Q_{i} x}+b_{i}^{T}x-c_{i} ,i=1,2,\cdots ,m \right\} :{\mathbb R}^n \rightarrow \mathbb R^m. \end{aligned}$$
(6)

The indicator is defined by

$$ \mathscr {I}(\varvec{\varepsilon })=\left\{ {\begin{array}{ll} {0,} &{} {\hbox {if} ~ \varvec{\varepsilon }\le 0\in \mathbb R^m},\\ {+\infty ,} &{} {\hbox {otherwise}}. \end{array}}\right. $$

With the indicator, the quadratic constraints in \((\mathscr {P}_{qq})\) can be relaxed and \((\mathscr {P}_{qq})\) takes the unconstrained form as following

$$\begin{aligned} ({\mathscr {P}}): \;\; \min \left\{ P({ x})=\mathscr {I}(\varvec{\varepsilon }(x))+\frac{1}{2}{ x}^{T}{ A x}-{ f}^{T}{ x} \; : \;\; x \in \mathbb R^n \right\} . \end{aligned}$$
(7)

Because \(\mathscr {I}(\varvec{\varepsilon })\) is convex and lower semi-continuous on \(\mathbb R^m\), their canonical dual variable \(\varvec{\sigma }\) satisfies the following duality relation

$$\begin{aligned} \varvec{\sigma }\in \partial ^{-}\mathscr {I}(\varvec{\varepsilon })\Leftrightarrow \varvec{\varepsilon }\in \partial ^{-}\mathscr {I}^{*}(\varvec{\sigma })\Leftrightarrow \mathscr {I}(\varvec{\varepsilon })+\mathscr {I}^{*}(\varvec{\sigma })=\varvec{\varepsilon }^T\varvec{\sigma }, \end{aligned}$$
(8)

where \(\partial ^-\) is called the sub-differential of \(\mathscr {I}\) in convex analysis. \(\mathscr {I}^{*}(\varvec{\sigma })\) is Fenchel sup-conjugate of \(\mathscr {I}\) by

$$\begin{aligned} \mathscr {I}^{*}(\varvec{\sigma }) =\sup _{\varvec{\varepsilon }\in \mathbb R^m} \{\varvec{\varepsilon }^T\varvec{\sigma }- \mathscr {I}(\varvec{\varepsilon })\}=\left\{ {\begin{array}{ll} {0,} &{} {if ~ \varvec{\sigma }\geqslant 0},\\ {+\infty ,} &{} {otherwise}. \end{array}}\right. \end{aligned}$$
(9)

The canonical dual function of P(x) is defined by the following equation (referred to [8])

$$\begin{aligned} P^d(\varvec{\sigma })=Q^{{\varLambda }}(\varvec{\sigma })- \mathscr {I}^{*}(\varvec{\sigma }), \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{array}{ll} {Q^{{\varLambda }}(\varvec{\sigma })}&{}{={sta} \; \left\{ \varvec{\varepsilon }^T\varvec{\sigma }+ \frac{1}{2}{ x}^{T}{ A x}-{ f}^{T}{ x}\right\} } \\ {}&{}{=-{\frac{1}{2}}F(\varvec{\sigma })^T G(\varvec{\sigma })^{-1}F(\varvec{\sigma })-c^{T}\varvec{\sigma }}, \end{array} \end{aligned}$$
(11)

in which the notation \(sta \{*: x\in \mathbb R^n \}\) is the operator to find out the stationary point in the space \( \mathbb R^n\), \(G(\varvec{\sigma })\), \(F(\varvec{\sigma })\) and c are defined by

$$\begin{aligned} G(\varvec{\sigma })=(A+\sum \limits _{i=1}^{m}Q_{i}{\sigma }_{i}), ~~{F(\varvec{\sigma })}=(f-\sum \limits _{i=1}^{m}b_{i} {\sigma }_{i}),~~ c=(c_1,c_2,\cdots ,c_m)^{T},\quad \end{aligned}$$
(12)

where \({\sigma }_{i}\) is the i-th element of \(\varvec{\sigma }\).

The dual feasible space is defined by

$$\begin{aligned} \mathscr {S}\triangleq \left\{ \varvec{\sigma }\in \mathbb R^m|\varvec{\sigma }\geqslant 0\in \mathbb R^m,~~\det (G(\varvec{\sigma })) \ne 0 \right\} . \end{aligned}$$
(13)

The canonical dual problem (\(\mathscr {P}^{d}\) in short) associated with \((\mathscr {P}_{qq})\) can be eventually formulated as follows

$$\begin{aligned} (\mathscr {P}^{d}): \max \limits _{\varvec{\sigma }\in \mathscr {S}} \left\{ P^d(\varvec{\sigma })\right\} . \end{aligned}$$
(14)

2.3 Two Important Theorems

In order to show that there is no duality gap, the following theorem is presented.

Theorem 1

If \(A, Q_{i}, b_{i}, f_{i}, c_{i},\) \(i=1,2,\cdots ,m,\) are given with definitions in \((\mathscr {P}_{qq})\) such that the dual feasible space

$$\begin{aligned} \mathscr {Y}\triangleq \left\{ \varvec{\sigma }\in \mathscr {S}~|~ {G(\varvec{\sigma })}^{-1}{F(\varvec{\sigma })}\in \mathscr {X} \right\} \end{aligned}$$
(15)

is not empty, the problem

$$\begin{aligned} (\mathscr {P}^{d}): \max \limits _{\varvec{\sigma }\in \mathscr {Y}}\left\{ P^d(\varvec{\sigma })\right\} , \end{aligned}$$
(16)

is canonically (perfectly) dual to \((\mathscr {P}_{qq})\). In another words, if \(\bar{\varvec{\sigma }}\) is a solution of the dual problem \((\mathscr {P}^d)\),

$$\begin{aligned} \bar{x} =G(\bar{\varvec{\sigma }})^{-1}F(\bar{\varvec{\sigma }}) \end{aligned}$$
(17)

is a solution of \((\mathscr {P}_{qq})\) and

$$\begin{aligned} P({\bar{x}}) = P^d (\bar{\varvec{\sigma }}) . \end{aligned}$$
(18)

Proof.

If \(\bar{\varvec{\sigma }}\) is a solution of the dual problem \((\mathscr {P}^d)\) such that (17) holds, it must satisfy the KKT conditions . Then, according to the complementarity conditions, we have

$$\begin{aligned} \begin{array}{l}{\bar{\varvec{\sigma }}\perp \nabla P^d(\bar{\varvec{\sigma }})~~~ \hbox {and} ~~~P^d(\bar{\varvec{\sigma }})=0.}\end{array} \end{aligned}$$
(19)

Let us pay attention to the (13) and \(\bar{x}\) must satisfy the constraints, we have

$$\begin{aligned} \begin{array}{l}{ \frac{1}{2} \bar{x}^{T} Q_{i} \bar{x}+b_{i}^{T}\bar{x}}-{c_{i}}\leqslant 0,\\ \bar{{\sigma }}_{i} \perp { \frac{1}{2} \bar{x}^{T} Q_{i} \bar{x}+b_{i}^{T}\bar{x}}-{c_{i}},\\ \bar{{\sigma }}_{i} \geqslant 0, i=1,2, \cdots , m. \end{array} \end{aligned}$$
(20)

This result shows that \(\bar{x} =G(\bar{\varvec{\sigma }})^{-1}F(\bar{\varvec{\sigma }})\) is a KKT point of \((\mathscr {P}_{qq})\).

Next, we show the equivalence between the primal problem and canonical duality one. According to complementarity conditions (20), we have

$$\begin{aligned} {c_{i}}\bar{{\sigma }}_{i}= \frac{1}{2} { \bar{x}}^{T}Q_{i}\bar{{\sigma }}_{i}{ \bar{x}+b_{i}^{T}\bar{{\sigma }}_{i}\bar{x}}, i=1,2, \cdots , m. \end{aligned}$$
(21)

Thus, in terms of \(\bar{x} =G(\bar{\varvec{\sigma }})^{-1}F(\bar{\varvec{\sigma }})=({ A}+\sum \limits _{i=1}^{m}Q_{i}\bar{{\sigma }}_{i})^{-1}(f-\sum \limits _{i=1}^{m}b_{i} \bar{{\sigma }}_{i})\), we have

$$\begin{aligned} \sum \limits _{i=1}^{m}Q_{i}\bar{{\sigma }}_{i}\bar{x}+\sum \limits _{i=1}^{m}b_{i} \bar{{\sigma }}_{i}=f-{ A}\bar{x}, \end{aligned}$$
(22)

then

$$\begin{array}{ll} {P^d(\bar{\varvec{\sigma }})}&{} {=-\frac{1}{2}F(\bar{\varvec{\sigma }})^{T}G(\bar{\varvec{\sigma }})^{-1}F(\bar{\varvec{\sigma }})-c^T\bar{\varvec{\sigma }},}\\ {}&{} {=-\frac{1}{2}\bar{x}^T G(\bar{\varvec{\sigma }})\bar{x}-{\sum \limits _{i=1}^{m}{(\frac{1}{2} { \bar{x}}^{T}Q_{i}\bar{{\sigma }}_{i}{ \bar{x}+b_{i}^{T}\bar{{\sigma }}_{i}\bar{x}})}},}\\ {}&{} {=-\frac{1}{2}\bar{x}^T A\bar{x}-({f - A \bar{x}})^T \bar{x},}\\ {}&{}{=\frac{1}{2}{ \bar{x}}^{T}{ A}{ \bar{x}}-{ f}^{T}{ \bar{x}},}\\ {}&{}{=P({ \bar{x}}),}\end{array} $$

which shows that there is no duality gap between \((\mathscr {P}_{qq})\) and \((\mathscr {P}^{d})\). The proof of the theorem is concluded.

In order to get the optimization solution of \((\mathscr {P}_{qq})\), we introduce the following subset

$$\begin{aligned} \mathscr {S}_{+} = \left\{ \varvec{\sigma }\in \mathscr {S}\;\;| \;\; G(\varvec{\sigma }) \text { is positive definite}\right\} . \end{aligned}$$
(23)

In order to hold on the uniqueness of optimal duality solution, the following existence theorem is presented.

Theorem 2

For any given symmetrical matrixes \( A, Q_i,\in \mathbb R^{n \times n}, \) \(\mathscr {G}_+(A)\) (defined by (5)) is the complementary positive definite matrix group of A, \(f, b_i \in \mathbb R^n, c_{i}\in \mathbb R\), \(i=1,2,\cdots ,m,\) if the following two conditions are satisfied  

\(C_{1}:\) :

\(\sum \limits _{i=1}^{m}Q_i \in \mathscr {G}_+(A)\) ;

\(C_{2}:\) :

there must exist one \( k (1\le k \le m)\) such that \(Q_k\) is positive definite and \(Q_k\in \mathscr {G}_+(A)\), moreover,

$$\begin{aligned} \Vert D_kA^{-1}f\Vert >\Vert b_k^TD_k^{-1}\Vert +\sqrt{\Vert b_k^TD_k^{-1}\Vert ^2+2|c_k|}, \end{aligned}$$
(24)

where \(Q_k=D_k^TD_k\) and \(\Vert *\Vert \) is some vector norm .

  Then, the canonical duality problem (16) has a unique nonzero solution \(\bar{\varvec{\sigma }}\) in the space \(\mathscr {S}_{+}\).

Proof.

If the condition \(C_{1}\) is satisfied, the dual feasible space defined by (23) is nonempty.

If \(C_{2}\) is also satisfied, we can get two results, the first one is that there is one positive definite matrix \(D_{k}\) such that

$$Q_k=D_k^TD_k. $$

The second one is that the stationary point of quadratic objective function is out of the convex constraint defined by \(\frac{1}{2}x^TQ_kx+b_{k}^Tx\le c_{k}\). The first one is easy to be proved because \(Q_k\) is symmetrical positive definite. Next, we will show how to get the the second result. Because \(D_{k}\) from the first result is also positive definite, we have

$$ \begin{array}{l} \frac{1}{2}f^T(A^{-1})^TQ_{k}A^{-1}f+b_{k}^TA^{-1}f \\ =\frac{1}{2}f^T(A^{-1})^TD_{k}^TD_{k}A^{-1}f+b_{k}^TD_{k}^{-1}D_{k}A^{-1}f \\ \ge |\frac{1}{2}f^T(A^{-1})^TD_{k}^TD_{k}A^{-1}f|-|b_{k}^TD_{k}^{-1}D_{k}A^{-1}f| \\ \ge \frac{1}{2}\Vert D_{k}A^{-1}f\Vert ^2-\Vert b_{k}^TD_{k}^{-1}\Vert \Vert D_{k}A^{-1}f\Vert \\ =\frac{1}{2}(\Vert D_{k}A^{-1}f\Vert -\Vert b_{k}^TD_{k}^{-1}\Vert )^2-\frac{1}{2}\Vert b_{k}^TD_{k}^{-1}\Vert ^2,\end{array} $$

if we pay attention to (24), from the above inequalities, the following inequalities are easy to obtain,

$$ \begin{array}{l} \frac{1}{2}f^T(A^{-1})^TQ_{k}A^{-1}f+b_{k}^TA^{-1}f \\ \ge |c_{k}|\ge c_{k}.\end{array} $$

So, \(A^{-1}f\) is out of the constraint. According to complementary theory,

$$ {\bar{{\sigma }}_k}\ne 0. $$

Then, there is nonzero solution for the canonical duality problem in the space \(\mathscr {S}_{+}\). Because the objective function is concave and differentiable in the space \(\mathscr {S}_{+}\), the canonical duality solution is unique. The proof of theorem is concluded.

3 Algorithm

In this section, an algorithm is proposed to solve the problem \((\mathscr {P}_{qq})\). The basic procedures are listed in Algorithm 1.

figure a

The algorithm has two important parts. The first one is to judge the conditions. The other one is to get the duality optimization solution.

In the first part, we need to complete two important steps, they are from the computation of eigenvalues of \(A+\sum _{k=1}^m Q_k\) and \(A+Q_i\). If we recall the parameters, n is the dimensional number of input variable x and m is the number of constrains. The complexity of the first part is

$$\begin{aligned} T(m,n)=O(m\times n^2). \end{aligned}$$
(25)

In the other part, the time complexity comes from the method to solve the canonical duality problem. The complexity is

$$\begin{aligned} T(m,n)=O(n\times m^2). \end{aligned}$$
(26)

The complexity of the final time complexity of our proposed algorithm is

$$\begin{aligned} T(m,n)=O(m\times n^2)+O(n\times m^2). \end{aligned}$$
(27)

4 Applications

In this section, several examples are illustrated to show how to use the presented theory to solve the problems. We employ the Quasi-Newton method to solve the canonical duality problems.

Example 1. First of all, let us consider two-dimensional quadratic minimization problem with one quadratic constraint. If we take \(A=\left( \begin{array}{cc}{2}&{} {0}\\ {0}&{} {-1} \end{array}\right) ,\) \(Q=\left( \begin{array}{cc}{4}&{} {0}\\ {0}&{} {2} \end{array}\right) ,f=\left( \begin{array}{c}{3}\\ {3}\end{array}\right) ,\) \(b=\left( \begin{array}{c}{0}\\ {-2}\end{array}\right) ,c=3\), the following minimization problem is obtained,

$$\begin{aligned} \begin{array}{ll} {{\min \limits _{x\in \mathbb R^2}}}&\left\{ P({ x})=x_{1}^2-0.5*x_{2}^2-3x_{1}-3x_{2}\right\} \end{array} \end{aligned}$$
(28)

such that

$$\begin{aligned} {2x_{1}^2}+(x_{2}-1)^2\le 4. \end{aligned}$$
(29)

This problem is to search the global minimize value of P(x) in the inner part of elliptic sphere whose boundary is determined by \({2x_{1}^2}+(x_{2}-1)^2=4\)(can be seen in Fig. 2).

Fig. 2
figure 2

The graph of p(x) on the quadratic constraint

Full size image

We can easily verify that condition \(C_1\) in Theorem 2 is satisfied because the eigenvalues of matrix \(A+Q\) are 6 and 1. \(C_{2}\) is also satisfied because \(\Vert DA^{-1}f\Vert =5.1962\) and

$$\Vert b^TD^{-1}\Vert +\sqrt{\Vert b^TD^{-1}\Vert ^2+2|c|}=4.2426.$$

where \(Q=D^TD\).

The corresponding dual problem is

$$\begin{aligned} \begin{array}{cl} {{\max \limits _{{\sigma }\in \mathbb R}}}&\left\{ P^{d}({{\sigma }})=-\frac{1}{2} (\frac{9}{4{\sigma }+2}+\frac{(3+2{\sigma })^2}{2{\sigma }-1})-3{\sigma }\right\} \end{array} \end{aligned}$$
(30)

such that \({\sigma }\geqslant 0.\)

Then we can present the solution of this problem. This dual problem has a unique solution:

$$ \bar{{\sigma }}=1.5358. $$

The canonical duality global maximize value is

$$ P^{d}(\bar{{\sigma }})=-14.0576. $$

The graph of the canonical duality problem \(P^{d}({\sigma })\) on the interval \([-5,5]\) is shown in Fig. 3. In this figure, we easily see that \(\bar{{\sigma }}=1.5358\) is the global maximizer and \(\max P^{d}({\sigma })=P^{d}(1.5)=-14.0576.\)

Fig. 3
figure 3

The graph of \(P^{d}({\sigma })\) on the interval \([-5,5]\)

Full size image

The optimal solution of primal problem can be obtained by

$$ \bar{x}=(A+\bar{{\sigma }}Q)^{-1}{(f-b\bar{{\sigma }})}=\left( \begin{array}{c}0.3684\\ 2.9309\end{array}\right) . $$

It is very easy to verify that

$$ P(\bar{x})=-14.0576=P^{d}(\bar{{\sigma }}). $$

Let us pay attention to the solution, \(\bar{{\sigma }}=1.5358\) shows that the solution \(\bar{x}\) is on the boundary of the feasible space, in fact, we can understand this from Fig. 2. We can easily check that \(\bar{x}= \left( \begin{array}{c}0.3684 \\ 2.9309\end{array}\right) \) satisfies \({2x_{1}^2}+(x_{2}-1)^2=4\).

Example 2. We now consider three-dimensional quadratic minimization problem with two quadratic constraints. If we take \(A=\left( \begin{array}{ccc}{-2}&{} {0}&{} {0}\\ {0}&{} {2}&{} {0}\\ {0}&{} {0}&{} {-2} \end{array}\right) ,\) \(Q_{1}=\left( \begin{array}{ccc}{4}&{} {0}&{} {0}\\ {0}&{} {4}&{} {0}\\ {0}&{} {0}&{} {4} \end{array}\right) ,\) \(Q_{2}=\left( \begin{array}{ccc}{4}&{} {0}&{} {0}\\ {0}&{} {-1}&{} {0}\\ {0}&{} {0}&{} {4} \end{array}\right) ,\) \(f=\left( \begin{array}{c}{4}\\ {2}\\ {4}\end{array}\right) ,\) \(b_{1}=\left( \begin{array}{c}{0}\\ {0}\\ {0}\end{array}\right) ,b_{2}=\left( \begin{array}{c}{-3}\\ {0}\\ {0}\end{array}\right) ,c_{1}=2,c_{2}=2\), the following minimization problem is obtained,

$$\begin{aligned} \begin{array}{ll} {{\min \limits _{x\in \mathbb R^3}}}&\left\{ P({ x})=-x_{1}^2+x_{2}^2-x_{3}^2-4x_{1}-2x_{2}-4x_{3}\right\} \end{array} \end{aligned}$$
(31)

such that

$$\begin{aligned} {2x_{1}^2}+2x_{2}^2+2x_{3}^2 \leqslant 2, \end{aligned}$$
(32)

and

$$\begin{aligned} {2x_{1}^2}-0.5x_{2}^2+2x_{3}^2-3x_{1} \leqslant 2. \end{aligned}$$
(33)

This problem is to look for the global minimize value of P(x) in the communal inner part of one parabolic and one sphere which boundary is determined by \(2{x_{1}^2}+2x_{2}^2+2x_{3}^2= 2\) and \(2{x_{1}^2}-0.5x_{2}^2+2x_{3}^2-3x_{1}=2\) (can be seen in Fig. 4).

Fig. 4
figure 4

Two quadratic constrains figure bounded by \({2x_{1}^2}+2x_{2}^2+2x_{3}^2 \leqslant 2\) and \(2x_{1}^2-0.5x_{2}^2+2x_{3}^2-3x_{1} \leqslant 2\)

Full size image

Also, we can easily verify that condition \(C_{1}\) in Theorem 2 is satisfied because the eigenvalues of \(A+Q_{1}+Q_{2}\) are 5, 6 and 6, the eigenvalues of \(A+Q_{1}\) are 2, 2 and 6. \(C_{2}\) is satisfied because \(\Vert D_1A^{-1}f\Vert =6\) and

$$ \Vert b_1^TD_1^{-1}\Vert +\sqrt{\Vert b_1^TD_1^{-1}\Vert ^2+2|c_1|}=2. $$

where \(Q_1=D_1^TD_1\).

According to canonical duality theory, the canonical dual problem of (31) is as follows:

$$\begin{aligned} \begin{array}{rl} {{\max \limits _{({\sigma }_{1},{\sigma }_{2})\in \mathbb R^2}}} &{} \{P^{d}({\sigma }_{1},{\sigma }_{2})=-\frac{1}{2}(\frac{(4+3{\sigma }_{2})^2}{4({\sigma }_{1}+{\sigma }_{2})-2}+\frac{4}{4{\sigma }_{1}-{\sigma }_{2}+2}+ \\ {}&{} \frac{16}{4({\sigma }_{1}+{\sigma }_{2})-2})-2{\sigma }_{1}-2{\sigma }_{2}\} \end{array} \end{aligned}$$
(34)

such that \({\sigma }_{1}\geqslant 0, {\sigma }_{2}\geqslant 0.\)

Then we can get the solution of this problem as following:

$$ \bar{{\sigma }}_{1}=1.9447,\bar{{\sigma }}_{2}=0. $$

The canonical duality global maximized value is

$$ P^{d}(\bar{{\sigma }}_{1},\bar{{\sigma }}_{2})=-6.8627. $$

The graph of canonical duality problem objective function \(P^{d}(\bar{{\sigma }}_{1},0)\) on the interval [1.8, 2.2] is shown in Fig. 5. In its figure, we easily guarantee that \((\bar{{\sigma }}_{1}=1.9447,\bar{{\sigma }}_{2}=0)\) is the global maximize point and \(\max P^{d}({\sigma }_{1},0)=P^{d}(1.9447,0)=-6.8627.\)

Fig. 5
figure 5

The graph of \(P^{d}({\sigma }_{1},0)\) on the interval [1.8, 2.2]

Full size image

The optimal solution of primal problem can be obtained by

$$ \bar{x}=(A+\bar{{\sigma }}_{1}Q_{1}+\bar{{\sigma }}_{2}Q_{2})^{-1}{(f-b_{1}\bar{{\sigma }}_{1}-b_{2}\bar{{\sigma }}_{2})}=\left( \begin{array}{c}0.6922\\ 0.2045\\ 0.6922\end{array}\right) . $$

It is very easy to verify that

$$ P(1.9447,0)=-6.8627=P^{d}(0.6922,0.2045,0.6922). $$

Example 3. We now consider four-dimensional quadratic minimization problem with three quadratic inequalities. constraint. If we take

$$ A=\left( \begin{array}{cccc}{2}&{} {0}&{} {0}&{} {0}\\ {0}&{} {2}&{} {0}&{} {0}\\ {0}&{} {0}&{} {-20}&{} {0}\\ {0}&{} {0}&{} {0}&{} {4} \end{array}\right) ,Q_{1}=\left( \begin{array}{cccc}{2}&{} {0}&{} {0}&{} {0}\\ {0}&{} {2}&{} {0}&{} {0}\\ {0}&{} {0}&{} {24}&{} {0}\\ {0}&{} {0}&{} {0}&{} {2} \end{array}\right) ,Q_{2}=\left( \begin{array}{cccc}{1}&{} {0}&{} {0}&{} {0}\\ {0}&{} {2}&{} {0}&{} {0}\\ {0}&{} {0}&{} {2}&{} {0}\\ {0}&{} {0}&{} {0}&{} {2} \end{array}\right) ,$$
$$Q_{3}=\left( \begin{array}{cccc}{2}&{} {0}&{} {0}&{} {0}\\ {0}&{} {-2}&{} {0}&{} {0}\\ {0}&{} {0}&{} {1}&{} {0}\\ {0}&{} {0}&{} {0}&{} {2} \end{array}\right) ,f=\left( \begin{array}{c}{4}\\ {12}\\ {-2}\\ {2}\end{array}\right) , b_{1}=\left( \begin{array}{c}{0}\\ {0}\\ {0}\\ {0}\end{array}\right) , b_{2}=\left( \begin{array}{c}{-1}\\ {0}\\ {0}\\ {0}\end{array}\right) , $$

\(b_{3}=\left( \begin{array}{cccc}{0}&{0}&{-1}&{0}\end{array}\right) ^T, c_{1}=9,c_{2}=c_{3}=8.5\), the following minimization problem is obtained,

$$\begin{aligned} \begin{array}{ll} {{\min \limits _{x\in \mathbb R^4}}}&\left\{ P({ x})=(x_{1}-1)^2+x_{2}^2-10x_{3}^2-4x_{4}^2-12x_{2}+2x_{3}-2x_{4}\right\} \end{array} \end{aligned}$$
(35)

such that

$$\begin{aligned} {x_{1}^2}+x_{2}^2+x_{3}^2+x_{4}^2 \leqslant 9, \end{aligned}$$
(36)

and

$$\begin{aligned} {\frac{1}{2}(x_{1}-1)^2}+x_{2}^2+12x_{3}^2+x_{4}^2 \leqslant 9, \end{aligned}$$
(37)

and

$$\begin{aligned} {x_{1}^2}-x_{2}^2+\frac{1}{2}(x_{3}-1)^2+x_{4}^2 \leqslant 9. \end{aligned}$$
(38)

The equality of the first constraint is sphere, the second one is ellipsoid and the last one is hyperboloid.

Also, we can easily verify that condition \(C_{1}\) in Theorem 2 is satisfied because the eigenvalues of \(A+Q_{1}+Q_{2}+Q_{3}\) are 4, 7, 7 and 10, the eigenvalues of \(A+Q_{1}\) are 4, 4, 4 and 6. \(C_{2}\) is satisfied because \(\Vert D_1A^{-1}f\Vert =8.9855\) and

$$\Vert b_1^TD_1^{-1}\Vert +\sqrt{\Vert b_1^TD_1^{-1}\Vert ^2+2|c_1|}=4.2426.$$

where \(Q_1=D_1^TD_1\).

According to canonical duality theory, the canonical dual problem of (35) is as follows

$$\begin{aligned} \begin{array}{rl} {{\max \limits _{({\sigma }_{1},{\sigma }_{2},{\sigma }_{3})\in \mathbb R^3}}}&{} \left\{ {P^{d}({\sigma }_{1},{\sigma }_{2},{\sigma }_{3})=-\frac{1}{2}(\frac{(4+{\sigma }_{2})^2}{2{\sigma }_{1}+{\sigma }_{2}+2{\sigma }_{3}+2} +\frac{144}{2({\sigma }_{1}+{\sigma }_{2}-{\sigma }_{3})+2} +}\right. \\ {}&{}\left. {\frac{({\sigma }_{3}-2)^2}{24{\sigma }_{1}+2{\sigma }_{2}+{\sigma }_{3}-20}+\frac{4}{2({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3})+4})-9{\sigma }_{1}-8.5{\sigma }_{2}-8.5{\sigma }_{3}}\right\} \end{array} \end{aligned}$$
(39)

such that \({\sigma }_{i}\geqslant 0,i=1,2,3.\)

Then we can get the solution of this problem as following:

$$ \bar{{\sigma }}_{1}=1.1983,\bar{{\sigma }}_{2}=0,\bar{{\sigma }}_{3}=0. $$

The canonical duality global maximized value is

$$ P^{d}(\bar{{\sigma }}_{1},\bar{{\sigma }}_{2},\bar{{\sigma }}_{3})=-29.5216. $$

The optimal solution of primal problem can be obtained by

$$ \bar{x}=(A+\bar{{\sigma }}_{1}Q_{1}+\bar{{\sigma }}_{2}Q_{2}+\bar{{\sigma }}_{3}Q_{3})^{-1}{(f-b_{1}\bar{{\sigma }}_{1}-b_{2}\bar{{\sigma }}_{2}-b_{3}\bar{{\sigma }}_{3})}=\left( \begin{array}{c}0.9098\\ 2.7293\\ -0.2283\\ 0.3127\end{array}\right) . $$

It is very easy to verify that

$$ P(1.1983,0,0)=-29.5216=P^{d}(0.9098,2.7293,-0.2283,0.3127). $$

Example 4. Here, we present a ten-dimensional nonconvex quadratic programming with two quadratic constraints. If we let

$$ A=\left( \begin{array}{cccccccccc} -2 &{} 0.5 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5\\ 0.5 &{}-13 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1\\ 1 &{} 1 &{} -14 &{} 0.5 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0.5 &{} -2 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0 &{} 0.5 &{} 3 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} -6 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} -1 &{} 0.5 &{} 1&{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} -13 &{} 0.5 &{} 1\\ 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 1 &{} 0.5 &{} -14 &{} 0.5\\ 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0 &{} 0 &{} 1 &{} 0.5 &{} -5 \end{array}\right) ,$$
$$ Q_{1}=\left( \begin{array}{cccccccccc} 10 &{} 0.5 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5\\ 0.5 &{} 25 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1\\ 1 &{} 1 &{} 24 &{} 0.5 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0.5 &{} 12 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0 &{} 0.5 &{} 9 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 12 &{} 0.5 &{} 0.5 &{} 0.5&{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 9 &{} 0.5 &{} 1 &{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 25 &{} 0.5 &{} 1\\ 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 1 &{} 0.5 &{} 31 &{} 0.5\\ 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0 &{} 0 &{} 1 &{} 0.5 &{} 9 \end{array}\right) ,$$
$$ Q_{2}=\left( \begin{array}{cccccccccc} 5 &{} 0.5 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5\\ 0.5 &{} 9 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1\\ 1 &{} 1 &{} 8 &{} 0.5 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0.5 &{} 6 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5\\ 1 &{} 1 &{} 0 &{} 0.5 &{} 4 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 6 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 1 &{} 0.5 &{} 0.5 &{} 4 &{} 0.5 &{} 1 &{} 0\\ 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 13 &{} 0.5 &{} 1\\ 0.5 &{} 0.5 &{} 0.5 &{} 0.5 &{} 1 &{} 0.5 &{} 1 &{} 0.5 &{} 13 &{} 0.5\\ 0.5 &{} 1 &{} 0.5 &{} 0.5 &{} 0.5 &{} 0 &{} 0 &{} 1 &{} 0.5 &{} 4 \end{array}\right) , $$

the other corresponding coefficients are listed as follows

$$ \begin{array}{c} f=\begin{array}{cccccccccc}(-27 &{} 1 &{} 8 &{} 6 &{} -18 &{} 6 &{} 30 &{} 1 &{} 13 &{} 4)\end{array},\\ b_{1}=\begin{array}{cccccccccc}(10 &{} 8 &{} 6 &{} 10 &{} 14 &{} 9 &{} 9 &{} 9 &{} 11 &{} 8),\end{array}\\ b_{2}=\begin{array}{cccccccccc}(16 &{} 9 &{} 14 &{} 15 &{} 9 &{} 7 &{} 9 &{} 13 &{} 6 &{} 11),\end{array}\end{array} $$

and \(c_{1}=c_{2}=20\).

Similar with the other three examples, we can easily verify that condition \(C_{1}\) in Theorem 2 is satisfied because the eigenvalues of \(A+Q_{1}+Q_{2}\) are listed as follows \(\{6.3635,\) 8.7851,  10.4295,  11.0365,  14.1675,  16.3225,  17.7796,  22.3263,  26.8958,  \( 36.8937\}\), the eigenvalues of \(A+Q_{1}\) are listed as follows \(\{2.8501,\) 4.6238,  5.8963,  6.9364,  8.6136,  9.8704,  10.7933,  11.8424,  15.0207,  \( 22.5531\}\). \(C_{2}\) is satisfied because \(\Vert D_1A^{-1}f\Vert =615.4753\) and

$$ \Vert b_1^TD_1^{-1}\Vert +\sqrt{\Vert b_1^TD_1^{-1}\Vert ^2+2|c_1|}=11.3815. $$

where \(Q_1=D_1^TD_1\).

The canonical duality solution is

$$ \bar{{\sigma }}_{1}=1.6894,\bar{{\sigma }}_{2}=0. $$

The canonical duality global maximize value is

$$ P^{d}(\bar{{\sigma }}_{1},\bar{{\sigma }}_{2})=-149.6523. $$

The optimal solution of primal problem can be obtained by

$$ \begin{array}{ll} {\bar{x}=}&{}{(-2.6417, -0.1485, 0.1268, -0.2010, -1.9168, -0.3058,}\\ {}&{}{1.5580, -0.3112, 0.0087, -0.2020).} \end{array} $$

It is very easy to verify that

$$ P(1.6984,0)=-149.6523=P^{d}(\bar{x}). $$

5 Conclusions

Nonconvex quadratic minimization problems with quadratic constraints are well known because they are very difficult to find out the global optimization solutions. In this paper, we have employed the canonical duality to convert them into a concave maximization dual problem over a convex set. With the presented conditions in Theorem 2, we have proved that the canonical duality problem (16) has a unique nonzero solution \(\bar{\varvec{\sigma }}\) in the space \(\mathscr {S}_{+}\). With Theorem 1, we can find out the global optimization solutions \(\bar{x}\) of the class of nonconvex quadratic minimization problems with quadratic constraints by (17). Several numerical examples can show that the given conditions and results in Theorems 1 and 2 are correct.