1 Introduction

An important choice needs to be taken when setting up direct numerical simulations (DNS) of turbulent channel flows, regarding how the flow is driven through the channel. Two classic possibilities are to drive the flow at constant flow rate (CFR) or at constant pressure gradient (CPG). While the different choices yield similar turbulent statistics for canonical flows [7], the main difference being, for instance, in the tails of the probability density function of wall shear stress, they have crucial implications on statistics of drag-reduced turbulent flows. For instance, with CFR drag reduction manifests as a reduction of friction but as an increase of bulk velocity with CPG. In neither case, the power transferred to the flow remains constant upon application of drag-reducing control nor so does the rate of production and dissipation of turbulent kinetic energy. Since the uncontrolled and drag-reduced flows differ energetically, it is difficult, if not impossible, to address the physics of drag reduction techniques from the energetic standpoint.

In this work, we exploit the recently-proposed constant total power input (CtPI) approach [4], in which the power transferred to the flow through pumping and imposition of a control is kept constant, to address how drag-reduction obtained via several wall-based strategies modifies energetic properties of turbulent channel flows. First, the effect of the control on the integral production and dissipation of mean and turbulent kinetic energy are computed [9]. Then, starting from the generalized form of the Kolmogorov equation [2, 6], the scale energy fluxes simultaneously occurring in the space of scales and in the physical space of wall-turbulent flows are preliminary studied to highlight differences among controlled drag-reduced and unmodified flows.

The structure of the paper is as follows. Section 2 describes the numerical method and procedures, as well as the control strategies adopted in the present study. In Sect. 3 the main results are presented and discussed, while Sect. 4 contains concluding remarks.

2 Numerical Method

Direct numerical simulation (DNS) of turbulent channel flows driven at CPI have been performed at a power-based Reynolds number, kept constant across all cases, of \(Re_\varPi = U_\varPi h / \nu = 6500\), corresponding in the reference unmanipulated channel to \(Re_\tau =u_\tau h / \nu = 199.7\) and \(Re_b=U_b h / \nu = 3176.8\). In the previous definitions, \(U_\varPi \) is the bulk velocity of a laminar driven at the given power, \(u_\tau \) and \(U_b\) are respectively the friction and the bulk velocity, h the channel semi-height and \(\nu \) is the kinematic viscosity. Two active flow control strategies for turbulent skin-friction drag reduction, which require a control power input \(\varPi _c\) in order to be applied, have been considered, namely the spanwise-oscillating wall ([8]) and the oppoition control [1]. In such cases, the calculations are performed while keeping a Constant total Power Input (CtPI) [3] in time. The total power input \(\varPi _t\) is defined as the sum of the control power input \(\varPi _c\) and the pumping power \(\varPi _c\), so that active control requires a fraction \(\gamma =\varPi _c/\varPi _c\) of the total power to be spent for applying the control instead of directly pumping the flow.

Fig. 1
figure 1

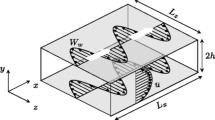
Sketch of the two control strategies addressed in the present work. Left opposition control [1]. The wall-normal velocity is sensed at wall-parallel plane located a distance \(y_p\) from the wall and fed back at the wall as blowing and suction with opposite sign, so as to damp near-wall quasi streamwise vortices. Right spanwise wall oscillations [8]

Full size image

The two control strategies of the present study (Fig. 1) have been selected due to their very different input power requirements, yielding different values of \(\gamma \). The ocillating-wall forcing requires a significant amount of energy to operate, while the opposition control, which enforces a distributed vertical velocity v at the wall opposing the same component at a plane located at a prescribed wall distance \(y_p\), requires minimal control power. The control parameters have been set in order to maximize the control performance, which in the CtPI framework means to maximize the increase in bulk mean velocity \(U_b\) (thereby decreasing the wall shear stress \(\tau _w\)) at a fixed total power \(\varPi _t\). This choice corresponds to an oscillating period of \(T^+=125.5\) and a maximum spanwise wall velocity of about \(W_w^+=4.5\) for the oscillating wall, and to a detection plane located at \(y_p^+=13\) for the opposition control. Hereinafter, the superscript \(+\) denotes quantities that have been nondimensionalized by the actual friction velocity and kinematic viscosity. In these configurations, the oscillating wall achieved \(Re_\tau =186.9\) and \(Re_b=3268\) with a \(\gamma =0.098\), while the opposition control achieved \(Re_\tau =190.5\) and \(Re_b=3474\) with the much smaller \(\gamma =0.0035\).

The employed DNS solver is the one developed by Luchini and Quadrio [5], which uses a mixed spatial dicretization with Fourier series expansion in the two homogeneous span- and streamwise direction and fourth-order explicit compact finite differences in the wall-normal direction. The computational domain has a streamwise length of \(L_x=4\pi h\) and a spanwise width of \(L_z=2\pi h\). 256 Fourier modes are used to expand the velocity in the streamwise and spanwise direction before dealiasing (additional modes are added for avoiding aliasing), while the velocity is discretized in the wall-normal direction with 256 unevenly spaced points, in order to improve the resolution in the near-wall region. The corresponding spatial resolutions before dealiasing in viscous wall units are \(\varDelta x^+=9.8\), \(\varDelta z^+=4.9\), \(\varDelta y^+_{\mathrm {min}}=0.47\) at the wall and \(\varDelta y^+=2.59\) at the channel centerline.

The governing equation are advanced in time with implicit temporal discretization for the viscous term and a third-order low-storage Runge-Kutta explicit scheme for the nonlinear terms. The time step is chosen to yield an averaged value of the Courant-Friedrichs-Levy number of 1.1. The calculations start from an initial condition where the flow is statistically stationary for the specific case and are advanced for about 25,000 viscous time units. For the oscillating-wall case, 200 field are saved for each of 8 different oscillation phases, for a total of 1600 flow fields.

3 Results

Table 1 Integral power budget for the uncontrolled and controlled channels. MKE and TKE are abbreviations for Mean and Turbulent Kinetic Energy respectively. All values are given in fraction of the total power \(\varPi _t\)
Full size table

Table 1 summarizes the volume integrals of the inbound and outbound energy fluxes, normalized by the total power input \(\varPi _t\). The flow is fed a pumping power \(\varPi _p\) and possibly a control input power \(\varPi _c\), whose sum is by constraint constant. The flow dissipates the total power input directly as dissipation of the mean kinetic energy or via production of turbulent fluctuations as dissipation of turbulent kinetic energy. At the present low value of the Reynolds number, 59% of the total input power is dissipated directly by the mean flow, while the remaining 41% is “wasted” to produce turbulent kinetic energy and then dissipated as turbulent dissipation. When control is applied within the CtPi framework, all the global energy fluxes change in a way which strongly depends on the type of control considered or, in particular, on the control-to-total power ratio \(\gamma \). In the case of the oscillating wall, for instance, 10% of the total power is used for applying the control, while only the remaining 90% is available for pumping. Nonetheless, the control results into an increase of the mean bulk velocity compared to the uncontrolled flow, which highlights how well the spanwise forcing class of control strategy performs, despite the high power requirement. The dissipation of mean kinetic energy decreases with the oscillating wall, in spite of the fact that \(U_b\) is increased, while the turbulent dissipation, which also accounts for the 10% of control input power considered as purely temporal velocity fluctuations, increases. The very opposite trend is observed for the opposition control, for which the dissipation of the mean kinetic energy is increased to 64% while the turbulent dissipation decreased to 36%.

Fig. 2
figure 2

Definition of the velocity difference, required to compute the second-order structure function. See text

Full size image

Closer insights into the physics of such control techniques for turbulent drag reduction can be obtained by analysing the Kolmogorov equation generalized for anisotropic flows with mean shear. A detailed discussion of such equation is out of the scope of the present manuscript and the interested reader is demanded to the discussion by Cimarelli, De Angelis and Casciola [6]. In the following we will discuss only the budget of the second order structure function \(\langle \delta u^2 \rangle = \delta u_i \delta u_i\), where \(\delta u_i\) is the velocity difference (Fig. 2) between two points that are separated in space by a vector \(\mathbf {r}\) and whose midpoint is located at the point \(\mathbf {X_c}\). The angular brackets denote space and time averaging. In a channel flow, the second order structure function depends only on the three components \(r_i\) of the vector \(\mathbf {r}\) and on the wall-normal coordinate \(Y_c\) of the midpoint \(\mathbf {X_c}\). The second order structure function can be interpreted, according to its definition, as the amount of fluctuation energy at a scale \(r_i\) and at the spatial position \(Y_c\) and therefore will be called hereinafter scale energy. In the following only the properties only spanwise separations \(r_z\) and the wall-normal position \(Y_c\) will be addressed.

Fig. 3
figure 3

Scale energy source map for an uncontrolled channel flow (a), for a channel modified by opposition control (b) and by spanwise wall oscillations (c). In all cases the total power is kept constant

Full size image

Figure 3 shows the maps of scale energy source term, positive when scale energy is produced and negative when dissipated, as colour maps. The vector field shows the fluxes of the scale energy in the \(Y_c-r_z\) plane while the solid lines represent some field lines which originate at the singular point of the vector field. Only the near wall region for the uncontrolled channel and for the channel manipulated via opposition control and spanwise wall oscillations are represented. Clearly, the morphology of scale energy production and dissipation is structurally modified by the control, also in this non trivial case in which the total power input to the system is kept constant. In the oscillating wall case, the peak scale-energy production decreases strongly and is located further from the wall compared to the reference case. The vertical shift of the peak scale energy production is observed also for the opposition control case. The presence of a wall vertical velocity causes the appearance of an intermediate region of positive scale energy production, located between the wall and the peak production. This intermediate region strongly modifies the morphology of the scale energy fluxes in the near-wall region.

4 Conclusions

The constant total power input (CtPI) approach is found to be a necessary and enabling step to address control-induced modifications of the energy transfer rates in turbulent flows without incurring in biases related to particular choice of scaling and normalizations of the results. The present study shows that no trivial general pattern can be found between the change of the global energy transfer rate and successful drag reduction, which in the CtPI results in an increase of bulk velocity compared to an unmanipulated flow. If the control input power is not accounted for in the turbulent dissipation, successful control results into a reduction of turbulent kinetic energy dissipation but not necessarily into an increase of mean kinetic energy dissipation.

The generalized Kolmogorov equation is a powerful tool to address the physics of turbulent drag reduction strategies from the energetic standpoint. The present preliminary results show a significant control-induced modification of both the scale energy production and scale energy fluxes in the near-wall region. Further analysis is required, considering all possible scale separations other than spanwise, to link the present evidence with fundamental properties of turbulent drag reduction.