Adaptive One-Class Support Vector Machine for Damage Detection in Structural Health Monitoring

Abstract

Machine learning algorithms have been employed extensively in the area of structural health monitoring to compare new measurements with baselines to detect any structural change. One-class support vector machine (OCSVM) with Gaussian kernel function is a promising machine learning method which can learn only from one class data and then classify any new query samples. However, generalization performance of OCSVM is profoundly influenced by its Gaussian model parameter $\sigma$. This paper proposes a new algorithm named Appropriate Distance to the Enclosing Surface (ADES) for tuning the Gaussian model parameter. The semantic idea of this algorithm is based on inspecting the spatial locations of the edge and interior samples, and their distances to the enclosing surface of OCSVM. The algorithm selects the optimal value of $\sigma$ which generates a hyperplane that is maximally distant from the interior samples but close to the edge samples. The sets of interior and edge samples are identified using a hard margin linear support vector machine. The algorithm was successfully validated using sensing data collected from the Sydney Harbour Bridge, in addition to five public datasets. The designed ADES algorithm is an appropriate choice to identify the optimal value of $\sigma$ for OCSVM especially in high dimensional datasets.

1 Introduction

Structural health monitoring (SHM) is an automated process to detect the damage in the structures using sensing data. It has earned a lot of interests in recent years and has attracted many researchers working in the area of machine learning [6, 9, 17]. With the advances in the sensing technology, it is becoming more feasible to develop an approach for detection of structural damage based on the information gathered from the sensor networks mounted to the structure [5]. The focus now is to build a decision-making model that is able to detect damage on the structure using sensor data. This can be solved using a supervised learning approach such as a support vector machine (SVM) [2]. However, because of the lack of available data from the damaged state of the structure in most cases, this leads to the development of the OCSVM classification model [15]. The design of OCSVM is well suited this kind of problems where only observations from the positive (healthy) samples are required. Moreover, OCSVM has been extensively used in the area of SHM for detecting different types of anomalies [3, 8, 11].

The rational idea behind OCSVM is to map the data into a high dimensional feature space via a kernel function and then learn an optimal decision boundary that separates the training positive observations from the origin. Several kernel functions have been used in SVM such as Gaussian and polynomial kernels. However, the Gaussian kernel function defined in Eq. (1) has gained much more popularity in the area of machine learning and it has turned out to be an appropriate setting for OCSVM in order to generate a non-linear decision boundary.

$$\begin{aligned} K(x_i, x_j) = \exp (-\dfrac{||x_i-x_j ||^{2}}{2\sigma ^2}) \end{aligned}$$

(1)

This kernel function is highly affected by a free critical parameter called the Gaussian kernel parameter denoted by $\sigma$ which determines the width of the Gaussian kernel. This parameter has a great influence on the construction of a classification model for OCSVM as it controls how loosely or tightly the decision boundary fits the training data. To demonstrate the effect of the parameter $\sigma$ on the decision boundary, we used a two-dimensional Banana-shaped data set. We applied the OCSVM on the dataset using different values of parameter $\sigma$, and then we plotted the resultant decision boundary of OCSVM for three different values of $\sigma$ as shown in Fig. 1. Comparing the lower and upper bounds of $\sigma$, it can be clearly seen that the enclosing surface is very tight in Fig. 1a, while it is loose in Fig. 1b. The optimal one is shown in Fig. 1c as the decision boundary precisely describes the form of the data. At that point the issue is changed over into how to estimate the suitability of the decision boundary.

Fig. 1.

Illustrations for enclosing surfaces at different values of $\sigma$. (a) $\sigma$ = 0.2. (b) $\sigma$ = 1.3. (c) $\sigma$ = 0.8.

Several researchers have addressed the problem of selecting the proper value of $\sigma$ [4, 16, 18]. However, they are not considered as appropriate methods to be applied on high dimensional datasets. Furthermore, tuning the Gaussian kernel for the OCSVM is still an open problem as stated by Tax and Duin [16] and Scholkopf et al. [15].

This paper addresses the problem of tuning the Gaussian kernel parameter $\sigma$ in OCSVM to ensure the generalization performance of the constructed model to unseen high dimensional data. Following the geometrical approach, we proposed a Gaussian kernel parameter selection method which is implemented in two steps. The first step aims to select the edge and interior samples in the training dataset. The second step constructs OCSVM models at different settings of the parameter $\sigma$ and then we measure the distances from the selected edge-interior samples to the enclosing surface of each OCSVM. Following these steps, we can select the optimal value of $\sigma$ which provides the maximum difference in the average distances between the interior and edge samples to the enclosing surface. The algorithm was validated using a real high dimensional data collected using a network of accelerometers mounted underneath the deck on the Sydney Harbour Bridge in Australia.

The rest of this paper is organized as follows: Sect. 2 briefly presents some related work for tuning $\sigma$. The Gaussian kernel parameter selection method is provided in Sect. 3. Section 4 presents experimental results using different datasets. Section 5 presents some concluding remarks.

2 Related Work

Several methods have been developed for tuning the parameter $\sigma$ in Gaussian kernel function. For instance, Evangelista et al. [4] followed a statistics-based approach to select the optimal value of $\sigma$ using the variance and mean measures of the training dataset. This method is known as VM measure which aims to evaluate ${\hat{\sigma }}$ by computing the ratio of the variance and the mean of the lower (or upper) part of the kernel matrix using the following formula:

$$\begin{aligned} {\hat{\sigma }} = \max _{\sigma }(\dfrac{v}{{\bar{m}}+\xi }) \end{aligned}$$

(2)

where v is the variance, m is the mean and $\xi$ is a small value in order to avoid zero division. This method often generates a small value for ${\hat{\sigma }}$ which results in a very tight model that closely fits to a limited set of data points. Khazai et al. [7] followed a geometric approach and proposed a method called MD to estimate the optimal value of $\sigma$ using the ratio between the maximum distance between instances and the number of samples inside the sphere as in the following equation:

$$\begin{aligned} {\sigma ^2} = \dfrac{d_{max}}{\sqrt{-\ln (\delta )}} \end{aligned}$$

(3)

where the appropriate value for $\delta$ is calculated by:

$$\begin{aligned} \delta = \dfrac{1}{N(1-\nu )+1} \end{aligned}$$

(4)

This method often produces a large value of $\sigma$ which yields to construct a very simple and poor performance model especially when the training dataset has a small number of samples. In this case, the value of the dominator term in Eq. (3) (${\sqrt{-\ln (\delta )}}$) becomes small. Xiao et al. [18] proposed a method known as MIES to select a suitable kernel parameter based on the spatial locations of the interior and edge samples. The critical requirement of this method is to find the edge-interior samples in order to calculate the optimal value of $\sigma$. The authors in [18] adopted the Border-Edge Pattern Selection (BEPS) method proposed by Li and Maguire [10] to select the edge-interior samples. This method performs well in selecting edge and interior samples when the data exists in a low dimensional space. However, it failed completely when it dealt with very high dimensional datasets where all the samples are selected as edge samples.

In this paper, we propose a method for tuning the Gaussian kernel parameter following a geometrical approach by introducing a new objective function and a new algorithm, inspired by [1], for finding the edge-interior samples of datasets exist in high dimensional space.

3 Gaussian Kernel Parameter Selection Method

The idea of the ADES method is based on the spatial locations of the edge and interior samples relative to the enclosing surface. The geometric locations of edge-interior samples with respect to the hyperplane plays a significant role in judging the appropriateness of the enclosing surface. In other words, the enclosing surface of OCSVM is very close to the interior samples when it has tightly fitted the data (as shown in Fig. 1a), and it is very far from the interior and edge samples when it is loose (as shown in Fig. 1b). However, the enclosing surface precisely fits the form of the data in Fig. 1c where the enclosing surface is far from the interior sample but at the same time is very close to the edge ones. This situation is turned up to be our objective in selecting the appropriateness of the enclosing surface. Therefore, we proposed a new objective function $f({\sigma _i})$ described in Eq. (5) to calculate the optimal value of ${\hat{\sigma }} = \underset{\sigma _i}{argmax} (f({\sigma _i}))$.

$$\begin{aligned} f({\sigma _i}) = mean (d_N(x_n)_{x_n\in \varOmega _{IN}}) - mean (d_N(x_n)_{x_n\in \varOmega _{ED}}) \end{aligned}$$

(5)

where $\varOmega _{IN}$ and $\varOmega _{ED}$, respectively, represent the sets of interior and edge samples in the training positive data points, and $d_N$ is the normalized distance from these samples to the hyperplane. This distance can be calculated using the following equation:

$$\begin{aligned} d_N(x_n) =\dfrac{d(x_n)}{1-d_{\pi }} \end{aligned}$$

(6)

where $d_{\pi }$ is the distance of a hyperplane to the origin described as $d_{\pi } = \frac{\rho }{||w ||}$, and $d(x_n)$ is the distance of the sample $x_n$ to the hyperplane obtained using the following equation:

$$\begin{aligned} d(x_n) =\dfrac{f(x_n)}{||w ||} = \dfrac{\sum _{i=1}^{sv}\alpha _i k(x_i,x_n)-\rho .}{\sqrt{\sum _{ij}^n\alpha _i\alpha _j K(x_i, x_j)}} \end{aligned}$$

(7)

where w is a perpendicular vector to the decision boundary, $\alpha$ are the Lagrange multipliers and $\rho$ known as the bias term.

The aim of this objective function is to find the hyperplane that is maximally distant from the interior samples but not from the edge samples. In this new objective function, we use the average distances from the interior and edge samples to the hyperplane in order to reduce the effect of improper selection possibility of the interior and edge samples in high dimensional space datasets. The key point of this method now is how to identify the interior and edge samples in a given high dimensional dataset. Therefore, we propose a new method based on linear SVM to select the interior and edge samples in high dimensional space. This algorithm is described as follows: given a dataset of $x_i(i = 1, \ldots , n)$, the unit vector of each point $x_i$ with its k closest points $x_j$ is computed as follows:

$$\begin{aligned} v_{j}^k = \dfrac{x_j-x_i}{||x_j-x_i ||} \end{aligned}$$

(8)

Then we employ a hard margin linear SVM to separate $v_{j}^k$, the closest points to $x_i$, from the origin by solving the OCSVM optimization problem of the obtained unit vectors in Eq. (8). Once we get the optimal solution ${\alpha _j, j=1, \ldots , k}$ and calculating $\rho$, we estimate the value of the decision function using,

$$\begin{aligned} f(v_{j}) = \sum _{i=1}^{sv}\alpha _i v_{i}. v_{j}-\rho . \end{aligned}$$

(9)

The next step is to evaluate the optimization of the constructed linear OCSVM using the following equation

$$\begin{aligned} s_i = \frac{1}{k}\sum _{j=1}^{k}f(v_{j}) > 0 \end{aligned}$$

(10)

where $s_i$ represents the success accuracy rate of the model. If all the closest points $v_{j}^k$ are successfully separated from the origin, then we count $x_i$ as an edge sample. This approach may end up with a few number of edge samples. Therefore, we have used a threshold $1-\gamma$ ($\gamma$ is a small positive parameter), to control the number of edge samples by setting up a percentage of the acceptable success rate for each sample $x_i$ to be an edge sample. For $\gamma =0.05$, if 95% of the closest points to a sample $x_i$ are successfully separated from the origin, then the sample $x_i$ can be added to the edge sample set $\varOmega _{ED}$. We have also extended this method to select the interior samples based on the furthest neighbours of the edge samples. The assumption made is that the furthest neighbour samples to the edge sample should be added to the interior sample set $\varOmega _{IN}$. This method is presented in Algorithm 1.

The algorithm starts with the entire set of positive samples. Two parameters are used in this algorithm; k, the number of the nearest neighbours which has been thoroughly studied by [10] and they set $k=5 \ln n$, where $\gamma$ take values in the range [0, 0.1].

Once the edge and interior samples are identified, we start optimizing our objective function presented in Eq. 5. The complete proposed method of ADES is presented in Algorithm 2.

4 Experimental Results

Three experiments were carried to evaluate the performance of our proposed algorithm. We initially applied our method on two-dimensional toy datasets as it allows us to visually observe the performance of OCSVM by plotting its decision boundary. The performance was also tested on benchmark datasets that allows us to objectively compare our obtained results to the previously published ones. The final experiments were applied on datasets obtained from an actual structure, the Sydney Harbour Bridge, to demonstrate the ability of the proposed algorithm to detect damage in steel reinforced concrete jack arches.

4.1 Experiments on Artificial Toy Datasets

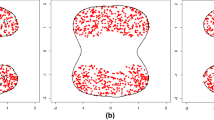
Three toys, {Round, Banana and Ring}-shaped, datasets were used in this section to visualize the performance of our method. The R package mlbench was used in order to generate these different geometric shaped datasets that vary in their characteristics. Figure 2 shows the selected edge and interior samples denoted by red “” and green “”, respectively. As it can be clearly observed that the proposed edge samples selection method has the ability to select the edge samples especially on the Ring-shaped dataset while the inner edge samples play a significant role in constructing the decision boundary.

Fig. 2.

Selected edge and interior samples: (a) Banana-shaped (b) Ring-shaped (c) Round-shaped. (Color figure online)

Figures 3 and 4 show the resultant decision boundary of each toy dataset. The enclosed surface of ADES method shown in each sub Figs. {3-4}(a) precisely fit the shape of each toy dataset without suffering from the overfitting nor the under-fitting problems. The MD and VM methods generate a loosely and tight decision boundary, respectively. The same results appeared with the Ring-shaped dataset (referring to Figs. 4(c) and (d)). The MIES method works well on the Banana-shaped dataset but failed in finding the optimal decision boundary in the Ring-shaped dataset. All the methods successfully enclosed the surface of the Round-shaped dataset with an optimal fitted decision boundary.

Fig. 3.

Performance on the Banana-shaped dataset: (a) ADES (b) MIES (c) MD (d) VM.

Fig. 4.

Performance on the Ring-shaped dataset: (a) ADES (b) MIES(c) MD (d) VM.

4.2 Experiments on Benchmark Datasets

We further investigated the performance of our method using five publicly available datasets downloaded from the machine learning repository¹. These datasets were previously used in previous related studies [18, 19]. The main characteristics of these datasets are summarized in Table 1. Each dataset has been pre-processed using the following procedure:

• 1. Label the class with a large number of samples as positive and the others as negative.

• 2. Randomly select 80% of the positive samples for training and 20% for testing in addition to the samples in the negative classes.

• 3. Normalize the training data to zero mean and unity variance.

• 4. Normalize the test data based on the mean and variance of the relating training dataset.

Table 1. Details of machine learning repository datasets.

Table 2. Optimal values of $\sigma$ selected by different methods for the benchmark datasets along with g-means, TPR and FPR.

For each dataset, we generated 20 bootstrap samples from the training dataset to train OCSVM with $\sigma$ parameter to be selected using Algorithm 2 and $\nu$ = 0.05 for all tests. Once we construct the OCSVM model, we evaluate its classification performance on the test dataset and calculate the accuracy using g-mean metric defined as

$$\begin{aligned} g\text {-}mean=\sqrt{TPR^+\times TNR^-} \end{aligned}$$

(11)

where TPR and TNR are the true positive rate and the true negative rate, respectively. Table 2 shows the classification performance comparison between ADES and the other methods described in Sect. 2. As shown in Table 2, the average g-mean of our method outperformed the other state-of-the-art methods on four datasets. ADES performed better than MIES algorithm on four datasets and generated a comparable result on the Biomed dataset. We can also notice that no results were reported in Table 2 for MIES method on the Sonar dataset. This is due to the fact that MIES algorithm does not work on high dimensional dataset where all the training data points are selected as edge samples.

Further, it was observed from the results that the MD method achieves high classification accuracy on the positive samples represented by the value of the TPR, and low accuracy on the negative samples represented by the FPR measurement. This is what we anticipated discovering from the MD method based on the decision boundary resulted from the toy datasets. The same expectation with the VM method which achieves a high accuracy on the negative samples but a very low TPR. These findings also reflect what we have obtained using the toy datasets. Further, the VM method selects a very small value of $\sigma$ when applied to the Heart and Sonar datasets. These small values lead to over-fit in the OCSVM model which completely failed to classify positive samples in the test datasets. This explains why we can see zero values for FPR and g-means. According to these results in Table 2, ADES has the capability to select the optimal value of $\sigma$ without causing the OCSVM model neither to over-fit nor to under-fit. Moreover, ADES can work on high dimensional datasets while still being able to select the edge and interior samples which are crucial for the objective function presented in Eq. 5.

4.3 Case Studies in Structural Health Monitoring

This work is part of the efforts to apply SHM to the iconic Sydney Harbour Bridge. This section presents two case studies to illustrate how OCSVM using our proposed method for tuning sigma is capable to detect structural damage. The first case study was conducted using real datasets collected from the Sydney Harbour Bridge and the second case study is a reinforced concrete cantilever beam subjected to increasingly progressive crack which replicates one of the major structural components in the Sydney Harbour Bridge.

Case Study I: Sydney Harbour Bridge.

Experiments Setup and Data Collection. Our main experiments were conducted using structural vibration based datasets acquired from a network of accelerometers mounted on the Sydney Harbour Bridge. The bridge has 800 joints on the underside of the deck of the bus lane. However, only six joints were used in this study (named 1 to 6) as shown in Fig. 5. Within these six joints, only joint number four was known as a cracked joint [13, 14]. Each joint was instrumented with a sensor node connected to three tri-axial accelerometers mounted on the left, middle and right side of the joint, as shown in Fig. 5. At each time a vehicle passes over the joint, defined as event, it causes vibrations which are recorded by the sensor node for a period of 1.6 s at a sampling rate of 375 Hz. An event is triggered when the acceleration value exceeds a pre-set threshold. Hence, 600 samples are recorded for each event. The data used in this study contains 36952 events as shown in Table 3 which were collected over a period of three months. For each reading of the tri-axial accelerometer (x,y,z), we calculated the magnitude of the three vectors and then the data of each event is normalized to have a zero mean and one standard variation. Since the accelerometer data is represented in the time domain, it is noteworthy to represent the generated data in the frequency domain using Fourier transform. The resultant six datasets (using the middle sensor of each joint) has 300 features which represent the frequencies of each event. All the events in the datasets (1, 2, 3, 5, and 6) are labeled positive (healthy events), where all the events in dataset 4 (joint 4) are labeled negative (damaged events). For each dataset, we randomly selected 70% of the positive events for training and 30% for testing in addition to the unhealthy events in dataset 4.

Fig. 5.

Evaluated joints on the Sydney Harbour Bridge.

Table 3. Number of samples in each joint of the bridge dataset.

We trained the OCSVM for each joint (1, 2, 3, 5 and 6) using different values of the Gaussian parameter calculated using the three methods ADES, MD and VM. The MIES method was not used here because it does not work in high dimensional datasets.

Table 4. Optimal selection of the $\sigma$ values based on different methods using the bridge datasets along with g-means, TPR and FPR.

Table 5. Average values of g-means, TPR and FPR over the five bridge datasets.

Results and Discussions. This section presents the classification performance of the OCSVM for each of the parameter selection methods. As shown in Table 4, the ADES method significantly outperformed the other two methods on the six experimented joints. The average g-mean value of ADES was equal to 0.971 compared to MD and VM, with their average values being 0.943 and 0.04, respectively. The VM method performed badly on the five joints due to the generation of a small value of $\sigma$ which yields to over-fit the OCSVM model. It can be clearly noticed in the results presented in Table 4 where the FPR of the VM method was equal to zero which means that the model was able to fully predict the negative samples but completely failed in predicting the positive ones. With respect to the MD method, it is known from our discussion and experiments in Sect. 4.1 that MD often generates a large value of $\sigma$ which yields to produce a loose decision boundary. As we expected, MD behaved similarly as it can be seen from Table 4 but with better results, since the number of samples was very large in these experiments which results in producing a small value of $\sigma$ for the MD method. However, the values of FPR for the MD method are still consistently higher than ADES.

We further investigated the classification performance among the three methods by conducting a paired t-test (ADES vs MD and ADES vs VM) to determine whether the differences in the g-means between ADES and the two other methods are significant or not. The p-values were used in this case to judge the degree of the performance improvement. The paired t-test of ADES vs MD resulted in a p-value of 0.01 which indicates that the two methods do not have the same g-means values and they were significantly different. As shown in Table 5, the average g-means value of ADES is 0.971 compared to MD which has a mean value equal to 0.943. This indicates a statistical classification improvement of ADES over MD. The same t-test procedure was used to compare the classification performance of ADES and VM. The t-test generated a very small p-value of $2\mathrm {e}{-13}$ which indicates a very large difference between the two approaches. The average g-means value indicates that ADES significantly outperformed VM method and suggests not to consider VM method in the next experiments.

Case Study II: A Reinforced Concrete Jack Arch.

Experiments Setup and Data Collection. The second case study is a lab specimen which was replicated a jack arch from the Sydney Harbour Bridge. A reinforced concrete cantilever beam with an arch section was manufactured and tested as shown in Fig. 6 [12]. Ten accelerometers were mounted on the specimen to measure the vibration response resulting from impact hammer excitation. A data acquisition system was used to capture the impact force and the resultant acceleration time histories. An impact was applied on the top surface of the specimen just above the location of sensor A9. A total of 190 impact test responses were collected from the healthy condition. A crack was later introduced into the specimen in the location marked in Fig. 6 using a cutting saw. The crack is located between sensor locations A2 and A3 and it is progressively increasing towards sensor location A9. The length of the cut was increased gradually from 75 mm to 270 mm, and the depth of the cut was fixed to 50 mm. After introducing each damage case (four cases), a total of 190 impact tests were performed on the structure in the location prescribed earlier.

Fig. 6.

Test specimen: intact structure with arrow indicating the cut location

Classification performance evaluation was carried out in the same way that was performed for the previous case study. The resultant 5 datasets has 950 samples separated into two main groups, Healthy (190 samples) and Damaged (760 samples). Each sample was measured for vibration responses resulted in a feature vectors with 8000 attributes representing the frequencies of each sample. The same scenario was applied here where the damaged cases were sub-grouped into 4 different damaged cases with 190 samples each.

Results and Discussions. In this section the classification results obtained using the OCSVM algorithm are presented for each of the parameter selection methods. Two sensors were used in this study, A1 and A4. As we mentioned in the above section, this dataset has four different levels of damage. The first level of damage, that is Damage Case 1, is very close to the healthy samples. This will allow us to thoroughly investigate the performance of the parameter selection methods considering the issues of under fitting and over-fitting. Table 6 shows the obtained results of each of the damage cases using sensors A1 and A4, respectively. Considering Damage Case 1 dataset, the results obtained by ADES are promising in comparison to MD. Although the samples in these dataset have a minor damage, ADES generated an optimal OCSVM hyperplane that was able to detect 80% of the damaged samples using sensors A1 and A4. 95% and 100% of the healthy samples were successfully classified using sensors A1 and A4, respectively. These results reveal the appropriateness of the generated enclosing surface of OCSVM using ADES. MD, on the other hand, detected only 43% of the damaged samples using A1 sensor, and 63% using A4 sensor. These results again reflect the general behavior of the MD method which often generates a loose OCSVM model. The results were improved with Damage Case 2 dataset where the severity of damage is not as close to the healthy samples. ADES also performs better than MD where the FPRs are 0.12 and 0.03 using A1 and A4, respectively. Both methods have similar performance on the two datasets, Damage Case 3 and Damage Case 4. MD performed well in these cases because the data points in these datasets were very far from the healthy samples.

Table 6. Optimal values of $\sigma$ selected by different methods using specimen datasets (A1) along with g-means, TPR and FPR.

5 Conclusions

The capability of OCSVM as a warning system for damage detection in SHM highly depends upon the optimal value of $\sigma$. This paper has proposed a new algorithm called ADES to estimate the optimal value of $\sigma$ from a geometric point of view. It follows the objective function that aims to select the optimal value of $\sigma$ so that a generated hyperplane is maximally distant from the interior samples but at the same time close to the edge samples. In order to formulate this objective function, we developed a method to select the edge and interior samples which are crucial to the success of the objective function. The experimental results on the three 2-D toy datasets showed that the ADES algorithm generated optimal values of $\sigma$ which resulted in an appropriate enclosing surface for OCSVM that precisely fitted the form of the three different shape datasets. Furthermore, the experiments on the five benchmark datasets demonstrated that ADES has the capability to work on high dimensional space datasets and capable of selecting the optimal values of $\sigma$ for a trustworthy OCSVM model. We have also conducted our experiments on the bridge datasets to evaluate the performance of the OCSVM model for damage detection. Our ADES method performed well on these datasets and promising results were achieved. We obtained a better classification result on the five joint datasets with a low number of false alarms.

Overall, ADES algorithm for OCSVM classifier was superior in accuracy to VM, MD and MIES on the toy datasets, five publicly available learning datasets and Sydney Harbour Bridge datasets.